| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |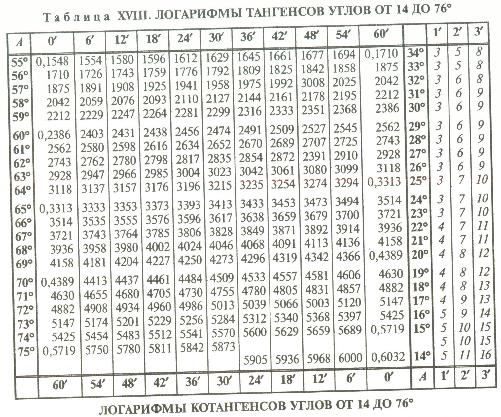
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Синус, косинус, тангенс углов от 0° до 180° — ГЕОМЕТРИЯ — Уроки для 9 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК № 1
Тема.
Синус, косинус, тангенс углов от 0° до 180°
Цель урока: формирование понятий синуса, косинуса, тангенса углов от 0° до 180°. Формирование умений находить тригонометрические функции тупых углов.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Соотношение между сторонами и углами треугольника» [13].
Требования к уровню подготовки учащихся: объясняют, что такое синус, косинус, тангенс углов от 0° до 180°.
Ход урока
И. Организационный этап
Вступительное слово учителя. Мы продолжаем изучение геометрии. В девятом классе вы ознакомитесь с новыми разделами геометрии: решения произвольных треугольников; правильные многоугольники; декартовы координаты на плоскости; геометрические преобразования; векторы на плоскости; начальные сведения из стереометрии. Впереди вас ждут новые теоремы о свойствах геометрических фигур, интересные задачи.
Желаю вам преодолеть препятствия, которые встанут на вашем пути лабиринтами геометрии.
Пусть изучение геометрии принесет вам радость от полученных побед.
II. Актуализация опорных знаний
Фронтальная беседа
Для повторения сведений о тригонометрические функции острых углов прямоугольного треугольника можно использовать таблицу из пособия [13].
1. Сформулируйте определение синуса, косинуса, тангенса острого угла прямоугольного треугольника.
2. Найдите по рис. 1 sinα, cosα, tgα, cosβ, sinβ, tgβ.
3. Как связаны sinα и cosα, если α — острый угол прямоугольного треугольника?
4. Упростите выражение:
а) 1 + sin2α + cos2α;
б) 2cos2α + sin2α — 1.
5. Какой зависимостью связаны sinα, cosα, tgα?
6. Найдите tgα, если:
а) sinα = , cosα = ;
б) sinα = , cosα = .
7. Укажите значение выражений:
а) sin 30°, cos 30°, tg 30°;
б) sin 45°, cos 45°, tg 45°;
в) sin 60°, cos 60°, tg 60°.
III. Поэтапное восприятие и осознание нового материала
Определение синуса, косинуса и тангенса углов от 0° до 180°
Изучение нового материала можно провести так. Построим окружность с центром в начале координат и радиусом 1 (рис. 2). Такой круг называется единичным. Построим острый угол а, который образует радиус ОА этого круга с положительным направлением оси Ох. Пусть точка А имеет координаты (х; у). Тогда для прямоугольного треугольника АОВ имеем:
sinα = = = в;
cosα = = = x;
tgα = = .
Таким образом: синусом угла α есть ордината точки единичной окружности, причем радиус ОА образует с положительным направлением оси Ох угол α. Косинусом угла α является абсцисса точки единичной окружности, причем радиус ОА образует с положительным направлением оси Ох угол α. Тангенсом угла α есть отношение ординаты точки А до абсциссы этой точки, причем радиус ОАутворює с положительным направлением оси Ох угол α.
Нахождение значений синуса, косинуса и тангенса тупых углов
Пользуясь предоставленными определениями, дадим определение для любого угла α, 0° α 180°. Тогда sin 0° = 0, cos 0° = 1, tg 0° = 0; sin 180° = 0, cos 180° = -l, tg 180° = 0.
Если угол α — тупой (0° α 90°), то ордината точки А (рис. 3) положительная (т.е. sin α > 0), абсцисса — отрицательная (то есть cosα 0), и отношение ординаты к абсциссы — отрицательное (т.е. tgα 0).
Следовательно, косинус, тангенс тупого угла отрицательные.
Если α — тупой угол (рис. 4), то cos α = ОС = — OD = -cos (180°- α),
sinα = AC = AD = sin (180° — α), тогда tg α = = — = -tg(180° — α).
Итак, чтобы найти синус тупого угла, достаточно найти синус смежного угла; чтобы найти косинус, тангенс тупого угла, надо найти число, противоположное косинуса, тангенса смежного угла.
Например, sin 120° = sin (180° — 120°) = sin 60° = ,
cos 150o = — cos (180° — 150°) = — cos 30° = — ,
tg 135° = -tg (180° — 135°) = — tg 45° = — 1.
Если учащиеся класса имеют недостаточную математическую подготовку, то можно упростить объяснение. Достаточно сказать, что синус тупого угла равна синуса смежного угла, а косинус и тангенс тупого угла равны числу, противоположном косинуса и тангенса смежного угла.
Синус 0° равна 0, синус 180° равен 0, синус 90 градусов равен 1, а косинус 0° равна 1, косинус 180° равен -1, косинус 90 градусов равен 0; тогда тангенс 0° и 180° равны 0, а тангенс 90° не существует.
IV. Закрепление и осмысление нового материала
Выполнение упражнений
1. Вычислите синус, косинус и тангенс угла:
а) 120°; б) 135°; в) 150°.
2. Пользуясь калькулятором (таблицами), найдите:
a) sin 100°, sin 132°, sin 175°;
б) cos 95°, cos 127°, cos l70°;
в) tg 93°, tg 129°, tg 172°.
V. Домашнее задание
1. Изучить определение синуса, косинуса, тангенса углов от 0° до 180°.
2. Пользуясь калькулятором (таблицами), вычислить:
a) sin 105°, sin 140°, sin 165°;
б) cos 100°, cos 130°, cos 160°;
в) tg 103°, tg 131°, tg 163°.
VI. Подведение итогов урока
Задача класса
1. Дайте определение синуса, косинуса, тангенса углов от 0° до 180°.
2. Пользуясь рис. 5, найдите:
а) sin α; б) cos α; в) tg α.
| Содержание | Вперед |
Это уравнение для прямой, но мы еще не использовали тот факт, что прямая должна проходить через нашу точку $(x_0,y_0)$. Или нам все еще нужно убедиться, что $(x_0,y_0)$ удовлетворяет уравнению для $C$. Теперь мы перепишем приведенное выше выражение следующим образом (мы переместили члены в $a,h,c$ и добавили и вычли члены в g,f,c):
$$
\начать{массив}{с}
а(2x_0x)
+ 2ч(ху_0+х_0у)
+ б(2г_0г)
+ г (х + х_0)
+ f(y+y_0) + 2c +\\
-(ax_0^2+2hx_0y_0+by_0^2+gx_0+fy_0+c)=0.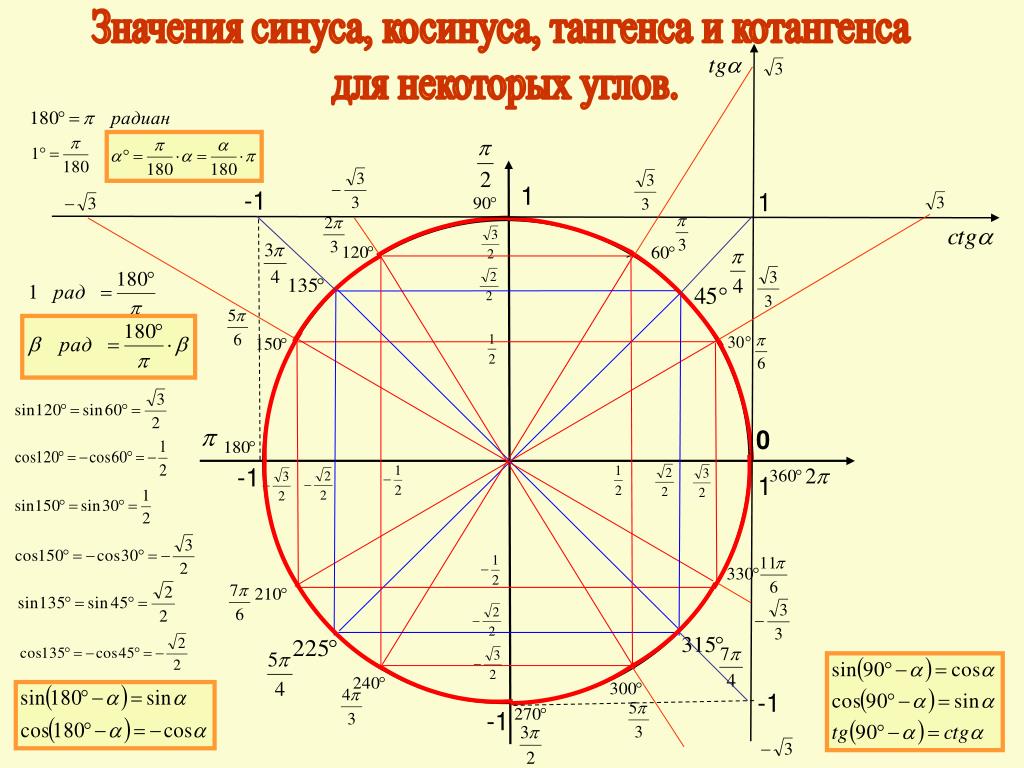
\конец{массив}
$$
Сказать, что $(x_0,y_0)$ проходит через $C$, значит сказать, что вторая строка исчезает! Итак, у нас наконец осталось: $$ 2ax_0x + 2ч(ху_0+х_0у) + 2by_0г + г (х + х_0) + f(y+y_0) + 2c=0. $$
Разделив обе части на $2$, мы получим именно вашу формулу.
(Да, это довольно долгий и сложный процесс. Я не могу придумать более простого, не теряющего ясности и не использующего сложные вычисления. Наверное, поэтому в старших классах это никогда не доказывают! В любом случае, я был бы очень-очень рад увидеть более короткое элементарное доказательство.)
Касательные и наклоны
Касательные и наклоныОпределение касательной
Синус и косинус — не единственные тригонометрические функции, используемые в тригонометрии. Многие другие использовались на протяжении веков, такие как гаверсины и спреды. Наиболее полезным из них является тангенс. С точки зрения диаграммы единичного круга, касательной является длина вертикальной линии ED , касательной к окружности из точки касания E до точки D , где эта касательная пересекает луч AD , образующий угол.
| Если ваш браузер поддерживает Java, вы можете перетаскивать точку B , чтобы увидеть, как синус, косинус и тангенс изменяются при изменении угла. (Дополнительную информацию об управлении фигурой см. в разделе Об апплете.) |
Тангенс относительно синуса и косинуса
Поскольку два треугольника ADE и ABC подобны, имеемНо ED = tan A, AE = 1, CB = sin A, и AC = cos AB. Следовательно, мы получили фундаментальное тождество
Касательные и прямоугольные треугольники
Точно так же, как синус и косинус можно найти как отношение сторон прямоугольного треугольника, можно найти и тангенс. Мы будем использовать три отношения, которые у нас уже есть. Во-первых, tan A = sin A / cos A.
Во-вторых, sin A = a/c. В-третьих, cos A = b/c. Разделив a/c на b/c и убрав появляющиеся c , мы заключаем, что tan A = a/b. Это означает, что касательная — это противолежащая сторона, деленная на прилежащую сторону:
Наклоны линий
Одна из причин, по которой касательные так важны, заключается в том, что они дают наклоны прямых линий. Рассмотрим прямую линию, проведенную в координатной плоскости x-y .Точка B находится там, где линия пересекает ось y . Мы можем принять координаты B равными (0, b ), так что b, , называемое точкой пересечения y , указывает, насколько выше x -ось B лежит. (Эти обозначения противоречат обозначению сторон треугольника a, b, и c, , поэтому не будем сейчас обозначать стороны.)
Вы можете видеть, что точка на 1 единицу вправо от начала координат помечена 1, и ее координаты, конечно же, (1,0).
Пусть C будет точкой, где эта вертикальная линия пересекает горизонтальную линию через B. Тогда C имеет координаты (1, b ).
Точка A находится там, где вертикальная линия выше 1 пересекает исходную линию. Пусть м обозначает расстояние, на котором А выше С. Тогда А имеет координаты (1, b + м ). Это значение м называется уклоном линии. Если вы переместитесь вправо на одну единицу в любом месте по линии, то вы переместитесь вверх на м единиц.
Теперь рассмотрим угол СВА. Назовем это угол наклона. Тангенс CA/BC = м /1 = м. Таким образом, наклон представляет собой тангенс угла наклона.
Углы возвышения и депрессии
Термин «угол места» относится к углу над горизонталью от зрителя. Если вы находитесь в точке А, и АХ это горизонтальная линия, то угол возвышения до точки B над горизонтом находится угол BAH.
Аналогично, «угол депрессии» к точке С ниже горизонта составляет угол САН.
Касательные часто используются для решения задач, связанных с углами возвышения и депрессии.
Опять общие углы
Мы можем расширить нашу таблицу синусов и косинусов общих углов до тангенсов. Вам не нужно запоминать всю эту информацию, если вы можете просто запомнить отношения сторон 45°-45°-9треугольник 0° и треугольник 30°-60°-90°. Отношения являются значениями триггерных функций.Обратите внимание, что тангенс прямого угла указан как бесконечность. Это потому, что по мере того, как угол увеличивается до 90°, его тангенс неограниченно растет. Может быть, лучше сказать, что касательная 90 ° не определена, поскольку, используя определение окружности, луч, исходящий из начала координат под углом 90 °, никогда не пересекается с касательной.
| Угол | Градусов | Радиан | косинус | синус | тангенс |
|---|---|---|---|---|---|
| 90° | π /2 | 900 59 01 | бесконечность | ||
| 60° | π /3 | 1/2 | √3 / 2 | √3 | |
| 45° | π /4 | √2 / 2 | √2 / 2 | 1 | |
| 30 ° | π /6 | √3 / 2 | 1/2 | 1/√3 | |
| 0° | 0 900 60 | 1 | 0 | 0 |
Упражнения
29.
В прямоугольном треугольнике a = 30 ярдов и тангенс A = 2. Найдите b и c.
49. cos t = 2 тангенс t. Найдите значение sin т.р.
Примечание: В следующих задачах расстояние означает расстояние по горизонтали, если не указано иное; под высотой объекта понимается его высота над горизонтальной плоскостью через точку наблюдения. Высота глаза наблюдателя не должна приниматься во внимание, если это специально не оговорено. В задачах, связанных с тенью объекта, предполагается, что тень падает на горизонтальную плоскость через основание объекта, если не указано иное.
151. Угол возвышения дерева на расстоянии 250 футов составляет 16° 13′. Найдите высоту.
152. Найти высоту колокольни на расстоянии 321 фут, угол возвышения 35° 16′.
153. С корабля угол возвышения верхней части маяка на высоте 200 футов над водой составляет 2° 20′.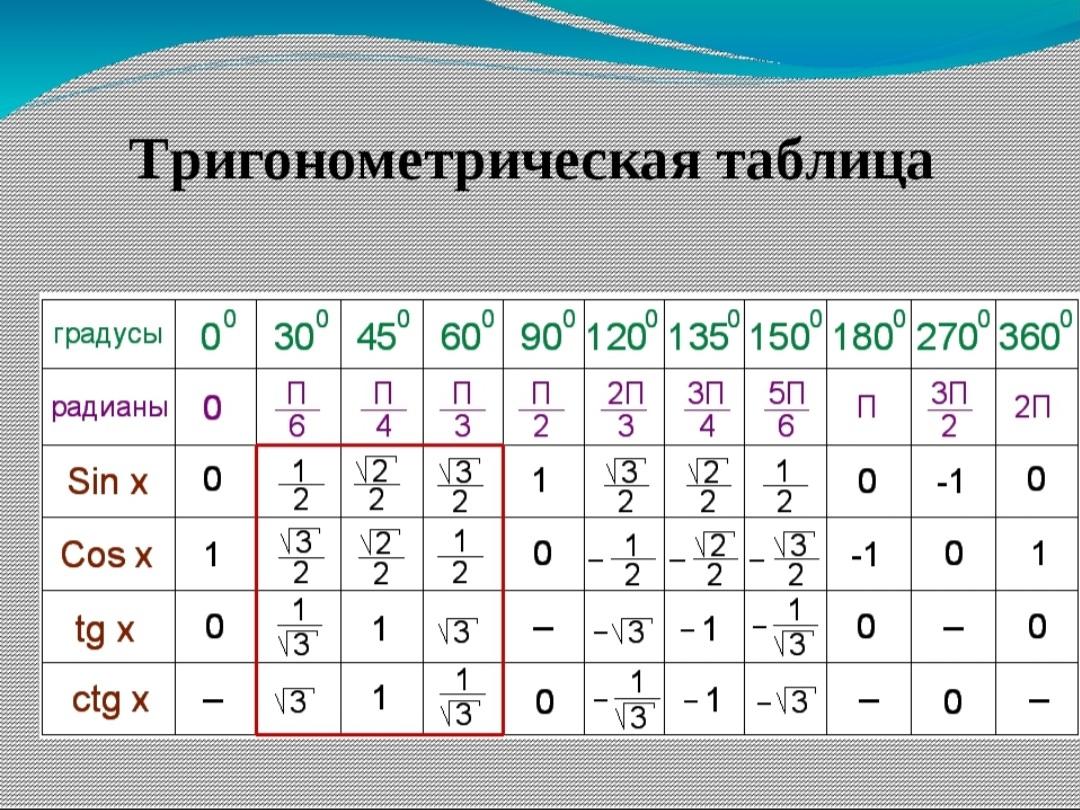
Найдите расстояние.
154. С вершины маяка на высоте 165 футов над водой угол депрессии корабля составляет 3° 50′. Найдите расстояние.
159. Найдите высоту башни на расстоянии 186 футов, угол возвышения 40° 44′.
160. С одной стороны ручья шест высотой 50 футов имеет с противоположной точки угол возвышения 5° 33′. Найдите ширину потока.
164. От одного холма вершина другого на 128 футов выше имеет угол возвышения 2° 40′. Найдите расстояние.
165. С одного холма на вершину другого далекого 6290 футов имеет угол возвышения 4° 9′. Найдите, на сколько высота второго холма больше высоты первого.
189. Фронтон крыши имеет ширину 40 футов у основания и 26 футов от основания до конька. Под каким углом наклон стропил?
Советы
Общий совет для всех этих упражнений: сначала нарисуйте фигуру. 29. Так как вы знаете a и коричневый А, можно найти б.
Затем можно определить c по теореме Пифагора, или с помощью синусов, или с помощью косинусов.
49. Вам понадобятся две личности. Во-первых, tan t = sin t / cos t. Во-вторых, тождество Пифагора, sin 2 t + cos 2 t = 1. Тогда вам нужно решить квадратное уравнение.
151. Помните, что тангенс угла прямоугольного треугольника равен противолежащей стороне, деленной на прилежащую сторону. Вы знаете смежную сторону (расстояние до дерева) и знаете угол (угол возвышения), поэтому можете использовать касательные для нахождения высоты дерева.
152. Вы знаете угол (опять же, угол возвышения) и прилежащую сторону (расстояние до шпиля), поэтому используйте касательные, чтобы найти противоположную сторону.
153. Используя угол и противоположную сторону, используйте тангенс, чтобы найти соседнюю сторону.
154. Та же подсказка, что и в 153.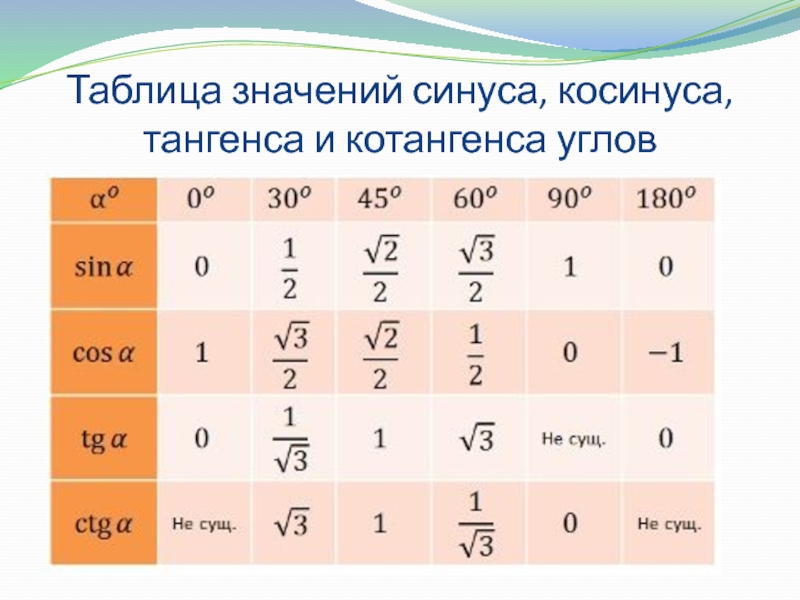
159. Та же подсказка, что и в 152.
160. Та же подсказка, что и в 153.
164. Та же подсказка, что и в 153.
165. Та же подсказка, что и в 152.
189. Фронтон крыши представляет собой равнобедренный треугольник. Если провести перпендикулярную линию от хребта, то получится два конгруэнтных прямоугольных треугольника. Вы знаете две стороны треугольников, поэтому можете определить угол наклона стропил с помощью арктангенса.
Ответы
29. b = a /tan A = 30/2 = 15 ярдов. c = 33,5 ярда.
49. Так как cos t = 2 tan t, поэтому cos t = 2 sin t /cos t, so cos 2 t = 2 sin t, и, по тождеству Пифагора вы получаете 1 – sin 2 t = 2 sin t. Получается квадратное уравнение sin 2 t + 2 sin t – 1 = 0.