Вопросы-головоломки на собеседованиях с ответами. Часть 2 — Work.ua
Work.ua продолжает публиковать ответы на самые сложные и неожиданные вопросы на собеседованиях, в которых кандидат должен проявить свою смекалку, логическое мышление и фантазию.
В предыдущей статье мы писали, что вопросы-головоломки порой могут не иметь единственного правильного ответа, а предназначены для того, чтобы проверить поведение кандидата в нестандартных ситуациях, узнать как он размышляет, и как справляется со сложными ситуациями.
Work.ua подготовил еще 5 головоломок, которые могут встретиться на вашем пути.
Бильярдные шары
Этот вопрос чаще всего задают IT-специалистам, чтобы проверить способность логически мыслить.
Вопрос: Есть 8 бильярдных шаров. Один из них немного тяжелее других. За какое минимальное количество взвешиваний на рычажных весах без гирь можно найти этот шар?
Ответ: 2 взвешивания. Нужно разделить все шары на три части: по 3 шара в двух частях, и 2 шара в третьей части.
Сначала взвешиваете первые две части по 3 шара. Если одна из частей оказалась тяжелее, то взвешиваем между собой любые 2 шара из нее. Или один из них будет искомым шаром, или не взвешенный, если они оказались равны. В случае равного веса частей при первом взвешивании, более тяжелый шар окажется в третьей части из двух шаров.
Дом
Вопрос: Нарисуйте дом.
Ответ: Казалось бы, что может быть проще. Рисуем квадрат, пару прямоугольников и треугольник наверху. А вот и нет. Этот тест рассчитан для должностей, которые требуют от сотрудника нестандартных решений и индивидуального подхода к каждой задаче (дизайнеров, менеджеров по рекламе). Во-первых, нужно проявить креативность, а не рисовать шаблонный дом. Во-вторых, нужно сперва уточнить для кого этот дом: кто в нем будет жить, и сколько будет этих жильцов. Не стоит приступать к работе, не узнав всех нюансов.
Вас могут попросить нарисовать не только дом, а все что угодно. Но всегда нужно узнавать все подробности, чтобы итоговый результат был правильным.
А сам процесс будет значить намного больше, чем этот итоговый результат.
Слон
Вопрос: Как узнать вес слона без весов?
Ответ: Вариантов может быть очень много, вы ограничены лишь своей находчивостью и фантазией. Например, слона можно поставить на баржу и отметить ее осадку. Затем убрать слона и ставить на баржу предметы, вес которых вам известен — пятилитровые бутылки с водой, допустим. А когда осадка баржи будет такого же уровня как и со слоном, умножаем количество предметов на их вес. Тут главное — ваша изобретательность.
Драже M&M’s
Вопрос: Почему глазурь на известных драже M&M’s идеально гладкая? Как их делают, они что летают в воздухе?
Ответ: Еще один вопрос, правильный ответ на который не настолько важен, как варианты, предложенные кандидатом. Как бы вы решили эту задачу, если бы внезапно попали на производство? Держали бы драже на воздушном потоке? Приклеивали бы на нитку, где расположен логотип? На самом деле их опрыскивают глазурью во вращающемся барабане.
Таким образом их поверхность остается гладкой, а глазурь наносится равномерно. Но ваш индивидуальный подход к решению этой задачи будет значить намного больше.
Русская рулетка
Решение этой задачи зависит от специфики вашей профессии. Ответ можно найти как с помощью точных вычислений, так и просто используя логику.
Вопрос: Есть шестизарядный револьвер. В нем 2 пули, обе расположены рядом друг с другом. Ваш оппонент раскручивает барабан, приставляет дуло к виску и нажимает на курок. Выстрела не произошло. Как поступите вы: сразу нажмете на курок или сперва снова раскрутите барабан?
Ответ: Правильный ответ один — сразу нажать на курок. Если произвести точные вычисления, то вероятность остаться в живых в этом случае составляет 75%, а если сперва раскрутить барабан — снижается до 66,7%. Так как пули расположены рядом друг с другом, можно логически определить, что лучше жать на курок сразу.
Читайте также: Вопросы-головоломки на собеседованиях с ответами.
Получать новости в Telegram
Чтобы оставить комментарий, нужно войти.
Math.ru
Григорий Александрович Гальперин, Александр Николаевич Земляков
М.: Наука, 1990. 288 с.
ISBN 5-02-014080-5; Тираж 130000 экз.
Серия Библиотечка «Квант», выпуск 77
| |||||||||||
Рассказывается о поведении бильярдного шара на столе произвольной формы без луз. Описание этого поведения приводит к решению разнообразных вопросов математики и механики: задач о переливании жидкости, об освещении зеркальных комнат, об осциллографе и фигурах Лиссажу и др.
На доступном школьникам языке вводятся понятия конфигурационного
и фазового пространства, понятия геодезических на простейших двумерных поверхностях, предлагаются (с решениями) многочисленные интересные задачи.
Для школьников 9-10-х классов.
Содержание
Предисловие.
Введение.
Часть I. БИЛЬЯРДЫ В ВЫПУКЛЫХ ОБЛАСТЯХ С КРИВОЛИНЕЙНОЙ ГРАНИЦЕЙ.
Глава 1. Бильярд в круге.
§ 1. Шар в круглом бильярде без луз.
§ 2. Теорема Якоби. Применение к теории чисел.
§ 3. Теорема Пуанкаре о возвращении. Конфигурационное и фазовое пространства. Парадокс Цермело и модель Эренфестов.
Глава 2. Бильярд в эллипсе.
§ 4. Эллипс и его бильярдные свойства. Каустики.
§ 5*. Задача об освещении невыпуклой области.
§ 6. Экстремальные свойства бильярдных траекторий. Принцип Ферма и теорема Биркгофа.
Часть II. ГЕОМЕТРИЯ И ФИЗИКА ПРЯМОУГОЛЬНОГО БИЛЬЯРДА.
Глава 3. Геометрия прямоугольного бильярда.
§ 7. Бильярдный шар на прямоугольном столе без луз.
§ 8. Top и его обмотки.
§ 9. Бильярд в прямоугольнике и тор.
Глава 4. Физика прямоугольного бильярда.
§ 10. Фигуры Лиссажу.
§ 11. Бильярд в прямоугольнике и осциллограф.
§ 12. Задача о пеленге.
Часть III. ГЕОМЕТРИЯ И АРИФМЕТИКА СТОЛКНОВЕНИЙ.
Глава 5. Одномерный «газ» из двух молекул.
§ 13. Два упруго сталкивающихся шара на отрезке.
§ 14. Два шара на отрезке: сведение к бильярду в треугольнике.
§ 15. Два шара на полупрямой: сведение к бильярду в угле.
Глава 6. Одномерный «газ» из большого числа молекул.
§ 16. Три упругих шара на прямой.
§ 17. n упругих шаров на прямой.
§ 18*. Число столкновений между молекулами одномерного «газа».
Глава 7**. Многомерный «газ».
§ 19. Конфигурационное пространство «газа» из n молекул в пространстве и сосуде.
§ 20. Сведение «газа» в пространстве и сосуде к бильярду.
§ 21. Рост числа столкновений между молекулами «газа».
Часть IV. БИЛЬЯРДЫ В МНОГОУГОЛЬНИКАХ И МНОГОГРАННИКАХ.
Глава 8. Геометрия многоугольного бильярда.
§ 22. Бильярды в «торических» многоугольниках.
§ 23. Склейка поверхностей из многоугольников.
§ 24. Бильярды в рациональных многоугольниках и поверхности.
Глава 9. Поведение бильярдных траекторий в многоугольниках.
§ 25. Траектории в рациональных многоугольниках и обмотки кренделей.
§ 26. Может ли непериодическая траектория в выпуклом многоугольнике не быть всюду плотной в нем?
§ 27. Периодические траектории в многоугольниках и многогранниках.
Заключение.
Список литературы.
| |||||||||||
49)Постоянный адрес этой страницы: http://math.ru/lib/bmkvant/77
Проблема бильярдного шара. Индус
Видеть, как бильярдные шары рикошетят от подушки бильярдного стола, ударяются друг о друга и погружаются в лузу на столе, — одно из величайших удовольствий в жизни. Математики и многие другие были большими поклонниками пула или бильярда, и неудивительно! Игра требует мастерства и утонченности, но также потворствует нашей чувствительности к поиску закономерностей. Присоединяйтесь к Дэниелу Финкелю, который познакомит вас с головоломкой, основанной на бильярдном шаре.
Сегодняшняя головоломка — это классика, которую я впервые увидел в замечательном учебнике Гарольда Джейкоба. Математика: человеческая деятельность . Копайте, и это не разочарует.
Головоломка 1.
Я разработал новый бильярдный стол и приглашаю вас поиграть.
Вы кладете биток прямо перед лузой в левом нижнем углу стола и бросаете его под углом 45 градусов поперек стола. Он будет продолжать катиться, пока не упадет в один из угловых карманов.
Можете ли вы предсказать, в каком углу окажется мяч?
Здесь, конечно, есть проблема, так как у нас недостаточно информации: я никогда не говорил вам размеры стола. И размеры имеют значение. Например, если бы стол был размером 5 на 10, мяч оказался бы в правом нижнем углу.
С другой стороны, если увеличить ширину таблицы с 10 до 11, мы получим совершенно другой путь и совершенно другой конечный карман: верхний правый.
Так что же происходит? Это загадка. Учитывая размеры стола, можете ли вы предсказать, в каком углу окажется мяч?
Большой совет, с чего начать: попробуйте решить эту задачу с кучей таблиц.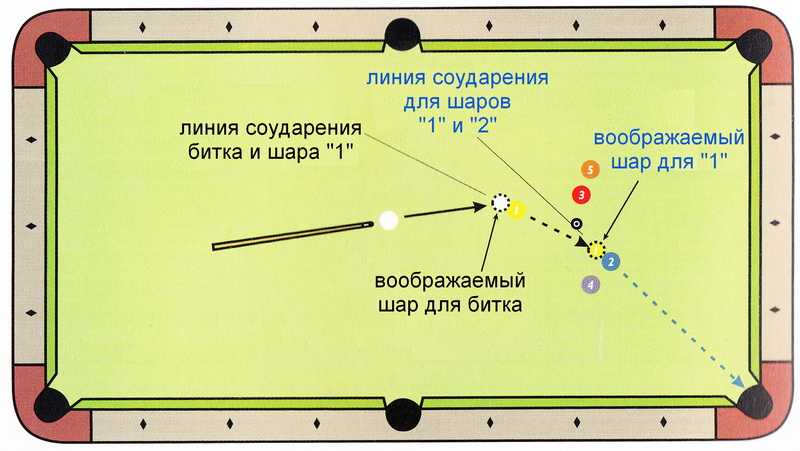
Вот некоторые конкретные таблицы, чтобы попробовать.
2 на 6
2 на 7
3 на 4
3 на 5
3 на 6
3 на 7
4 70 0 6 9 0
4 0002 4 по 10Если можете проделав все это, сможете ли вы найти закономерность, которая поможет вам предсказать, в каком углу окажется мяч за этими большими столами?
26 на 47
35 на 99
501 на 998
600 на 10 000
На мой взгляд, лучший способ разобраться в этой проблеме — попробовать несколько примеров. Вы могли заметить, что четность , или четность и нечетность, играет определенную роль.
| Размеры стола | Угол, в который мяч попадает |
| Нечетное по нечетному | Верхний правый |
| 0069 | Нижний правый |
| Четный по нечетному | Верхний левый |
| Четный по четному | Варьируется… |
2 по
кажется странным, но с этим можно справиться простое наблюдение: стол 2 на 6 идентичен столу 1 на 3 (если хотите, если смотреть с более близкого расстояния).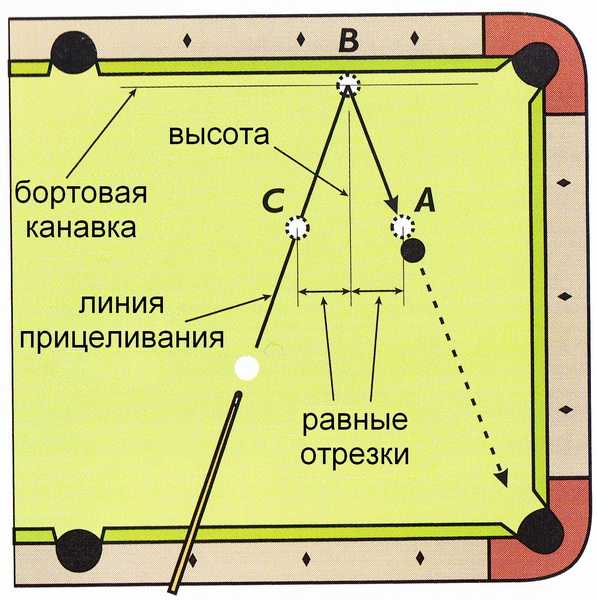
В общем, всякий раз, когда у вас есть таблица с двумя четными числами в качестве ее измерений, вы можете делить их оба на 2 до тех пор, пока хотя бы одно из них не перестанет быть четным, и вы не изменили природу таблицы.
Мы можем предсказать, в соответствии с этим шаблоном, где шар окажется на больших столах:
26 на 47 — вверху слева
35 на 99 — вверху справа
501 на 998 — внизу справа
600 на 10 000 — внизу справа, потому что 600 на 10 000 на самом деле просто масштабная модель стола 3 на 50.
Теперь реальный вопрос: почему четность объясняет путь бильярдных шаров? Я хочу предложить два объяснения, одно элегантное, другое яркое.
Во-первых, элегантное объяснение. Для любой таблицы нарисуйте ее на сетке – или решетка , как мы иногда говорим — и раскрасим точки сетки в шахматном порядке.
Нажмите здесь, чтобы увидеть ответ.
Ничего не заметили? Путь бильярдного шара не может измениться с синих точек на красные точки.
Это означает, что нам нужно только выяснить, какой из четырех углов будет синим или другим цветом, соответствующим нижнему левому углу. Цвет уголков, как видите, зависит только от соотношения размеров стола.
Нажмите здесь, чтобы увидеть ответ.
Итак, это элегантная идея, и она легко проходит быстро. Вот еще один прием. Представьте, что мяч катится к концу стола, и вместо того, чтобы отскакивать, представьте, что он проходит «через зеркало» в зеркальное отражение существующего стола.
Нажмите здесь, чтобы увидеть ответ.
Затем он снова отскакивает в зеркальном отражении. Продолжайте расширять зеркальные изображения, и мы сможем изобразить наш мяч на прямолинейном пути. Мало того, его путешествие по этим таблицам зеркального отображения является в точности зеркальным отражением его реального пути. В частности, если мы будем отслеживать угол, мы все равно сможем правильно предсказать, где он окажется.
В этом случае, используя таблицу 3 на 4, мы можем поставить 4 из них встык по вертикали и 3 впритык по горизонтали.
Раскрашивая углы исходной таблицы, чтобы отслеживать, я вижу, что зеркальное отражение прямого пути мяча заканчивается в правом нижнем углу.
Нажмите здесь, чтобы увидеть ответ.
Что здесь важно? Только паритет, сколько столов я должен был сложить вправо и сколько я должен был сложить. Четность и нечетность, опять же, все объясняют.
В обоих этих аргументах нужно проработать некоторые детали, и я рекомендую это сделать. Четность необычайно распространена в математике и математических головоломках, и с ней стоит познакомиться из-за ее простоты и силы.
Задачи с бильярдным шаром:
Перейти к основному содержанию
источник изображения гуглАншу Пандей
Аншу Пандей
Наставник по математике | Наставник JEE Mains/JEE Advanced/OLYMPIADS | AP Исчисление ТРЕНЕР | Миссия по созданию 100000 ИИТианцев | 5000+ подписчиков
Опубликовано 21 декабря 2020 г.
+ Подписаться
Задачу о бильярдном шаре можно рассматривать как одну элегантную математическую задачу. В этой статье мы проанализируем его математически.
Прежде чем мы начнем, давайте сначала посмотрим на проблему. Ниже приведена ситуация. Можете ли вы предсказать, в какую лузу попадет шарик?
Теперь свяжем эту задачу с математической обусловленностью. Мы все хорошо знаем свойство отражения. Теперь вы подумали, что всякий раз, когда мяч ударяется о какое-либо зеркало, он входит в прямоугольник, который является его зеркальным отражением. Теперь просто продолжайте строить прямоугольники, взяв общие стороны CD и BC (изначально), а затем и их отражения.
Помните одну вещь: мяч будет продолжать двигаться в своем направлении, пока не достигнет одной из вершин наших видимых прямоугольников. и, следовательно, очевидно, что нет. таких видимых прямоугольников, которые вам понадобятся в горизонтальном направлении, будет 67, а в вертикальном направлении — 100 (наименьший возможный).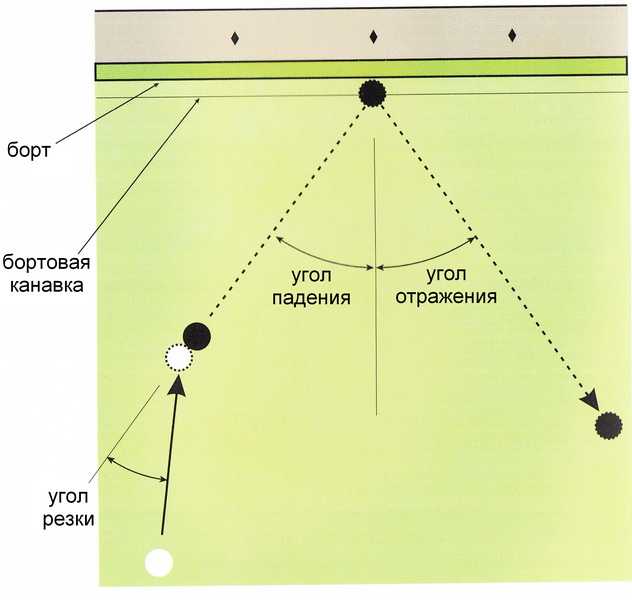
следовательно, поскольку 67 нечетно, очевидно, что оно попадет либо в C, либо в D, а если 100 будет четным, оно в конечном итоге попадет в D.
В качестве альтернативы мы можем думать, что, чтобы попасть из нижнего левого кармана в любой другой карман, мяч должен пройти целое число, кратное длине и ширине (то есть, мяч должен пройти так, чтобы он оказался либо вверху, либо снизу и справа/слева от бильярдного стола, чтобы попасть в лузу). Мы также знаем, что, поскольку он запускается под углом 45 градусов, его скорость равномерно делится на горизонтальную и вертикальную составляющие (это означает, что в любой точке он пройдет одно и то же расстояние по горизонтали и вертикали).
Если мы допустим, что пройденная длина по горизонтали равна «x», а пройденная ширина по вертикали равна «y», тогда:
100x = 67y, где x, y — целые числа
И первое значение (я), которое это работает для x=67 и y=100. Это означает, что мяч прошел нечетное количество длин (оказался справа) и четное количество ширин (оказался внизу), и из этого мы можем легко заключить, что он окажется в правом нижнем углу, давая ответ Д.
Подожди, подумай еще раз! До сих пор мы только и делали, что вычисляли наименьшее общее кратное длины и ширины для задачи, которая казалась намного более сложной. Разве это не умопомрачительно!
Делает ли практика вас совершенным?
14 декабря 2022 г.
Четыре друга!
26 ноября 2022 г.
Муравей на резинке-парадокс
31 октября 2022 г.
Нахождение логарифма числа с помощью висячей цепи: определение контактной сети Лейбницем!
29 июня 2022 г.
Представление чисел площадью или объемом объектов
22 мая 2022 г.
Как улучшить свое творческое воображение? Может ли математика помочь вам?
16 мая 2022 г.
Мотивация и вдохновение: ключ к достижению ваших целей
5 мая 2022 г.
