Тау решение задач: Решения 🤴 и примеры задач по теории автоматического управления (ТАУ) по всем темам и готовыми ответами

Решение задач по ТАУ

Решение задач по ТАУ
(смотрите также решение задач по материаловедению)

Как и многие другие специальные дисциплины, теория автоматического управления способна вызвать проблемы у студентов, которые сталкиваются с ней впервые. Теория вызывает чувство недоумения, а решение задач по ТАУ кажется чем-то не для земного ума. На самом деле, конечно, там нет ничего запредельно сложного (по крайней мере, в учебном курсе). Однако как переубедить эмоции, которые криком кричат – «Это какой-то кошмар!»?

ТАУ – это не только специальная, но и специфическая дисциплина. Понимание теории в ней само по себе требует достаточно специфического склада ума (впрочем, на профильных факультетах это нормально), но и затрат времени, не говоря уже о решении задач по ней. Увы, не все студенты могут затратить достаточно времени и сил на все предметы своего расписания. Некоторые работают и вынуждены тратить время на зарабатывание денег, другие предпочитают уделить внимание более важным для своего будущего предметам. Тем более далеко не во всех случаях ТАУ оказывается предметом, важным в реальной практической работе.

Но попробуйте объяснить это преподавателю, который ждёт от студентов полного погружения в свой предмет, и для него неважно, сколько ещё экзаменов в вашей сессии! Он потребует от вас понимания предмета, на которое надо тратить много времени. К тому же специфика здесь такова, что примеры задач по ТАУ не получится механически приложить к другим исходным условиям – нужно действительно понимать суть дисциплины.

Пример оформления задач по ТАУ нашими специалистами:

Есть ли универсальные методы решения задач по ТАУ? Как ни парадоксально, есть. Один из таких методов – решение задач по ТАУ на заказ. Мы предлагаем вам решения от самых лучших специалистов, преподавателей, знакомых не только с теорией автоматического управления как таковой, но и с учебными курсами по этому предмету. Предлагаем решение задач по различным системам автоматического управления (дискретным, линейным, нелинейным).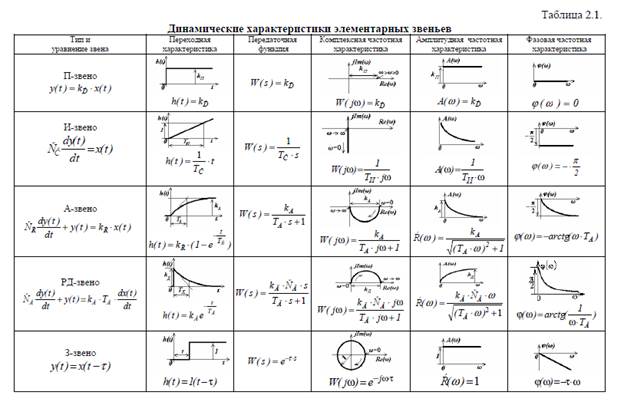

Мы поможем вам разобраться с самыми разными заданиями по ТАУ, с контрольными работами по этому предмету, с подготовкой к лабораторным работам, с решением задач для курсовых и дипломных работ и с подготовкой к защите учёных степеней. Мы также можем помочь вам с решением исследовательских задач в рамках исследовательских действий.

Выполненные нашими специалистами решения задач по ТАУ будут не только верными, но и подробными, с пояснениями по каждому шагу. Более того, такие задачи можно не только показать преподавателю и рассчитывать на хорошую оценку. Они станут для вас подспорьем в реальном освоении ТАУ, когда вы возьмётесь за это дело. А вы ведь возьмётесь, правда? Нам бы хотелось, чтобы наши услуги стали для вас не поводом отказываться от самостоятельной работы, а помощью в ней.

Вникнув в ход решения задачи, вы сможете не только вручить преподавателю распечатку, но и аргументированно пояснить своему преподавателю все шаги решения задачи. Кроме ответа, вы получаете набор практических знаний и рекомендаций по дальнейшему решению задач. Благодаря прямому сотрудничеству с автором вы получаете постоянные консультации в реальном времени, возможность уточнять и корректировать задание, и всё это за более чем разумную плату. В случае каких-либо изменений в содержании задания или сроках его сдачи вы можете сразу сообщить об этом нам, чтобы мы откорректировали план действий. Мы предлагаем также большой выбор вариантов оплаты (электронные деньги, банковские переводы и т.д.)

Примеры решений задач по ТАУ вы можете увидеть на нашем сайте (однако помните, что предмет достаточно нетривиален, и механическая подстановка данных одних задач в условия других может и не дать верного ответа!)

Заказать нам работу!

Примеры решения задач

Задача 1. С помощью преобразования Лапласа решить дифференциальное уравнение с заданными начальными условиями:

.

При решении уравнения с использованием преобразования Лапласа необходимо его преобразовать по Лапласу с учетом начальных условий:

.

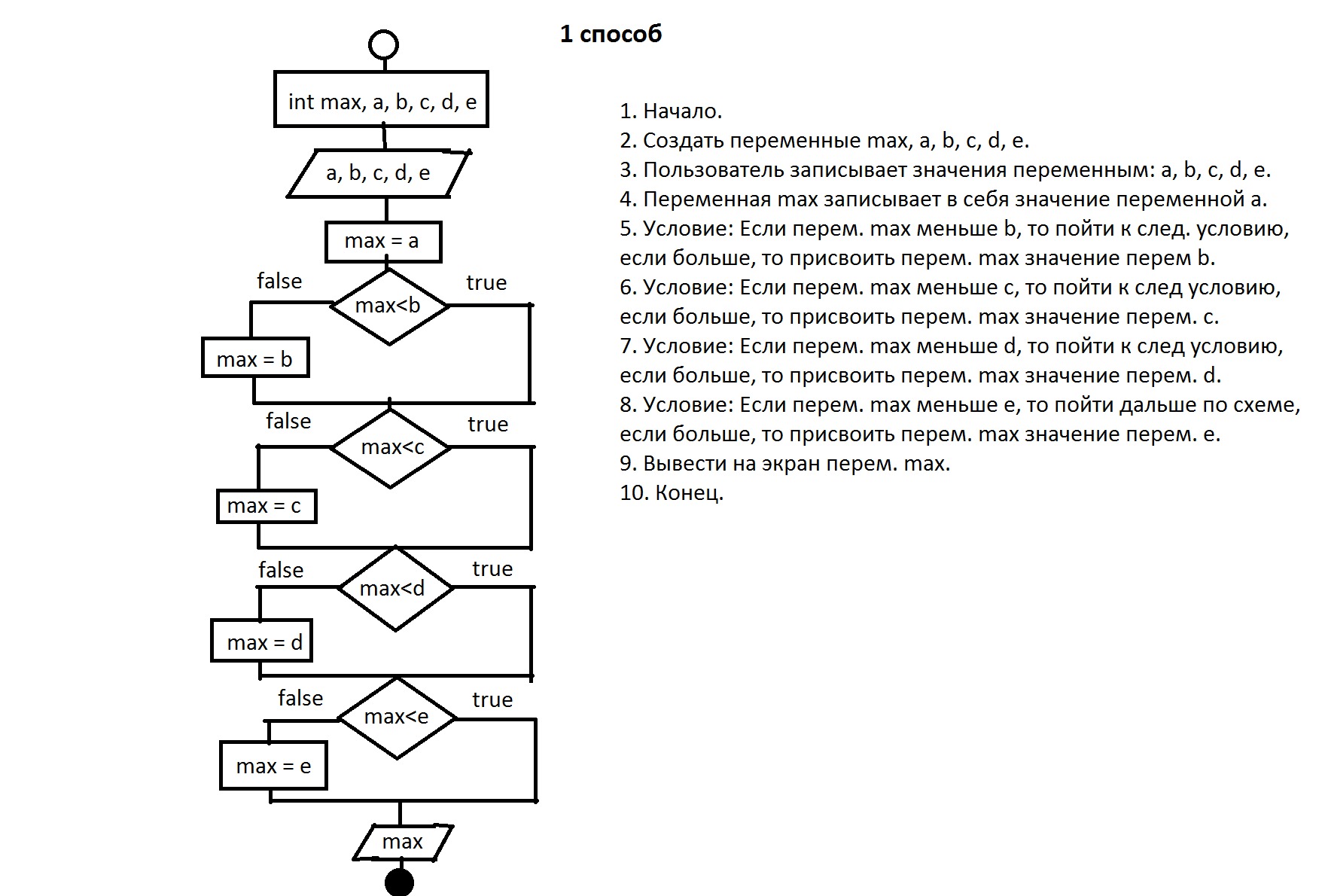
Из последнего выражения определяется y(s) , которое и является решением уравнения, которое записано в терминах преобразования Лапласа. Для получения решения уравнения во временной области полученная дробь раскладывается на простейшие дроби, от которых в последствии по таблицам необходимо взять обратное преобразование Лапласа. В результате разложения получаем следующее выражение:

Приравнивая коэффициенты при одинаковых степенях s в числителе, записываем систему алгебраических уравнений для определения неизвестных коэффициентов:

Решение системы:

Таким образом, дробь разложена на следующие простейшие дроби:

Взяв обратное преобразование Лапласа от последнего выражения, получим:

Функция y(t) является решением дифференциального уравнения.

Задача 2. По известной кривой разгона и весовой функции линейного элемента найти:

1. Реакцию на входной сигнал x(t).

2. Весовую функцию или кривую разгона соответственно.

3. Передаточную функцию элемента.

Задано: кривая разгона – h(t) = 2t; весовая функция – ω(t) = 1- te^—t; входной сигнал – x(t) = 1- e^—t sin t.

1) Реакция элемента на входной сигнал определяется по интегралу Дюамеля, который может быть записан через кривую разгона или через весовую функцию.

Если известна кривая разгона, то интеграл Дюамеля записывается следующим образом: следовательно,

Если известна весовая функция, то интеграл Дюамеля имеет вид:

и тогда выходной сигнал в данной задаче будет записан как:

2) Между кривой разгона и весовой функцией существует взаимная связь. Если известна кривая разгона, то весовая функция определяется как: т.е.

Если же известна весовая функция, то кривая разгона следовательно, в нашем случае

3) Передаточная функция, которая представляет собой отношение преобразованного по Лапласу выходного сигнала к преобразованному по Лапласу входному сигналу при нулевых начальных условиях, может быть определена как через кривую разгона, так и через весовую функцию:

Для нашей задачи:

Задача 3. По известной передаточной функции элемента W(s) найти его кривую разгона, весовую функцию, частотные характеристики – АФХ, ФЧХ, АЧХ, ВЧХ, построить графики. Записать дифференциальное уравнение элемента, связывающее выходную координату и входную координату.

Задана следующая передаточная функция: .

По определению передаточная функция представляет собой W(s) = y(s)/x(s). Для получения дифференциального уравнения запишем y(s)/ x(s) = (3s + 4)/((2s + 3)(4s +1)) . Полученное выражение преобразуем следующим образом:

или

это есть не что иное, как дифференциальное уравнение, но записанное в терминах преобразования Лапласа. Для получения дифференциального уравнения в привычной временной форме записи необходимо взять обратное преобразование Лапласа с учетом нулевых начальных условий, т.е.

Временные характеристики: кривая разгона и весовая функция связаны с передаточной функцией соотношениями:

Таким образом, кривая разгона определяется выражением:

а весовая функция выражением:

Кроме того, если определена кривая разгона, то весовая функция может быть получена по ней, так как они связаны между собой формулой т. е. имеем

Графики функций h(t) и ω(t) представлены на рис. 3, а и б соответственно.

Для отыскания частотных характеристик в передаточной функции производится замена , т.е..

Амплитудно-фазовая характеристика является комплексной функцией, которую записывают в показательной форме с выделением амплитудно-частотной характеристики (АЧХ) и фазо-частотной характеристики (ФЧХ) или в алгебраической форме с выделением вещественно-частотной характеристики (ВЧХ) и мнимой частотной характеристики (МЧХ).

Показательная форма записи АФХ имеет вид: .

Рис. 3 Временные характеристики:

а – кривая разгона; б – весовая функция

Рассматриваемый элемент является линейным и поэтому для него выполняется принцип суперпозиции, в связи с которым его амплитудно-частотная характеристика определяется как отношение АЧХ числителя к АЧХ знаменателя, так выражение для АФХ представляет собой дробь, т.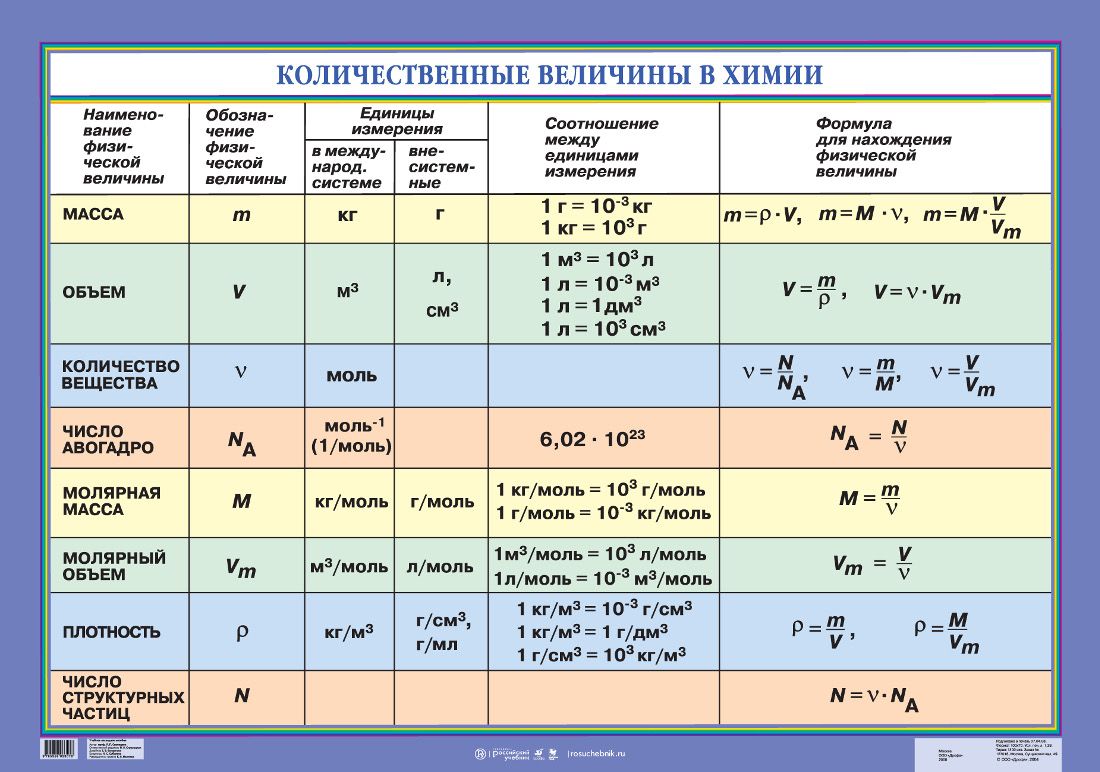 е.Числитель и знаменатель АФХ записаны в алгебраической форме, в этом случае модуль определяется как

Таким образом, выражение для АЧХ запишется в виде:

Фазо-частотная характеристика определяется как разность фаз числителя и знаменателя –которые, в свою очередь, определяются какесли известна алгебраическая запись комплексной функции.

Таким образом, получаем следующее выражение для ФЧХ:

Амплитудно-фазовая характеристика в показательной форме записывается в виде: .

Графики функции ипредставлены на рис. 4, а и б. Анализ характера АЧХ и ФЧХ показывает, что

а) б)

Рис. 4 Частотные характеристики:

а – АЧХ; б – ФЧХ

Годограф АФХ W(iω) представлен на рис.

5.

Запишем теперь выражение для АФХ в алгебраической форме, для этого надо освободиться от мнимости в знаменателе. С этой целью умножим и знаменатель, и числитель на сопряженные выражения относительно

комплексных составляющих знаменателя.

Проведем следующие математические преобразования:

Из последнего выражения записываем:

ВЧХ МЧХ

Рис. 5 Годограф АФХ

График функции представлен на рис. 6.

Рис. 6 Вещественно-частотная характеристика

Задача 4. Преобразовать структурную схему (рис. 7) и записать передаточную функцию.

Считается, что известны передаточные функции отдельных элементов и входной сигнал.

Рис. 7 Структурная схема

Для записи передаточной функции сложной структурной схемы ее необходимо преобразовать в соответствии с правилами преобразования структурных схем. Для того чтобы развязать перекрестные связи в заданной структурной схеме, перенесем узел 1 через звено с передаточной функцией W₃(s) и через узел 2 в соответствии с правилами преобразования структурных схем. В результате проведенных преобразований получаем структурную схему (рис. 8), в которой четко прослеживаются основные типы соединений: последовательное соединение и вложенные друг в друга соединения с обратной связью.

Рис. 8 Преобразованная структурная схема

Записывая последовательно передаточные функции отдельных элементов схемы, придем к выражению передаточной функции всей схемы:

.

Задача 5. Исследовать устойчивость системы автоматического регулирования (рис. 9):

1) с помощью критерия Рауса–Гурвица;

2) с помощью критерия Михайлова.

Рис. 9 Структурная схема системы автоматического регулирования

Заданы следующие исходные данные: передаточные функции объекта и регулятора:

1) Для исследования устойчивости систем автоматического регулирования с помощью критерия Рауса–Гурвица необходимо знать дифференциальное или характеристическое уравнение системы. Знаменатель передаточной функции всегда представляет собой характеристический полином, поэтому необходимо, прежде всего, записать передаточную функцию замкнутой одноконтурной системы (рис. 9):

Характеристическое уравнение определяется путем приравнивания к нулю знаменателя передаточной функции замкнутой системы:

с учетом конкретных значений передаточных функций объекта и регулятора получим:

откуда характеристическое уравнение запишется в виде:

Задачу будем решать с использованием формулировки критерия устойчивости по Гурвицу. Для этого необходимо из коэффициентов характеристического уравнения составить главный определитель Гурвица по определенному правилу: вдоль главной диагонали записываются коэффициенты, начиная с а_{n – 1}, выше главной диагонали записываются коэффициенты с индексом на единицу меньше, ниже главной диагонали записываются коэффициенты с индексом на единицу больше.

Порядок определителя соответствует порядку характеристического уравнения. Из этого определителя составляются диагональные миноры, которых должно быть n – 1.

Система автоматического управления будет устойчивой тогда и только тогда, когда все диагональные миноры главного определителя будут положительны.

Для нашей задачи главный определитель Гурвица имеет вид:

Вычислим последовательно диагональные миноры:

Все диагональные миноры отрицательны, следовательно, система неустойчива. Следует отметить, что для исследования устойчивости не обязательно вычислять все миноры. Если при вычислении миноров получают, что его значение отрицательно, дальнейшие расчеты можно прекратить и сделать вывод, что система неустойчива.

2) Исследуем эту же систему автоматического управления на устойчивость с использованием частотного критерия устойчивости Михайлова.

В соответствии с этим критерием необходимо построить годограф Михайлова, который для устойчивых систем имеет строго определенный вид. И тогда система автоматического управления будет устойчивой, если годограф Михайлова начинается на положительной вещественной полуоси, обходит последовательно, нигде не обращаясь в нуль, n квадрантов координатной плоскости, уходя в бесконечность в n квадранте, где n – порядок характеристического уравнения.

Для записи математического выражения годографа Михайлова необходимо в характеристическом уравнении перейти в частотную область, т.е. в уравнении сделать замену – s = iω. В результате получим комплексное выражение в котором выделим вещественную часть –и мнимую часть –

Первая называется вещественной функцией Михайлова, а вторая – мнимой функций Михайлова.

По вещественной и мнимой функциям Михайлова строится годограф Михайлова в координатах методом контрольных точек. Для этого задается значение частоты, для которой определяются значения функцийГрафик годографа Михайлова представлен на рис. 10, его анализ показывает, что годограф начинается на вещественной положительной полуоси и располагается только в первом квадранте, что свидетельствует о том, что система неустойчива.

Рис. 10 Годограф Михайлова

На практике для исследования устойчивости систем автоматического управления удобно пользоваться не критерием Михайлова, а следствием из этого критерия. Для этого необходимо записать уравнения, которые получаются приравниванием к нулю вещественной мнимой функций Михайлова, найти их корни. Следствие гласит, для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы корни уравнений были действительными чередующимися между собой и выполнялись условия

Для ответа на вопрос об устойчивости системы необходимо решить следующие уравнения:

;

В результате решения этих уравнений получаем, что корни уравнения -а уравнения-

Как видно из расчетов, корни не чередуются и даже являются комплексно-сопряженными, что свидетельствует о том, что система неустойчива.

Задача 6. Исследовать на устойчивость систему автоматического регулирования (рис. 11) с помощью критерия Найквиста.

Исходными данными являются передаточные функции объекта и регулятора:

Рис. 11 Структурная схема АСР с запаздыванием

Критерий устойчивости Найквиста, в отличие от предыдущих критериев, применяется для исследования устойчивости систем автоматического управления с запаздыванием, поэтому в данной задаче рассматривается объект с запаздыванием. Критерий Найквиста дает ответ об устойчивости замкнутой системы по АФХ разомкнутой системы. Он имеет три формулировки в зависимости от того устойчива, нейтральна или неустойчива разомкнутая система. Поэтому, прежде всего, необходимо ответить на вопрос об устойчивости разомкнутой системы.

Исследуем на устойчивость разомкнутую систему известными методами. Для записи передаточной функции разомкнутой системы разорвем обратную связь в замкнутой системе.

Разомкнутая система представляет собой последовательно соединенные между собой объект и регулятор, ее передаточная функция запишется в виде: .

Характеристическое уравнение разомкнутой системы – это знаменатель передаточной функции, приравненный к нулю, будет .

Корни характеристического уравнения . В соответствии с необходимым и достаточным условием устойчивости разомкнутая система будет нейтральной. Критерий Найквиста в этом случае звучит: если разомкнутая система нейтральна, то для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы АФХ разомкнутой системы с добавлением в бесконечность не охватывала точку (–1, i0).

Для ответа на вопрос об устойчивости замкнутой системы по критерию Найквиста проще всего построить АФХ разомкнутой системы и посмотреть охватывает она точку (–1, i0) или нет, поэтому запишем выражение для АФХ разомкнутой системы:

;

откуда АЧХ: ,

ФЧХ: .

Задаваясь значениями частот построим годограф АФХ разомкнутой системы (рис. 12).

Как видно из рисунка АФХ разомкнутой системы охватывает точку (–1, i0), что говорит о том, что замкнутая система неустойчива.

Рис. 12 Годограф АФХ разомкнутой системы

Объяснение корреляции рангов Кендалла

. | Джозеф Магия

А как насчет ранговой корреляции Кендалла (также известной как тау-б Кендалла)? Что это такое? Как начать? Когда я использую тау-б Кендалла? Эй, просто научите меня всему, что вы знаете о ранговой корреляции Кендалла. “ — Любознательный ум.

Что такое корреляция?

Корреляция — это двуфакторный анализ, который измеряет силу связи между двумя переменными и направление связи. По силе связи значение коэффициента корреляции колеблется от +1 до -1. Значение ± 1 указывает на идеальную степень связи между двумя переменными. По мере приближения значения коэффициента корреляции к 0 взаимосвязь между двумя переменными будет слабее. Направление связи указывается знаком коэффициента; знак + указывает на положительную связь, а знак — указывает на отрицательную связь.

Обычно в статистике мы измеряем четыре типа корреляций:

• Корреляция Пирсона (параметрическая)
• Ранговая корреляция Кендалла (непараметрическая)
• Корреляция Спирмена (непараметрическая)
• Точечная бисериальная корреляция.

Ранговая корреляция Кендалла

Также широко известна как «тау-коэффициент Кендалла». Тау-коэффициент Кендалла и ранговый коэффициент корреляции Спирмена оценивают статистические ассоциации на основе рангов данных. Ранговая корреляция Кендалла (непараметрическая) — это альтернатива корреляции Пирсона (параметрическая), когда данные, с которыми вы работаете, не соответствуют одному или нескольким предположениям теста. Это также лучшая альтернатива корреляции Спирмена (непараметрическая), когда размер вашей выборки невелик и имеет много связанных рангов.

Ранговая корреляция Кендалла используется для проверки сходства в упорядочении данных при их ранжировании по количеству. Другие типы коэффициентов корреляции используют наблюдения в качестве основы корреляции, коэффициент корреляции Кендалла использует пары наблюдений и определяет силу связи на основе закономерностей соответствия и несоответствия между парами.

• Согласованность: Упорядочены одинаково (непротиворечивость), т.е. они расположены в одном и том же порядке по отношению к каждой переменной. Например, пара наблюдений X и Y считается согласованной, если (x1 < x2) и (y1 < x2) или (x1 > x2) и (y1 > x2)
• Несоответствие: Различный порядок (несогласованность), т. е. значения расположены в противоположных направлениях. Например, пара наблюдений X и Y считается дискордантной, если (x1 < x2) и (y1 > x2) или (x1 > x2) и (y1 < x2)

Тау-коэффициент корреляции Кендалла обычно меньше значений, чем Ро-корреляция Спирмена. Расчеты основаны на согласованных и несогласных парах. Нечувствителен к ошибкам. Значения P более точны при меньших размерах выборки.

Вопросы, на которые отвечает ранговая корреляция Кендалла.

1. Корреляция между экзаменационной оценкой учащегося (A, B, C…) и временем, потраченным на обучение, по категориям (<2 часов, 2–4 часа, 5–7 часов…)
2. Удовлетворенность клиентов (например, очень доволен, Удовлетворен, Нейтрально…) и время доставки (< 30 минут, 30 минут — 1 час, 1–2 часа и т. д.)
3. Третий вопрос я оставил вам и вселенной… Веселитесь!

Допущения

Прежде чем приступить к использованию ранговой корреляции Кендалла, необходимо убедиться, что ваши данные удовлетворяют предположениям. Это гарантирует, что у вас будут действительные результаты, которые вы действительно сможете использовать, а не просто цифры на вашем мониторе.

1. Переменные измеряются по порядковой или непрерывной шкале. Порядковые шкалы обычно являются мерой нечисловых понятий, таких как удовлетворение, счастье, дискомфорт. например Очень доволен, в некоторой степени удовлетворен, нейтрально, в некоторой степени неудовлетворен, очень неудовлетворен. Непрерывные шкалы — это, по сути, интервал (т. е. температура, например, 30 градусов) или переменные отношения (например, вес, рост).
2. Желательно , если ваши данные следуют монотонному соотношению . Проще говоря, по мере увеличения значения одной переменной увеличивается и другая переменная, а по мере увеличения значения одной переменной уменьшается другая переменная. Вот почему: ранговая корреляция Кендалла измеряет силу и направление существующей связи (определяет, есть ли монотонная связь) между двумя переменными. Зная это, имеет смысл проверить наличие монотонной связи. Но, как я уже сказал, это желательно .

Монотонные и немонотонные отношения

А-а, вот и все! Коротко и сладко! Вы можете идти!

Вы также можете проверить:

• Кендалл Рейнг Корреляция- Python
• Коэффициент корреляции Pearson объяснил
• Коэффициент корреляции Pearson- Python
• My Profile для большего на Data

100.

Kendall’s Tau Tau Tau Tau-Tau Tau Tau Tau Tau Tau27

10011129.

2.12.12.1112.1111111112.1112.112.11111119.

.

. Основные понятия

Если имеется большое количество связей, то знаменатель в определении тау Кендалла (см. Основные понятия тау Кендалла) следует заменить на

, где n _x  – количество пар с ничьей в переменной x и  n _y  – количество пар с ничьей в переменной y. Эту версию Тау Кендалла часто называют тау-б (вместо предыдущей версии, которая называлась тау-а ).

Расчет n _y аналогичен расчету D , описанному в тесте тау-гипотезы Кендалла, а именно для каждого i , подсчитайте количество j > i , для которых x _i  = x _j . Эта сумма равна n _y . Вычисление n _x аналогично, хотя потенциально проще, поскольку x _i  вычисляются в порядке возрастания.

Так как вообще C ( m , 2) = 1 + 2 +⋯+ ( m –1), то

Здесь t i1 в i -я группа связей среди значений x . u _j = количество элементов в j -й группе связей среди значений y. Пример 1. тау (со связями)

Как и в примере 1 проверки гипотезы Тау Кендалла, мы сначала сортируем данные, помещая результаты в диапазон D3:E18. На этот раз мы видим, что есть связи.

Расчет аналогичен тому, что использовался для примера 1 нормального приближения Тау Кендалла, за исключением того, что нам нужно учитывать связи. В частности, нам нужно изменить формулу инверсий ( D ). Например. ячейка F4 на рисунке 1 содержит формулу =СЧЁТЕСЛИМН(E5:E$19, «<"&E4, D5:D$19,">» & D4).

Чтобы рассчитать модифицированный знаменатель для тау, нам нужно вычислить n _x  и  n _y . Например. расчет за n _x  выполняется путем помещения формулы =СЧЁТЕСЛИ(D5:D$19”=”&D4) в ячейку h5. Затем мы выделим диапазон h5:h28 и нажмем Ctrl-D , чтобы скопировать эту формулу во все соответствующие ячейки столбца H. Поместив формулу = СУММ(h5:h28) в ячейку h29, мы получим значение n _x . . Аналогичным образом можно рассчитать значение n _y (ячейка I19).

Мы можем вычислить значение  C  как сумму элементов соответствия способом, аналогичным тому, который использовался для расчета  Д .

ячейка G4 содержит формулу =СЧЁТЕСЛИМН(E5:E$19″,>»&E4, D5:D$19″,>» & D4). В качестве альтернативы отметим, что C = C ( N , 2) — D — T. Теперь C ( N , 2) = C (15, 2) = 105 ( Cell M5), D = 72 (ячейка F19) и T = N _x + N _Y — N _{X & Y} = 7 + 4 — 1 = 10. количество ничьих равно количеству ничьих в x  плюс количество связей y минус количество связей для x и y,  n _x&y . Мы вычисляем n _x&y  как сумму ячеек в столбце J, где, например, ячейка J4 содержит формулу =СЧЁТЕСЛИМН(D5:D$19,”=”&D4,E5:E$19”,=”&E4) .

Тау Кендалла (ячейка M8) рассчитывается по формуле =(M7-M6)/SQRT((M5-h29)*(M5-I19)).

Модификация стандартной ошибки

Если есть много связей, нам также необходимо изменить расчет стандартной ошибки следующим образом:

Таким образом

Пример 2 : Повторите анализ для анализа

2 : Повторите для анализа для анализа

2 : Повторный Пример 1 с использованием улучшенной версии стандартной ошибки и z , описанных выше.

Мы показываем анализ на рисунке 2.

Рисунок 2 – Проверка гипотезы для тау Кендалла: улучшенная версия

C  и D  рассчитываются, как и раньше, но на этот раз мы обрабатываем связи по формулам ), которые являются первыми из группы связей. Это значение на единицу меньше, чем количество связей в этой группе. Точно так же столбец I обрабатывает связи из столбца E (значения y). Например. значение 78 встречается 4 раза в столбце D. Первый из них встречается в ячейке D12, поэтому ячейка h22 содержит значение 4 – 1 = 3. Это делается по формуле

=ЕСЛИ(СЧЁТЕСЛИ(D$3:D11,D12)=0,СЧЁТЕСЛИ(D13:D$19,D12),0)

Таким образом, имеется C (4, 2) = 6 пар со значением 78 .

Так как для любых м , C ( м , 2) = м ( м– 1)/2, мы можем вычислить количество связей для 1 х 0 , а именно x  =   C ( t _i , 2) по формуле =СУММПРОИЗВ(h5:h28,h5:h28+1)/2. Мы можем сделать то же самое для n _y . Точно так же мы можем вычислить значения всех формул в предыдущем наблюдении, как показано на рисунке 3.

(ячейка L9) и z-показатель (ячейка L12), как показано на рисунке 2.

No related posts.