Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376111 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype.
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
RU
- Class
RU
Теорема Фалеса | это… Что такое Теорема Фалеса?
- Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему.
Теорема Фалеса — одна из теорем планиметрии.
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. |
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.
Доказательство в случае секущих
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые и при этом .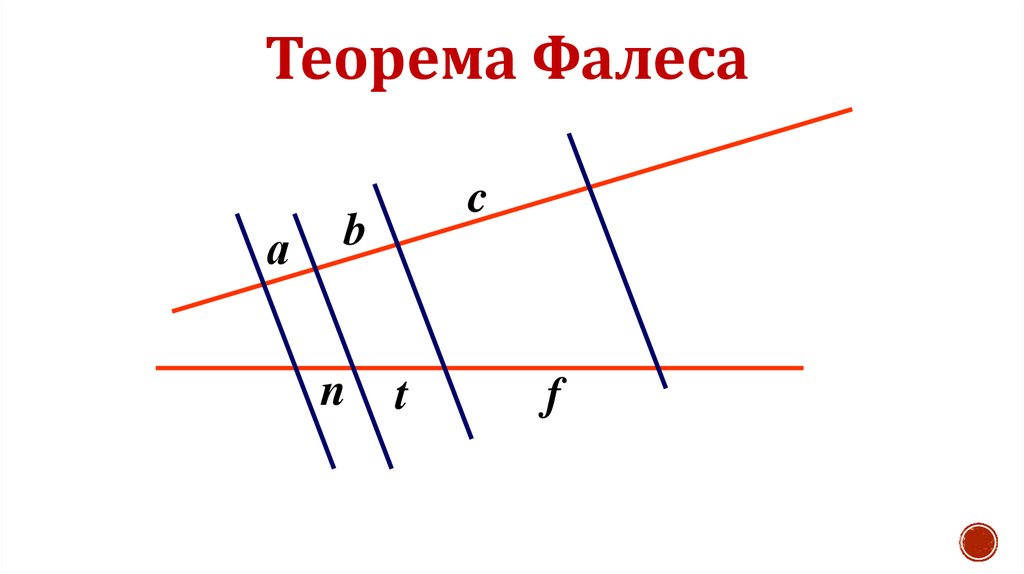
- Проведём через точки и прямые, параллельные другой стороне угла. Получим два параллелограмма и . Согласно свойству параллелограмма: и .
- Треугольники и равны на основании второго признака равенства треугольников:
- согласно условию теоремы,
- как соответственные, образовавшиеся при пересечении параллельных и прямой BD.
- Аналогично каждый из углов и оказывается равным углу с вершиной в точке пересечения секущих.
- как соответственные элементы в равных треугольниках.
- ■
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Также существует обобщённая теорема Фалеса:
- Параллельные прямые отсекают на секущих пропорциональные отрезки:
Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.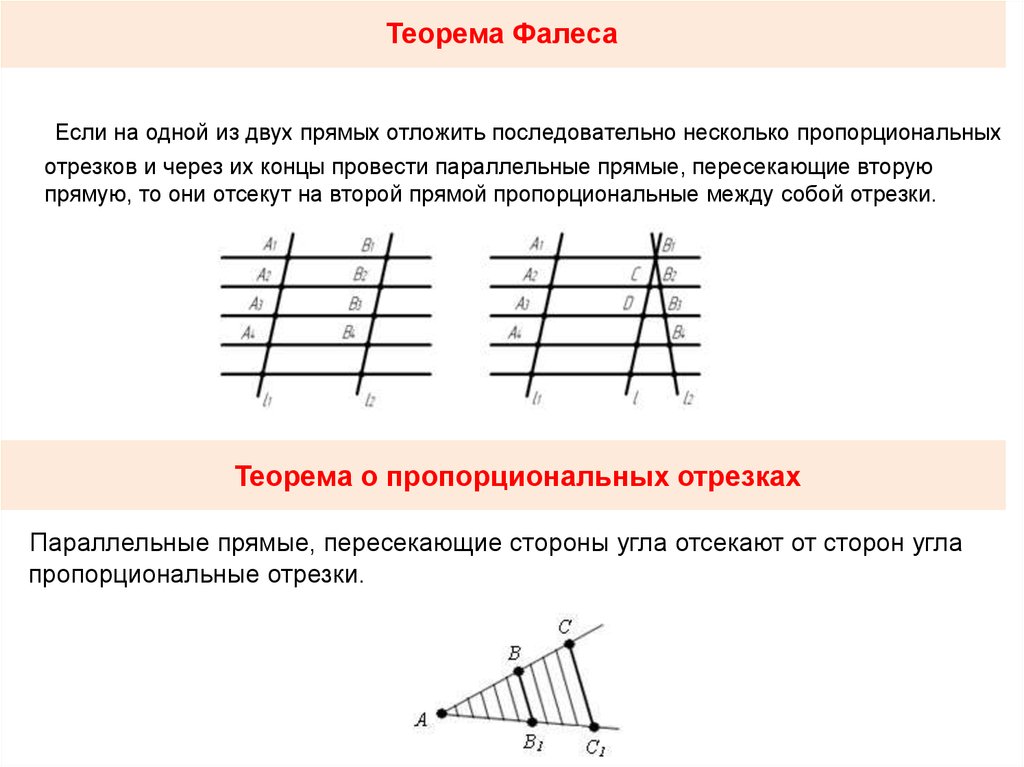
Содержание
|
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
Таким образом (см. рис.) из того, что следует, что прямые .
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).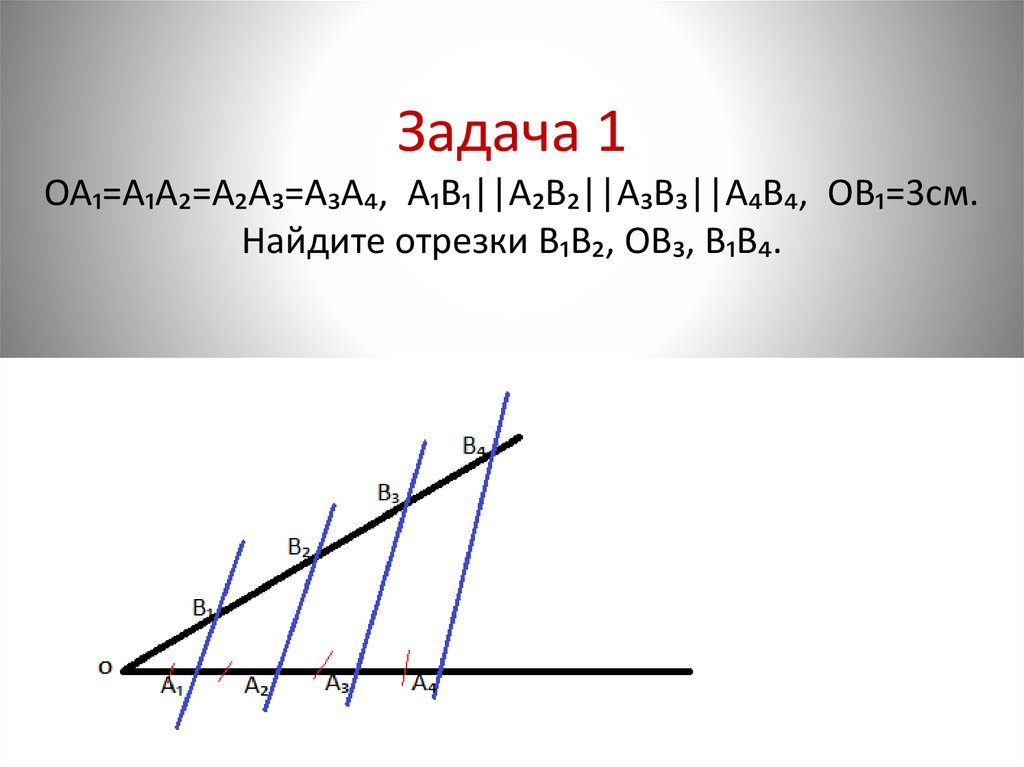
Вариации и обобщения
Следующее утверждение, двойственно к лемме Соллертинского:
Пусть — проективное соответствие между точками прямой и прямой . Тогда множество прямых будет множеством касательных к некоторому коническому сечению (возможно, вырожденному). |
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни[1] приводится доказательство для прямой теоремы для пропорциональных отрезков.
Интересные факты
- Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
- Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Литература
- Атанасян С.Л. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
- ↑ El Teorema de Thales por Les Luthiers en You Tube
Теорема Фалеса — объяснение и примеры
Теорема Фалеса говорит нам, что диаметр окружности всегда образует прямоугольный треугольник, когда мы соединяем его с любой точкой, расположенной на окружности окружности. Эту теорему можно доказать, используя два равнобедренных треугольника, вписанных в окружность, и используя их углы.
Здесь мы рассмотрим более подробное объяснение теоремы Фалеса. Кроме того, мы научимся доказывать эту теорему и использовать ее для решения некоторых практических примеров.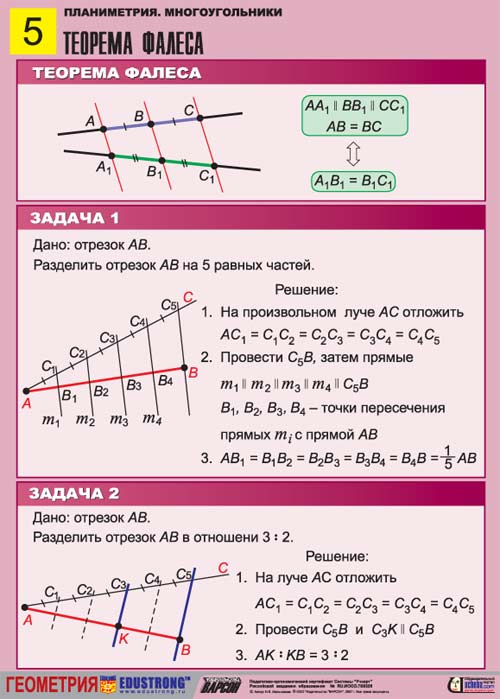
ГЕОМЕТРИЯ
Актуально для …
Изучение теоремы Фалеса на примерах.
См. объяснение
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение теоремы Фалеса.
См. объяснение
Объяснение теоремы Фалеса
Теорема Фалеса считается частным случаем теоремы о вписанных углах. Теорема Фалеса применяется к прямоугольным треугольникам, вписанным в окружность.
Мы собираемся использовать следующую диаграмму для описания теоремы Фалеса.
Теорема Фалеса показывает, что если точки A, B, C — различные точки, расположенные на окружности с центром O, где прямая AC — диаметр окружности, треугольник ΔABC имеет прямой угол (90°) в точке B.
Следовательно, треугольник ΔABC прямоугольный. Это означает, что диаметр окружности всегда образует прямой угол с любой точкой окружности.
Доказательство теоремы Фалеса
Мы можем доказать теорему Фалеса несколькими различными способами, используя алгебраические и геометрические методы.
Однако здесь мы сосредоточимся на геометрическом методе, использующем биссектрисы и сумму внутренних углов.
Соединив центр окружности O с точкой B, мы получим два треугольника ΔABO и ΔOBC. Оба треугольника равнобедренные, так как отрезки OA, OC, OB равны, так как являются радиусами окружности.
Мы знаем, что углы при основании равнобедренного треугольника равны. Следовательно, углы α треугольника ΔABO равны. Аналогично углы β треугольника ΔOBC равны.
Мы также знаем, что сумма внутренних углов любого треугольника всегда равна 180°. Таким образом, в треугольнике ΔABC имеем:
$латекс \альфа+(\альфа+\бета)+\бета=180$°
$латекс 2\альфа+2\бета=180$°
Разделив выражение на 2 имеем:
$latex \alpha+\beta=90$°
Угол α+β есть угол треугольника ΔABC в точке B. Таким образом, мы доказали теорему.
Примеры с ответами теоремы Фалеса
ПРИМЕР 1
Отрезок AB соответствует диаметру окружности. Определите меру угла X.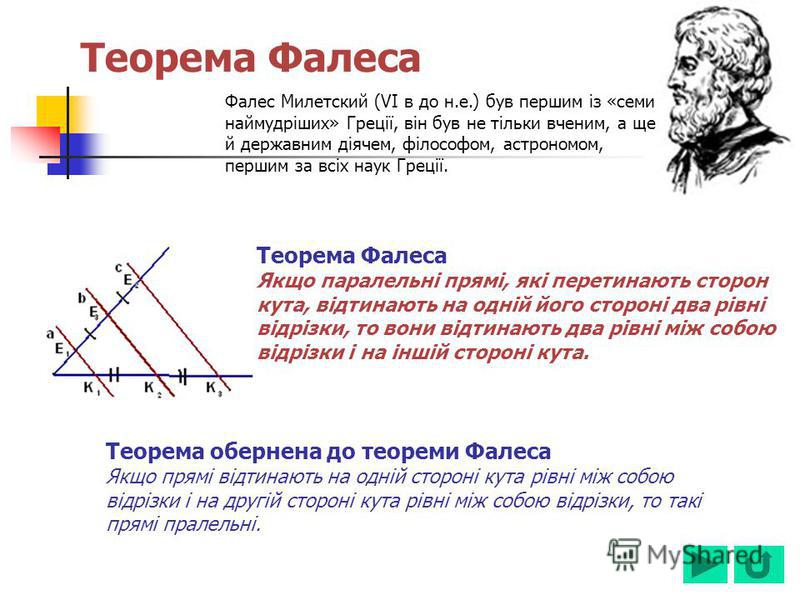
Решение: Поскольку отрезок AB является диаметром, по теореме Фалеса мы знаем, что угол, образованный при вершине C, равен 90°. Также известно, что сумма внутренних углов любого треугольника равна 180°. Следовательно, имеем:
90°+60°+X=180°
150°+X=180°
X=180°-150°
X=30°
Угол X равен 30 °.
ПРИМЕР 2
Точка M является центром окружности. Чему равен угол Z?
Решение: Если точка M является центром, это означает, что отрезок XZ является диаметром окружности, поэтому мы можем применить теорему Фалеса. Следовательно, мы знаем, что угол, образованный при вершине Y, равен 90°. Мы можем использовать сумму внутренних углов треугольника, чтобы получить меру Z:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
92}=61$$латекс c=7,81$
Длина сегмента XY составляет 7,81 ед.
ПРИМЕР 4
Определите угол ∠ABC, считая точку C центром окружности.
Решение: Точка C является центром окружности, поэтому отрезок AD является диаметром, и мы можем применить теорему Фалеса.
Ранее мы видели, что треугольники ABC и BCD должны быть равнобедренными. Итак, имеем:
∠ CBD = ∠ CDB =60°
По теореме Фалеса мы знаем, что:
∠ ABD =90°
Следовательно, имеем:
∠ ABC = 90°-60°=30° Таким образом, угол
,900 ∠ABC равен 30°.
См. также
Хотите узнать больше о теореме Тале? Взгляните на эти страницы:
- Проблемы с теоремой Фалеса
- Примеры с теоремой Фалеса
Примеры с теоремой Фалеса — Мехамат
Теорема Фалеса говорит нам, что треугольник вписан в окружность, где гипотенуза соответствует диаметру окружности, всегда является прямоугольным треугольником. Эту теорему можно доказать, используя сумму внутренних углов.
Здесь мы рассмотрим краткое изложение теоремы Фалеса.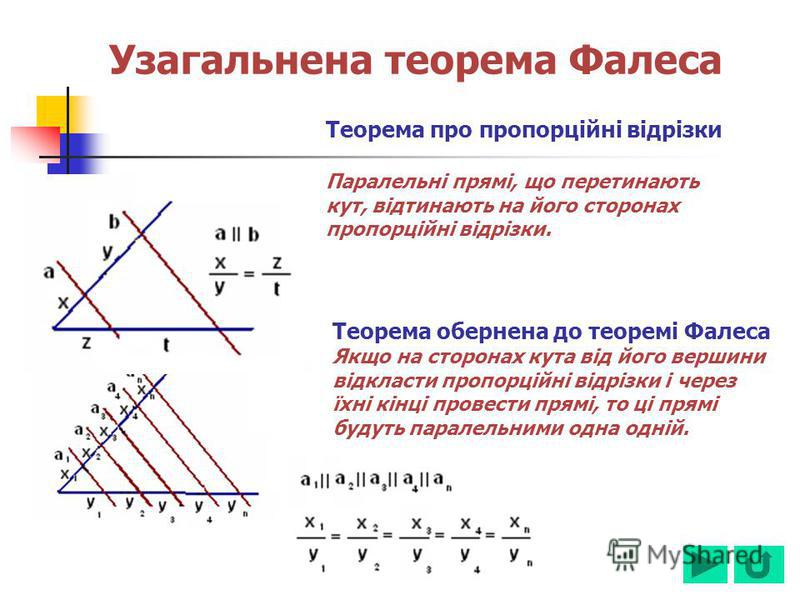
Затем мы научимся применять эту теорему для решения некоторых практических задач.
ГЕОМЕТРИЯ
Актуально для …
Учимся решать примеры с теоремой Фалеса.
См. примеры
Содержание
ГЕОМЕТРИЯ
Актуально для …
Учимся решать примеры с теоремой Фалеса.
См. примеры
Резюме теоремы Фалеса
Теорема Фалеса рассматривается как частный случай теоремы о вписанных углах. Эта теорема говорит нам, что если у нас есть треугольник, вписанный в окружность, как показано на следующей диаграмме, угол, образованный при вершине B, всегда прямой.
Следовательно, если на окружности расположены три точки A, B и C, где прямая AC — диаметр окружности, то угол ∠ABC — прямой (90°).
Эту теорему можно доказать, проведя биссектрису из центра в вершину B, а затем используя углы образующихся равнобедренных треугольников и тот факт, что сумма внутренних углов любого треугольника равна 180°.
Вы можете посмотреть полное доказательство в этой статье.
Теорема Фалеса – примеры с ответами
Следующие примеры показывают применение теоремы Фалеса. Каждый пример имеет свое решение, но рекомендуется попробовать решить примеры самостоятельно, прежде чем смотреть решение.
ПРИМЕР 1Отрезок AC – это диаметр окружности. Чему равен угол Z?
Решение
Отрезок AC — это диаметр окружности, поэтому мы можем использовать теорему Фалеса. Следовательно, мы знаем, что угол при вершине B равен 9угол 0°. Так как сумма внутренних углов в любом треугольнике равна 180°, то имеем:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
Угол Z равен 40°.
ПРИМЕР 2Если M — центр окружности, определите угол Z.
Решение
Поскольку точка M — центр окружности, мы знаем, что отрезок XZ — диаметр окружности. . Следовательно, мы можем использовать теорему Фалеса.
По теореме мы знаем, что угол при вершине Y прямой, то есть угол 90°. Мы можем использовать сумму внутренних углов треугольника, чтобы получить меру Z:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
Угол Z равен 40°.
ПРИМЕР 3Отрезок AC – это диаметр окружности. Какова длина диаметра?
Решение
Используя теорему Фалеса, мы можем определить, что треугольник ABC прямоугольный. Это означает, что угол В прямой. Следовательно, мы можем использовать теорему Пифагора, чтобы найти длину диаметра: 92}=36$
$латекс a=6$
Длина отрезка АВ равна 6 единицам.
ПРИМЕР 5Если C является центром окружности, то какова мера угла ∠ABC?
Решение
Поскольку точка C является центром окружности, мы знаем, что отрезок AD является диаметром. Следовательно, мы можем применить теорему Фалеса.
Две стороны треугольников ABC и BCD равны, так как они соответствуют радиусам окружности.