Теория комплексные числа: Национальный исследовательский университет «Высшая школа экономики»

Содержание

Урок 38. определение комплексного числа. действия с комплексными числами — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №38. Определение комплексного числа. Действия с комплексными числами.

Перечень вопросов, рассматриваемых в теме

1) понятие мнимой единицы;

2) определение комплексного числа;

3) действия с комплексными числами и действия над ними.

Глоссарий по теме

Определение. Комплексным числом называется выражение вида a + bi, где a и b — действительные числа.

Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.

Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

Определение. Суммой комплексных чисел z₁ = a₁ + b₁i и z₂ = a₂ + b₂i называется комплексное число z, действительная часть которого равна сумме действительных частей z₁ и z₂, а мнимая часть — сумме мнимых частей чисел z₁ и z₂, то есть z = (a₁ + a₂) + (b₁ + b₂) i.

Числа z₁ и z₂ называются слагаемыми.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z,

что z + z₂ = z₁.

Теорема. Разность комплексных чисел существует и притом единственная.

Определение. Произведением комплексных чисел z₁=a₁+ b₁ i и z₂=a₂+b₂ i называется комплексное число z, определяемое равенством:

z = (a₁a₂ – b₁b₂) + (a₁b₂ + a₂b₁) i.

Числа z₁ и z₂ называются сомножителями.

Определение. Разделить комплексное число z₁ на комплексное число z₂, значит найти такое комплексное число z, что z · z₂ = z₁.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i ² = —1.

Исходя из этого, получим следующее определение комплексного числа.

Определение. Комплексным числом называется выражение вида a + bi, где a и b — действительные числа. При этом выполняются условия:

а) Два комплексных числа a₁ + b₁i и a₂ + b₂i равны тогда и только тогда, когда a₁=a₂, b₁=b₂.

б) Сложение комплексных чисел определяется правилом:

(a₁ + b₁i) + (a₂ + b₂i) = (a₁ + a₂) + (b₁ + b₂) i.

в) Умножение комплексных чисел определяется правилом:

(a₁ + b₁i) (a₂ + b₂i) = (a₁a₂ — b₁b₂) + (a₁b₂ — a₂b₁) i.

Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0

Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.

Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.

Два комплексных числа z = a + bi и = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.

Над комплексными числами в алгебраической форме можно выполнять следующие действия.

1) Сложение.

Определение. Суммой комплексных чисел z₁ = a₁ + b₁ i и z₂ = a₂ + b₂i называется комплексное число z, действительная часть которого равна сумме действительных частей z₁ и z₂, а мнимая часть — сумме мнимых частей чисел z₁ и z₂, то есть z = (a₁ + a₂) + (b₁ + b₂) i.

Числа z₁ и z₂называются слагаемыми.

Сложение комплексных чисел обладает следующими свойствами:

1º. Коммутативность: z₁ + z₂ = z₂ + z₁.

2º. Ассоциативность: (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃).

3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0

Пример 1. Выполните сложение (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Вычитание.

Определение. Вычесть из комплексного числа z₁ комплексное число z₂, значит найти такое комплексное число z, что z + z₂ =z₁.

Теорема. Разность комплексных чисел существует и притом единственная.

Пример 2. Выполните вычитание (4 – 2i) — (-3 + 2i).

(4 – 2i) — (-3 + 2i) = (4 — (-3)) + (-2 — 2) i = 7 – 4i.

3) Умножение.

Определение. Произведением комплексных чисел z₁=a₁+ b₁ i и z₂=a₂+b₂i называется комплексное число z, определяемое равенством:

z = (a₁ a₂ – b₁b₂) + (a₁b₂ + a₂b₁) i.

Числа z₁ и z₂ называются сомножителями.

Умножение комплексных чисел обладает следующими свойствами:

1º. Коммутативность: z₁z₂ = z₂ z₁.

2º. Ассоциативность: (z₁z₂)z₃ = z₁ (z₂z₃)

3º. Дистрибутивность умножения относительно сложения:

(z₁ + z₂) z₃ = z₁z₃ + z₂z₃.

4º. z · = (a + bi) (a – bi) = a² + b²— действительное число.

На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.

В следующем примере рассмотрим умножение комплексных чисел двумя способами: по правилу и умножением суммы на сумму.

Пример 3. Выполните умножение (2 + 3i) (5 – 7i).

1 способ. (2 + 3i) (5 – 7i) = (2⋅ 5 – 3⋅ (- 7)) + (2⋅ (- 7) + 3⋅ 5)i =

= (10 + 21) + (- 14 + 15)i = 31 + i.

2 способ. (2 + 3i) (5 – 7i) = 2⋅ 5 + 2⋅ (- 7i) + 3i⋅ 5 + 3i⋅ (- 7i) =

= 10 – 14i + 15i + 21 = 31 + i.

4) Деление.

Теорема. Частное комплексных чисел существует и единственно, если z₂ ≠ 0 + 0i.

На практике частное комплексных чисел находят путем умножения числителя и знаменателя на число, сопряженное знаменателю.

Пусть z₁ = a₁ + b₁i, z₂ = a₂ + b₂i, тогда

В следующем примере выполним деление по формуле и правилу умножения на число, сопряженное знаменателю.

Пример 4. Найти частное

1 способ.

2 способ.

5) Возведение в целую положительную степень.

а) Степени мнимой единицы.

Пользуясь равенством i² = -1, легко определить любую целую положительную степень мнимой единицы. Имеем:

i³= i²i = -i,

i⁴= i²i² = 1,

i⁵ = i⁴i = i,

i⁶= i⁴i² = -1,

i⁷= i⁵i² = -i,

i⁸ = i⁶i² = 1 и т. д.

Это показывает, что значения степени iⁿ, где n – целое положительное число, периодически повторяется при увеличении показателя на 4 .

Поэтому, чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.

Пример 5. Вычислите: (i ³⁶ + i ¹⁷) · i ²³.

i ³⁶ = (i ⁴)⁹= 1 ⁹ = 1,

i ¹⁷= i ^{4⋅ 4+1} = (i ⁴)⁴⋅ i = 1 · i = i.

i ²³ = i ^{4⋅ 5+3} = (i ⁴)⁵⋅ i³ = 1 · i³ = — i.

(i ³⁶ + i ¹⁷) · i ²³ = (1 + i) (- i) = — i + 1= 1 – i.

б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.

Пример 6. Вычислите: (4 + 2i) ³

(4 + 2i) ³= 4 ³ + 3⋅ 4²⋅ 2i + 3⋅ 4⋅ (2i)² + (2i)³ = 64 + 96i – 48 – 8i = 16 + 88i.

Стоит отметить. что с помощью комплексных чисел можно решать квадратные уравнения, у которых отрицательный дискриминант.

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен.

Пример 7. Решите уравнения:

а) x² – 6x + 13 = 0; б) 9x² + 12x + 29 = 0.

Решение. а) Найдем дискриминант по формуле
D = b²– 4ac.

Так как a = 1, b = – 6, c = 13, то
D = (– 6)² – 4×1×13 = 36 – 52 = – 16;

Корни уравнения находим по формулам

б) Здесь a = 9, b = 12, c = 29. Следовательно,
D = b² – 4ac =122 – 4×9×29 = 144 – 1044 = – 900,

Находим корни уравнения:

Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня.

Разбор решения заданий тренировочного модуля

№1. Тип задания: единичный выбор

Вычислите сумму (2 + 3i)+ (5 – 7i).

7 +4i
7 — 4i
6 — 3i
6 + 3i

Решение: 2 + 3i + 5 — 7i = (2 + 5) + (3 — 7)i = 7 — 4i.

Можем сделать вывод, что верный ответ

2. 7 — 4i.

№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Чему будет равно частное: (5 + 3i):(1 — 2i)=______

Решение:

Ответ: -0. 2 + 2.6i

1.4.1. Понятие комплексного числа

Глава 1. Арифметика

1.4.

1.4.1.

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
a = c и b = d.
Суммой двух комплексных чисел a + ib и c + id называется комплексное число
a + c + i(b + d).
Произведением двух комплексных чисел a + ib и c + id называется комплексное число
ac – bd + i(ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z.

Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i.

Чисто мнимое число i1 = 1i = i обладает удивительным свойством:

Таким образом,

С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства то и перемножать эти числа можно как многочлены. В самом деле,

то есть как раз получается нужная формула.

Пример 1

Вычислить z₁ + z₂ и z₁z₂, где z₁ = 1 + 2i и z₂ = 2 – i.

Показать решение

Рисунок 1.

4.1.1

Мы хорошо помним, что геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.

Очень важной является интерпретация комплексного числа z = a + ib как вектора с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор и наоборот, каждому вектору соответствует, и притом единственное, число z = a + ib.

Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости.

Модель 1.14. Комплексные числа на плоскости


	Модулем комплексного числа называется длина вектора, соответствующего этому числу:

Модуль комплексного числа z обычно обозначается или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).

Рисунок 1.4.1.2

Если то то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что для всех При этом тогда и только тогда, когда


	Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.

Угол φ, аргумент комплексного числа, обозначается φ = arg z.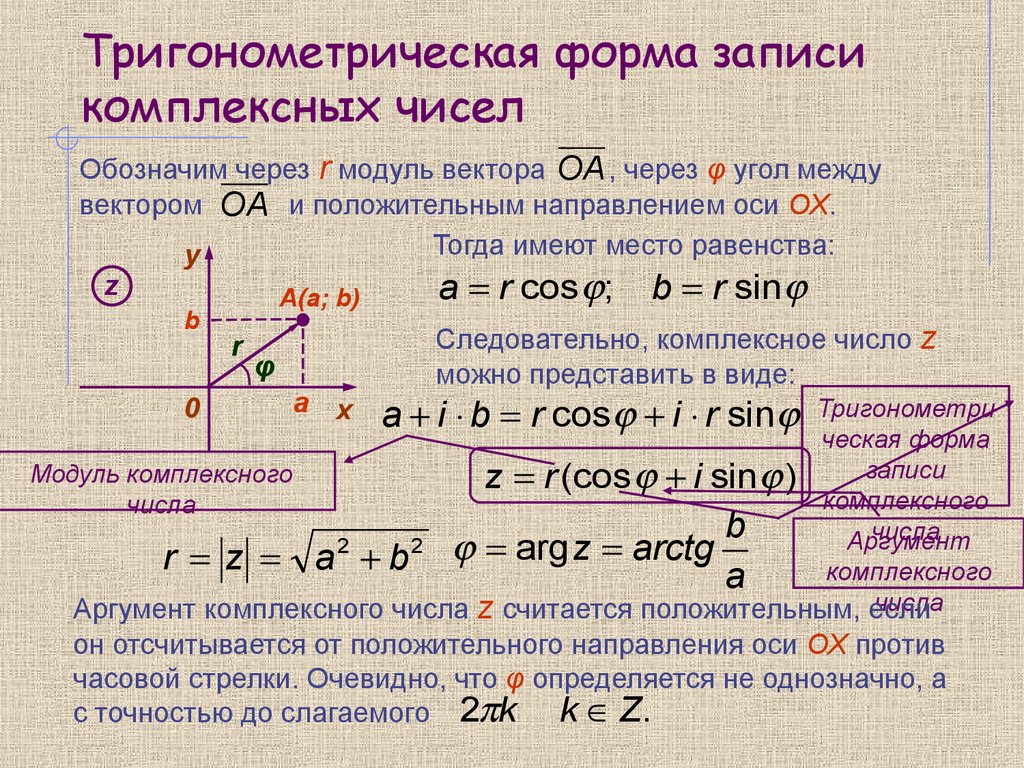 Для числа z = 0 аргумент не определён.

Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет. Действительно, если φ = arg z – аргумент этого комплексного числа, то все числа вида φ + 2πn также будут аргументами этого комплексного числа. Например, аргументами комплексного числа z = 1 + i являются углы и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π.

Заданием только лишь своего модуля определяется только комплексное число z = 0.

Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система

Пример 2

Найти модуль и аргумент комплексного числа z = –1 – i.

Показать решение

Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн

Кирпич

Уникальный прочный кирпич с гайкой. Гарантия долговечности. Стройте на века

oooservisstroy.ru

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.

А также: online подготовка к ЕГЭ на College.ru, библиотека ЭОРов и обучающие программы на Multiring.ru.

Комплексные числа и операции с ними

Содержание

Введение

Комплексная плоскость и мнимая единица

Модуль и фаза комплексного числа

Показательная форма комплексного числа. Формула Эйлера

Операции над комплексными числами. Комплексно-сопряженные числа

Выводы

Список литературы

DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов

Распространяется под лицензией LGPL v3

Страница проекта на SourceForge

Обнаружили ошибку? Выделите ее мышью и нажмите

Введение

Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Например функция определена для , аналогично можно вспомнить, что функция определена для , а функция определена для .

Однако, ограниченная область определения функций на множестве вещественных чисел не означает, что , или не имеют смысла. Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том, что не может быть представлено вещественным числом. Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .

При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.

Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1), на которой мы можем откладывать рациональные и иррациональные вещественные числа. Но на этой прямой нет числа , значит его надо искать вне числовой прямой. Таким образом мы должны расширить множество вещественных чисел до множества в котором значения , или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве, как на множестве вещественных чисел.

Комплексная плоскость и мнимая единица

Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано число .

Рисунок 1. Расширение множества вещественных чисел до множества комплексных числел

Значение вещественного числа однозначно определяет его позицию на числовой прямой, однако для определения позиции на плоскости одного числа недостаточно.

Для «навигации» по комплексной плоскости вводятся две прямые и , которые пересекаются в начале координат.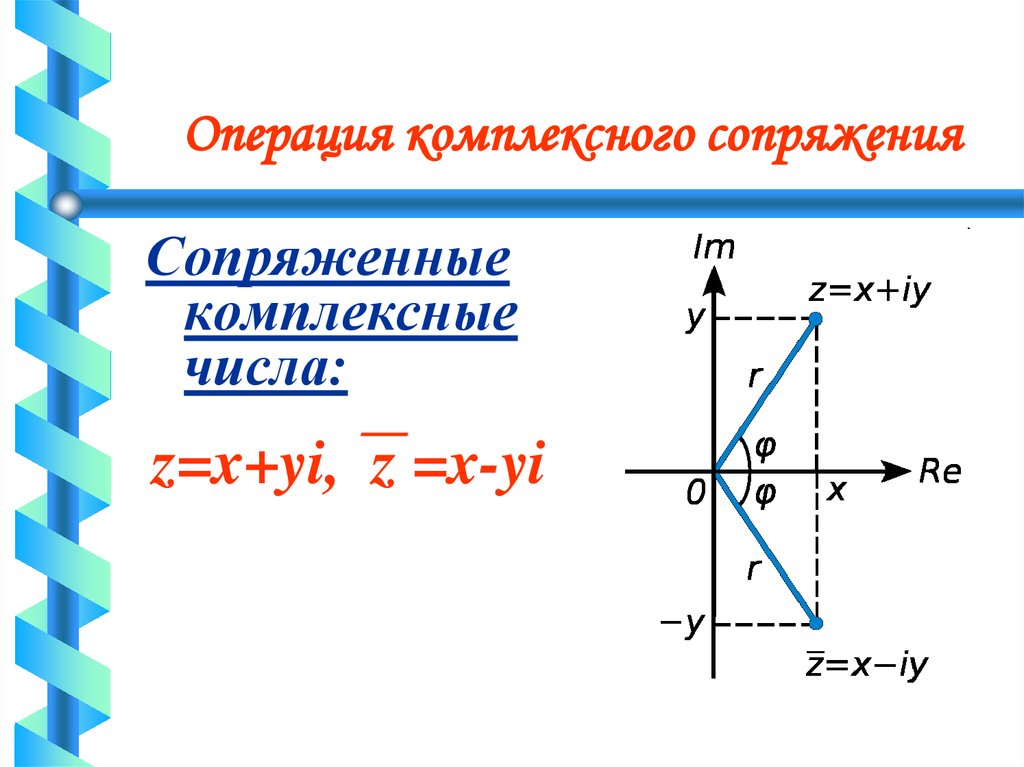 Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа. Прямая называется мнимой осью и она перпендикулярна реальной оси . Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.

Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно. При этом само комплексное число можно записать как , где называется реальной частью и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью и задает координату точки комплексной плоскости на мнимой оси .

Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей .

Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой .

Если и , тогда число является действительным и располагается на реальной оси .

Если и , тогда число является чисто мнимым и располагается на мнимой оси .

Если и , тогда число располагается в одной из четвертей комплексной плоскости.

Модуль и фаза комплексного числа

Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как

(1)

— неотрицательное вещественное число характеризующее длину вектора и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно реальной оси на некоторый угол , называемый фазой. Фаза комплексного числа может быть положительной или отрицательной, в зависимости от того в каком направлении относительно оси отсчитывать угол. Если угол поворота вектора на комплексной плоскости отсчитывать против часовой стрелки (как это показано на рисунке 1), то фаза будет принимать положительные значения, а если по часовой — то отрицательные.

Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:

(2)

Тогда комплексное число можно представить в тригонометрической форме:

(3)

Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа, представленного в алгебраической форме:

(4)

тогда

(5)

где учитывает четверть комплексной плоскости в которой расположено число :

(6)

Необходимость поправки возникает из-за того, что функция периодическая функция с периодом рад.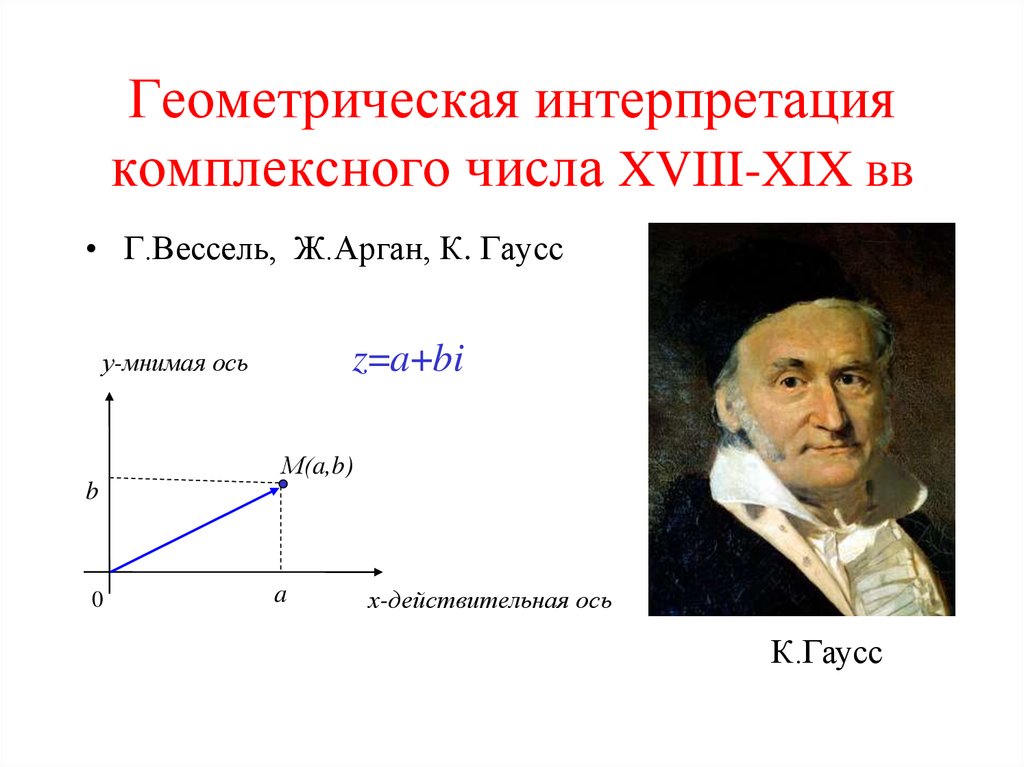 В результате возвращает корректные значения только в интервале . Таким образом функция арктангенса не отличает четверть I от четверти III (в обоих случаях отношение положительное), а также не отличает четверть II от четверти IV (отношение отрицательное).

На рисунке 2 показаны значения параметра , в зависимости от того в какой четверти комплексной плоскости расположено число.

Рисунок 2. Значение поправки фазы комплексного числа в зависимости от расположения на комплексной плоскости.

На рисунке 2а исходное комплексное число расположено в первой четверти комплексной плоскости и .

Тогда и значение фазы комплексного числа равно:

(7)

Рассмотрим случай, когда комплексное число расположено во второй четверти комплексной плоскости (рисунок 2б), т.е. и . В этом случае и угол также будет отрицательным (красная пунктирная линия). Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:

(8)

Пусть комплексное число расположено в третьей четверти комплексной плоскости (рисунок 2в), т. е. и . В этом случае и угол будет положительным (красная пунктирная линия). Тогда для того, чтобы получить корректное значение фазы необходимо ввести поправку рад:

(9)

Если расположено в четвертой четверти комплексной плоскости (рисунок 2г), т.е. и , то в этом случае и угол будет отрицательным и равным фазе комплексного числа без поправок ( рад):

(10)

Функция которая позволяет получить фазу комплексного числа c учетом четверти комплексной плоскости в которой расположено комплексное число называется функция арктангенс-2 и обозначается .

Функция арктангенс-2 присутствует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.

Показательная форма комплексного числа. Формула Эйлера

Мы уже рассмотрели алгебраическую и тригонометрическую формы записи комплексного числа. Помимо алгебраической и тригонометрической формы существует также показательная форма комплексного числа:

(11)

связанная с тригонометрической формой формулой Эйлера:

(12)

Cоотношение (12) легко доказать, если произвести разложение экспоненты в ряд Тейлора:

(13)

Представим ряд (13) в виде суммы четных и нечетных членов последовательности:

(14)

Рассмотрим более подробно мнимую единицу в четной и нечетной степенях.

Из определения мнимой единицы можно сделать вывод, что , тогда , в свою очередь .

Таким образом, можно сделать вывод что .

Построим аналогичным образом соотношение для нечетных степеней: , тогда , в свою очередь и окончательно можно записать: . Тогда (14) можно представить как:

(15)

В выражении (15) первая сумма по четным степеням дает разложение в ряд Тейлора функции , а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции . Таким образом, получено доказательство справедливости формулы Эйлера (12).

Необходимо отметить, что формула Эйлера является одной из важнейших в теории функций комплексного переменного. Так например при помощи формулы Эйлера можно связать математические константы и с использованием мнимой единицы :

(16)

Операции над комплексными числами. Комплексно-сопряженные числа

В данном параграфе мы кратко рассмотрим операции над комплексными числами. Сумма двух комплексных чисел и представляет собой комплексное число :

(17)

При сложении реальные и мнимые части комплексного числа также складываются. На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3а).

Рисунок 3. Операции над комплексными числами

Разность двух комплексных чисел и представляет собой комплексное число

(18)

При вычитании реальные и мнимые части комплексного числа также вычитаются. На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов по правилу параллелограмма (рисунок 3б). На первом шаге из вектора формируется вектор (обозначенный пунктирной линией на рисунке 3б), после чего вектор складывается с вектором по правилу параллелограмма.

Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:

(19)

Умножение комплексных проще выполнять если числа представлены в показательной форме:

(20)

При перемножении в показательной форме модули комплексных чисел перемножаются а фазы складываются. Операция произведения комплексных чисел показано на рисунке 3в.

Введем понятие комплексно-сопряженного числа. Число является комплексно-сопряженным числу .

Комплексно-сопряженные числа отличаются знаком перед мнимой частью.

Графически комплексно-сопряженные числа показаны на рисунке 3г.

При этом можно заметить, что модули комплексно-сопряженных чисел равны , а фазы имеют противоположные знаки.

Произведение комплексно-сопряженных чисел

(21)

представляет собой действительное число равное квадрату модуля этих чисел.

Из элементарных операций нам осталось рассмотреть лишь деление комплексных чисел. Рассмотрим результат деления комплексных чисел в показательной форме:

(22)

Таким образом, при делении комплексных чисел модуль частного равен частному модулей исходных чисел, а фаза равна разности фаз исходных чисел.

При этом необходимо потребовать, чтобы был не равен нулю, иначе у нас появится деление на ноль при расчете модуля частного.

Рассмотрим теперь деление комплексных чисел в алгебраической форме:

(23)

Домножим и числитель и знаменатель на число, комплексно-сопряженное знаменателю:

(24)

Выводы

В данной статье введено понятие комплексного числа и рассмотрены основные его свойства. Введено понятие мнимой единицы.

Подробно рассмотрена комплексная плоскость и представление комплексных чисел в алгебраической, тригонометрической и показательной формах. Введены понятия модуля и фазы комплексного числа.

Рассмотрены основные арифметические операции над комплексными числами.

Показано как выполнять операции сложения, вычитания в алгебраической форме, введено понятие комплексно-сопряженных чисел, а также операции умножения и деления в показательной и алгебраической формах.

Информация была полезна? Поделитесь с друзьями!

Список литературы

[1] Пантелеев А.В., Якимова А.С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. М: Высшая школа, 2011.

[2] Дубровин В.Т. Теория функций комплексного переменного. Теория и практика Казань: Казанский государственный университет, 2010. [PDF]

Последнее изменение страницы: 12.05.2022 (19:41:15)

Страница создана Latex to HTML translator ver. 5.20.11.14

Комплексные числа, 3 формы записи, основные операции

Часть 2. Теория функций комплексной переменной.

Лекция 1.

Комплексные числа, 3 формы записи, основные операции.

Алгебраическая форма записи комплексного числа z=x+iy, x = Re z – действительная часть (real), y = Im z – мнимая часть комплексной числа (imagine), i – мнимая единица (i² = -1). Степени мнимой единицы: i⁰ =1, i¹ = i, i² = -1, i³ = -i, i⁴ = 1, i⁵ = i, i⁶ = -1, i⁷ =-i, i⁸ =1,….значения повторяются через 4. Например, i²³= i²⁰ i³= -i, i⁶¹ = i⁶⁰ i = i, и т.д. Если ввести в комплексной плоскости декартову систему координат, то x откладывают на действительной оси в комплексной плоскости (оси абсцисс), y – на мнимой оси (оси ординат).

Если ввести в комплексной плоскости полярную систему координат (полярные координаты ),

то комплексное число можно записать в тригонометрической форме .

Комплексное число можно ассоциировать с его радиусом – вектором. Полярная координата — это модуль радиуса – вектора или просто модуль комплексного числа , а полярный угол — аргумент комплексного числа, .

Аргумент определяется так сложно, потому что имеет область значений , а необходимо обеспечить возможность изменения полярного угла в диапазоне .

Пример. Записать в тригонометрической форме. .

Записать в тригонометрической форме. .

Справедлива формула Эйлера . Это – одна из самых красивых и фундаментальных формул в математике. Достаточно сказать, что из нее следует равенство , связывающее почти все основные математические константы: 0, 1, i, .

Используя формулу Эйлера, можно записать комплексное число в показательной форме . Алгебраическая, тригонометрическая и показательная формы – три формы записи комплексных чисел.

Рассмотрим операции над комплексными числами. Сложение и вычитание комплексных чисел удобнее всего производить в алгебраической форме записи.

. Например, . Заметим, что числа называются комплексно сопряженными числами.

Сложение или вычитание комплексных чисел соответствует сложению или вычитанию их радиусов векторов и может быть проведено по «правилу параллелограмма » или «правилу треугольника » .

Умножение и деление комплексных чисел тоже можно выполнять в алгебраической форме.

Примеры. ,

. Здесь числитель и знаменатель дроби умножают на число, сопряженное знаменателю, чтобы получить в знаменателе действительное число.

Удобнее выполнять умножение или деление в тригонометрической или показательной формах:

Итак, действует правило: при умножении комплексных чисел их модули перемножаются, а аргументы складываются. При делении комплексных чисел их модули делятся, а аргументы вычитаются.

Особенно удобно использовать тригонометрическую и показательную формы при возведении комплексного числа в степень.

. С другой стороны, .

Из сопоставления этих выражений получается знаменитая формула Муавра

. Ее удобно применять для выражения синусов и косинусов кратных углов через степени синусов и косинусов самого угла. Например,

Отделяя действительные и мнимые части, получим

Например, .

Здесь можно было .

Рассмотрим «пятое действие арифметики » – извлечение корня.. Пусть . Тогда . Получим формулу . .

Из формулы ясно, что все корней лежат в комплексной плоскости на круге радиуса с центром в начале координат на равном угловом расстоянии друг от друга , причем первый корень расположен под углом к действительной оси.

Найдем, например, . Определяем

Все корни лежат на круге радиусом 2 с центром в начале координат, на угловом расстоянии друг от друга, причем первый корень лежит под углом к действительной оси.

Множества на комплексной плоскости.

Для того, чтобы правильно строить типичные кривые на комплексной плоскости, прежде всего надо помнить, что . Следовательно, — это окружность радиуса с центром в точке на комплексной плоскости (расстояние от точки до точки равно ). — это круговое кольцо с центром в точке , включая внутреннюю окружность радиусом , исключая внешнюю окружность радиусом .

— это прямая линия на комплексной плоскости , — угол наклона прямой к действительной оси. Некоторые часто встречающиеся кривые и области изображены ниже

При построении двух последних областей надо вспомнить определение эллипса (геометрическое место точек плоскости, сумма расстояний которых от двух фиксированных точек плоскости постоянна и равна ()) и определение параболы (геометрическое место точек плоскости, расстояние которых от фиксированной точки плоскости равно расстоянию до фиксированной прямой ).

Открытые и замкнутые множества, односвязное множество.

называется множество .

Точка называется внутренней точкой множества, если существует ее окрестность, целиком принадлежащая этому множеству. Например, все точки круга — внутренние.

Точка называется граничной точкой множества, если в любой ее окрестности найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Границей множества называется совокупность его граничных точек. Например, окружность — граница круга .

Множество называется открытым, если оно состоит только из внутренних точек. Например, круг — открытое множество.

Замыканием множества называется объединение множества и его границы. Замкнутым называется множество, совпадающее со своим замыканием.

Множество называется ограниченным, если его можно накрыть кругом конечного радиуса.

Открытой областью (или просто областью) называется открытое множество, любые две точки которого можно соединить ломаной, целиком принадлежащей множеству.

Замкнутой областью называется объединение открытой области и ее границы.

Рассмотрим последовательность комплексных чисел . Последовательность называется неограниченно возрастающей, если . То есть все элементы неограниченно возрастающей последовательности нельзя накрыть кругом конечного радиуса.

По определению полагают, что все неограниченно возрастающие последовательности сходятся к (единственной) бесконечно удаленной точке ( или БУТ), которая не принадлежит комплексной плоскости. Пополняя комплексную плоскость, мы получаем расширенную комплексную плоскость.

Пояснить единственность бесконечно удаленной точки можно, рассматривая сферу Римана

Кривой на комплексной плоскости называется однопараметрическое семейство точек плоскости . Точкой самопересечения или кратной точкой кривой называется точка, отвечающая двум или более значениям параметра.

Кривая, не содержащая кратных точек, называется простой или жордановой кривой. Кривая называется замкнутой, если ее начало совпадает с ее концом.

Теорема Жордана. Любая замкнутая жорданова кривая делит расширенную комплексную плоскость на две области, общей границей которых она является. Одна из этих областей ограничена и называется внутренностью кривой. Вторая не ограничена и называется внешностью кривой.

Множество называется односвязным, если для любой замкнутой кривой либо внутренность кривой принадлежит , либо внешность кривой принадлежит . Например, множества , да и все изображенные на рисунках области, за исключением кругового кольца — односвязные, они «не содержат дыр » .

«Комплексные числа» обобщающий урок математики с использованием интерактивной доски

Цели урока

Систематизировать теоретический материал по теме.

Повторить перевод чисел из алгебраической в тригонометрическую форму записи комплексных чисел, действия с комплексными числами.

Обобщить знания учащихся по теме и рассмотреть вопросы по теме «Функция комплексного переменного» в межпредметной связи с темой «Преобразования на плоскости».

Развивать: способности анализировать, планировать, контролировать свою деятельность (взаимо- и самоконтроль).

Формировать коммуникативные навыки, оперировать математической терминологией.

Продолжить освоение интерактивной доски.

План проведения урока

I. Организационный момент

Учащиеся записывают тему урока «Комплексные числа».

Учитель: Впервые в истории комплексными числами стали заниматься в XVI веке в связи с решением уравнений. Несмотря на то, что с комплексными числами оперировать ничуть не сложнее, чем с действительными, но до начала XIX века комплексные числа рассматривались как очень сложные, почти мистические объекты.

Вы привыкли видеть высказывания ученых-математиков на наших уроках, я предлагаю вам прочитать четверостишье русского писателя Валерия Яковлевича Брюсова о числах.

(Презентация «Комплексные числа». Приложение.)

Слайд 3 «Девиз урока».

Вам поклоняюсь, вас желаю, числа!
Свободные, бесплотные как тени,
Вы радугой связующей повисли
К раздумиям с вершины вдохновенья!
Валерий Яковлевич Брюсов (русский писатель 1873-1924).

Учитель: Как появилось понятие комплексные числа, и кто из ученых работал в этой области математики?

Слайд 4 «Историческая справка».

Итальянский математик Джерсламс Кардано (1501-1576), решая задачу о представлении числа 10 в виде суммы двух слагаемых так, чтобы произведение этих слагаемых равнялось 40, встретился с ситуацией, что система не имеет действительных решений. Величины, квадрат которых равен отрицательному числу Кардано назвал «софически отрицательными», считал, что они лишены всякого реального содержания. Писал: «Для осуществления таких действий нужна была бы новая арифметика, которая была бы настолько же утонченной, насколько бесполезной».

Слайд 5 «Основатели теории комплексных чисел».

Бомбелли — итальянский алгебраист в 1572г. ввёл правила арифметических действий.

Р. Декарт — французский математик и философ в 1637г. Дал название «мнимые числа».

Эйлер-русский математик, швейцарец по происхождению, ввёл символ i , а в 1748г. нашел формулу, носящую теперь его имя.

из формулы получается таинственное равенство единения арифметики, алгебры, геометрии и анализа.

К.Гаусс в 1799г. доказал основную теорему алгебры, в 1831г. предложил геометрическую интерпретацию, независимо от него датчанином Весселем (1797) и французом Аргоном (1806) предложено геометрическое толкование комплексных чисел.

Начиная с XIX века, и позже применение комплексных чисел значительно возросло.

Софья Ковалевская решила, используя теорию функции комплексного переменного, задачу о вращении твердого тела вокруг неподвижной точки.

Русский ученый в области механики, основоположник современной гидродинамики Николай Егорович Жуковский, вывел формулу для определения подъемной силы крыла, которая теперь носит его имя.

Учитель: Какие термины встречаются при изучении темы?

Слайд 6 «Словарь терминов».

Комплексный-лат. составной, сложный. Термин введён Гауссом.
i — первая буква французского слова imaginaire, мнимый.
Инверсия, inversio — лат. переворачивание, перестановка.

Учитель:
Продумаем план проведения урока. Что вы предлагаете повторить по теме?
Какие вопросы вас интересуют? Что, по вашему мнению, требует углубления?
Какие виды контроля считаете наиболее рациональными на этом уроке?

После обсуждения учащиеся знакомятся с предполагаемым планом.

Слайд 7 «Цели урока и план работы на уроке»

1 этап — повторение вопросов теории.
2 этап — вычислительная работа.
3 этап — практическая работа, выход на новый материал.
4 этап – итоговый контроль.

Учитель: Вы согласны, что эти этапы необходимы?

II. Работа с теоретическим материалом

Учитель: Вы готовились к теоретическому зачету. Проверьте себя. Работайте устно в парах. Основные формулы и теоремы записывайте в тетради.

Слайд 8 «Этап 1.1. Повторение вопросов теории».

1) Сформулируйте определение комплексного числа.
2) Как изображается комплексное число на плоскости?
3) Как вычислить модуль комплексного числа?
4) Что называется аргументом?
5) В каких границах заключен главный аргумент?
6) Как записать число в тригонометрической форме?
7) Какое число называется сопряженным? Свойство сопряженных чисел?
8) Запишите теоремы о модуле и аргументе
9) Формула Муавра для Z в степени n.

Проводится проверка и коррекция ошибок.

Слайд 9 «Этап 1.2.Основные определения».

Число вида z=a+bi называется комплексным, а и b-действительные числа, i-мнимая единица Re z=a, Im z=b

Модулем комплексного числа называется

Аргументом комплексного числа z называется угол между положительным направлением полуоси ОХ и радиус-вектором ОМ, М(а,b)

Главный аргумент arg z заключен в границах

Тригонометрическая форма комплексного числа

Слайд 10 «Этап 1.3.Основные формулы».

III. Вычислительный практикум

Учитель: Проверим, как вы умеете применять формулы. В какой форме удобнее выполнять задание (алгебраической или тригонометрической)? Запишите только номер задания и ответ.

Слайд 11 «Этап 2.1. Вычислительная работа».

Выполните действия, ответы запишите в тетрадь.

1) (3+2i)+3(-1+3i)

2) i-2-(6-5i)

3) (1+i)(1-i)

4) i³, i¹⁰¹

5) 3/i

6) (1 +i)⁴

Разложите на множители в комплексных числах:

7) x² + 1, 8) a² + 4b², 9) x⁴ — 16

Выполните самопроверку.

Слайд 12 «Этап 2.2. Проверь себя!»

1) 11i

2) -8+6i

3) 2

4) –i, I

5) -3i

6) -4

7) (x-i)(x+i)

8) (a+2bi)(a-2bi)

9) (x-2)(x+2)(x-2i)(x+2i)

Учитель: Работаем с тригонометрической формой комплексного числа. Как изображается комплексное число?

Слайд 13 «Этап 2.3. Тригонометрическая форма комплексного числа».

Изобразите комплексное число на плоскости z=-2+2i

Запишите данное число в тригонометрической форме.

Выполняется проверка с помощью режима интерактивной доски, вызывается ученик со своим решением.

Проанализируйте, как изображение комплексного числа помогает при решении задачи?

Какие варианты ответов? Кто не согласен с ответом? Какие дополнения, уточнения?

Слайд 14 «Этап 2.4. Решите задачу различными способами в алгебраической и тригонометрической форме»

Найдите z⁶, если

В режиме интерактивной доски рассматриваются решения учащихся. Для тех, кто затрудняется, предлагается следующий слайд.

Слайд 15 «Этап 2.5. Указания к решению».

1 способ

Если z=x+iy, то получаем уравнение 3x+3yi-x+yi=-4+8i, x+2yi=-2+4i,

Используем условие равенства комплексных чисел, получаем, что х=-2, у=2.

При возведении в квадрат, получаем число -8i, которое возводим в куб.

Ответ: 512i

2 способ

Представленное в тригонометрической форме число возвести по формуле Муавра в 6-ю степень.

Учитель: Какие этапы плана выполнили? Что еще необходимо повторить? (Построение ГМТ, удовлетворяющих заданным условиям) Вернемся к слайду 7.

IV. Выход на новый материал

Учитель: Выполните практическую работу в тетради (с обоснованием построения).

Слайд 16 «Этап 3.1.Геометрическое место точек»

Изобразите на плоскости ГМТ, удовлетворяющих условиям:

Учитель оказывает индивидуальную помощь.

Фронтальное обсуждение результатов практической работы с использованиемрежима интерактивной доски. (Учитель может заранее приготовить варианты построений, но без нумерации. Ребята выбирают правильные решения.)

Итак, проверьте правильность выполненных построений.

Слайд 17 «Этап 3.2.1. Полученные ГМТ»

№1. Окружность с центром (0;-1) и радиусом 1,5

№2. Полуплоскость

№3. Угол, заключенный между заданными лучами.
№4. Прямые у=х и у=-х.
№5. Точки, расположенные в вершинах правильного 6-тиугольника с центром (0;0).

Модуль равен 1. Простейший аргумент

Учитель: У кого возникли затруднения? Кому нужна помощь, консультация? Предлагаю подробное решение задач.

Слайд 18 «Этап 3.2.2. Решения задач».

V. Освоение нового материла

Слайд 19 «Этап 3.3. Функции комплексного переменного».

Задайте условиями четверть круга с центром в точке (0;0), радиусом 2.

Выполните преобразования и постройте ГМТ w, удовлетворяющее условию:

Выполните:

I вариант — а, в, д
II вариант — б, г, д.

В режиме интерактивной доски проводится проверка всех заданий.

Учитель: Какие виды геометрических преобразований использовали при решении задач?

Слайд 20 «Этап 3.4.1.Решения задач».

Слайд 21 «Этап 3.4.2.Решения задач».

Внутренние точки переходят во внешние, штриховка фигуры.
Такое преобразование называется инверсией.

Выводы учащихся: выполняли преобразования — параллельный перенос; гомотетия; поворот.

Встретился и новый вид — преобразование инверсия, что в переводе с латинского, переворачивание, перестановка.

VI. Контрольный элемент

Слайд 22 «Этап 4.1. Итоговый тест. Проверь себя! («да» или «нет»)»

1. Число 1+i является действительным?
2. -2(cos90 0+i sin90 0)-является тригонометрической формой комплексного числа?
3. Многочлен (х+4) можно разложить на множители в комплексных числах?
4. Если комплексное число равно своему сопряженному, то оно является действительным?

Число

имеет аргумент равный

Проверка решения учащимися. Тетради сдаются учителю.

Слайд 23 «Этап 4.2. Ответы»

1. Нет

2. Нет

3. Да

4. Да

5. Нет

VII. Итог урока

Слайд 7 «Цели урока и план работы на уроке».

Учитель: Удалось ли реализовать цели данного урока? Что узнали нового? Что не совсем получилось?

На основании геометрической интерпретации применение комплексных чисел эффективно в тех областях, где приходится оперировать с величинами, которые можно представить в виде точки на плоскости или плоского вектора. Поэтому теория функции комплексного переменного нашла широкое употребление для решения вопросов теоретической физики, гидродинамики, электротехники, кораблестроения, картографии.

Те из вас, кто продолжит свое образование в технических вузах, смогут глубже ознакомиться с теорией функции комплексного переменного и её приложениями в различных областях науки и техники.

Спасибо за урок.

Комплексные числа для чайников

Не занимайтесь комплексными числами после комплексного обеда

На данном уроке мы познакомимся с понятием комплексного числа, рассмотрим алгебраическую, тригонометрическую и показательную форму комплексного числа. А также научимся выполнять действия с комплексными числами: сложение, вычитание, умножение, деление, возведение в степень и извлечение корня. Не беспокойтесь, я вас напугал, я вас и рассмешу. Для освоения комплексных чисел не требуется каких-то специальных знаний из курса высшей математики, и материал доступен даже школьнику. Достаточно уметь выполнять основные алгебраические действия с «обычными» числа, и немного рубить в тригонометрии, впрочем, если что забылось, я напомню.

Урок состоит из следующих параграфов: 1) Понятие комплексного числа. 2) Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел. 3) Тригонометрическая и показательная форма комплексного числа. 4) Возведение комплексных чисел в степень. 5) Извлечение корней из комплексных чисел.

На любой вкус и цвет – кому, что интересно. А комплексные числа действительно становятся наиболее интересной темой, после того, как студенты знакомятся с другими разделами высшей алгебры =). Если Вы являетесь чайником, или только-только приступили к изучению комплексных чисел, то параграфы лучше прочитать по порядку, без «перескоков».

Сначала вспомним «обычные» школьные числа. В математике они называются множеством действительных чисел и обозначаются буквой (в литературе, рукописях заглавную букву «эр» пишут жирной либо утолщённой). Все действительные числа сидят на знакомой числовой прямой:

Компания действительных чисел очень пёстрая – здесь и целые числа, и дроби, и иррациональные числа. При этом каждой точке числовой обязательно соответствует некоторое действительное число.

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве. Если хотите, комплексное число – это двумерное число. И курить бессмысленно. … Так, кто тут улыбается? Видимо, действительно не помогло.

Комплексным числом называется число вида , где и – действительные числа, – так называемая мнимая единица. Число называется действительной частью ()комплексного числа , число называется мнимой частью () комплексного числа .

– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости: Как упоминалось выше, буквой принято обозначать множество действительных чисел.Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей: – действительная ось – мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать размерность, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа: , , , , , , ,

По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии. Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел является подмножеством множества комплексных чисел .

Числа , , – это комплексные числа с нулевой мнимой частью.

Числа , , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому-что они сливаются с осями.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились, – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность: Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Комплексные числа

Комплексный номер

Комплексное число представляет собой комбинацию
Действительного числа и Воображаемого числа

Реальные числа — это такие числа, как:

12,38

−0,8625

3/4

√2

1998

Почти любое число, которое вы можете придумать, является действительным числом!

Мнимые числа, когда в квадрате дают отрицательный результат .

Обычно этого не происходит, потому что:

когда мы возводим в квадрат положительное число, мы получаем положительный результат, а
, когда мы возводим в квадрат отрицательное число, мы также получаем положительный результат (поскольку отрицательное число, умноженное на отрицательное, дает положительный результат), например, −2 × −2 = +4

Но представьте, что такие числа существуют, потому что они нам нужны.

Поговорим еще о мнимых числах…

«Единичное» мнимое число (например, 1 для действительных чисел) равно i, которое является квадратным корнем из −1

Потому что, возведя i в квадрат, мы получим −1

i ² = −1

Примеры мнимых чисел Номера:

1.04i

−2,8i

3i/4

(√2)я

1998i

И мы держим здесь маленькую букву «i», чтобы напомнить себе, что нам нужно умножить на √−1

Комплексные числа

Когда мы объединяем действительное число и мнимое число, мы получаем комплексное число :

Примеры:

1 + я

39 + 3i

0,8 − 2,2i

−2 + πi

√2 + i/2

Может ли число быть комбинацией двух чисел?

Можем ли мы составить число из двух других чисел? Мы можем точно!

Мы постоянно делаем это с дробями. Дробь ³ / ₈ — это число, состоящее из 3 и 8. Мы знаем, что это означает «3 из 8 равных частей».

Комплексное число — это всего лишь два числа, сложенные вместе (действительное и мнимое число).

Любая часть может быть равна нулю

Итак, у комплексного числа есть действительная и мнимая части.

Но любая часть может быть 0 , поэтому все действительные числа и мнимые числа также являются комплексными числами.

Комплексный номер	Реальная часть	Воображаемая часть
3 + 2i	3	2
5	5	0	Чисто настоящий
−6i	0	−6	Чисто воображаемый

Сложно?

Комплекс , а не означает сложный.

Это означает, что два типа чисел, действительные и мнимые, вместе образуют комплекс , точно так же, как комплекс зданий (здания, соединенные вместе).

Визуальное объяснение

Вы знаете, как идет числовая линия влево-вправо ?

Хорошо, пусть мнимые числа идут вверх-вниз :

И получаем Сложный Самолет

Комплексное число теперь может отображаться в виде точки:

Комплекс № 3+4 i

Добавление

Чтобы сложить два комплексных числа, складываем каждую часть отдельно:

(а+б я ) + (с+г я ) = (а+с) + (б+г) я

Пример: добавьте комплексные числа

3 + 2 i и 1 + 7 i

добавьте действительные числа и
добавить мнимые числа:

(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7) i
= 4 + 9i

Попробуем еще:

Пример: добавьте комплексные числа

3 + 5 i и 4 − 3 i

(3 + 5 I ) + (4 — 3 I )
= 3 + 4 + (5 — 3) I
= 7 + 2 I

. На комплексной плоскости это:

Умножение

Чтобы умножить комплексные числа:

Каждая часть первого комплексного числа умножается на
каждая часть второго комплексного числа

Просто используйте «FOIL», что означает » F первоначальных, O маточных, I внутренних, L астровых» (подробнее см. Биномиальное умножение):

Первые: a × c
Внешний: a × d i
Внутренние: b i × c
Колодки: b i × d i

(A + B I ) (C + D I ) = AC + AD I + BC I + BD I ² 9006 I ²

I ² I ²

Вот так:

Пример: (3 + 2i)(1 + 7i)

(3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i

= 3 + 21i + 2i + 14i ²

= 3 + 21i + 2i − 14 (поскольку i ² = −1)

= −11 + 23i

А это:

Пример: (1 + i)

(1 + i)(1 + i)= 1×1 + 1×i + 1×i + i ²

= 1 + 2i − 1 (потому что i ² = −1)

= 0 + 2i

Но есть более быстрый способ!

Используйте это правило:

(a+b i )(c+d i ) = (ac−bd) + (ad+bc) i

Пример: (3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i

Почему это правило работает?

Это просто метод «ФОЛЬГА» после небольшой работы:

(a+b i )(c+d i ) =ac + ad i + bc i + bd i ² метод FOIL i i

0 i − bd (потому что i ² = −1)

= (ac − bd) + (ad + bc) i (собирая подобные термины)

И здесь у нас есть (ac − bd) + (ad + bc) i шаблон.

Это правило, безусловно, быстрее, но если вы его забудете, просто запомните метод FOIL.

Попробуем i

²
Ради интереса воспользуемся методом вычисления i ²
Пример: i
²
Мы можем записать i с действительной и мнимой частями как 0 + i
i ² = (0 + i) ²
= (0 + i)(0 + i )
= (0×0 − 1×1) + (0×1 + 1×0) i
= −1 + 0 i
= −1
И это хорошо согласуется с определением, что я ² = −1
Так все замечательно работает!
Дополнительные сведения см. в разделе Умножение комплексных чисел.
Конъюгаты
Через минуту нам нужно будет узнать о конъюгатах!
В сопряжении мы меняем знак в середине следующим образом:
Спряжение часто пишется с чертой над ним:
Пример:
5 − 3 i = 5 + 3 i
Разделение
Конъюгат используется для облегчения сложного деления.
Хитрость заключается в том, чтобы умножить верхнее и нижнее на сопряженное нижнее .
Пример: Do This Division:
2 + 3 I 4 — 5 I

Умножение верхней и нижней 4 − 5 i × 4 + 5 i 4 + 5 I = 8 + 10 I + 12 I + 15 I ² 16 + 20 I — 20 I — 25 I 666995595959559559559559559559559595959595959595959595959595959595959595959595959595959595959595959595959595959595959595959595959595959н.

Теперь помните, что I ² = −1, так:

= 8 + 10 I + 12 I — 15 16 + 200009 I — 20 I + 25 9000

Добавьте условия «Нравится» (и обратите внимание, как внизу 20 i − 20 i Отменить!):

= −7 + 22 I 41

Наконец, мы должны поместить ответ в A + B I Форма:

= —7 41

+ — 7 41 + — 7 41 + —7 41 + —7 419 41952 + — 7 4110 41952 = —7 4110 4106. 22 41 i

ГОТОВО!

Да, нужно немного посчитать. Но это можно сделать.

Умножение на сопряженное

Однако есть более быстрый способ.

В предыдущем примере интересно было то, что произошло внизу:

(4 — 5 i )(4 + 5 i ) = 16 + 20 i — 20 i — 25 i ²

Средние члены (20 i − 20 i ) сокращаются:

(4 — 5 i )(4 + 5 i ) = 16 — 25 i ²

Также i ² = −1 :

(4 — 5 i )(4 + 5 i ) = 16 + 25

А 16 и 25 — это (магически) квадраты 4 и 5:

(4 — 5 i )(4 + 5 i ) = 4 ² + 5 ²

Довольно простой результат. Общее правило:

(a + b i ) (a − b i ) = a ² + b ²

Это может сэкономить нам время при делении, например:

Пример: попробуем еще раз

2 + 3 i 4 − 5 i

Умножить верх и низ на сопряженное число 4 − 5 I :

2 + 3 I 4 — 5 I × 4 + 5 I 4 + 5 + = 8 + 10999999999999

11110 = 8 + 109. 199999999999

10 . I + 15 I ² 16 + 25

= −7 + 22 I 41

, а затем обратно в A + B I :

9 40002 = = = = x = x . 7 41 + 22 41 я

ГОТОВО!

Обозначение

Мы часто используем z для комплексного числа. И Re() для действительной части и Im() для мнимой части, например:

Что выглядит на комплексной плоскости так:

Набор Мандельброта

Прекрасное множество Мандельброта (на фото) основано на комплексных числах.

Это график того, что происходит, когда мы берем простое уравнение z ² + c (оба комплексных числа) и возвращаем результат обратно в z снова и снова.

Цвет показывает, как быстро растет z ² + c , а черный означает, что он остается в определенном диапазоне.

Вот изображение, полученное путем увеличения множества Мандельброта

А вот центр предыдущего увеличен еще больше:

440, 1070, 273, 1071, 1072, 443, 3991, 271, 3992, 3993

комплексных чисел | Brilliant Math & Science Wiki

Энди Хейс, Рам Мохит, Тадеуш Абий, а также

способствовал

Содержимое

Сложный самолет
Воображаемая единица III
Арифметика комплексных чисел
Комплексные конъюгаты
Гауссовские целые числа
Комплексный модуль и аргумент
Сложные корни
Формула Эйлера
Корни единства
Комплексные числа в геометрии
Приложения в физике
Множество Мандельброта

Основная статья: Сложный самолет

Комплексные числа часто представляются на комплексной плоскости , иногда известной как плоскость Аргана или диаграмма Аргана . В комплексной плоскости имеется действительных осей и перпендикуляр мнимой оси . Комплексное число a+bia+bia+bi изображается на этой плоскости точно так же, как упорядоченная пара (a,b)(a,b)(a,b) изображается на плоскости декартовых координат. Действительная ось соответствует оси xxx, а воображаемая ось соответствует оси yyy.

Комплексные числа, изображенные на комплексной плоскости

Основное преимущество комплексных чисел перед упорядоченными парами заключается в том, что операции сложения и умножения определены для комплексных чисел, тогда как эти операции не определены для упорядоченных пар.

В комплексном числе Z = a + ib, Z = a + ib, Z = a + ib,

Z = a⏟partreal+i⏟unitimaginaryb⏟partimaginary.Z = \underbrace{a} _{\overset{ \text{real}}{\text{part}}} + \underbrace{i}_{\overset{\text{воображаемый}}{\text{единица}}} \underbrace{b}_{\overset{\ text{воображаемый}}{\text{part}}}. Z=partreala+unitimaginaryipartimaginaryb.

Здесь iii называется мнимой единицей , и математически его значение равно i=−1.i = \sqrt{-1}.i=−1.

В этом разделе мы обсудим некоторые важные свойства i:i:i: 9{200}\big).(11+12+i3+i4)+(i5+i6+i7+i8)+⋯+(i193+i194+i195+i196)+(i197+i198+i199+i200).

Теперь, исходя из приведенного выше результата, значение в каждой скобке становится равным 000 как сумма 4 последовательных степеней iii, равная 000. Имеется 50 скобок, и каждая скобка равна 0.

Следовательно, 50(0)=0. □50(0)=0.\ _\квадрат50(0)=0. □

Сложение комплексных чисел следует алгебраическому принципу объединения одинаковых терминов. Действительные части комплексных чисел считаются одинаковыми, а комплексные части считаются одинаковыми.

Добавление комплексных номеров:
Даны комплексные числа a+bi a + bi a+bi и c+di c+di c+di, их сумма равна
(а+с)+(б+г)я. (а+в) + (б+г)я. (а+в)+(б+г)я.

Что такое (4+3i)+(2+2i)?(4+3i)+(2+2i)?(4+3i)+(2+2i)?
Складывая по отдельности действительную и мнимую части, получаем
4+3i+2+2i=(4+2)+(3+2)i=6+5i. □ 4+3i+2+2i = (4+2) + (3+2)i = 6+5i.\ _\square4+3i+2+2i=(4+2)+(3+2)i= 6+5и. □

Обратите внимание, что действительные числа добавлялись только к другим действительным числам, а мнимые числа добавлялись только к другим мнимым числам.

Несколько дополнительных примеров:

(3−4i)+(3+2i)=6−2i(3-4i)+(3+2i) = 6-2i(3−4i)+(3+2i) )=6−2i
(4−2i)−(−2−5i)=6+3i(4-2i)-(-2-5i) = 6+3i(4−2i)−(−2−5i)=6+3i
(3i)+(3+5i)=3+8i(3i)+(3+5i) = 3+8i(3i)+(3+5i)=3+8i

Умножение комплексных чисел следует принципу умножения биномов. Одно заметное отличие состоит в том, что при умножении мнимых членов получается действительное число. 92\\ &= (ac) + (ad+bc)i + (bd)(-1) \\ &= (ac — bd) + (ad+bc)i . \end{выровнено} (a+bi)×(c+di)=a(c+di)+bi(c+di)=(ac)+(ad)i+(bc)i+(bd)i2=( ac)+(ad+bc)i+(bd)(-1)=(ac-bd)+(ad+bc)i. 4?i2+i6+i4? 92-2х+5\большой)\левый(х+4\правый) + 7х + 5\\ &= 0 \cdot (x+4) + 7x +5 \qquad \qquad \qquad \big(\text{by}(1)\big) \\ &= 7(1+2i) + 5 \\ &= 12 + 14i. \ _\площадь \end{выровнено} x3+2×2+4x+25=(x2−2x+5)(x+4)+7x+5=0⋅(x+4)+7x+5(by (1))=7 (1+2i)+5=12+14i. □

Отдел комплексных номеров:
Если Z1=a+ibZ_1 = a + ibZ1=a+ib и Z2=c+idZ_2 = c + idZ2=c+id — любые два комплексных числа, то деление двух комплексных чисел выполняется простым рационализаторством комплекс номер или умножение и деление на сопряженное число знаменателя .
Это обсуждается в следующем разделе.

Основная статья: Комплексные конъюгаты

Комплексное сопряжение комплексного числа a+bia+bia+bi есть a-bia-bia-bi.

Назовите комплексно-сопряженные числа следующих чисел:
Их комплексные сопряжения следующие:
−5+6i ⟹ −5−6i-5+6i \ подразумевает -5-6i−5+6i⟹−5−6i
83−i ⟹ 83+i\frac{8}{3}-i \подразумевает \frac{8}{3}+i38−i⟹38+i
−2i ⟹ 2i:-2i \ подразумевает 2i:−2i⟹2i: комплексное сопряжение мнимого числа есть отрицание этого числа.
17 ⟹ 17:17 \подразумевает 17:17⟹17: комплексно-сопряженным вещественным числом является само число. □_\квадрат□

Комплексное сопряжение также можно рассматривать как отражение комплексного числа относительно действительной оси на комплексной плоскости.

Комплексно-сопряженные пары на комплексной плоскости

Комплексно-сопряженные пары полезны для рационализации знаменателей, содержащих комплексные числа. Процесс рационализации сложного знаменателя очень похож на то, как этот процесс работает для радикалов.

Рационализируйте знаменатель и запишите в стандартной форме:
3+2i5−2i.\frac{3+2i}{5-2i}.5−2i3+2i.
Сопряжение знаменателя равно 5+2i.5+2i.5+2i. Умножьте числитель и знаменатель на это число:
3+2i5−2i=(3+2i)(5+2i)(5−2i)(5+2i)=11+16i29=1129+1629i. □\begin{выровнено} \frac{3+2i}{5-2i} &= \frac{(3+2i)(5+2i)}{(5-2i)(5+2i)} \\ \\ &= \frac{11+16i}{29} \\ \\ &= \frac{11}{29}+\frac{16}{29}i. \ _\квадрат \end{align}5−2i3+2i=(5−2i)(5+2i)(3+2i)(5+2i)=2911+16i=2911+2916i. □

Кроме того, теорема о комплексно-сопряженных корнях утверждает, что комплексные корни многочленов всегда входят в сопряженные пары.

Теорема о комплексно-сопряженном корне: 92-2х+2, \end{выровнено}x2+bx+c=(x−1−i)(x−1+i)=x2−2x+2,
, что подразумевает b=-2b=-2b=-2 и c=2,c=2,c=2, поэтому b+c=0.b+c=0.b+c=0. □_\квадрат□

Если ∣z1∣=∣z2∣=∣z3∣=…=∣zn∣=1,\left|z_1\right|=\left|z_2\right|=\left|z_3\right|=\ldots=\left |z_n\right|=1,∣z1∣=∣z2∣=∣z3∣=…=∣zn∣=1, то докажите, что
∣1z1+1z2+1z3+⋯+1zn∣=∣z1+z2+z3+⋯+zn∣.\left|\frac{1}{z_1}+\frac{1}{z_2}+\frac{1}{ z_3}+\cdots+\frac{1}{z_n}\right|=\left|z_1+z_2+z_3+\cdots+z_n\right|.∣∣∣∣z11+z21+z3 1+⋯+zn1∣∣∣∣=∣z1+z2+z3+⋯+zn∣. 92&=1 \\\\ z_1\overline{z_1}=1, z_2\overline{z_2}=1, z_3\overline{z_3}=1, \ldots, z_n\overline{z_n}&=1\\\\ \frac{1}{z_1}=\overline{z_1}, \frac{1}{z_2}=\overline{z_2}, \frac{1}{z_3}=\overline{z_3}, \ldots, \frac {1}{z_n}&=\overline{z_n}\\\\ \влево| \frac{1}{z_1}+ \frac{1}{z_2}+ \frac{1}{z_3}+ \cdots+\frac{1}{z_n}\right|&=\left|\overline{z_1} + \overline{z_2}+ \overline{z_3}+ \cdots+\overline{z_n}\right|\\\\ &=\left|\overline{z_1+ z_2+z_3+ \cdots+z_n}\right|\\\\ &=\влево|z_1+ z_2+z_3+ \cdots+z_n\вправо| \qquad \big(\text{с} \left|\overline{z}\right|=\left|z\right|\big)\\\\ \Стрелка вправо\влево| \frac{1}{z_1}+ \frac{1}{z_2}+ \frac{1}{z_3}+ \cdots+\frac{1}{z_n}\right|&=\left|z_1+ z_2+z_3+ \ cdots+z_n\справа|. \ _\квадрат \end{выровнено}∣z1∣=∣z2∣=∣z3∣=…=∣zn∣∣z1∣2=∣z2∣2=∣z3∣2=…=∣zn∣ 2z1z1=1,z2z2=1,z3z3=1,…,znznz11=z1,z21=z2,z3 1=z3,…,zn1∣∣∣∣z11+z21+z31+⋯+zn1∣∣∣∣⇒∣∣∣∣ z11+z21+z31+⋯+zn1∣∣∣∣=1=1=1=zn=∣z1+z2+z3 +⋯+zn∣=∣z1+z2+z3+⋯+zn∣=∣z1+z2+z3+⋯+zn∣(поскольку ∣z∣=∣z∣ )=∣z1+z2+z3+⋯+zn∣. □

Основная статья: Гауссовы целые числа

Гауссово целое число — это комплексное число a+bi,a+bi,a+bi, где aaa и bbb — целые числа. Следует отметить, что целое число Гаусса равно , а не , если мнимая часть не равна 0.

Целые числа Гаусса:
3+2i3+2i3+2i
7-8i7-8i7-8i
141414
−92i-92i−92i
Негауссовские целые числа:

Гауссовы целые числа представляют интерес в теории чисел, потому что проблемы квадратичной, кубической и четвертой взаимности удобнее формулировать как задачи о гауссовских целых числах.

Основная статья: Комплексные числа — абсолютные значения
См. также: Преобразование декартовых координат в полярные

Следует отметить, что процесс нахождения модуля и аргумента комплексного числа почти идентичен процессу преобразования декартовых координат в полярные координаты.

Абсолютное значение действительного числа определяется как положительное расстояние от 0 до этого числа. Точно так же определяется абсолютное значение комплексного числа, за исключением того, что это расстояние измеряется на комплексной плоскости.

Поскольку отрезок, соединяющий 0 с комплексным числом, является гипотенузой прямоугольного треугольника, расстояние до этого отрезка вычисляется по теореме Пифагора. Это расстояние иногда называют .2}=5.\ _\квадрат∣−3+4i∣=(−3)2+42=5. □

Угол, который положительная вещественная ось образует с лучом, соединяющим 000 с комплексным числом, называется аргументом этого комплексного числа. \text{nd}2-м квадранте, поэтому к этому углу следует добавить π\piπ, чтобы получить правильный аргумент: 9{-1}\left(-\frac{4}{3}\right)+\pi.\ _\squareθ=tan−1(−34)+π. □

Полный оборот комплексного числа 2π2\pi2π радиан создаст изображение, котерминальное комплексному числу. Поэтому каждое комплексное число имеет бесконечно много аргументов.

Если θ\thetaθ является аргументом комплексного числа, то θ+2kπ\theta+2k\piθ+2kπ также является аргументом этого комплексного числа, где kkk — целое число.

Основная статья: Основная теорема алгебры 92 — 4\times1\times10 = -4 .D=b2−4ac=62−4×1×10=−4.
Это меньше 000 и, таким образом, мы можем заключить, что квадратичный имеет пару комплексных корней с мнимыми компонентами. Чтобы их найти, воспользуемся квадратичной формулой следующим образом:
x=-b±D2a=-6±-42×1=-6±2-12=-3±i.\begin{выровнено} х &= \frac{ -b \pm \sqrt{D}}{2a} \\ & = \frac{-6 \pm \sqrt{-4}}{ 2 \times 1} \\ & = \frac{-6 \pm 2\sqrt{-1}}{2} \\ &=-3 \pm i . \end{выровнено}x=2a−b±D=2×1−6±−4=2−6±2−1=−3±i.
92 — 4\х3\х7 = -109. D=b2-4ac=(5i)2-4×3×7=-109.
Это действительно меньше 000, и, таким образом, мы можем заключить, что квадратное число имеет пару комплексных корней. Чтобы их найти, воспользуемся квадратичной формулой следующим образом:
x=-b±D2a=-5i±-1092×3=-5i±109-16.\begin{выровнено} х &= \frac{ -b \pm \sqrt{D}}{2a} \\ &= \frac{-5i \pm \sqrt{-109}}{ 2 \times 3} \\ &= \frac{-5i \pm \sqrt{109} \sqrt{-1}}{6}. \end{выровнено} x=2a−b±D=2×3−5i±−109=6−5i±109−1.
Таким образом, корней
x=(−5−1096)iandx=(−5+1096)i. □\begin{array}{c}&x =\left (\frac{-5-\sqrt{109}}{6}\right)i &\text{and} &x = \left(\frac{-5+) \sqrt{109}}{6}\right)i .\end{массив} \ _\squarex=(6−5−109)iandx=(6−5+109) я. □

Основная статья: Формула Эйлера
См. также: Теорема Муавра.

Форма a+bia+bia+bi известна как стандартная форма комплексного числа. Формула Эйлера позволяет представить комплексное число в экспоненциальной форме. 9n \right \}A={(21+3i)n} — набор комплексных чисел, где nnn — целое положительное число. Сколько различных элементов в множестве A?A?A?

Основная статья: Комплексные числа в геометрии

Из-за круговых отношений, связанных с комплексными числами, они полезны для многих задач геометрии. Например, вращение точки или твердой фигуры можно выполнить с помощью комплексных чисел гораздо проще, чем это можно сделать с помощью тригонометрии.

Чтобы повернуть точку θ\thetaθ радиан против часовой стрелки вокруг начала координат, 9{\pi i/6}=\frac{\sqrt{3}}{2}+\frac{i}{2}.eπi/6=23+2i.
Умножьте эти комплексные числа, чтобы получить изображение вращения:
(2+5i32)(32+i2)=3−52+i(1+532).\влево(2+5i\vphantom{\frac{\sqrt{3}}{2}}\вправо)\влево (\ frac {\ sqrt {3}} {2} + \ frac {i} {2} \ right) = \ sqrt {3} — \ frac {5} {2} + i \ left (1+ \ frac { 5\sqrt{3}}{2}\right).(2+5i23)(23+2i)=3−25+i(1+253).
Соответствующая упорядоченная пара: (3−52, 1+532). \left(\sqrt{3}-\frac{5}{2},\ 1+\frac{5\sqrt{3}}{2} \справа).(3−25, 1+253). □_\квадрат□

Есть несколько других применений комплексных чисел в геометрии на вики-странице по этой теме.

Цитировать как: Комплексные числа. Brilliant.org . Извлекаются из https://brilliant.org/wiki/complex-numbers/

Комплексное число — определение, формула, свойства, примеры

Комплексные числа помогают найти квадратный корень из отрицательных чисел. Концепция комплексных чисел была впервые упомянута в I веке греческим математиком Героем Александрийским, когда он пытался найти квадратный корень из отрицательного числа. Но он просто изменил отрицательное значение на положительное и просто взял числовой корень. Кроме того, реальная идентичность комплексного числа была определена в 16 веке итальянским математиком Джероламо Кардано в процессе нахождения отрицательных корней кубических и квадратичных полиномиальных выражений.

Комплексные числа находят применение во многих научных исследованиях, обработке сигналов, электромагнетизме, гидродинамике, квантовой механике и анализе вибрации. Здесь мы можем понять определение, терминологию, визуализацию комплексных чисел, свойства и операции с комплексными числами.

1.	Что такое комплексные числа?
2.	График комплексных чисел
3.	Свойства комплексных чисел
4.	Операции над комплексными числами
5.	Алгебраические тождества комплексных чисел
6.	Решенные примеры
7.	Практические вопросы
8.	Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа?

Комплексное число – это сумма действительного числа и мнимого числа. Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом.

Примерами комплексных чисел являются $2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2$ и т. д.

Степень of i

Алфавит i называется йотой и полезен для представления мнимой части комплексного числа. Кроме того, йота (i) очень полезна для нахождения квадратного корня из отрицательных чисел. У нас есть значение i ² = -1, и оно используется для нахождения значения √-4 = √i ² 4 = 9. 1613 + 2i Значение i ² = -1 является основным аспектом комплексного числа. Давайте попробуем понять больше о возрастающих силах i.

я = √-1
i ² = -1
i ³ = i.i ² = i(-1) = -i
i ⁴ = (i ² ) ² = (-1) ² = 1
i ⁴ⁿ = 1
i ^{4n + 1} = i
i ^{4n + 2} = -1
i ^{4n + 3} = -i

График комплексных чисел

Комплексное число состоит из действительной и мнимой частей, которые можно рассматривать как упорядоченную пару (Re(z), Im(z)) и представлять в виде точек координат на евклидовой плоскости. Евклидова плоскость применительно к комплексным числам называется комплексной плоскостью или Плоскостью Аргана, названной в честь Жана-Роберта Аргана. Комплексное число z = a + ib представлено действительной частью — a относительно оси x и мнимой частью -ib относительно оси y. {-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)).

Свойства комплексного номера

Следующие свойства комплексных чисел помогают лучше понять комплексные числа, а также выполнять различные арифметические операции над комплексными числами.

Сопряжение комплексного числа

Сопряжение комплексного числа образуется путем взятия той же действительной части комплексного числа и замены мнимой части комплексного числа на ее аддитивную обратную. Если сумма и произведение двух комплексных чисел являются действительными числами, то они называются сопряженными комплексными числами. Для комплексного числа z = a + ib его сопряженным является $\bar z$ = a — ib.

Сумма комплексного числа и его сопряженного равна $z + \bar z$ = (a + ib) + (a — ib) = 2a, а произведение этих комплексных чисел $z.\bar z $ = (a + ib) × (a — ib) = a ² + b ² .

Обратная величина комплексного числа

Обратная величина комплексных чисел полезна в процессе деления одного комплексного числа на другое комплексное число. {-1}\).

Равенство комплексных чисел

Равенство комплексных чисел аналогично равенству действительных чисел. Два комплексных числа $z_1 = a_1 + ib_1$ и $z_2 = a_2 + ib_2 $ называются равными, если относительная часть обоих комплексных чисел равна $a_1 = a_2$, и мнимая части обоих комплексных чисел равны $b_1 = b_2 $. Кроме того, два комплексных числа в полярной форме равны тогда и только тогда, когда они имеют одинаковую величину, а их аргумент (угол) отличается на целое кратное 2π.

Упорядочивание комплексных чисел

Упорядочивание комплексных чисел невозможно. Действительные числа и другие связанные системы счисления можно упорядочить, но нельзя упорядочить комплексные числа. Комплексные числа не имеют структуры упорядоченного поля, и нет упорядоченности комплексных чисел, совместимой со сложением и умножением. Также нетривиальная сумма квадратов в упорядоченном поле есть число $\neq 0$, а в комплексном числе нетривиальная сумма квадратов равна i ² + 1 ² = 0. Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат.

Формула Эйлера: В соответствии с формулой Эйлера для любого действительного значения θ мы имеем e ^iθ = Cosθ + iSinθ, и оно представляет комплексное число в координатной плоскости, где Cosθ – действительная часть, представленная относительно ось x, Sinθ – мнимая часть, представленная относительно оси y, θ – угол, образованный по отношению к оси x и воображаемой линии, соединяющей начало координат и комплексное число. Согласно формуле Эйлера и функциональному представлению x и y имеем e ^{x + iy} = e ^x (уютно + isiny) = e ^x уютно + т.е. ^x сине. Это разлагает экспоненциальную функцию на ее действительную и мнимую части.

Операции над комплексными числами

Различные операции сложения, вычитания, умножения, деления натуральных чисел можно выполнять и для комплексных чисел. Детали различных арифметических операций с комплексными числами заключаются в следующем.

Сложение комплексных чисел

Сложение комплексных чисел аналогично сложению натуральных чисел. Здесь в комплексных числах действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Для двух комплексных чисел вида $z_1 = a + id$ и $z_2 = c + id$ сумма комплексных чисел $z_1 + z_2 = (a + c) + i(b + d) $. Комплексные числа следуют всем следующим свойствам сложения.

Закон замыкания: Сумма двух комплексных чисел также является комплексным числом. Для двух комплексных чисел $z_1$ и $z_2$ сумма $z_1 + z_2$ также является комплексным числом.
Коммутативный закон: Для двух комплексных чисел $z_1$, $z_2$ имеем $z_1 + z_2 = z_2 + z_1$.
Ассоциативный закон: Для данных трех комплексных чисел $z_1, z_2, z_3$ имеем $z_1 + (z_2 + z_3) = (z_1 + z_2)+z_3 $. 2 = -1\). Для двух комплексных чисел $z_1$ = a + ib, $z_2$ = c + id произведение равно $z_1.z_2$ = (ca — bd) + i(ad + bc).
Умножение комплексных чисел в полярной форме немного отличается от упомянутой выше формы умножения. Здесь абсолютные значения двух комплексных чисел перемножаются, а их аргументы складываются для получения произведения комплексных чисел. Для комплексных чисел $z_1 = r_1(Cos\theta_1 + iSin\theta_1)$ и z ₂ = $z_2 = r_1(Cos\theta_2 + iSin\theta_2)$ произведение комплексные числа $z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))$. 92 + 2z_1z_2 +2z_2z_3 +2z_3z_1\)

Связанные темы:

Комплексное сопряжение
Калькулятор комплексных чисел
Тригонометрия
Координатная плоскость
Координатная геометрия

Комплексные числа Советы и подсказки:

Все действительные числа являются комплексными числами, но не все комплексные числа должны быть действительными числами.
Все мнимые числа являются комплексными числами, но все комплексные числа не обязательно должны быть мнимыми числами. 9{2}-4(1)(1)}}{2(1)} \\[0,2 см]
&=\frac{-1 \pm \sqrt{-3}}{2}\\[0,2 см]
\text{Здесь } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0,2 см]
x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0,2 см]
\end{align} \]
Таким образом, корнями данного квадратного уравнения являются: $\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\ , \ frac{-1}{2}- i\frac{\sqrt{3}}{2}$
Пример 2: Выразите сумму, разность, произведение и частное следующих комплексных чисел в виде комплексного числа.
\[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \]
Решение:
Сумма:
\[ \begin{ выровнять} z_1+z_2&= (-2+i)+(1-2i)\\[0,2 см] &=(-2+1)+ (i-2i)\\[0,2 см] &= -1-i \end{align}\]
Разница:
\[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0,2 см] &=(-2-1) + (i+2i)\\[0,2 см] &= -3+3i \end{align}\]
Продукт:
\[ \begin{align} z_1\cdot z_2&= (-2+i)( 1-2i)\\[0,2см] &=-2+4i+i-2i^2\\[0,2см] &=-2+4i+i+2 \,\,\, [\потому что i^2 =-1]\\[0,2 см] &=5i \end{выравнивание}\] 92=-1]\\[0,2 см] &= \dfrac{-4-3i}{5}\\[0,2 см] &=- \dfrac{4}{5}- i \dfrac{3}{5 }\end{align}\]
Следовательно, имеем:
Сумма = -1 — i
Разница = -3 + 3i
Продукт = 5i
Деление = -4/5 — 3i/5

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа в математике?

Комплексное число представляет собой комбинацию действительных и мнимых значений. Обозначается z = a + ib, где a, b — действительные числа, а i — мнимое число. i = $\sqrt{-1}$ и никакое действительное значение не удовлетворяет уравнению i ² = -1, поэтому I называется мнимым числом.

Для чего используются комплексные числа?

Комплексное число используется для простого нахождения квадратного корня из отрицательного числа. Здесь мы используем значение i ² = -1 для представления отрицательного знака числа, что помогает легко найти квадратный корень. Здесь мы имеем √-4 = √i ² 4 = + 2i. {-1}\frac{b}{a} \)).

Что такое действительные и комплексные числа?

Комплексные числа являются частью действительных чисел. Некоторые действительные числа с отрицательным знаком трудно вычислить, и мы представляем отрицательный знак с помощью йоты «i», и такое представление чисел вместе с «i» называется комплексным числом. Дополнительные комплексные числа полезны для нахождения квадратного корня из отрицательного числа, а также для нахождения отрицательных корней квадратного или полиномиального выражения.

Как делить комплексные числа? 92)}\).

Как строить графики комплексных чисел?

Комплексное число вида z = a + ib может быть представлено в плоскости арганда. Комплексное число z = a + ib может быть представлено в виде координат точки как (Re(z), Im(z)) = (a, ib). Здесь действительная часть представлена относительно оси x, а мнимая часть представлена относительно оси y.

Как преобразовать комплексные числа в полярную форму?

Комплексный номер можно легко преобразовать в полярную форму. {-1}\). 9p$, когда $a$ отрицательно… Но это скрывает некоторые замечательные математические основы, в том числе и особенно странность и удивительность мнимых и комплексных чисел! Давайте познакомимся с этими математическими объектами в этой статье! Наш подход будет в высшей степени геометрическим и, я думаю, гораздо более проницательным, чем тот, которому вы научились (или будете учиться) в школе.

Геометрия $n$-го корня

Чтобы понять, что только что произошло, давайте сосредоточимся на первом равенстве, а именно на $-2 = \sqrt[3]{-8}$. Он гласит: «$-2$ — это кубический корень из $-8$». Но что это значит? 93 = x \times (-2) \times (-2) \times (-2) = x \times (-8)$. Таким образом, теперь мы можем видеть операцию «$\times (-2)$» как операцию над числами, которая при трехкратном применении эквивалентна операции «$\times (-8)$»!

Я до сих пор не знаю, куда ты клонишь…

Вот это самое интересное. Эти операции соответствуют геометрическим преобразованиям числовой прямой (это симметрии)! Например, умножение на $(-2)$ соответствует инвертированию и увеличению в 2 раза. Это то, что делается ниже три раза! 9{1/3}$ на геометрическую фразу: Трижды инвертировать числовую прямую эквивалентно ее однократному инвертированию . Сладко, не так ли?

Да! Но я все равно не вижу в этом смысла…

Хе-хе! Ключевая идея комплексных чисел заключается в следующем вопросе… Является ли $(-1)$ единственным кубическим корнем из $(-1)$?

Думаю, да… Если вы возьмете положительное число, его куб будет положительным… Таким образом, работает только число $-1$…

Не думайте числами! Весь смысл моей конструкции состоял в том, чтобы рассмотреть задачу геометрически!

Гм…

Другими словами, существует ли геометрическая операция над числовой прямой, которая при трехкратном применении соответствует ее инвертированию?

Гм…

Давай! Вы можете найти это!

Я знаю! Как насчет поворота числовой линии на 6 оборота?

Бинго!

На самом деле, есть две такие операции шестого хода, в зависимости от того, по часовой стрелке или против часовой стрелки. Ниже описаны эти две операции, каждая из которых применяется к числовой прямой трижды.

В дополнение к операции «$\times (-1)$» это дает нам всего три кубических корня из $(-1)$!

Есть ли у $(-8)$ несколько кубических корней? А как насчет 6-го корня из $64$?

Отличные вопросы! На самом деле, вы должны попытаться ответить самостоятельно!

Хм… Я думаю, кубический корень из $(-8)$ можно получить за 6-ю часть хода (например, $(-1)$) в сочетании с растяжением числовой прямой, не так ли?

Точно! Точно так же корни 6-й степени из $ 64 $ включают расширение в 2 раза в сочетании с поворотом на одну или две 6-х оборота по часовой стрелке или против часовой стрелки. Плюс еще есть операции «$\times (-2)$» и «$\times 2$». Это дает нам шесть шестых корней из $64$. И, как вы можете догадаться (или доказать!), вообще, любое число имеет $n$ $n$-го корня!

Слышал про квадратный корень из $(-1)$… Получается так же, как мы делали??

Еще раз, ты должен дать мне ответ!

Гм. ..

Другими словами, существует ли геометрическое преобразование, которое при двойном применении к числовой прямой эквивалентно простому ее обращению?

Я знаю! Вращения четверть оборота!

Ну вот! По соглашению мы называем вращение на четверть оборота против часовой стрелки как $i$. Этот $i$ настолько важен, что мы дали ему разные имена… что мне всем не нравится! Он известен как мнимое число (воображаемое? число?), квадратный корень из $(-1)$ или, что хуже всего, $\sqrt{-1}$.

Что не так с $\sqrt{-1}$?

Что очень неправильно, так это то, что $i$ не единственный квадратный корень из $(-1)$. Вращение на четверть оборота по часовой стрелке тоже является квадратным корнем из $(-1)$! Кроме того, если вы не можете написать $\sqrt[3]{-8}$, то вы точно не сможете написать $\sqrt{-1}$!

ОК… Это круто, но я не понимаю, как это решает парадокс введения!

Хе-хе… Теперь мы можем элегантно ответить на этот вопрос!

Решение парадокса

Главный недостаток заключается в неединственности $n$-го корня. Это то, что французский математик XIX века Эварист Галуа назвал неоднозначностью корней $n$-го порядка. Точнее, ни кубического корня из $(-8)$, ни уникальности корня шестой степени из $64$ не существует. В частности, $(-2)$ — это корень шестой степени из $64$, но это не тот корень, на который мы ссылаемся через $\sqrt[6]{64}$. 9{1/6}$. Буквально там говорится, что кубический корень из $(-8)$ является корнем в шестой степени из квадрата $(-8)$.

Хм… не уверен, что понял…

И снова наше спасение придет от геометрии! Геометрически это означает, что операция, эквивалентная $\times (-8)$ при трехкратном применении, равна операции, которая при шестикратном применении эквивалентна двукратному применению $\times (-8)$. Ниже приведен рисунок, иллюстрирующий это утверждение.

Как видно из рисунка выше, любой кубический корень из $(-8)$ также является корнем 6-й степени из $64$. Действительно, шестикратное применение зеленой операции будет эквивалентно двукратному применению «$\times (-8)$». Но некоторые из корней шестой степени из $64$ не являются кубическими корнями из $(-8)$! Несложно доказать, что это кубический корень из 8$, а другой квадратный корень из 64$. Предлагаю сделать это в качестве упражнения!

Теперь, обозначив $\sqrt[3]{-8}$ множество всех кубических корней из $-8$ и $\sqrt[6]{64}$ множество всех шестых корней из $64$, мы можно элегантно исправить парадокс! Эти обозначения очень нетрадиционны, и меня обвиняют в их использовании. Но я считаю, что это обеспечивает проницательное и красивое решение парадокса. Кроме того, если вы сможете отличить $n$-ые корни от классической записи $\sqrt[n]{x}$ при $x \geq 0$, то вы совершите огромный прорыв в понимании $n$-ые корни. 9Тогда q$ будет корректно определен для любого $q \in \mathbb Q$.

Гомотетии и вращения

Несмотря на проницательность, описания комплексных чисел, которые мы дали до сих пор, не очень строги.

Итак, каково точное определение комплексных чисел?

С геометрической точки зрения комплексные числа следует фактически рассматривать как определенный набор преобразований плоскости, а не линии. Эта плоскость называется сложной плоскостью . Он бесконечен во всех направлениях и имеет единственный центр, называемый 9-м.0549 происхождение . Кроме того, одна из его осей, проходящая через начало координат, известна как прямая с действительными числами . Ось, перпендикулярная линии действительного числа, известна как линия мнимого числа .

Так о каких трансформациях самолета идет речь?

Преобразования, соответствующие комплексным числам, — это те, которые мы использовали до сих пор: гомотетии и повороты с центром в начале координат. Эти две операции и есть симметрии, описанные ниже:

Ключевым аспектом этих операций является то, что можно комбинировать любое количество вращений и гомотетий, а порядок, в котором они комбинируются, не имеет значения. Говоря технически, мы говорим, что все эти геометрические преобразования являются 90 549 ассоциативными 90 552 и 90 549 коммутативными 90 552. Еще одним важным фактом является то, что все обычные числа можно однозначно сопоставить с помощью одной такой геометрической операции. Например, какая операция соответствует числу $2$?

И я предполагаю, что это соответствует гомотетии с коэффициентом 2…

Да, что также известно как «$\times 2$»! А как насчет числа $(-1)$?

Операция «$\times (-1)$» инвертировала числовую прямую… Так что, думаю, это симметрия вдоль воображаемой оси!

Нет… Имейте в виду, что мы можем использовать только гомотетии и повороты!

Арг… Гм… Я знаю! Это пол-оборота!

Отлично! Позвольте мне привести вам последний пример: $(-2)$ является гомотетией множителя 2 в сочетании с поворотом на пол-оборота. Теперь, в более общем смысле, любая комбинация гомотетии и поворота образует комплексные номера .

Подождите… Комплексное число?

Да! Теперь гомотетия определяется положительным фактором, называемым по модулю , и обычно обозначается $\rho$. По соглашению вращение определяется углом 90 545 против часовой стрелки на 90 548 оборотов, называемым 90 549 аргументом 90 552 и часто обозначаемым $\theta$. Поскольку эти два параметра однозначно определяют комбинацию гомотетии и поворота, каждое комплексное число может быть представлено парой $(\rho, \theta)$. 9* \times SO(3)) \cup \{0\}$ (технически «повороты» $\mathbb H$ образуют двойное покрытие $SO(3)$). Однако кватернионы немного сложнее, поскольку они не коммутативны. Действительно, как вы можете видеть, играя в кубик Рубика, два вращения в пространстве вообще не коммутируют. Если можно, напишите о кватернионах!

А любое число является комплексным?

Ну, как мы уже говорили, любое положительное число — это просто гомотетия. Это включает поворот на угол $0$. Таким образом, любое положительное число $x$ является комплексным числом $(x, 0)$. Теперь, если $x$ — положительное число, то $(-x)$ соответствует гомотетии множителя $x$ и половины оборота. Поскольку полуоборот соответствует углу $\pi$, число $(-x)$, таким образом, является комплексным числом $(x, \pi)$.

Что? Половина оборота равна $\pi$? Не лучше ли дать полному обороту имя вроде $\tau$, а половинному обороту назвать $\tau/2$?

Я знаю! Некоторые математики даже считают, что $\pi$ следует убрать из всех уравнений и заменить на $\pi = \tau/2$. Есть даже манифест, подтверждающий это… как вы можете видеть в следующем замечательном видео от ViHart:

Лично я предпочитаю $\tau$ $\pi$… Поскольку вы, вероятно, выучили $\pi$, я постараюсь вставить его в эту статью, но большую часть я буду делать с $\tau$. В частности, обратите внимание, что если $x > 0$, то $(-x)$ — это комплексное число $(x, \tau/2)$.
Как насчет числа ноль?
Хм… Хорошее замечание. Нам нужно новое преобразование, соответствующее нулю! Это преобразование состоит в свертывании всей комплексной плоскости в ее начало.
Меня беспокоит одно… Вы говорили, что комплексные числа — это геометрические преобразования? В каком возможном смысле они являются числами?
Точно не в явном! Но, во-первых, мы можем умножать комплексные числа. Это соответствует последовательному выполнению геометрических операций, связанных с комплексными числами. И что прекрасно, так это то, что у этого есть алгебраический перевод! Под этим я подразумеваю, что умножение $(\rho_1, \theta_1)$ на $(\rho_2, \theta_2)$ соответствует двум гомотетиям на множители $\rho_1$ и $\rho_2$ и двум поворотам углов $\theta_1 $ и $\тета_2$. Теперь две гомотетии множителей $\rho_1$ и $\rho_2$ объединяются в гомотетию множителя $\rho_1 \times \rho_2$, а два поворота углов $\theta_1$ и $\theta_2$ приводят к повороту угла $\тета_1+\тета_2$. Таким образом, мы имеем произведение $(\rho_1, \theta_1) \times (\rho_2, \theta_2) = (\rho_1 \times \rho_2, \theta_1 + \theta_2)$. Насколько это сладко? 9{it}$ дает элегантное описание этих движений, что значительно облегчает вычисления! Но это все еще только верхушка айсберга. Чтобы раскрыть истинную магию комплексных чисел, нам нужно копнуть глубже!
Точки комплексной плоскости

В 19 веке немецкий математик Карл Фридрих Гаусс, король математики, представил мощную визуализацию комплексных чисел. Чтобы добраться туда, обратите внимание на невероятный факт, что $1 \times x=x$, когда $x$ — число. Таким образом, если я покажу вам геометрическое преобразование «$\times x$», то вы легко сможете найти, какое $x$ я выбрал, посмотрев, в какую точку отправлено число $1$. Точно так же, если я дам вам геометрическое преобразование $(\rho, \theta)$, то вы сможете узнать значения $\rho$ и $\theta$, так как они будут полярными координатами точки $1$ отправляется! Эта точка называется 9.0549 изображение из 1.

Полярные координаты? Можете ли вы привести пример?

Конечно! Ниже приведена комбинация гомотетии в 2 раза и поворота на угол $2\tau/3$ (2/3 оборота).

Коэффициент гомотетии $\rho$ – это расстояние между образом 1 и началом координат, а угол поворота $\theta$ – это угол (против часовой стрелки) от $1$ до его образа.

Похоже на полярные координаты!

Точно! Это показывает, что любое геометрическое преобразование можно перевести в точку на комплексной плоскости, полярные координаты которой задаются коэффициентом гомотетии и углом поворота! И это взаимно однозначное соответствие между геометрическими преобразованиями и точками! Таким образом, мы можем отождествить геометрическое преобразование с точками на комплексных плоскостях. 92$. Таким образом, мы можем отождествить оба множества, и мы называем их оба $\mathbb C$.

Можно ли перевести эти координаты обратно в классические декартовы?

Да! Но перед этим давайте сначала посмотрим, с какой точкой комплексной плоскости связано геометрическое преобразование $i$:

Итак, $i$ — это точка прямо над началом координат? Забавно…

Я знаю! Что также особенно интересно, так это то, что теперь мы можем описывать евклидову планарную геометрию с помощью комплексных чисел!

Векторы комплексной плоскости

Чтобы завершить построение комплексных чисел, нам нужно связать любую точку комплексной плоскости с вектором.

Вектор? Что это за фигня?

Вектор — это движение в комплексной плоскости. Это движение часто изображается стрелкой от начальной точки к конечной. Но важно помнить, что вектор соответствует движению, а не стрелке. Две стрелки могут соответствовать одному и тому же движению, даже если они не начинаются в одних и тех же начальных точках, как показано стрелками одного цвета на рисунке справа.

Так как же связать любую точку комплексной плоскости с вектором?

Учитывая точку на комплексной плоскости, мы можем провести стрелку из начала координат в эту точку. Этот вектор, связанный с этой стрелкой, будет вектором, связанным с точкой комплексной плоскости. Например, $i$ связано со стрелкой от $0$ до $i$, что соответствует зеленым стрелкам на рисунке справа.

Кажется, я понял… Но какой смысл в сопоставлении точек с векторами?

Теперь мы можем определять сложение комплексных чисел!

Как нам это сделать?

Комбинируя движения, связанные с векторами! Например, сочетание фиолетового и зеленого движений — это движение на одну единицу вправо и на две единицы вверх. Это эквивалентно только синему движению! Это означает, что $фиолетовый + зеленый = синий$. И это можно визуализировать геометрически, если фиолетовая и синяя стрелки начинаются в одной точке, а зеленая стрелка помещается в конец фиолетовой стрелки. Фиолетовые, зеленые и синие стрелки должны образовать треугольник, как показано ниже:

А поскольку все векторы соответствуют комплексным числам, теперь мы можем складывать комплексные числа, складывая соответствующие им векторы!

Круто!

Теперь самое главное. Все векторы можно однозначно разложить на сумму $1$ и $i$ . Например, фиолетовый вектор можно получить комбинацией вектора, связанного с $1$, и вектора, связанного с $i$. Таким образом, $purple = 1+i$. Точно так же синий вектор представляет собой комбинацию $1$ и двух умноженных на $i$. Следовательно, $blue = 1+2i$.

Значит, все векторы есть определенное количество раз $1$ плюс определенное количество раз $i$?

Точно! А так как все векторы соответствуют комплексным числам, то все комплексные числа можно записать как $a+bi$, где $a$ и $b$ — обычные числа. Это разложение позволяет выполнять простые вычисления сложения комплексных чисел! В самом деле, если рассмотреть любые два комплексных числа $z_1$ и $z_2$, то мы уже знаем, что каждое из них можно разложить как $z_1 = a_1+b_1i$ и $z_2 = a_2 + b_2 i$. Тогда сумма $z_1$ и $z_2$ определяется как $z_1 + z_2 = (a_1+b_1i) + (a_2+b_2i) = (a_1+a_2) + (b_1+b_2)i$.

Следует также отметить, что каждому комплексному числу $z$ также соответствует операция «$+z$» над точками комплексной плоскости. Геометрически эта операция состоит в переносе вектора, которому соответствует $z$. Фактически это отображение $z$ в $+z$ является изоморфизмом евклидова векторного пространства между пространством комплексных чисел и множеством сдвигов комплексной плоскости.

Это декартово описание комплексных чисел было бы весьма полезным, если бы не более общий подход линейной алгебры к определению векторов. 92$. В частности, это дает пространству $(\mathbb C, +)$ структуру коммутативной группы. Этот изоморфизм тривиален для классического построения комплексных чисел, но в построении этой статьи он весьма впечатляет! Напомним, что мы ввели $\mathbb C$ как комбинацию гомотетий и поворотов!

Поле комплексных чисел

Подведем итог тому, что мы уже обсуждали. Прелесть комплексных чисел в том, что их можно отождествить с несколькими различными математическими объектами. Их можно рассматривать как комбинации гомотетий и поворотов комплексной плоскости, как точки на комплексной плоскости и как векторы на комплексных плоскостях. Первое понимание комплексных чисел описывает умножение, а третье — сложение. Размышление о каждом из значений комплексных чисел по отдельности уже довольно завораживает, но поистине умопомрачительное свойство комплексных чисел проявляется, когда мы их смешиваем!

Что ты имеешь в виду?

Посмотрим, что получится, если у нас есть и умножение, и сложение! В частности, давайте сосредоточимся на простейшем возможном случае, а именно на $(x+y) \times z$, где $x$, $y$ и $z$ — комплексные числа.

Гм… не знаю, с чего начать!

Ну, выражение начинается со сложения $x$ и $y$…

ОК… Итак, чтобы выполнить сложение, нам нужно думать об этих комплексных числах как о векторах, верно?

Точно! Нарисуем $x$, $y$ и их сумму $x+y$. Но тогда нам нужно умножить эти члены на $z$. Как мы это делаем?

Я знаю! Нам нужно думать о $z$ как о $\times z$, что является комбинацией поворота и гомотетии!

Очень хорошо! Это означает, что $xz$, $yz$ и $(x+y)z$ будут образом геометрического преобразования $\times z$ $x$, $y$ и $z$. Вот что нарисовано ниже:

Теперь происходит волшебство, когда мы замечаем, что любое геометрическое преобразование $\times z$ сохраняет формы треугольников. В результате треугольник $x$, $y$, $x+y$ трансформируется в треугольник $xz$, $yz$, $(x+y)z$. А это значит, что сумма сторон $xz$ и $yz$ равна последней стороне $(x+y)z$! Другими словами, $xz+yz=(x+y)z$. это главное 92$ по-прежнему действительны для комплексных чисел! Именно это сильное сходство с манипуляциями привело математиков к тому, чтобы называть комплексные числа… числами. В терминах чистой алгебры мы говорим, что комплексные числа образуют поле .

Заключение

Подытожим: комплексное число — очень сложный математический объект, который можно рассматривать под разными углами. В основном его можно рассматривать как комбинацию гомотетии и вращения, как точку на комплексной плоскости или как вектор размерности 2. Эти три интерпретации показаны ниже.

Но что делает комплексные числа такими особенными, так это не разные углы, под которыми их можно увидеть, а их комбинация, вроде того, как квантовые объекты не являются просто классическими волнами или классическими частицами. А именно, раскрывается полная природа комплексных чисел, поскольку они рассматриваются как поле. В частности, именно к этой области применяется основная теорема алгебры .

Что это за теорема?

Эта теорема, впервые доказанная Карлом Фридрихом Гауссом, утверждает, что все полиномиальные комплексные уравнения имеют решения. Это так просто. Это свойство также известно как тот факт, что комплексные числа образуют 92+1)\mathbb R[X]$ и, таким образом, является полем. Это так красиво, что я чуть не заплакал, когда впервые увидел это!

В чем смысл этой теоремы?

Теперь можно решить гораздо больше уравнений! И я говорю не только о полиномиальных уравнениях. Что еще более важно, естественные и простые решения появляются в дифференциальных уравнениях, электромагнетизме, поиске собственных значений, преобразовании Фурье и теории чисел среди многих других областей. В частности, комплексные числа оказались подходящей структурой для описания физики элементарных частиц! Прочтите мою статью о динамике волновой функции в квантовой механике, чтобы увидеть комплексные числа в действии!

Объяснение комплексных чисел.

Когда мы думаем о комплексных числах, мы часто думаем о выполнении алгебры с этим странным термином i , и все это кажется немного произвольным и легко забываемым. На самом деле то, что мы делаем, осязаемо и может быть визуализировано.

Так что будьте готовы.

После этого поста вы, вероятно, никогда больше не будете думать о комплексных числах как раньше… и да, это хорошо.

Примечание: Если вы не знаете, что такое мнимые числа и как они работают на сложной плоскости, проверьте этот пост .

Комплексные числа представляют собой сумму действительного и мнимого чисел, представленную как a + b i. Используя комплексную плоскость, мы можем отображать комплексные числа подобно тому, как мы наносим координаты на декартовой плоскости.

Вот несколько примеров:

3 + 2 i

1 – 4 i

-3 + 3,5 i

Просто поставьте точку на пересечении реальной части, расположенной на горизонтальной оси, и мнимой части, расположенной на вертикальной оси .

Это самая простая и интуитивно понятная операция. Добавление/вычитание действительных чисел переводит точку вправо/влево на действительной оси, а добавление/вычитание мнимых чисел переводит точку вверх/вниз по мнимой оси.

Арифметически это работает так же, как объединение одинаковых терминов в алгебре.

Например, если мы вычтем 1 – 4 i из 3 + 2 i, , мы просто вычислим реальную разницу:

3 – 1 = 2,

и мнимую разницу:

2 i – (-4 i ) = 2 i + 4 i = 6 i.

Это то же самое, что нарисовать точку 3+2 i и перевести ее влево 1 единица и до 4 шт. . Полученная точка и есть ответ: 2+6 i.

Мы также можем думать об этих точках как о векторах .

Сначала распределите знак минус, чтобы получилось сложение: (3+2 i ) + (-1+4 i ).

Затем нанесите две точки с отрезками, исходящими из начала координат.

Чтобы добавить эти точки, просто сложите одну поверх другой. Поскольку сложение коммутативно, не имеет значения, как мы их складываем.

Это может показаться излишеством, но вот в чем дело: понимание векторного представления значительно облегчит умножение и деление комплексных чисел.

Эта операция менее очевидна и оставляет нас в недоумении:

Что означает умножение двух комплексных чисел?

В общем, мы знаем, что умножение на действительное число масштабирует значение, и мы узнали в последнем посте, что умножение на i поворачивает значение на 90˚ против часовой стрелки, а как насчет этого?

Чтобы лучше понять, давайте распределим первый двучлен через второй.

Хорошо, теперь мы можем выполнить сложение, сложив векторы после выполнения преобразований. Давайте попробуем.

Сначала имеем (3+2 i )(1), что равно (3+2 i ) в масштабе 1. ). Здесь происходят две вещи: масштабирование и вращение.

Сначала увеличим его в 4 раза, умножив (4)(3+2 и ), чтобы получить (12 + 8 и ).

Еще надо умножить на — т.е. Вспомните умножив на — i это 90˚ поворот по часовой стрелке .

Примечание: Это соответствует алгебре, если бы мы подставили в i = √-1:

Последний шаг — выполнить сложение путем суммирования векторов.

Наш окончательный ответ: 11 – 10 i .

Теперь вы можете подумать,

«Бретт, почему мы не можем просто решить это с помощью алгебры??»

И это правда, мы можем решить это с помощью алгебры. На самом деле, это самый эффективный способ решения проблемы (хотя ему не хватает понимания, которое вы получаете, рисуя графики).

Я был бы паршивым математиком, если бы не показал вам оба пути. Итак, для всех моих любящих алгебру друзей, вот как расширить и упростить приведенную выше задачу:

Давайте разделим (3+2 i )/(1–4 i ).

В этот момент вы можете подумать, что можете просто разделить действительные и мнимые части… но не так быстро.

Нет! Даже не думай!!
Как и в алгебре, мы должны разделить знаменатель на оба члена числителя, что оставляет нас с той же проблемой:
Что на самом деле означает деление на комплексное число?
По правде говоря, это сбивает с толку, и этому нет хорошего объяснения. Было бы неплохо, если бы мы могли избавиться от мнимого числа в знаменателе??
Хорошие новости → Именно этим мы и займемся!
Комплексное сопряжение
Ключом к решению этой проблемы является выяснение того, как преобразовать знаменатель в обычное действительное число.
Проще всего это сделать с помощью комплексного сопряжения .
Чтобы найти комплексное сопряжение, просто переверните знак мнимой части. Например, комплексное сопряжение (1–4 90 545 i 90 548 ) равно (1 + 4 90 545 i 90 548 ).
Когда я умножаю их вместе, я получаю 17:
Конечно, я не могу просто умножить знаменатель на (1+4 i ). Как и любая дробь, если я хочу умножить знаменатель на значение, я должен также умножить числитель на это значение.
Теперь это имеет смысл. У нас есть два комплексных числа, которые умножаются в числителе, с которым мы знаем, как обращаться из предыдущего раздела, и мы масштабируем все это на 1/17.
Вы можете решить это с помощью графика или использовать ярлык алгебры:
Это было не так уж и плохо, не так ли?
Что мне нравится в том, что проблемы решаются несколькими способами, так это то, что вы получаете возможность по-настоящему познакомиться с концепцией и полностью понять ее так, как вы бы не смогли, если бы не видели оба метода. Мало того, что у вас больше шансов наткнуться на заветную ага! На данный момент в вашем арсенале теперь гораздо больше инструментов для решения более сложных задач.
Спасибо за внимание!
Реальность мнимых чисел
Несколько лет назад я обучал студента-психолога кое-какой предварительной математике, необходимой для занятий по статистике.
Мы говорили о…
medium.com
Как визуально «заполнить квадрат»
и проблемы с запоминанием
medium.com
Ходьба пьяницы и объяснение процессов Маркова
9000 Случайные блуждания
medium.com
10 главных тайн треугольника Паскаля 9x$ и $\log(x)$), векторы и матрицы, степенные ряды. Сложные моменты отмечены. (Для студентов в Великобритании начальные разделы должны быть доступны для всех, кто сдает экзамен GCSE или выше, но некоторые из более поздних разделов соответствуют стандарту A-level.) Повсюду есть упражнения для вы, чтобы проверить свое понимание, с ответами на спине.
Я пытался сделать упражнения менее похожими на стандартные вычислительные, которые вы получаете в школе, но это означает, что некоторые из них довольно сложны.
В этой статье я использовал радианы и градусы для измерения углов. Вы, возможно, не видели, чтобы раньше использовались радианы, это просто еще один способ измерения углов. 2)$ через $\textrm{Re}(z)$ и $\textrm{Im} (г)$. 9п$? Для тех из вас, кто встречался с математической индукцией, можете ли вы это доказать?
Плоскость Аргана
Мы еще не добрались до самого удивительного в комплексных числах — геометрической интерпретации. Как вы знаете, комплексное число $z$ можно записать как $a+i b$, где $a$ и $b$ — вещественные числа. Если вы когда-либо работали с векторами, это будет выглядеть очень знакомо, 2D-вектор можно записать как $a\mathbf{i} +b\mathbf{j}$, где $\mathbf{i}$ и $\mathbf{j} $ — единичные векторы. Итак, комплексное число $z = a+i b$ соответствует точке на двумерной плоскости, заданной как $a\mathbf{i} +b\mathbf{j}$. Если вы не создали векторы, используя приведенные выше обозначения, $a+ib$ просто соответствует точке в 2D с координатами $x$ $a$ и $y$-координатой $b$.
Как насчет суммы двух комплексных чисел, $z+w$. Оказывается, сложить два комплексных числа — это то же самое, что сложить два вектора. Если вы не знаете, как сложить два вектора, посмотрите на следующую картинку:
Итак, сложение векторов соответствует сложению комплексных чисел. Двумерная плоскость комплексных чисел называется плоскостью Аргана или диаграммой Аргана. Что ж, это мило, но не так здорово. Удивительно, что происходит, когда вы умножаете два вектора. Прежде чем мы перейдем к этому, нам нужна пара новых идей. 9{-1} (\textrm{Im}(z) /\textrm{Re}(z))$ (если только $\textrm{Re}(z) = 0$). Надеюсь, следующий рисунок объясняет модуль и аргумент комплексного числа:
Упражнение 12 Пусть $w = (1+i)/\sqrt{2}.$ Что такое $|w|$ и $\arg(w )$?
Упражнение 13 Что такое $|z|-|\textrm{Conj}(z)|$? Объясните геометрически, что такое $\textrm{Conj}(z)$ в терминах $z$. Используя это, что такое $\arg(\textrm{Conj}(z))+\arg(z)$?
Теперь мы можем обсудить удивительную вещь, связанную с геометрией комплексных чисел. Если $z$ и $w$ — два комплексных числа, то $|z w| = | г | |w|$ и $\arg(z w) = \arg(z)+\arg(w)$. Другими словами, если вы умножаете два комплексных числа, вы умножаете их длины и складываете их углы. Мы не сможем доказать второе уравнение до следующего раздела, но мы можем доказать первое. Если $z = a+i b$ и $w = x+i y$, то $z w = (a x- b y)+i(a y+b x)$. Так 9{\ circ} / п) $. Найдите все $n$ решений относительно этого решения.
Полярные координаты и формула де Муавра
Помимо $a+i b$ существует и другой способ записи комплексных чисел. Поскольку комплексное число похоже на точку на комплексной плоскости, мы можем вычислить расстояние от этой точки до начала координат, $r$, и угол, который линия от начала до точки образует с осью $x$. , $\тета$. После того, как мы разобрались с ними, мы можем записать комплексное число как $(r,\theta)$, это называется записью в полярных координатах. Эти числа $r$ и $\theta$ — это просто модуль и аргумент $x+i y$, с которыми мы познакомились выше.
Итак, комплексное число $z = a+i b$ можно записать как $z = (|z|,\arg(z))$. Кроме того, для заданного комплексного числа $(r,\theta)$ мы можем преобразовать его в обозначение $x+i y$ (это то, о чем Q1) как $(r, \theta) = r(\cos\theta +i \sin\тета)$.
Итак, мы можем переключаться между двумя разными способами записи комплексных чисел, но какой в этом смысл? Ну, это очень полезно по причине, которая станет очевидной, если вы прочитаете следующий раздел (что немного сложнее), но также полезно по нескольким другим причинам. 7} {7!} + \dots$$ 9{-z}] /2$. Найдите разложение в степенной ряд для $\cosh(z)$ и докажите, что $\cosh(i z) = \cos(z)$.
Прикольная штука
Теперь мы знаем основы работы сложных чисел, что мы можем с ними делать?
Предположим, у нас есть комплексное число $z = (r, \theta)$ в полярных координатах и другое комплексное число $w = (1, \phi)$ с модулем 1. Произведение этих двух комплексных чисел равно $z w = (г, \тета + \фи)$. Другими словами, $z w$ — это $z$, повернутый на угол $\phi$. Мы можем использовать их для расчета матрицы, которая поворачивает вектор на угол $\phi$. Предположим, что $z = x+i y$ и $w = (1, \phi) = \cos\phi + i\sin\phi$, тогда $z w = (x+i y)(\cos\phi + i\sin\phi) = (x\cos\phi — y\sin\phi) + i(x\sin\phi + y\cos\phi)$. Другими словами, $x$-координата (эквивалентная действительной части комплексного числа) вектора, повернутого на угол $\phi$, равна $x’ = xcos\phi — y\sin\phi$ и координата $y$ (мнимая часть) равна $y’ = xsin\phi — y\cos\phi$. Мы можем представить это как произведение матрицы:
\[\left( \begin{array}{c} x’\\ y’\end{array}\right) = \left(\begin{array}{cc} \cos\phi & -\sin\ phi \\ \sin\phi & \cos\phi \end{массив}\right) \left(\begin{array}{c} x \\ y \end{массив}\right)\]
Другими словами , матрица вращения $M$, которая поворачивает вектор $\textbf{v}$ в вектор $M\mathbf{v}$ на угол $\phi$, равна:
\[\mathbf{M} = \left (\begin{array}{cc} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{array}\right)\]
В начале я упоминал, что вы можете решить любое полиномиальное уравнение, используя комплексные числа, это известно как основная теорема алгебры, и известный математик, известный как Гаусс, дал около 98 = 1$. Это называется восьмым корнем из единицы.
Ответ 8 $ \quad X = \pm i$.
Ответ 9 $ \quad X = \pm w = \pm 1+i /\sqrt{2}$. Другими решениями являются $- w$ , $i w$ и $- i w$.
Ответ 10 Решение с использованием квадратичной формулы $$ x = \frac { -2\pm i \sqrt{4-8}} {2}\ = 1\pm \sqrt{-1}\ = — 1 \pm i $$
Ответ 11 Раскрывая каждое из уравнений и упрощая, мы получаем 1 в каждом случае (включая общий случай). Доказательство см. в разделе о формуле де Муавра. 9n) = n\arg(z)$.
Ответ 15 Используя подсказку, что $z = (z /w )w$ и тот факт, что $|u v| = |и| |v|$ получаем, что $|z| = |(z/w)| |w|$ , поэтому $|(z /w )| = | г | /|ш|$ . Точно так же, взяв аргумент обеих сторон, мы получаем $\arg(z) = \arg(z/w)+\arg(w)$ и, таким образом, $\arg(z/w) = \arg(z)- \ аргумент(ш)$.
Ответ 16 $\quad |z| = r$ и $\arg(z) = \theta$. Итак, $z = |z| (\cos(\arg(z))+i\sin(\arg(z)))$. Теперь мы можем доказать, что $|z w| = | г | |w|$ и $\arg(z w) = \arg(z)+\arg(w)$, раскрывая скобки, используя это разложение $z$ и $w$ и тригонометрическую формулу для $\cos(A +B) = \cos(A)\cos(B)-\sin(A)\sin(B)$ и $\sin(A+B) = \cos(A)\sin(B)+\sin(A)\sin(B)$.
Итак, если $|z| = г_1, |ш| = r_2$, $\arg(z) = \theta_1$ и $\arg(w) = \theta_2$, то $z = r_1 (\cos\theta_1 +i\sin\theta_1)$ и $w = = r_2 ( \cos\theta_2 +i\sin\theta_2)$. Расширение
\begin{eqnarray} z w &=& r_{1} r_{2}\cos\theta_{1} +i\sin\theta_{1})(\cos\theta_{2} +i\sin \theta_{2})\\ &=& r_{1} r_{2} ((\cos\theta_{1} \cos\theta_{2} — \sin\theta_{1} \sin\theta_{2} )+i(\cos\theta_{1} \sin\theta_{2} + \cos\theta_{2} \sin\theta_{1} )) \\ &=& r_1 r_2 (\cos(\theta_{1 } + \theta_{2} )+i\sin(\theta_{1} + \theta_{2} )) \end{eqnarray} 9{-z}] /2$ тогда $\sinh(i z) = i\sin(z)$. Кроме того, $\cos(i z) = \cosh(z)$ и $\sin(i z) = i\sinh(z)$.
Cool Stuff
Ответ 25 Мы пытаемся доказать это по индукции, поэтому нам нужно сначала доказать, что это верно для $n = 1$. Если $n = 1$, то $p(z) = z + a_0$ для некоторого комплексного числа $a_0$. В этом случае $p(z)$ можно записать как $p(z) = (x- (- a_0 ))$, и теорема верна. Далее нам нужно доказать, что если это верно для $n$, то верно и для $n+1$.
No related posts.
Навигация по записям
Предыдущая статьяНайдите область определения функции с корнем: § Область определения функции
Следующая статьяЧетвертой степени уравнение как решать: Онлайн калькулятор: Решение уравнения 4-й степени
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Геометрия
Математика
Физика
Химия
Школьная жизнь
Разное
© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»
Карта сайта