ТЕОРИЯ
1. Справочный материал
2. Решение неравенств
Определение и основные свойства неравенств.
Определения:
где a и
b могут быть числами или функциями.
Символы <(≤), >(≥) называются знаками неравенства и читаются соответственно :
меньше(меньше или равно) ,больше(больше или равно).
Неравенства , которые записываются с помощью знаков > и <,называются строгими,
а неравенства, в записи которых участвуют знаки ≥ и ≤,- нестрогими.
Неравенства вида a<x<b (a≤x≤b) называются двойными неравенствами
и читаются соответственно :x больше a,но меньше b (x больше или равно a,но меньше или равно b ).
Различают два вида неравенств: числовые (2>0,7 ;½<6) и неравенства с переменной (5x-40>0 ; x²-2x<0).
Свойства числовых неравенств :
- Если
a>b , то
b<a; если a<b,
то
b>a.
- Если a<b и b<c, то a<c.
- Если a<b и c-любое число, то a +c<b+c.
- Если a<b и c>0,то ac<bc. Если a<b и c<0,то ac>bc.
- Если a<b и c<d,то a +c<b +d.
Числовые промежутки
| Неравенство |
Числовой промежуток |
Название промежутка |
Геометрическая интерпретация |
| замкнутый промежуток(отрезок) с концами a и b ,a<b |
|
||
|
|
открытый промежуток (интервал) с концами a и b ,a<b |
|
|
|
|
|
полуоткрытые промежутки (полуинтервалы) концами a и b ,a<b |
|
|
|
|
бесконечные промежутки (лучи) |
|
|
|
|
бесконечные промежутки (открытые лучи) |
|
| бесконечный промежуток (числовая прямая) |
Вверх
Основные
определения и свойства.
Определения:
Решением неравенства с одной переменной называется значение переменной,
которое обращает его в верное числовое неравенство.
Решить неравенство — значит найти все его решения или доказать, что решений нет.
Неравенства, имеющие одни и те же решения, называются равносильными.
Неравенства, не имеющие решений, также считают равносильными.
При решении неравенств используются следующие свойства:
1) Если из одной части неравенства перенести в
другую слагаемое с противоположным знаком,
то получится равносильное ему неравенство.
2) Если обе части неравенства умножить или
разделить на одно и то же положительное число,
то получится равносильное ему неравенство.
3) Если обе части неравенства умножить или
разделить на одно и то же отрицательное число,
изменив при этом знак неравенства на противоположный,
то получится равносильное ему неравенство.
Многие неравенства в процессе преобразований сводятся к линейным неравенствам.
Неравенства вида ах>b ( ах <b ,ax≤b или ax≥b), где а и b — некоторые числа,
называют
линейными неравенствами с одной
переменной.
Если a>0 ,то неравенство ax>b равносильно неравенству
и множество решений неравенства есть промежуток
Если a<0 ,то неравенство ax>b равносильно неравенству
и множество решений неравенства есть промежуток
неравенство примет вид 0∙x>b, т.е. оно не имеет решений ,если b≥0
,и верно при любых x ,если b<0.
Аналитический способ решения неравенств с одной переменной.
Алгоритм решения неравенства с одной переменной
- Преобразовать обе части неравенства.
- Привести подобные слагаемые.
- Привести неравенства к простейшему виду, на основании свойств неравенств.
- Записать ответ.
Приведем примеры решения неравенств .
Пример 1. Решить неравенство 3x≤15.
Решение:
Обе части неравенства
разделим на положительное число 3 (свойство 2) : x≤5.
Множество решений
неравенства представляет собой числовой промежуток (-∞;5].
Ответ :(-∞;5]
Пример 2. Решить неравенство -10x≥34.
Решение:
Обе части неравенстваразделим на отрицательное число -10 ,
при этом знак неравенства изменим на противоположный (свойство 3) : x≤-3,4.
Множество решений неравенства представляет собой промежуток (-∞;-3,4].
Ответ : (-∞;-3,4].
Пример 3. Решить неравенство 18+6x>0.
Решение:
Перенесем слагаемое 18 с противоположным знаком в левую часть неравенства (свойство 1): 6x>-18.
Разделим обе части на 6 (свойство 2) :
x>-3.
Множество решений неравенства представляет собой промежуток (-3;+∞).
Ответ : (-3;+∞).
Пример 4.Решить неравенство 3(x-2)-4(x+2)<2(x-3)-2.
Решение:
Раскроем скобки : 3x-6-4x-8<2x-6-2.
Перенесем члены ,содержащие неизвестное ,в левую часть ,
а члены не содержащие неизвестное , в правую часть (свойство 1):
3x-4x-2x<6+8-6-2.
Приведем подобные члены: -3x<6.
Разделим обе части на -3 (свойство 3) :
x>-2.
Множество решений неравенства представляет собой промежуток (-2;+∞).
Ответ
: (-2;+∞).
Пример 5. Решить неравенство
Решение:
Умножим обе части неравенства на наименьший общий знаменатель дробей,
входящих в неравенство, т. е. на 6 (свойство 2).
Получим:
,2x-3x≤12.
Отсюда , —x≤12 , x≥-12.
Ответ : [-12;+∞).
Пример 6. Решить неравенство 3(2-x)-2>5-3x.
Решение:
Упростим неравенство ,раскрыв скобки:
6-3x-2>5-3x, 4-3x>5-3x, -3x+3x>5-4.
Приведем подобные члены в левой части неравенства и запишем
результат в виде 0∙x>1.
Полученное неравенство не имеет решений, так как при любом значении x
оно обращается в числовое неравенство 0 < 1, не являющееся верным.
Значит, не имеет решений и равносильное ему заданное неравенство.
Ответ : решений нет.
Пример 7.Решить неравенство 2(x+1)+5>3-(1-2x).
Решение:
Упростим неравенство ,раскрыв скобки:
2x+2+5>3-1+2x, 2x+7>2+2x,2x-2x>2-7, 0∙x>-5.
Полученное неравенство является верным при любом значении x,
так как левая часть при любом x равна нулю, а 0>-5.
Множеством решения неравенства является промежуток (-∞;+∞).
Ответ
:
(-∞;+∞).
Пример 8. При каких значениях x имеет смысл выражение:
a)
b)
Решение:
а)По определению арифметического квадратного корня
должно выполнятся следующее неравенство 5x-3≥0.
Решая, получаем 5x≥3, x≥0,6.
Итак, данное выражение имеет смысл при всех x из промежутка [0,6;+∞).
Ответ : [0,6;+∞).
б)С учетом свойств арифметического квадратного корня и знаменателя дроби
должно выполнятся следующее неравенство 2-3x>0.
Отсюда ,-3x>-2
(свойство 3), x<2/3.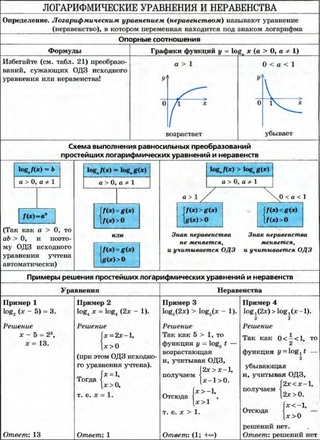
Данное выражение имеет смысл при всех x из промежутка (-∞;2/3).
Ответ :(-∞;2/3).
Пример 9.При каких значениях a квадратное уравнение x-8x2-4a=0 имеет два корня ?
Решение:
Квадратное уравнение будет иметь два корня ,если дискриминант D будет больше нуля.
D=(-8)2-4∙(-4a)=64+16a,
64+16a>0,
16a>-64,
a>-4.
Таким образом , при всех значениях a из промежутка (-∞;-4)
данное квадратное уравнение будет иметь два корня.
Ответ
:
при всех
a из промежутка
(-∞;-4)
.
Пример 10.Решите задачу:
В одном бассейне налито 100 л воды, а во втором 150 л воды.
Каждый час в первый бассейн вливается 15 л воды, а во второй — 5 л воды.
В какие моменты времени в первом бассейне будет больше воды, чем во втором?
Решение:
Пусть за x ч в первый бассейн вольется 15x л воды и в нем станет 100+15x л воды.
Тогда через x ч во втором бассейне будет 150+5x л воды.
Надо найти такие значения x , для которых выполняется неравенство
100+15x>150+5x.
Преобразовав ,получаем
15x-5x>150-100,
10x>50,
x>5.
Итак ,в первом бассейне окажется больше воды ,чем во втором, при x>5,
т.е. после 5ч с начала вливания воды.
Ответ : после 5ч с начала вливания воды.
Пример 11. При каких значениях x значения функции Y=-1/3x+8 принадлежит промежутку (-1,1)?
Решение: -1<-1/3x+8<1,
-9<-1/3x<7,
27>x>21,
21<x<27.
Ответ : (21;27).
Вопросы.
1. Что называется неравенством первой степени с одним неизвестным?
2. Что называется решением неравенства с одним неизвестным?
3.
Что значит решить неравенство с одним неизвестным?
4. Каким способом можно решить неравенство первой степени с одним неизвестным?
.Графический способ решения неравенств с одной переменной.
Покажем, как можно, применяя графический метод, решить неравенства вида
kx+ b> 0 (1)
или
kx + b<0, (2)
где k и b — заданные числа и k≠0.
В декартовой системе координат Оху рассмотрим прямую
y = kx + b. (3)
На рис. 1 изображена такая прямая при
k>
0, а на рис.
2 изображена такая прямая при
k<0.
рис1. рис.2.
Решить неравенство (1) — это значит найти все решения х,
для которых прямая y = kx-b расположена выше оси х.
Здесь важную роль играет точка А пересечения прямой (3) с осью х.
Абсциссу точки А
обозначим
через
xo.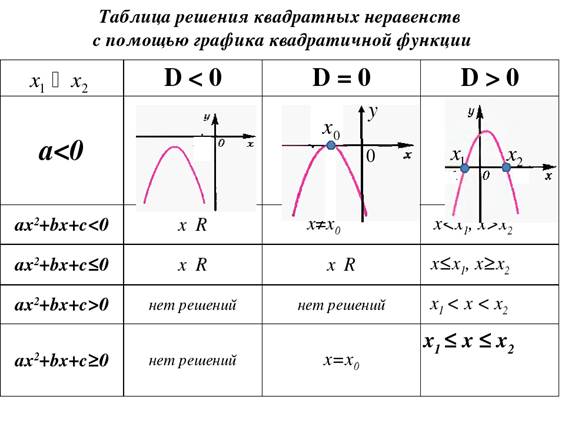
Так как ее ордината равна нулю, то
xo
удовлетворяет уравнению
O = kxo + b, откуда
xo=-b/k.
Обратимся к рис. 1, соответствующему случаю k> 0. Мы видим , что прямая y = kx+b
расположена выше оси
х
для всех х,
находящихся правее
точки xo, т. е. для всех х из интервала (-∞,
+ ∞), и
расположена ниже оси
х
для
всех х,
находящихся левее точки
xo,
т. е. для всех х
из интервала (—∞,xo).
Итак, при k> 0 неравенство (1) выполняется на интервале (xo, + ∞), а неравенство (2) —на интервале (—∞,xo).
При k<0, как это видно из рис. 2, неравенство (1) выполняется на интервале (—∞,xo),
а неравенство (2) — на интервале (xo, + ∞).
Пример 1. Решить, применяя графический метод, неравенства
2X+1 >0, (4)
2X+1 <0. (5)
Решение :
Начертим в декартовой системе координат Оху прямую
у = 2X+1.
(6)
рис3.
Для этого нужно знать две ее точки. В качестве первой точки возьмем точку пересечения прямой с осью х. Она все равно будет нужна. Полагая в формуле (6) у = 0, получим уравнение
0 = 2х+1.
Его решение есть абсцисса точки А пересечения прямой с осью х. Итак, А ( —1/2 ,0).
В качестве второй точки можно взять точку В
пересечения
прямой с осью у.
Ее абсцисса
X=0, а ордината
y=2∙0+1, y=1.
Итак, В(0, 1).
Через точки А и В проводим прямую. Это и есть прямая y=2X+1 (рис. 3).
Из рис. 3 видно, что неравенство (4) выполняется на интервале ( — 1/2 , + ∞) а (5) — на интервале (— ∞, —1/2).
Вопрос.
Как можно решать неравенства первой степени, применяя графический метод?
Питирим Сорокин и «Теория неравенства»
Октябрьская революция 1917 года и приход к власти большевиков в корне изменили судьбу тысяч россиян. Многим пришлось покинуть Родину, чтобы сохранить жизнь своим близким и себе.
Речь идёт о тех, кто был не согласен с политикой большевиков и их идеологией. Те же, кто решил остаться в советской России, либо погибли в лагерях, как П.А. Флоренский, либо вынуждены были принять идеологию большевиков, как Лосев А.Ф. Мы не случайно упоминаем имена известных русских философов, потому что решили посвятить нашу работу выдающемуся российско – американскому учёному Питириму Сорокину.
Рисунок 1. П.А.Сорокин
23 сентября 1922 года поездом Москва — Рига отправилась крупная партия «инакомыслящих» в изгнание, в числе которых был и П.А. Сорокин — выдающийся русский философ. Пароходы и поезда, на которых эмигрировала русская интеллигенция, получили собирательное название «философский пароход» [2].
Рисунок 2. Пароход «Oberbürgermeister Haken»
Оказавшись за границей, П.Сорокин, уже известный как автор ряда статей философского значения, прославился как социолог, автор «Теории социальной стратификации» [1]. Он первым отказался делить общество на классы, а ввёл такое понятие как «страты» («слои»).
В Советском Союзе, где царила пропаганда равенства всех, независимо от статуса, его теория была неприемлема. Всё население делилось на два класса – рабочих и крестьян. Интеллигенция вообще считалась «прослойкой». Сегодня ни для кого не секрет, что неравенство всегда присутствовало и будет присутствовать среди людей, исходя из тех критериев, которые П.Сорокин и приводит как доказательство: доход, власть, образование, профессия. Человек может повысить свой социальный статус, если у него есть способности, желание, стремление достичь поставленной цели. «Только от нас зависит наше будущее»: писал П.Сорокин. Его книга «Социальная культурная динамика», в которой он излагал принципы теории социальной стратификации, получила всемирную известность. В октябре 1923 году П.Сорокин был приглашён в США для чтения курса лекций по истории русской революции. А в 1931 году он основал социологический факультет в Гарвардском университете и руководил им до 1942 года. С 1931 по 1959 годы П.Сорокин — профессор Гарвардского университета, первый профессор социологии в этом университете.
А в 1965 году он стал президентом Американской социологической ассоциации.
Рисунок 3. Гарвардский университет
Таким образом, П. Сорокин приобрёл всемирную известность и признание, но он оставался патриотом своей Родины, даже будучи гражданином США. После нападения Гитлера на Советский Союз П.Сорокин и его жена активно включились в работу общественной организации «Помощь воюющей России», читал лекции на темы «Россия в борьбе с общим врагом», «Русские и американцы» [3]. Это содействовало большому пониманию значения войны, которую вёл Советский Союз, и большому состраданию к народу, на долю которого выпали тяжёлые испытания. Учёный не раз повторял: «Величие современного Советского Союза невозможно игнорировать». Он не раз говорил о необходимости открыть второй фронт, об объединении сил двух великих держав – СССР и США в борьбе с Гитлером общим народом.
Таким образом, Питирим Сорокин, объявленный в СССР врагом и предателем, повёл себя как друг и помогал ему как мог.
Вот только на Родине оценили его слишком поздно. Только в годы перестройки вспомнили о П.Сорокине и признали его как учёного. А он к тому времени уже умер…
Питирим Сорокин – великая потеря для отечественной науки – и как философа, и как социолога. Сегодня его труды, переведённые на десятки языков, изучаются и в России. Но как много можно было бы сделать для развития отечественной социологии, если бы не эмиграция, отторжение такого учёного как Питирим Сорокин! Увы, его теория неравенства оказалась применима к нему самому и советской властью.
9.2: Теории несправедливости и неравенства
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 150255
- Дженнифер Хасти, Дэвид Г. Льюис и Марджори М. Снайпс
- OpenStax
Льюис и Марджори М. Снайпс
0; Университет Райса и OpenStax) Рисунок 9.6 Оркестр West-Eastern Divan Orchestra объединяет музыкантов со всего Ближнего Востока с целью способствовать взаимопониманию между культурными различиями. (кредит: «Barenboim WEDO Salzburg 2013» от WolfD59/Wikimedia Commons, общественное достояние)Эта страница под названием 9.2: Теории неравенства и неравенства распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Дженнифер Хасти, Дэвидом Г. Льюисом, Марджори М. Снайпс. , & Марджори М. Снайпс (OpenStax) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- автор @ Дэвид Г. Льюис
- автор @ Дженнифер Хасти
- автор@Марджори М. Снайпс
- источник@https://openstax.org/details/books/introduction-anthropology
- автор @ Дэвид Г.
Льюис8.6: Социологические теории и глобальное неравенство
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 57071
- Boundless (теперь LumenLearning)
- Безграничный
Функционалисты считают, что высокая заработная плата и статус, предоставляемые юристам, действуют как стимул, побуждающий квалифицированных людей смириться с этими недостатками.- 900:30 Мемориал Маркса в Москве: Этот мемориал Карлу Марксу в Москве гласит: «Пролетарии всех стран, соединяйтесь! Марксизм связан с точкой зрения на стратификацию, которая противопоставляет владельцев средств производства рабочим. Конгресс США в настоящее время: Используя теорию стратификации Вебера, члены Конгресса США находятся на вершине социальной власть и статус, несмотря на относительно небольшое богатство в среднем.
Карта империй и колоний: 1800: к концу 19 в.В 19 веке большая часть Америки находилась под контролем европейских колониальных империй. В настоящее время большая часть Южной и Центральной Америки по-прежнему экономически зависит от иностранных государств в плане капитала и экспортных рынков.