Как построить график сложной функции: Построение графиков сложных функций

График сложных функции

Цель урока:

Систематизировать и расширить знания учащихся по теме: “Графики функций”

Задачи урока:

1. Использовать графики функций в задачах с параметром.
2. Расширить знания при построении графиков функций, связанных с модулем.
3. Исследовать и строить графики суперпозиции функций.
4. Получить новые знания при построении графиков суммы, разности, произведения, частного функций.

План урока:

1. Формулировка темы, цели, задач урока.
2. Обсуждение домашнего задания с приобщением задач с параметром.
3. Исследование и построение графиков функций, связанных с модулем (работа у доски, в парах, в группах).
4. Исследование и построение графиков суммы и произведения функций.
5. Исследование и построение графиков суперпозиции функций.
6. Домашнее задание в виде творческой работы.
7. Итоги урока. Рефлексия.

1. Обсуждение домашнего задания:

Построить график функций и описать свойства:

а)

б)

Правильность построения графиков проверяется с помощью мультимедийного проектора. Свойства функций проговариваются учащимися устно.

Дополнительный вопрос учителя по домашнему заданию:

Найдите все значения параметра a , при каждом из которых уравнение

а)

б)

имеет ровно один, ровно два и ровно один корень.

Вопрос к классу: Сформулируйте определение функции.

2. Построение графиков функций, связанных с модулем (работа в тетрадях).

Построить графики следующих функций:

а)
б)
в)
г)
д)
е)

С помощью ранее построенных графиков, постройте графики следующих функций:

а)
б)
в)
г)
д)
е)

Укажите особенности графиков функций.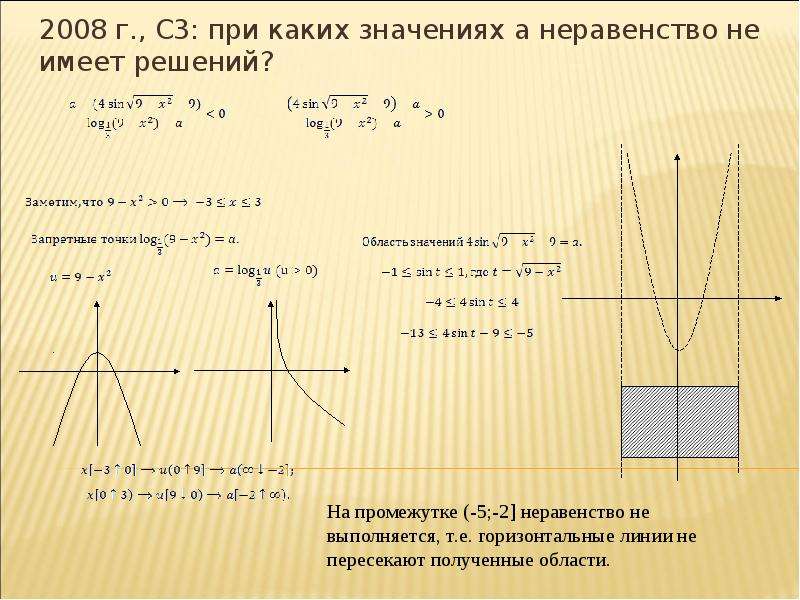

Правильность построения графиков проверяется с помощью мультимедийного проектора. Работа в парах, с последующей проверкой и оценкой.

Вывод:

Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОХ или выше, и симметрично отразить относительно оси ОХ ту часть графика функции, которая расположена ниже оси ОХ.

Для построения графика функции надо сохранить ту часть графика функции, точки которой находятся на оси ОУ или справа от нее, и симметрично отразить эту часть относительно оси ОУ.

Вопрос классу: Сформулируйте определение графика функции?

Работа в группах.

Построить график и описать свойства следующих функций:

а)
б)
в)
г)
д)
е)
ж)
з)

Работают 6 групп, два — три человека работают у доски. Заранее желательно обсудить какая функция является исходной.

Правильность построения графиков проверяется с помощью мультимедийного проектора.

Учащиеся, работавшие у доски, должны назвать особенности построенных графиков функций. Уполномоченные в группах должны назвать вертикальные и горизонтальные асимптоты для графиков своих функций.

Вопрос классу: Сформулируйте определение сложной функции?

3. Два учащихся выполняют задание у доски:

Построить графики и описать свойства следующих функций:

а)

б)

В это время идет исследование:

Как построить график суммы функций ?

1. Найти область определения функции.
2. Произвести сложение ординат точек графиков.

Например: Постройте график функции

Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.

Проверка с помощью мультимедийного проектора.

Здесь же, с помощью проектора, рассмотреть другой пример графика суммы функций

По аналогии обсудить: как построить график разности функций.

Как построить график произведения функций ?

1. Найти область определения функции.
2. Произвести умножение ординат точек графиков.

Например: Постройте график функции

Учащиеся самостоятельно выполняют эту работу. Возможны консультации в парах и группах.

Проверка с помощью мультимедийного проектора. С помощью проектора рассмотреть другой пример графика произведения функций

По аналогии обсудить: как построить график частного функций.

Рассмотреть с помощью проектора график функции

4. С помощью проектора, проверить правильность построения графиков суперпозиции функций (проанализировать работу двух учащихся, которые ранее работали у доски, показать особенности графиков).

Творческое домашнее задание:

Построить графики суммы, разности произведения функций, график сложной функции (подсказка в учебнике после п.2).

Итог урока:

Построение графиков функций один из самых интересных вопросов в курсе алгебры. Графики сложных функций чаще всего получаются очень красивыми и необычными. Поэтому изучение этого материала приносит не только практическую пользу

(например: в физике при изучении волновых явлений), но и эстетическое наслаждение.

Рефлексия:

1. Что вам понравилось (или не понравилось) на уроке?
2. Что нового вы узнали?
3. Ваши пожелания?

Приложение.

Построение графиков сложных функций на основе свойства монотонности

Похожие презентации:

Исследовательская работа по теме: Построение графиков сложных функций на основе свойства монотонности

Степенные функции, их свойства и графики

Степенные функции, их свойства и графики

Функции, их свойства и графики

Преобразование графиков тригонометрических функций и их свойства

Свойства и графики тригонометрических функций

Логарифмическая функция, ее свойства и график

Функции и их свойства

Функции и их свойства.

Предел последовательности и функции. Производная функции и дифференциал

Основные свойства функций и их графики

y
y
k
y
x
k
y
x
k 0
o
k 0
o
x
x
y
y
y sin x
o
y x2
x
o
x
y
y
y
x
y arc tgx
o
o
x
x
y
y
y log a x
o
a 1
0 a 1
a 1
x
0 a 1
o
y ax
x
Итак, рассмотрим функцию :
y arctg 2 x
Это сложная функция. Она является композицией двух функций:
v 2 x (назовём её внутренней функцией )
y arctgv (назовём её внешней функцией).
Каждая из них является элементарной.
Построим графики этих функций в системе координат.
v
y
v 2x
y
y arctg 2 x
y arctgv
2
2
o
x
o
v
o
2
Внутренняя функция является строго возрастающей: х возрастает от до ;

v возрастает от 0 до .
По графику внешней функции определяем: v возрастает от 0 до ;
y возрастает от 0 до 2 .
Итак, при возрастании х от до ,
у возрастает от 0 до 2 .
Контрольная точка: x = 0; y =
4
x
y 2
Построить график функции
Внутренняя функция v= 1/x. Внешняя функция
Строим графики внутренней и внешней функций.
y
v
1
v
x
y 2
1
x
.
y 2v
.
y
v
y 2
1
x
y(1)=2; y(1/2)=4 ; y(-1)= ½.
o
x
o
v
o
Промежутки монотонности внутренней функции:
x возрастает от до 0; v убывает от 0 до
x возрастает от 0 до ; v убывает от до 0
Такому изменению v соответствует убывание y от 1 до 0 и от до 1
Для более точного построения следует использовать контрольные точки,
выбирая те значения x, при которых легко вычислять точные значения y.
y(1) = 2; y(1/2) = 4 ; y(-1) = ½.
x
Итак, построение графика сложной функции y = f (v(x)) в не которых случаях можно осуществить по следующему плану:
1
Начертить графики:
внутренней v = v(x) функции
внешней y = f(v) функции
И построить систему координат ХОУ.
2
Определить промежутки монотонности внутрен
ней функции
и отметить их на оси ОХ плоскости ХОУ.
3
На каждом промежутке определить границы изме
нения внутренней функции, выбирая те значения
y = v(x), которые попадают в область определения
функции y= f(v).
4
По графику внешней функции y= f (v) найти харак
тер изменения функции y.
5
В системе координат ХОУ начертить график
y= y(x).
y
Построить график функции
Строим графики
v x2 1 и
v
y
1
x2 1
1
v
y
1
2
1 2
1
y
v
v x 1
o
x
o
y
v
y
o
х возрастает от 0 до ; v возрастает от 1 до
v возрастает от 1 до ; у убывает от 1 до 0.
Воспользовавшись чётностью функции, получаем такой график
1
x2 1
x
При построении графиков следует иметь
в виду, что область определения сложной
функции Y = f(v(x)) может быть уже области
определения внутренней функции !
Построить график функции
Строим графики элементарных функций
y ln x 2 3x 2
v x 2 3x 2
и
v
y ln v
y ln x 2 3x 2
v x 3x 2
2
.
y
y
y ln v
o
x
o
v
o
x
х возрастает от до 1; v убывает от до 0.
х возрастает от 2 до ; v возрастает от 0 до
На отрезке [ 1;2 ] функция v(x) = 0 либо v(x)< 0 .
Следовательно, при этих значениях функция y = f (v(x)) не определена
И х = 1, х = 2 — вертикальные асимптоты.
v убывает от до 0; у убывает от до .
v возрастает от 0 до ; у возрастает от до .
Построить график функции
y 2
sin x
.
Достаточно построить график на отрезке , длина которого равна
периоду функции.
v
Строим графики v sin x и y 2 .
y
v sin x
y
v
y 2 sin x
y 2v
o
x
o
v
o
х возрастает на отрезке ; v возрастает от -1 до 1
2 2
у возрастает от ½ до 2 . .
х убывает на отрезке
у убывает от 2 до ½.
3
2 ; 2 ; v убывает от 1 до -1;
Контрольные точки: х = 0, у = 1; х = -п/2, у = ½ ; х = п/2, у = 2 ;
х = 3п/2, у = 1/2
x
1
2х
Построить график функции
2
4 х 3
Данная функция является композицией трёх функций:
v 1
u x 2 4x 3
y 2v
u
Отсюда последовательно получаем три графика.
u
y
v
1
1
v 2
x 4x 3
y 2 x 4 x 3
2
u x 2 4x 3
o
x
o
x
o
x
Здесь мы обошлись без графиков функций v = 1/u и y = 2 v , свойства
монотонности которых хорошо известны.
Построить график функции
y
1
.
1 2 x
Конечно, при построении графиков сложных функций надо использовать весь
арсенал элементарных средств: переносы, отражения, сложение графиков и т.д.
Рассмотрим ещё примеры.
y
u
v
v 1 u x
u1 2 x
o
x
y
o
u
1
1 2 x
o
u 2 x
1. Строим график
2. Строим график
x
.
u1 2
u 2 x ,
(симметрия относительно оси ОХ).
3. Строим график v=1+u(x), (смещение на 1 вдоль оси ОУ вверх).
4. Строим график y= 1/v(x), на основании монотонности функций
x
Построить график функции
y lg sin x
Освоив данный метод построения графиков сложных функций,
можно достаточно быстро строить эскизы этих графиков .
v lg u
u sin x
y lg sin x
y
2
o
2
3
x
Итак, на сегодняшнем занятии мы познакомились ещё
с одним из способов построения графиков функций.
Для овладения данной методикой необходима практика.
Этим мы и займёмся на следующих наших занятиях.
Домашнее задание:
Построить графики функций:
1.
2.
3.
4.
y arctg ( x2 4 x 5)
y ln sin x
y 2tgx
y arccos(1 x3 )
?

English     Русский Правила

GeoGebra Tutorial — Комплексные числа

В GeoGebra вы можете ввести комплексное число в строке ввода, используя \(i\) в качестве мнимой единицы; например w=2+3i . Число появляется в графическом представлении в виде точки, и вы можете перемещать его. Вы также можете используйте инструмент Комплексный номер .

Существуют некоторые функции GeoGebra, которые работать как с точками, так и с комплексными числами. Функции abs(w), arg(w) и conjugate(w) говорят сами за себя. Чтобы получить действительную или мнимую часть, используйте x(w) или y(w) соответственно.

Можно выполнять арифметические операции над комплексными числами и использовать некоторые сложные функции.

Сложные функции

Для функции \(\mathbb{C} \rightarrow \mathbb{C}\) нельзя построить график. Вместо этого вы можете визуализировать, как один набор точек отображается на другой набор точек.

Мы будем использовать следующие методы в GeoGebra для визуализации сложных функций.

Пусть \(z\) и \(w\) — комплексные числа такие, что \(w = f(z)\) для некоторой функции \(f\).

• Введите функцию \(f(x)\) (переменной \(x\)) в строке ввода GeoGebra. Скрыть график функции.
• Используйте инструмент Комплексный номер , чтобы добавить точку как комплексное число. Точка будет называться \(z_1\), и вы не сможете переименовать ее в \(z\), так как \(x, y, z\) являются предопределенными именами переменных.
• Напишите f(z_1) , чтобы создать еще одно комплексное число. Переименуйте его в \(w\).

Метод 1 можно использовать для изучения того, как точки отображаются на точки.

Если вы хотите изучить, как отображается набор точек, образующих некоторую кривую, вы можете использовать инструмент Locus .

Пусть \(z\) и \(w\) — комплексные числа такие, что \(w = f(z)\) для некоторой функции \(f\).

Начните с создания какой-нибудь кривой, например круга, линии или графика функции.

• Введите функцию \(f(x)\) (переменной \(x\)) в строке ввода GeoGebra. Скрыть график функции.
• Используйте инструмент Комплексный номер и поместите комплексную точку на кривую. Точка будет называться \(z_1\).
• Напишите f(z_1) , чтобы создать еще одно комплексное число. Переименуйте его в \(w\).
• Используйте инструмент Locus . Сначала нажмите на \(w\), а затем на \(z_1\). Скройте точки \(z_1\) и \(w\).

Если вы хотите нанести на карту многоугольник, вы можете разместить комплексную точку на каждой стороне многоугольника, а затем использовать метод 2 для каждой точки. Делать это утомительно, если вы хотите отобразить несколько полигонов. Более эффективным подходом является использование электронной таблицы.

Пусть \(z\) и \(w\) — комплексные числа такие, что \(w = f(z)\) для некоторой функции \(f\).

Начните с создания кривой, например, с помощью инструмента Правильный многоугольник .

• Введите функцию \(f(x)\) (переменной \(x\)) в строке ввода GeoGebra. Скрыть график функции.
• Используйте инструмент Комплексный номер и поместите комплексную точку на каждой стороне многоугольника. Переименуйте точки в \(A1, A2, A3, \ldots\), чтобы они отображались в столбце A электронной таблицы.
• Напишите f(A1) в ячейке B1 и сделайте соответствующие копии по столбцу B.
• Напишите Locus(B1, A1) в ячейке C1 и сделайте соответствующие копии по столбцу C

Обратите внимание, что эти методы не работают с функциями, которые явно зависят от \(\text{Re } z \), \(\text{Im } z\), \(\text{arg } z\) или \(\ бар{г}\). Методы также не будут работать для полиномиальных функций, имеющих комплексные коэффициенты. Методы будут работать только в том случае, если вы используете функции, которые также можно рассматривать как действительные функции реальной переменной.

Если вы хотите использовать простую функцию, такую ​​как \(f(z) = az + b\), где \(a\) и \(b\) — комплексные коэффициенты, вы можете написать выражение a*z_1+ b , чтобы создать сопоставленную точку.

Преобразования Мёбиуса

Загрузить рабочий лист GeoGebra

Переместите ползунки a,b,c,d, чтобы увидеть различные преобразования Мёбиуса красных фигур.
Из-за большого количества объектов рекомендуется хороший браузер (Chrome).

Преобразование Мёбиуса — это функция \(\mathbb{C} \rightarrow \mathbb{C}\), определяемая равенством

\[f(z) = \frac{az+b}{cz+d}\]

, где \(a, b, c\) и \(d\) — комплексные числа такие, что \(ad-bc\ne 0\).

Преобразование Мёбиуса не определено, когда \(z = -d/c\), так как это означало бы деление на ноль. Если вместо этого мы используем так называемую расширенную комплексную плоскость , эта плоскость также содержит точку в бесконечности. Расширенная комплексная плоскость представлена ​​точками на так называемой сфере Римана , где точка в бесконечности является самой верхней точкой сферы.

Используя сферу Римана, которую мы можем записать как \(\mathbb{C} \cup \{\infty \} \), мы можем определить преобразование Мёбиуса \(\mathbb{C} \cup \{\infty \ } \rightarrow \mathbb{C} \cup \{\infty \} \) следующим образом:

Предположим, что \(ad-bc\ne 0\).

Если \(c \ne 0 \) мы определяем функцию как

\[ f(z) = \begin{случаи} \frac{az+b}{cz+d} &\text{ if } z \ne \infty, z \ne -d/c \\ a/c &\text{ если } z = \infty \\ \infty &\text{ если } z = -d/c \end{случаи} \]

Если \(c = 0\), мы определяем функцию как

\[ f(z) = \begin{случаи} \frac{az+b}{d} &\text{ if } z \ne \infty \\ \infty &\text{ если } z = \infty \end{случаи} \]

Обратите внимание, что если \(c \ne 0\), то \(d = 0\) не может быть, так как \(ad-bc\ne 0\).

Легко показать следующие свойства преобразования Мёбиуса:

1. Если \(f\) и \(g\) — преобразования Мёбиуса, то \(f \circ g\) также является преобразованием Мёбиуса. Другими словами, \(f(g(z)\) является преобразованием Мёбиуса. 9{-1}(f(z)) = z\).

То, что композиция двух преобразований Мёбиуса является другим преобразованием Мёбиуса, означает, что повторяющиеся преобразования могут быть описаны как составные функции.

Упражнения

В большинстве упражнений предполагается, что вы знакомы с инверсией окружности: Неевклидова геометрия ‐ Инверсия в круге.

Упражнение 1

Наборы в комплексной плоскости

Опишите следующие наборы с помощью бумаги и ручки.

• \(1 < \text{Re} z < 5\)
• \(0 < \arg z < \pi/4\)
• \(|z-(2+i)| < 3\)

Упражнение 2

Найти набор

Пусть \(z\) и \(w\) — комплексные числа такие, что

\[ w = \frac{z-1}{z+1}. \]

• Используйте метод 1, чтобы создать построение карты GeoGebra.

• Множество \(\text{Re } z > 0 \) отображается на множество, которое может быть определено уравнением в \(w\). Используйте свою конструкцию GeoGebra, чтобы найти этот набор и сделать предположение. Подсказка: ставьте следы по точкам! 9{-1}\) из \(f(z) = (z-1)/(z+1)\).

Упражнение 3

Сравнение с инверсией окружности

Комплексная карта \[f(z) = \frac{1}{z},\] имеет некоторое сходство с инверсией в единичном круге.

• Создайте комплексную точку \(z_1\) в GeoGebra. Создайте точку \(1/z_1\).

  Создайте единичный круг и отразите \(z_1\) в единичном круге с помощью инструмента Reflect about Circle .

  Сравните две операции \(1/z\) и обращение \(z\) в единичной окружности. Объясните, как связаны эти две операции.

• Найдите комплексную функцию, соответствующую инверсии в единичной окружности. Чем эта функция отличается от функции \(f\)?

• Повороты, отражения и перемещения — это преобразования, сохраняющие углы. Ранее мы также показали, что обращение по окружности сохраняет углы. Сохраняет ли функция \(f(z) = 1/z\) углы или нет? Объясните свое мышление. {i\theta}\). 92.\]

  Когда ваше построение завершено, вы можете изменить окружность, перетащив определяющие ее точки. Пусть две кривые имеют разные цвета, чтобы вы могли легко увидеть, какая кривая относится к какой функции.

  • Для функции \(f\) вы должны угадать, на какую кривую нанесена окружность. Объясните, что вы думаете об этой кривой.

  • Существуют ли простые частные случаи окружностей, для которых можно объяснить отображение функции \(g\)? 9я.\]

    • Для функции \(f\) вы должны уметь угадывать, на какую кривую нанесена линия. Объясните, что вы думаете об этой кривой.

    • Существуют ли простые частные случаи прямых, для которых можно объяснить отображение функции \(g\)?

    Упражнение 7

    Отображение квадрата и треугольника

    • Используйте метод 3, чтобы показать, как квадрат и равносторонний треугольник отображаются с помощью функции

      \[f(z) = \frac{1}{z}.\]

    • Показать, как полигоны отображаются функцией

      \[г(г) = аз\]

      и

      \[ч(г) = г + а\]

      , где \(а\) — комплексный коэффициент. Создайте комплексную точку, представляющую \(a\).

      Используйте столбцы D и E, чтобы показать сопоставления полигонов с помощью \(g\). Используйте столбцы F и G, чтобы показать отображения многоугольников \(h\). Вы не можете использовать для этого функции GeoGebra, но вы можете напрямую писать выражения функций.

    • Опишите и объясните преобразования \(f, g\) и \(h\).

    Упражнение 8

    Преобразование Мебиуса многоугольника

    Для простоты мы будем использовать только действительные коэффициенты \(a, b, c, d\). Сделайте ползунок для каждого коэффициента и напишите функцию \(f(x)\) для преобразования Мёбиуса, определяемого ползунками.

    Создайте конструкцию GeoGebra, визуализирующую, как функция преобразует правильный многоугольник.

    Еще один способ визуализации сложных функций — Википедия: Раскраска домена

    Смотрите захватывающее видео YouTube ‐ Открыты преобразования Мёбиуса

    Малин Кристерссон в рамках Creative Commons Attribution-Noncommercial-Share Alike 2. 5 Швеция Лицензия

    www.malinc.se

     

    Графические функции с комплексными числами

    Все ресурсы Algebra II

    10 диагностических тестов 630 практических тестов Вопрос дня Карточки Учитесь по концепции

    Алгебра II Помощь » Математические отношения и основные графики » Воображаемые числа » Графические функции с комплексными числами

    Найдите

    Возможные ответы:
    Правильный ответ:
    Объяснение:

    Используйте формулу изменения основания для логарифмических функций и учтите тот факт, что и

    Или

     можно решить с помощью 

    Сообщить об ошибке

    Где на числовой прямой окажется  

    Возможные ответы:

    Невозможно определить

    слева от

    в

    справа от

    Правильный ответ: 90 007

    Невозможно определить

    Пояснение:

    Мнимые числа не попадают на числовую прямую — они по определению не действительные числа.

    ** Если задать вопрос, где на числовой прямой находится  , ответ будет слева от 0, потому что .

    Сообщить об ошибке

    Запишите комплексное число в полярной форме, где полярная форма выражает результат в терминах расстояния от начала координат на комплексной плоскости и угла от положительной -оси, , измеряемого в радианах.

    Возможные ответы:
    Правильный ответ:
    Объяснение:

    Чтобы увидеть, какова полярная форма числа, полезно изобразить его на графике, где горизонтальная ось — мнимая часть, а вертикальная ось — действительная часть. Это называется комплексной плоскостью.

    Чтобы найти угол, мы можем найти его дополнительный угол и вычесть его из радианов, так что.

    Используя тригонометрические соотношения,    и  .

    Тогда .

     

    Чтобы найти расстояние , нам нужно найти расстояние от начала координат до точки . Используя теорему Пифагора, найти гипотенузу или .

    Сообщить об ошибке

    Где находится числовая линия?

    Возможные ответы:

    Слева от 0

    На 0

    Справа от 0

    Невозможно определить

    Правильный ответ:

    Слева от 0

    Объяснение:

     Мнимые числа не попадают на числовую прямую по определению, поскольку они не являются действительными числами. Однако, хотя i — мнимое число, равное квадратному корню из -1,  — действительное число, поскольку . Поэтому, . Отрицательные числа падают слева от 0 на числовой прямой.

     

     

    Сообщить об ошибке

    Какое комплексное число представляет этот график?

    Действительные числа представлены по оси X, а мнимые числа представлены по оси Y.

    Возможные ответы:
    Правильный ответ:
    Объяснение:

    В комплексных числах вида а представляет действительную часть числа, а b представляет мнимую часть числа. Чтобы построить график на плоскости, в которой действительные числа представлены по оси X, а мнимые числа представлены по оси Y, поместите точку на a единиц справа от начала координат и на b единиц выше начала координат. На графике показана точка на 2 единицы правее и на 3 единицы выше начала координат, поэтому представленное комплексное число равно .

    Сообщить об ошибке

    Какое комплексное число представляет этот график?

    Действительные числа представлены по оси X, а мнимые числа представлены по оси Y.

    Возможные ответы:
    Правильный ответ:
    Объяснение:

    В комплексных числах вида а представляет действительную часть числа, а b представляет мнимую часть числа. Чтобы построить график на плоскости, в которой действительные числа представлены по оси X, а мнимые числа представлены по оси Y, поместите точку на a единиц справа от начала координат и на b единиц выше начала координат. На графике показана точка на 5 единиц левее и на 2 единицы ниже начала координат, поэтому представленное комплексное число равно .

    Сообщить об ошибке

    Что из нижеперечисленного представляет вещественный компонент комплексного числа?

    Возможные ответы:
    Правильный ответ:
    Объяснение:

     В комплексных числах формы а представляет действительную часть числа, а b представляет мнимую часть числа. В комплексном числе , и .

     

     

    Сообщить об ошибке

    Что из следующего представляет собой мнимую часть комплексного числа -3 + ki, в котором k является константой?

    Возможные ответы:
    Правильный ответ:
    Объяснение:

     В комплексных числах формы  представляет действительную часть числа и представляет мнимую часть числа. В комплексном номере и 

     

     

    Сообщить об ошибке

    Какое комплексное число представляет этот график?

    Действительные числа представлены по оси X, а мнимые числа представлены по оси Y.

    Возможные ответы:
    Правильный ответ:
    Объяснение:

     В комплексных числах формы а представляет действительную часть числа, а b представляет мнимую часть числа. Чтобы построить график на плоскости, в которой действительные числа представлены по оси X, а мнимые числа представлены по оси Y, поместите точку на a единиц справа от начала координат и на b единиц выше начала координат. На графике показана точка на 4 единицы правее и на 7 единиц ниже начала координат, поэтому представленное комплексное число равно .

    Сообщить об ошибке

    Какое комплексное число представляет этот график?

    Действительные числа представлены по оси X, а мнимые числа представлены по оси Y.

    Возможные ответы:
    Правильный ответ:
    Объяснение:

    В комплексных числах вида а представляет действительную часть числа, а b представляет мнимую часть числа.

    No related posts.