Сложение и умножение вероятностей | Математика
Суммой двух событий A и B называется событие C=A+B, состоящее в появлении или события A, или события B, или обоих вместе. Ключевое слово «или» («либо»).
Произведением двух событий A и B называется событие C=AB, состоящее в совместном выполнении события A и события B. Ключевое слово «и».
Два события называются несовместными, если они не могут появиться одновременно.
Теорема сложения.
для несовместных событий;
для совместных событий.
Два события называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого.
Условной вероятностью называют вероятность события A, вычисленную в предположении, что событие B уже наступило.
Теорема умножения.
для независимых событий;
для зависимых событий.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.26. В урне 3 красных и 4 белых шара, 5 красных, 2 белых и 6 черных кубов. Из урны наудачу вынимается одно изделие. Найти вероятность того, что выбранное изделие а) либо белое, либо черное; б) либо красное, либо куб.
РЕШЕНИЕ: а) Рассмотрим события:
A — изделие белое; , так как всего изделий 20, а белых шесть.
B — изделие черное, .
Событие C — изделие либо белое, либо черное можно представить как сумму событий A и B. Следовательно, .
События A и B несовместны, так как вынутое изделие не может быть одновременно и белым и черным. Тогда .
б) Введем события
D — изделие красное; ;
E — изделие куб; ;
F — изделие либо красное, либо куб; .
События D и E совместны, так как вынутое изделие может оказаться красным кубом . Тогда
.
ПРИМЕР 13.2.27. В ящике 10 деталей, 3 из которых бракованные. Наудачу вынимают два изделия. Найти вероятность того, что оба изделия бракованные, если первое изделие: а) возвращается в ящик; б) в ящик не возвращается.
РЕШЕНИЕ. Введем события
A — первое изделие бракованное,
B — второе изделие бракованное,
C — оба изделия бракованные.
Событие C представляет собой произведение событий A и B; C=AB.
а) Если первое изделие возвращается в ящик, то вне зависимости от того, какое изделие было первое, то есть A и B — независимые события. Тогда .
б) Если изделие не возвращается, то вероятность события B будет меняться в зависимости от того, какое изделие было вынуто первым (бракованное или небракованное). Найдем вероятность события B в предположении, что первое изделие оказалось бракованным. , так как всего осталось 9 изделий, два из которых бракованные. Тогда
.
ПРИМЕР 13.2.28. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадет: а) только один из стрелков; б) хотя бы один стрелок.
РЕШЕНИЕ. Рассмотрим события
первый стрелок попал; ;
первый стрелок промахнулся; ;
второй стрелок попал; ;
второй стрелок промахнулся; .
а) Событие B попал только один стрелок, используя алгебру событий, можно представить в виде
.
Тогда по теореме сложения вероятностей несовместных и умножения независимых событий имеем:
.
б) Событие C попал хотя бы один стрелок можно представить как сумму двух несовместных событий: B — попал только один стрелок и D- попали оба стрелка
.
Однако вероятность события C можно найти другим способом. Рассмотрим событие оба промахнулись,
.
Тогда .
ПРИМЕР 13.2.29. Вероятность выхода из строя хотя бы одного их трех станков в течение смены равна 0,488. Найти вероятность выхода из строя одного станка за смену, если вероятности выхода из строя каждого станка одинаковы.
РЕШЕНИЕ. Пусть A — выход из строя хотя бы одного станка. Тогда нормальная работа всех трех станков; . Обозначим через p вероятность нормальной работы каждого станка, тогда или . Вероятность выхода из строя каждого станка вычисляется .
Примеры и задачи для самостоятельного решения
Решить задачи, используя теоремы сложения и умножения вероятностей
13.2.4.1. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
13.2.4.2. В урне белых и черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара будут белыми, если выемку производить: а) с возвращением; б) без возвращения.
13.2.4.3. В мешке смешаны нити, среди которых 30% белых, а остальные – красные. Определить вероятности того, что вынутые наудачу две нити будут а) одного цвета; б) разных цветов.
13.2.4.4. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы за определенный промежуток времени первого, второго и третьего элемента соответственно равны 0,6;0,7;0,8. Найти вероятности того, что за это время безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента; г) хотя бы два элемента.
13.2.4.5. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.
13.2.4.6. Вероятность одного попадания в цель при одном залпе из двух орудий равно 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.
13.2.4.7. Брошены три игральные кости. Найти вероятности следующих событий: а) на каждой из выпавших граней появится пять очков; б) на всех выпавших гранях появится одинаковое число очков; в) на двух выпавших гранях появится одно очко, а на третьей грани – другое число очков; г) на всех выпавших гранях появится разное число очков.
13.2.4.8. Вероятность попадания в мишень стрелком при одном выстреле равна 0,8. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью меньшей 0,4, можно было ожидать, что не будет ни одного промаха?
13.2.4.9. Сколько раз нужно бросить игральную кость, чтобы с вероятностью, не меньшей 0,9, хотя бы один раз выпала «шестерка»?
13.2.4.10. Монета бросается до тех пор, пока 2 раза подряд она не выпадет одной и той же стороной. Найти вероятности следующих событий: а)опыт окончится до шестого бросания; б) потребуется четное число бросаний.
13.2.4.11. Числитель и знаменатель рациональной дроби написаны наудачу. Какова вероятность того, что эта дробь несократима на 5?
13.2.4.12. Из цифр 1,2,3,4,5 сначала выбирается одна, а затем из оставшихся четырех – вторая цифра. Предполагается, что все 20 возможных исходов равновероятны. Найти вероятность того, что будет выбрана нечетная цифра а) в первый раз; б) во второй раз; в) в оба раза.
13.2.4.13. Найти вероятность того, что наудачу взятое натуральное число, не превосходящее 100, будет делиться а) на 2 или на 5; б) и на 2, и на 5.
13.2.4.14. Три команды спортивного общества состязаются соответственно с тремя командами общества . Вероятности того, что команды общества выиграют матчи у команд общества таковы: при встрече с 0,8; с 0,4; с 0,4. Для победы необходимо выиграть не менее двух матчей из трех (ничьи во внимание не принимаются). Победа какого из обществ вероятнее?
13.2.4.15. Возле остановки останавливаются трамваи маршрутов 2,4,5,9. Для рабочего попутными являются маршруты 5 и 9. Вычислить вероятность того, что к остановке первым подойдет трамвай маршрута попутного для него номера, если по линиям маршрутов №2,4,5,9 курсируют соответственно 15,12,10,13 поездов. Протяженности маршрутов считаются одинаковыми.
13.2.4.16. Вероятность того, что в мужской обувной секции магазина очередной будет продана пара обуви 46-го размера равна 0,01. Сколько должно быть продано пар обуви в магазине, чтобы с вероятностью, не меньшей 0,9 можно было ожидать, что будет продана хотя бы одна пара обуви 46-го размера.
13.2.4.17. В урне имеется пять шаров с номерами от 1 до 5. Наудачу по одному извлекают три шара без возвращения. Найти вероятность следующих событий: а) последовательно появятся шары с номерами 1,4,5; б) извлеченные шары будут иметь номера 1,4,5 независимо от того, в какой последовательности они появились.
13.2.4.18. В круг радиуса вписан правильный треугольник. Внутрь круга наудачу брошены четыре точки. Найти вероятности следующих событий: а) все четыре точки попадут внутрь треугольника; б) одна точка попадет внутрь треугольника и по одной точке попадает на каждый «малый» сегмент. Предполагается, что вероятность попадания точки в фигуру пропорциональна площади фигуры и не зависит от ее расположения.
13.2.4.19. Отрезок разделен на три равные части. На этот отрезок наудачу брошены три точки. Найти вероятность того, что на каждую из трех частей отрезка попадет по одной точке. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
13.2.4.20. Три самолета независимо друг от друга производят одиночное бомбометание по некоторой цели. Первый самолет сбрасывает 4 бомбы по 250 кг, второй – 2 бомбы по 500 кг, третий – 1 бомбу в 1000 кг. Вероятность попадания для первого самолета равна 0,2, для второго – 0,3, для третьего – 0,4. Для разрушения цели достаточно попадания одной бомбы весом не менее 500 кг или двух – весом по 250 кг. Найти вероятность разрушения цели.
13.2.4.21. При одном цикле обзора радиолокационной станции, следящей за космическим объектом, объект обнаруживается с вероятностью . Обнаружение объекта в каждом цикле происходит независимо от других циклов сканирования. Найти вероятность того, что при циклах объект будет обнаружен.
13.2.4.22. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча и после игры их кладут обратно. При выборе мячей новые от использованных не отличают. Какова вероятность того, что после трех игр не останется новых мячей?
13.2.4.23. Слово «лотос», составленное из букв – карточек, рассыпано на отдельные буквы, которые тщательно перемешаны. Из них выбираются последовательно три карточки. Какова вероятность того, что при этом появится слово «сто»?
13.2.4.24. Подбрасываются две игральные кости. Найти вероятность того, что произведение числа очков на первой и второй кости будет четным числом.
13.2.4.25. Вероятность попадания в первую мишень для данного стрелка равна 2/3. Если при первом выстреле зафиксировано попадание, то стрелок получает право на второй выстрел по другой мишени. Вероятность поражения обеих мишеней при двух выстрелах равна 0,5. Определить вероятность поражения второй мишени.
13.2.4.26. На пяти карточках написаны цифры от 1 до 5. Друг за другом вытаскивают три карточки и в порядке поступления записывают число. Вероятность какого события выше: “число меньше 450” или ”число больше 200”?
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Теорема сложения вероятностей, следствия и формулы
Теорема сложения вероятностей совместных событий
В случае если события и несовместны, то есть , то имеет место следующая теорема.
Теорема сложения вероятностей несовместных событий
Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий , равна сумме вероятностей этих событий
Следствие 2. Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
Следствие 3. Сумма противоположных событий равна единице, то есть
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Урок 33. вероятность события. сложение вероятностей — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Глоссарий по теме
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Равновозможные события — такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9. сс.242-261.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Рассмотрим пример:
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
Варианты ответов:
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Определение.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
- Процесс доставания предмета из коробки является испытанием.
- Результат доставания предмета из корзины является событием.
- Событие «вынутый предмет окажется клубком» является достоверным событием.
- События «вынутый предмет не окажется клубком» или «вынутый предмет окажется красным клубком» являются невозможными событиями.
- Событие «вынутый предмет окажется зеленым клубком» является вероятным событием.
А={вынутый предмет оказался клубком}.
В={вынутый предмет не оказался клубком.
С={вынутый предмет оказался зеленым клубком}.
D ={вынутый предмет оказался красным клубком}.
2. Определим еще несколько важных понятий теории вероятностей
Определение
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω= {w 1, w 2, w 3, w 4, w 5, w6}, где wi— выпадение i очков.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Например:
- A – сдал экзамен по математике;
- Ᾱ – не сдал экзамен по математике.
Определение.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Пример .
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпало два «орла»
— Выпало две «решки»
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Определение.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Пример.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число 
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
2 .Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Например:
- Пусть А — идет дождь, B — идет снег, тогда А + В – «идет снег или дождь»
- При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 — «произошло не больше двух попаданий»
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C⋅D — из урны вынули два белых шара
- Пусть С — из урны вынули белый шар, D — из урны вынули белый шар, тогда C
 ⋅- из урны вынули два шара: белый и не белый
⋅- из урны вынули два шара: белый и не белый
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Р(А+В)=Р(А)+Р(В)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Решение:
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
Теоремы сложения и умножения вероятностей
Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то событие А+В – попадание хотя бы при одном выстреле (или при первом выстреле, или при втором, или в обоих случаях).
Теорема сложения вероятностей:
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B)
Следствие: Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An)
Теорема 1:
Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна единице:
P(A1)+P(A2)+…+P(An)=1
Теорема 1*: (частный случай теоремы 2)
Сумма вероятностей противоположных событий равна единице:
P(A)+P(Ᾱ)=1 или p+q=1, где P(A)=p, Р(Ᾱ)=q
Пример:
Пусть в результате испытания возможны только два единственно возможных события. Например, а) при одном бросании монеты — «выпал герб» и «выпала цифра»; б) при одном бросании игральной кости — «выпало 6 очков» и «не выпало 6 очков»; в) при одном выстреле — «попадание в мишень» и «не попадание в мишень». В каждой паре событий появление одного исключает появление второго. Действительно, если монета выпала гербом, то уже не может выпасть цифрой; игральная кость не может одновременно выпасть сразу двумя гранями; стрелок попадая в мишень, исключает промах. Итак, в данных примерах противоположными событиями являются: а) A={выпал герб}, Ᾱ={выпала цифра}; б) А={выпало 6 очков}, Ᾱ={не выпало 6 очков}; в) А={попадание в мишень}, Ᾱ={не попадание в мишень}, а Р(А)+Р(Ᾱ)=1.Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена.
Теорема умножения вероятностей:
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
P(AB)=P(A)•P(B)
Теорема сложения вероятностей несовместных событий —
Пусть события А и В ― несовместные, причем вероятности этих событий известны. Вопрос: как найти вероятность того, что наступит одно из этих несовместных событий? На этот вопрос ответ дает теорема сложения.
Теорема. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
p(А + В) = p(А) + p(В) (1.6)
Доказательство. Действительно, пусть n – общее число всех равновозможных и несовместных (т.е. элементарных) исходов. Пусть событию А благоприятствует m1 исходов, а событию В – m2 исходов. Тогда согласно классическому определению вероятности этих событий равны: p(А) = m1 / n, p(B) = m2 / n .
Так как события А и В несовместные, то ни один из исходов, благоприятствующих событию А, не благоприятствует событию В (см. схему ниже).

Поэтому событию А+В будут благоприятствовать m1 + m2 исходов. Следовательно, для вероятности p(А + В) получим:
p(А + В) =  =
=  +
+ = p(А) + p(В).
= p(А) + p(В).
Что и требовалось доказать.
Используя метод математической индукции, теорему сложения двух несовместных событий можно обобщить на случай любого числа попарно несовместных событий, которая в этом случае примет формулировку: вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий.
p(А1 + А2 + … + Аn) = p(А1) + p(А2) + … + p(Аn),
или
 =
=  .
.
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице:
p(А) + p(В) + p(С) + … + p(D) = 1.
Действительно, пусть события А, В, С, … , D образуют полную группу. В силу этого они являются несовместными и единственно возможными. Поэтому событие А + В + С + …+ D, состоящее в появлении ( в результате испытания) хотя бы одного из этих событий, является достоверным, т.е. А+В+С+…+D =  и p(А+В+С+ …+D) = 1.
и p(А+В+С+ …+D) = 1.
В силу несовместности событий А, В, С, …, D справедлива формула:
p(А+В+С+ …+ D) = p(А) + p(В) + p(С) + … + p(D) = 1.
Пример. В урне 30 шаров, из них 10 красных, 5 синих и 15 белых. Найти вероятность извлечения красного или синего шара при условии, что из урны извлекли только один шар.
Решение. Пусть событие А1 – извлечение красного шара, а событие А2 – извлечение синего шара. Данные события несовместны, причём p(А1) = 10 / 30 = 1 / 3; p(А2) = 5 / 30 = 1 /6. По теореме сложения получим:
p(А1 + А2) = p(А1) + p(А2) = 1 / 3 + 1 / 6 = 1 / 2.
Замечание 1. Подчеркнём, что по смыслу задачи необходимо прежде всего установить характер рассматриваемых событий – являются ли они несовместными. Если приведённую теорему применять к совместным событиям, то результат получится неверным.
Формулы сложения вероятностей — Студопедия
В случаях, когда интересующее событие является суммой других событий, для нахождения его вероятности используется формула сложения.
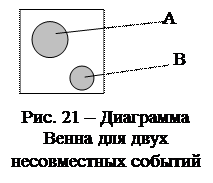 Формула сложения имеет две основные разновидности – для совместных и для несовместных событий. Обосновать эти формулы можно, используя диаграммы Венна (рис. 21). Напомним, что на этих диаграммах вероятности событий численно равны площадям соответствующих этим событиям зон.
Формула сложения имеет две основные разновидности – для совместных и для несовместных событий. Обосновать эти формулы можно, используя диаграммы Венна (рис. 21). Напомним, что на этих диаграммах вероятности событий численно равны площадям соответствующих этим событиям зон.
Для двух несовместных событий :
Р(А+В) = Р(А) + Р(В).(8, а)
Для N несовместных событий, вероятность их суммы равна сумме вероятностей этих событий:
 =
= 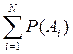 .(8б)
.(8б)
Из формулы сложения несовместных событий имеются два важных следствия.
Следствие 1.Для событий, образующих полную группу, сумма их вероятностей равна единице:
 = 1.
= 1.
Это объясняется следующим. Для событий, образующих полную группу, в левой части выражения (8б) находится вероятность того, что произойдёт одно из событий Аi ,но так как полная группа исчерпывает весь перечень возможных событий, то одно из таких событий произойдёт обязательно. Таким образом, в левой части записана вероятность события, которое обязательно произойдёт – достоверного события. Вероятность его равна единице.
Следствие 2.Сумма вероятностей двух противоположных событий равна единице:
Р(А) + Р(Ā) = 1.
Это следствие вытекает из предыдущего, так как противоположные события всегда образуют полную группу.
Пример 15
Вероятность работоспособного состояния технического устройства равна 0,8. Найти вероятность отказа этого устройства за тот же период наблюдений.
Решение.
Важное замечание. В теории надёжности принято вероятность работоспособного состояния обозначать буквой р, а вероятность отказа — буквой q. В дальнейшем будем использовать эти обозначения. Как та, так и другая вероятности являются функциями времени. Так, для больших периодов времени вероятность работоспособного состояния любого объекта приближается к нулю. Вероятность отказа любого объекта близка к нулю для малых периодов времени. В тех случаях, когда период наблюдения в задачах не указан, подразумевается, что он одинаков для всех рассматриваемых объектов.
 Нахождение устройства в состояниях работоспособности и отказа – противоположные события. Пользуясь следствием 2, получим вероятность отказа устройства:
Нахождение устройства в состояниях работоспособности и отказа – противоположные события. Пользуясь следствием 2, получим вероятность отказа устройства:
q = 1 – р = 1 – 0,8 = 0,2.
Для двух совместных событий формула сложения вероятностей имеет вид:
Р(А+В) = Р(А) + Р(В) – Р(АВ), (9)
что иллюстрирует диаграмма Венна (рис. 22).
Действительно, чтобы найти всю заштрихованную площадь (она соответствует сумме событий А + В), нужно из суммы площадей фигур А и В вычесть площадь общей зоны (она соответствует произведению событий АВ), так как иначе она будет учтена дважды.
Для трех совместных событий формула сложения вероятностей усложняется:
Р(А+В+С)=Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС).(10)
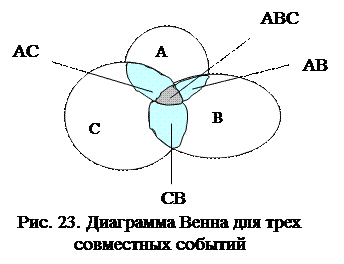 На диаграмме Венна (рис. 23) искомая вероятность численно равна общей площади зоны, образованной событиями А, В и С (для упрощения рисунка единичный квадрат на нем не показан).
На диаграмме Венна (рис. 23) искомая вероятность численно равна общей площади зоны, образованной событиями А, В и С (для упрощения рисунка единичный квадрат на нем не показан).
После того, как из суммы площадей зон А, В и С вычтены площади зон АВ, АС и СВ получилось, что площадь зоны АВС была просуммирована трижды и трижды вычтена. Поэтому для учета этой площади она должна быть добавлена в окончательное выражение.
При увеличении числа слагаемых формула сложения становится всё более и более громоздкой, но принцип её построения остаётся прежним: сначала суммируются вероятности событий взятых по одиночке, затем вычитаются вероятности всех по парных комбинаций событий, прибавляются вероятности событий взятых тройками, вычитаются вероятности комбинаций событий взятых четверками и т.д.
В итоге следует подчеркнуть: формула сложения вероятностей совместных событий при количестве слагаемых от трех и более громоздка и неудобна к применению, использование ее при решении задач нецелесообразно.
Пример 16
Для ниже приведенной схемы электроснабжения (рис. 24) определить вероятность отказа системы в целом QС по вероятностям отказа qi отдельных элементов (генератора, трансформаторов и линии).

 Состояния отказа отдельных элементов системы электроснабжения, так же как и состояния работоспособности, всегда являются попарно совместными событиями, так как нет никаких принципиальных препятствий к тому, чтобы одновременно производился ремонт, например, линии и трансформатора. Отказ системы наступает при отказе любого её элемента: или генератора, или 1-го трансформатора, или линии, или 2-го трансформатора, или при отказе любой пары, любой тройки или всех четырёх элементов. Следовательно, искомое событие – отказ системы является суммой отказов отдельных элементов. Для решения задачи может быть использована формула сложения совместных событий:
Состояния отказа отдельных элементов системы электроснабжения, так же как и состояния работоспособности, всегда являются попарно совместными событиями, так как нет никаких принципиальных препятствий к тому, чтобы одновременно производился ремонт, например, линии и трансформатора. Отказ системы наступает при отказе любого её элемента: или генератора, или 1-го трансформатора, или линии, или 2-го трансформатора, или при отказе любой пары, любой тройки или всех четырёх элементов. Следовательно, искомое событие – отказ системы является суммой отказов отдельных элементов. Для решения задачи может быть использована формула сложения совместных событий:
Qс = q г + q т1 + q л + q т2 – q гq т1 – q гq л – q гq т2 – q т1q л – q т1q т2 – q лq т2 + qгqт1qл + q гq лq т2 + q гq т1q т2 + q т1q т2q л – qг q т1q лq т2.
Это решение ещё раз убеждает в громоздкости формулы сложения для совместных событий. В дальнейшем будет рассмотрен другой более рациональный способ решения данной задачи.
Полученное выше решение может быть упрощено с учётом того, что вероятности отказов отдельных элементов системы электроснабжения для применяемого обычно в расчётах надежности периода в один год достаточно малы (порядка 10-2). Поэтому все слагаемые кроме первых четырех можно отбросить, что практически не повлияет на численный результат. Тогда можно записать:
Qс≈q г + q т1 + q л + q т2.
 Однако к подобным упрощениям надо относится осторожно, внимательно изучая их последствия, так как часто отбрасываемые слагаемые могут оказаться соизмеримыми с первыми.
Однако к подобным упрощениям надо относится осторожно, внимательно изучая их последствия, так как часто отбрасываемые слагаемые могут оказаться соизмеримыми с первыми.
Пример 17
Определить вероятность работоспособного состояния системы РС, состоящей из трех резервирующих друг друга элементов.
Решение. Резервирующие друг друга элементы на логической схеме анализа надёжности изображаются соединенными параллельно (рис. 25):
Резервированная система работоспособна, когда работоспособен или 1-й, или 2-й, или 3-й элемент, или работоспособна любая пара, или все три элемента совместно. Следовательно, работоспособное состояние системы есть сумма работоспособных состояний отдельных элементов. По формуле сложения для совместных событий Рс = Р1 + Р2 + Р3 – Р1Р2 – Р1Р3 – Р2Р3 + Р1Р2Р3., где Р1, Р2 и Р3 – вероятности работоспособного состояния элементов 1, 2 и 3 соответственно.
В данном случае упрощать решение, отбрасывая по парные произведения нельзя, поскольку такое приближение даст значительную погрешность (эти произведения обычно числено близки к первым трём слагаемым). Как и в примере 16, эта задача имеет другое более компактное решение.
Пример 18
 Для двухцепной линии электропередачи (рис. 26) известна вероятность отказа каждой цепи: q1 = q2 = 0,001. Определить вероятности того, что линия будет иметь стопроцентную пропускную способность – Р(R100), пятидесяти процентную пропускную способность — Р(R50), и вероятность того, что система откажет – Q.
Для двухцепной линии электропередачи (рис. 26) известна вероятность отказа каждой цепи: q1 = q2 = 0,001. Определить вероятности того, что линия будет иметь стопроцентную пропускную способность – Р(R100), пятидесяти процентную пропускную способность — Р(R50), и вероятность того, что система откажет – Q.
Линия имеет стопроцентную пропускную способность, когда работоспособна и 1-я и 2-я цепь:
Р(100%) = р1р2 = (1 – q1)(1 – q2) =
= (1 – 0,001)(1 – 0,001) = 0,998001.
Линия отказывает, когда отказывает и 1-я и 2-я цепь:
Р(0%) = q1 q2 =0,001∙0,001 = 10-6.
Линия имеет пятидесяти процентную пропускную способность, когда работоспособна 1-я цепь и отказала 2-я, или когда работоспособна 2-я цепь и отказала 1-я:
Р(50%)= р1q2 + р2 q1 = 2∙0,999∙10-3 = 0,001998.
В последнем выражении использована формула сложения для несовместных событий, каковыми они и являются.
События, рассмотренные в этой задаче, составляют полную группу, поэтому сумма их вероятностей составляет единицу.
3. Теоремы сложения вероятностей.
Суммой
двух событий А+В 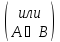 называется
событие, которое состоит в том, что
произойдёт или событие А или событие В
или оба они одновременно.
называется
событие, которое состоит в том, что
произойдёт или событие А или событие В
или оба они одновременно.
Суммой нескольких событий (А₁+А₂+А₃+…..+Аn) называется событие, которое состоит в том, что произойдёт хотя бы одно из этих событий.
Теорема
1: Вероятность двух несовместных событий
равна сумме вероятностей этих событий: 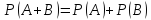
Теорема 2: Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:
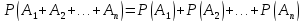
Следствие 1:Сумма вероятностей событий, которые образуют полную группу, равна 1:
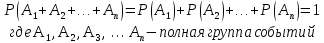
Следствие 2: Сумма вероятностей противоположных событий равна 1:
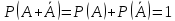
Теорема 3: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность совместного их появления:
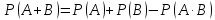
Пример: Бросаем 2 кубика: А – выпадет чётное число на первом кубике
В — выпадет чётное число на втором кубике
(А+В)
– выпадет чётное число на первом или
втором кубике или на первом и втором
одновременно: 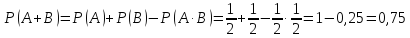
4. Теоремы умножения вероятностей.
События бывают зависимыми и независимыми.
Событие В не зависит от события А, если Р(В) не изменяется от того, что произошло событие А.
Событие В зависит от события А, если Р(В) изменяется от того, что произошло событие А.
Р(В/А) – вероятность события В, при условии, что произошло событие А – это условная вероятность события В.
Произведением
двух событий А·В 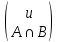 ,
называется событие, которое состоит в
том, что произойдёт и событие А и событие
В.
,
называется событие, которое состоит в
том, что произойдёт и событие А и событие
В.
Произведением нескольких событий А·В·С·D·… называется событие, которое состоит в том, что произойдут все эти события.
Теорема 1. Вероятность совместного появления двух независимых событий равна произведению их вероятностей.
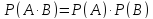
Теорема 2. Вероятность совместного появления двух зависимых событий (В зависит от А) равна произведению вероятности события А на условную вероятность события В.
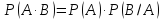
5. Формула полной вероятности.
Иногда
событие А может произойти только
совместно с одним из нескольких других
событий, их принято называть гипотезами и обозначать 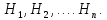 Тогдаполная
вероятность события А вычисляется по формуле:
Тогдаполная
вероятность события А вычисляется по формуле:

Пример:  Н₃
Н₃ 
Н₁ Н₂ СобытиеА:попадёмв домик.
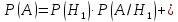
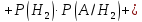


6. Формулы Байеса.
До
проведения опыта мы имели вероятности гипотез 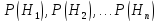
(В
примере 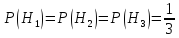 ).
).
После проведения опыта:
Пусть
событие А произошло (т.е. попали в домик),
вероятности гипотез 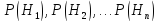 изменились. Для того, чтобы вычислить
вероятности гипотез, при условии, что
произошло событие А используют формулы
Байеса:
изменились. Для того, чтобы вычислить
вероятности гипотез, при условии, что
произошло событие А используют формулы
Байеса:
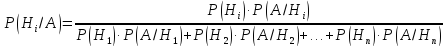
Пример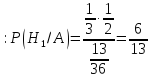
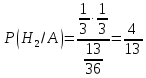
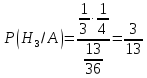
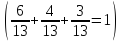
Теорема сложения о вероятности | Бесплатная помощь с домашним заданием
Вероятность наступления события можно легко найти, используя определение вероятности. Но просто определение не может быть использовано для определения вероятности наступления хотя бы одного из данных событий. Теорема, известная как «Теорема сложения», решает эти типы проблем. Формулировка и доказательство «теоремы сложения» и ее использования в различных случаях заключаются в следующем.
Взаимоисключающие события:
Два или более события считаются взаимоисключающими, если у них нет общего элемента.то есть, если возникновение одного из событий предотвращает возникновение других, то эти события считаются взаимоисключающими.
Пример:
Событие получения 2 решек, A и событие получения 2 решек, B , когда подбрасываются две монеты, являются взаимоисключающими.
Потому что A = {HH}; B = {TT}.
Взаимно исчерпывающие события:
Два события считаются взаимоисключающими, если есть уверенность в том, что произойдет хотя бы одно из этих двух событий.то есть одно из этих событий обязательно произойдет.
Если A и B являются двумя взаимно исчерпывающими, то вероятность их объединения равна 1.
, то есть P (AUB) = 1.
Пример:
Событие выпадения головы и событие выпадения хвоста при подбрасывании монеты являются взаимоисключающими.
Теорема сложения о вероятности:
Если A и B — любые два события, то вероятность наступления хотя бы одного из событий определяется как P (AUB) = P (A) + P (B) — P (A ∩B).
Проба:
Поскольку события представляют собой не что иное, как наборы,
Из теории множеств имеем
n (AUB) = n (A) + n (B) — n (A∩B).
Разделив приведенное выше уравнение на n (S), (где S — это пространство выборки)
n (AUB) / n (S) = n (A) / n (S) + n (B) / n (S) — n (A∩B) / n (S)
Тогда по определению вероятности
P (AUB) = P (A) + P (B) — P (A∩B).
Пример:
Если вероятность решения задачи двумя учениками, Джорджем и Джеймсом, равна 1/2 и 1/3 соответственно, то какова вероятность того, что проблема будет решена.
Решение:
Пусть A и B будут вероятностями решения проблемы Джорджем и Джеймсом соответственно.
Тогда P (A) = 1/2 и P (B) = 1/3.
Проблема будет решена, если ее решит и хотя бы один из них.
Итак, нам нужно найти P (AUB).
По теореме сложения вероятностей имеем
P (AUB) = P (A) + P (B) — P (A∩B).
P (AUB) = 1/2 +.1/3 — 1/2 * 1/3 = 1/2 + 1 / 3-1 / 6 = (3 + 2-1) / 6 = 4/6 = 2/3
Примечание:
Если A и B — любые два взаимоисключающих события, то P (A∩B) = 0.
Тогда P (AUB) = P (A) + P (B).
Вам также нужна помощь по географии? Взгляните на наши услуги репетиторства по географии.
SchoolTutoring Academy — ведущая компания в сфере образовательных услуг для школьников и школьников. Мы предлагаем программы репетиторства для учеников K-12, AP и колледжей.Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Окотоксе, посетите: Репетиторство в Окотоксе.
.Что такое теоремы сложения и умножения о вероятности?
Что такое теоремы сложения и умножения о вероятности?
Теорема вероятности сложения и умножения
Сформулируйте и докажите вероятностную теорему сложения и умножения на примерах
Теорема сложения и умножения
Обозначения:
- P (A + B) или P (A∪B) = вероятность наступления события A или B
= вероятность наступления событий A или B или обоих
= вероятность наступления по крайней мере одного события A или B - P (AB) или P ( A∩B) = Вероятность совершения событий A и B вместе.
(1) Если события не являются взаимоисключающими:
Если A и B — два события, которые не исключают друг друга, тогда
P (A∪B) = P (A) + P (B) — P ( A∩B)
или P (A + B) = P (A) + P (B) — P (AB)
Для любых трех событий A, B, C
P (A∪B∪C) = P (A ) + P (B) + P (C) — P (A∩B) — P (B∩C) — P (C∩A) + P (A∩B∩C)
или P (A + B + C ) = P (A) + P (B) + P (C) — P (AB) — P (BC) — P (CA) + P (ABC)
(2) Когда события являются взаимоисключающими:
Если A и B являются взаимоисключающими событиями, то
n (A∩B) = 0 ⇒ P (A∩B) = 0
∴ P (A∪B) = P (A) + P (B) .
Для любых трех событий A, B, C, которые являются взаимоисключающими,
P (A∩B) = P (B∩C) = P (C∩A) = P (A∩B∩C) = 0
∴ P (A∪B∪C) = P (A) + P (B) + P (C).
Вероятность возникновения любого из нескольких взаимоисключающих событий равна сумме их вероятностей, , т.е. , если A 1 , A 2 ……… A n являются взаимоисключающими событиями, тогда
P (A 1 + A 2 +… + A n ) = P (A 1 ) + P (A 2 ) + …… + P (A n )
i.е. P (Σ A i ) = Σ P (A i ).
(3) Когда события независимы:
Если A и B являются независимыми событиями, то P (A∩B) = P (A) .P (B)
∴ P (A∪B) = P (A) + P (B) — P (A) .P (B)
(4) Некоторые другие теоремы
- Пусть A и B — два события, связанные со случайным экспериментом, тогда
- Обобщение теоремы сложения:
Если A 1 , A 2 ……… A n — n событий, связанных со случайным экспериментом, то - Неравенство Були: Если A 1 , A 2 ……… A n — это n событий, связанных со случайным экспериментом, затем
Эти результаты могут быть легко получены с помощью принципа математической индукции.
Условная вероятность
Пусть A и B — два события, связанные со случайным экспериментом. Тогда вероятность появления A при условии, что B уже произошло и P (B) ≠ 0, называется условной вероятностью и обозначается P (A / B).
Таким образом, P (A / B) = вероятность появления A, учитывая, что B уже произошло.
Аналогично, P (B / A) = вероятность появления B, учитывая, что A уже произошло.
Иногда P (A / B) также используется для обозначения вероятности появления A при возникновении B.Точно так же P (B / A) используется для обозначения вероятности появления B при возникновении A.
Теорема вероятности умножения
- Если A и B — это два события, связанные со случайным экспериментом, то P (A∩B) = P (A) .P (B / A), если P ( A ) ≠ 0 или P (A∩B) = P (B) .P (A / B), если P (B) ≠ 0.
- Расширение теоремы умножения:
Если A 1 , A 2 ……… A n — это n событий, связанных со случайным экспериментом, затем
P (A 1 ∩A 2 ∩A 3 ∩… ∩A n ) = P ( A 1 ) P (A 2 / A 1 ) P (A 3 / A 1 ∩A 2 ) …… P (A n / A 1 ∩A 2 ∩… ∩A n − 1 ),
где P (A i / A 1 ∩A 2 ∩… ∩A i − 1 ), представляет собой условную вероятность события, учитывая, что события A 1 , A 2 ……… A i — 1 уже произошли. - Теоремы умножения для независимых событий:
Если A и B являются независимыми событиями, связанными со случайным экспериментом, то P (A∩B) = P (A) .P (B) то есть вероятность одновременного наступления двух независимых событий равна произведению их вероятностей. По теореме умножения P (A∩B) = P (A) .P (B / A). Поскольку A, и B, являются независимыми событиями, поэтому P (B / A) = P (B). Следовательно, P (A∩B) = P (A).П (В). - Расширение теоремы умножения для независимых событий:
Если A 1 , A 2 ……… A n являются независимыми событиями, связанными со случайным экспериментом, то
P (A 1 ∩A 2 ∩A 3 ∩… ∩A n ) = P (A 1 ) P (A 2 ) ..… P (A n ).
По теореме умножения имеем
P (A 1 ∩A 2 ∩A 3 ∩… ∩A n ) = P (A 1 ) P (A 2 / A 1 ) P (A 3 / A 1 ∩A 2 ) …… P (A n / A 1 ∩A 2 ∩… ∩A n − 1 )
Так как A 1 , A 2 ……… A n-1 , A n являются независимыми событиями, поэтому
P (A 2 / A 1 ) = P (A 2 ), P (A 3 / A 1 ∩A 2 ) = P (A 3 ), ……, P (A n / A 1 ∩A 2 ∩… ∩A n −1 ) = P (A n )
Следовательно, P (A 1 ∩A 2 ∩A 3 ∩… ∩A n ) = P (A 1 ) P (A 2 )..… P (A n ).
Вероятность хотя бы одного из n независимых событий:
Если p 1 , p 2 ……… p n будет вероятностями возникновения n независимых событий A 1 , A 2 ……… A n соответственно, затем
Полная вероятность и правило Бая
(1) Закон полной вероятности:
Пусть S будет пространством выборки и пусть E 1 , E 2 ……… E n — это n взаимоисключающие и исчерпывающие события, связанные со случайным экспериментом.Если A — любое событие, которое происходит с E 1 или E 2 или… или E n , тогда
P (A) = P (E 1 ) P (A / E 1 ) + P (E 2 ) P (A / E 2 ) +… .. P (E n ) P (A / E n ).
(2) Правило Байя:
Пусть S будет пробным пространством и E 1 , E 2 ……… E n будет n взаимоисключающими событиями, так что
Мы можем думать о E и как причины, приведшие к исходу эксперимента.Вероятности P (E i ), i = 1, 2,… .., n называются априорными вероятностями. Предположим, что эксперимент приводит к результату события A , где P (A)> 0. Нам нужно найти вероятность того, что наблюдаемое событие A было причиной E i , то есть мы ищем условное вероятность P (E i / A). Эти вероятности называются апостериорными вероятностями, которые по правилу Байя задаются как
теория вероятностей | Определение, примеры и факты
Применение простых вероятностных экспериментов
Фундаментальный компонент теории вероятностей — это эксперимент, который можно повторить, по крайней мере, гипотетически, в по существу идентичных условиях и который может привести к различным результатам в разных испытаниях. Набор всех возможных результатов эксперимента называется «пробелом». Эксперимент по подбрасыванию монеты один раз приводит к пространству выборки с двумя возможными исходами: «орлом» и «решкой».«Бросок двух игральных костей имеет пространство выборки с 36 возможными исходами, каждый из которых может быть идентифицирован с помощью упорядоченной пары ( i , j ), где i и j принимают одно из значений 1, 2, 3, 4, 5, 6 и обозначают лица, изображенные на отдельных кубиках. Важно думать о кубиках как о идентифицируемых (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1). «Событие» — это четко определенное подмножество пространства выборки. Например, событие «сумма лиц, показанных на двух кубиках, равна шести», состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1).
Britannica Premium: удовлетворение растущих потребностей искателей знаний. Получите 30% подписки сегодня. Подпишись сейчасТретий пример — извлечь n шаров из урны, содержащей шары разного цвета. Общий результат этого эксперимента — набор n , где i -я запись определяет цвет шара, полученного при розыгрыше i -го ( i = 1, 2,…, n ) . Несмотря на простоту этого эксперимента, глубокое понимание дает теоретическую основу для опросов общественного мнения и выборочных опросов.Например, люди в группе населения, поддерживающие конкретного кандидата на выборах, могут быть идентифицированы с помощью шариков определенного цвета, лица, выступающие за другого кандидата, могут быть идентифицированы другим цветом и так далее. Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение предназначено для получения сведений об электоральных предпочтениях населения на основе выборки, взятой из этого населения.
Еще одно применение простых моделей урн — клинические испытания, призванные определить, лучше ли новое лечение болезни, новое лекарство или новая хирургическая процедура, чем стандартное лечение.В простом случае, когда лечение можно рассматривать как успешное или неудачное, цель клинических испытаний — выяснить, приводит ли новое лечение к успеху чаще, чем стандартное лечение. Больных можно идентифицировать по шарикам в урне. Красные шары — это те пациенты, которых вылечили с помощью нового лечения, а черные шары — это те пациенты, которые не вылечились. Обычно есть контрольная группа, получающая стандартное лечение. Они представлены второй урной с возможно другой долей красных шаров.Цель эксперимента по извлечению некоторого количества шаров из каждой урны — определить на основе образца, в какой урне больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины. Возможно, самым крупным и самым известным примером является испытание вакцины Солка от полиомиелита, проведенное в 1954 году. Оно было организовано Службой общественного здравоохранения США и охватило почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здоровья в промышленно развитых частях мира.Строго говоря, эти приложения являются задачами статистики, основу которых составляет теория вероятностей.
В отличие от описанных выше экспериментов, многие эксперименты имеют бесконечно много возможных результатов. Например, можно подбрасывать монету до тех пор, пока «орел» не появится впервые. Количество возможных бросков — n = 1, 2,…. Другой пример — крутить спиннер. Для идеализированного спиннера, сделанного из отрезка прямой линии без ширины и повернутого в его центре, набор возможных результатов — это набор всех углов, которые конечное положение спиннера образует с некоторым фиксированным направлением, что эквивалентно всем действительным числам в [0 , 2π).Многие измерения в естественных и социальных науках, такие как объем, напряжение, температура, время реакции, предельный доход и т. Д., Производятся в непрерывных масштабах и, по крайней мере, теоретически включают бесконечно много возможных значений. Если повторные измерения на разных предметах или в разное время на одном и том же предмете могут привести к разным результатам, теория вероятностей является возможным инструментом для изучения этой изменчивости.
Из-за их сравнительной простоты сначала обсуждаются эксперименты с конечным пространством выборок.На раннем этапе развития теории вероятностей математики рассматривали только те эксперименты, для которых казалось разумным, исходя из соображений симметрии, предположить, что все результаты эксперимента были «одинаково вероятными». Затем в большом количестве испытаний все исходы должны происходить примерно с одинаковой частотой. Вероятность события определяется как отношение количества случаев, благоприятных для данного события, т. Е. Количества исходов в подмножестве выборочного пространства, определяющего событие, к общему количеству случаев.Таким образом, 36 возможных исходов при броске двух кубиков считаются равновероятными, а вероятность получения «шести» равна количеству благоприятных случаев, 5, деленному на 36, или 5/36.
Теперь предположим, что монета была подброшена n раз, и рассмотрим вероятность события «орел не выпадет» при n подбрасываниях. Результатом эксперимента является набор n , k -я запись которого идентифицирует результат k -го броска. Поскольку существует два возможных результата для каждого броска, количество элементов в пространстве выборки составляет 2 n .Из них только один исход соответствует отсутствию орла, поэтому требуемая вероятность равна 1/2 n .
Немного сложнее определить вероятность «не более одной головы». В дополнение к единственному случаю, в котором не происходит никакого выпадения, существует n случаев, в которых возникает ровно одна выпадение, потому что это может произойти при первом, втором,… или n -м броске. Следовательно, существует n + 1 случаев, благоприятных для получения не более одной головы, и желаемая вероятность равна ( n + 1) / 2 n .
.
 ⋅- из урны вынули два шара: белый и не белый
⋅- из урны вынули два шара: белый и не белый