Теорвер формула бернулли: Математическое Бюро. Страница 404

Формула Бернулли и повторные независимые испытания. Теория вероятностей

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Краткая теория

---

Схема Бернулли

Теория вероятностей имеет дело с такими экспериментами, которые можно повторять (по крайней мере теоретически) неограниченное число раз. Пусть некоторый эксперимент повторяется  раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:

1) результатом каждого испытания является один из двух возможных исходов, называемых соответственно  «успехом» или «неудачей».

2) вероятность «успеха»,  в каждом последующем испытании не зависит от результатов предыдущих испытаний и остается постоянной.

Схему испытаний Бернулли называют также биномиальной схемой, а соответствующие вероятности – биномиальными, что связано с использованием биномиальных коэффициентов .

Теорема Бернулли

Если производится серия из  независимых испытаний Бернулли, в каждом из которых «успех» появляется с вероятностью , то вероятность того, что «успех» в  испытаниях появится ровно  раз, выражается формулой:

где  – вероятность «неудачи».

 – число сочетаний  элементов по   (см. основные формулы комбинаторики)

Эта формула называется формулой Бернулли.

Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей - при достаточно большом количестве испытаний.

Если число испытаний n велико, то пользуются:

• локальной формулой Муавра — Лапласа
• интегральной формулой Муавра — Лапласа
• формулой Пуассона

Примеры решения задач

---

Пример 1

Всхожесть семян некоторого растения составляет 70%. Какова вероятность того, что из 10 посеянных семян взойдут: 8, по крайней мере 8; не менее 8?

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Решение

Воспользуемся формулой Бернулли:

В нашем случае

Пусть событие  – из 10 семян взойдут 8:

 

Пусть событие  – взойдет по крайней мере 8 (это значит 8, 9 или 10)

 

Пусть событие  – взойдет не менее 8 (это значит 8,9 или 10)

Ответ: P(A)=0.2335;P(B)=0.3828;  P(C)=0.3828

---

Пример 2

В результате обследования были выделены семьи, имеющие по четыре ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней:

а) одного мальчика;

б) двух мальчиков.

Решение

Вероятность появления мальчика или девочки равна . Вероятность появления мальчика в семье, имеющей четырех детей, находится по формуле Бернулли:

В нашем случае:

 

б) Вероятность появления в семье двух мальчиков:

Ответ: а) ; б) .

---

Пример 3

Два равносильных противника играют в шахматы. Что вероятнее а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.

Решение

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Играют равносильные шахматисты, поэтому вероятность выигрыша , следовательно вероятность проигрыша тоже равна 1/2. Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли:

а) Вероятность выиграть 1 партию из двух:

Вероятность выиграть 2 партии из четырех:

Вероятнее выиграть одну партию из 2-х.

 

б) Вероятность выиграть не менее 2-х партий из 4:

 

Вероятность выиграть не менее 3-х партий из 5:

Вероятнее выиграть не менее 2-х партий из 4.

Ответ: а) Вероятнее выиграть одну партию из 2-х; б) Вероятнее выиграть не менее 2-х партий из 4.

Задачи контрольных и самостоятельных работ

---

Задача 1

Всхожесть семян данного сорта имеет вероятность 0. 7. Оценить вероятность того, что из 9 семян взойдет не менее 4 семян.

---

Задача 2

Найти вероятность того, что в n независимых испытаниях событие A появится ровно k раз, зная, что в каждом испытании вероятность появления события равна p.

.

---

Задача 3

а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4.  б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

---

Задача 4

В ралли участвует 10 однотипных машин. Вероятность выхода из строя за период соревнований каждой из них 1/20.

Найти вероятность того, что к финишу придут не менее 8 машин.

---

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Задача 5

Баскетболист бросает мяч 4 раза. Вероятность попадания при каждом броске равна 0,7. Найти вероятность того, что он попадет в корзину: а) три раза; б) менее 3 раз; б) более трех раз.

---

Задача 6

В семье пятеро детей. Считая, что вероятность рождения мальчика равна 0.4, найти вероятность того, что среди этих детей есть не менее двух девочек.

---

Задача 7

В микрорайоне пять машин технической службы. Для бесперебойной работы необходимо, чтобы не меньше трех машин были в исправном состоянии. Считая верояность исправного состояния для всех машин одинаковой и равной 0,75, найти вероятность бесперебойной работы технической службы в микрорайоне.

---

Задача 8

В среднем каждый десятый договор страховой компании завершается выплатой по страховому случаю. Компания заключила пять договоров. Найти вероятность того, что страховой случай наступит: а) один раз; б) хотя бы один раз.

 

---

Задача 9

В мастерской работают 6 моторов. Для каждого мотора вероятность перегрева к обеленному перерыву равна 0,8. Найти вероятность того, что к обеденному перерыву перегреются 4 мотора.

---

Задача 10

Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта.

---

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Задача 11

Контрольное задание состоит из 5 вопросов, на каждый из которых дается 4 варианта ответа, причем один из них правильный, а остальные неправильные. Найдите вероятность того, что учащийся, не знающий ни одного вопроса, дает: а) 3 правильных ответа; б) не менее 3-х правильных ответов (предполагается, что учащийся выбирает ответы наудачу).

---

Задача 12

Стрелок попадает в мишень с вероятностью 0,6. Производится серия из 4 выстрелов.

а) Какова вероятность того, что число промахов будет равно числу попаданий?

б) Найти вероятность хотя бы одного промаха.

---

Задание 13

Дана вероятность p=0.5 появления события A в серии из  независимых испытаний. Найти вероятность того, что в этих испытаниях событие  появится:

а) ровно  раза

б) не менее  раз

в) не менее  раза и не более  раза.

---

Задача 14

Применяемый метод лечения в 80% случаев приводит к выздоровлению. Найти вероятность того, что из четырех больных поправятся:

а) трое;

б) хотя бы один;

в) найти наивероятнейшее количество поправившихся больных и соответствующую этому событию вероятность.

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Теория вероятности формула и примеры для чайников, задачи с решениями, как найти классическую вероятность в математике, как обозначается и в чем выражается вероятность

В высшей математике существует раздел, изучающий статистику. По сути, это теоретическая база. Направление изучает закономерности и случайные явления, систематизирует данные для обоснования принятых решений. Основой науки является теория вероятности, чьи формулы используются для предположения о свершении того или иного события. Существует и алгоритм, с помощью которого решаются все задачи.

Содержание

• Развитие науки
• Сущность предмета
• Алгоритм решения
• Теорема Муавра — Лапласа
• Сочетание взаимных событий

Развитие науки

Изучение вероятности наступления того или иного события берёт своё начало со Средних веков. Первоначально наблюдаемые закономерности не имели математического описания и основывались на различных эмпирических фактах. Ранние работы были непосредственно связаны с азартными играми. Французские учёные Паскаль и Ферма пытались выявить и рассчитать закономерности при бросании костей.

Независимо от них этим вопросом занимался и голландский физик Гюйгенс. В своей работе он оперировал такими понятиями, как величина шанса, математическое ожидание, цена случайности. Он первый, кто попробовал применить теоремы сложения и умножения в описание вероятности.

Фундаментальное значение для развития науки имели труды Бернулли, Байеса, Лапласа и Пуассона. Их стараниями были сформулированы и доказаны предельные теоремы, предложены первые формулы и примеры. В теории вероятности начали использовать анализ ошибочного наблюдения. Но лишь Карл Гаусс детально смог разобраться в нормальном распределении случайной величины.

В XIX веке русские и европейские учёные смогли доказать сделанные ранее предложения. В первую очередь это касалось закона больших чисел и центральной предельной теоремы. Формальная система для описания теории была принята в 1933 году. Предложил её академик СССР Андрей Колмогоров. Руководствуясь идеями теории множеств, меры и интегрирования, он смог систематизировать аксиомы и с их помощью описать классическую теорию вероятности. На основании его работ была создана новая теория — случайных процессов.

В его систему входит:

• алгебра событий — состоит из множества подмножеств, называемых событиями и их пространства;
• существование возможности появления событий — каждому случаю приписывается в соответствие вещественная вероятность наступления;
• нормировка — состояние, при котором вещественное число имеет вероятность свершения равное единице;
• аддитивность — если 2 события не пересекаются, их вероятность находится суммированием.

Объекты, удовлетворяющие системе, были названы полем вероятности (вероятностным пространством). Было принято, что аксиомы не могут противоречить друг другу. Аксиоматизация позволила привести все предположения к строгому математическому виду и стала восприниматься как один из разделов математического вычисления.

Сущность предмета

Предметом изучения науки являются закономерности, появляющиеся в случайных событиях, результат которых нельзя установить заранее. Но не все эксперименты можно изучать с помощью теории, а лишь те, что повторяются при одних и тех же условиях.

Существует понятие «статистической устойчивости». Если существует некоторое событие «А», которое может наступить в результате события или не произойти, то часть экспериментов должна стабилизироваться. При этом с увеличением числа экспериментов вероятность повторения стремится к определённому числу Р(А). Оно и является характеристикой, определяющей степень возможности наступления события «А».

Объяснить основы теории вероятности для чайников можно с помощью классических понятий:

Вероятность, что событие «А» сможет произойти описывается выражением: Р (А) = m/n, где: n — общее количество исходов эксперимента, имеющих равные возможности; m — число исходов, соответствующих событию «А».

Для геометрического определения вместо чисел используется мера. В числитель формулы подставляется показатель, выражающий количество благоприятных исходов наступления рассматриваемого события, а в знаменатель — геометрическая мера. Например, ширина, плотность, объём.

При расчётах принимается, что полная группа событий образует вероятность равную единице: P (A1) + P (A2) + + P (An) = 1, при этом сумма противоположных событий также будет равна одному.

Шанс, что одно из двух несовместимых событий обязательно случится, определяется сложением этих вероятностей. Это формулировка справедлива и к любому количеству ожидаемых исходов: P (C +B +A) = Р(С) + Р (B) +P (A).

Исход, что любое из двух событий сбудется, равен вероятности суммы без учёта возможного их совместного появления: P (А+В) = Р (А) + Р (B) — P (АВ).

Основополагающими формулами являются выражения Байеса и Бернулли.

Согласно первому, если существует гипотеза «Вн», а событие уже наступило, вероятность её правдивости определяется как Pа (Вн) = Р (Вн) * Рв (А) / Р (А). Это выражение ещё называют формулой полной вероятности. Равенство же Бернулли помогает оценить вероятность, что конкретное событие «А» случится n количество раз при m вариантах: P = C ⁿ * p ⁿ * q^{n — m}.

Алгоритм решения

Теория вероятностей используется, когда необходимо сделать прогноз на выпадение того или иного шанса в эксперименте. Случайность является основным понятием предмета. Она обозначает явление, для которого невозможно точно вычислить периодичность наступления, поэтому в задачах находят именно число возможностей. По своей сути вероятность — функция, способная принимать 3 значения:

• ноль — ожидание никогда не выполнится;
• единица — событие произойдёт при любых условиях;
• паритет — существует равная возможность выполнения или невыполнения ожидания.

Чтобы высчитать случайность, рекомендуется придерживаться разработанного алгоритма. Следует внимательно изучить задание и определить, вероятность чего необходимо вычислить, а также события, от которых случайность будет изменяться. Определив схему задачи, подобрать формулу и, подставив в неё все имеющиеся данные, рассчитать шанс. Чтобы правильно определиться с нужной схемой, необходимо знать о количестве экспериментов, существовании между ними зависимости, возможности применения нескольких гипотез.

Для понятия принципа нахождения случайности часто предлагается к решению следующая задача. В закрытом ящике лежит 6 разноцветных перемешанных между собой шаров. Из них 2 красного цвета, 3 зелёного и 1 белый. Нужно посчитать, насколько шансов достать белый шар меньше, чем цветной.

Случайность доставания цветного шара обозначают как событие «А». Согласно определению вероятность «А» определяется отношением благоприятствующих шансов к общему числу исходов. Существует 6 различных возможностей вытянуть шар, из них 5 относятся к благоприятным, поэтому эксперимент покажет, что вероятность достать из ящика цветной шар будет составлять P = 5 / 6 = 0,83(3). Это и есть показатель оценки степени случайности.

Таким способом можно узнать различную вероятность любого исхода, не прибегая к собиранию статистики и её анализу, то есть решить задачу математически, как, например, следующую. В таксопарке используется 2 синих, 9 красных и 4 чёрных машины. Нужно определить, какая существует возможность приезда по вызову красного автомобиля. Решение простое. Так как всего имеется 15 машин, вероятность приезда именно красной составит Р = 9/15 или 0,6.

Теорема Муавра — Лапласа

Это предельное определение, предложенное Лапласом в 1812 году. В основе теоремы используется формула Бернулли, но применяется она к довольно большому количеству экспериментов. Суть её в следующем: если при независимых экспериментах n существует вероятность свершения случайного события N равная нулю или единице, при этом число испытаний равняется m, искомое значение близко к интегральной функции Лапласа.

Стандартные значения, соответствующие нормальному распределению, сведены в статистические таблицы. Взять их можно в решебниках задач по теории. Под приведёнными значениями понимается площадь кривой от нуля до числа x. Например, если придумать какую-либо величину площади между числами 0 и 2,34, согласно таблице она составит 0,49036.

При рассмотрении свершения m событий в n экспериментах существует вероятность, заключённая в определённом отрезке между значениями a и b, поэтому выражение для нахождения можно найти из формулы: Р(m) = (n! * pm * qn-m) / m!(n-m)!. Уравнение требует сложных и громоздких расчётов, поэтому, чтобы найти вероятность, в математике из формулы используют асимптотическое распределение. Но возможно это только при условии, что Р(m) неизменное, а число экспериментов будет стремиться к бесконечности.

Реальная формула, описывающая теорему сложна, поэтому используется приближённая:

Р(m) = 1 / ((2p*n*p*q)1/2) exp (-X2m/2).

Использовать её рекомендуют только при значениях событий больше 20, а экспериментов 100. Например, брак выпускаемых изделий составляет 15%. Поступает товар в упаковках по 100 штук. Нужно найти вероятность, что случайно взятая коробка будет укомплектована 13 бракованными изделиями. При этом число товара низкого качества в упаковке не превысит 20.

За испытание необходимо принять изготовление. Вероятность появления события, которое необходимо искать составит p = 0,15. Далее, находится случайность: n * p = 15 и n * p * q = 12,75. Исходные данные подставляют в формулу Лапласа:

Таким образом, примерно 9,5% упаковок от общего количества содержат 13 товаров плохого качества, а в 92% случаях число изделий с браком не превышает 20.

Сочетание взаимных событий

При рассмотрении задач может возникнуть вопрос, как различные события могут зависеть друг от друга. Для характеристики их взаимосвязи вводится понятие условная вероятность. Например, имеются 2 случайных исхода одного эксперимента «А» и «В».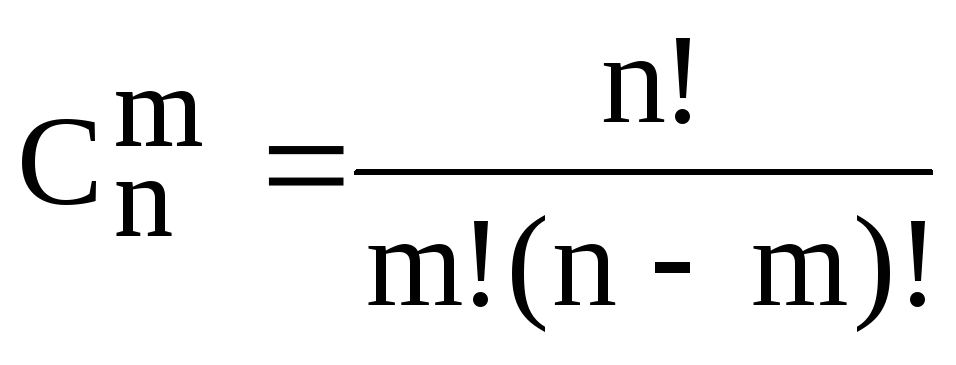 Тогда условной вероятностью первого события «А» при условии, что второе произошло, называется отношение P (AB) / P (B).

Необходимо определить, с какой вероятностью в семье с ребёнком-девочкой родится мальчик. За вероятность появления в семье двух мальчиков нужно взять «А», а за ребёнка противоположного пола событие «В». Существует 4 возможных исхода, поэтому справедливо будет записать: P (AB) = 1/4, P(B) = 3/4. Подставив эти значения в формулу можно рассчитать вероятность: P (A/B) = (1/4) / (3/4) = 0,3. Первый исход считается независимым от второго, если наступление события «В» не оказывает влияние.

Если же события взаимны, они влияют друг на друга. В этом случае используется их перемножение: P(AB) = P(A) *PB (А). Например, в пачке 26 лотерей, из которых 3 призовых. Нужно определить шанс, что первый билет будет призовой и вероятность, что второй билет также будет с выигрышем, но при условии, что первый билет уже убрали.

Для решения задачи вначале нужно найти шанс, что первый билет будет с выигрышем: P (A) = 3/26 = 0,115. Затем рассчитать вероятность двух выигрышей подряд: P(AB) = P(A) * P(B) = (3/26) * (2/25) = 0,009.

Это довольно простые задачи, но существуют задания, для решения которых понадобится применять несколько формул. Такой расчёт вероятности наступления того или иного события может быть трудным, требующим повышенного внимания. Для облегчения вычислений существуют специальные интернет-порталы. Они предлагают рассчитать исход события даже тем, кто и вовсе не разбирается в теории. Например, allcalc.ru, kontrolnaya-rabota.ru, matburo.ru, math.semestr.ru.

На этих сайтах от пользователей требуется лишь заполнить предлагаемые формы исходными данными и нажать кнопку «Рассчитать». Все калькуляторы совмещают в себе быстроту нахождения ответа и ознакомление с подробным описанием решения.

Предыдущая

АлгебраРешение систем линейных уравнений алгоритмы общих и частных методов нахождения корней, основные правила и теоремы и примеры их использования, онлайн калькулятор

Следующая

АлгебраКак найти область определения функции заданной формулой, примеры и способы решения 10 класс, ручной и автоматизированный методы, онлайн-калькулятор

🎓 Теория вероятности — презентация на Slide-Share.

ru

1

Первый слайд презентации: Теория вероятности

Независимые повторные испытания.

Изображение слайда

2

Слайд 2: Содержание презентации

Независимые повторные испытания. Формула Бернулли. Наивероятнейшее число появлений события. Локальная теорема Лапласа. Интегральная теорема Лапласа. Формула Пуассона. Независимые повторные испытания. Схема.

Изображение слайда

3

Слайд 3: Независимые повторные испытания

Изображение слайда

4

Слайд 4: Независимые повторные испытания

Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми повторными испытаниями. В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.

Изображение слайда

5

Слайд 5: Независимые повторные испытания

Примеры: Подбрасываем игральный кубик n раз. Выпадение числа очков от 1 до 6 происходит с вероятностью 1/6 в каждом из испытаний; Приобретаем n лотерейных билетов. Для каждого из лотерейных билетов вероятность выигрыша есть величина постоянная; Подбрасывается n раз монета. Выпадение орла или решки происходит с вероятностью ½ в каждом испытании. Пример 1 и примеры 2,3 отличаются друг от друга тем, что в первом примере возможно появление 6-ти событий, а во втором и третьем – появление только 2-х событий: выиграл — не выиграл, орел – решка, т. е. условно можно назвать такие исходы «успех – неуспех». Такие испытания называются испытаниями Бернулли.

Изображение слайда

6

Слайд 6: Независимые повторные испытания

Независимые повторные испытания, в каждом из которых возможно появление события А (успех) с постоянной вероятностью p или непоявление события А (неуспех) с постоянной вероятностью q=1-p, называются испытаниями Бернулли или схемой Бернулли. Швейцарский математик Якоб Бернулли (1654-1705).

Изображение слайда

7

Слайд 7: Независимые повторные испытания

Формула Бернулли.

Изображение слайда

8

Слайд 8: Формула Бернулли

Пусть производится n испытаний Бернулли. Вероятность того, что в этих испытаниях событие А произойдет ровно m раз можно найти по формуле Бернулли: n – число испытаний p – вероятность появления события А в одном испытании q — вероятность непоявления события А в одном испытании Р n (m) – вероятность того, что событие А появится ровно m раз в n испытаниях

Изображение слайда

9

Слайд 9: Формула Бернулли

Пример. Вероятность того, что расход электроэнергии в продолжении суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшую неделю расход электроэнергии в течении четырех суток не превысит норму. Решение. Обозначим А- расход не превысит норму. По условию n = 7, m = 4, p = P(A) = 0.75. По формуле Бернулли: Ответ: вероятность того, что в ближайшую неделю расход электроэнергии в течении четырех суток не превысит норму равна 0,1969

Изображение слайда

10

Слайд 10: Формула Бернулли

Пример. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть одному из них 2 партии из 4-х или 3 партии из 6-ти? Решение. Найдем вероятность выиграть одному из них 2 партии из 4-х: n=4, m=2, p=1/2, q=1/2. По формуле Бернулли: 2) Найдем вероятность выиграть одному из них 3 партии из 6-ти: n= 6, m= 4, p=1/2, q=1/2. По формуле Бернулли: Сравним полученные результаты: т.к. 3/8 > 5/16, то вероятнее выиграть одному из них 2 партии из 4-х.

Изображение слайда

11

Слайд 11: Формула Бернулли

Пример. Две электрические лампочки включены в цепь параллельно. Вероятность того, что при некотором повышении напряжения в цепи выше номинального перегорит только одна лампочка, равна 0,18. найти вероятности перегореть для каждой из этих лампочек, если известно, что эти вероятности превосходят 0,7 и равны между собой. Решение. Испытание состоит в проверке работы электрической лампочки. Общее число испытаний n = 2. А – при повышении напряжения лампочка не перегорит. По условию P 2 (1)=0, 18. Требуется найти вероятность р наступления события А в каждом испытании. Это уравнение имеет два корня: р=0,9 и р=0,7. По условию р > 0,7. Поэтому р=0,7 не удовлетворяет условию задачи. Ответ: Вероятность того, что каждая из лампочек не перегорит р=0,9.

Изображение слайда

12

Слайд 12: Независимые повторные испытания

Наивероятнейшее число появлений события.

Изображение слайда

13

Слайд 13: Наивероятнейшее число появлений события

Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных. Решение. Вероятность изготовления бракованной детали Р = 1 — 0,8 = 0,2. Искомые вероятности находим по формуле Бернулли: P 5 (0)=0,32768; P 5 (3)=0,0512; P 5 (1)=0,4096; P 5 (4)= 0,0064; P 5 (2)= 0,2048; P 5 (5)=0,00032. Полученные вероятности изобразим графически точками с координатами ( m, P n (m) ). Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей.

Изображение слайда

14

Слайд 14: Наивероятнейшее число появлений события

Рассматривая многоугольник распределения вероятностей мы видим, что есть такие значения m (в данном случае, одно — m 0 =1), обладающие наибольшей вероятностью Р n (m). 0,1 0,2 0,3 0,4 1 2 3 4 5 m 0 P n (m)

Изображение слайда

15

Слайд 15: Наивероятнейшее число появлений события

Число m 0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события Р n ( m 0 ) по крайней мере не меньше вероятностей других событий Р n (m) при любом m. Для нахождения m 0 используется двойное неравенство: n • p — q ≤ m 0 ≤ n • p + p

Изображение слайда

16

Слайд 16: Наивероятнейшее число появлений события

Так как наивероятнейшее число может быть только целым, то: Если границы дробные, то m 0 может принимать только одно значение; Если границы целые, то m 0 может принимать два значения, равные граничным. Тогда для определения наивероятнейшего числа нужно сравнить вероятности на границах.

Изображение слайда

17

Слайд 17: Наивероятнейшее число появлений события

Пример. В результате многолетних наблюдений вероятность дождя 21 июля в городе N составляет 0,3. Найти наивероятнейшее число дождливых дней 21 июля на ближайшие 30 лет. Решение. По условию: p=0.3, q=0.7, n=30. n ∙ p — q ≤ m 0 ≤ n ∙ p + p 0.3 ∙ 30 – 0.7 ≤ m 0 ≤ 0.3 ∙ 30 + 0.3 8.3 ≤ m 0 ≤ 9.3 m 0 = 9 Ответ: наивероятнейшее число дождливых дней 21 июля на ближайшие 30 лет равно 9. Т.е. вероятнее всего 9 раз за 30 лет 21 июля будет дождливым.

Изображение слайда

18

Слайд 18: Наивероятнейшее число появлений события

Пример. Сколько раз необходимо подбросить игральную кость, чтобы наивероятнейшее выпадение тройки было равно 10? Решение. По условию: p= 1/6, q= 5/6, m 0 = 10. n ∙ p-q ≤ m 0 ≤ n ∙ p+p n ∙1/6 – 5/6 ≤ 10 ≤ n ∙1/6 + 1/6 (умножим на 6) n -5 ≤ 60 ≤ n +1 (запишем в виде двух неравенств) n -5 ≤ 60 n ≤ 65 n+1 ≥ 60 n ≥ 59 Следовательно, 59 ≤ n ≤ 65. Ответ: чтобы наивероятнейшее выпадение тройки было равно 10, игральную кость необходимо подбросить 59, 60, 61, 62, 63, 64 или 65 раз.

Изображение слайда

19

Слайд 19: Независимые повторные испытания

Локальная теорема Лапласа.

Изображение слайда

20

Слайд 20: Локальная теорема Лапласа

Пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами. Например, если n = 50, m = 30, р=0,1, то для отыскания вероятности P 30 (50) надо вычислить выражение Нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Локальная теорема Лапласа и дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытаний достаточно велико.

Изображение слайда

21

Слайд 21: Локальная теорема Лапласа

Лаплас Пьер Симон (23.03.1749 — 05.03.1827), Нормандия «То, что мы знаем, так ничтожно по сравнению с тем, что мы не знаем».

Изображение слайда

22

Слайд 22: Локальная теорема Лапласа

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р n ( m ) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n ) где

Изображение слайда

23

Слайд 23: Локальная теорема Лапласа

Замечание. Для частного случая, а именно для р=1/2, асимптотическая формула была найдена в 1730 г. Муавром. В 1783 г. Лаплас обобщил формулу Муавра для произвольного р, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра—Лапласа. Абрахам де Муавр (26.05.1667 – 27.11.1754), Франция. По легенде, Муавр точно предсказал день собственной смерти. Обнаружив, что продолжительность его сна стала увеличиваться в арифметической прогрессии, он легко вычислил, когда она достигнет 24 часов, и, как всегда, не ошибся.

Изображение слайда

24

Слайд 24: Локальная теорема Лапласа

Для упрощения расчетов, связанных с применением формулы составлена таблица значений функции. Пользуясь этой таблицей, необходимо иметь в виду свойства функции : 1. Функция является четной, т.е.. 2. Функция — монотонно убывающая при положительных значениях х, причем при (Практически можно считать, что уже при х > 5 ). Теорему Муавра-Лапласа применяют при n ∙ p ∙ q ≥ 10.

Изображение слайда

25

Слайд 25: Локальная теорема Лапласа

Пример. Вероятность выхода из строя кодового замка в течение месяца равна 2%. Какова вероятность того, что в партии из 600 замков, установленных фирмой, 20 замков выйдут из строя в течение месяца. Решение. По условию n=600, m=20, p=0.02, q=0.98. Нужно найти Р 600 (20). n ∙ p ∙ q=600 ∙ 0.02 ∙ 0.98=11.76, следовательно, локальную теорему Лапласа можно применять. ; ; по таблице найдем ; .

Изображение слайда

26

Слайд 26: Локальная теорема Лапласа

( npq=64, x=0, φ (0) ≈ 0,3989, ) Локальная теорема Лапласа. Задача. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2. Задача. Вероятность поражения мишени стрелком при одном выстреле р = 0,75. Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз. ( npq =1.875, x =0.36, φ ( 0.36 ) ≈ 0,3739, ) Если решать эту задачу с помощью формулы Бернулли, то результат будет несколько иным: Р 10 (8) ≈ 0,282. Такое расхождение ответов объясняется тем, что в настоящем примере n имеет малое значение (формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях n ).

Изображение слайда

27

Слайд 27: Локальная теорема Лапласа

npq = 400 ∙ 0,8∙ (1—0,8) = 64 > 10, следовательно можно применять локальную формулу Муавра—Лапласа. ; ; По таблице найдем ; . Пример. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники. Решение. Вероятность того, что семья имеет холодильник, равна р = 80/100 = 0,8; n = 400, m = 300, q = 0,2.

Изображение слайда

28

Слайд 28: Локальная теорема Лапласа

Пусть в условиях предыдущего примера необходимо найти вероятность того, что от 300 до 360 семей (включительно) имеют холодильники. В этом случае по теореме сложения вероятность искомого события: В принципе вычислить каждое слагаемое можно по локальной формуле Муавра—Лапласа, но большое количество слагаемых делает расчет весьма громоздким. В таких случаях используется интегральная теорема Лапласа.

Изображение слайда

29

Слайд 29: Независимые повторные испытания

Интегральная теорема Лапласа

Изображение слайда

30

Слайд 30: Интегральная теорема Лапласа

Интегральная теорема Муавра—Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна где

Изображение слайда

31

Слайд 31: Интегральная теорема Лапласа

Функция Ф(х) называется функцией Лапласа. Свойства функции Ф(х) : Функция Ф(х) нечетная, т.е. Ф(-х) = — Ф(х). Функция Ф(х) монотонно возрастающая, причем при (практически можно считать, что уже при х > 5 Ф(х) ≈ 0,5). Интегральную теорему Лапласа применяют при n ∙ p >10. Для функции Лапласа также имеются статистико-математические таблицы.

Изображение слайда

32

Слайд 32: Интегральная теорема Лапласа

Пример. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей от 300 до 360 семей (включительно) имеют холодильники. Решение. р = 80/100 = 0,8; n = 400, q = 0,2, a = 300, b = 360. np = 0.8 ∙ 400 = 320 > 10, значит, можно применить интегральную теорему Лапласа. ;. Ф (-2,5)= -Ф (2,5) ≈ -0,4938, Ф (5) ≈ 0,499997; . Ответ: вероятность того, что от 300 до 360 семей (включительно) имеют холодильники равна 0,993793.

Изображение слайда

33

Слайд 33: Независимые повторные испытания

Формула Пуассона.

Изображение слайда

34

Слайд 34: Формула Пуассона

Если число независимых испытаний n достаточно велико, а вероятность появления события в каждом испытании отлична от 0 и 1 и мала ( p – близка к 0), так что n ∙ p ≤ 10, то для вычисления вероятности появления события k раз применяют формулу Пуассона. Пуассон Симеон (21.06.1781 — 25.04.1840) Французский учёный, член Парижской АН, почётный член Петербургской АН. Труды Пуассона относятся к теоретической и небесной механике, математике и математической физике.

Изображение слайда

35

Слайд 35: Формула Пуассона

Теорема. Если вероятность p наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, то вероятность того, что в n независимых испытаниях событие А наступит m раз приближенно равна где Формулу Пуассона можно применять при λ ≤ 10. Существуют статистико-математические таблицы для распределения Пуассона.

Изображение слайда

36

Слайд 36: Формула Пуассона

Пример. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета? Решение. Вероятность того, что день рождения студента 1 сентября, равна р = 1/365. Так как р = 1/365 — мала, n = 1825 — велико и λ = n р = 1825 • (1/365 ) = 5 < 10, то применяем формулу Пуассона: По таблицам можно точнее и быстрее найти Р( m, λ ). Так для данного примера P 1825 (4) = P(m, λ ) = P(4,5) ≈ 0.17547. Ответ: вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета равна 0, 17547.

Изображение слайда

37

Слайд 37: Формула Пуассона

Задача 1. Некоторое электронное устройство выходит из строя, если откажет определенная микросхема. Вероятность ее отказа в течение 1 ч работы устройства равна 0,004. Какова вероятность того, что за 1000 ч работы устройства придется пять раз менять микросхему? Задача 2. Телефонный коммутатор обслуживает 2000 абонентов. Для каждого абонента вероятность позвонить в течение часа равна 0,0025. Найти вероятность того, что в течение часа позвонят на коммутатор: а) три абонента; б) не менее четырех абонентов. (Р 1000 (5) ≈ 0,1563) ( Р 2000 (3) ≈ 0,1404 )

Изображение слайда

38

Последний слайд презентации: Теория вероятности: Независимые повторные испытания. Схема

Независимые повторные испытания n невелико, р (или q) не очень мало n велико, р (или q) не очень мало n велико, р (или q) очень мало Формула Бернулли Формула Лапласа Формула Пуассона Таблица для φ ( x) Таблица функции Пуассона

Изображение слайда

Уравнение Бернулли

Загрузка

 

Даниил Бернулли (Гронинген, 29 января 1700 г. — 27 июля 1782 г.) был швейцарским математиком, который провел большую часть своей жизни в Базеле, где и умер. Член талантливой семьи математиков, физиков и философов, он особенно известен своими приложениями математики к механике, особенно гидромеханике, а также новаторскими работами в области вероятности и статистики. (Википедия)

Простейшие и наиболее популярные объяснения аэродинамической подъемной силы основаны на принципе Бернулли, который, в свою очередь, выводится из теоремы Бернулли. Его уравнение, исследованное в начале 1700-х годов Даниэлем Бернулли, определяет физические законы, на которых основано большинство аэродинамических правил. Это ныне известное уравнение является абсолютно фундаментальным для изучения воздушных потоков. Каждая попытка улучшить то, как машина Формулы-1 пробивает себе дорогу через молекулы воздуха, основывается на этой естественной взаимосвязи между скоростью жидкости (газа или жидкости) и давлением. Существует несколько форм уравнения Бернулли, три из которых обсуждаются в последующих абзацах: течение по одной линии тока, течение по многим линиям тока и течение по аэродинамической поверхности.

Все три уравнения были выведены с использованием нескольких предположений, возможно, наиболее важным из которых является то, что плотность воздуха не изменяется с давлением (т. е. воздух остается несжимаемым). Поэтому их можно применять только в дозвуковых ситуациях.

Так как автомобили F1 движутся намного медленнее, чем 1 Маха, эти уравнения могут быть использованы для получения очень точных результатов.

Низкоскоростное течение жидкости вдоль одной или нескольких линий тока интерпретируется на рисунке 1. На рисунке перечислены допущения относительно применения уравнения Бернулли к этому сценарию. В этой ситуации существует связь между скоростью, плотностью и давлением. Поскольку одиночный поток жидкости течет по трубе с изменяющейся площадью поперечного сечения (например, воздухозаборник F1), его скорость уменьшается от первой до второй станции, а его полное давление остается постоянным. При наличии нескольких линий тока общее давление равно одной и той же константе вдоль каждой линии тока. Однако это имеет место только в том случае, если перепады высот между линиями тока пренебрежимо малы. В противном случае каждая линия тока имеет уникальное полное давление.

 

 

Математическое и графическое объяснение уравнения Бернулли применительно к потоку жидкости через трубу с изменяющейся площадью поперечного сечения.
Применительно к низкоскоростным аэродинамическим профилям (например, крыльям прижимной силы F1) воздушный поток несжимаем, и его плотность остается постоянной. Тогда уравнение Бернулли сводится к простому соотношению между скоростью и статическим давлением.

(давление) + 0,5 (плотность) X (скорость)2 = константа

Из этого уравнения следует, что увеличение давления должно сопровождаться уменьшением скорости и наоборот. Интегрирование статического давления по всей поверхности аэродинамического профиля дает полную аэродинамическую силу, действующую на тело. Компоненты подъемной силы и сопротивления могут быть определены путем разложения этой силы.

 

 

Чтобы обсудить подъемную силу и прижимную силу, может оказаться полезным дать дополнительное объяснение связи, возникающей в приведенной выше форме уравнения Бернулли. Если жидкость обтекает объект с разными скоростями, более медленная жидкость будет оказывать большее давление на объект, чем более быстрая жидкость. Затем объект будет вынужден приближаться к более быстро движущейся жидкости. Результатом этого события является либо подъемная сила, либо прижимная сила, каждая из которых зависит от положения более длинной хорды крыла. Подъемная сила возникает, когда более длинная хорда направлена ​​вверх, а прижимная сила возникает, когда она направлена ​​вниз.

Подъемная сила в соответствии с применением уравнения Бернулли

 

Хотя принцип Бернулли является основным источником подъемной или прижимной силы в крыле самолета или гоночного автомобиля, эффект Коанда играет еще большую роль в создании подъемной силы. Чтобы узнать больше о взаимодействии принципа Бернулли и эффекта Коанда, ознакомьтесь с моей статьей здесь.

В то время как принцип Бернулли часто используется для объяснения явления аэродинамической подъемной силы, создаваемой воздушным потоком вокруг профиля крыла, существуют альтернативные объяснения, которые используют в той или иной комбинации: «эффект Коанды», понятие циркуляции и третий закон Ньютона. закон. Эти альтернативные объяснения, по крайней мере, столь же правомерны, как и объяснение, основанное на принципе Бернулли, и среди аэродинамиков считаются в некоторой степени превосходящими объяснение Бернулли.
Гордон МакКейб опубликовал отличную статью по этому аргументу «Объяснение и открытие в аэродинамике» от 2 февраля 2008 года. Вы можете скачать его работу здесь.

Из реферата:

«Цель этой статьи состоит в том, чтобы обсудить и прояснить объяснения, обычно приводимые для аэродинамической подъемной силы, создаваемой крылом, а затем проанализировать, в качестве примера инженерного открытия, аэродинамические революции, которые произошли в Формуле 1 в за последние 40 лет. Статья начинается с введения, в котором дается краткое изложение математики гидромеханики».

 

Вернуться к началу страницы

 

Демонстрация теоремы Бернулли – Лабораторное руководство по прикладной гидромеханике

Энергия представлена ​​в виде давления, скорости и подъема в жидкостях без обмена энергией из-за вязкой диссипации, теплопередачи или работы вала (насоса или другого устройства). Взаимосвязь между этими тремя формами энергии была впервые установлена ​​Даниэлем Бернулли (1700-1782) на основе принципа сохранения энергии. Теорема Бернулли, относящаяся к линии тока, основана на трех допущениях: стационарное течение, несжимаемая жидкость и отсутствие потерь от жидкостного трения. Справедливость уравнения Бернулли будет проверена в этом эксперименте.

Теорема Бернулли предоставляет математические средства для понимания механики жидкостей. Он имеет множество реальных применений, начиная от понимания аэродинамики самолета; расчет ветровой нагрузки на здания; проектирование водопроводных и канализационных сетей; измерение расхода с использованием таких устройств, как водосливы, лотки Паршалла и вентуриметры; и оценка просачивания через почву и т. д. Хотя выражение для теоремы Бернулли простое, принцип, используемый в уравнении, играет жизненно важную роль в технологических достижениях, направленных на улучшение качества человеческой жизни.

Целью этого эксперимента является исследование правильности уравнения Бернулли, когда оно применяется к установившемуся потоку воды через сужающийся канал.

В этом эксперименте справедливость уравнения Бернулли будет проверена с использованием конического воздуховода (система Вентури), соединенного с манометрами для измерения напора и полного напора в известных точках вдоль потока.

Для демонстрации эксперимента с уравнением Бернулли требуется следующее оборудование:

• Гидравлический стол F1-10,
• Оборудование для испытаний аппарата Бернулли F1-15 и
• Секундомер для измерения расхода.

Прибор Бернулли состоит из конического канала (вентури), ряда манометров, вставленных в трубку Вентури для измерения напора, и подкожного зонда, который можно перемещать по центру испытательного участка для измерения общего напора. Испытательный участок представляет собой круглый воздуховод переменного диаметра с углом наклона 14° с одной стороны и углом наклона 21° с другой стороны. Для подключения манометров к испытательному участку предусмотрен ряд отводов давления в боковых отверстиях (рис. 2.1).

Рисунок 2.1: Испытательное оборудование аппарата Бернулли Armfield F1-15 Манометры

позволяют одновременно измерять напор на всех шести участках воздуховода. Размеры испытательного участка, места врезки и диаметры испытательного участка показаны на рис. 2.2. Раздел теста включает в себя два объединения, по одному на каждом конце, чтобы упростить обращение для конвергентного или дивергентного тестирования. Зонд предназначен для измерения общего напора вдоль испытательного участка путем размещения его на любом участке воздуховода. Этот зонд можно перемещать после ослабления гайки сальника, которую следует снова затянуть вручную. Во избежание повреждения датчик должен быть полностью вставлен во время транспортировки/хранения. Отводы давления соединены с манометрами, установленными на плинтусе. Расход через испытательную секцию можно регулировать регулирующим клапаном аппарата или стендовым регулирующим клапаном [2].

Рисунок 2.2: Испытательные участки, положения манометров и диаметры воздуховода вдоль испытательного участка

Теорема Бернулли предполагает, что поток без трения, установившийся и несжимаемый. Эти предположения также основаны на законах сохранения массы и энергии. Таким образом, входная масса и энергия для данного контрольного объема равны выходной массе и энергии:

Эти два закона, а также определение работы и давления являются основой теоремы Бернулли и могут быть выражены следующим образом для любых двух точек, расположенных на одной линии тока в потоке:

где:

Р: давление,

g: ускорение свободного падения,

v : скорость жидкости и

z: вертикальное возвышение жидкости.

В этом эксперименте, поскольку воздуховод горизонтальный, разницей в высоте можно пренебречь, т. е. z ₁ = z ₂

Гидростатическое давление (P) вдоль потока измеряется манометрами, вставленными в воздуховод. Таким образом, напор (h) рассчитывается как:

Следовательно, уравнение Бернулли для рабочего участка можно записать так:

в котором называется скоростным напором (h _d ).

Общий напор (h _t ) может быть измерен поперечным подкожным зондом. Этот зонд вставляется в воздуховод так, чтобы его торцевое отверстие было обращено к потоку, так что поток локально застаивался на этом конце; таким образом:

Закон сохранения энергии или уравнение Бернулли можно выразить следующим образом:

Скорость потока измеряется путем сбора объема жидкости (V) за период времени (t). Расход рассчитывается как:

Скорость потока на любом участке воздуховода с площадью поперечного сечения  определяется как:

Для несжимаемой жидкости также должен выполняться закон сохранения массы в испытательном сечении (уравнение 1а), т. е.:

• Поместите прибор на стол для гидравлики и убедитесь, что выпускная трубка расположена над мерным резервуаром, чтобы упростить сбор данных по времени.
• Выровняйте основание аппарата, отрегулировав его ножки. (Для этого к основанию крепится спиртовой уровень.) Для точного измерения высоты с помощью манометров прибор должен находиться в горизонтальном положении.
• Установите тестовую секцию так, чтобы сужающаяся под углом 14° секция сужалась в направлении потока. Если тестовую секцию необходимо перевернуть, датчик полного напора должен быть втянут, прежде чем освобождать монтажные муфты.
• Подсоедините впускное отверстие аппарата к источнику потока стенда, закройте клапан стенда и клапан управления потоком аппарата и запустите насос. Постепенно откройте клапан стенда, чтобы заполнить испытательную секцию водой.
• Для удаления воздуха из точек отбора давления и манометров необходимо предпринять следующие шаги:
  • Закройте клапан стенда и клапан управления потоком аппарата.
  • Снимите колпачок с воздушного клапана, подсоедините маленькую трубку от воздушного клапана к мерному резервуару и откройте винт для выпуска воздуха.
  • Откройте клапан стенда и дайте потоку пройти через манометры, чтобы удалить из них весь воздух, затем затяните винт для выпуска воздуха и частично откройте клапан стенда и клапан управления расходом аппарата.
  • Слегка приоткройте винт для выпуска воздуха, чтобы воздух попал в верхнюю часть манометров (для этого может потребоваться отрегулировать оба клапана), и снова затяните винт, когда уровни манометра достигнут удобной высоты. Максимальный расход будет определяться максимальным (h ₁ ) и минимальным (h ₅ ) показаниями манометра на плинтусе.

При необходимости уровни манометра можно отрегулировать с помощью воздушного насоса для повышения давления. Этого можно добиться, подсоединив трубку ручного насоса к воздухоотводному клапану, открыв винт и накачав воздух в манометры. Закройте винт после прокачки, чтобы сохранить давление в системе.

• Снимать показания манометров с h ₁ по h ₆ при стабильном уровне воды в манометрах. Зонд полного давления должен быть отведен от испытательной секции во время этого считывания.
• Измерьте общий напор, проведя датчиком полного давления вдоль испытательного участка от h ₁ до h ₆ .
• Измерьте скорость потока с помощью синхронизированного сбора объема. Для этого закройте шаровой кран и с помощью секундомера измерьте время, необходимое для накопления известного объема жидкости в баке, который считывается по смотровому стеклу. Вы должны собирать жидкость не менее одна минута , чтобы свести к минимуму ошибки синхронизации. Вы можете повторить измерение расхода дважды, чтобы проверить повторяемость. Убедитесь, что во время этого измерения датчик общего давления отведен от контрольной секции.
• Уменьшите расход, чтобы разница напора между манометрами 1 и 5 составляла около 50 мм (h ₁ -h ₅ ). Это эксперимент с минимальным потоком. Измерьте напор, общий напор и расход.
• Повторите процесс для еще одного расхода с (ч ₁ -h ₅ ) разница примерно посередине между значениями, полученными для минимального и максимального расхода. Это эксперимент со средним потоком.
• Переверните тестовую секцию ( сужающаяся под углом 21° секция , сужающаяся в направлении потока), чтобы наблюдать влияние более быстро сужающейся секции. Убедитесь, что датчик полного давления полностью выведен из контрольной секции, но не вытянут из направляющей в выходной муфте. Отвинтите две муфты, снимите тестовую секцию и переверните ее, затем снова соберите ее, затянув муфты.
• Выполните три набора измерений расхода и выполните измерения давления и расхода, как указано выше.

Перейдите по этой ссылке, чтобы получить доступ к рабочей книге Excel для этого эксперимента.

9.1. Результаты

Введите результаты теста в таблицы необработанных данных.

 

 

Таблица исходных данных

Положение 1: сужение от 14° до 21°
Испытательная секция	Объем (литр)	Время (сек)	Напор (мм)	Общий напор (мм)
ч 1
ч 2
ч 3
ч 4
ч 5
ч 6
ч 1
ч 2
ч 3
ч 4
ч 5
ч 6
ч 1
ч 2
ч 3
ч 4
ч 5
ч 6

  Таблица исходных данных

Позиция 2: конусность от 21° до 14°
Испытательная секция	Объем (литр)	Время (сек)	Напор (мм)	Общий напор (мм)
ч 1
ч 2
ч 3
ч 4
ч 5
ч 6
ч 1
ч 2
ч 3
ч 4
ч 5
ч 6
ч 1
ч 2
ч 3
ч 4
ч 5
ч 6

9. 2 Расчеты

Для каждого набора измерений рассчитайте скорость потока; скорость потока, скоростной напор и общий напор (напор + скоростной напор). Запишите свои расчеты в таблицу результатов.

Таблица результатов

Положение 1: сужение от 14° до 21°
Тест №	Испытательная секция	Расстояние до воздуховода (м)	Площадь потока (м²)	Расход (м³/с)	Скорость (м/с)	Напор (м)	Скорость напора (м)	Расчетный общий напор (м)	Измеренный общий напор (м)
1	h2	0	0,00049
	h3	0,06028	0,00015
	h4	0,06868	0,00011
	h5	0,07318	0,00009
	h5	0,08108	0,000079
	h6	0,14154	0,00049
2	ч2	0	0,00049
	h3	0,06028	0,00015
	ч4	0,06868	0,00011
	h5	0,07318	0,00009
	h5	0,08108	0,000079
	h6	0,14154	0,00049
3	ч2	0	0,00049
	h3	0,06028	0,00015
	h4	0,06868	0,00011
	h5	0,07318	0,00009
	ч5	0,08108	0,000079
	h6	0,14154	0,00049

 

Позиция 2: конусность от 21° до 14°
Тест №	Испытательная секция	Расстояние до воздуховода (м)	Площадь потока (м²)	Расход (м³/с)	Скорость (м/с)	Напор (м)	Скорость напора (м)	Расчетный общий напор (м)	Измеренный общий напор (м)
1	ч2	0	0,00049
	h3	0,06028	0,00015
	h4	0,06868	0,00011
	h5	0,07318	0,00009
	h5	0,08108	0,000079
	h6	0,14154	0,00049
2	ч2	0	0,00049
	h3	0,06028	0,00015
	h4	0,06868	0,00011
	h5	0,07318	0,00009
	h5	0,08108	0,000079
	h6	0,14154	0,00049
3	ч2	0	0,00049
	h3	0,06028	0,00015
	h4	0,06868	0,00011
	h5	0,07318	0,00009
	h5	0,08108	0,000079
	h6	0,14154	0,00049

 

Используйте предоставленный шаблон для подготовки лабораторного отчета для этого эксперимента. Ваш отчет должен включать следующее:

• Таблица(и) исходных данных
• Таблицы результатов
• Для каждого испытания нанесите общий напор (рассчитанный и измеренный), напор и скоростной напор (ось Y) в зависимости от расстояния до воздуховода (ось X) от манометра 1 до 6, всего шесть графиков. Соедините точки данных, чтобы наблюдать тенденцию на каждом графике. Обратите внимание, что направление потока в позиции 1 воздуховода от манометра 1 до 6; в положении 2 – от манометра 6 до 1.
• Комментарий о справедливости уравнения Бернулли при схождении и расхождении потока вдоль канала.
• Комментарий к сравнению рассчитанного и измеренного общего напора в этом эксперименте.
• Обсудите свои результаты, обращая внимание, в частности, на следующее:
  • потери энергии и как они проявляются по результатам этого эксперимента и
  • компоненты уравнения Бернулли () и то, как они изменяются по длине испытательного участка. Укажите точки максимальной скорости и минимального давления.

Вывод уравнения Бернулли и его приложения

Механика

Уравнение Бернулли определяется как сумма давления, кинетической энергии и потенциальной энергии на единицу объема при стационарном течении несжимаемой и невязкой жидкости остается постоянной в каждой точке своего пути. Струя воздуха — примеры теоремы Бернулли, а бейсбольная кривая, кровоток — несколько приложений принципа Бернулли.

Принципиальная формула Бернулли

P+ ρgh +1/2 ρv ² = константа

Уравнение Бернулли, являющееся фундаментальным соотношением в гидромеханике, не является новым принципом, но выводится из основных законов ньютоновской механики. Мы находим удобным вывести его из теоремы о работе-энергии, так как по сути это формулировка теоремы о работе-энергии для потока жидкости.

Вывод уравнения Бернулли

Рассмотрим стационарное, несжимаемое, невязкое и безвихревое течение жидкости через трубопровод или трубу потока, как показано на рисунке. Участок трубы, показанный на рисунке, имеет одинаковое поперечное сечение А ₁ , слева. Там она горизонтальна на высоте y ₁ над некоторым исходным уровнем. Он постепенно расширяется и поднимается и справа имеет однородное поперечное сечение A ₂ . Там она горизонтальна на высоте y ₂ . Во всех точках узкой части трубы давление p ₁ и скорость v ₁ ; во всех точках широкой части давление равно p ₂ и скорость v ₂ .

Теорема о работе-энергии гласит: Работа, совершаемая результирующей силой, действующей на систему, равна изменению кинетической энергии системы. На рисунке силы, совершающие работу над системой, если предположить, что мы можем пренебречь вязкими силами, представляют собой силы давления p ₁ A ₁ и p ₂ A ₂ , действующие на левый и правый концы системы соответственно и сила тяжести. По мере того, как жидкость течет по трубе, возникает чистый эффект. Мы можем найти работу W совершаемая над системой равнодействующая сила следующим образом:

1. Работа, совершаемая над системой силой давления 1 .
2. Работа, совершаемая над системой силой давления Обратите внимание, что оно отрицательно, потому что сила действует в направлении, противоположном горизонтальному смещению.
3. Работа силы тяжести над системой связана с подъемом элемента жидкости с высоты y ₁ на высоту y ₂ и равна -Δmg(y ₂ – y
   6 , где Δm — масса жидкости в любой области. Этот вклад также отрицательный, поскольку сила тяжести действует в направлении, противоположном вертикальному смещению.

Сеть W, проделанная над системой всеми силами, находится путем сложения этих трех членов, или

W = p ₁ A ₁ Δl ₁ – p ₂ A ₂ Δl ₂  -Δmg(y ₂ – y ₁ )

Now A ₁ Δl ₁ and A ₂ Δl ₂ is the volume of the fluid element which we can write as Δm  _{/ρ ,}  in which ρ     is the constant плотность жидкости.