Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень 8 класс онлайн-подготовка на
113. Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень.
При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним. Например:
27+37=2+37=57.
Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:
ac+bc=a+bc,
где а, b и с — многочлены, причем с — ненулевой многочлен.
Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:
Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.
Вычитание рациональных дробей выполняется аналогично сложению:
ac-bc=a-bc.
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
Пример 1. Сложим дроби:
3a-7b15ab+2a+2b15ab=3a-7b+2a+2b15ab=5a-5b15ab=5(a-b)15ab=a-b3ab.
Пример 2. Вычтем дроби:
a2+95a-15-6a5a-15=a2+9-6a5a-15=a-325a-3=a-35.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.
Пример 3. Сложим дроби x4a3b+56ab4.
Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен 12а3b4. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей.
Имеем
x4a3b+56ab4=x∙3b3+5∙2a212a3b4=3b3x+10a212a3b4.
Пример 4. Преобразуем разность a+3a2+ab-b-3ab+b2.
Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:
a+3a2+ab-b-3ab+b2=a+3a(a+b)-b-3b(a+b).
Простейшим общим знаменателем служит выражение ab(a+b). Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.
Имеем:
a+3a(a+b)-b-3ba+b=a+3b-b-3aaba+b=ab+3b-ab+3aaba+b=3a+baba+b=3ab.
Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.
Пример 5. Упростим выражение a-1-a2-3a+1
Представим выражение a-1 в виде дроби со знаменателем 1 и выполним вычитание дробей:
a-1-a2-3a+1=a-11-a2-3a+1=a-1a+1-a2-3a+1=a2-1-a2+3a+1=2a+1.
Умножение и деление дробей. Возведение дроби в степень.
При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например: 23∙45=2∙43∙5=815.
Таким же образом перемножают любые рациональные дроби:
ab∙cd=acbd,
где а, b, с и d — некоторые многочлены, причем b и d — ненулевые многочлены. Это равенство выражает правило умножения рациональных дробей:
чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.
Пример 6. Умножим дроби a34b2∙6ba2.
Воспользуемся правилом умножения дробей:
a34b2∙6ba2=a3∙6b4b2∙a2=6a3b4a2b2=3a2b.
Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:
Например:
ab∙cd∙mn=acbd∙mn=acmbdn.
Выясним теперь, как выполняется возведение рациональной дроби в степень.
Рассмотрим выражение abn, являющейся n-й степенью рациональной дроби ab и докажем, что
abn=anbn.
По определению степени имеем
abn=ab·ab∙…∙ab (n раз).
Применяя правило умножения рациональных дробей и определение степени, получим
ab·ab∙…∙ab=a∙a∙…∙ab∙b∙…∙b=anbn.
Следовательно, abn=anbn.
Из доказанного тождества следует правило возведения рациональной дроби в степень:
чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.
Пример 7. Возведем дробь 2a2b4 в третью степень.
Воспользуемся правилом возведения в степень:
2a2b43=(2a2)3(b4)3=8a6b12.
Деление дробей
При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например: 38:25=38∙52=1516.
Так же поступают при делении любых рациональных дробей:
ab:cd=ab∙dc=adbc,
где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.
Это равенство выражает правило деления рациональных дробей:
чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Пример 8. Разделим дроби 7a2b3:14ab.
Воспользуемся правилом деления дробей:
7a2b3:14ab=7a2b3·b14a=7a2b14ab3=a2b2.
Контрольные работы по алгебре 8 класс | Тест по алгебре (8 класс) на тему:
Опубликовано 16. 03.2016 — 15:23 — Ронжина Анна Александровна
03.2016 — 15:23 — Ронжина Анна Александровна
Контрольные работы по алгебре 8 класс
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
«Математика» № 30/02, 12/03
А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 1 | А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 2 |
1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при а = 4, b = –12. 4. Упростите выражение . | 1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при х = –18, у = 4,5. 4. Упростите выражение . | ||
А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 3 | А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 4 |
1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при а = 7, b = –15. 4. Упростите выражение . | 1. а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при х = 3,5, у = –14. 4. Упростите выражение . | ||
А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 1 | А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 2 |
1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при а = 4, b = –12. 4. Упростите выражение . | 1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при х = –18, у = 4,5. 4. Упростите выражение . | ||
А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 3 | А–8 | КР–1 «Сумма и разность дробей» ВАРИАНТ 4 |
1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при а = 7, b = –15. 4. Упростите выражение . | 1. Сократите дробь: а) ; б) ; в) . 2. Выполните вычитание или сложение дробей: а) ; б) . 3. Найдите значение выражения при х = 3,5, у = –14. 4. Упростите выражение . | ||
www. MetodKopilka.com
MetodKopilka.com
По теме: методические разработки, презентации и конспекты
вводная контрольная работа в 11 классе по алгебре
Контрольная работа составлена в формате ЕГЭ за курс алгебры и начала анализа 10 класса, рассчитана на 1 урок….
итоговая контрольная работа по алгебре 8 класс
Итоговая контрольная работа представлена в виде теста на основе демонстрационных материалов ГИА. Данная работа может быть использована и при проведении вводного диагностического контроля по алгебре в …
контрольные работы по алгебре в 7 классе к учебнику Макарычев Ю.Н. и др. ( ИЗ АВТОРСКОЙ ПРОГРАММЫ ПО АЛГЕБРЕ. 2012ГОДА)
Данная работа взята из авторской программы по алгебре для 7-9классов издательства «Просвещение » 2012года. Удобно использовать для рабочей программы ….
Итоговая контрольная работа по алгебре 8 класс,по математике 5 класс
Предлагаемые вниманию учителей контрольные работы составлены в соответствии с программой по математике . Могут быть использованы во всех типах учебных заведений….
Могут быть использованы во всех типах учебных заведений….
Контрольная работа по алгебре 10 класс (11 класс) по теме «Показательная функция»
Разноуровневая Контрольная работа по алгебре 10 класс (учебник Муравиных) по теме «Показательная функция». Может быть испольхована для учебников других авторов в 10-11 классе, а т…
Комплект тематических контрольных работ по алгебре за 7 класс к УМК «Алгебра 7кл», Ю.Н. Макарычев, Н.Г. Миндюк и другие (под редакцией С.А.Теляковского)
Данный комплект содержит комплект тематических контрольных работ с №1 по №9 + №10 (годовая) – к УМК «Алгебра 7кл», Ю.Н. Макарычев, Н.Г. Миндюк и другие (под редакцией С.А…
Контрольно-измерительные материалы для проведения итоговой контрольной работы по алгебре в 7 классе.
Материал может использоваться для проведения переводного экзамена по алгебре в 7 классе.Критерии по оцениванию:Каждый пункт оценивается как отдельное задание.Все задания решены верно &nda…
Алгебра 7-9 классы.
 14. Решение типовых заданий по теме: «Дробные рациональные выражения»
14. Решение типовых заданий по теме: «Дробные рациональные выражения»
- Подробности
- Категория: Алгебра 7-9 классы
Сумма и разность дробей
Сложение и вычитание дробей с одинаковыми знаменателями
При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним. Например:
Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:
где а, b и с — многочлены, причем с — ненулевой многочлен.
Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:
чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же
Вычитание рациональных дробей выполняется аналогично сложению:
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
Пример 1. Сложим дроби
Пример 2. Вычтем дроби
Пример 3. Упростим выражение
Здесь удобно сложение и вычитание дробей выполнять не последовательно, а совместно:
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.
Пример 1. Сложим дроби
Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен . Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей соответственно равны .
Дополнительные множители к числителям и знаменателям этих дробей соответственно равны .
Имеем
Пример 2. Преобразуем разность
Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:
Простейшим общим знаменателем служит выражение Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.
Имеем
Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.
Пример 3. Упростим выражение
Представим выражение а — 1 в виде дроби со знаменателем 1 и выполним вычитание дробей:
Произведение и частное дробей
Умножение дробей.
 Возведение дроби в степень
Возведение дроби в степень
При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например:
Таким же образом перемножают любые рациональные дроби:
где а, b, с и
чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.
Пример 1. Умножим дробь на дробь
Воспользуемся правилом умножения дробей:
Пример 2. Умножим дробь на дробь
Имеем
Пример 3. Представим произведение в виде рациональной дроби.
Представим произведение в виде рациональной дроби.
Имеем
Пример 4. Умножим дробь на многочлен
При умножении дроби на многочлен этот многочлен записывают в виде дроби и затем применяют правило умножения дробей:
Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:
Выясним теперь, как выполняется возведение рациональной дроби в степень.
Рассмотрим выражение , являющейся n-й степенью рациональной дроби и докажем, что
По определению степени имеем
Применяя правило умножения рациональных дробей и определение степени, получим
Следовательно ,
Из доказанного тождества следует правило возведения рациональной дроби в степень:
чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.
Пример 5. Возведем дробь в третью степень.
Воспользуемся правилом возведения в степень:
Деление дробей
При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например:
Так же поступают при делении любых рациональных дробей:
где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.
Это равенство выражает правило деления рациональных :
чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Пример 1. Разделим дробь на дробь .
Воспользуемся правилом деления дробей:
Пример 2. Разделим дробь на дробь
Имеем
Пример 3. Разделим дробь на многочлен a + 3.
Разделим дробь на многочлен a + 3.
При делении дроби на многочлен этот многочлен записывают в виде дроби и затем применяют правило деления дробей:
Преобразование рациональных выражений
Рациональное выражение представляет собой частное от деления суммы рациональных дробей многочлен. Деление на можно заменить умножением на дробь Поэтому преобразование данного выражения сводится к сложению дробей и умножению результата на дробь Вообще преобразование любого рационального выражения можно свести к сложению, вычитанию, умножению или делению рациональных дробей.
Из правил действий с дробями следует, что сумму, разнос произведение и частное рациональных дробей всегда можно предс вить в виде рациональной дроби. Значит, и всякое рациональное выражение можно представить в виде рациональной дроби.
Пример 1. Преобразуем в рациональную дробь выражение
Сначала выполним умножение дробей, затем полученный результат вычтем из многочлена x + 1:
Запись можно вести иначе:
Пример 2. Представим выражение
Представим выражение
в виде рациональной дроби.
Сначала сложим дроби, заключенные в скобки, затем найденный результат умножим на дробь и, наконец, к полученному произведению прибавим 1:
Тест Дроби с разными знаменателями 6 класс с ответами
Тестовые задания для 6 класса по теме: Дроби с разными знаменателями.
Правильный вариант ответа отмечен знаком +
1. ⅗ — ½ = …
a. 1/10 +
b. ⅔ -
c. 4/7 -
d. 2/7 -
2. Результатом любого вычитания является …
a. сумма -
b. разность +
c. произведение -
d. частное -
3. Какое равенство является неверным?
a. ¾ — ½ = 7/12 — ⅓ -
b. 6/7 — ½ = 13/14 — 4/7 —
c. ⅘ — ⅔ = 7/15 — ⅓ -
d. 2 ⅖ — ¾ = 3 ½ — 1 ⅔ +
4.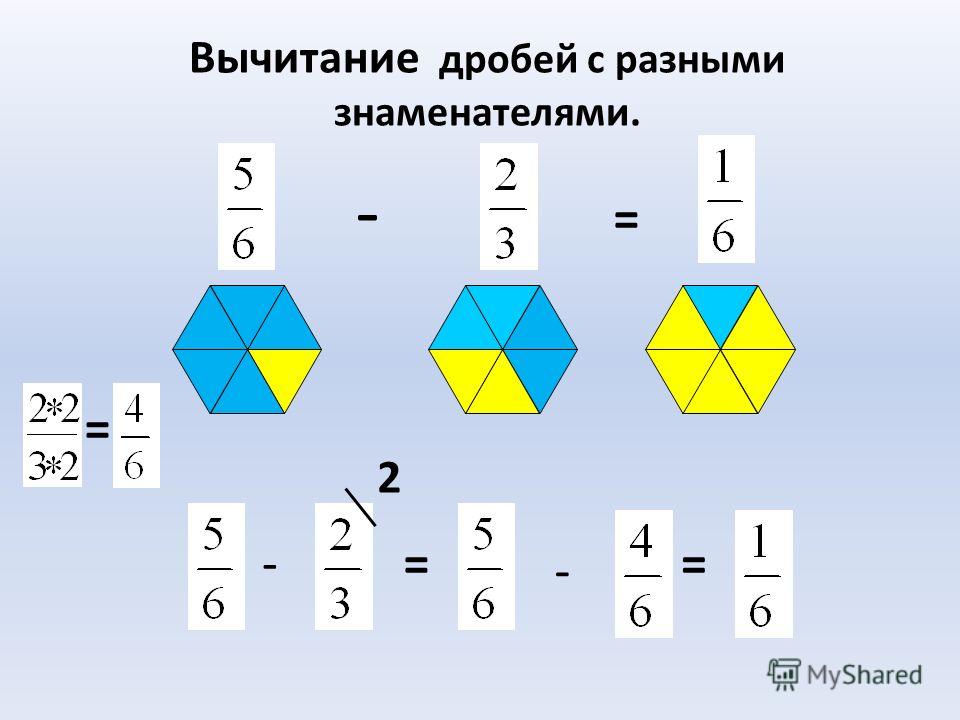 Какой общий знаменатель будет у дробей в примере 1 ⅞ — ⅚?
Какой общий знаменатель будет у дробей в примере 1 ⅞ — ⅚?
a. 48 -
b. 24 +
c. 96 -
d. 144 -
5. Чему равен x в уравнении 1 8/21 — x = ⅔?
a. 5/7 +
b. 4/21 -
c. 3/7 -
d. 6/7 -
6. На тарелке лежали 2 целых яблока и половина яблока. Вася съел ¾ от общего количества фруктов. Сколько яблок осталось на тарелке?
a. 2 ⅓ -
b. 1 ⅚ -
c. 1 ¾ +
d. 2 ¼ -
7. Что нужно сделать сперва при вычитании дробей с разными знаменателями?
a.привести дроби к общему знаменателю +
b. привести дроби к общему числителю -
c. вычесть сумму знаменателей от суммы числителей -
d. сложить знаменатели -
8. -⅘ — ⅜ = …
a. -2 1/40 -
b. 1 7/13 -
c. -1 7/40 +
d. 2 1/13 -
9. Какое неравенство составлено верно?
Какое неравенство составлено верно?
a. 2 ⅝ — ¾ > 2 27/40 — 1 ⅞ +
b. 9/11 — 1/22 > 37/44 — 17/22 -
c. 1 6/7 — ⅔ < 1 4/21 — 1 3/42 -
d. 6/7 — ½ < 5/14 — 2/7 -
тест 10. Чему равна разность чисел 1 7/15 и ⅘?
a. 1 1/15 -
b. 11/15 -
c. ⅗ -
d. ⅔ +
11. … — 3/10 = ⅙
a. 7/15 +
b. 9/13 -
c. ⅘ -
d. 6/11 -
12. Каким знаком обозначается процесс вычитания?
a. + -
b. — +
c. : -
d. × -
13. Чему равна разность в примере на картинке?
a. 26/45 +
b. 14/45 -
c. 21/44 -
d. 1 2/45 -
14. В каком из вариантов дополнительные множители равны 2 и 3?
a. ¾ — ⅔ -
b. 1 4/9 — ⅓ -
c. 2 ¾ — ⅜ -
2 ¾ — ⅜ -
d. 1 ⅚ — 1 ¼ +
15. В каком выражении содержится ошибка?
a. ⅝ — ⅗ = 1/40 -
b. 1 ⅙ — ⅔ = ½ -
c. 2 ¼ — ⅘ = 2 9/20 +
d. 11/12 — ⅙ = ¾ -
16. Какую часть времени осталось пройти Паше от дома до школы, если он уже прошел ⅔ часа?
a. ⅓ +
b. ⅚ -
c. 2/9 -
d. ¼ -
17. На какую часть опустилась температура воздуха, если днем было 14°C, а вечером — 7°C?
a. на ⅗ -
b. на ¼ -
c. на 2/9 -
d. на ½ +
18. 11/22 — 9/11 = …
a. 1/11 -
b. -2/11 -
c. -7/22 +
d. 8/27 -
19. Какой знак сравнения нужно поставить между выражениями 1 ¼ — ⅔ и 1 5/12 — ⅚?
a. > -
b. = +
c. < -
d. ≈ -
тест-20. Какой наименьший знаменатель у дробей 12/17 и ½?
a. 34 +
34 +
b. 68 -
c. 136 -
d. 17 -
21. Как называл отрицательные числа математик из Индии Брахмагупта?
a. обязательства -
b. долги +
c. беспроцентные займы -
d. хвосты -
22. 4 ⅜ — … = 4 ⅜
a. 1 -
b. -4 ⅜ -
c. 0 +
d. 8/35 -
23. На сколько число 15/19 меньше, чем 37/38?
a. 7/38 +
b. на 11/19 -
c. на ½ -
d. на 17/38 -
24. В коробке было 10 шоколадных конфет. Миша запил с чаем 6 ½ конфет, а Катя — на 3 конфеты меньше. Сколько конфет съела Катя?
a. 4 ½ -
b. 3 ⅖ -
c. 2 ⅝ -
d. 3 ½ +
25. Как записать пример 0,8 — 0,5 в виде вычитания обыкновенных дробей?
a. ⅘ — ½ +
b. 10/8 — 10/5 -
c. 5/4 — ½ -
d.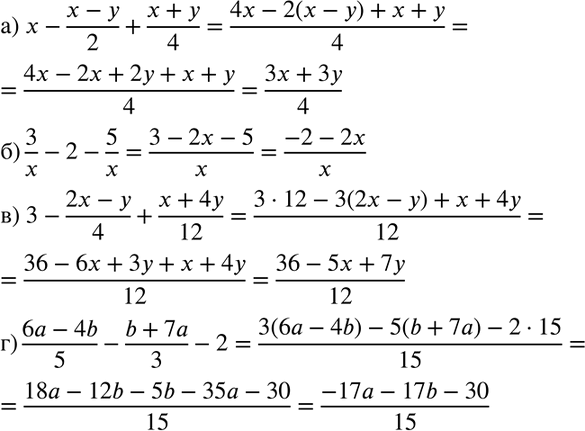 1 ¼ — 2 -
1 ¼ — 2 -
26. (⅚ — ⅓) — … = 1/10
a. ⅜ -
b. ⅖ +
c. ⅙ -
d. ⅘ -
27. Какое арифметическое действие будет решаться первым в выражении 1/20 : (⅜ — ½) × (1 ¾ + ½)?
a. сложение -
b. деление -
c. умножение -
d. вычитание +
28. Какое число самое большое?
a. -¾ -
b. -1 ¼ -
c. -½ +
d. -⅘ -
29. 1 5/18 — 7/9 = …
a. ½ +
b. ⅓ -
c. ¼ -
d. ⅕ -
тест_30. Какой круг закрашен на ⅔?
a. 1 -
b. 2 +
c. 3 -
d. 4 —
правила, примеры, решения, решение дробей
Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
58-28
В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Определение 1Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Пример 1Вычтите из дроби 2415 обыкновенную дробь 1715.
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.
Наши подсчеты можно записать так: 2415-1715=24-1715=715
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Пример 2Найдите разность 3712-1512.
Решение
Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 116. Это неправильная дробь, из которой мы выделим целую часть: 116=156.
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Сформулируем определение:
Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Пример 3Вычтите из 29 дробь 115.
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.
Подсчитаем: 29=2·59·5=1045115=1·315·3=345
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745
Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
Пример 4Найдите разность 199 — 736.
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.
Считаем ответ: 7636-736=76-736=6936
Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 11112.
Краткая запись всего решения — 199-736=11112.
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Пример 5Найдите разность 8321 – 3.
Решение
3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Из дроби 8321 при выделении целой части получится 8321=32021.
Теперь просто вычтем 3 из него: 32021-3=2021.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Проиллюстрируем это примером.
Найдите разность: 7-53.
Решение
Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Определение 3Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.
Пример 7Вычислите разность 1 065 -1362.
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Получается, что 1-1362=11-1362=6262-1362=4962.
Теперь вспомним про 1064 и сформулируем ответ: 10644962.
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Пример 8Вычислите разность 644 — 735.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
735=1435
Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Рассмотрим, как использовать их при решении примеров.
Найдите разность 244-32-56.
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:
254-32=244-64=194194-56=5712-1012=4712
Преобразуем ответ, выделив из него целую часть. Итог — 31112.
Краткая запись всего решения:
254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Пример 10Н айдите разность 98+1720-5+35.
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35
Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Онлайн тест действия с рациональными числами. Тест по математике на тему «Все действия с рациональными числами» (6 класс)
Тест по математике для проведения контроля
по теме «Все действия с рациональными числами»
Цель: установление уровня сформированности предметных, метапредметных и личностных результатов обучающихся по теме «Рациональные числа».
Требования стандарта :
Личностные результаты:
Метапредметные результаты:
Предметные результаты:
Инструкция по выполнению работы
На выполнение всей работы отводится 30 минут.
Работа состоит из 7 заданий. Среди них 3 задания с выбором одного верного ответа из четырех предложенных (задания 2, 3, 5), 1 задание на соотнесение (задание 1), 1 задание с кратким ответом (задание 4), 1 задание на составление выражения и нахождения значения (задание 7) и 1 задание, требующее составить уравнения по заданному условию (задание 6).
Задания 2. К заданию приводится 2 варианта ответа, один из которых верный. (1 балл)
Задания 3. К заданию приводится 4 варианта ответа, один из которых верный. (1 балл)
Задание 5. К заданию приводится 4 варианта ответа, один из которых верный. (2 балла)
Задание 1 на соотнесение. Учащиеся вписывают в приведенную в ответе таблицу под каждой цифрой соответствующую букву. За каждую верно указанную пару начисляется 0,5 балл. Максимальный балл за задание 2.
За каждую верно указанную пару начисляется 0,5 балл. Максимальный балл за задание 2.
Задание 4 со свободным ответом. Учащиеся представляют решение на черновике и выписывают в бланк полученный ответ. Максимальный балл за задание 3.
Задание 6 на составление уравнений имеющих заданный ответ. Максимальный балл 4.
Задание 7 на составление выражения по заданным условиям, на основе имеющихся знаний по теме и нахождении значения выражения. Максимальный балл за задание 4.
Максимальное количество баллов за всю работу – 17.
Вариант 1
- Значение выражения
Установите соответствие между выражениями и их ответами. Результат запишите в таблицу.
Значение выражения
является отрицательным числом?3. Выясните корнем, какого уравнения является число 2. Выпишите правильный ответ.
1)
2)
3)
4)
4. Вычислите:
А)
Б)
Ответ_______________________
5. Выберите номер рисунка соответствующего неравенству -а>b .
6. Придумайте и запишите четыре уравнения с различными математическими действиями, корнем, которых является число -6.
__________________________________________________________________
7. Запишите выражение: модуль разности числа b и суммы чисел a и c . Найдите значение выражения при a = –5, b = –0,5 и c = –0,05.

Ответ_______________________________________________________
Критерии оценивания тестового контроля знаний
Уровни деятельностиУУД
Критерии
№ задания
Макс. балл
Эмоц.-психол.
Личностные
Регуля-тивный
Регуля-тивные
Соци-альный
Комму-
никати-вные
Анали-тичес-кий
Позна-
ватель-
ные
Знание понятия противоположного числа
Умение находить числа изображённые точками на координатной прямой.
Умение сравнивать числа изображённые на координатной прямой
Творчс-кий
Личност-ные
Умение составить выражение по заданным условиям и на основе имеющихся знаний по теме.
Самосовершенствова-ния
Регуля-
тивные
Решение составленного выражения содержащего модуль и нахождение его значения.
Ответы
Результаты тестовой работыКласс: 6А Предмет: математика Педагог: Дата проведения:
Цель: установление уровня сформированности предметных, метапредметных и личностных результатов у обучающихся в соответствии с требованиями ФГОС
Эмоц. —
—псих..
Регулятивный
Социальный
Аналитический
Творческий
Самосовер
шенствования
Итого баллов
% выполнения
Отметка
Номер задания
4 (а)
4 (б)
ФИО обучающихся
/баллы
17
5
6.5
3
4
2
8.5
4
6.5
3
6
3
9
4
7
3
10
4
5
3
5.5
3
9
4
12
4
3
2
3.5
2
3
2
5.5
3
14
5
2.
 5
5 2
9.5
4
8
4
4
2
4.5
2
5
3
Реал. баллы
35.5
4 0
Макс. баллы
% достижен.
77
87
13
57
36
21
УУД
Личностные
Регулятивные
Коммуникативные
Познавательные
% достижения
55.5
54
13
57
Аналитическая записка по результатам тестовой работы
по теме « Все действия с рациональными числами »
Цель : установление уровня образовательных достижений обучающихся по теме «Рациональные числа » на основе требований ФГОС.
Класс: 6 Дата проведения тестовой работы:
Тестовая работа устанавливала уровень сформированности следующих предметных, метапредметных и личностных результатов:
формирование ответственного отношения к учению,
формирование готовности и способности обучающегося к саморазвитию и самообразованию на основе мотивации к обучению и познанию.

умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач,
умение оценивать правильность выполнения учебной задачи.
Овладение приемами вычисления рациональных чисел,
Развитие умения использовать приёмы для решения различных математических задач.
По итогам тестирования получены следующие результаты :
Предметные результаты :
На высоком уровне сформированности
знания:Простейшие действия с рациональными числами
Умение выполнять вычисления с рациональными числами, взятыми под знак модуля.
На низком уровне сформированности
умения:Метапредметные результаты :
Наиболее сформированными являются следующие компоненты деятельности:
регулятивный,
познавательные
Наименее сформированными являются следующие компоненты деятельности:
и универсальные учебные действия:
коммуникативные.

Уровни достижения компонентов деятельности :
Эмоционально — психологический 77 %
Регулятивный 87 %
Социальный 13 %
Аналитический 57 %
Творческий 36 %
Самосовершенствования 21 %.
Уровни сформированности универсальных учебных действий:
Регулятивные УУД 54 %,
Коммуникативные УУД 13 %
Познавательные УУД 57 %
Личностные УУД 55,5 %
Выводы :
1. По результатам тестирования выявлен высокий уровень сформированности теоретических знаний по предмету, умение находить и сравнивать числа изображённые точками на координатной прямой; эмоционально-психологические и регулятивные компоненты деятельности, познавательные УУД.
2. Выявились недостатки в подготовке обучающихся:
Недостаточно сформировано умение решать выражения в несколько действий, менее сформирован творческий компонент и самосовершенствования, коммуникативные УУД.

Предложения :
В ходе учебных занятий необходимо уделить внимание формированию компонентов деятельности и универсальных учебных действий, освоению предметных и личностных результатов:
Повышать уровень сложности задания, включать задачи нестандартного характера, требующие творческого подхода к решению, создавать для обучающихся условия, способствующие самосовершенствованию.
3. Выясните корнем, какого уравнения является число 3. Выпишите правильный ответ.
1)
2)
3)
4)
4. Вычислите:
А)
Б)
Ответ_______________________
5. Выберите номер рисунка соответствующего неравенству а
6. Придумайте и запишите четыре уравнения с различными математическими действиями, корнем, которых является число -4.
7. Запишите выражение: модуль разности числа a и суммы чисел b и c . Найдите значение выражения при a = –5, b = –0,5 и c = –0,05.
Тест «Все действия с рациональными числами»
Вариант 2
2-е изд., перераб. и доп. — М.: 2015. — 128 с. М.: 2013. — 128 с.
Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения). Пособие содержит тестовые задания по математике ко всем учебникам математики 6 класса, включенным в Федеральный перечень учебников. Тесты даются в двух вариантах по всем темам, изучаемым в 6 классе. В конце предлагается итоговый тест в двух вариантах. Ко всем заданиям имеются ответы.
Формат: pdf (2015, 128с.)
Размер: 2,3 Мб
Смотреть, скачать: drive. google
google
Формат: djvu (2013, 128с.)
Размер: 772 Кб
Смотреть, скачать: yandex.disk
Формат: pdf
Размер: 4 Мб
Смотреть, скачать: yandex.disk
ОГЛАВЛЕНИЕ
ТЕСТ 1. Отношения
чисел и величин 5
ТЕСТ 2. Масштаб 7
ТЕСТ 3. Деление числа в данном отношении 9
ТЕСТ 4. Пропорции 11
ТЕСТ 5. Прямая и обратная пропорциональность 13
ТЕСТ 6. Понятие о проценте 15
ТЕСТ 7. Задачи на проценты 17
ТЕСТ 8. Круговые диаграммы 19
ТЕСТ 9. Отрицательные целые числа 23
ТЕСТ 10. Противоположные числа. Модуль числа 25
ТЕСТ 11. Сравнение целых чисел 27
ТЕСТ 12. Сложение целых чисел 29
ТЕСТ 13. Законы сложения целых чисел 31
ТЕСТ 14. Разность целых чисел 33
ТЕСТ 15. Произведение целых чисел 35
ТЕСТ 16. Частное целых чисел 37
ТЕСТ 17. Распределительный закон 39
ТЕСТ 18. Раскрытие скобок и заключение в скобки 41
ТЕСТ 19. Действия с суммами нескольких слагаемых 43
ТЕСТ 20. Представление целых чисел на координатной оси 45
Представление целых чисел на координатной оси 45
ТЕСТ 21. Отрицательные дроби 47
ТЕСТ 22. Рациональные числа 49
ТЕСТ 23. Сравнение рациональных чисел 51
ТЕСТ 24. Сложение и вычитание дробей 53
ТЕСТ 25. Умножение и деление дробей 55
ТЕСТ 26. Законы сложения и умножения 57
ТЕСТ 27. Смешанные дроби произвольного знака 59
ТЕСТ 28. Изображение рациональных чисел на координатной оси 61
ТЕСТ 29. Уравнения 63
ТЕСТ 30. Решение задач с помощью уравнений 65
ТЕСТ 31. Понятие положительной десятичной дроби 67
ТЕСТ 32. Сравнение положительных десятичных дробей 69
ТЕСТ 33. Сложение и вычитание положительных десятичных дробей 71
ТЕСТ 34. Перенос запятой в положительной десятичной дроби 73
ТЕСТ 35. Умножение положительных десятичных дробей 75
ТЕСТ 36. Деление положительных десятичных дробей 77
ТЕСТ 37. Десятичные дроби и проценты 79
ТЕСТ 38. Сложные задачи на проценты 81
ТЕСТ 39. Десятичные дроби произвольного знака 83
ТЕСТ 40. Приближение десятичных дробей 85
Приближение десятичных дробей 85
ТЕСТ 41. Приближение суммы, разности, произведения и частного двух чисел
87
ТЕСТ 42. Разложение положительной обыкновенной дроби в конечную
десятичную дробь 89
ТЕСТ 43. Бесконечные периодические десятичные дроби 91
ТЕСТ 44. Длина отрезка 93
ТЕСТ 45. Длина окружности. Площадь круга 95
ТЕСТ 46. Координатная ось 97
ТЕСТ 47. Декартова система координат на плоскости 99
ТЕСТ 48. Столбчатые диаграммы и графики 102
Итоговый тест 106
Ответы 122
Калькулятор вычисления сумм и разностей дробей
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Используйте
Оцените суммы и разности для положительных правильных дробей, n/d (числитель/знаменатель), где n ≤ d и 0 ≤ n/d ≤ 1. Используйте округление для оценки ответов при сложении или вычитании правильных дробей.
Расчет дробей путем округления
Первоначально этот онлайн-калькулятор был настроен для вычисления путем округления дробей до ближайшей 1/2. Дроби округлялись до 0, 1/2 или 1. Для более точной оценки мы добавили возможность округлять дроби до ближайших 1/4 или 1/8. См. раздел «Значение оценки дробей» ниже.
Оценка сумм и разностей дробей с точностью до 1/2
- Дроби < 1/4 округляются в меньшую сторону до 0
- Дроби ≥ 1/4 и ≤ 3/4 округляются до 1/2
- Дроби > 3/4 округляются до 1
Оценка сумм и разностей дробей с точностью до 1/4
- Дроби < 1/8 округляются до 0
- Дроби ≥ 1/8 и < 3/8 округляются до 2/8=1/4
- Дроби ≥ 3/8 и < 5/8 округляются до 4/8=2/4=1/2
- Дроби ≥ 5/8 и < 7/8 округляются до 6/8=3/4
- Дроби ≥ 7/8 округляются до 8/8=1
Оценка сумм и разностей дробей с точностью до 1/8
- Дроби < 1/16 округляются до 0
- Дроби ≥ 1/16 и < 3/16 округляются до 2/16=1/8
- Дроби ≥ 3/16 и < 5/16 округляются до 4/16=2/8=1/4
- Дроби ≥ 5/16 и < 7/16 округляются до 6/16=3/8
- Дроби ≥ 7/16 и < 9/16 округляются до 8/16=4/8=1/2
- Дроби ≥ 15/16 округляются до 16/16=8/8=1
Таблица фракций для половинок, кварталов, восьмых и шестнадцатых с десятичными эквивалентами
таблица фракций для 16 TH , 8 TH , 4 TH и 1/2 эквивалентов
0/2
0/4 9 9 9/2. 0003
0003
0/8
0/16
0.00000
1/16
0.06250
1/8
2/16
0.12500
3/16
0.18750
1/4
2/8
4/16
0,25000
90000,25000
90000,25000
0,25000
0,25000
9000
0,25000
9000 9000
5/16
0.31250
3/8
6/16
0.37500
7/16
0.43750
1 /2
2/4
4/8
8/16
0.50000
9/16
0.56250
5/8
10/16
0. 62500
62500
11/16
0.68750
3/4
6/8
12/16
0.75000
13/16
0.81250
7/8
14/16
0.87500
15/16
0,93750
1
2/2
4/4
8/8
16/16
9000 1000См. таблица дробей.
Значение оценки дробей
Во-первых, всегда следуйте указаниям, которые дает вам учитель, для оценки сумм и разностей дробей.
Вычисление операций над правильными дробями таким способом иногда более точно выполняется человеком, чем калькулятором. Калькулятор, безусловно, может сделать оценку на основе определенных параметров в формуле, и во многих приложениях оценка очень хорошо выполняется с помощью калькуляторов (или компьютеров). Однако в этом случае более точная оценка может быть достигнута человеком.
Однако в этом случае более точная оценка может быть достигнута человеком.
Например, стандартной практикой вычисления сумм и разностей дробей для учащихся начальной школы является округление до ближайшей 1/2 путем округления до 0, 1/2 или 1. Это хорошо работает с помощью калькулятора, например, если вы добавляют 3/8 + 11/16. 3/8 ближе всего к 1/2, а 11/16 меньше 3/4, поэтому оно также ближе всего к 1/2. Оценивая, мы имеем 1/2 + 1/2 = 1. Если мы действительно сложим эти члены 3/8 + 11/16, с общим знаменателем 16 мы получим 6/16 + 11/16 = 17/16 = 1 + 1/16, что действительно близко к нашей оценке 1. Если мы теперь попробуем 1/8 + 3/4, по правилам округления до ближайшей 1/2, 1/8 ближе всего к 0, а 3/4 округляется до 1/2. При оценке получаем 0 + 1/2 = 1/2. Однако реальный ответ таков: 1/8 + 3/4 = 1/8 + 6/8 = 7/8. Это намного ближе к 1, чем к 1/2, поэтому наша оценка не очень точна. Имейте в виду, что оценка по определению является приблизительный расчет .
Если вы попытаетесь сложить несколько дробей одним и тем же методом, например, 1/8 + 1/16 + 2/8 + 3/16, вы можете получить очень приблизительную оценку. Таким образом, вы должны использовать здравый смысл в процессе оценки.
Об этих и некоторых других основных методах работы с дробями см. также Помогите с дробями.
Подписаться на калькуляторSoup:
Складывать и вычитать дроби с разными знаменателями (включая смешанные числа), заменяя данные дроби эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (В общем, a/b + c/d = (ad + bc)/bd.)
Экспорт
Распечатать
Связанные точки доступа
Альтернативная версия этого контрольного показателя для учащихся со значительными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Уроки STEM — Активность по моделированию
Клуб няни Развлечение с дробями MEA:
В этом MEA учащиеся будут применять свои знания о сложении, вычитании и сравнении дробей с одинаковыми и разными знаменателями. Babysitters ‘R Us потребует от учащихся анализа данных в виде дробных единиц времени, чтобы выбрать лучшую няню для семьи Cryin’ Ryan.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, внедренных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Формирующие оценки MFAS
Сложение дробей с разными знаменателями:
Учащихся просят сложить две пары дробей с разными знаменателями.
Сложение других дробей с разными знаменателями:
Учащихся просят сложить пары дробей с разными знаменателями.
Вычитание дробей:
Учащимся предлагается вычитать дроби с разными знаменателями.
Вычитание дополнительных дробей:
Учащихся просят вычитать неправильные дроби и смешанные числа с разными знаменателями.
Оригинальные учебники для учащихся по математике — классы K-5
Сложение зелий с непохожими дробями Часть 1:
Узнайте, как складывать дроби меньше единицы с непохожими знаменателями в этом волшебном интерактивном учебном пособии.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом эталонном тесте.
Оригинальный учебник для студентов
Сложение зелий с непохожими дробями Часть 1:
Узнайте, как складывать дроби меньше единицы с непохожими знаменателями в этом волшебном интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Образовательная игра
Викторина дроби:
Проверьте свои навыки дроби, отвечая на вопросы на этом сайте. В этом тесте вам предлагается упростить дроби, преобразовать дроби в десятичные числа и проценты, а также ответить на вопросы по алгебре, связанные с дробями. Вы даже можете выбрать уровень сложности, типы вопросов и ограничение по времени.
Тип: Обучающая игра
Задачи решения проблем
Сравнение сумм дробей единиц:
Цель этого задания – помочь учащимся понять сложение дробей; он задуман как учебная задача. Обратите внимание, что учащимся не предлагается найти сумму, поэтому это может быть дано учащимся, которые ограничены вычислением суммы дробей с одним и тем же знаменателем. Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Тип: Задача решения проблем
Смешанные числа с разными знаменателями:
Цель этого задания — помочь учащимся понять, что существуют разные способы сложения смешанных чисел, и это наиболее подходит для использования в учебных целях. Два основных способа, которыми учащиеся могут складывать, — это преобразование смешанных чисел в дроби, большие 1, или сложение целых чисел и дробных частей по отдельности. Для учащихся полезно развить чувство того, какой подход будет лучше в конкретном контексте.
Тип: Задание на решение задач
Приготовление S’Mores:
Целью этого учебного задания является мотивация обсуждения сложения дробей и значения общего знаменателя. В различных частях задания учащиеся перемещаются между абстрактным представлением дробей и значением дробей в контексте.
Тип: Задание на решение задач
Бег-а-Тон:
Цель этого задания — представить учащимся ситуацию, когда естественно складывать дроби с разными знаменателями; его можно использовать как для оценки, так и для учебных целей. Учителя должны предусмотреть два типа решений: в одном учащиеся вычисляют расстояние, которое пробежал Алекс, чтобы определить ответ, а в другом учащиеся сравнивают две части его бега с эталонными дробями.
Тип: Задание по решению задач
Нахождение общих знаменателей для вычитания:
В части (a) этого задания учащимся предлагается использовать два разных знаменателя для вычитания дробей. Цель этого состоит в том, чтобы помочь учащимся понять, что любой общий знаменатель будет работать, а не только наименьший общий знаменатель. Часть (b) не требует от учащихся делать это более чем одним способом; цель состоит в том, чтобы дать им возможность выбрать знаменатель и, возможно, сравнить с другим студентом, который выбрал другой знаменатель. Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Тип: Задание по решению задач
Нахождение общих знаменателей для сложения:
В части (a) этого задания учащимся предлагается найти и использовать два различных общих знаменателя для сложения данных дробей. Цель этого вопроса — помочь учащимся понять, что они могут использовать любой общий знаменатель для поиска решения, а не только наименьший общий знаменатель. Часть (б) не просит студентов решить данную задачу на сложение более чем одним способом. Вместо этого цель этого вопроса состоит в том, чтобы дать учащимся возможность выбрать знаменатель и, возможно, сравнить свой метод решения с другим учащимся, выбравшим другой знаменатель. Цель части (с) — дать учащимся, готовым к символической работе, возможность работать более эффективно.
Тип: Задача-решение
Египетские дроби:
Одна из целей этого задания — помочь учащимся научиться легко и комфортно складывать дроби с разными знаменателями. Другая цель состоит в том, чтобы помочь им развить чувство числа дробей, попросив учащихся разложить дроби.
Тип: Задание на решение задач
Складывают ли они?:
В этом задании рассматриваются распространенные ошибки, которые допускают учащиеся при интерпретации словесных задач на сложение дробей. Учащимся очень важно понимать, что они складывают дроби только тогда, когда дроби относятся к одному и тому же целому, а также когда дроби складываемого целого не перекрываются. Этот набор вопросов предназначен для улучшения понимания учащимися того, когда уместно и неуместно складывать дроби.
Тип: Задача решения проблем
Учебники
Создание общих знаменателей:
В этом учебном пособии рассматривается сложение и вычитание дробей с разными знаменателями. Используя числовую прямую, этот математический процесс можно легко визуализировать и связать с конечной стратегией умножения знаменателей (a/b + c/d = ad +bc/bd). Строка номера видео показывает отрицательные числа, которые выходят за рамки элементарных стандартов, поэтому учителю начальных классов необходимо подумать о том, обогатит ли это видео знания учащихся или вызовет путаницу.
Используя числовую прямую, этот математический процесс можно легко визуализировать и связать с конечной стратегией умножения знаменателей (a/b + c/d = ad +bc/bd). Строка номера видео показывает отрицательные числа, которые выходят за рамки элементарных стандартов, поэтому учителю начальных классов необходимо подумать о том, обогатит ли это видео знания учащихся или вызовет путаницу.
Тип: Учебное пособие
Наименьшие общие знаменатели:
В этом учебном пособии учащиеся познакомятся со стратегией нахождения наименьшего общего знаменателя для определенных случаев. Учителя начальных классов должны помнить, что это не является обязательным требованием для начальных стандартов, и подумать, будет ли это видео способствовать углублению знаний учащихся или создаст путаницу. В этой главе объясняется, как найти наименьший возможный общий знаменатель. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12.
Тип: Учебное пособие
Сложение и вычитание дробей:
Это учебное пособие для учащихся поможет лучше понять правила сложения и вычитания дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Виртуальный манипулятор
Дробная игра:
Этот виртуальный манипулятор позволяет отдельным учащимся работать с отношениями дробей. (Есть также ссылка на версию для двух игроков.)
Тип: Виртуальный манипулятивный
Ресурсы для родителей
Проверенные ресурсы воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Задачи решения проблем
Сравнение сумм дробей единиц:
Цель этого задания – помочь учащимся понять сложение дробей; он задуман как учебная задача. Обратите внимание, что учащимся не предлагается найти сумму, поэтому это может быть дано учащимся, которые ограничены вычислением суммы дробей с одним и тем же знаменателем. Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Обратите внимание, что учащимся не предлагается найти сумму, поэтому это может быть дано учащимся, которые ограничены вычислением суммы дробей с одним и тем же знаменателем. Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Тип: Задание на решение задач
Смешанные числа с разными знаменателями:
Цель этого задания — помочь учащимся понять, что существуют разные способы сложения смешанных чисел, и оно наиболее подходит для использования в учебных целях. Два основных способа, которыми учащиеся могут складывать, — это преобразование смешанных чисел в дроби, большие 1, или сложение целых чисел и дробных частей по отдельности. Для учащихся полезно развить чувство того, какой подход будет лучше в конкретном контексте.
Тип: Задание на решение задач
Приготовление S’Mores:
Целью этого учебного задания является мотивация обсуждения сложения дробей и значения общего знаменателя. В различных частях задания учащиеся перемещаются между абстрактным представлением дробей и значением дробей в контексте.
В различных частях задания учащиеся перемещаются между абстрактным представлением дробей и значением дробей в контексте.
Тип: Задание на решение задач
Бег-а-Тон:
Цель этого задания — представить учащимся ситуацию, когда естественно складывать дроби с разными знаменателями; его можно использовать как для оценки, так и для учебных целей. Учителя должны предусмотреть два типа решений: в одном учащиеся вычисляют расстояние, которое пробежал Алекс, чтобы определить ответ, а в другом учащиеся сравнивают две части его бега с эталонными дробями.
Тип: Задание по решению задач
Нахождение общих знаменателей для вычитания:
В части (a) этого задания учащимся предлагается использовать два разных знаменателя для вычитания дробей. Цель этого состоит в том, чтобы помочь учащимся понять, что любой общий знаменатель будет работать, а не только наименьший общий знаменатель. Часть (b) не требует от учащихся делать это более чем одним способом; цель состоит в том, чтобы дать им возможность выбрать знаменатель и, возможно, сравнить с другим студентом, который выбрал другой знаменатель. Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Тип: Задание по решению задач
Нахождение общих знаменателей для сложения:
В части (a) этого задания учащимся предлагается найти и использовать два различных общих знаменателя для сложения данных дробей. Цель этого вопроса — помочь учащимся понять, что они могут использовать любой общий знаменатель для поиска решения, а не только наименьший общий знаменатель. Часть (б) не просит студентов решить данную задачу на сложение более чем одним способом. Вместо этого цель этого вопроса состоит в том, чтобы дать учащимся возможность выбрать знаменатель и, возможно, сравнить свой метод решения с другим учащимся, выбравшим другой знаменатель. Цель части (с) — дать учащимся, готовым к символической работе, возможность работать более эффективно.
Тип: Задача-решение
Египетские дроби:
Одна из целей этого задания — помочь учащимся научиться легко и комфортно складывать дроби с разными знаменателями. Другая цель состоит в том, чтобы помочь им развить чувство числа дробей, попросив учащихся разложить дроби.
Тип: Задание на решение задач
Складывают ли они?:
В этом задании рассматриваются распространенные ошибки, которые допускают учащиеся при интерпретации словесных задач на сложение дробей. Учащимся очень важно понимать, что они складывают дроби только тогда, когда дроби относятся к одному и тому же целому, а также когда дроби складываемого целого не перекрываются. Этот набор вопросов предназначен для улучшения понимания учащимися того, когда уместно и неуместно складывать дроби.
Тип: Задача решения проблем
Учебники
Сложение и вычитание дробей:
Этот учебник для учащихся поможет учащимся лучше понять правила сложения и вычитания дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Вычитание дробей:
В этом веб-учебнике учащиеся изучают процедуры вычитания дробей. Учебник включает в себя визуальные представления задач с использованием пиццы, анимацию алгоритма и ссылки на соответствующие уроки, рабочие листы и практические задачи.
Тип: Учебное пособие
Практический тест ATI Math для сложения и вычитания дробей
Ниже приведен практический тест для сложения и вычитания дробей, , который обычно рассматривается на экзамене ATI TEAS*. Я расскажу, как складывать и вычитать смешанные дроби, неправильные дроби и правильные дроби (с разными знаменателями). Экзамен ATI TEAS проверяет абитуриентов по различным предметам математики. Большинство учащихся нервничают из-за сдачи математической части экзамена ATI (или экзамена HESI), потому что они плохо разбираются в математике. Однако ключом к успеху в математическом разделе экзамена ATI TEAS является повторение математических задач снова и снова.
Экзамен ATI TEAS проверяет абитуриентов по различным предметам математики. Большинство учащихся нервничают из-за сдачи математической части экзамена ATI (или экзамена HESI), потому что они плохо разбираются в математике. Однако ключом к успеху в математическом разделе экзамена ATI TEAS является повторение математических задач снова и снова.
Какой тип математики входит в экзамен ATI TEAS? ATI TEAS math Участники секции тестируют сложение и вычитание дробей, вычитание целых чисел, отношения, метрические разговоры и т. Д. В течение следующих недель RegisteredNurseRN.com будет разрабатывать бесплатные математические викторины и лекции по практике, чтобы помочь вам подготовиться к ATI Teas экзамен V или HESI.
Краткие советы:
Во-первых, вы должны преобразовать любые смешанные дроби в задаче в неправильные дроби, чтобы их можно было складывать или вычитать. Если знаменатели одинаковы, вы можете складывать и вычитать дроби (неважно, правильные они, неправильные или их комбинация). Если знаменатели разные, вы должны найти наименьший общий знаменатель, чтобы продолжить.
Если знаменатели разные, вы должны найти наименьший общий знаменатель, чтобы продолжить.
- M = Смешанные фракции. Если есть смешанная дробь, преобразуйте ее в… неправильную дробь (I внизу)
- I =Неправильная дробь. Все смешанные дроби должны быть преобразованы в это. Вы можете складывать неправильные дроби или правильные дроби без проблем.
- L = Наименьший общий знаменатель. Когда все дроби приведены в правильную или неправильную форму, у вас должен быть один и тот же знаменатель, чтобы складывать или вычитать их. Если знаменатели разные, необходимо найти наименьший общий знаменатель.
- E =Выполнить. Если у вас есть одинаковые знаменатели и нет смешанных дробей, вы можете выполнить (решить) задачу.
- S = Упрощение. Вы хотите упростить свой ответ, чтобы он был настолько мал, насколько может быть дробь (наименьший общий множитель единицы).

Этот практический тест проверит вашу способность решать дроби.
Практический тест ATI по математике | Сложение и вычитание дробей
Этот практический тест ATI TEAS проверит ваши знания о сложении и вычитании дробей.- Чему равна сумма 2 ½ и 3 ¼?*
- 5 ¾
- 46/8
- 5/2
- 1/2
- Упростите выражение: 6 2/3 – 1 5/8*
- 13/8
- 9 2/6
- 5 1/24
- 6 2/3
- Вычислить разницу 10 – 2 3/8*
- 8/19
- 7 5/8
- 5/8
- 3 5/9
- Упростим выражение: 5/9 + 1/3 =*
- 1/6
- 3/15
- 2/3
- 8/9
- Чему равна сумма 3 6/10 и 1 1/3?*
- 4 14/15
- 148/30
- 6 14/23
- Ни один из вариантов не является правильным.

- Упростим выражение: 2/3 + 1 14/15 =*
- 2 1/5
- 2 3/5
- 6 2/3
- 9 1/5
- Вычислить разницу 10 – 6 2/3 =*
- 4 2/3
- 1/3
- 3 1/3
- 6 2/3
- Упростим выражение: 2/3 – 1/5 =*
- 7/15
- 1/3
- 15 сентября
- 2 3/4
- Чему равна сумма 2 и 2 5/10?*
- 2 1/2
- 6
- 4 ½
- 2/3
- Упростите выражение 65 ½ + 3 25/40 =*
- 63 9/2
- 69 1/8
- 56 1/2
- Ни один из вариантов не является правильным.
(ПРИМЕЧАНИЕ. Когда вы нажмете «Отправить», будет обновлена эта же страница. Прокрутите вниз, чтобы увидеть результаты.)
Когда вы нажмете «Отправить», будет обновлена эта же страница. Прокрутите вниз, чтобы увидеть результаты.)
- Чему равна сумма 2 ½ и 3 ¼?
- Упростите выражение: 6 2/3 – 1 5/8
- Вычислить разницу между 10 и 2 3/8
- Упростите выражение: 5/9 + 1/3 =
- Чему равна сумма 3 6/10 и 1 1/3?
- Упростите выражение: 2/3 + 1 14/15 =
- Вычислите разницу 10 – 6 2/3 =
- Упростите выражение: 2/3 – 1/5 =
- Чему равна сумма 2 и 2 5/10?
- Упростите выражение 65 ½ + 3 25/40 =
Ключ ответа
1.) 5 ¾
2.) 5 1/24
3.) 7 5/8
4.) 8/9
5.) 4 14/15
6.) 2 3/5
7.) 3 1/3
8.) 7/15
9.) 4 ½
10.) 69 1/8
Не забудьте рассказать друзьям об этом тесте, поделившись им в Facebook, Twitter, и другие социальные сети. Вы также можете принять участие в более забавных викторинах по уходу за больными.
*Отказ от ответственности. Хотя мы делаем все возможное, чтобы предоставить учащимся точные и подробные тесты для изучения, этот тест/викторина предназначен только для образовательных и развлекательных целей. Пожалуйста, обратитесь к последним книгам обзоров Teas V для официального обзора исследования. TEAS и HESI являются зарегистрированными товарными знаками, не связанными с нашим сайтом. Авторские права на этот тест принадлежат RegisteredNurseRn.com. Пожалуйста, не копируйте этот тест напрямую на другие сайты; однако, пожалуйста, поделитесь ссылкой на эту страницу со студентами, друзьями и другими людьми.
Хотя мы делаем все возможное, чтобы предоставить учащимся точные и подробные тесты для изучения, этот тест/викторина предназначен только для образовательных и развлекательных целей. Пожалуйста, обратитесь к последним книгам обзоров Teas V для официального обзора исследования. TEAS и HESI являются зарегистрированными товарными знаками, не связанными с нашим сайтом. Авторские права на этот тест принадлежат RegisteredNurseRn.com. Пожалуйста, не копируйте этот тест напрямую на другие сайты; однако, пожалуйста, поделитесь ссылкой на эту страницу со студентами, друзьями и другими людьми.
7.2 Тождества суммы и разности — предварительное исчисление 2e
Цели обучения
В этом разделе вы:
- Используйте формулы суммы и разности для косинуса.
- Использовать формулы суммы и разности для синуса.
- Используйте формулы суммы и разности для тангенса.
- Используйте формулы суммы и разности для кофункций.
- Используйте формулы суммы и разности для проверки идентичности.

Рисунок 1 Денали (бывшая гора Мак-Кинли) в национальном парке Денали на Аляске возвышается на 20 237 футов (6 168 м) над уровнем моря. Это самая высокая вершина в Северной Америке. (кредит: Дэниел А. Лейфхейт, Flickr)
Как можно измерить высоту горы? Что можно сказать о расстоянии от Земли до Солнца? Как и многие, казалось бы, неразрешимые проблемы, мы полагаемся на математические формулы, чтобы найти ответы. Тригонометрические тождества, обычно используемые в математических доказательствах, веками применялись в реальном мире, в том числе для расчета больших расстояний.
Тригонометрические тождества, которые мы рассмотрим в этом разделе, восходят к персидскому астроному, жившему около 950 г. н.э., но древние греки открыли те же самые формулы намного раньше и сформулировали их в терминах аккордов. Это специальные уравнения или постулаты, верные для всех значений, вводимых в уравнения, и с бесчисленными приложениями.
В этом разделе мы изучим методы, которые позволят нам решать проблемы, подобные описанным выше. Следующие формулы упростят многие тригонометрические выражения и уравнения. Имейте в виду, что в этом разделе термин формула используется как синоним слова тождество .
Следующие формулы упростят многие тригонометрические выражения и уравнения. Имейте в виду, что в этом разделе термин формула используется как синоним слова тождество .
Использование формул суммы и разности для косинуса
Найти точное значение синуса, косинуса или тангенса угла часто проще, если мы можем переписать заданный угол через два угла, для которых известны тригонометрические значения. Мы можем использовать специальные углы, которые мы можем рассмотреть в единичной окружности, показанной на рисунке 2.9.0003
Рисунок 2 Единичный круг
Мы начнем с формул суммы и разности для косинуса, чтобы мы могли найти косинус заданного угла, если мы можем разбить его на сумму или разность двух специальных углов. См. Таблицу 1.
| Формула суммы для косинуса | cos(α+β)=cosαcosβ−sinαsinβcos(α+β)=cosαcosβ−sinαsinβ |
| Формула разности для косинуса | cos(α−β)=cosαcosβ+sinαsinβcos(α−β)=cosαcosβ+sinαsinβ |
Стол 1
Сначала докажем формулу разности косинусов. Рассмотрим две точки на единичной окружности. См. рисунок 3. Точка PP находится под углом αα от положительной оси x- с координатами (cosα,sinα)(cosα,sinα), а точка QQ находится под углом ββ от положительной оси x- с координатами (cosβ,sinβ).(cosβ,sinβ). Обратите внимание, что мера угла POQPOQ равна α−β.α−β.
Рассмотрим две точки на единичной окружности. См. рисунок 3. Точка PP находится под углом αα от положительной оси x- с координатами (cosα,sinα)(cosα,sinα), а точка QQ находится под углом ββ от положительной оси x- с координатами (cosβ,sinβ).(cosβ,sinβ). Обратите внимание, что мера угла POQPOQ равна α−β.α−β.
Обозначьте еще две точки: AA под углом (α−β)(α−β) от положительной оси x- с координатами (cos(α−β),sin(α−β));(cos (α−β),sin(α−β)); и точка BB с координатами (1,0).(1,0). Треугольник POQPOQ является вращением треугольника AOBAOB и, таким образом, расстояние от PP до QQ такое же, как расстояние от AA до B.B.
Рисунок 3
Мы можем найти расстояние от PP до QQ, используя формулу расстояния.
Затем мы применяем тождество Пифагора и упрощаем.
=(cos2α+sin2α)+(cos2β+sin2β)−2cosαcosβ−2sinαsinβ=1+1−2cosαcosβ−2sinαsinβ=2−2cosαcosβ−2sinαsinβ=(cos2α+sin2α)+(cos2β+sin2β)−2cosαcosβ−2sin=1αsinβ−2sin +1−2cosαcosβ−2sinαsinβ=2−2cosαcosβ−2sinαsinβ
Точно так же, используя формулу расстояния, мы можем найти расстояние от AA до B. B.
B.
dAB=(cos(α−β)−1)2+(sin(α−β)−0)2 =cos2(α−β)−2cos(α−β)+1+sin2(α−β)dAB =(cos(α−β)−1)2+(sin(α−β)−0)2 =cos2(α−β)−2cos(α−β)+1+sin2(α−β)
Применяя тождество Пифагора и упрощая, получаем:
=(cos2(α−β)+sin2(α−β))−2cos(α−β)+1=1−2cos(α−β)+1=2 −2cos(α−β)=(cos2(α−β)+sin2(α−β))−2cos(α−β)+1=1−2cos(α−β)+1=2−2cos(α− р)
Поскольку два расстояния одинаковы, мы приравняем их друг к другу и упростим.
2−2cosαcosβ−2sinαsinβ=2−2cos(α−β) 2−2cosαcosβ−2sinαsinβ=2−2cos(α−β) 2−2cosαcosβ−2sinαsinβ=2−2cos(α−β) 2−2cosαcosβ−2sinαsinβ=2 −2cos(α−β)
Наконец, мы вычитаем 22 из обеих частей и делим обе части на −2,−2.
cosαcosβ+sinαsinβ=cos(α−β) cosαcosβ+sinαsinβ=cos(α−β)
Итак, у нас есть разностная формула для косинуса. Мы можем использовать аналогичные методы для получения косинуса суммы двух углов.
Формулы суммы и разности для косинуса
Эти формулы можно использовать для вычисления косинуса суммы и разности углов.
cos(α+β)=cosαcosβ−sinαsinβcos(α+β)=cosαcosβ−sinαsinβ
cos(α−β)=cosαcosβ+sinαsinβcos(α−β)=cosαcosβ+sinαsinβ
Как
Даны два угла. Найдите косинус разности углов.
- Напишите формулу разности для косинуса.
- Подставить значения заданных углов в формулу.
- Упростить.
Пример 1
Нахождение точного значения с помощью формулы для косинуса разности двух углов
С помощью формулы для косинуса разности двух углов найдите точное значение cos(5π4−π6).cos(5π4−π6 ).
Решение
Используйте формулу косинуса разности двух углов. Имеем
cos(α−β)=cosαcosβ+sinαsinβcos(5π4−π6)=cos(5π4)cos(π6)+sin(5π4)sin(π6) =(−22)(32)−(22)( 12) =−64−24 = −6−24 cos(α−β)=cosαcosβ+sinαsinβcos(5π4−π6)=cos(5π4)cos(π6)+sin(5π4)sin(2π6) = (32)−(22)(12) =−64−24 =−6−24
Попытайся #1
Найдите точное значение cos(π3−π4). cos(π3−π4).
cos(π3−π4).
Пример 2
Нахождение точного значения по формуле суммы двух углов для косинуса
Нахождение точного значения cos(75∘).cos(75∘).
Решение
Поскольку 75∘=45∘+30∘, 75∘=45∘+30∘, мы можем оценить cos(75∘)cos(75∘) как cos(45∘+30∘).cos(45∘+30∘ ). Таким образом,
cos (45∘+30∘) = cos (45∘) cos (30∘) −sin (45∘) sin (30∘) = 22 (32) −22 (12) = 64–24 = 6 −24cos (45∘+30∘) = cos (45∘) cos (30∘) −sin (45∘) sin (30∘) = 22 (32) −22 (12) = 64–24 = 6–24 9
Попытайся #2
Найдите точное значение cos(105∘).cos(105∘).
Использование формул суммы и разности для синуса
Формулы суммы и разности для синуса можно вывести так же, как и для косинуса, и они напоминают формулы косинуса.
Формулы суммы и разности для синуса
Эти формулы можно использовать для вычисления синусов сумм и разностей углов.
sin(α+β)=sinαcosβ+cosαsinβsin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβsin(α-β)=sinαcosβ-cosαsinβ
Как
Даны два угла. Найдите синус разности углов.
- Напишите формулу разности для синуса.
- Подставить данные углы в формулу.
- Упростить.
Пример 3
Использование тождеств суммы и разности для оценки разности углов
Использование тождеств суммы и разности для оценки разности углов и демонстрации того, что часть a соответствует части b.
- ⓐ sin(45∘−30∘)sin(45∘−30∘)
- ⓑ sin(135∘−120∘)sin(135∘−120∘)
Решение
- ⓐ Начнем с того, что напишем формулу и подставим заданные углы.

sin(α−β)=sinαcosβ−cosαsinβsin(45∘−30∘)=sin(45∘)cos(30∘)−cos(45∘)sin(30∘) sin(α−β)=sinαcosβ−cosαsinβsin (45∘−30∘)=sin(45∘)cos(30∘)−cos(45∘)sin(30∘)
Далее нам нужно найти значения тригонометрических выражений.
sin(45∘)=22,cos(30∘)=32,cos(45∘)=22,sin(30∘)=12sin(45∘)=22,cos(30∘)=32,cos(45 ∘)=22,sin(30∘)=12
Теперь мы можем подставить эти значения в уравнение и упростить.
sin(45∘−30∘)=22(32)−22(12) =6−24sin(45∘−30∘)=22(32)−22(12) =6−24
- ⓑ Снова пишем формулу и подставляем заданные углы.
sin(α−β)=sinαcosβ−cosαsinβsin(135∘−120∘)=sin(135∘)cos(120∘)−cos(135∘)sin(120∘) sin(α−β)=sinαcosβ−sinαsin (135∘−120∘)=sin(135∘)cos(120∘)−cos(135∘)sin(120∘)
Далее находим значения тригонометрических выражений.
sin(135∘)=22,cos(120∘)=−12,cos(135∘)=−22,sin(120∘)=32sin(135∘)=22,cos(120∘)=−12, cos(135∘)=−22,sin(120∘)=32
Теперь мы можем подставить эти значения в уравнение и упростить его.

sin(135∘−120∘)=22(−12)−(−22)(32) = −2+64 =6−24sin(135∘−120−120∘)=22(2) (32) = −2+64 = 6–24sin (135∘ —120∘) = 22 (−12) — ( — 22) (32) = −2+64 = 6–24sin (135∘ — 1220∘) = 22(−12)−(−22)(32) =−2+64 =6−24
Пример 4
Нахождение точного значения выражения, содержащего обратную тригонометрическую функцию
Нахождение точного значения sin(cos-112+sin-135).sin(cos-112+sin-135).
Решение
В этой задаче отображается шаблон sin(α+β).sin(α+β). Пусть α=cos-112α=cos-112 и β=sin-135.β=sin-135. Тогда мы можем записать
cosα=12,0≤α≤πsinβ=35,−π2≤β≤π2cosα=12,0≤α≤πsinβ=35,−π2≤β≤π2
Мы будем использовать тождества Пифагора для найти sinαsinα и cosβ.cosβ.
SINα = 1 -COS2α = 1-14 = 34 = 32COSβ = 1-SIN2β = 1–925 = 1625 = 45SINα = 1 -COS2α = 1-14 = 34 = 32COSβ = 1-SIN2β = 1–925 = 1625 = 34 = 32COSβ = 1-SIN2β = 1–925 = 1625 = 34 45
Используя формулу суммы для синуса: sin−135)=sin(α+β)=sinαcosβ+cosαsinβ=32⋅45+12⋅35=43+310
Использование формул суммы и разности для касательной
Нахождение точных значений тангенса суммы или разности двух углов немного сложнее, но опять же, это вопрос распознавания закономерности.
Чтобы найти формулу суммы двух углов для тангенса, нужно взять частное из формул суммы для синуса и косинуса и упростить. Напомним, tanx=sinxcosx,cosx≠0.tanx=sinxcosx,cosx≠0.
Выведем формулу суммы для тангенса.
tan(α+β)=sin(α+β)cos(α+β) =sinαcosβ+cosαsinβcosαcosβ−sinαsinβ =sinαcosβ+cosαsinβcosαcosβcosαcosβ−sinαsinβcosαcosβDivide the numerator and denominator by cosαcosβ =sinαcosβcosαcosβ+cosαsinβcosαcosβcosαcosβcosαcosβ−sinαsinβcosαcosβ =sinαcosα+sinβcosβ1−sinαsinβcosαcosβ =tanα+tanβ1−tanαtanβtan(α+β)=sin(α+β)cos(α+β) =sinαcosβ+cosαsinβcosαcosβ−sinαsinβ =sinαcosβ+cosαsinβcosαcosβcosαcosβ−sinαsinβcosαcosβDivide the numerator and denominator by cosαcosβ =sinαcosβcosαcosβ+cosαsinβcosαcosβcosαcosβcosαcosβ−sinαsinβcosαcosβ =sinαcosα +sinβcosβ1−sinαsinβcosαcosβ =tanα+tanβ1−tanαtanβ
Аналогичным образом можно вывести формулу разности для тангенса.
Формулы суммы и разности для касательной
Формулы суммы и разности для тангенса следующие:
tan(α+β)=tanα+tanβ1−tanαtanβtan(α+β)=tanα+tanβ1−tanαtanβ (α−β)=tanα−tanβ1+tanαtanβ
Как
Даны два угла, найдите тангенс суммы углов.
- Напишите формулу суммы для тангенса.
- Подставить данные углы в формулу.
- Упростить.
Пример 5
Нахождение точного значения выражения, содержащего тангенс
Нахождение точного значения tan(π6+π4).tan(π6+π4).
Решение
Давайте сначала напишем формулу суммы для тангенса и подставим в формулу заданные углы.
tan(α+β)=tanα+tanβ1−tanαtanβtan(π6+π4)=tan(π6)+tan(π4)1−(tan(π6))(tan(π4))tan(α+β)= tanα+tanβ1−tanαtanβtan(π6+π4)=tan(π6)+tan(π4)1−(tan(π6))(tan(π4))
Затем мы определяем отдельные тангенсы по формуле: +π4)=13+11−(13)(1) =1+333−13 =1+33(33−1) =3+13−1tan(π6+π4)=13+11−(13)(1 ) =1+333−13 =1+33(33−1) =3+13−1
Попытайся #3
Найдите точное значение tan(2π3+π4). tan(2π3+π4).
tan(2π3+π4).
Пример 6
Нахождение кратных сумм и разностей углов
Учитывая sinα=35,0<α<π2,cosβ=−513,π<β<3π2,sinα=35,0<α<π2,cosβ=−513,π< β<3π2, найти
- ⓐ sin(α+β)sin(α+β)
- ⓑ потому что (α + β) потому что (α + β)
- ⓒ загар(α+β)загар(α+β)
- ⓓ загар (α-β) загар (α-β)
Решение
Мы можем использовать формулы суммы и разности для определения суммы или разности углов, когда для каждого из отдельных углов задано отношение синуса, косинуса или тангенса. Для этого мы строим так называемый эталонный треугольник, чтобы помочь найти каждый компонент формул суммы и разности.
- ⓐ
Чтобы найти sin(α+β),sin(α+β), мы начинаем с sinα=35sinα=35 и 0<α<π2.0<α<π2. Сторона, противоположная αα, имеет длину 3, гипотенуза имеет длину 5, а αα находится в первом квадранте.
 См. рис. 4. Используя теорему Пифагора, мы можем найти длину стороны
См. рис. 4. Используя теорему Пифагора, мы можем найти длину стороныa:a2+32=52 a2=16 a=4a:a2+32=52 a2=16 a=4
Рисунок 4
Поскольку cosβ=−513cosβ=−513 и π<β<3π2,π<β<3π2, сторона, примыкающая к ββ, равна −5,−5, гипотенуза равна 13, а ββ находится в третьем квадранте. См. рис. 5. Опять же, используя теорему Пифагора, мы имеем
(−5)2+a2=13225+a2=169a2=144a=±12(−5)2+a2=13225+a2=169a2=144a=±12
Поскольку ββ находится в третьем квадранте, a=– 12.а=–12.
Рисунок 5
Следующим шагом является нахождение косинуса αα и синуса β.β. Косинус αα — это прилежащий катет к гипотенузе. Мы можем найти его из треугольника на рисунке 5: cosα=45.cosα=45. Мы также можем найти синус ββ из треугольника на рисунке 5, как противоположную сторону от гипотенузы: sinβ=−1213.sinβ=−1213. Теперь мы готовы вычислить sin(α+β).sin(α+β).
sin (α+β) = sinαCosβ+cosαSinβ = (35) ( — 513)+(45) ( — 1213) = −1565–4865 = −6365sin (α+β) = sinαcosβ+cosαSinβ = (35) ( — 513)+(45)(-1213) =−1565−4865 =−6365
- ⓑ Мы можем найти cos(α+β)cos(α+β) аналогичным образом.
 Подставляем значения по формуле.
Подставляем значения по формуле.COS (α+β) = COSαCOSβ -SINαSINβ = (45) ( — 513) — (35) ( — 1213) = −2065+3665 = 1665COS (α+β) = COSαCOSβ -SINα = (45) (α+β) = COSαCOSβ -SINα = (45) (513 )−(35)(−1213) =−2065+3665 =1665
- ⓒ Для tan(α+β),tan(α+β), если sinα=35sinα=35 и cosα=45,cosα=45, то
tanα=3545=34tanα=3545=34
Если sinβ=-1213sinβ=-1213 и cosβ=-513,cosβ=-513, затем
tanβ=−1213−513=125tanβ=−1213−513=125
Затем
TAN (α+β) = TANα+TANβ1 -TANαTANβ = 34+1251–34 (125) = 6320–1620 = -6316TAN (α+β) = TANα+TANβ1 -TANαTANβ = 34+1251–34 (125) = 6320−1620 = 6316
- ⓓ Чтобы найти tan(α−β),tan(α−β), у нас есть нужные значения. Мы можем подставить их и оценить.
TAN (α -β) = TANα -TANβ1+TANαTANβ = 34–1251+34 (125) = -33205620 = −3356TAN (α -β) = TANα -TANβ1+TANαTANβ = 34–1251+34 (125) = — — 33205620 =−3356
Анализ
Распространенная ошибка при решении таких задач, как эта, заключается в том, что у нас может возникнуть соблазн думать, что αα и ββ являются углами одного и того же треугольника, что, конечно же, не так. Также обратите внимание, что
Также обратите внимание, что
tan(α+β)=sin(α+β)cos(α+β)tan(α+β)=sin(α+β)cos(α+β)
Использование формул суммы и разности для кофункций
Теперь, когда мы можем найти функции синуса, косинуса и тангенса для сумм и разностей углов, мы можем использовать их, чтобы сделать то же самое для их кофункций. Вы можете вспомнить из тригонометрии прямоугольного треугольника, что если сумма двух положительных углов равна π2,π2, эти два угла являются дополнительными, а сумма двух острых углов в прямоугольном треугольнике равна π2,π2, поэтому они также являются дополнительными. На рисунке 6 обратите внимание, что если один из острых углов помечен как θ, θ, то другой острый угол должен быть помечен (π2−θ).(π2−θ).
Обратите также внимание на то, что sinθ=cos(π2−θ):sinθ=cos(π2−θ): против гипотенузы. Таким образом, когда два угла дополняют друг друга, мы можем сказать, что синус θθ равен кофункции дополнения θ.θ. Точно так же тангенс и котангенс являются кофункциями, а секанс и косеканс являются кофункциями.
Рисунок 6
Из этих отношений формируются тождества кофункций.
Кофункциональные тождества
Идентичности кофункций приведены в таблице 2.
| sinθ=cos(π2−θ)sinθ=cos(π2−θ) | cosθ=sin(π2−θ)cosθ=sin(π2−θ) |
| tanθ=cot(π2−θ)tanθ=cot(π2−θ) | cotθ=tan(π2−θ)cotθ=tan(π2−θ) |
| secθ=csc(π2−θ)secθ=csc(π2−θ) | cscθ=сек(π2−θ)cscθ=сек(π2−θ) |
Стол 2
Обратите внимание, что формулы в таблице можно также обосновать алгебраически, используя формулы суммы и разности. Например, используя
cos(α−β)=cosαcosβ+sinαsinβ,cos(α−β)=cosαcosβ+sinαsinβ,
мы можем написать
cos (π2−θ) = cosπ2cosθ+sinπ2sinθ = (0) cosθ+(1) sinθ = sinθcos (π2−θ) = cosπ2cosθ+sinπ2du Пример 7
Нахождение кофункции с тем же значением, что и заданное выражение
Запишите tanπ9tanπ9 через его кофункцию.
Решение
Кофункция tanθ=cot(π2−θ).tanθ=cot(π2−θ). Таким образом,
tan(π9)=cot(π2−π9) =cot(9π18−2π18) =cot(7π18)tan(π9)=cot(π2−π9) =cot(9π18−2π18) =cot(7π18)
Попытайся #4
Запишите sinπ7sinπ7 через его кофункцию.
Использование формул суммы и разности для проверки идентичности
Проверка идентичности означает демонстрацию того, что уравнение верно для всех значений переменной. Это помогает быть хорошо знакомым с тождествами или иметь их список, доступный во время работы над задачами. Просмотр общих правил из раздела «Решение тригонометрических уравнений с тождествами» может помочь упростить процесс проверки тождества.
Как
Имея тождество, проверьте его, используя формулы суммы и разности.
- Начните с выражения со стороны знака равенства, которое кажется наиболее сложным.
 Перепишите это выражение, пока оно не совпадет с другой стороной знака равенства. Иногда нам, возможно, придется изменить обе стороны, но наиболее эффективно работать только с одной стороной.
Перепишите это выражение, пока оно не совпадет с другой стороной знака равенства. Иногда нам, возможно, придется изменить обе стороны, но наиболее эффективно работать только с одной стороной. - Ищите возможности использовать формулы суммы и разности.
- Преобразовать суммы или разности частных в отдельные частные.
- Если процесс становится громоздким, перепишите выражение в терминах синусов и косинусов.
Пример 8
Проверка идентичности с использованием синуса
Проверка идентичности sin(α+β)+sin(α−β)=2sinαcosβ.sin(α+β)+sin(α−β)=2sinαcosβ.
Решение
Мы видим, что в левую часть уравнения входят синусы суммы и разности углов.
sin(α+β)=sinαcosβ+cosαsinβsin(α−β)=sinαcosβ−cosαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α−β)=sinαcosβ−cosαsinβ
Мы можем переписать каждое из них, используя формулы суммы и разности.
sin(α+β)+sin(α−β)=sinαcosβ+cosαsinβ+sinαcosβ−cosαsinβ=2sinαcosβsin(α+β)+sin(α−β)=sinαcosβ+cosαsinβ+sinαcosβ−cosαsinβ=2sinαcosβ
Мы убедитесь, что личность подтверждена.
Пример 9
Проверка идентичности с участием касательной
Проверьте следующую идентичность.
sin(α−β)cosαcosβ=tanα−tanβsin(α−β)cosαcosβ=tanα−tanβ
Решение 908:40
Начнем с того, что перепишем числитель в левой части уравнения.
sin(α−β)cosαcosβ=sinαcosβ−cosαsinβcosαcosβ=sinαcosβcosαcosβ−cosαsinβcosαcosβRewrite using a common denominator.=sinαcosα−sinβcosβCancel.=tanα−tanβRewrite in terms of tangent.sin(α−β)cosαcosβ=sinαcosβ−cosαsinβcosαcosβ=sinαcosβcosαcosβ− cosαsinβcosαcosβПереписать с использованием общего знаменателя.=sinαcosα−sinβcosβОтмена.=tanα−tanβПереписать в терминах касательной.
Видим, что личность подтверждена. Во многих случаях проверку тождества тангенса можно успешно выполнить, записав тангенс в терминах синуса и косинуса.
Попытайся #5
Проверить идентичность: tan(π−θ)=−tanθ.tan(π−θ)=−tanθ.
Пример 10
Использование формул суммы и разности для решения прикладной задачи
Пусть L1L1 и L2L2 обозначают две невертикальные пересекающиеся прямые, а θθ обозначает острый угол между L1L1 и L2.L2. См. рисунок 7. Покажите, что
tanθ=m2−m11+m1m2tanθ=m2−m11+m1m2
, где m1m1 и m2m2 — наклоны L1L1 и L2L2 соответственно. ( Подсказка: Используйте тот факт, что tanθ1=m1tanθ1=m1 и tanθ2=m2.tanθ2=m2. )
Рисунок 7
Решение
Используя формулу разности для тангенса, эта проблема не кажется такой сложной, как могла бы.
tanθ=tan(θ2−θ1) =tanθ2−tanθ11+tanθ1tanθ2 =m2−m11+m1m2tanθ=tan(θ2−θ1) =tanθ2−tanθ11+tanθ1tanθ2 0 0 =m2−m1
Пример 11
Исследование проблемы с растяжкой
Для стены для скалолазания растяжка RR крепится на высоте 47 футов к вертикальному столбу. Дополнительная поддержка обеспечивается другой растяжкой SS, прикрепленной на высоте 40 футов над землей к тому же столбу. Если провода прикреплены к земле на расстоянии 50 футов от столба, найдите угол αα между проводами. См. рис. 8.
Дополнительная поддержка обеспечивается другой растяжкой SS, прикрепленной на высоте 40 футов над землей к тому же столбу. Если провода прикреплены к земле на расстоянии 50 футов от столба, найдите угол αα между проводами. См. рис. 8.
Рисунок 8
Решение
Давайте сначала обобщим информацию, которую мы можем собрать из диаграммы. Поскольку известны только стороны, прилегающие к прямому углу, мы можем использовать функцию касательной. Обратите внимание, что tanβ=4750,tanβ=4750 и tan(β−α)=4050=45.tan(β−α)=4050=45. Затем мы можем использовать формулу разности для тангенса.
tan(β−α)=tanβ−tanα1+tanβtanαtan(β−α)=tanβ−tanα1+tanβtanα
Теперь, подставляя известные нам значения в формулу, имеем
45 = 4750 -TANα1+4750TANα4 (1+4750TANα) = 5 (4750 -TANα) 45 = 4750 -TANα1+4750TANα4 (1+4750TANα) = 5 (4750–TANα)
Используйте свойство распределения, а затем упрощение. функции.
4(1)+4(4750)tanα=5(4750)−5tanα4+3,76tanα=4,7−5tanα5tanα+3,76tanα=0,78,76tanα=0,7tanα≈0,07991tan−1(0,07991)≈0,0797414(1) +4(4750)tanα=5(4750)−5tanα4+3,76tanα=4,7−5tanα5tanα+3,76tanα=0,78,76tanα=0,7tanα≈0,07991tan−1(0,07991)≈0,079741
Теперь мы можем вычислить угол в градусов.
α≈0,079741(180π)≈4,57∘α≈0,079741(180π)≈4,57∘
Анализ
Иногда, когда появляется приложение, включающее прямоугольный треугольник, мы можем подумать, что решение — это вопрос применения теоремы Пифагора. Это может быть частично правдой, но это зависит от того, что задает проблема и какая информация предоставляется.
7.2 Секционные упражнения
Вербальный
1.
Объясните основу тождеств кофункций и когда они применяются.
2.
Есть ли только один способ вычислить cos(5π4)?cos(5π4)? Объясните, как настроить решение двумя разными способами, а затем вычислить, чтобы убедиться, что они дают одинаковый ответ.
3.
Объясните тому, кто забыл четно-нечетные свойства синусоидальных функций, как формулы сложения и вычитания могут определить эту характеристику для f(x)=sin(x)f(x)=sin(x) и g(x) =cos(x). g(x)=cos(x). (Подсказка: 0−x=−x0−x=−x )
g(x)=cos(x). (Подсказка: 0−x=−x0−x=−x )
Алгебраический
Для следующих упражнений найдите точное значение.
4.
потому что (7π12) потому что (7π12)
5.
потому что (π12) потому что (π12)
6.
грех (5π12) грех (5π12)
7.
грех(11π12)грех(11π12)
8.
тангенс(-π12)тангенс(-π12)
9.
загар(19π12)загар(19π12)
Для следующих упражнений перепишите в терминах sinxsinx и cosx.cosx.
10.
грех(х+11π6) грех(х+11π6)
11.
грех(х-3π4) грех(х-3π4)
12.
потому что (х-5π6) потому что (х-5π6)
13.
cos(x+2π3)cos(x+2π3)
Для следующих упражнений упростите данное выражение.
14.
csc(π2−t)csc(π2−t)
15.
сек(π2−θ)сек(π2−θ)
16.
раскладушка(π2−x)раскладушка(π2−x)
17.
тангенс (π2−x) тангенс (π2−x)
18.
sin(2x)cos(5x)−sin(5x)cos(2x)sin(2x)cos(5x)−sin(5x)cos(2x)
19.
загар(32x)−загар(75x)1+загар(32x)загар(75x)загар(32x)−загар(75x)1+загар(32x)загар(75x)
Для следующих упражнений найдите требуемую информацию.
20.
Учитывая, что sina=23sina=23 и cosb=−14,cosb=−14, aa и bb оба находятся в интервале [π2,π),[π2,π], найдите sin(a+b)sin(a +b) и cos(a−b). cos(a−b).
cos(a−b).
21.
Учитывая, что sina=45,sina=45 и cosb=13,cosb=13, причем aa и bb оба находятся в интервале [0,π2),[0,π2], найдите sin(a−b)sin( a−b) и cos(a+b).cos(a+b).
В следующих упражнениях найдите точное значение каждого выражения.
22.
sin(cos-1(0)-cos-1(12))sin(cos-1(0)-cos-1(12))
23.
cos(cos-1(22)+sin-1(32))cos(cos-1(22)+sin-1(32))
24.
тангенс (sin-1(12)-cos-1(12))tan(sin-1(12)-cos-1(12))
Графический
В следующих упражнениях упростите выражение, а затем начертите оба выражения как функции, чтобы убедиться, что графики идентичны.
25.
cos(π2−x)cos(π2−x)
26.
sin(π−x)sin(π−x)
27.
тангенс(π3+x)тангенс(π3+x)
28.
sin(π3+x)sin(π3+x)
29.
тангенс (π4−x) тангенс (π4−x)
30.
потому что (7π6+x) потому что (7π6+x)
31.
sin(π4+x)sin(π4+x)
32.
потому что (5π4+x) потому что (5π4+x)
В следующих упражнениях используйте график, чтобы определить, являются ли функции одинаковыми или разными. Если они одинаковые, покажите, почему. Если они разные, замените вторую функцию на ту, которая идентична первой. (Подсказка: думайте, что 2x=x+x.2x=x+x. )
33.
f(x)=sin(4x)−sin(3x)cosxf(x)=sin(4x)−sin(3x)cosx, g(x)=sinxcos(3x)g(x)=sinxcos(3x)
34.
f(x)=cos(4x)+sinxsin(3x),g(x)=-cosxcos(3x)f(x)=cos(4x)+sinxsin(3x),g(x)=-cosxcos( 3x)
35.
f(x)=sin(3x)cos(6x)f(x)=sin(3x)cos(6x), g(x)=-sin(3x)cos(6x)g(x)=-sin (3x)cos(6x)
36.
f(x)=sin(4x)f(x)=sin(4x), g(x)=sin(5x)cosx-cos(5x)sinxg(x)=sin(5x)cosx-cos(5x )синкс
37.
f(x)=sin(2x)f(x)=sin(2x), g(x)=2sinxcosxg(x)=2sinxcosx
38.
f(θ)=cos(2θ)f(θ)=cos(2θ), g(θ)=cos2θ−sin2θg(θ)=cos2θ−sin2θ
39.
f(θ)=tan(2θ)f(θ)=tan(2θ), g(θ)=tanθ1+tan2θg(θ)=tanθ1+tan2θ
40.
f(x)=sin(3x)sinxf(x)=sin(3x)sinx, g(x)=sin2(2x)cos2x−cos2(2x)sin2xg(x)=sin2(2x)cos2x−cos2( 2x)sin2x
41.
f(x)=tan(-x)f(x)=tan(-x), g(x)=tanx-tan(2x)1-tanxtan(2x)g(x)=tanx-tan(2x )1−tanxtan(2x)
Технология
Для следующих упражнений найдите точное значение алгебраически, а затем подтвердите ответ с помощью калькулятора с точностью до четвертого десятичного знака.
42.
грех(75∘)грех(75∘)
43.
грех(195∘)грех(195∘)
44.
потому что (165∘) потому что (165∘)
45.
потому что (345∘) потому что (345∘)
46.
тан(-15∘)тан(-15∘)
Расширения
Для следующих упражнений докажите представленные тождества.
47.
tan(x+π4)=tanx+11−tanxtan(x+π4)=tanx+11−tanx
48.
tan(a+b)tan(a-b)=sinacosa+sinbcosbssinacosa-sinbcosbtan(a+b)tan(a-b)=sinacosa+sinbcosbsinacosa-sinbcosb
49.
cos(a+b)cosacosb=1-tanatanbcos(a+b)cosacosb=1-tanatanb
50.
cos(x+y)cos(x−y)=cos2x−sin2ycos(x+y)cos(x−y)=cos2x−sin2y
51.
cos(x+h)-cosxh=cosxcosh-1h-sinxsinhhcos(x+h)-cosxh=cosxcosh-1h-sinxsinhh
В следующих упражнениях докажите или опровергните утверждения.
52.
tan(u+v)=tanu+tanv1−tanutanvtan(u+v)=tanu+tanv1−tanutanv
53.
tan(u-v)=tanu-tanv1+tanutanvtan(u-v)=tanu-tanv1+tanutanv
54.
tan(x+y)1+tanxtanx=tanx+tany1−tan2xtan2ytan(x+y)1+tanxtanx=tanx+tany1−tan2xtan2y
55.
Если α, β,α, β и γγ являются углами одного и того же треугольника, то докажите или опровергните sin(α+β)=sinγ.sin(α+β)=sinγ.
56.
Если α,β,α,β и γγ являются углами одного и того же треугольника, то докажите или опровергните tanα+tanβ+tanγ=tanαtanβtanγtanα+tanβ+tanγ=tanαtanβtanγ
Тригонометрические тождества суммы и разности (Видео)
Привет, и добро пожаловать в этот обзор тригонометрических тождеств суммы и разности ! В этом видео мы расскажем много полезных формул, так что давайте начнем!
Прежде чем мы углубимся, давайте на минутку рассмотрим единичный круг. Единичный круг дает вам значения синуса и косинуса для некоторых из наиболее распространенных мер угла.
Единичный круг дает вам значения синуса и косинуса для некоторых из наиболее распространенных мер угла.
С помощью этой информации в сочетании с некоторыми формулами, которые мы сегодня рассмотрим, мы можем найти точные тригонометрические значения еще большего количества углов на единичной окружности, и все это без использования калькулятора.
Начнем с суммы тождеств. Первое, что мы будем использовать, — это формула для нахождения синуса суммы двух углов. Давайте посмотрим на формулу:
\(sin(a+\beta)=sin\text{ }\alpha \text{ }cos\text{ }\beta + cos\text{ }\alpha \text{ }sin\text{ }\beta\ )
Итак, если мы хотим найти синус 75 градусов, мы можем сделать это, найдя два угла, сумма которых равна 75, и используя их как \(\alpha\) и \(\beta\). К счастью, это легко найти на нашем единичном круге. Поскольку \(30+45=75\), мы можем использовать 30 как \(\alpha\) и 45 как \(\beta\). Мы также можем использовать 45 как \(\alpha\) и 30 как \(\beta\). На самом деле это не имеет значения.
На самом деле это не имеет значения.
Во-первых, давайте запишем информацию, которая нам нужна для наших двух углов. Мы используем 30 градусов как \(\альфа\), поэтому мы запишем, \(\альфа\)=30°, а затем мы найдем наши значения косинуса и нашего синуса из нашего единичного круга. .
\(\alpha=30°\)
\(cos(30°)=\frac{\sqrt{3}}{2}\)
\(sin(30°)=\frac{1 }{2}\)
Затем мы делаем то же самое для \(\beta\), которое мы установили равным 45 градусам.
\(\бета=45°\)
\(cos(45°)=\frac{\sqrt{2}}{2}\)
\(sin(45°)=\frac{\sqrt{2}}{2}\)
Теперь мы запишем нашу формулу для тождества суммы синусов.
\(sin(\alpha +\beta)=sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)\)
Тогда мы заменим 30 градусов на \(\alpha\), 45 градусов для \(\beta\), а затем подставьте все наши значения синуса и косинуса в правую часть нашей формулы.
\(sin(30°+45°)=sin(30°)cos(45°)+cos(30°)sin(45°)\)
Затем мы подставим значения синуса и косинуса.
\(sin(75°)=(\frac{1}{2})(\frac{\sqrt{2}}{2})+(\frac{\sqrt{3}}{2}) (\frac{\sqrt{2}}{2})\)
Теперь мы собираемся упростить, немного умножив.
\(sin(75°)=\frac{\sqrt{2}}{4}+\frac{\sqrt{6}}{4}\)
Наконец, поскольку оба термина имеют тот же знаменатель, мы можем записать наш ответ в виде одной дроби.
\(sin(75°)=\frac{2+\sqrt{6}}{4}\)
Как видите, для этого важно уметь обращаться с радикалами и дробями. тип работы. Мы можем проверить наш ответ с помощью калькулятора. Если мы добавим \(\sqrt{2}\) к \(\sqrt{6}\) и затем разделим на 4, мы получим примерно 0,966.
\(sin(75°)=\frac{\sqrt{2}+\sqrt{6}}{4}\приблизительно 0,966\)
Если затем использовать калькулятор для нахождения синуса 75°, мы получаем то же самое.
Но возникает вопрос: «Почему бы нам просто не использовать калькулятор, чтобы найти синус, вместо того, чтобы делать всю эту работу?» Ответ заключается в том, что калькулятор дает нам приблизительное значение синуса 75 градусов. Если мы хотим узнать точное значение , нам нужно пройти долгий путь. Если при прохождении стандартизированного теста вы видите слово «точный» в отношении такой проблемы, значит, вы знаете, как выполнить этот процесс.
Что если мы хотим найти точное значение косинуса 75 градусов? У нас есть формула тождества суммы и для этого:
\(cos(\alpha+\beta)=cos(\alpha) cos(\beta)-sin (\alpha) sin (\beta)\)
Это работает аналогичным образом. Мы можем подставить наши значения и довольно быстро найти косинус.
Начнем с записи тождества суммы косинусов. Если вы этого не сделаете, очень легко перепутать значения, так что это всегда хорошая идея.
\(cos(\alpha+\beta)=cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)\)
Затем мы заменим 30 градусов на \(\alpha\), 45 градусов для \(\beta\), а затем подставьте все наши значения синуса и косинуса в правую часть формулы, как мы сделали с последней задачей.
\(cos(30°+45°)=cos(30°)cos(45°)-sin(30°)sin(45°)\)
Затем подставим наш синус и значения косинуса. Итак, сначала мы просто обработаем эту левую сторону.
\(cos(75°)=(\frac{\sqrt{3}}{2})(\frac{\sqrt{2}}{2})-(\frac{1}{2}) (\frac{\sqrt{2}}{2})\)
Еще раз произведем умножение и запишем наш ответ в виде одной дроби.
\(cos(75°)=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2 }}{4}\)
Как и в предыдущей задаче, мы можем проверить нашу работу, оценив это подкоренное выражение на калькуляторе, а затем найдя на калькуляторе приблизительное значение косинуса 75°.
\(\frac{\sqrt{6}-\sqrt{2}}{4}=0,25881
0252\)
\(cos(75°)=0,258810252\)
мы сделали что-то правильно!
Для тангенса также существует тождество суммы:
\(tan(\alpha + \beta)=\frac{tan\text{ }\alpha + tan\text{ }\beta}{1-tan\text{ }\alpha\text{ }tan\text{ }\beta}\)
Давайте воспользуемся этим тождеством, чтобы ответить на вопрос:
Каково точное значение тангенса 75 градусов?
Чтобы это понять, нам нужно найти тангенс 30 градусов и тангенс 45 градусов. Но этой информации нет в нашем единичном круге. К счастью, мы можем найти его достаточно легко, потому что знаем, что:
Но этой информации нет в нашем единичном круге. К счастью, мы можем найти его достаточно легко, потому что знаем, что:
\(tan(\alpha)=\frac{sin\text{ }\alpha}{cos\text{ }\beta}\)
Мы могли бы сделать это дважды для каждого из двух углов, которые нам нужны, а затем подставить его в тождество суммы для тангенса, но поскольку мы только что нашли точное значение для синуса и косинуса 75 градусов, используя тождества суммы для синуса и косинус, мы можем подставить эти ответы непосредственно в это более простое тождество, чтобы найти наш ответ:
\(sin(75°)=\frac{\sqrt{2}+\sqrt{6}}{4}\)
\(cos(75°)=\frac{\sqrt{6}- \sqrt{2}}{4}\)
Теперь мы запишем нашу касательную идентичность.
\(tan(\alpha)=\frac{sin(\alpha)}{cos(\alpha)}\)
Итак, если мы хотим узнать \(tan(75°)\) , мы просто подставляем \(sin(75°)\), а затем делим его на \(cos(75°)\).
\(tan (75°) = \ frac {sin (75°)} {cos (75°)} = \ frac {\ frac {\ sqrt {2} + \ sqrt {6}} {4}} {\ гидроразрыва {\ sqrt {6} — \ sqrt {2}} {4}} \)
Теперь, чтобы упростить это, мы можем переписать это как деление дробей.
\(\frac{\frac{\sqrt{2}+\sqrt{6}}{4}}{\frac{\sqrt{6}-\sqrt{2}}{4}}=\frac {\ sqrt {2} + \ sqrt {6}} {4} \ div \ frac {\ sqrt {6} — \ sqrt {2}} {4} = \ frac {\ sqrt {2} + \ sqrt {6 }}{4} \frac{4}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2 }}\)
Теперь помните, что когда мы делим дроби, мы переворачиваем вторую дробь и умножаем их.
\(\frac{\sqrt{2}+\sqrt{6}}{4}\div \frac{\sqrt{6}-\sqrt{2}}{4}=\frac{\sqrt{ 2}+\sqrt{6}}{4}\cdot \frac{4}{\sqrt{6}-\sqrt{2}}\)
Теперь мы можем перемножить их вместе.
\(\frac{\sqrt{2}+\sqrt{6}}{4} \cdot \frac{4}{\sqrt{6}-\sqrt{2}}=\frac{\sqrt{ 2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}\)
Если бы мы не знали синуса и косинуса 75 градусов, имело бы смысл использовать нашу тождество суммы для касательной. Итак, давайте рассмотрим, как это будет выглядеть.
Итак, давайте рассмотрим, как это будет выглядеть.
Как обычно, мы начинаем с записи всей информации, которая нам понадобится. В этом случае мы должны использовать тот факт, что \(tan=\frac{sin}{cos}\), чтобы найти наши значения для тангенса 30 и 45 градусов.
\(tan(30°)=\frac{sin(30°)}{cos (30°)}=\frac{\frac{1}{2}}{\frac{\sqrt{3}} {2}}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)
Это получается из рационализации знаменателя, которую мы рассмотрим немного больше позже в этом видео.
\(tan (45°) = \ frac {sin (45°)} {cos (45°)} = \ frac {\ frac {\ sqrt {2}} {2}} {\ frac {\ sqrt {2}}{2}}=1\)
Затем мы записываем тождество суммы тангенсов.
\(tan(\alpha+\beta)=\frac{tan(\alpha+\beta)=\frac{tan(tan(\alpha)+tan(\beta)}{1-tan(\alpha)tan(\beta)}\)
Затем мы заменим 30 градусов на \(\alpha\), 45 градусов на \(\beta\), а затем подставим все наши значения тангенса в нашу формулу.
\(tan(30°+45°)=\frac{tan(30°)+tan(45°)}{1-tan(30°)tan(45°)}\)
Теперь давайте подставим значения касательной.
\(тангенс (30+45) = \ frac {\ frac {\ sqrt {3}} {3} +1} {1- (\ frac {\ sqrt {3}} {3}) (1) } = \ frac {\ frac {\ sqrt {3}} {3} + \ frac {3} {3}} {1- \ frac {\ sqrt {3}} {3}} = \ frac {\ frac { \sqrt{3}+3}{3}}{\frac{3-\sqrt{3}}{3}}= \frac{\sqrt{3}+3}{3}\div \frac{3- \sqrt{3}}{3}=\frac{\sqrt{3}+3}{3}\cdot \frac{3}{3-\sqrt{3}}=\frac{\sqrt{3}+ 3}{3-\sqrt{3}}\)
Обратите внимание, что два ответа для наших двух разных методов не кажутся одинаковыми. Но если мы введем их в калькулятор, то получим одно и то же значение:
\(\frac{\sqrt{3}+3}{3-\sqrt{3}}=3,7320508075\)
\(\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}=3,7320508075\)
Это то же значение, которое мы получаем, когда мы спросите калькулятор для загара 75 градусов тоже!
\(tan(75°)=3,7320508075\)
Причина, по которой ответы выглядят по-разному, заключается в том, что они не были полностью упрощены. Если вы заметили, в знаменателе есть радикал. Чтобы исправить оба ответа, нам нужно умножить верхнюю и нижнюю часть наших ответов на сопряженное число знаменателя, которое выглядит так же, как знаменатель, но имеет противоположный знак между двумя членами. Затем мы можем еще больше упростить и посмотреть, сможем ли мы сделать так, чтобы ответы выглядели одинаково.
Если вы заметили, в знаменателе есть радикал. Чтобы исправить оба ответа, нам нужно умножить верхнюю и нижнюю часть наших ответов на сопряженное число знаменателя, которое выглядит так же, как знаменатель, но имеет противоположный знак между двумя членами. Затем мы можем еще больше упростить и посмотреть, сможем ли мы сделать так, чтобы ответы выглядели одинаково.
Начнем с первого. Во-первых, нам нужно сделать сопряженную версию знаменателя и умножить ответ. , сопряженное с , означает, что знак между двумя терминами изменится.
\(\frac{\sqrt{2}+\sqrt{6}}{\sqrt{6}-\sqrt{2}}\cdot \frac{\sqrt{6}+\sqrt{2}} {\sqrt{6}+\sqrt{2}}\)
Эта дробь упрощается до 1, поэтому мы вообще не меняем значение нашей дроби. Теперь мы можем использовать FOIL , чтобы перемножить наши числители и знаменатели вместе.
\(\frac{\sqrt{12}+\sqrt{4}+\sqrt{36}+\sqrt{12}}{\sqrt{36}+\sqrt{12}+(-\sqrt{ 12})+(-\sqrt{4})}\)
Теперь мы немного упростим наши радикалы.
\(\frac{2\sqrt{3}+2+6+2\sqrt{3}}{6+2\sqrt{3}-2\sqrt{3}-2}\)
Теперь мы можем комбинировать одинаковые члены в нашем числителе.
\(\frac{4\sqrt{3}+8}{4}\)
Отсюда мы можем вынести 4 из нашего числителя.
\(\frac{4(\sqrt{3}+2)}4\)
Наши 4 отменят друг друга, и мы останемся с \(\sqrt{3}+2 \).
Хорошо, теперь я сделаю то же самое с другим. Опять же, мы собираемся умножить на дробь, которая имеет сопряженное число как в числителе, так и в знаменателе. Таким образом, сопряжение \(3-\sqrt{3}\) равно \(3+\sqrt{3}\).
\(\frac{\sqrt{3}+3}{3-\sqrt{3}}\cdot \frac{3+\sqrt{3}}{3+\sqrt{3}}\)
Затем мы собираемся ИСПРАВИТЬ наши числители и знаменатели и упростить наши корни.
\(\frac{3\sqrt{3}+\sqrt{9}+9+3\sqrt{3}}{9+3\sqrt{3}+(-3\sqrt{3})+ (-\sqrt{9})}=\frac{3\sqrt{3}+3+9+3\sqrt{3}}{9-3}\)
Теперь мы можем объединить одинаковые члены в нашем числителе и знаменателе, и фактор 6 из числителя для упрощения.
\(\frac{6\sqrt{3}+12}{6}=\frac{6(\sqrt{3}+2)}{6}=2+\sqrt{3}\)
Итак, мы видим, что оба наших значения равны одному и тому же, хотя изначально они выглядели немного по-разному. И это гораздо более приятная цифра. Так что рационализация знаменателя иногда может быть действительно полезной.
У нас также есть тождества для нахождения разности двух углов, а не суммы. Это разностные тождества для синуса, косинуса и тангенса:
\(sin(\alpha-\beta)=sin (\alpha) cos (\beta)-cos (\alpha) sin (\beta)\)
\(cos(\alpha-\beta)=cos (\alpha) cos (\beta)+sin (\alpha) sin (\beta)\)
\(tan(\alpha-\beta)=\ frac{tan (\alpha) – tan (\beta)}{1 + tan (\alpha) tan (\beta)}\)
Мы используем их так же, как мы используем тождества суммы, но они позволяют нам найти несколько меньших углов. Например, мы могли бы использовать тождество разности синусов, чтобы найти синус 15 градусов, используя 45 градусов как \(\альфа\) и 30 градусов как \(\бета\).
Опять же, мы начинаем со сбора необходимой информации и определения наших углов \(\альфа\) и \(\бета\), чтобы все было организовано и сводилось к минимуму риск ошибки. Итак, для этой задачи мы говорим, что \(\alpha=45°\). Поскольку мы ищем меньший угол, наша альфа должна быть больше, чем наша бета. Итак, \(\бета=30°\).
\(\alpha=45°~~~~~~~~\beta=30°\)
\(sin(45°)=\frac{\sqrt{2}}{2}~~~ ~~~~~sin(30°)=\frac{1}{2}\)
\(cos(45°)=\frac{\sqrt{2}}{2}~~~~~~~ ~ cos (30 °) = \ frac {\ sqrt {3}} {2} \)
Теперь мы запишем нашу сумму разности.
\(sin(\alpha-\beta)=sin(\alpha)cos(\beta)-cos(\alpha)sin(\beta)\)
Затем мы просто подставляем все подходящие значения в формулу.
\(sin(45°-30°)=sin(45°)cos(30°)-cos(45°)sin(30°)\)
\(sin(75°)=(\frac {\ sqrt {2}} {2}) (\ frac {\ sqrt {3}} {2}) — (\ frac {\ sqrt {2}} {2}) (\ frac {1} {2}) \)
Теперь мы можем немного умножить и упростить.
\(sin(15°)=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2 }}{4}\)
На этот раз в нашем знаменателе нет радикала, поэтому нам не нужно рационализировать его.
Мы можем проверить это значение на калькуляторе, найдя \(sin(15°)\). Это дает нам приблизительное значение 0,259.
Помните, что наш ответ с радикалами — это точное значение для \(sin(15°)\).
Тождества разностей косинусов и тангенсов работают одинаково. Мы просто подключаем наши ценности и наслаждаемся работой с радикалами, пока не получим ответ.
Я надеюсь, что это видео помогло вам лучше понять сумму и разность триггерных функций. Спасибо за просмотр и удачной учебы!
Как вычитать дроби с разными знаменателями
Вычитание дробей, особенно с разными знаменателями, может показаться сложным на первый взгляд. Однако, как только вы освоите некоторые основные правила, все будет довольно просто.
Во-первых, нам нужно понять состав дроби. Здесь есть две части – числитель и знаменатель, разделенные разделительной чертой.
Здесь есть две части – числитель и знаменатель, разделенные разделительной чертой.
Знаменатель — это нижняя цифра. Это показывает нам, на сколько равных частей было разделено одно целое. Числитель является верхней цифрой и показывает, сколько частей целого присутствует.
Чтобы успешно отделить одну дробь от другой, нужно добиться того, чтобы целое, с которым мы имеем дело, в обоих случаях делилось на одинаковое количество равных частей, т. е. чтобы знаменатели были одинаковыми.
Есть несколько быстрых приемов, которые можно использовать при вычитании дробей с разными знаменателями. Ниже мы объясняем традиционный метод, поскольку именно его вам нужно будет применить, когда вас попросят показать свои работы на любом официальном экзамене.
Одни и те же правила применяются при работе с правильными дробями (где числитель меньше знаменателя) или неправильными дробями (где числитель больше знаменателя).
4 простых шага, как вычитать дроби с разными знаменателями:
Шаг 1.
 Найдите наименьший общий знаменатель
Найдите наименьший общий знаменательНаименьший общий знаменатель (НОД) — это наименьшее общее кратное двух знаменателей, с которыми вы работаете.
Например, если нас попросили вычесть 2/3 из 2/6, мы знаем, что 6 кратно 3, поэтому 6 — это наш LCD.
Шаг 2: Найдите эквивалентную дробь
После того, как вы нашли ЖК-дисплей, вам нужно сохранить значение ваших дробей прежним. Таким образом, при изменении знаменателя вам нужно применить то же изменение к числителю.
Используя приведенный выше пример, чтобы заменить знаменатель на 6, мы умножаем 3 на 2. Чтобы сохранить дробь равного значения, мы также должны умножить 2 (числитель) на 2. Это дает нам эквивалент дроби 4 /6.
Повторите этот процесс и для второй фракции. В нашем примере знаменатель уже равен 6, поэтому никаких изменений не требуется.
Теперь у нас есть пересмотренное уравнение 4/6 — 2/6.
Шаг 3: Вычтите новые числители
Следующий этап прост: просто вычтите числители, которые есть в вашем новом уравнении. В этом случае 4 — 2 = 2.
В этом случае 4 — 2 = 2.
Возьмите полученную цифру и поместите ее над общим знаменателем. Это дает нам 2/6.
Шаг 4: При необходимости упростите ответ
Последний шаг – по возможности упростить дробь. Для этого вам нужно найти наибольший общий множитель, общий для обеих частей дроби, и разделить их на него.
В случае 2/6 наибольший общий делитель равен 2. Поскольку 2 ÷ 2 = 1, а 6 ÷ 2 = 3, наша упрощенная дробь равна 1/3.
2/3 — 2/6 = 1/3
Примеры вопросов
Ниже вы найдете два примера вопросов, в которых вам предлагается вычесть дроби с разными знаменателями. Первое выражается в виде стандартного уравнения, второе — в виде более сложной словесной задачи.
Пример вопроса 1
Сколько будет 5/6 минус 13/25?
Начните с поиска ЖК-дисплея. В этом примере это не так просто, поэтому вам может быть полезно записать кратные наибольшему текущему знаменателю, чтобы помочь вам: 25, 50, 75, 100, 125, 150…
Теперь мы можем видеть, что первое кратное 25 делится на 6 равно 150, так что это наш ЖК-дисплей.
Затем нам нужно найти наши эквивалентные дроби:
6 x 25 = 150, поэтому нам нужно использовать то же значение, чтобы умножить числитель, что даст 5 x 25 = 125. Таким образом, наша первая эквивалентная дробь будет 125/150.
Теперь перейдем ко второй:
25 х 6 = 150 и 13 х 6 = 78. Наша вторая эквивалентная дробь 78/150.
Вычтите числители и поместите результат на ЖК-дисплей: 125/150 — 78/150 = 47/150.
Эта фракция уже имеет простейшую форму.
Ответ: 5/6 минус 13/25 = 47/150
Пример вопроса 2
Эмма готовится к марафону и поставила перед собой цель пробежать к концу недели. В понедельник она пробегает 7/15 дистанции. В среду она пробегает 4/5 дистанции.
Насколько дальше пробежала Эмма в среду по сравнению с понедельником?
Чтобы решить эту задачу, нам нужно вычесть расстояние, которое Эмма пробежала в понедельник, из того, сколько она пробежала в среду, поэтому наше уравнение будет выглядеть так: 4/5 — 7/15.


 Сократите дробь:
Сократите дробь:
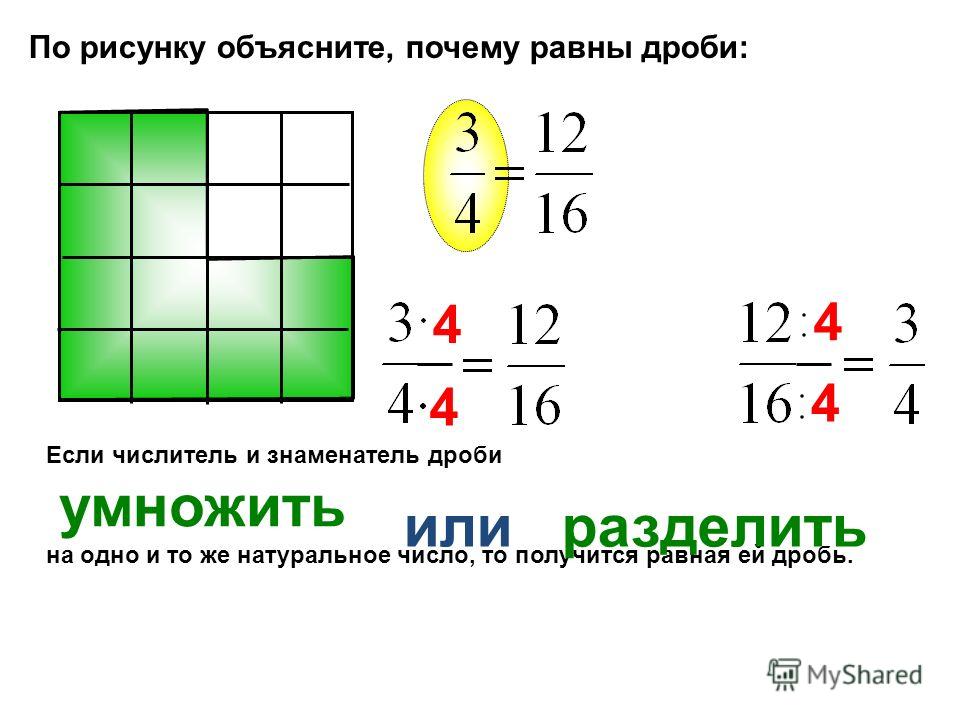
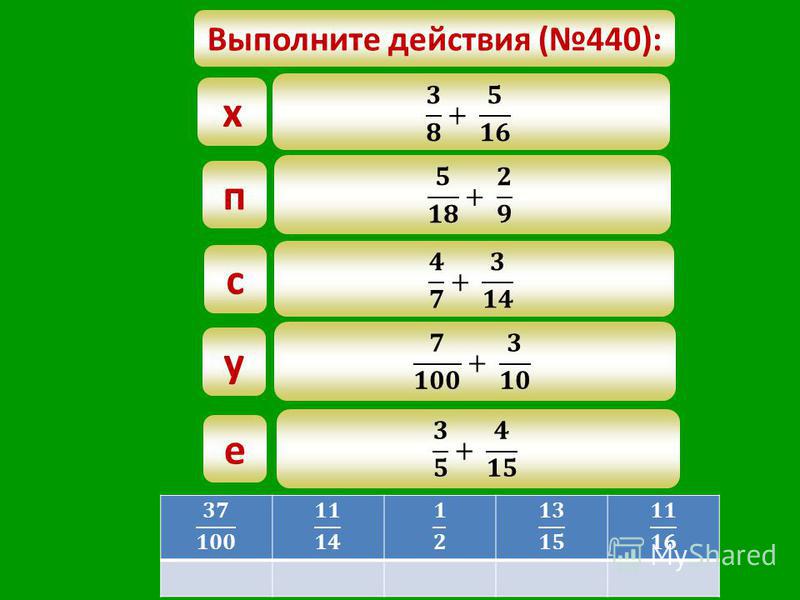 —
— 5
5 




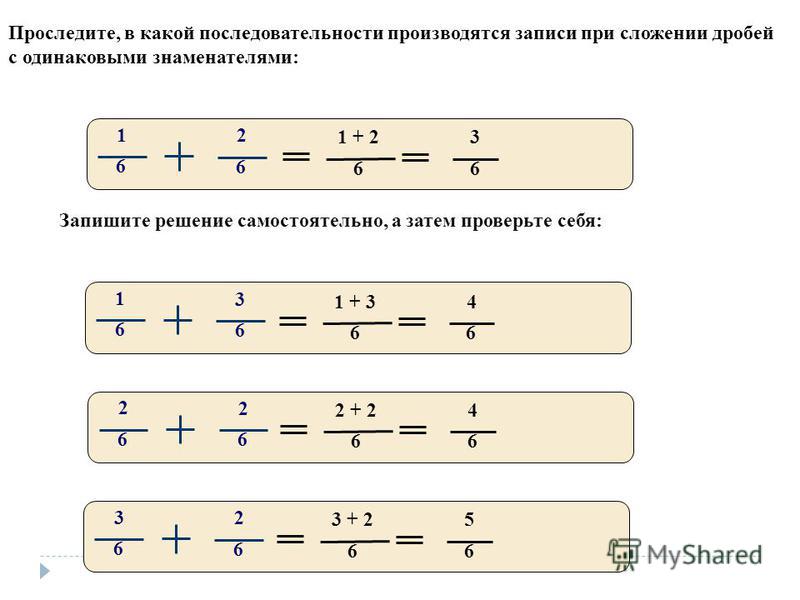


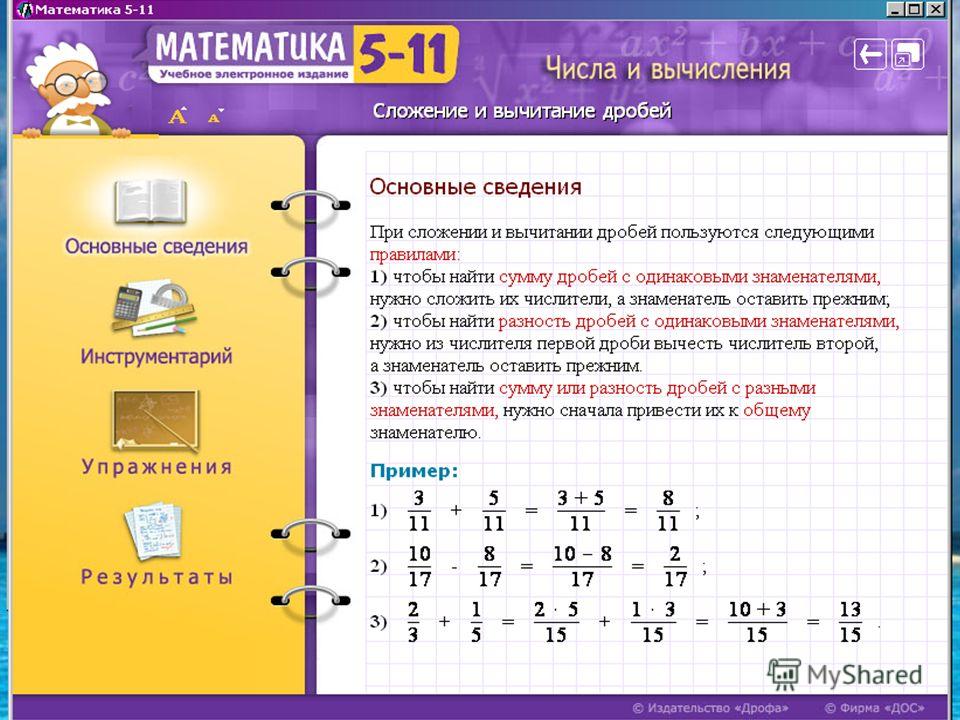 См. рис. 4. Используя теорему Пифагора, мы можем найти длину стороны
См. рис. 4. Используя теорему Пифагора, мы можем найти длину стороны Подставляем значения по формуле.
Подставляем значения по формуле. Перепишите это выражение, пока оно не совпадет с другой стороной знака равенства. Иногда нам, возможно, придется изменить обе стороны, но наиболее эффективно работать только с одной стороной.
Перепишите это выражение, пока оно не совпадет с другой стороной знака равенства. Иногда нам, возможно, придется изменить обе стороны, но наиболее эффективно работать только с одной стороной.