Статистика | Онлайн-тест – «На Урок»
Запитання 1
Статистика как наука изучает:
варіанти відповідей
единичные явления;
массовые явления;
периодические события.
Запитання 2
Термин «статистика» происходит от слова:
варіанти відповідей
статика;
статный;
статус.
Запитання 3
Статистика зародилась и оформилась как самостоятельная учебная дисциплина:
варіанти відповідей
до новой эры, в Китае и Древнем Риме;
в 20 веке, в СССР;
в 17-18 веках, в Европе.
Запитання 4
Статистика изучает явления и процессы посредством изучения:
варіанти відповідей
признаков различных явлений;
определенной информации;
статистических показателей.
Запитання 5
Основными задачами статистики на современном этапе являются:
варіанти відповідей
исследование преобразований экономических и социальных процессов в обществе;
регламентация и планирование хозяйственных процессов;
анализ и прогнозирование тенденций развития экономики;
Запитання 6
Статистический показатель дает оценку свойства изучаемого явления:
варіанти відповідей
количественную;
качественную;
количественную и качественную.
Запитання 7
Основные стадии экономико-статистического исследования включают:
варіанти відповідей
сбор первичных данных,
статистическая сводка и группировка данных,
контроль и управление объектами статистического изучения,
анализ статистических данных.
Запитання 8
Статистическое наблюдение – это:
варіанти відповідей
научная организация регистрации информации;
оценка и регистрация признаков изучаемой совокупности;
работа по сбору массовых первичных данных;
обширная программа статистических исследований.
Запитання 9
Назовите основные организационные формы статистического наблюдения:
варіанти відповідей
перепись и отчетность;
разовое наблюдение;
опрос.
Запитання 10
Является ли статистическим наблюдением наблюдения покупателя за качеством товаров или изменением цен на городских рынках?
варіанти відповідей
Запитання 11
Статистическая сводка — это:
варіанти відповідей
систематизация и подсчет итогов зарегистрированных фактов и данных;
форма представления и развития изучаемых явлений;
анализ и прогноз зарегистрированных данных.
Запитання 12
Статистическая группировка — это:
варіанти відповідей
объединение данных в группы по времени регистрации;
расчленение изучаемой совокупности на группы по существенным признакам;
образование групп зарегистрированной информации по мере ее поступления.
Запитання 13
Статистические группировки могут быть: а) типологическими; б) структурными; в) аналитическими; г) комбинированными
варіанти відповідей
а,б,в,г
Запитання 14
Ряд распределения — это:
варіанти відповідей
упорядоченное расположение единиц изучаемой совокупности по группам;
ряд значений показателя, расположенных по каким-то правилам.
Запитання 15
Статистический показатель — это
варіанти відповідей
размер изучаемого явления в натуральных единицах измерения;
количественная характеристика свойств в единстве с их качественной определенностью;
результат измерения свойств изучаемого объекта.
Запитання 16
В каких единицах выражаются абсолютные статистические показатели?
варіанти відповідей
в коэффициентах;
в натуральных;
в трудовых.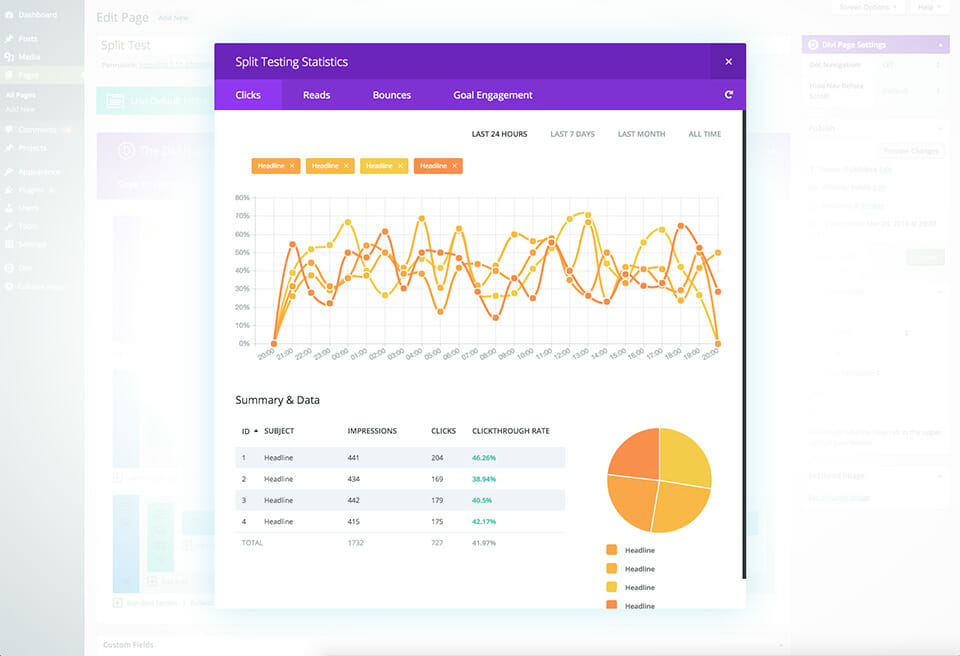
Запитання 17
В каких единицах будет выражаться относительный показатель, если база сравнения принимается за единицу?
варіанти відповідей
в натуральных;
в процентах;
в коэффициентах.
Запитання 18
Относительные показатели по своему познавательному значению подразделяются на показатели: а) выполнения и сравнения, б) структуры и динамики, в) интенсивности и координации, г) прогнозирования и экстраполяции
варіанти відповідей
а, б, г
б, в, г
а, б, в
Запитання 19
Статистические показатели по сущности изучаемых явлений могут быть: а) качественными б) объёмными
варіанти відповідей
Запитання 20
Статистические показатели в зависимости от характера изучаемых явлений могут быть: а) интервальными б) моментными
варіанти відповідей
Запитання 21
Требуется вычислить средний стаж деятельности работников фирмы: 6,5,4,6,3,1,4,5,4,5. Какую формулу Вы примените?
варіанти відповідей
средняя арифметическая;
средняя арифметическая взвешенная
средняя гармоническая.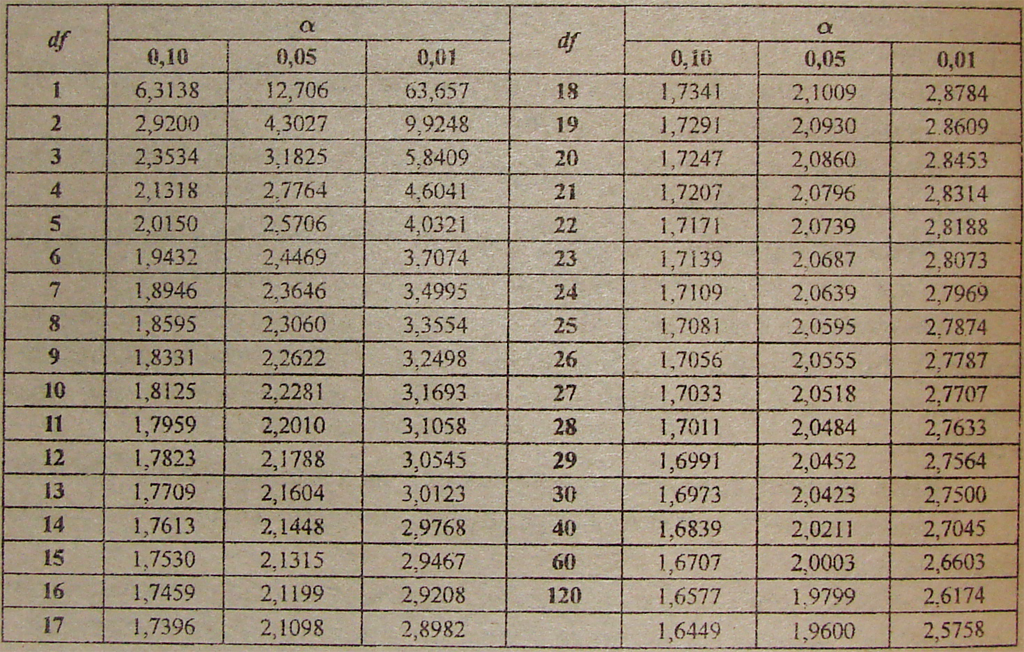
Запитання 22
По какой формуле производится вычисление средней величины в интервальном ряду?
варіанти відповідей
средняя гармоническая взвешенная
средняя арифметическая взвешенная
Запитання 23
Средняя геометрическая — это:
варіанти відповідей
корень из произведения индивидуальных показателей;
произведение корней из индивидуальных показателей.
Запитання 24
Значения признака, повторяющиеся с наибольшей частотой, называется
варіанти відповідей
модой;
медианой.
Запитання 25
Средняя хронологическая исчисляется
варіанти відповідей
в моментных рядах динамики с равными интервалами;
в интервальных рядах динамики с равными интервалами;
в интервальных рядах динамики с неравными интервалами.
Запитання 26
Медиана в ряду распределения с четным числом членов ряда равна
варіанти відповідей
полусумме двух срединных членов.
полусумме двух крайних членов
Запитання 27
Что понимается в статистике под термином «вариация показателя»?
варіанти відповідей
изменение размерности показателя
изменение величины показателя
изменение названия показателя
Запитання 28
Размах вариации исчисляется как
варіанти відповідей
разность между первым и последним членом ряда распределения
разность между максимальным и минимальным значением показателя;
Запитання 29
Выборочный метод в статистических исследованиях используется для:
варіанти відповідей
повышения точности прогноза
анализа факторов взаимосвязи
экономии времени и снижения затрат на проведение статистического исследования
Запитання 30
Ряд динамики характеризует: а) структуру совокупности по какому-то признаку; б) изменение характеристик совокупности во времени; в) определенное значение признака в совокупности; г) величину показателя на определенную дату или за определенный период
варіанти відповідей
Запитання 31
Прогнозирование в статистике ‑ это:
варіанти відповідей
предсказание предполагаемого события в будущем;
оценка возможной меры изучаемого явления в будущем.
Запитання 32
Статистический индекс — это:
варіанти відповідей
критерий сравнения относительных величин
сравнительная характеристика двух абсолютных величин
относительная величина сравнения двух показателей.
Запитання 33
Индексы позволяют соизмерить социально-экономические явления:
варіанти відповідей
во времени
в пространстве и во времени
в пространстве
Запитання 34
Можно ли утверждать, что индивидуальные индексы по методологии исчисления адекватны темпам роста:
варіанти відповідей
можно;
нельзя.
Запитання 35
Сводные индексы позволяют получить обобщающую оценку изменения:
варіанти відповідей
по товарной группе;
одного товара за несколько периодов.
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
Створити тест
Натисніть «Подобається», щоб слідкувати за оновленнями на Facebook
Результаты тестов и опросов
Вы можете просматривать статистические сводки о своих тестах и опросах.
Статистические данные помогают оценивать эффективность тестов и опросов. Например, можно узнать, сколько учащихся (в процентах) выбрали определенный ответ на вопрос с множественным выбором в одном из ваших тестов.
В этой таблице приведены сведения о доступных отчетах и их использовании.
| Статистический отчет | Предоставленная информация | Функция |
|---|---|---|
| Статистика столбца | Отражает общую успеваемость в классе в соответствии с элементом Центра оценок, который включает среднюю оценку и среднеквадратическое отклонение. Перечисляет количество отправленных материалов для элемента, который находится в обработке и требует оценки. | Тесты Опросы Задания Оцененные обсуждения, вики-страницы, блоги, журналы |
| Статистики попыток | Отображает среднюю оценку и распределение ответов учащихся для каждого вопроса. | Тесты Опросы |
| Анализ элементов | Формируется статистика общей успеваемости по тесту и отдельным вопросам. Эти данные помогают выявить вопросы, которые плохо отражают успеваемость учащихся. Можно использовать эту информацию для совершенствования вопросов будущих тестов или для корректировки дополнительных баллов в текущих попытках. Это средство содержит часть той же информации, что и статистические данные столбца и попыток, но представленной иным образом. Дополнительная информация об анализе элементов | Тесты |
Просмотр статистики столбцов
Для каждого теста и опроса в Центре оценок можно просмотреть статистику столбцов касательно общей успеваемости в классе.
- Статистика, например среднеквадратическое отклонение и средняя оценка.
- Количество попыток, которые сейчас выполняются, требуют оценки или освобождены.
- Распределение оценки
Эта информация поможет вам быстро проанализировать, насколько хорошо учащиеся усвоили материал.
Вы можете также сравнить успеваемость текущего класса с результатами по другим разделам или предыдущим периодам.
Выберите в Центре оценок пункт Статистика столбца из меню столбца теста или опроса. Появится страница Статистика столбца, и можно будет ознакомиться со статистикой по следующим пунктам.
Подсчет. Количество оцененных тестов или пройденных опросов.
Минимальное значение. Самая низкая оценка за тест.
Максимальное значение. Самая высокая оценка за тест.
Период. Этот диапазон оценок служит основным показателем вариабельности оценок за тест.
Среднее. Сумма всех баллов, разделенная на количество оценок.
Медиана. Оценка в средней точке распределения баллов. Выше и ниже этой оценки находится одинаковое количество оценок.
Стандартное отклонение. Показатель степени отклонения оценки от среднего балла.
Дисперсия. Показатель дисперсии оценок — среднеквадратическое от дисперсии является среднеквадратическим отклонением.
Поскольку у опросов нет значения, для некоторых статистических данных опросов отображается ноль.
Просмотр статистики попыток
Статистика попыток показывает успехи учащихся по каждому вопросу. Общее качество теста зависит от качества отдельных вопросов. Используйте статистические данные, чтобы определить, было ли содержимое неясным и были ли вопросы неправильно истолкованы.
Вы можете также использовать статистику попыток для просмотра результатов опросов.
- В Центре оценок перейдите к столбцу теста или опроса.
- Откройте меню столбца и выберите Статистики попыток. Результаты отобразятся на странице Статистика.
Предоставляется следующая информация.
- Среднюю оценку за каждый вопрос.
- Количество оцененных попыток учащегося.
- Количество вопросов без ответов.
- Распределение ответов учащихся по каждому вопросу
Каждый возможный ответ показан в виде процента или процента ответивших. Для вопроса с вариантами ответа высокий процент ответивших неправильно на определенный вопрос может указывать на общее неправильное понимание среди учащихся.
Вы могли также выбрать ответ incorrect при создании вопроса. Высокий процент ответов incorrect может свидетельствовать также о плохой формулировке вопроса.
Поскольку опросы анонимны, вы не можете просмотреть ответы отдельных учащихся. Если вы включили в опрос открытый вопрос, отобразится список всех ответов.
Загрузка результатов
В Центре оценок в меню каждого теста или опроса также отображается параметр Загрузить результаты. Вы можете объединить вопросы и ответы в одну электронную таблицу для просмотра в автономном режиме.
Загружаемые результаты теста в виде электронной таблицы содержат имена учащихся и их имена пользователей. В отличие от тестов опросы предназначены для сбора мнений учащихся. Поскольку анонимность обеспечена, учащиеся могут отвечать честно. При этом загружаемые результаты не содержат сведений, позволяющих установить личности каждого учащегося.
Загружаемые результаты тестов и опросов не содержат статистических сведений.
Параметры форматирования
Вы можете выбрать тип разделителя для загружаемых результатов теста или опроса.
Файлы с разделителями-запятыми (CSV) содержат элементы данных, разделенные запятыми. Файлы с разделителями табуляцией (TXT) содержат элементы данных, разделенные табуляцией.
Можно добавить .txt к имени загруженного файла, а затем импортировать его в приложение для просмотра электронных таблиц.
Если в процессе создания вопросов и ответов были вставлены сведения о тесте или опросе из документа HTML или Word, в таблице может отобразиться код HTML.
7.1.3. Что такое статистические тесты?
7.1.3. Что такое статистические тесты?| 7.
Сравнение продуктов и процессов 7.1. Вступление
| |||
| Что подразумевается под статистическим тестом? | Статистический тест обеспечивает механизм для проведения количественных
решения о процессе или процессах.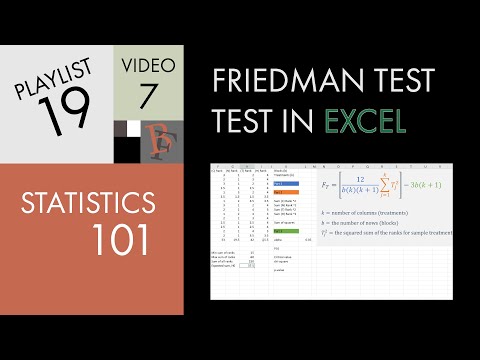 Цель состоит в том, чтобы определить
достаточно ли доказательств, чтобы «отклонить»
предположение или гипотеза о процессе. Гипотеза
называется нулевой гипотезой. Не отвергать может быть хорошим результатом
если мы хотим продолжать действовать так, как будто мы «верим» в нуль
гипотеза верна. Или это может быть неутешительный результат, возможно,
указывает на то, что у нас может быть недостаточно данных, чтобы «доказать» что-то путем
отвергая нулевую гипотезу. Подробнее о значении статистической гипотезы см.
тест, см. главу 1. | ||
| Концепция нулевой гипотезы | Классическое использование статистического теста происходит в управлении технологическим процессом.
исследования. Например, предположим, что мы заинтересованы в обеспечении
что фотомаски в производственном процессе имеют среднюю ширину линии
500 микрометров. Нулевая гипотеза в данном случае состоит в том, что
средняя ширина линии составляет 500 мкм. Неявно в этом утверждении
необходимость помечать фотомаски со средней шириной линии,
либо намного больше, либо намного меньше 500 мкм. Этот
переводится в альтернативную гипотезу о том, что средние ширины линий
не равны 500 мкм. Это двусторонний вариант
потому что он защищает от альтернатив в противоположных направлениях;
а именно, что ширина линий слишком мала или слишком велика. | ||
| Односторонние проверки гипотезы | Нулевая и альтернативная гипотезы также могут быть односторонними. Например,
чтобы убедиться, что у многих лампочек средний срок службы
не менее 500 часов, реализуется программа испытаний. Нуль
Гипотеза в данном случае состоит в том, что среднее время жизни больше, чем
или равно 500 часам. Дополнительная или альтернативная гипотеза
от чего следует защищаться, так это того, что средний срок службы меньше
чем 500 часов. Тестовая статистика сравнивается с более низким
критическое значение, а если оно меньше этого предела, нуль
гипотеза отвергается.Таким образом, для статистической проверки требуется пара гипотез; а именно,
| ||
| Уровни значимости | Нулевая гипотеза — это утверждение об убеждении. Мы можем сомневаться, что
нулевая гипотеза верна, возможно, поэтому мы ее «проверяем».
Альтернативная гипотеза могла бы, на самом деле, быть тем, во что мы верим.
истинный. Процедура испытаний построена таким образом, что риск отказа
нулевая гипотеза, когда она действительно верна, мала. | ||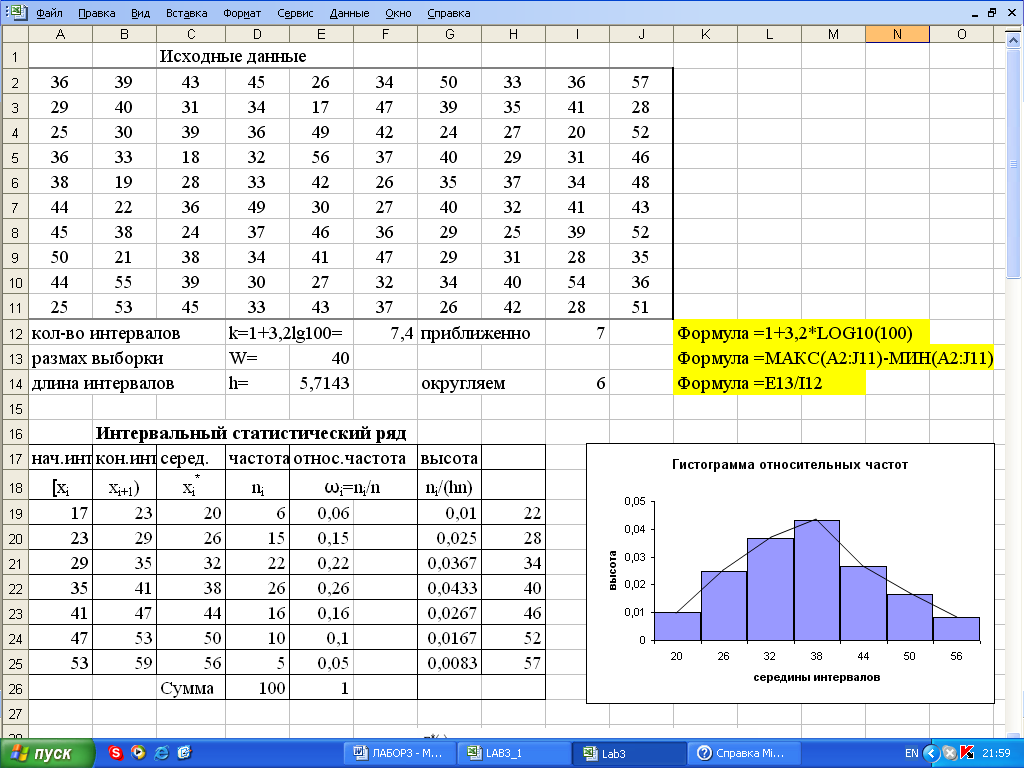
| Ошибки второго рода | Риск не отклонить нулевую гипотезу, когда она находится в
fact false не выбирается пользователем, а определяется как один
можно было бы ожидать, по величине реального несоответствия. Этот риск,
\(\бета\), обычно называют ошибка второго рода . Большой
расхождения между реальностью и нулевой гипотезой легче
обнаруживать и приводить к малым ошибкам второго рода; пока маленький
несоответствия труднее обнаружить и приводят к большим ошибкам
второго рода. Также риск \(\beta\) возрастает по мере того, как риск \(\alpha\) уменьшается. Риски ошибок второго рода обычно
резюмируется кривой рабочей характеристики (OC) для
тест. Кривые ОС для нескольких типов тестов показаны на рис. (Натрелла, 19 лет62). | ||
| Указания в этой главе | В этой главе представлены методы построения тестовой статистики и
соответствующие им критические значения как для одностороннего, так и для
двусторонние тесты для конкретных ситуаций, изложенных в
объем. Он также содержит рекомендации по
размеры выборки, необходимые для этих испытаний. Дополнительные рекомендации по проверке статистических гипотез, значимость уровней и критических областей, приведен в Глава 1. | ||
7. Критерии Стьюдента
Ранее мы рассмотрели, как проверить нулевую гипотезу об отсутствии разницы между средним значением выборки и средним значением генеральной совокупности, а также между средними значениями двух выборок. Мы получили разницу между средними путем вычитания, а затем разделили эту разницу на стандартную ошибку разницы. Если разница в 196 раз превышает стандартную ошибку, она, вероятно, возникает случайно с частотой всего 1 к 20 или меньше.
Для небольших выборок, где необходимо учитывать больше случайных вариаций, эти отношения не совсем точны, поскольку неопределенностью в оценке стандартной ошибки не учитывалась. Необходима некоторая модификация процедуры деления разности на ее стандартную ошибку, и в качестве метода следует использовать критерий t . Его основы были заложены В. С. Госсетом, писавшим под псевдонимом «Студент», поэтому его иногда называют тестом Стьюдента t . Процедура не сильно отличается от той, что используется для больших выборок, но предпочтительнее при числе наблюдений менее 60 и уж точно при их количестве 30 и менее.
Теперь будет рассмотрено применение распределения t к следующим четырем типам задач.
- Расчет доверительного интервала для выборочного среднего.
- Рассчитываются среднее значение и стандартное отклонение выборки, и постулируется значение среднего значения генеральной совокупности. Насколько значительно выборочное среднее отличается от постулируемого среднего значения генеральной совокупности?
- Рассчитываются средние значения и стандартные отклонения двух образцов.
Могли ли обе выборки быть взяты из одной и той же популяции? - Парные наблюдения проводятся на двух образцах (или последовательно на одном образце). Каково значение разницы между средними значениями двух наборов наблюдений?
Могли ли обе выборки быть взяты из одной и той же популяции?В каждом случае задача, по существу, одна и та же, а именно: установить кратные стандартные ошибки, к которым можно привязать вероятности. Эти кратные представляют собой количество раз, которое разность может быть разделена на ее стандартную ошибку. Мы видели, что при больших выборках 1,96-кратная стандартная ошибка имеет вероятность 5 % или менее, а 2,576-кратная стандартная ошибка имеет вероятность 1 % или менее (таблица А в Приложении). При малых выборках эти множители больше, и чем меньше выборка, тем больше они становятся.
Доверительный интервал для среднего из небольшой выборки
Редкое врожденное заболевание, синдром Эверли, обычно вызывает снижение концентрации натрия в крови. Считается, что это является полезным диагностическим признаком, а также ключом к пониманию эффективности лечения.
Мало что известно об этом предмете, но известно, что директор дерматологического отделения в лондонской клинической больнице интересуется этой болезнью и видел больше случаев, чем кто-либо другой. Несмотря на это, он видел только 18 пациентов. Все пациенты были в возрасте от 20 до 44 лет.0030
Средняя концентрация натрия в крови в этих 18 случаях составила 115 ммоль/л со стандартным отклонением 12 ммоль/л. Предполагая, что концентрация натрия в крови имеет нормальное распределение, каков 95% доверительный интервал, в пределах которого можно ожидать, что находится среднее значение общей совокупности таких случаев?
Данные представлены следующим образом:
Чтобы найти 95% доверительный интервал выше и ниже среднего, нам нужно найти множитель стандартной ошибки. В больших выборках мы видели, что кратность равна 1,9.6 (глава 4). Для небольших образцов мы используем таблицу t , приведенную в Приложении Таблица B.pdf. По мере того, как выборка становится меньше, t становится больше для любого конкретного уровня вероятности.
Наоборот, по мере увеличения выборки t становится меньше и приближается к значениям, приведенным в таблице А, достигая их для бесконечно больших выборок.
Поскольку размер выборки влияет на значение t, размер выборки учитывается при соотнесении значения t с вероятностями в таблице. Некоторые полезные части полной таблицы t приведены в . Левая колонка озаглавлена d.f. для «степеней свободы». Их использование было отмечено при расчете стандартного отклонения (глава 2). На практике количество степеней свободы в этих обстоятельствах на одну меньше числа наблюдений в выборке. С этими данными имеем 18 – 1 = 17 ф.р. Это связано с тем, что для определения выборки необходимо только 17 наблюдений плюс общее количество наблюдений, а 18-е определяется вычитанием.
Чтобы найти число, на которое мы должны умножить стандартную ошибку, чтобы получить 95-процентный доверительный интервал, мы входим в таблицу B под номером 17 в левой колонке и читаем в столбце с заголовком 0,05, чтобы найти число 2,110.
95% доверительные интервалы среднего значения теперь установлены следующим образом:
Среднее + 2,110 SE к среднему – 2,110 SE
, что дает нам: ммоль/л.
Тогда мы можем сказать с вероятностью 95 %, что диапазон 109От 0,03 до 120,97 ммоль/л включает среднее значение по популяции.
Аналогично таблице B.pdf 99% доверительный интервал среднего выглядит следующим образом:
Среднее + 2,898 SE к среднему – 2,898 SE
что дает:
115 – (2,898 x 2,83) до 115 + ( 2,898 х 2,83) или от 106,80 до 123,20 ммоль/л.
Отличие среднего значения выборки от среднего значения популяции (один образец t тест)
Оценки концентрации кальция в плазме у 18 пациентов с синдромом Эверли дали среднее значение 3,2 ммоль/л со стандартным отклонением 1,1. Предыдущий опыт ряда исследований и опубликованных отчетов показал, что среднее значение обычно близко к 2,5 ммоль/л у здоровых людей в возрасте 20-44 лет, возрастной диапазон пациентов. Является ли среднее значение у этих пациентов аномально высоким?
Мы устанавливаем цифры следующим образом:
t разница между средними, деленная на стандартную ошибку выборочного среднего./MIR/7/2.jpg)
Игнорируя знак значения t и входя в таблицу B с 17 степенями свободы, мы находим, что 2,69 находится между значениями вероятности 0,02 и 0,01, другими словами, между 2% и 1% и т. д. Таким образом, маловероятно, что выборка со средним значением 3,2 была получена из совокупности со средним значением 2,5, и мы можем заключить, что среднее значение выборки, по крайней мере, статистически, необычно велико. Вопрос о том, следует ли считать его клинически аномально высоким, должен рассматриваться отдельно лечащим врачом.
Разница между средними двумя выборками
Здесь мы применяем модифицированную процедуру для нахождения стандартной ошибки разницы между двумя средними и проверки размера разницы по этой стандартной ошибке (см. главу 5 для больших выборок). Для больших выборок мы использовали стандартное отклонение каждой выборки, рассчитанное отдельно, для расчета стандартной ошибки разницы между средними значениями. Для небольших выборок мы рассчитываем комбинированное стандартное отклонение для двух выборок.
Предположения:
- что данные количественные и правдоподобно Нормальные
- что две выборки взяты из распределений, которые могут отличаться по своему среднему значению, но не по стандартному отклонению
- что наблюдения независимы друг от друга .
- Третье предположение является наиболее важным. Как правило, повторные измерения одного и того же человека не являются независимыми. Если у нас было 20 язв голени на 15 пациентов, то мы имеем только 15 независимых наблюдений.
Следующий пример иллюстрирует процедуру.
Добавление отрубей в рацион приносит пользу пациентам с дивертикулезом. Доступно несколько различных препаратов отрубей, и клиницист хочет проверить эффективность двух из них на пациентах, поскольку для каждого были сделаны положительные заявления. Одним из последствий введения отрубей, требующих тестирования, является время прохождения через пищеварительный тракт. Различается ли он в двух группах пациентов, принимающих эти два препарата?
Нулевая гипотеза состоит в том, что две группы происходят из одной и той же популяции.
Методом случайного распределения клиницист выбирает две группы больных в возрасте 40-64 лет с дивертикулезом сопоставимой степени тяжести. Образец 1 содержит 15 пациентов, получающих лечение А, а образец 2 содержит 12 пациентов, получающих лечение В. Время прохождения пищи через кишечник измеряют стандартным методом с отмеченными гранулами, и результаты записывают в порядке возрастания. время в таблице 7.1.
Таблица 7.1
Эти данные показаны на рис. 7.1. Предположение о приблизительной нормальности и равенстве дисперсии выполнено. Дизайн предполагает, что наблюдения действительно независимы. Поскольку разница в среднем времени прохождения для AB может быть положительной или отрицательной, мы будем использовать двусторонний тест.
Рисунок 7.1
При лечении А среднее время прохождения составило 68,40 ч, а при лечении В — 83,42 ч. В чем смысл разницы, 15.02h?
Процедура следующая:
Получите стандартное отклонение для образца 1:
Получите стандартное отклонение для образца 2:
Умножьте квадрат стандартного отклонения для образца 1 на количество степеней свободы, т.
е. субъектов минус один:
Повторите для образца 2
Сложите два вместе и разделите на общее количество степеней свободы
Стандартная ошибка разницы между средними значениями равна
, что может быть записано как
Когда разница между средними делится на эту стандартную ошибку, результат равен t . Таким образом,
Таблица распределения t Таблица B (приложение), которая дает двусторонние значения P, вводится по степеням свободы.
Для времени прохождения из таблицы 7.1,
показывает, что при 25 степенях свободы (то есть (15 – 1) + (12 – 1)), t = 2,282 лежит между 2,060 и 2,485. Следовательно, эта степень вероятности меньше условного уровня в 5%. Таким образом, нулевая гипотеза об отсутствии различий между средними значениями несколько маловероятна.
95% доверительный интервал определяется следующим образом:
83,42 – 68,40 2,06 x 6,582
15,02 – 13,56 до 15,02 + 13,56 или 1,46 до 18,58 ч.
Неравные стандартные отклонения
Если стандартные отклонения в двух группах заметно различаются, например, если отношение большего к меньшему больше двух, то одно из допущений t-теста (что две выборки взяты из популяции с одинаковым стандартным отклонением) вряд ли будет выполняться. Приблизительный тест, предложенный Саттервейтом и описанный Армитажем и Берри, (1) допускающий неравные стандартные отклонения, выглядит следующим образом.
Вместо того, чтобы использовать объединенную оценку дисперсии, вычислите
Это аналогично вычислению стандартной ошибки разности двух пропорций при альтернативной гипотезе, как описано в главе 6. статистика, в которой степени свободы:
Хотя это может показаться очень сложным, его можно очень легко вычислить на калькуляторе, не записывая промежуточные шаги (см. ниже). Он может дать степень свободы, которая не является целым числом и поэтому недоступна в таблицах. В этом случае следует округлить до ближайшего целого числа.
Многие статистические пакеты теперь выполняют этот тест по умолчанию, и чтобы получить статистику с равными отклонениями, нужно специально запрашивать его. Неравная дисперсия 9Тест 0097 t имеет тенденцию быть менее мощным, чем обычный тест t , если дисперсии фактически одинаковы, поскольку он использует меньше предположений. Однако его не следует использовать без разбора, потому что, если стандартные отклонения различны, как мы можем интерпретировать, например, незначительную разницу в средних значениях? Часто лучшей стратегией является попытка преобразования данных, например логарифмирования, как описано в главе 2. Преобразования, приближающие распределения к нормальности, часто также делают аналогичными стандартные отклонения. Если преобразование журнала прошло успешно, используйте обычные t проверка зарегистрированных данных. Применив этот метод к данным таблицы 7.1, метод калькулятора (с использованием Casio fx-350) для расчета стандартной ошибки будет следующим:
Разность между средними значениями парных выборок (парные
t тесты).
Когда сравниваются эффекты двух альтернативных методов лечения или экспериментов, например, в перекрестных исследованиях, рандомизированных исследованиях, в которых рандомизация проводится между подобранными парами, или в исследованиях с сопоставлением случай-контроль (см. Главу 13), иногда можно провести сравнения в пары. Сопоставление элементов управления для сопоставленных переменных, что может привести к более эффективному исследованию.
Тест основан на тесте одиночного образца t с использованием следующих предположений.
- Данные количественные
- Распределение различий (не исходных данных), вероятно, нормальное.
- Различия не зависят друг от друга.
Первый случай, который следует рассмотреть, — это когда каждый член выборки действует как собственный контроль. Применяется ли лечение А или лечение В первым или вторым для каждого члена выборки, должно быть определено с использованием таблицы случайных чисел Таблица F (Приложение).
Таким образом можно свести к минимуму любое влияние одного лечения на другое, даже косвенно, например, через отношение пациента к лечению. Иногда можно проводить оба вида лечения одновременно, например, при лечении кожных заболеваний путем нанесения лекарства на кожу на противоположных сторонах тела.
Возьмем в качестве примера исследования отрубей при лечении дивертикулеза, которые обсуждались ранее. Клиницист задается вопросом, будет ли время транзита короче, если отруби давать в той же дозировке три раза в день (лечение А) или в один прием пищи (лечение Б). Выбирается случайная выборка пациентов в возрасте от 20 до 44 лет с сопоставимой тяжестью заболевания, и два вида лечения назначаются два раза подряд, причем порядок лечения также определяется по таблице случайных чисел. Время пищевого транзита и различия для каждой пары обработок указаны в Таблице 7.2.
Таблица 7.2
При вычислении t по парным наблюдениям мы работаем с разностью d между членами каждой пары.
Наша первая задача состоит в том, чтобы найти среднее значение различий между наблюдениями, а затем стандартную ошибку среднего значения, действуя следующим образом: , мы находим, что это значение находится между 0,697 и 1,796. Отсчитывая значение вероятности, мы видим, что 0,1
95%-й доверительный интервал для средней разности определяется как
В этом случае t 11 при P = 0,05 равен 2,201 (таблица B), поэтому 95%-й доверительный интервал равен:
-6,5 – 2,201 x 4,37 до -6,5 + 2,201 х 4,37 ч. или от -16,1 до 3,1 ч.
Это довольно широко, поэтому мы не можем сделать вывод, что эти два препарата эквивалентны, и должны обратиться к более крупному исследованию.
Второй случай парного сравнения, который следует рассмотреть, — это когда выбираются две выборки, и каждый член выборки 1 объединяется в пару с одним членом выборки 2, как в сопоставленном исследовании случай-контроль. Поскольку цель состоит в том, чтобы проверить разницу, если таковая имеется, между двумя типами лечения, выбор членов для каждой пары разработан таким образом, чтобы сделать их как можно более похожими.
Чем более они похожи, тем более очевидными будут любые различия, вызванные лечением, потому что их нельзя будет спутать с различиями в результатах, вызванными различиями между членами пары. Сходство внутри пар относится к атрибутам, относящимся к рассматриваемому исследованию. Например, в тесте на лекарство, снижающее артериальное давление, цвет глаз пациентов, вероятно, не будет иметь значения, но их диастолическое артериальное давление в покое вполне может послужить основой для выбора пар. Другим (возможно, родственным) основанием является прогноз заболевания у пациентов: в целом больных со схожим прогнозом лучше всего объединять в пары. Какие бы критерии ни были выбраны, важно, чтобы пары были составлены до того, как будет назначено лечение, поскольку на составление пар не должно влиять знание эффектов лечения.
Дополнительные методы
Предположим, у нас было клиническое испытание с более чем двумя видами лечения. Недопустимо сравнивать каждую обработку с другой обработкой с использованием t тестов, потому что общая частота ошибок типа I будет больше, чем обычный уровень, установленный для каждого отдельного теста.
Метод контроля для этого с использованием одностороннего дисперсионного анализа. (2)
Общие вопросы
Должен ли я проверить свои данные на нормальность перед использованием теста t ?
Казалось бы логичным, что, поскольку тест t предполагает Нормальность, сначала нужно проверить Нормальность. Проблема в том, что тест на нормальность зависит от размера выборки. При небольшой выборке незначительный результат не означает, что данные получены из нормального распределения. С другой стороны, при большой выборке значимый результат не означает, что мы не можем использовать тест t , поскольку тест t устойчив к умеренным отклонениям от нормальности, то есть полученное значение P может быть правильно истолковано. Есть что-то нелогичное в использовании одного теста значимости в зависимости от результатов другого теста значимости. В общем, это вопрос знания и просмотра данных. Данные можно «на глазок» посмотреть, и если распределения не очень асимметричны, и особенно если (для двух выборок t тест) количество наблюдений одинаково в двух группах, то тест t будет верным.
Основная проблема часто заключается в том, что выбросы увеличивают стандартные отклонения и делают тест менее чувствительным. Кроме того, обычно не принимается во внимание тот факт, что если данные получены из рандомизированного контролируемого исследования, то процесс рандомизации обеспечит достоверность I-теста независимо от исходного распределения данных.
Должен ли я проверить равенство стандартных отклонений перед использованием обычного т тест?
Здесь преобладает тот же аргумент, что и в предыдущем вопросе о Нормальности. Тест на равенство дисперсий зависит от размера выборки. Эмпирическое правило заключается в том, что если отношение большего стандартного отклонения к меньшему больше двух, то следует использовать тест неравной дисперсии. С помощью компьютера можно легко выполнить тест равной и неравной дисперсии t и посмотреть, различаются ли ответы.
Зачем мне использовать парный тест, если мои данные парные? Что произойдет, если я этого не сделаю?
Спаривание предоставляет информацию об эксперименте, и чем больше информации может быть предоставлено в анализе, тем более чувствительным является тест.
Одним из основных источников изменчивости является изменчивость между субъектами. Повторяя измерения внутри субъектов, каждый субъект действует как собственный контроль, и изменчивость между субъектами устраняется. В целом это означает, что если между парами есть истинное различие, парный тест с большей вероятностью его выявит: он более мощный. Когда пары генерируются путем сопоставления, критерии сопоставления могут не иметь значения. При этом парные и непарные тесты должны давать одинаковые результаты.
Ссылки
- Армитаж П., Берри Г. Статистические методы в медицинских исследованиях. 3-е изд. Оксфорд: Научные публикации Блэквелла, 1994: 112–13.
- Армитаж П., Берри Г. Статистические методы в медицинских исследованиях. 3-е изд. Оксфорд: Научные публикации Блэквелла, 1994: 207-14.
Упражнения
7.1 У 22 пациентов с необычным заболеванием печени определенная лаборатория показала, что щелочная фосфатаза плазмы имеет среднее значение 39 единиц Кинга-Армстронга, стандартное отклонение 3,4 единицы.
Ответ
7.2 У 18 пациентов с синдромом Эверли средний уровень фосфатов плазмы составил 1,7 ммоль/л, стандартное отклонение 0,8. Если принять средний уровень в общей популяции за 1,2 ммоль/л, какова значимость разницы между этим средним значением и средним значением этих 18 пациентов?
Ответы Глава 7.pdfОтвет
7.3 В двух палатах для пожилых женщин гериатрической больницы обнаружены следующие уровни гемоглобина:
Палата А: 12.2, 11.1, 14.0, 11.3, 10.8, 12.5, 12.2, 11.9, 13.6, 12.7, 13.4, 13.7 г /дл;
Отделение B: 11,9, 10,7, 12,3, 13,9, 11,1, 11,2, 13,3, 11,4, 12,0, 11,1 г/дл.
В чем разница между средними уровнями в двух отделениях и каково ее значение? Каков 95% доверительный интервал для различий в лечении?
Ответы Глава 7.pdf
7.4 Новое лечение варикозной язвы сравнивают со стандартным лечением на десяти соответствующих парах пациентов, где лечение между парами определяется с использованием случайных чисел.