Развёрнутый угол | это… Что такое Развёрнутый угол?
«∠», обозначение угла в математике
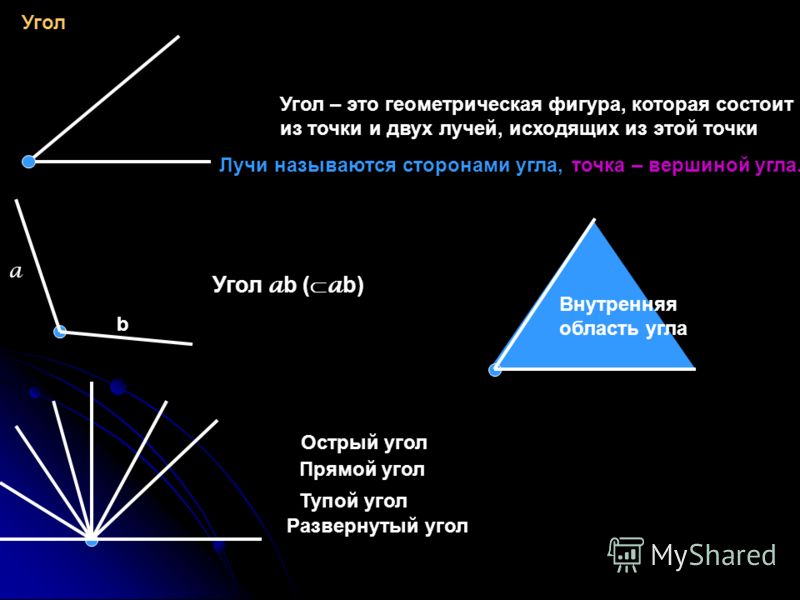
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Содержание
|
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r

1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:
Невыпуклый угол
Прямой угол
- Острые (от 0 до 90°)
- Прямые (90°)
- Тупые (от 90° до 180°)
- Развернутые (180°)
- Невыпуклые (от 180° до 360°)
- Полные (360°)
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на , считаются равными. Следует отметить, что ориентированный угол между прямыми
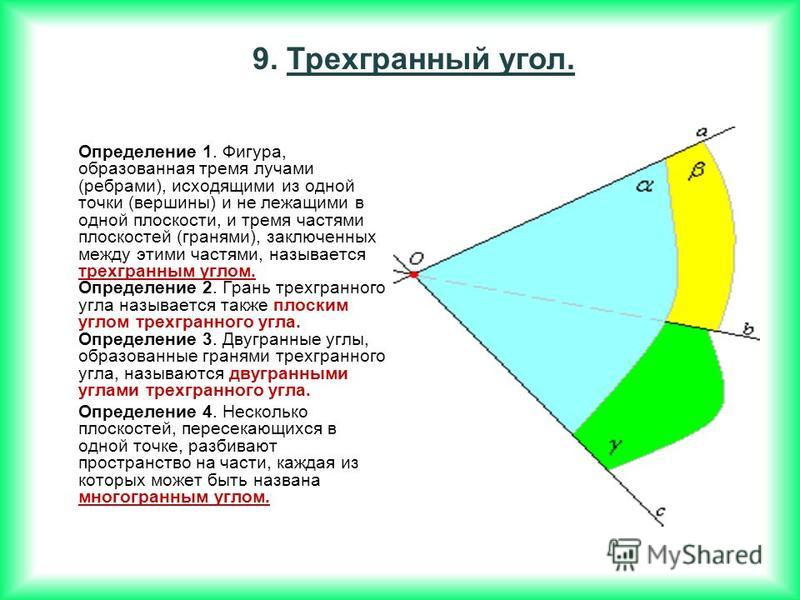
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Геометрия Многогранный угол
Материалы к уроку
Конспект урока
Многогранный угол
|
В планиметрии одним из объектов изучения является угол. Угол – это геометрическая фигура, состоящая из точки – вершины угла и двух лучей, исходящих из этой точки.
Два угла одна сторона, которых общая и две другие являются продолжением одна другой, в планиметрии называются смежными.
Циркуль можно рассматривать как модель плоского угла.
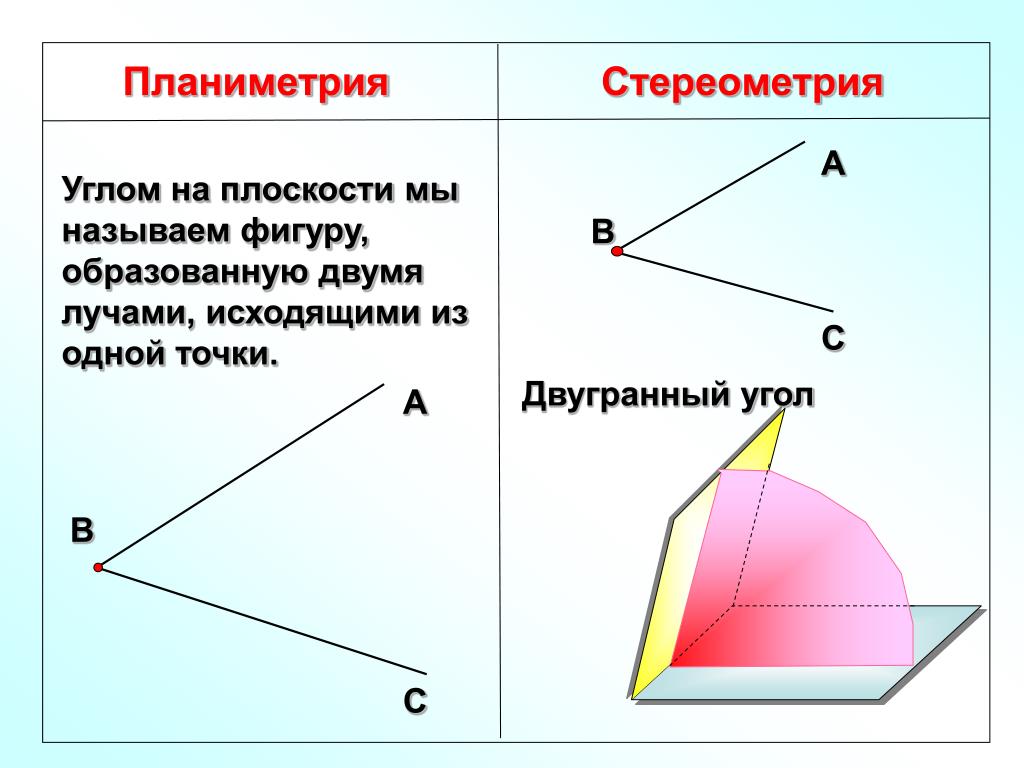
Вспомним понятие двухгранного угла. Это фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости в геометрии называется двугранным углом.
Крыша дома наглядно демонстрирует двухгранный угол.
Но крыша дома на рисунке два выполнена в виде фигуры образованной из шести плоских углов с общей вершиной так, что углы берутся в определенном порядке и каждая пара соседних углов, включая первый и последний, имеет общую сторону. Как называется такая форма крыши? |
На экране изображение и текст: Угол
На экране изображение:
На экране изображение Угол
На экране изображение Двугранный угол
|
||||||||
|
В геометрии фигура, составленная из углов А1ОА2, А2ОА3 и так далее АnОА1 и их внутренних областей так, что смежные не лежат в одной плоскости, а не смежные углы (с их внутренними областями) не имеют общих точек называется многогранный угол ОА1А2 А3…Аn.
А углы из которых составлен этот угол называются плоскими углами. Стороны плоских углов называются ребрами многогранного угла. Точка О называется вершиной угла.
Примеры многогранных углов можно найти в тетраэдре и параллелепипеде. Грани тетраэдра DBA, ABC, DBC образуют многогранный угол ВADC. Чаще он называется трёхгранным углом.
В параллелепипеде грани АА1D1D, ABCD, AA1B1B образую трехгранный угол AA1DB.
Ну а крыша дома выполнена в форме шестигранного угла. Она состоит из шести плоских углов. |
На экране изображение:
На экране изображение:
|
||||||||
|
Для многогранного угла справедлив ряд свойств. Сформулируем их и докажем. Здесь говорится, что утверждение |
|
||||||||
|
Во–первых, для любого выпуклого многогранного угла существует плоскость, пересекающая все его рёбра. Рассмотри для доказательства многогранный угол ОА1А2 А3…Аn.
По условию он выпуклый. Угол называется выпуклым, если он лежит по одну сторону от плоскости каждого из своих плоских углов.
Так как по условию этот угол выпуклый, то точки О, А1, А2 ,А3, Аn лежат по одну сторону от плоскости ОА1А2
Проведем среднюю линию KM треугольника ОА1А2 и выберем из ребер ОА3, ОА4, ОАn то ребро которое образует с плоскостью ОКМ, наименьший двугранный угол. Пусть это будет ребро ОАi.
Рассмотрим полуплоскость α с границей КМ, делящую двугранный угол ОКМАi на два двухгранных угла. Все вершины от А до Аn лежат по одну сторону от плоскости α, а точка О по другую сторону. Следовательно, плоскость α пересекает все ребра многогранного угла. Утверждение доказано. |
На экране текст: Для любого выпуклого многогранного угла существует плоскость, пересекающая все его рёбра.
На экране изображение:
Ткст: Угол называется выпуклым, если он лежит по одну сторону от плоскости каждого из своих плоских углов.
На экране обновляется изображение
На экране изображение: |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
простых способов определения углов
••• Hemera Technologies/PhotoObjects. net/Getty Images
net/Getty Images
Обновлено 24 апреля 2017 г. Углы можно рассчитать разными способами, в том числе с применением математических формул и логического вывода. Некоторые подходы к измерению углов требуют специальных инструментов.
Правило треугольника
Когда вас попросят вычислить сумму углов фигуры, подсчитайте, сколько треугольников можно составить из вершин фигуры. Вершины — это углы фигуры, точки, в которых встречаются две линии. Например, сумма углов квадрата составляет 360 градусов. Проведите линию от одного угла квадрата к противоположному диагональному углу. Это создает два треугольника. Если в квадрате два треугольника, значит, сумма углов треугольника будет равна половине 360 или 180 градусов.
Транспортир
Чтобы определить точную величину угла, используйте транспортир. Транспортир представляет собой инструмент в форме полукруга, на дуге которого нанесены два набора градусных мер. Поместите открытое отверстие транспортира над вершиной измеряемого угла, точкой, в которой встречаются два луча угла. Совместите линию 0 градусов с одним лучом угла. Число, которое появляется там, где другой луч пересекает внешний край транспортира, будет измерением угла.
Совместите линию 0 градусов с одним лучом угла. Число, которое появляется там, где другой луч пересекает внешний край транспортира, будет измерением угла.
Связанные углы
Используйте принципы связанных углов при работе с параллельными линиями, пересекаемыми секущей, которая представляет собой прямую линию, пересекающую параллельные линии. Следует помнить три ключевых момента. Во-первых, вертикальные углы или углы, образующие «х-образную форму», равны. Во-вторых, соответствующие углы или углы, находящиеся в одном и том же месте на параллельных прямых, равны. В-третьих, внутренние углы или два угла, которые примыкают друг к другу и при соединении образуют прямую линию, равны. Все эти связанные углы дадут в сумме 180 градусов.
Внешний угол треугольника
Другой способ найти угол треугольника — применить правило внешнего угла треугольника. Это правило гласит, что внешний угол равен сумме других внутренних углов в любом данном треугольнике. Чтобы проиллюстрировать эту концепцию, нарисуйте треугольник. Возьмите любую сторону треугольника и вытяните ее за пределы треугольника с помощью линейки. Угол, который образован вне треугольника, является внешним углом. С помощью транспортира измерьте внешний угол. Тогда можно вычислить дополнительный внутренний угол. Например, если внешний угол равен 50 градусам, вычитание 50 из 180 даст результат 130 градусов. Это измерение дополнительного внутреннего угла. Как только эта мера внутреннего угла известна, сумма оставшихся внутренних углов должна быть 50 градусов, потому что три угла любого треугольника должны составлять 180 градусов. Обратите внимание, что внешний угол равен сумме двух других углов внутри треугольника.
Чтобы проиллюстрировать эту концепцию, нарисуйте треугольник. Возьмите любую сторону треугольника и вытяните ее за пределы треугольника с помощью линейки. Угол, который образован вне треугольника, является внешним углом. С помощью транспортира измерьте внешний угол. Тогда можно вычислить дополнительный внутренний угол. Например, если внешний угол равен 50 градусам, вычитание 50 из 180 даст результат 130 градусов. Это измерение дополнительного внутреннего угла. Как только эта мера внутреннего угла известна, сумма оставшихся внутренних углов должна быть 50 градусов, потому что три угла любого треугольника должны составлять 180 градусов. Обратите внимание, что внешний угол равен сумме двух других углов внутри треугольника.
Статьи по теме
Ссылки
- Увлекательная математика: использование транспортира
Об авторе
С 2008 года Джен Ким является профессиональным писателем и блоггером, работающим в национальных изданиях, таких как Psychology Today и филиалах Chicago Tribune. . Она имеет степень магистра журналистики Северо-Западного университета.
. Она имеет степень магистра журналистики Северо-Западного университета.
Photo Credits
Hemera Technologies/PhotoObjects.net/Getty Images
Q1 Назовите угол данной фигуры…
Перейти к
- Упражнение 4.1
- Упражнение 4.2
- Упражнение 4.3
- Упражнение 4.4
- Упражнение 4.5
- Упражнение 4.
 6
6
- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 4. Основные геометрические идеи
>
Упражнение 4.3
>
Вопрос 1
Основные геометрические идеи
>
Упражнение 4.3
>
Вопрос 1
Вопрос 1 Упражнение 4.3
Q1: Назовите угол данной фигуры.
Ответ:
Решение 1:
На данной фигуре четыре угла
\угол ABC,\угол ADC,\угол DAB,\угол DCB
Стенограмма видео
«Сегодня выполни домашнее задание. Мы задаемся вопросом. Номер один, который назван углам на данной фигуре. Хорошо, сэр, вы должны назвать это так, чтобы образовавшийся угол был первым этим 1. Итак, как назовем этот угол, напишем его как угол a dc1, где угол находится здесь. Это можно записать как угол. См. быть другим, здесь. Это можно записать как угол d a, а также можно записать наоборот.Ладно,значит BD или ладно,и еще один вот здесь,который можно записать как Б.Ладно.Спасибо большое ребятам за просмотр видео. Если у вас есть какие-либо сомнения, пожалуйста, дайте мне знать в комментарии ниже.Также еще один момент.Можно написать наоборот арки.Например,если это KDC,то можно также написать ca
Они просили вас написать все возможное. Но да, мы можем написать доделать все эти дырки. Хорошо. Большое спасибо, ребята, пожалуйста, следите за обновлениями для новых видео. Большое спасибо.
Если у вас есть какие-либо сомнения, пожалуйста, дайте мне знать в комментарии ниже.Также еще один момент.Можно написать наоборот арки.Например,если это KDC,то можно также написать ca
Они просили вас написать все возможное. Но да, мы можем написать доделать все эти дырки. Хорошо. Большое спасибо, ребята, пожалуйста, следите за обновлениями для новых видео. Большое спасибо.
Связанные вопросы
Назовите углы на данном рисунке.
Q2. На данной диаграмме назовите точку (точки) (a) Внутри ∠DOE (b) Во внешней части ∠EOF (c) …
На данной диаграмме назовите точки(ы)(а) Внутри ∠DOE(b) Во внешности ∠EOF(c) На…
Начертите диаграмму двух углов так, чтобы они имели: а) одну общую точку; б) две общие точки…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 4.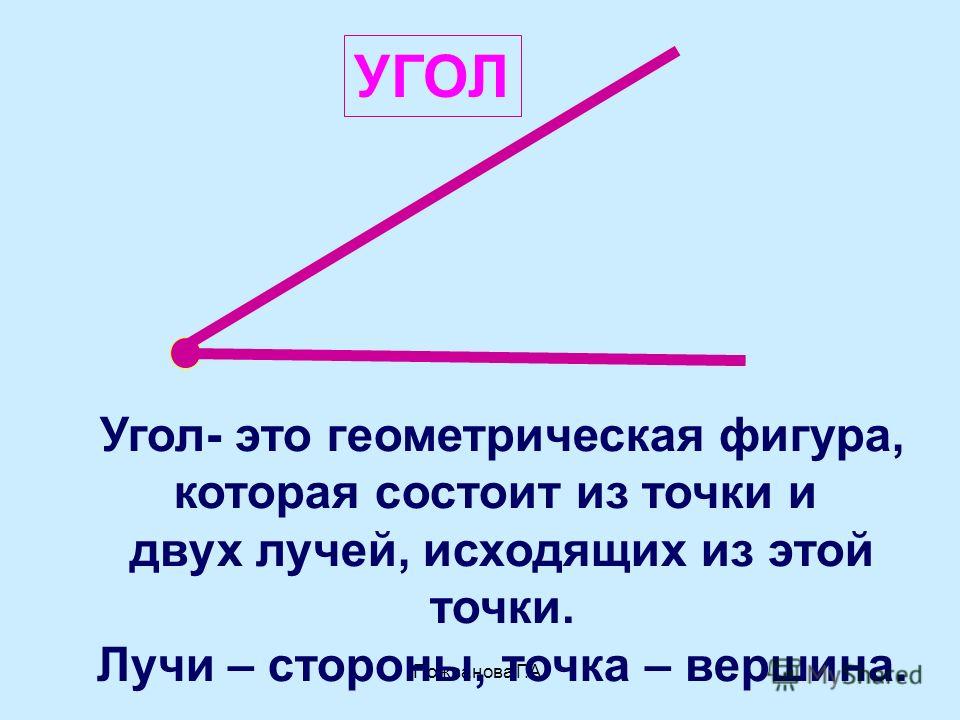

 Полуплоскости – это грани двугранного угла. Прямая а – это ребро двугранного угла.
Полуплоскости – это грани двугранного угла. Прямая а – это ребро двугранного угла.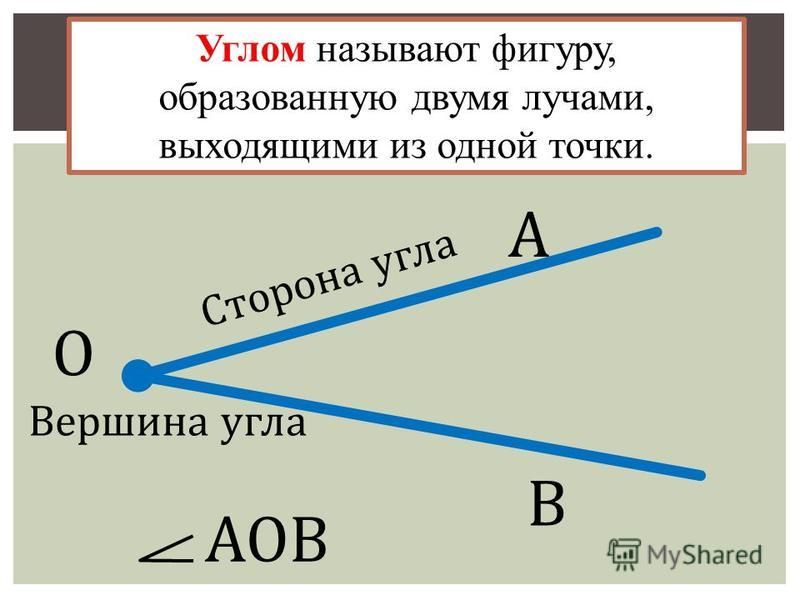


 (оа итое)
(оа итое) 6
6