tg 45 tg 30 tg 60
Вы искали tg 45 tg 30 tg 60? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и tg30 таблица, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «tg 45 tg 30 tg 60».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как tg 45 tg 30 tg 60,tg30 таблица,значение некоторых углов тригонометрических функций,значение синусов и косинусов и котангенсов,значение тригонометрических функций,значение тригонометрических функций некоторых углов,значение тригонометрических функций полная таблица,значение тригонометрических функций таблица,значение тригонометрических функций таблица полная,значение углов в тригонометрии,значения косинус и синус,значения тригонометрии,значения тригонометрические углов,значения тригонометрических углов,значения тригонометрических функций,значения тригонометрических функций для некоторых углов,значения тригонометрических функций таблица,значения тригонометрических функций таблица полная,значения тригонометрических функций углов,значения углов тригонометрических,значения углов тригонометрических функций,косинус 60 синус 45 тангенс 30,косинус и синус 90 градусов,косинус и синус значения,косинус синус тангенс и котангенс таблица,косинусы и синусы 45 30 и 60,основные значения синусов косинусов тангенсов котангенсов,полная таблица значение тригонометрических функций,полная таблица тригонометрических значений,синус и косинус 30 45 и 60,синус и косинус 90 градусов,синус косинус значения,синус косинус тангенс и котангенс таблица,синус косинус тангенс котангенс таблица,синусы косинусы тангенсы котангенсы таблица окружность,таблица значение тригонометрических функций полная,таблица значений основных тригонометрических функций,таблица значений тригонометрии,таблица значений тригонометрических функций,таблица значений тригонометрических функций основных,таблица значений тригонометрия,таблица значений углов тригонометрических функций,таблица значения тригонометрических функций,таблица косинусов и синусов тангенсов котангенсов на окружности,таблица основных значений тригонометрических значений,таблица основных значений тригонометрических функций,таблица приведения косинусов и синусов,таблица приведения синусов и косинусов,таблица синусов и косинусов тангенсов котангенсов на окружности,таблица синусов косинусов тангенсов и котангенсов в радианах,таблица тригоном,таблица тригонометрии значений,таблица тригонометрические функции,таблица тригонометрический,таблица тригонометрических значений,таблица тригонометрических значений полная,таблица тригонометрических значений углов,таблица тригонометрических функций,таблица тригонометрия,таблица тригонометрия значений,таблицы тригонометрии,таблицы тригонометрия,таблиця тригонометричних функцій,табличные значения,табличные значения тригонометрических функций,тангенс 60 градусов таблица,тригоном таблица,тригонометрии значения,тригонометрическая таблица значений,тригонометрическая таблица углов,тригонометрические значения,тригонометрические значения таблица,тригонометрические значения углов,тригонометрические функции синус косинус тангенс и котангенс таблица,тригонометрические функции таблица,тригонометрический таблица,тригонометрична таблиця,тригонометрия значения,тригонометрия значения синусов и косинусов,тригонометрия таблица,тригонометрия таблица значений.
Решить задачу tg 45 tg 30 tg 60 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
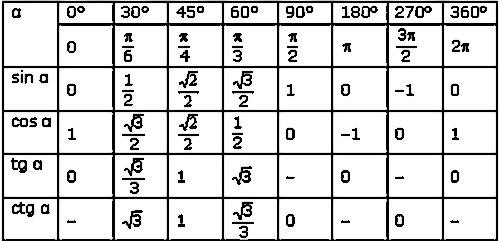
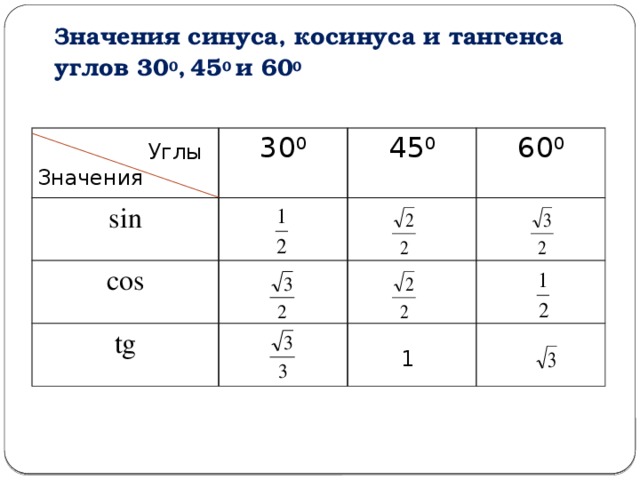
Значение тригонометрических функций углов 30°, 45° и 60°
Найдем значение Sin, Cos, Tg, Ctg трёх примечательных углов 30°, 45° и 60°.
30° и 60°
Начнём с синуса 30°. Для этого построим прямоугольный треугольник с острым углом в 30°.
И синус 30° – это будет отношение противолежащего короткого катета к гипотенузе. И для удобства установим длину гипотенузы единица.
И тогда получается что отношение длины катета к гипотенузе равно просто длине катета, и синус 30° будет равен просто а. Кроме того, сумма углов любого треугольника равна 180°, и 2й острый угол равен 180° – 90° – 30° = 60°. И для 2го острого угла отношение короткого катета к гипотенузе – это будет отношение прилежащего катета к гипотенузе то есть косинус. И значит, Cos(60°) тоже будет равен а. А теперь найдем, чему же равно это а. Для этого построим снизу ещё один такой же треугольник, равный исходному — только отраженный зеркально.
И вот что получается: во-первых приглядимся к углу, сложившемуся из двух прямых углов – он развернутый. Получается, что верхняя и нижняя точки треугольника и вершина прямых углов лежат на одном отрезке. А левый угол складывается из двух углов по 30°, то есть равен он 60°. Следовательно, можно стереть горизонтальный отрезок, и получается треугольник, у которого каждый угол равен 60°.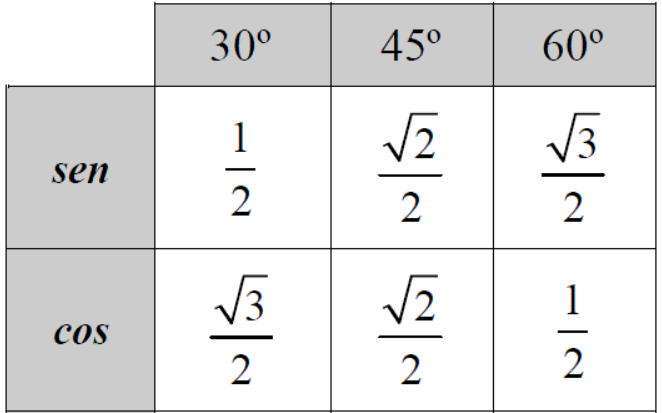
Равносторонний треугольник, у которого третья сторона равна первым двум сторонам и тоже равна единице. Получилось, что:
а + a = 1
А это означает, что
a = 1/2
И таким образом
Sin(30°) = Cos(60°) = 1/2
Теперь вернемся к исходному треугольнику. Короткий катет теперь известен – это 1/2. А чему же равен длинный катет? Обозначим его буквой b.
Для угла в 30° этот катет b – прилежащий, гипотенуза равна 1. И значит длина этого катета равна отношению длины прилежащего катета к гипотенузе, то есть Cos(30°). А для 60° этот длинный катет – противолежащий. И следовательно длина этого катета равна отношению противолежащего катета к гипотенузе, то есть Sin(60°). И значит
Cos(30°) = Sin(60°) = b
Ну а теперь найдем катет b с помощью теоремы Пифагора. Как известно, сумма квадратов катетов равна квадрату гипотенузы, то есть
(½)² + b² = 1²
¼ + b² = 1
b² = ¾
b = (√3)/2
Таким образом
Cos(30°) = Sin(60°) = (√3)/2
Теперь уже известны оба катета, и можно найти отношение двух катетов.
Сначала найдём отношение короткого катета к длинному катету. Для угла в 30° это будет отношение противолежащего катета к прилежащему катету, то есть Tg(30°). А для угла в 60° это будет наоборот – отношение прилежащего катета к противолежащему катету то есть Ctg(60°).
Tg(30°) = Ctg(60°) =
= (1/2) : ((√3)/2) =
= 1 : (√3)
А теперь наоборот длинный катет разделим на короткий катет. Для 30° это будет прилежащий катет разделить на противолежащий, то есть Ctg(30°). А для 60° это будет противолежащий катет разделить на прилежащий, то есть Tg(60°).
Ctg(30°) = Tg(60°) =
= ((√3)/2) : (1/2) =
= (√3) : 1 = √3
45°
Построим прямоугольный треугольник с острым углом 45 градусов. Гипотенузу опять сделаем единицу и противолежащий катет обозначим буквой e.
Отношение противолежащего катета к гипотенузе и будет равно Sin(45°). Но гипотенуза – единица – поэтому просто длина этого катета равна синусу Sin(45°). Теперь обратим внимание на 2й острый угол.
На два острых угла в прямоугольном треугольнике приходится 90°. Значит 2й острый угол равен 90° – 45° = 45°. Выходит что этот прямоугольный треугольник – равнобедренный, и второй катет тоже равен е. И получается что для угла 45° отношение прилежащего катета к гипотенузе такое же, как и противолежащего катета к гипотенузе
Cos(45°) = Sin(45°) = е
Кроме того, даже не зная, чему равно е, можно сказать, какой будет Tg(45°) и Ctg(45°), потому что отношение противолежащего катета к прилежащему или, наоборот, прилежащего катета к противолежащему – будет равно единице.
Tg(45°) = Ctg(45°) = e / e = 1
Ну а теперь можно уже наконец найти, чему равно е. И для этого воспользуемся теоремой Пифагора.
е² + e² = 1²
2 × е² = 1
е² = ½
e = 1/(√2) = (√2)/2
Получается, что:
Cos(45°) = Sin(45°) = (√2)/2
И таким образом найдены значения основных тригонометрических функций углов 30° 45° и 60°.
← Предыдущий урок
Оглавление
Следующий урок →
o =\sqrt3}$$Общий генератор (TG)
Нормативная информация Калифорнии
892.0303Артикул: ТГ
Обзор продукта
TG-10
TG-10 — очень эффективный генератор озона, производящий 10 г озона в час всего из 3 л/мин кислорода. TG-10 — это управляемый микропроцессором генератор озона, который будет работать практически при любом давлении и расходе, настраивая себя на оптимальную производительность.
Информация о системе
10 г/ч озона из 3 л/мин кислорода при 5% по весу
Регулируемый выход озона от 0 до 100%
Генератор озона с воздушным охлаждением, монтируемый в стойку
Дополнительный манометр и расходомер
Эффективное производство озона с низкими эксплуатационными затратами
Быстрая настройка для экономии времени
Низкая потребность в кислороде для выхода озона
Дополнительная информация | |
Концентрация при номинальном расходе | 5% |
Стандартное рабочее давление | от 0,0 до 80 фунтов на кв. |
Максимальное рабочее давление | 80 фунтов на квадратный дюйм (5,62 бар) |
Поставка газа | Кислород |
Регулируемый регулятор выхода озона | Да |
Охлаждение | С воздушным охлаждением |
Способ производства озона | Коронный разряд |
Рабочая частота | Высокая частота 5 000–30 000 Гц |
Соединения для озона/кислорода | 1/4 дюйма из нержавеющей стали |
| Выход озона | 10 г/ч. |
Размеры | 19 x 17 x 7 дюймов |
Вес | 23,0 фунта. |
Гарантия | 1 год |
Номинальный расход | 3 л/мин (6,36 стандартных кубических футов в час) |
|
|
| Общая информация о генераторе | |
|---|---|
Информация о гарантии
Продавец гарантирует, что все Продукты будут соответствовать Спецификациям и не будут иметь дефектов изготовления материалов и программирования. Претензии по Продукции, не соответствующей настоящей гарантии, должны быть предъявлены Покупателем не позднее 12 месяцев с даты поставки Покупателю. Продавец должен незамедлительно отремонтировать или заменить, по своему усмотрению и за свой счет, несоответствующую Продукцию. Отправка несоответствующих Продуктов Покупателем Продавцу и обратная отправка отремонтированных или замененных Продуктов Продавцом Покупателю осуществляется за счет Продавца, если только не будет установлено, что Покупатель вернул Продукт, соответствующий требованиям, и в этом случае расходы несет Покупатель, а в случае их оплаты Продавцом эти расходы возмещаются Покупателем в течение тридцати (30) дней с момента уведомления Продавцом.