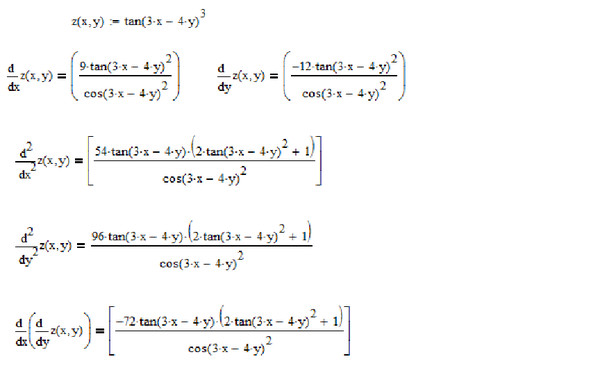Tg y 1 tg x y 2: Решить систему уравнений : tg x +tg y =1, x+y=п/4

Функции y = tg x, y = ctg x, их свойства и графики

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

y f (x)
у
х
Функции y = tg x, y = ctg x,
их свойства и графики.
Устно:
1. Вычислите:
tg
4
; tg
3
; tg 0; tg
2
; tg
6
2. Докажите, что число является периодом для
функции y = sin2x.
sin2(x — ) = sin2x = sin2(x + )
3. Докажите, что функция является нечётной:
f(x) = x⁵ ∙ cos3x
у
4.

Прочитайте
по графику
функцию:
-2
0
-4
5
2
5
х
Свойство 1.
Область определения функции y = tg x – множество
всех действительных чисел, за исключением чисел
вида x = /2 + k.
у
3
2
2
2
3
2
х
Свойство 2.
y = tg x – периодическая функция с
периодом .
tg(x — ) = tg x = tg(x + )
Свойство 3.
y = tg x – нечётная функция.
tg(- x) = — tg x
(График функции симметричен относительно
начала координат).
Свойство 4.
у
3
2
y = tg x
2
2
3
2
х
Функция возрастает на любом интервале вида:
График функции y = tg x
k ; k
называется тангенсоидой.
2
2
Свойство 5.
Функция y = tg x не ограничена ни снизу, ни сверху.
Свойство 6.
У функции y = tg x нет ни наибольшего, ни
наименьшего значений.
Свойство 7.
Функция y = tg x непрерывна на любом интервале
вида
k ; k
2
2
Свойство 8.
E( f ) ;
Пример 1.
Решите уравнение tg x = 3
у
у = 3
3
2
Ответ: x
3
2
32
k .
3 х
2
Пример 2.
Построить график функции y = — tg (x + /2).
у
3
2
y = ctg x
2
2
3
2
х
Т.к. — tg (x + /2) = ctg x, то построен график функции
y = ctg x.
Опишите свойства функции y = ctgx.
1) D(f): множество всех действительных чисел, кроме чисел
вида x = k.
2) Периодическая с периодом .
3) Нечётная функция.
4) Функция убывает на любом интервале вида ( k; + k).
5) Функция не ограничена ни снизу, ни сверху.
6) Функция не имеет ни наибольшего, ни наименьшего
значений.
7) Функция непрерывна на любом интервале вида ( k; + k).
8) E(f) = (- ; + ).

10. Разберём примеры 1-3, с. 67-70

11. В классе:

№ 254
№ 255
№ 256 (а, б)
№ 259 (а, б)

12. Домашнее задание:

№ 256 (в, г)
№ 257
№ 259 (в, г)

English     Русский Правила

Внеклассный урок — Тангенс сложения аргументов

Тангенс сложения аргументов

tg x + tg y                                                            tg (x + y) = ——————                                                                                 1 – tg x tg y                                                                                  tg x – tg y                                                            tg (x – y) = ——————                                                                                 1 + tg x tg y

 

Как мы получили эти формулы?

При всей кажущейся сложности решение простое. Мы покажем только решение для тангенса сложения аргументов: решение для тангенса разности такое же.
Итак…

Как вы знаете, тангенс – это отношение синуса к косинусу. Пишем эту дробь, затем применяем формулу синуса сложения аргументов (см.предыдущий раздел):

                       sin (x + y)           sin x cos y + cos x sin y
tg (x + y) = —————— = ———————————
                      cos (x + y)           cos x cos y – sin x sin y

Делим все части выражения на cos x cos y, чтобы привести выражение к более удобному для нас виду. Сокращаем подобные члены и приходим к решению:

   sin x cos y         cos x sin y
 ————— + —————
  cos x cos y       cos x cos y            tg x + tg y
———————————— = ——————
cos x cos y         sin x sin y           1 – tg x · tg y
————— – —————
 cos x cos y       cos x cos y

ПРИМЕЧАНИЕ:

При решении конкретных задач важно помнить, что задача имеет смысл лишь в том случае, если в процессе решения знаменатели нигде не оказываются равны нулю.

В заключение решим один пример по теме.

Пример: Вычислить tg 15º.

Решение.

Представим 15º в виде 45º – 30º. Вычислим синусы и косинусы этих углов:

                    π         √2
sin 45º = sin —  =  ——
                    4           2

                    π       1
sin 30º = sin — = —
                    6       2

                       π         √2
cos 45º = cos —  =  ——
                       4          2

                       π       √3
cos 30º = cos — = ——
                       6        2

Теперь найдем тангенс 45º:

               √2        √2
tg 45º = —— : ——  =  1
                2         2

Найдем тангенс 30º:

              1       √3      1        2         1             1 ∙ √3         √3
tg 30º = — : —— = — ∙ —— = ——  =  ———— = ——
              2        2        2      √3       √3          √3 ∙ √3          3

Мы уже можем применить формулу тангенса разности аргументов, так нам стали известны значения двух тангенсов. Следуя этой формуле, получаем следующее выражение:

          √3
  1 – ——
           3
——————
         √3
  1 + ——
           3

Получилось сложное выражение, поэтому будем действовать, «разбив» его на части.

Сначала приведем числитель этого выражения к общему знаменателю и преобразим его:

        √3        3 – √3
1 – —— = ————
         3             3

Теперь приведем к общему знаменателю знаменатель нашего выражения:

         √3        3 + √3
1 + —— = ————
          3             3

Формула требует разделить первое полученное выражение на второе – то есть найти соотношение числителя и знаменателя:

                            3 – √3      3 + √3     3 – √3          3            3 – √3
tg (45º – 30º)  =  ——— : ——— = ———  ∙  ———  =  ———
                                3             3              3           3 + √3        3 + √3

Упростим дробь, умножив числитель и знаменатель на 3 – √3:

(3 – √3) (3 – √3)            9 – 6√3 + 3        12 – 6√3            6 (2 – √3)
———————  =   —————— = —————  =  —————  = 2 – √3
(3 + √3) (3 – √3)               9 – 3                     6                         6

Пример решен.

 

3.6: Линейная независимость и вронскиан

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

401

• Ларри Грин
• Общественный колледж Лейк-Тахо

Напомним из линейной алгебры, что два вектора \(v\) и \(w\) называются линейно зависимыми, если существуют ненулевые константы \(c_1\) и \(c_2\) с

\[ c_1v + c_2w = 0. \]

Мы можем думать о дифференцируемых функциях \(f(t)\) и \(g(t)\) как о векторах в векторном пространстве дифференцируемых функций. Аналогичное определение приведено ниже.

Определение: линейная зависимость и независимость

Пусть \(f(t)\) и \(g(t)\) — дифференцируемые функции.

Тогда их называют 92 = 0 \nonnumber\]

для всех значений \(t\). Сначала пусть \(t = 1\). Тогда

\[ c_1 + c_2 = 0. \nonnumber\]

Пусть теперь \(t = 2\). Тогда

\[ 2c_1 + 4c_2 = 0\nonnumber \]

Это система из 2-х уравнений и двух неизвестных. Определитель соответствующей матрицы равен

\[4 — 2 = 2.\номер\]

Поскольку определитель не равен нулю, единственным решением является тривиальное решение. Это

\[ c_1 = c_2 = 0 .\nonnumber\]

Две функции линейно независимы.

В приведенном выше примере мы произвольно выбрали два значения для \(t\). Оказывается, есть систематический способ проверки на линейную зависимость. Следующая теорема утверждает это.

Теорема

Пусть \(f\) и \(g\) дифференцируемы на \([a,b]\). Если вронскиан \(W(f,g)(t_0)\) отличен от нуля для некоторого \(t_0\) в \([a,b]\), то \(f\) и \(g\) линейно независимы от \([а,б]\). Если \(f\) и \(g\) линейно зависимы, то вронскиан равен нулю для всех \(t\) в \([a,b]\).

9{2t})(1)\nonumber\]

Теперь подставьте \(t=0\), чтобы получить

\[ W(f, g )(0) = -1 \nonumber\]

, который не равен нулю . Мы можем заключить, что \(f\) и \(g\) линейно независимы .

Доказательство

Если

\[ C_1 f(t) + C_2g(t) = 0 \nonumber\]

Тогда мы можем взять производные от обеих сторон, чтобы получить

\[ C_1f»(t) + C_2g'( t) = 0 \nonumber\]

Это система двух уравнений с двумя неизвестными. Определитель соответствующей матрицы есть вронскиан. Следовательно, если вронскиан отличен от нуля при некотором \( t_0\), то только тривиальное решение существует, следовательно, они линейно независимы.{- \int p(t) dt}} \nonumber \]

где \(c\) — константа, зависящая только от \(y_1\) и \(y_2\), но не от \(t\). Вронскиан либо равен нулю для всех \(t\) в \([a,b]\), либо не равен нулю в \([a,b]\).

Доказательство

Первый вронскиан

\[ W = y_1y’_2 — y_1y_2 \nonumber\]

имеет производную

\[W’ = y_1y’_2 + y_1y»_2 — y»_1y’_2 — y_2 = у_1у»_2 — у»_1у_2.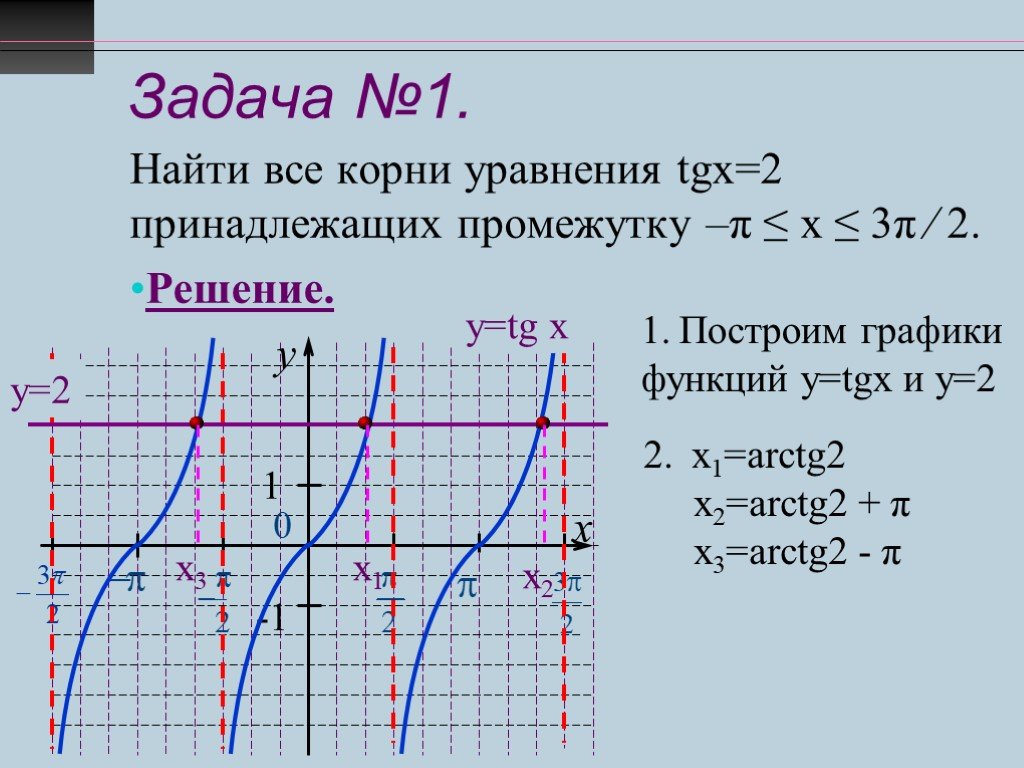 \nonumber\]

Так как \(y_1\) и \(y_2\) являются решениями дифференциального уравнения, мы имеем

\[ y»_1 + p(t)y’_1 + q(t)y_1 = 0 \не число\]

\[ y»_2 + p(t)y’_2 + q(t)y_2 = 0 . \nonumber\]

Умножение первого уравнения на \(-y_2\), второго на \(y_1\) и сложение дает

\[ (y_1y»_2 — y»_1y_2) + p(t)( y_1y’_2 — y_1y_2) = 0. \nonnumber\]

Это может быть записано как

\[ W’ + p(t)W = 0. \nonnumber\]

Это отделимое дифференциальное уравнение с

\[ \dfrac{dW}{W} = -p(t) dt.\nonumber \]

93. \nonumber \]

Обратите внимание, что вронскиан равен нулю в точке \(t = 0\), но отличен от нуля в точке \(t = 1\). По приведенному выше следствию \(y_1\) и \(y_2\) не могут быть одновременно решениями.

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Ларри Грин

   Показать страницу TOC

   нет

2. Теги

   1. Теорема Абеля
   2. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
   3. линейная независимость
   4. Вронскиан

1.

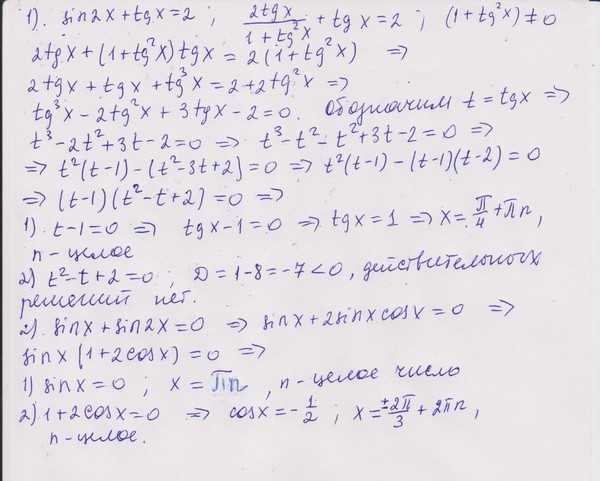Introduction DDNSDiscrete Dynamics in Nature and Society1607-887X1026-0226Hindawi Publishing Corporation10.1155/2015/317094317094Research ArticleExistence and Stability of Solutions for Hadamard-Stieltjes Fractional Integral EquationsAbbasSaïd ¹ AlaidarousEman ² BenchohraMouffak ^{2, 3} NietoJuan J ^{2, 4} БьянкаКарло ¹ Математическая лаборатория Университета СаидыП.О. Box 13820000 SaïdaAlgeriauniv-saida.dz ² Факультет математикиФакультет естественных наукУниверситет короля Абдулазиза им. Ящик 80203Джидда 21589Saudi Arabiakau.edu.sa ³ Лаборатория математикиУниверситет Сиди-Бель-АббесP.O. Box 8922000 Sidi Bel-AbbèsAlgeriauniv-sba.dz ⁴ Department of Mathematical Analysis, Faculty of MathematicsUniversity of Santiago de Compostela15782 Santiago de CompostelaSpainusc.es201530920152015160720150709201530920152015Copyright © 2015 Saïd Abbas et al.This is an open access article distributed under the Creative Commons Attribution License , который разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Мы приводим некоторые результаты существования и результаты устойчивости по Уламу для одного класса интегральных уравнений Адамара-Стилтьеса. Мы представляем два результата: первый — результат существования, основанный на теореме Шаудера о неподвижной точке, а второй — об обобщенной устойчивости Улама-Хайерса-Рассиаса.

1. Введение

Дифференциальные и интегральные уравнения дробного порядка в последнее время находят применение в различных областях техники, математики, физики, биоинженерии и других прикладных наук [1, 2]. В последние годы произошло значительное развитие обыкновенных и дифференциальных уравнений с частными дробями и интегральных уравнений; см. прекрасную классическую монографию Kilbas et al. [3] или недавняя монография Abbas et al. [4].

Первоначально вопрос об устойчивости функциональных уравнений был поднят Уламом в 1940 г. в докладе в Висконсинском университете. Проблема, поставленная Уламом, заключалась в следующем: при каких условиях существует аддитивное отображение вблизи приближенно аддитивного отображения? (подробнее см.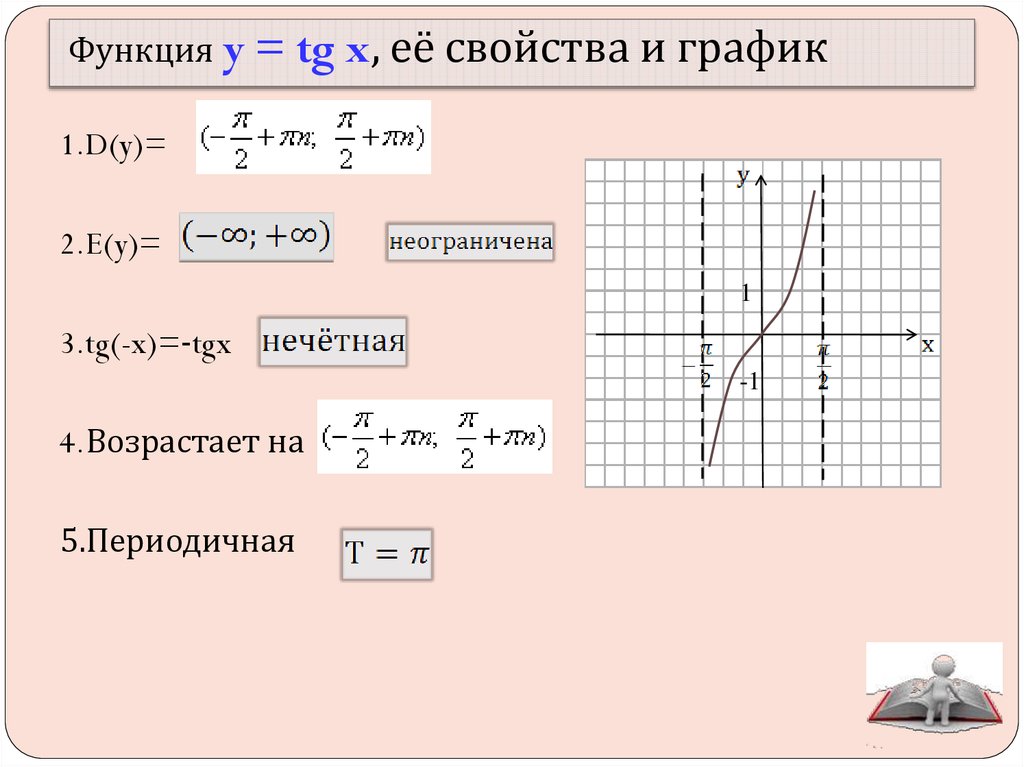 [5]). Первый ответ на вопрос Улама дал Хайерс в 1941 г. в случае банаховых пространств в [6]. В дальнейшем этот тип устойчивости называют стабильностью Улама-Хайерса. В 1978 г. Рассиас [7] дал замечательное обобщение устойчивости отображений по Уламу-Хайерсу, рассматривая переменные. Понятие устойчивости функционального уравнения возникает, когда мы заменяем функциональное уравнение неравенством, которое действует как возмущение уравнения. Таким образом, вопрос об устойчивости функциональных уравнений заключается в том, чем отличаются решения неравенства от решений данного функционального уравнения? Большое внимание уделялось изучению устойчивости по Уламу-Хайерсу и Уламу-Хайерсу-Рассиасу всех видов функциональных уравнений; можно ознакомиться с монографиями [8, 9]. Бота-Боричану и Петрусел [10], Петру и др. [11] и Рус [12, 13] обсуждали устойчивость по Уламу-Хайерсу для операторных уравнений и включений. Кастро и Рамос [14] и Юнг [15] рассмотрели устойчивость Хайерса-Улама-Рассиаса для класса интегральных уравнений Вольтерра.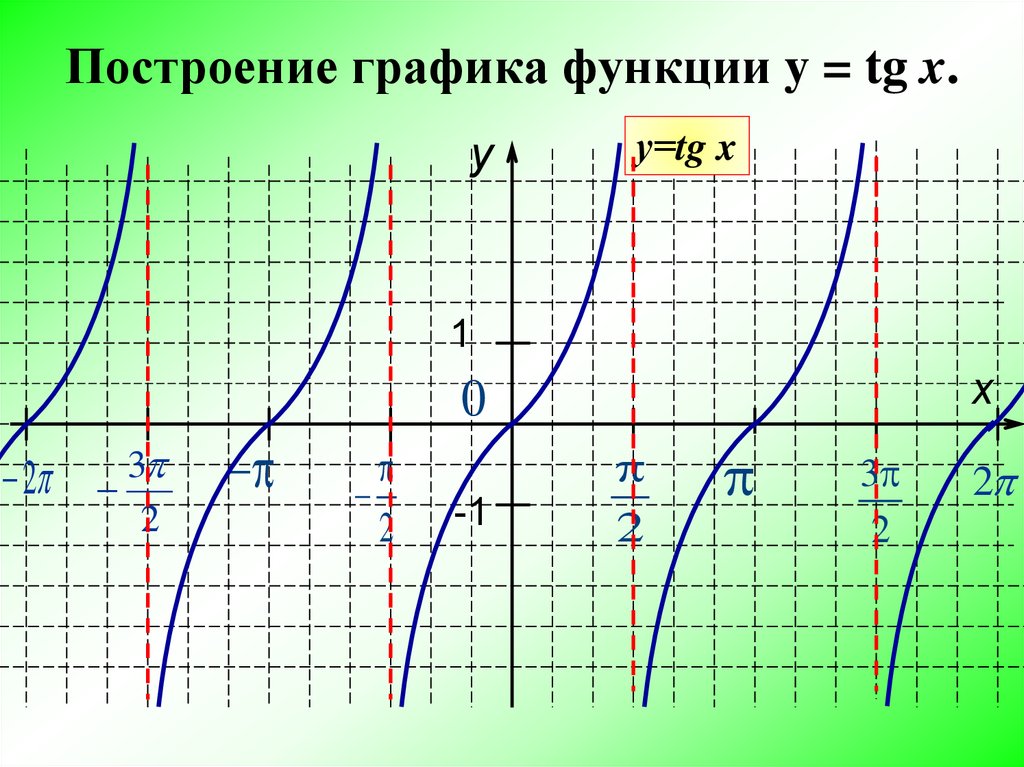

Более подробная информация с исторической точки зрения и недавние разработки таких устойчивых систем приведены в [12, 16].

В [17] Butzer et al. исследовать свойства дробного интеграла Адамара и производной. В [18] они получили преобразования Меллина дробных интегральных и дифференциальных операторов Адамара, а в [19], Pooseh et al. получены формулы разложения операторов Адамара по производным целого порядка. Многие другие интересные свойства этих операторов суммированы в [20] и приведенных там ссылках.

В этой статье рассматривается существование устойчивости по Уламу решений следующего интегрального уравнения Адамара-Стилтьеса: (1)ux,y=µx,y+∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,us, tstΓr1Γr2dtg2y,tdsg1x,s; если  x,y∈J, где J:=[1,a]×[1,b], a,b>1, r1,r2>0 и µ:J→R, f:J×R→R, g1 :[1,a]2→R, g2:[1,b]2→R — заданные непрерывные функции, а Γ(·) — гамма-функция Эйлера.

Наши исследования проводятся с применением теоремы Шаудера о неподвижной точке для существования решений интегрального уравнения (1).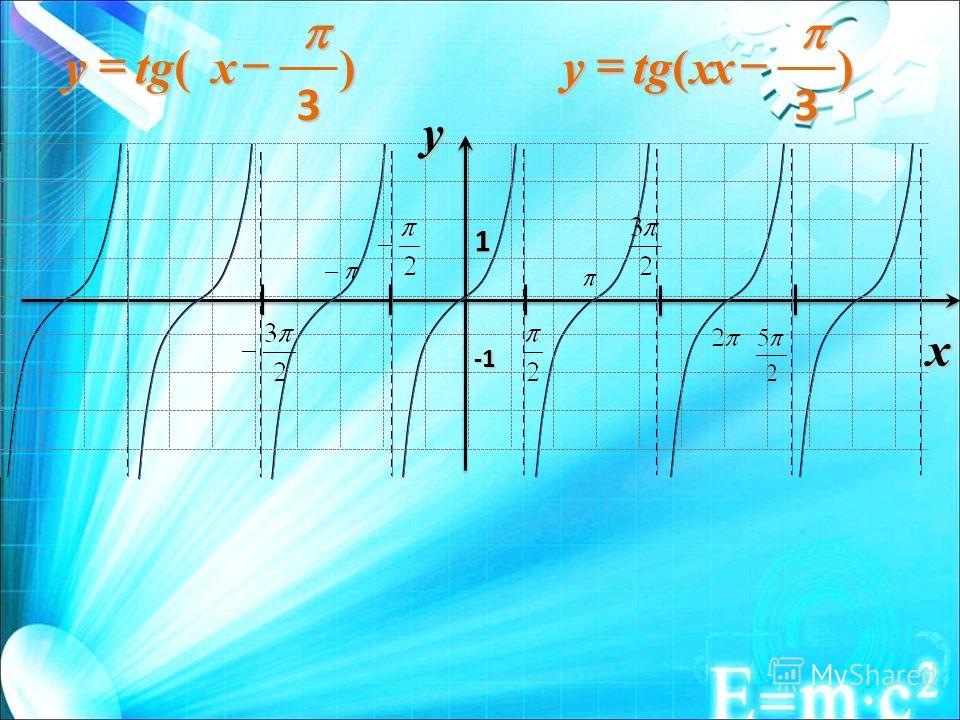 Также мы получаем некоторые результаты об обобщенной устойчивости по Уламу-Хайерсу-Рассиасу решений уравнения (1). Наконец, приведем пример, иллюстрирующий применимость наложенных условий.

Эта статья положила начало изучению существования и устойчивости по Уламу такого класса интегральных уравнений.

2. Предварительные занятия

В этом разделе мы вводим обозначения, определения и предварительные факты, которые используются на протяжении всей статьи. Обозначим через L1(J,R) банахово пространство функций u:J→R, интегрируемых по Лебегу с нормой (2)uL1=∫1a∫1bux,ydy dx. Пусть C:=C(J,R) — банахово пространство всех непрерывных функций u:J→R с нормой (3)uC=supx,y∈J⁡ux,y.

Определение 1 (см. [3, 21]).

Дробный интеграл Адамара порядка q>0 для функции g∈L1([1,a],R) определяется как (4)I1rHgx=1Γq∫1xlog⁡xsq-1gssds.

Определение 2.

Пусть r1,r2≥0, σ=(1,1) и r=(r1,r2). Для w∈L1(J,R) определим частный дробный интеграл Адамара порядка r выражением (5)IσrHwx,y=1Γr1Γr2∫1x∫1ylog⁡xsr1-1log⁡ytr2-1ws,tstdt ds.

Если u — действительная функция, определенная на интервале [a,b], то символ ⋁abu обозначает вариацию u на [a,b]. Мы говорим, что u имеет ограниченную вариацию на интервале [a,b], если ⋁abu конечно. Если w:[a,b]×[c,b]→R, то символ ⋁t=pqw(t,s) указывает на изменение функции t→w(t,s) на интервале [p,q ]⊂[a,b], где s произвольно фиксировано в [c,d]. Таким же образом мы определяем ⋁s=pqw(t,s). По свойствам функций ограниченной вариации мы отсылаем к [22].

Если u и φ — две действительные функции, определенные на отрезке [a,b], то при некоторых условиях (см. [22]) мы можем определить интеграл Стилтьеса (в смысле Римана-Стилтьеса) (6)∫abutdφt функции функция u относительно φ. В этом случае говорят, что u интегрируема по Стилтьесу на [a,b] относительно φ. Известно несколько условий, гарантирующих интегрируемость по Стилтьесу [22]. Одно из наиболее часто используемых требований состоит в том, что функция u непрерывна, а функция φ имеет ограниченную вариацию на [a,b].

В дальнейшем мы используем следующие свойства интеграла Стилтьеса ([23], п. 8.13).

Если u интегрируема по Стилтьесу на интервале [a,b] относительно функции φ ограниченной вариации, то (7)∫abutdφt≤∫abutd⋁atφ. Если u и v — интегрируемые по Стилтьесу функции на отрезке [a,b] относительно неубывающей функции φ такие, что u(t)≤v(t) при t∈[a,b], то (8)∫abutdφt≤ ∫abvtdφt.

В дальнейшем мы рассматриваем интегралы Стилтьеса вида (9)∫abutdsgt,s и интегралы Адамара-Стилтьеса дробного порядка вида (10)1Γr∫1tlog⁡tsq-1usdsgt,s, где g:[1,∞)×[1,∞)→R,  q∈(0 ,∞), а символ ds обозначает интегрирование по s.

Определение 3.

Пусть r1,r2≥0,  σ=(1,1) и r=(r1,r2). Для w∈L1(J,R) определим частный дробный интеграл Адамара-Стилтьеса порядка r выражением , где g1,g2:[1,∞)×[1,∞)→R.

Теперь рассмотрим устойчивость по Уламу для интегрального уравнения (1). Рассмотрим оператор N:C→C, определенный формулой (12)Nux,y=µx,y+∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,us,tstΓr1Γr2dtg2y,tdsg1x,s. Очевидно, что неподвижные точки оператор N являются решением интегрального уравнения (1).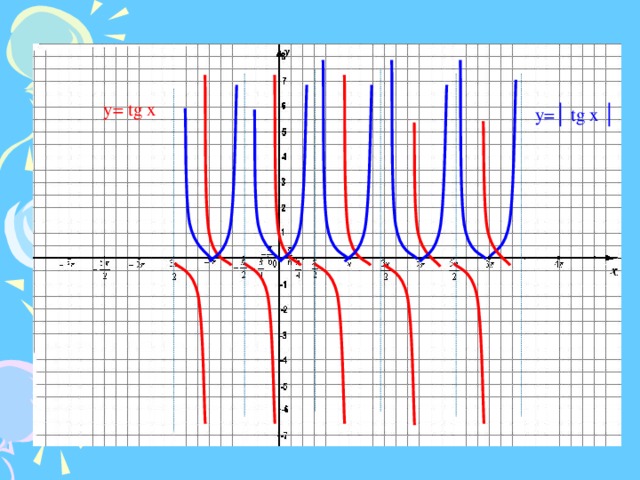 Пусть ϵ>0 и Φ:J→[0,∞) — непрерывная функция. Рассмотрим следующие неравенства: (13)ux,y-Nux,y≤ϵ; x,y∈J,(14)ux,y-Nux,y≤Φx,y; x,y∈J,(15)ux,y-Nux,y≤ϵΦx,y; х,у∈J.

Определение 4 (см. [12, 24]).

Уравнение (1) является устойчивым по Уламу-Хайерсу, если существует действительное число cN>0 такое, что для каждого ϵ>0 и каждого решения u∈C неравенства (13) существует решение v∈C уравнения (1) с (16)ux,y-vx,y≤ϵcN; х,у∈J.

Определение 5 (см. [12, 24]).

Уравнение (1) является обобщенным устойчивым по Уламу-Хайерсу, если существует cN:C(0,∞,[0,∞)) с cN(0)=0 такое, что для каждого ϵ>0 и для каждого решения u∈C уравнения неравенства (13) существует решение v∈C уравнения (1) с (17)ux,y-vx,y≤cNϵ; х,у∈J.

Определение 6 (см. [12, 24]).

Уравнение (1) является устойчивым по Уламу-Хайерсу-Рассиасу относительно Φ, если существует действительное число cN,Φ>0 такое, что для каждого ϵ>0 и для каждого решения u∈C неравенства (15) существует решение v∈C уравнения (1) с (18)ux,y-vx,y≤ϵcN,ΦΦx,y; х,у∈J.

Определение 7 (см. [12, 24]).

Уравнение (1) является обобщенным устойчивым по Уламу-Хайерсу-Рассиасу относительно Φ, если существует действительное число cN,Φ>0 такое, что для каждого решения u∈C неравенства (14) существует решение v∈C уравнения (1) с ux,y-vx,y≤cN,ΦΦ(x,y); (х,у)∈J.

Замечание 8.

Ясно, что (i) определение 4  ⇒ определение 5, (ii) определение 6  ⇒ определение 7 и (iii) определение 6 для Φ(·,·)=1  ⇒ определение 4.

Аналогичные замечания можно сделать и для неравенств (13) и (15).

3. Существование и результаты устойчивости по Уламу

В этом разделе мы обсуждаем существование решений и приводим условия устойчивости по Уламу для интегрального уравнения Адамара (1).

В дальнейшем будут использоваться следующие гипотезы.(h2)

Существуют функции p1,p2∈C(J,R+) такие, что для любых u∈R и (x,y)∈J, (19)fx,y,u≤p1x,y+p2x,y1+ux, Юкс, у,

с (20)pi∗=supx,y∈J⁡ sups,t∈1,x×1,y⁡log⁡xsr1-1log⁡ytr2-1pis,tstΓr1Γr2; я=1,2.

(ч3)

Для всех x1,x2∈[1,a], таких что x1 Кроме того, для всех y1,y2∈[1,b], таких что y1 (ч4)

Функции s↦g1(0,s) и t↦g2(0,t) неубывают на [1,a] или [1,b] соответственно.

(ч5)

Функции s↦g1(x,s) и x↦g1(x,s) непрерывны на [1,a] для каждого фиксированного x∈[1,a] или s∈[1,a] соответственно. Кроме того, функции t↦g2(y,t) и y↦g2(y,t) непрерывны на [1,b] для каждого фиксированного y∈[1,b] или t∈[1,b] соответственно.

(Н5)

Существует λΦ>0 такое, что для каждого (x,y)∈J выполняется (21)IσrHSΦx,y≤λΦΦx,y.

Положим (22)g∗=supx,y∈J⁡ ⋁k2=1yg2y,k2⋁k1=1xg1x,k1.

Теорема 9.

. Предположим, что выполнены гипотезы (h2)–(h5). Тогда интегральное уравнение (1) имеет решение, определенное на J.

Доказательство.

Пусть ρ>0 — константа такая, что (23)ρ>µ∞+g∗p1∗+p2∗. Воспользуемся теоремой Шаудера [25] для доказательства того, что оператор N, определенный в (12), имеет неподвижную точку. Доказательство будет дано в четыре шага.

Шаг 1 (N переводит шар Bρ:={u∈C:uC≤ρ} в себя). Для любого u∈Bρ и каждого (x,y)∈J имеем 1x∫1ylog⁡xsr1-1log⁡ytr2-1p2s,tus,tst1+us,tdtg2y,tdsg1x,s≤µC+1Γr1Γr2∫1x∫1ylog⁡xsr1-1log⁡ytr2-1p1s,t+p2s,tρstdt⋁k2=1tg2y, k2ds⋁k1=1sg1x,k1≤µC+p1∗+p2∗∫1x∫1ydt⋁k2=1tg2y,k2ds⋁k1=1sg1x,k1≤µC+g∗p1∗+p2∗≤ρ. Таким образом, (Nu)C≤ρ. Отсюда следует, что N переводит шар Bρ в себя.

Шаг 2 (N:Bρ→Bρ непрерывен). Пусть {un}n∈N — последовательность такая, что un→u в Bρ. Тогда (25)Nunx,y-Nux,y≤1Γr1Γr2∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,uns,t-fs,t,us,tstdtg2y,tdsg1x,s≤sups,t∈J⁡ fs,t,uns,t-fs,t,us,tΓr1Γr2∫1x∫1ylog⁡xsr1-1log⁡ytr2-1dt⋁k2=1tg2y,k2ds⋁k1=1sg1x,k1≤g∗f·,·,un·, ·-f·,·,u·,·C. Из теоремы Лебега о мажорируемой сходимости и непрерывности функции f получаем (26)Nunx,y-Nux,y⟶0 as  n⟶∞.

Шаг 3 (N(Bρ) ограничено). Это ясно, так как N(Bρ)⊂Bρ и Bρ ограничено.

Шаг 4 (N(Bρ) эквинепрерывна). Пусть (x1,y1),(x2,y2)∈J,  x1 Таким образом, получаем ,k2ds⋁k1=1sg1x1,k1+p1∗+p2∗∫x1x2∫y1y2dt⋁k2=1tg2y2,k2ds⋁k1=1sg1x2,k1+p1∗+p2∗∫1×1∫y1y2dt⋁k2=1tg2y2,k21ds ,k1+p1∗+p2∗∫x1x2∫1y1dt⋁k2=1tg2y2,k2ds⋁k1=1sg1x2,k1. Отсюда получаем (29)Nux2,y2-Nux1,y1≤µx1,y1-µx2,y2+p1∗+p2∗⋁k2=1y1g2y2,k2⋁k1=1x1g1x2,k1-⋁k2=1y1g2y1,k2⋁k1=1x1g1x1,k1+p1∗ +p2∗⋁k2=y1y2g2y2,k2⋁k1=x1x2g1x2,k1+p1∗+p2∗⋁k2=y1y2g2y2,k2⋁k1=1x2g1x2,k1+p1∗+p2∗⋁k2=1y2g2y2,k2⋁k1=x1x2g1x2,k2⋁k1=x1x2g1x2,k2⋁k1=1x2g1x2,k1+p1∗+p2∗⋁k2=1y2g2y2,k2⋁k1=x1x2g1x2, к1. При x1→x2 и y1→y2 правая часть приведенного выше неравенства стремится к нулю.

В результате выполнения шагов 1–4 вместе с теоремой Арцела-Асколи мы можем заключить, что N непрерывно и компактно. Из применения теоремы Шаудера [25] получаем, что N имеет неподвижную точку u, являющуюся решением интегрального уравнения (1).

Теперь нас интересует устойчивость решений интегрального уравнения (1).

Теорема 10.

Предположим, что выполняются (h2)–(H5). Кроме того, предположим, что существует qi∈CJ,R+,  i=1,2 такое, что для каждого (x,y)∈J имеем (30)pix,y≤qix,yΦx,y. Тогда интегральное уравнение (1) является обобщенно устойчивым по Уламу-Хайерсу-Рассиасу.

Доказательство.

Пусть u — решение неравенства (14). По теореме 9 существует v, являющееся решением интегрального уравнения (1). Отсюда (31)vx,y=µx,y+∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,vs,tstΓr1Γr2dtg2y,tdsg1x,s. В силу неравенства (14) для каждого (x,y)∈J имеем (32)ux,y-µx,y-∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,us,tstΓr1Γr2dtg2y,tdsg1x,s≤Φx,y. Положим (33)qi∗=supx,y∈J⁡qix,y; я=1,2. Для каждого (x,y)∈J имеем (34)ux,y-vx,y≤ux,y-µx,y-∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,us,tstΓr1Γr2dtg2y, tdsg1x,s+∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,us,t-fs,t,vs,tstΓr1Γr2dtg2y,tdsg1x,s≤Φx,y+1Γr1Γr2∫1x∫1ylog⁡xsr1-1log⁡ytr2- 12q1∗+q2∗us,t1+u+q2∗vs,t1+vΦs,tstdtg2y,tdsg1x,s≤Φx,y+2q1∗+q2∗IσrHSΦx,y≤1+2q1∗+q2∗λϕΦx,y≔cN ,ΦΦx,y. Следовательно, интегральное уравнение (1) является обобщенно устойчивым по Уламу-Хайерсу-Рассиасу.

4. Пример

. В качестве приложения наших результатов рассмотрим следующее интегральное уравнение Адамара-Стилтьеса (35)ux,y=µx,y+∫1x∫1ylog⁡xsr1-1log⁡ytr2-1fs,t,us,tstΓr1Γr2dtg2y,tdsg1x ,с; x,y∈1,e×1,e, где (36)r1,r2>0,µx,y=x+y2; x,y∈1,e×1,e,g1x,s=s,g2y,t=t; s,t∈1,e,fx,y,ux,y=xy2e-7+ux,yex+y+5; x,y∈1,e×1,e. Условие (h2) выполняется при p1(x,y)=xy2e-7 и p2∗=xy2/ex+y+5. Мы видим, что функции g1 и g2 удовлетворяют (h3)–(h5). Следовательно, из теоремы 9 следует, что интегральное уравнение Адамара (35) имеет решение, определенное на [1,e]×[1,e].

Также выполняется гипотеза (H5) с (37)Φx,y=e3,λΦ=1Γ1+r1Γ1+r2. Действительно, для каждого (x,y)∈[1,e]×[1,e] получаем (38)IσrHSΦx,y≤e3Γ1+r1Γ1+r2=λΦΦx,y. Следовательно, из теоремы 10 следует, что (35) обобщенно устойчиво по Уламу-Хайерсу-Рассиасу.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Работа J. J. Nieto была частично поддержана Министерством экономики и конкурентоспособности Испании в рамках гранта MTM2013–43014–P и Xunta de Galicia в рамках гранта R2014/002 и софинансирована Фондом Европейского сообщества FEDER.

1 Хилфер Р. Применение дробного исчисления в физике 2000 г. Сингапур World Scientific2 ТарасовВ. E. Дробная динамика: применение дробного исчисления к динамике частиц, полей и сред 2010 г.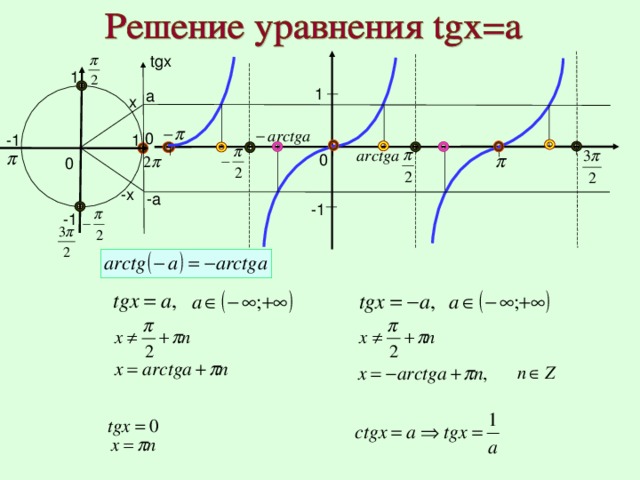 Пекин, Китай, Спрингер, Гейдельберг, Германия; Пресса о высшем образовании3 Килбас А. А. Шривастава Х. М. Трухильо Дж. J. Теория и приложения дробных дифференциальных уравнений2006204Амстердам, НидерландыElsevier ScienceNorth-Holland Mathematics StudiesMR22180734 Аббас С. Бенчохра М. Н’Гереката Г. M.Advanced Fractional Differential and Integral Equations2015New York, NY, USANova Science PublishersMR33095825 УламС. Сборник математических задач, 1968 г., Нью-Йорк, США, Interscience PublishersMR01201276 Хайерс Д. H. Об устойчивости линейного функционального уравнения. Proceedings of the National Academy of Sciences of the United States of America. РассиасТ. М. Об устойчивости линейного отображения в банаховых пространствах Proceedings of the American Mathematical Society197872229730010.2307/2042795MR5073278 Хайерс Д. Х.ИсакГ.РассиасТ. М. Устойчивость функциональных уравнений со многими переменными 1998Биркхойзер10.1007/978-1-4612-1790-9MR16398019 JungS.-M.Hyers-Ulam-Rassias Устойчивость функциональных уравнений в математическом анализе 2001 г. 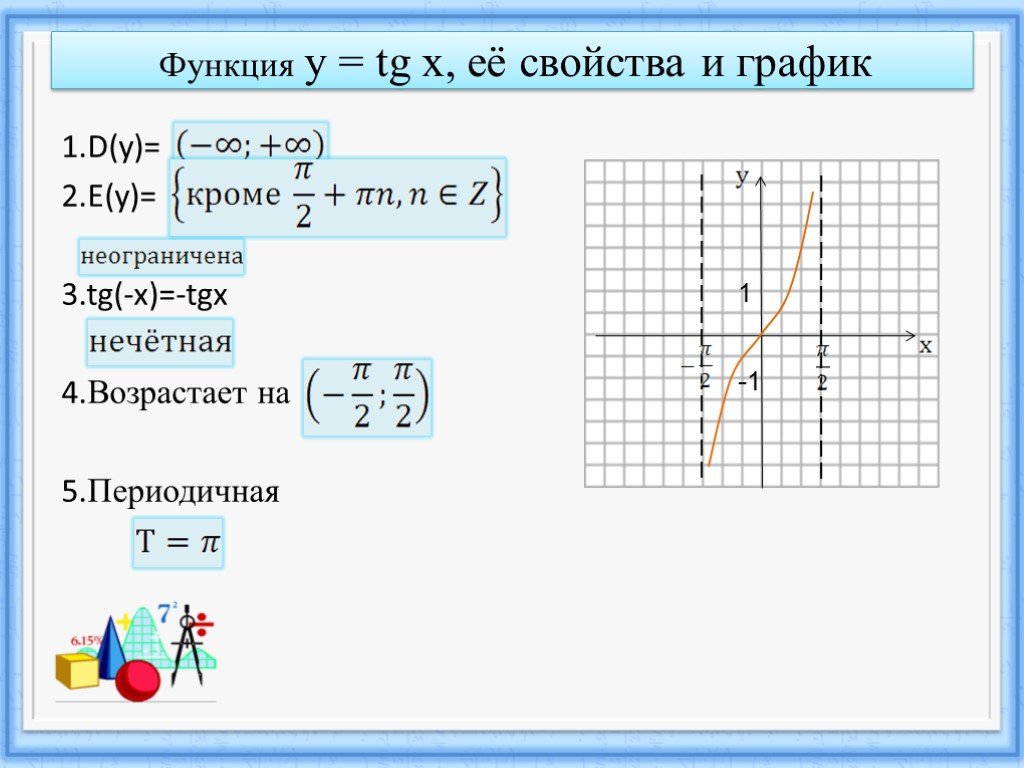Палм-Харбор, Флорида, СШАHadronic PressMR184118210 Бота-БоричануМ. F.PetruselA.Ulam-Hyers Устойчивость для операторных уравнений и включенийAnalele Universitatii “Al. И. Куза» Яссы201157657411 ПетруТ. P.PetruşelA.YaoJ.-C.Ulam-Hyers Устойчивость операторных уравнений и включений через несамостоятельные операторыTaiwanese Journal of Mathematics201115521952212MR28804002-s2.0-8005335729012 РусИ. А. Устойчивость обыкновенных дифференциальных уравнений по УламуStudia Universitatis Babeş-Bolyai, Series Mathematica2009412513313 РусИ. A. Замечания об устойчивости по Уламу операторных уравнений. Теория неподвижной точки2009102305320MR2564 КастроЛ. П.Рамос А. Устойчивость Хайерса-Улама-Рассиаса для класса интегральных уравнений ВольтерраBanach Journal of Mathematical Analysis20093364315 Юнг С.-М. Подход с фиксированной точкой к устойчивости интегрального уравнения Вольтерра. Теория фиксированной точки и ее приложения.16 JungS.-M.Hyers-Ulam-Rassias Устойчивость функциональных уравнений в нелинейном анализе2011New York, NY, USASpringerMR279077317 Батцер П.