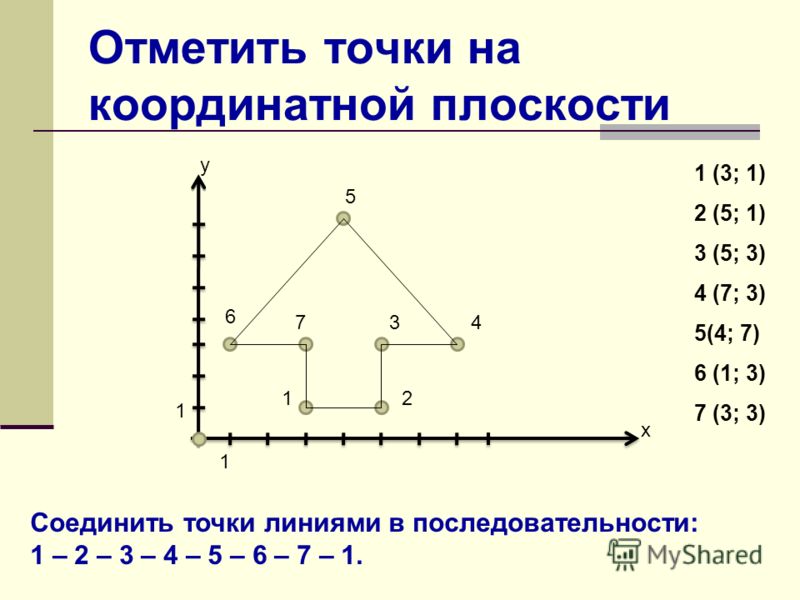
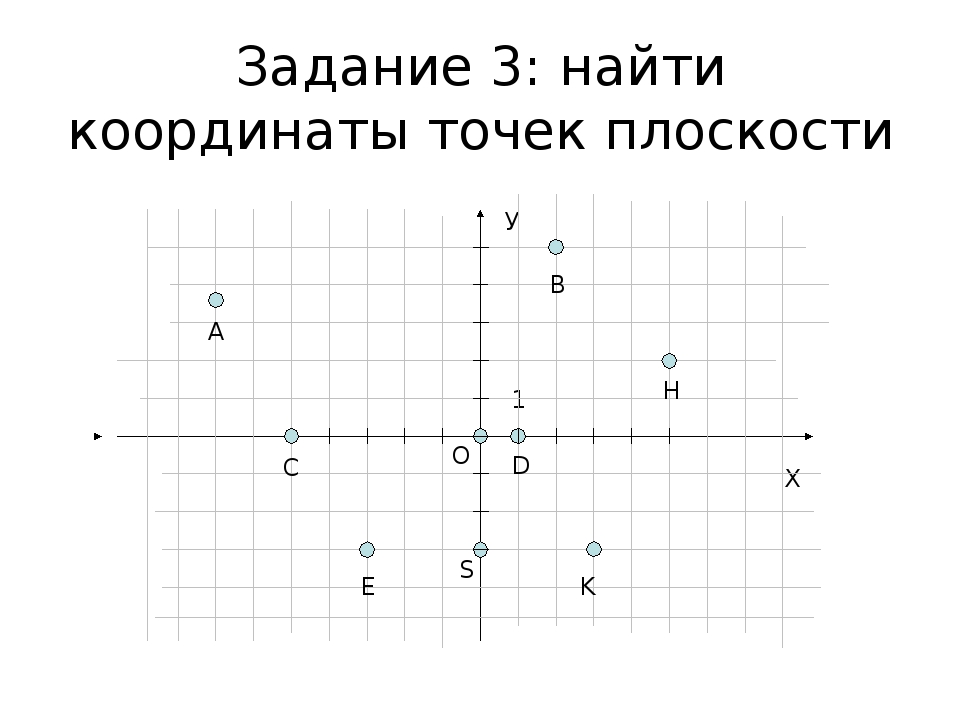
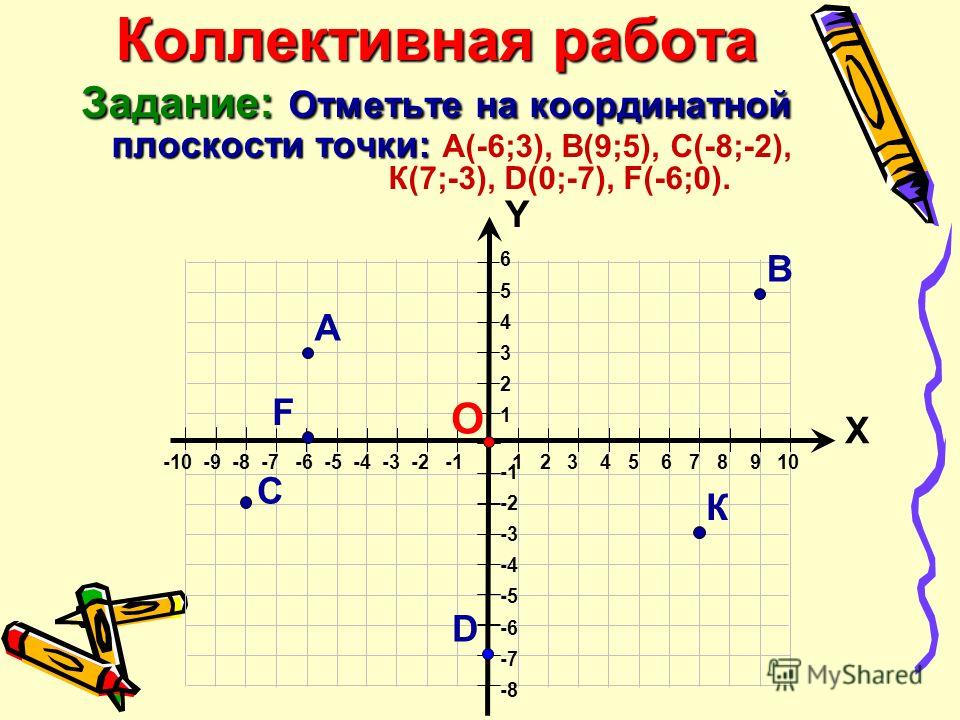
Как отметить точку на координатной плоскости?
Содержание
Как мы уже знаем, положение точки на плоскости задаётся координатами в виде 2 чисел $(x,y)$
Пример:
Отметим точку с координатами $(\color{#3D68EB}{2}, \color{#4DC46D}{4})$.
Координата $\color{#3D68EB}x$ в данном случае равна $\color{#3D68EB}2$
Координата $\color{#4DC46D}y$ равна $\color{#4DC46D}4$
Сначала отложим вправо $(\color{#3D68EB}{2}$ единичных отрезка на оси $\color{#3D68EB}{x}$
Затем отложим $\color{#4DC46D}{4}$ единичных отрезка вверх по оси $\color{#4DC46D}{y}$ и отмечаем нашу точку.
{
"questions": [{
"widgets": {
"graph": {
"type": "graph",
"func": "points",
"settings": { "cells": 12 },
"answer": ["0#1"]
}
},
"hints": ["Координата $x$ равна 0, значит точка будет лежать на оси $y$ (оси ординат).","Координата $y$ равна 1, значит поднимаем точку на 1 ед.
отрезок от начала координат, на цифру 1 на оси $y$."],
"content": "Отметьте точку c координатами $(0,1)$ [[graph]]"
}, {
"widgets": {
"graph": {
"type": "graph",
"func": "points",
"settings": { "cells": 12 },
"answer": ["1#1"]
}
},
"content": "Отметьте точку c координатами $(1,1)$ [[graph]]"
}, {
"widgets": {
"graph": {
"type":"graph",
"func": "points",
"settings": { "cells": 12 },
"answer": ["1#0"]
}
},
"hints": ["Координата $x$ равна 1, двигаем точку на цифру 1 на горизонтальной оси $x$ (на оси абсцисс).","Координата $y$ равна 0, значит точка будет лежать на оси абсцисс."],
"content": "Отметьте точку c координатами $(1,0)$ [[graph]]"
}]
}
5
Оценить урок
Поделиться уроком →
Что можно улучшить?
Изложение материала
Непонятное объяснение
Урок неполный, не хватает информации
Урок перегружен, слишком много информации
Тесты плохого качества
Тестов недостаточно
Тестов слишком много
Тесты слишком легкие
Тесты слишком сложные
Изображения
Изображения плохого качества
Изображений недостаточно
Изображений слишком много
Другое
Войдите, чтобы оценивать уроки
Что нужно исправить?
Спасибо, что помогаете нам стать лучше!
Проверим знания по теме?
Отметьте точки по координатам в первой четверти
Комментарии
Координатная плоскость | это.
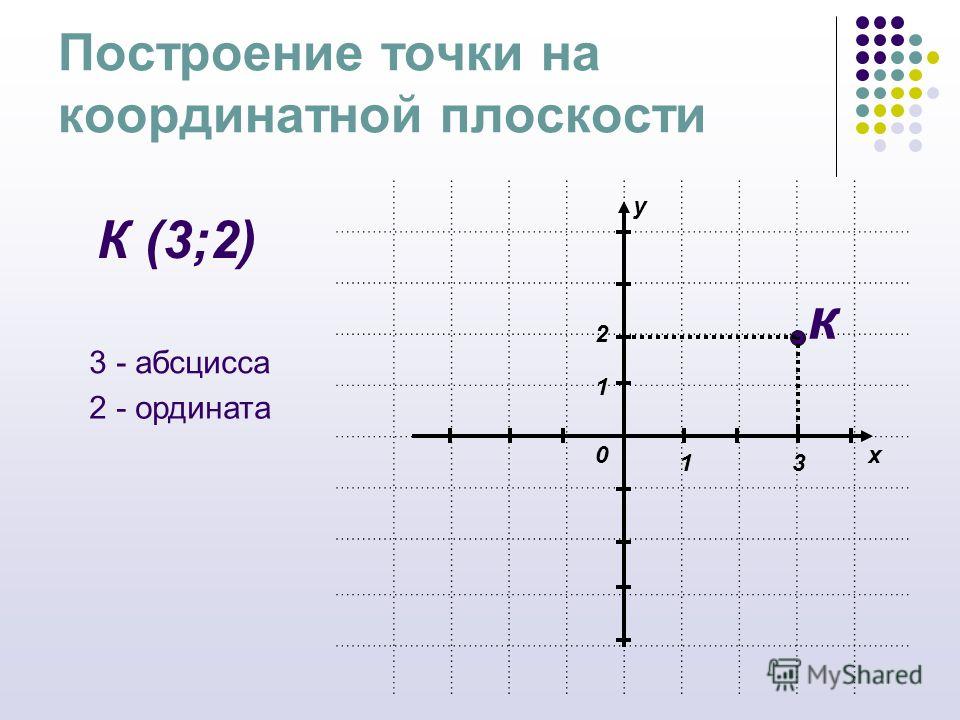.. Что такое Координатная плоскость?Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.
Содержание
|
Прямоугольная система координат на плоскости
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см.
Рис. 1).
Рис. 1
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ.
Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Рис. 2
Положение точки A в пространстве определяется тремя координатами x, y и z.
Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Орты
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются i j k или exeyez . При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:
- [i j]=k ;
- [j k]=i ;
- [k i]=j .
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См. также
Ссылки
Точки построения и координатная плоскость
Раздел 1.1 Нанесение точек и координатной плоскости
Координатная плоскость — мощный инструмент для визуализации математических концепций. В этом разделе мы обсудим связь между написанными точками и их положением на плоскости.Определение 1.1.1.
Координатная плоскость показана на изображении ниже.
Факт 1.1.2. Точки построения.
Очки записываются в виде двух чисел, разделенных запятой и заключенных в круглые скобки. Для построения точки \((a,b)\text{,}\) первое число — это \(x\)-координата, которая говорит вам, как двигаться слева направо по \(x\)- оси, а второе число — это координата \(y\), которая говорит вам, как перемещаться вверх и вниз по оси \(y\).
Иногда мы также называем эти упорядоченные пары, так как это пара чисел и порядок, в котором мы их записываем.
Пример 1.1.3.
Предположим, мы хотим нанести точку \((3,-5)\text{.}\) Мы видим, что координата \(x\) равна \(3\text{,}\), что означает, что мы хотим перейти к \(3\) по оси \(x\). Оттуда мы видим, что координата \(y\) равна \(-5\text{,}\), поэтому мы спустимся на 5 (поскольку она отрицательная).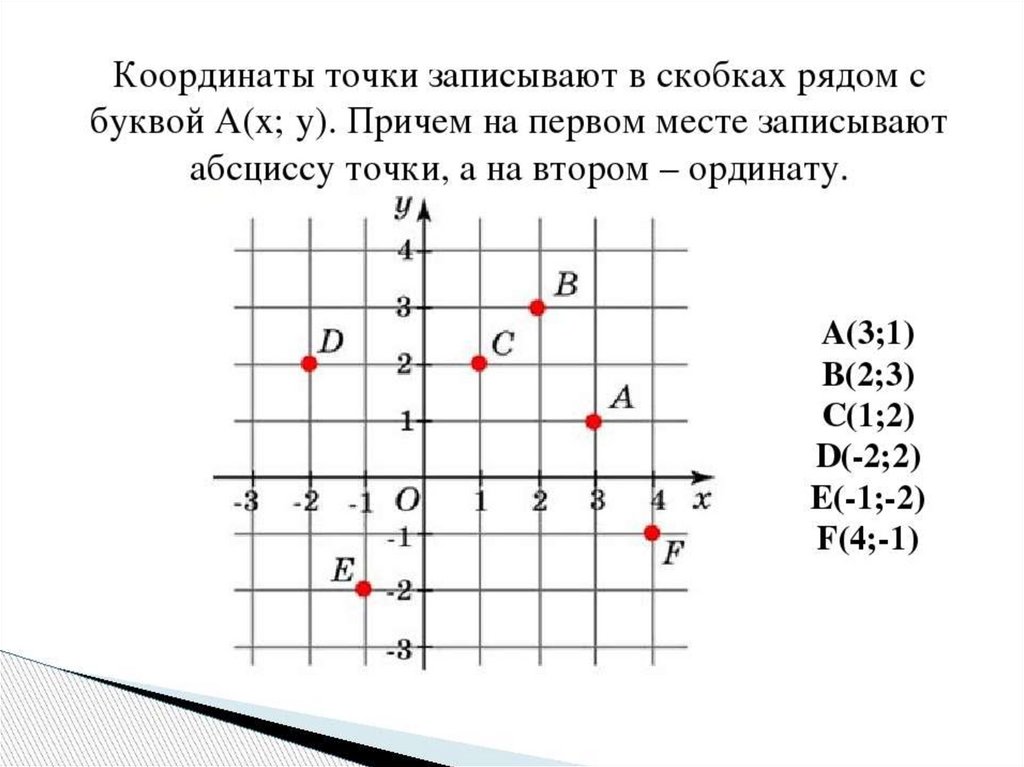
КПП 1.1.4.
Постройте точку \((-2,0)\text{.}\)
Ответ.
Раствор.
Мы видим, что координата \(x\) равна \(-2\text{,}\), что означает, что мы хотим перейти к \(-2\) по оси \(x\) (которая влево, так как оно отрицательное). Отсюда мы видим, что координата \(y\) равна \(0\text{,}\), что означает, что нам вообще не нужно двигаться вверх или вниз. Эта точка находится на оси \(х\). После того, как мы сделали оба этих движения, мы приземляемся в конечном пункте назначения, показанном на графике ниже.
Пример 1.1.5.
Предположим, мы хотим вычислить координаты точки, изображенной ниже:
Чтобы вычислить координату \(x\), мы проследим вверх/вниз по оси \(x\), чтобы увидеть, к какому числу мы приземлимся. В этом случае мы прослеживаем вниз и видим, что мы находимся в точке \(-5\text{,}\), так что это наша координата \(x\).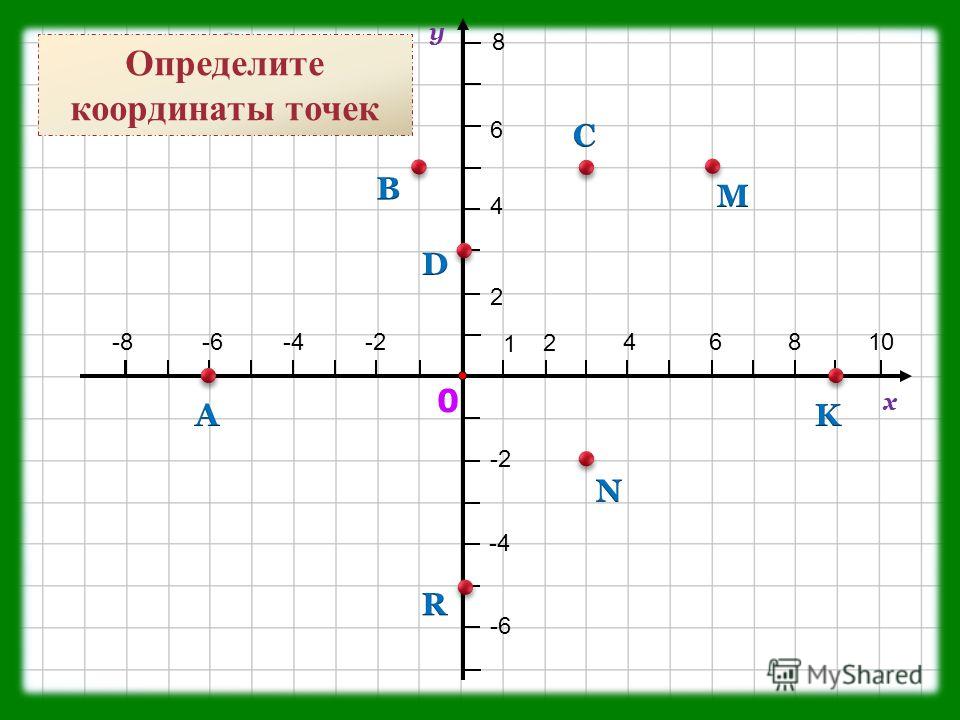
Чтобы вычислить \(y\)-координату, мы проследим слева/справа от \(y\)-оси, чтобы увидеть, к какому числу мы приземлимся. В этом случае мы проследим вправо и увидим, что мы находимся в точке \(1\text{,}\), так что это наша координата \(y\). Теперь, когда у нас есть обе координаты, мы можем собрать их вместе для нашего окончательного ответа: \((-5,1)\text{.}\)
КПП 1.1.6.
Определить координаты точки на графике ниже:
Ответ.
\((3,7)\)
Чтобы вычислить координату \(x\), мы проследим вверх/вниз по оси \(x\), чтобы увидеть, к какому числу мы приземлимся. В этом случае мы прослеживаем вниз и видим, что находимся в точке \(3\text{,}\), так что это наша координата \(x\). Чтобы вычислить \(y\)-координату, мы проследим слева/справа от \(y\)-оси, чтобы увидеть, к какому числу мы приземлимся. В этом случае мы проследим вправо и увидим, что мы находимся в точке \(7\text{,}\), так что это наша координата \(y\).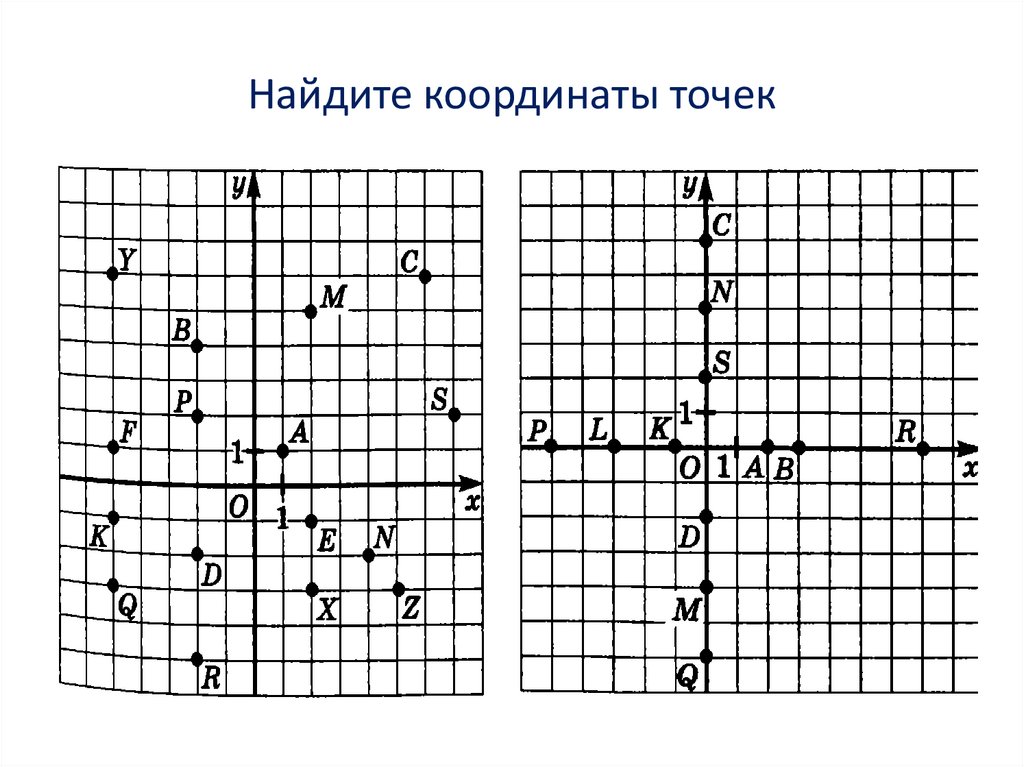
Теперь, когда у нас есть обе координаты, мы можем собрать их вместе для нашего окончательного ответа: \((3,7)\text{.}\)
Координатная плоскость Примечания — МАТЕМАТИЧЕСКИЕ ПОТРЕБНОСТИ
Цели:
- Определить словарь, связанный с координатной плоскостью (упорядоченная пара, начало координат, квадрант, ось x, ось y, координата x и координата y )
- Определение квадранта, в котором находится точка
- Нанесение точек на координатную плоскость
- Определение упорядоченной пары точек на координатной плоскости
Что такое координатная плоскость?
Координатная плоскость — это двумерная числовая линия. Горизонтальная линия – это ось x, а вертикальная линия – ось y. Начало координат — это точка пересечения осей x и y. Эта точка равна (0,0).
Координатная плоскость разбита на 4 квадранта: квадрант I, квадрант II, квадрант III и квадрант IV.
Точка, лежащая в квадранте I, будет иметь положительные координаты x и y. Точка, лежащая в квадранте II, будет иметь отрицательную координату x и положительную координату y. Точка, расположенная в квадранте III, будет иметь отрицательные координаты x и y. Точка, расположенная в квадранте IV, будет иметь положительную координату x и отрицательную координату y. |
Нам также нужно подумать о точке, которая попадает на ось X или ось Y. В каком квадранте должны лежать эти точки? Ответ состоит в том, что эти точки НЕ лежат ни в одном квадранте.
Мы можем записать точку в виде упорядоченной пары. Упорядоченная пара записывается как (x, y), где координата x записывается первой, а координата y записывается второй. Например, если у нас есть координата x, равная 2, и координата y, равная 4, то упорядоченная пара будет записана как (2,4). Эта точка находится в квадранте I, так как координаты x и y положительны. Давайте рассмотрим еще несколько примеров ниже!
Пример #1Ваша очередь! Учитывая приведенные ниже точки, определите, в каком квадранте находится каждая точка:
Нажмите ЗДЕСЬ, чтобы проверить свой ответ.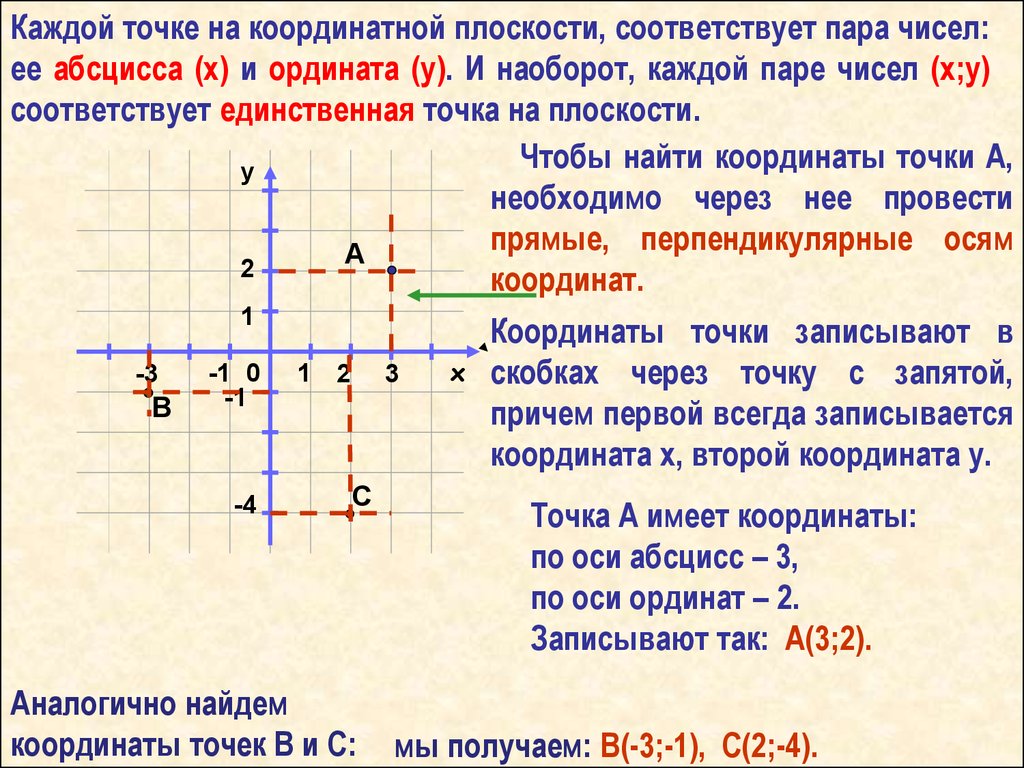
Нанесение точек на координатную плоскость путем «бегания», затем «возрастания».
Как было сказано ранее, мы всегда начинаем с координаты x, поскольку точки записываются как (x,y). Координата x говорит нам, сколько «бежать» влево или вправо. Координата Y говорит нам, насколько «подниматься» вверх или вниз.
Давайте рассмотрим пример ниже:
Пример #2Ваша очередь! Нанесите на координатную плоскость следующие точки:
Нажмите ЗДЕСЬ, чтобы проверить свой ответ.
Как написать упорядоченную пару по графу Чтобы написать упорядоченную пару, нам всегда нужно начинать с начала координат. Помните, что начало координат находится в (0,0). Следовательно, мы начнем с (0,0) и посмотрим, насколько точка находится левее или правее от начала координат. Это будет наша координата x. Далее мы посмотрим, насколько точка находится вверх или вниз от начала координат.