определение понятия и подробное решение примера
Математика
25829 1463 1 0
Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.
Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.
Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.
Содержание:
- Определение точки разрыва
- Точки разрыва первого и второго рода
- Как найти точки разрыва функции
- Видео
Определение точки разрыва
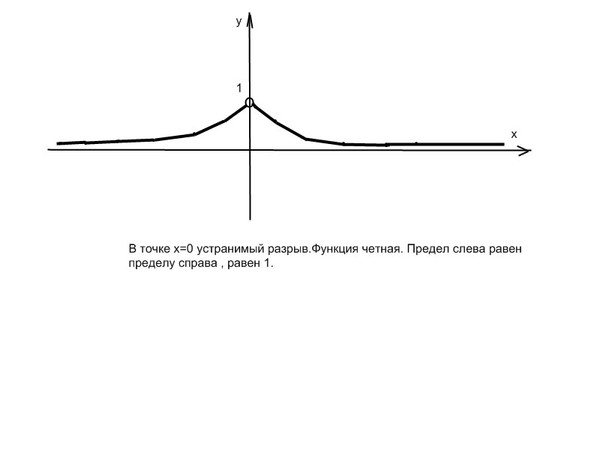
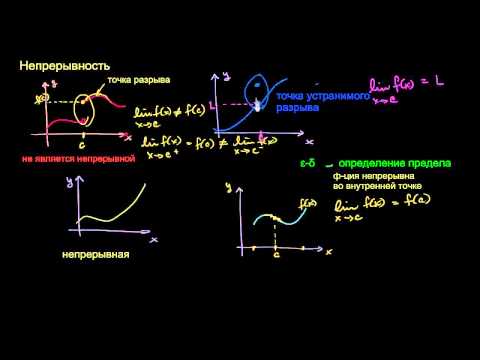
Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:
Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:
Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:
- первый род;
- второй род.
Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.
К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных.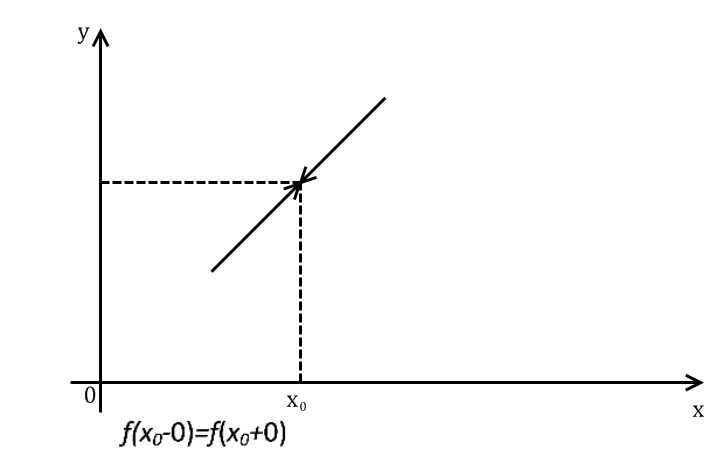 Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.
Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.
Классификация точек разрыва.
Точки разрыва первого и второго рода
Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:
- Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.
-
Точки конечного разрыва первого рода — скачок функции. Пределы могут быть вычислены, но в то же время не равны друг другу, и поэтому доопределение уравнения невозможно.
 Разница первого и второго называется скачком.
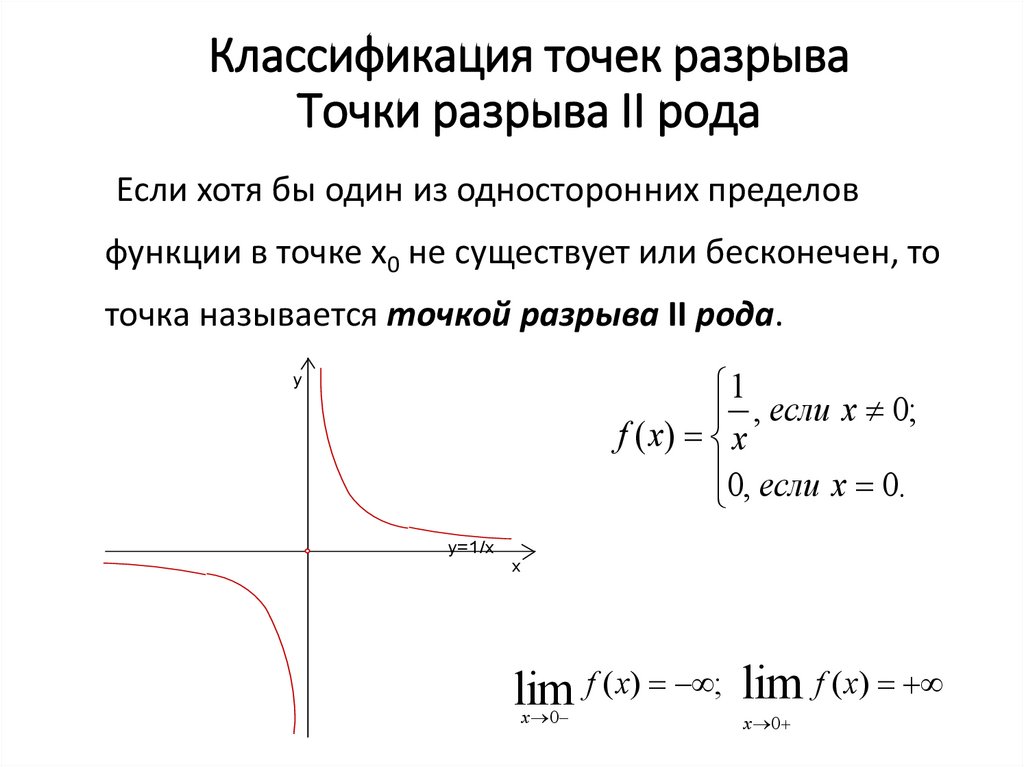
Разница первого и второго называется скачком. - Точки разрыва второго рода отличаются тем, что вычисляемые пределы не просто различны по значению, но результат хотя бы одного из них обязательно должен быть равен бесконечности или несуществующему числу.
Как найти точки разрыва функции
Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.
Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² — 25)/(y — 5):
- Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель.
 Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва. - Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
- Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.

Видео
Из этого видео вы узнаете, как исследовать непрерывность функции.
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Определение 1Функция f(x) является непрерывной в точке x0, если предел слева равен пределу справа и совпадает со значением функции в точке x0, т.е.: limx→x0-0f(x)=limx→x0+0f(x)=f(x0)
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Пример 1Дана функция f(x)=16(x-8)2-8. Необходимо доказать ее непрерывность в точке х0= 2.
Решение
В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов хn, сводящуюся к х0 =2·(хn<2). Например, такой последовательностью может быть:
Чтобы это сделать, используем последовательность аргументов хn, сводящуюся к х0 =2·(хn<2). Например, такой последовательностью может быть:
-2, 0, 1, 112, 134, 178, 11516,…, 110231024,…→2
Соответствующая последовательность значений функций выглядит так:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8.667; 2.667; 0.167; -0.958; -1.489; -1.747; -1.874;…;-1.998;…→-2
на чертеже они обозначены зеленым цветом.
Достаточно очевидно, что такая последовательность сводится к -2, значит limx→2-016(x-8)2-8=-2.
Определим существование предела справа: используем последовательность аргументов хn, сводящуюся к х0= 2 (хn>2). Например, такой последовательностью может быть:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Соответствующая последовательность функций:
f(6); f(4); f(3); f212; f214; f218; f2116;…; f211024;…==-7.333; -5.333; -3.833; -2.958; -2.489; -2.247; -2.247; -2.124;…; -2.001;…→-2
на рисунке обозначена синим цветом.
И эта последовательность сводится к -2, тогда limx→2+016(x-8)2-8=-2.
Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции f(x)=16x-82-8 в точке х0= 2, при этом limx→216(x-8)2-8=-2.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
limx→2-0f(x)=limx→2+0f(x)=f(2)=16(2-8)2-8=-2 что свидетельствует о непрерывности заданной функции в заданной точке.
Покажем графически:
Ответ: Непрерывность функции f(x)=16(x-8)2-8 в заданной части доказано.
Устранимый разрыв первого рода
Определение 2Функция имеет устранимый разрыв первого рода в точке х0, когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
limx→x0-0f(x)=limx→x0+0f(x)≠f(x0)
Пример 2Задана функция f(x)=x2-25x-5. Необходимо определить точки ее разрыва и определить их тип.
Решение
Сначала обозначим область определения функции: D(f(x))⇔Dx2-25x-5⇔x-5≠0⇔x∈(-∞; 5)∪(5; +∞)
В заданной функции точкой разрыва может служить только граничная точка области определения, т. е. х0= 5. Исследуем функцию на непрерывность в этой точке.
е. х0= 5. Исследуем функцию на непрерывность в этой точке.
Выражение x2-25x-5 упростим: x2-25x-5=(x-5)(x+5)x-5=x+5.
Определим пределы справа и слева. Поскольку функция g(x)=x+5 является непрерывной при любом действительном x, тогда:
limx→5-0(x+5)=5+5=10limx→5+0(x+5)=5+5=10
Ответ: пределы справа и слева являются равными, а заданная функция в точке х0= 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Определение 3Функция имеет неустранимый разрыв первого рода в точке х0, когда пределы справа и слева не являются равными, т.е.: limx→x0-0f(x)≠limx→x0+0f(x). Точка х0 здесь – точка скачка функции.
Пример 3
Задана кусочно-непрерывная функция f(x)=x+4, x<-1,x2+2, -1≤x<12x, x≥1. Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.
Решение
Разрывы данной функции могут быть лишь в точке х0=-1 или в точке х0=1.
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
- слева от точки х0=-1 заданная функция есть f(x)=x+4, тогда в силу непрерывности линейной функции: limx→-1-0f(x)=limx→-1-0(x+4)=-1+4=3;
- непосредственно в точке х0=-1 функция принимает вид: f(x)=x2+2, тогда: f(-1)=(-1)2+2=3;
- на промежутке (-1; 1) заданная функция есть: f(x)=x2+2. Опираясь на свойство непрерывности квадратичной функции, имеем: limx→-1+0f(x)=limx→-1+0(x2+2)=(-1)2+2=3limx→1-0f(x)=limx→1-0(x2+2)=(1)2+2=3
- в точке х0=-1 функция имеет вид: f(x)=2x и f(1)=2·1=2.
- справа от точки х0 заданная функция есть f(x)=2x. В силу непрерывности линейной функции: limx→1+0f(x)=limx→1+0(2x)=2·1=2
Ответ: в конечном счете мы получили:
- limx→-1-0f(x)=limx→-1+0f(x)=f(-1)=3 — это означает, что в точке х0=-1 заданная кусочная функция непрерывна;
- limx→-1-0f(x)=3, limx→1+0f(x)=2 — таким образом, в точке х0=1 определён неустранимый разрыв первого рода (скачок).

Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Определение 4Функция имеет разрыв второго рода в точке х0, когда какой-либо из пределов слева limx→x0-0f(x) или справа limx→x0+0f(x) не существует или бесконечен.
Пример 4Задана функция f(x)=1x. Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.
Решение
Запишем область определения функции: x∈(-∞; 0)∪(0; +∞).
Найдем пределы справа и слева от точки х0= 0.
Зададим произвольную последовательность значений аргумента, сходящуюся к х0 слева. К примеру:
-8; -4; -2; -1; -12; -14;…; -11024;…
Ей соответствует последовательность значений функции:
f(-8); f(-4); f(-2); f(-1); f-12; f-14;…; f-11024;…==-18;-14; -12; -1; -2; -4;…; -1024;…
Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда limx→0-0f(x)=limx→0-01x=-∞.
Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к х0 справа. К примеру: 8; 4; 2; 1; 12; 14;…; 11024;…, и ей соответствует последовательность значений функции:
f(8); f(4); f(2); f(1); f12; f14;…; f11024;…==18; 14; 12; 1; 2; 4;…; 1024;…
Эта последовательность — бесконечно большая положительная, а значит limx→0+0f(x)=limx→0+01x=+∞.
Ответ: точка х0= 0 — точка разрыва функции второго рода.
Проиллюстрируем:
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.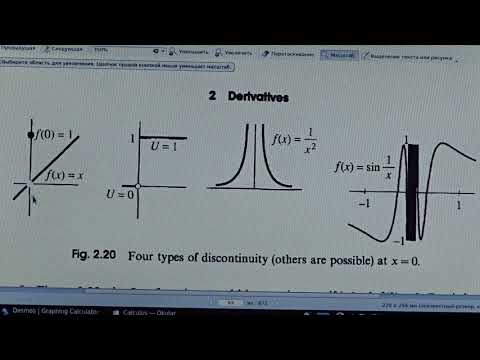 Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
2.2.2. Классификация точек разрыва
Доказательство |
|
|
|
|
| |
Найдем |
|
|
|
|
|
|
lim F(x) = lim (f (x) + g(x))= lim | f (x) + lim g(x) = f (x0 ) + g(x0 ) = F(x0 ) | |||||
x→х0 | x→х0 |
|
| x→х0 | x→x0 |
|
функция F(x) = f (x) + g(x) | ― непрерывная в точке x0 . | |||||
теоремы для произведения и частного. |
|
| ||||
Теорема 2.2.1 |
|
|
|
|
|
|
Если функция g(x) | непрерывна в точке x0 , а функция | f (u) ― в точке u0 = g(x0 ) , | ||||
то сложная функция f (g(x)) непрерывна в точке x0 . |
| |||||
Доказательство |
|
|
|
|
| |
|
| lim f (g(x)) = lim | f (u) = f (u0 ) = f (g(u0 )) . | |||
| x→х0 |
| u→u0 |
|
| |
Определение 2. 2.4 2.4 |
|
|
|
|
| |
Функция y = f (x) | называется непрерывной слева (справа) в точке x0 , если она | |||||
определена в точке x0 | и | lim | f (x) = f (x0 ) (или lim | f (x) = f (x0 ) ). | ||
|
| x→х0 −0 |
| x→х0 +0 |
| |
|
| |||||
Если функция | f (x) | не является непрерывной в точке x0 , то говорят, что она терпит в | ||||
этой точке разрыв.
Чтобы классифицировать точки разрыва функции дадим определение непрерывной в точке функции в развернутом виде.
Функция f (x) называется непрерывной в точке x0 , если:
1)f (x) определена в некоторой окрестности точки x0 ;Устранимый разрыв
2)существуют конечные односторонние пределы
lim f (x) = f (x0 − 0) и | lim f (x) = f (x0 + 0) ; | |
x→x0 −0 |
| x→x0 +0 |
3) эти пределы равны значению функции в точке x0 , т. | ||
lim | f (x) = lim | f (x) = f (x0 ) . |
x→х0 −0 | x→х0 +0 | |
Если в точке x0 хотя бы одно из условий непрерывности нарушается, точка x0 является точкой разрыва данной функции.
1. Устранимый разрыв
Пусть существуют конечные односторонние пределы:
lim f (x) = f (x0 − 0) и | lim | f (x) = f (x0 + 0) . |
x→x0 −0 | x→x0 +0 |
|
Если А= f (x0 − 0) = f (x0 + 0) ≠ f (x0 ) , то точка | x0 называется точкой устранимого | |
разрыва (рис. 2.1).
у
А= f (хо- 0) =
= f (хо+ 0)
|
|
| х |
0 | хо | ||
| Рис. |
| |
23
Для того, чтобы устранить разрыв, нужно доопределить (или переопределить) функцию в самой точке x0 , т.е. ввести новую функцию
f (x), если х ≠ x0 | . | ||
у = |
| х = x0 | |
А, | если |
| |
2. Неустранимый разрыв первого рода |
|
|
|
Пусть существуют конечные односторонние пределы: |
| ||
lim f (x) = f (x0 − 0) | и | lim f (x) = f (x0 + 0) . | |
x→x0 −0 | x→x0 +0 |
| |
Если f (x0 − 0) ≠ f (x0 + 0) , то точка x0 | называется точкой неустранимого разрыва | ||
первого рода (рис. 2.2). Величина δ = f (x0 + 0) − f (x0 − 0) называется скачком функции f (x) в точке x0 .
2.2). Величина δ = f (x0 + 0) − f (x0 − 0) называется скачком функции f (x) в точке x0 .
у
f (хо+ 0) f (хо- 0)
0 | хо | х |
| Рис. 2.2. |
|
3. Неустранимый разрыв второго рода
Если в точке x0 хотя бы один из односторонних пределов не существует или равен
∞, то точка x0 называется точкой неустранимого разрыва второго рода (рис. 2.3).
у
|
| 0 |
|
| хо |
|
| х |
|
|
|
|
| ||||
|
|
|
|
| ||||
|
|
|
|
|
| |||
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| |
|
|
|
| Рис. |
|
| ||
Задача 2.2.1 |
|
|
|
|
|
|
|
|
Исследовать функцию |
| x −1, | если 0 ≤ х < 3, | на непрерывность: | ||||
f (x) = | 3 − х, | если | 3 ≤ х ≤ 4. | |||||
|
|
|
|
| ||||
Решение
Изобразим график этой функции (рис. 2.4).
у |
|
2 |
|
0 | 3 4 |
— 1 | х |
| |
| Рис. |
Для функции f (x) точка х = 3 является точкой разрыва первого рода, так как
24
lim | f (x) = | lim | (x | −1) | = 2 |
|
x→3−0 |
| x→3−0 |
|
|
| разрыв первого рода, скачок δ = 2 . |
lim | f (x) = | lim | (3 |
|
| |
− x) = 0 |
| |||||
x→3+0 |
| x→3+0 |
|
|
| |
Следует отметить, что в точке х = 0 функция непрерывна справа, так как
| lim | f (x) = | lim (x −1) = −1 = f (0) . | ||
| x→0+0 |
|
| x→0+0 | |
А в точке х = 4 функция непрерывна слева, так как | |||||
| lim | f (x) = | lim (3 − x) = −1 = f (4) . | ||
| x→4−0 |
|
| x→4−0 | |
Задача 2.2.2 |
|
|
|
|
|
Исследовать функцию | y = | sin x | на непрерывность. | ||
| |||||
|
| x |
|
|
|
Решение
Функция f (х) не определена в точке x = 0 .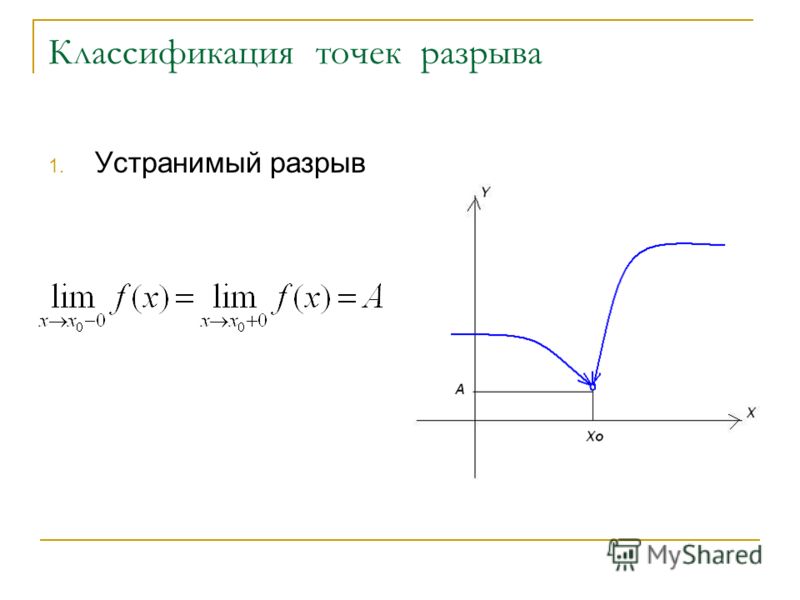 Эта точка является точкой устранимого разрыва, так как
Эта точка является точкой устранимого разрыва, так как
lim | sin x | = | lim | sin x | =1 . | |
x | x | |||||
x→0−0 |
| x→0+0 |
|
у
1
|
|
|
| 0 | х |
|
|
|
| Рис. 2.5. |
|
График функции | y = | sin x | изображен на рисунке 2.5. |
| |
|
| ||||
|
|
| x |
|
|
Доопределить функцию по непрерывности – это значит задать f (0) =1 , т.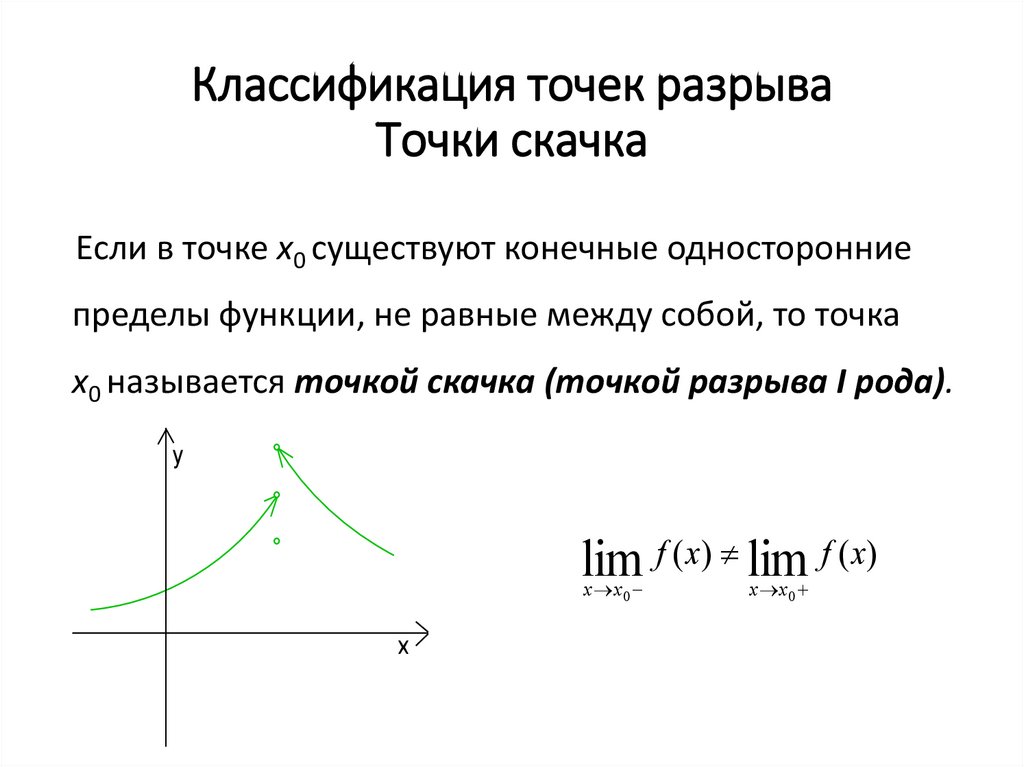 е. получить
е. получить
sin x | , x | ≠ 0 |
|
|
| |||
| x | x = 0 . | ||||||
функцию y = |
| , которая непрерывна в точке | ||||||
| x = 0 |
|
|
|
|
|
| |
1, |
|
|
|
|
|
| ||
Задача 2.2.3 |
|
|
|
|
|
|
|
|
Исследовать функцию y = sin | 1 | на непрерывность. |
|
|
| |||
|
|
|
| |||||
|
|
|
| x |
|
|
| |
Решение |
|
|
|
|
|
|
|
|
Точка x = 0 | является точкой разрыва второго рода, так как пределы lim sin | 1 | не | |||||
x→0±0 x
существуют.
у
Рис. 2.6.
25
Типы разрывов / разрывных функций
Содержание:
- Что такое разрывные функции?
- График разрывной функции
- Поиск разрывов
- Типы разрывов
- Основной разрыв (неустранимый)
- Бесконечный разрыв
- Прыжок (Шаг) Разрыв
- Колеблющийся разрыв
- Съемный (отверстие) разрыв
Разрывная функция — это функция, которая не является непрерывной в одной или нескольких точках. Большинство функций, как это ни удивительно, так или иначе разрывны [1].
Большинство функций, как это ни удивительно, так или иначе разрывны [1].
Быть «непрерывным в каждой точке» означает, что в каждой точке a:
- Функция существует в этой точке. Если вы можете вставить x-значение в свою функцию, и она вернет значение, в этот момент она будет непрерывной.
- Предел функции при переходе x в точку a существует. Другими словами, все значения функции, окружающие точку «а», приближаются к одному и тому же числу.
- И (1), и (2) равны.
В обозначениях мы можем записать это как:
На простом языке это означает, что функция проходит через каждую точку, и каждая точка близка к следующей: нет резких скачков (в отличие от разрывов скачков) . Когда вы рисуете график, вы можете рисовать функцию слева направо, не отрывая карандаша от бумаги.
Прерывистая функция — это функция, для которой вы должны оторвать карандаш от бумаги хотя бы один раз во время рисования.
Прерывистый прыжок.
Графически разрывная функция будет иметь либо дыру — одно пятно или несколько пятен, где функция не определена, — либо скачок, когда значение f(x) быстро меняется («скачет») по мере перехода от одного места в другое, бесконечно близкое.
Вертикальная асимптота. Функция приблизится к этой линии, но никогда не коснется ее.
У него также может быть асимптота, линия, где по мере приближения функция стремится к бесконечности. Функция никогда не сливается с этой линией, хотя может приближаться бесконечно близко.
Вернуться к началу
Если вашу функцию можно записать в виде рациональной функции (т. е. в виде дроби), любые значения x, при которых знаменатель стремится к нулю, будут разрывами вашей функции. Это места, где ваша функция не определена из-за деления на ноль.
Если у вас есть кусочная функция, точка, где заканчивается одна часть и другая часть, также является хорошим местом для проверки разрыва.
В противном случае самый простой способ найти неоднородности в вашей функции — построить ее график. Обратите внимание на любые дыры, асимптоты или скачки. Все они представляют собой разрывы, и достаточно одного разрыва, чтобы сделать вашу функцию разрывной.
Типы разрывов.
Классификация типов разрывов сложнее, чем кажется, из-за того, что разные авторы классифицируют их по-разному. Например:
- Некоторые авторы упрощают типы до двух общих терминов: съемный (отверстия) и неустранимый (скачки, бесконечные и существенные разрывы не могут быть удалены, поскольку они слишком далеко друг от друга или дикие в своем поведении). .
- Существенные разрывы (которые резко прыгают, когда функция приближается к пределу) иногда называют «неустранимый разрыв», исключающий скачки и бесконечность из определения неустранимого.
- Некоторые авторы также включают «смешанные» разрывы в качестве типа разрыва, где разрыв представляет собой комбинацию более чем одного типа.

Вывод: не существует «единой» системы классификации типов разрывов, с которой все согласны. Какую систему вы используете, будет зависеть от используемого вами текста и предпочтений вашего преподавателя. Следующий список следует воспринимать как руководство, а не как установленную систему классификации камней.
Вернуться к началу
- Существенный разрыв
- Существенная сингулярность
Существенный разрыв (также называемый вторым типом или неустранимым разрывом) — это разрыв, который резко скачет по мере приближения к пределу. Это затрудняет удаление разрыва (отсюда альтернативное название «неустранимый» разрыв) и выполнение каких-либо вычислений над функцией.
Существенный разрыв считается «наихудшим» из видов разрыва. Это потому, что поведение вокруг пределов должно быть , но ненормально, невозможно вычислить, а иногда просто безумно. На очень коротком расстоянии может быть много разрывов прыжков, или вы вообще не сможете зафиксировать какое-либо поведение. Графические калькуляторы могут не помочь (из-за аномального поведения), и вам, возможно, придется прибегнуть к ручке и бумаге, чтобы понять график.
Графические калькуляторы могут не помочь (из-за аномального поведения), и вам, возможно, придется прибегнуть к ручке и бумаге, чтобы понять график.
Подтипы
Существенные разрывы (т. е. неустранимые разрывы) могут быть далее разбиты на два типа разрывов в зависимости от того, являются ли односторонние пределы ограниченными или неограниченными (Bauldry, 2011):
- Ограниченный : колебательный разрыв . Паттерн вблизи предела подпрыгивает вверх и вниз, никогда не формируя паттерн, который можно было бы зафиксировать.
- Неограниченный : бесконечный разрыв . Пределы существуют, но они бесконечны и становятся больше по мере приближения к пределу.
Простые (устранимые) разрывы также можно разделить на два подтипа:
- Устранимый разрыв имеет зазор, который можно легко заполнить, поскольку предел одинаков с обеих сторон.
- Разрыв прыжка в точке имеет ограничения, которые существуют, но они разные по обе стороны разрыва.

В любом из этих двух случаев можно количественно определить предел и устранить разрыв; Существенный разрыв не может быть определен количественно. Обратите внимание, что разрывы скачков, которые происходят на кривой , не могут быть удалены и поэтому необходимы (Rohde, 2012).
Вернуться к началу
Существенная сингулярность — это плохо работающая «дыра» в неаналитической сложной функции, которую нельзя удалить/починить. Другими словами, нет простого способа превратить функцию с существенной особенностью в непрерывную и дифференцируемую.
Этот тип сингулярности подобен своему вещественному аналогу: существенной прерывности. С этими типами сингулярностей/разрывов трудно иметь дело из-за их патологического поведения в определенный момент.
Существенные особенности являются одним из трех типов особенностей в комплексном анализе. Два других — это полюса (изолированные сингулярности) и устранимые сингулярности, обе из которых ведут себя относительно хорошо. Существенных особенностей классифицируется по исключению: если не полюс и не устранимая сингулярность, то существенная.
Существенных особенностей классифицируется по исключению: если не полюс и не устранимая сингулярность, то существенная.
Пример функции с существенной особенностью
Функция exp (1/z) имеет существенную особенность при z = 0, где функция не определена (из-за деления на ноль). На данный момент функция не имеет предела, поэтому убрать сингулярность невозможно.
График оттенка-яркости exp(1/z) с центром в основной сингулярности в нуле. Функция ведет себя по-разному в зависимости от того, с какой стороны вы приближаетесь к функции. Кредит: Функтор Салат | Викисклад./>
В терминах ряда Лорана
Существенные разрывы можно определить, глядя на поведение ряда Лорана, представляющего окрестности вокруг сингулярности. В частности, особенность существенна, если главная часть ряда Лорана имеет бесконечно много ненулевых членов (Крамер, nd).
Основная часть серии Laurent.
В начало
Бесконечный разрыв имеет один или несколько бесконечных пределов — значения, которые становятся все больше и больше по мере приближения к разрыву в функции. Бесконечный разрыв — это подтип существенных разрывов, которые представляют собой широкий набор плохо ведущих себя разрывов, которые нельзя удалить.
Бесконечный разрыв — это подтип существенных разрывов, которые представляют собой широкий набор плохо ведущих себя разрывов, которые нельзя удалить.
Типы разрывов. Бесконечный разрыв справа имеет значения функции, которые продолжают стремиться к бесконечности.
Эта функция стремится к бесконечности только при x = 0 с одной стороны (справа), но она по-прежнему классифицируется как бесконечный разрыв.
Важно отметить, что только одна сторона должна стремиться к ±бесконечности, чтобы разрыв был классифицирован как бесконечный. Одна сторона может достигать определенного значения функции или быть неопределенной. Но пока одна сторона представляет собой либо отрицательную бесконечность, либо положительную бесконечность, это бесконечный разрыв.
Бесконечность может быть положительной или отрицательной
Функция может двигаться к бесконечности в одном и том же направлении или в разных направлениях. Например, функция может идти в направлении:
Например, функция может идти в направлении:
- Положительная бесконечность с обеих сторон,
- Отрицательная бесконечность с обеих сторон или
- Одна сторона может уйти в отрицательную бесконечность, а другая — в положительную бесконечность.
График y = 1/x, стремящийся как к отрицательной, так и к положительной бесконечности при x = 0.
График 1/x 2 , который стремится к отрицательной бесконечности в обоих направлениях при x = 0. (Графики, сделанные с помощью калькулятора Desmos) или разрыв первого рода ) — разрыв в графе, который резко скачет.
Следующий график переходит в начало координат (x = 0).
Чтобы разрыв считался скачком, пределы должны:
- существуют как (конечные) действительные числа по обе стороны пробела, а
- не могут быть равны. Если пределы равны , то это дыра, а не скачок (формальнее дыры называются устранимыми разрывами).

Разница между двумя пределами составляет скачков в этой точке (Сохраб, 2003). Удивительно, но количество прыжков в любой конкретной функции исчисляемо; Другими словами, невозможно иметь бесконечное количество переходов даже в непрерывных функциях (Сохраб, 2003).
Когда происходят прыжки?
Скачок разрыва обычно происходит только в кусочных или ступенчатых функциях.
Кусочные функции определяются на последовательности интервалов.
Пример ступенчатой функции (красный график). Эта конкретная ступенчатая функция непрерывна справа.
Ступенчатые функции являются подвидом кусочных функций, в которых имеется ряд одинаковых «лестничных» шагов.
Обозначение разрывов скачка
В обозначениях разрыв скачка может быть определен в терминах пределов по обе стороны от скачка. Допустим, у вас есть функция f(t), которая имеет разрыв скачка при t = 10. Следующие обозначения описывают скачок:
Левый предел:
Правый предел:
Скачок сама может быть определена через два предела:
f (10 +) – f (10 -) .
Прыжок против шага
Хотя термин «прерывистость шага» является довольно распространенным, он имеет тенденцию быть неформальным. Обычное название такого типа разрыва — скачкообразный разрыв. Однако, когда это выглядит как физический шаг, имеет смысл называть его так (а не прыжком, который наводит на мысль о большом разрыве по горизонтальной оси, что не всегда так!). Какой термин вы используете, обычно зависит от вашего личного выбора или выбора вашего инструктора.
Примеры разрыва ступени / разрыва скачка
Функция
имеет разрыв скачка при x = 1. В этой точке нет единого предела; хотя односторонние пределы L – и L + оба существуют, потому что они не равны. Если бы вы представили, что идете по кривой, вам пришлось бы серьезно подпрыгнуть, когда вы доберетесь до нее. Это показано ниже.
На приведенном ниже графике есть разрыв шага в -4, потому что левый и правый пределы существуют и не бесконечны, но различны. В точке 2 имеется разрыв еще одной ступени; правый предел равен -1, а левый предел равен 5. Однако разрыв в точке 4 не является ступенчатым разрывом, поскольку левый и правый пределы равны. Это еще один тип разрыва — съемная несплошность .
В точке 2 имеется разрыв еще одной ступени; правый предел равен -1, а левый предел равен 5. Однако разрыв в точке 4 не является ступенчатым разрывом, поскольку левый и правый пределы равны. Это еще один тип разрыва — съемная несплошность .
Вернуться к началу
Колеблющийся разрыв (также называемый бесконечно колеблющимся разрывом ) резко прыгает (т.е. колеблется) по мере приближения к пределу; нет никакого способа «починить» разрыв. Его часто определяют методом исключения: это не устранимый разрыв, разрыв скачка или бесконечный разрыв. Поэтому вы можете увидеть, что его называют «другим» типом разрыва.
Ограниченные и неограниченные функции
Осциллирующие разрывы ограничены. Другими словами, их колебания остаются между определенными линиями. Например, функция может быть ограничена между верхней точкой y = 3 и нижней точкой y = -3. Если функция неограничена с одной или обеих сторон, это бесконечный разрыв. Другими словами, функция должна быть полностью ограничена во всех точках, чтобы имел место осциллирующий разрыв. Кроме того, односторонних ограничений вообще не существует.
Другими словами, функция должна быть полностью ограничена во всех точках, чтобы имел место осциллирующий разрыв. Кроме того, односторонних ограничений вообще не существует.
Пример
Возможно, неудивительно, что многие осциллирующие функции имеют по крайней мере один осциллирующий разрыв.
Невозможно определить предел функции sin(1/x) в нуле.
Осциллирующие разрывы являются подтипом существенных или неустранимых разрывов.
Как найти колеблющийся разрыв
Самый простой способ идентифицировать этот тип разрыва — непрерывно увеличивать график: независимо от того, сколько раз вы увеличиваете масштаб, функция будет продолжать колебаться вокруг предела.
На TI-89 постройте график функции в маленьком окне (например, окно [-2,2,1]*[-2, 2, 1]. Нажмите клавишу Zoom, выберите функцию Zoom Box ( 1:ZBox) и нажмите Enter. Отметьте верхний левый угол поля, нажав Enter, затем увеличьте поле с помощью клавиш со стрелками. Нажмите Enter еще раз. Повторяйте до бесконечности. Полные инструкции и изображения того, как это сделать, см. в разделе Модуль 8: Непрерывность на веб-сайте TI
Нажмите Enter еще раз. Повторяйте до бесконечности. Полные инструкции и изображения того, как это сделать, см. в разделе Модуль 8: Непрерывность на веб-сайте TI
Вернуться к началу
Съемная неоднородность (также называемая разрыв отверстия ) имеет зазор, который можно легко заполнить, поскольку предел одинаков с обеих сторон. Вы можете думать об этом как о маленьком отверстии на оси X.
Устранимый разрыв иногда называют разрывом в точек , потому что функция не определена в одной (крохотной точке).
Удаление отверстия
Отверстие называется устранимым разрывом, потому что его можно заполнить или удалить, немного переопределив значения функции. Просто заменить значение функции в отверстии значением предела.
Пример
Возьмем следующую кусочную функцию:
На графике функция выглядит так:
Обратите внимание на небольшое отверстие в точке x = 0,5. Значение функции здесь (то есть значение y) равно 4, что создает проблему, если мы хотим выполнить дальнейшие вычисления с функцией (например, интегрирование).
На графике вы можете просто нарисовать дырку и удалить точку в (0,5, 4). Математически, если мы возьмем значения y очень близко к дыре, мы сможем заполнить ее таким образом. Кусочная функция задается как h(x) = 1,5 + 1/(x + 0,25) для каждой точки , кроме 0.5, поэтому мы можем игнорировать эту причуду и просто использовать функцию, чтобы заполнить дыру. Подставляя x = 0,5 в функцию, получаем:
h(x) = 1,5 + 1 / (0,5 + 0,25) = 17/6 &приблизительно; 2.83.
Типы разрывов: Ссылки
Изображение: Functor Salad [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)]
[1] Drago et. др. «Букет» разрывных функций для начинающих в математическом анализе. Получено 13 июля 2021 г. с: http://ceadserv1.nku.edu/longa//classes/mat420/days/highlights/PathologicalFunctions.pdf
[2] Раздел 1.4. Непрерывность. Получено 13 июля 2021 г. с: https://www.math.uh.edu/~beatrice/143114.pdf
Боулдри, В. (2011). Введение в реальный анализ: образовательный подход.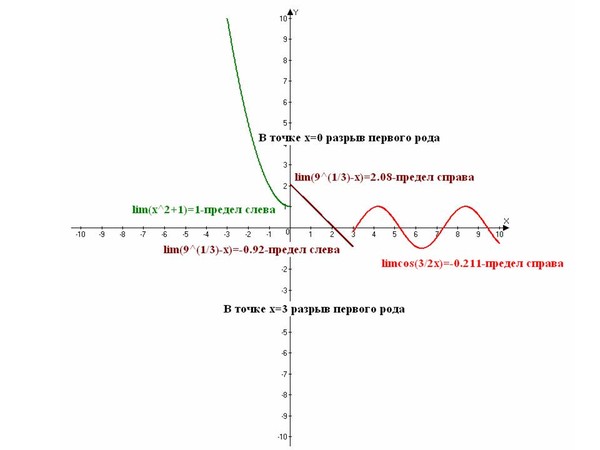 Джон Уайли и сыновья.
Джон Уайли и сыновья.
Богли, В. (1996). Устранимые разрывы. Получено 28 октября 2019 г. с: https://oregonstate.edu/instruct/mth351/cq/Stage4/Lesson/removable.html
Григориу, М. Стохастическое исчисление: приложения в науке и технике.
Бесконечный разрыв. Проверено 29 октября., 2019 г. из: http://www-math.mit.edu/~djk/18_01/chapter02/example03.html
Бесконечные разрывы. Получено 28 октября 2019 г. с: https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/1.-дифференциация/part-a-definition-and-basic- rules/session-5-discontinuity/MIT18_01SCF10_Ses5c.pdf
Кнопп, К. «Существенные и несущественные особенности или полюса». § 31 в Теории функций, части I и II, два тома, связанные как один, часть I. Нью-Йорк: Дувр, стр. 123–126, 19.96.
Крамер, П.Л.С. Примеры. Получено 22 августа 2020 г. с: http://eaton.math.rpi.edu/faculty/Kramer/CA13/canotes111113.pdf
Кранц С.Г. «Устранимые особенности, полюса и существенные особенности». §4.1. 4 в Справочнике комплексных переменных. Бостон, Массачусетс: Биркхойзер, с. 42, 1999.
4 в Справочнике комплексных переменных. Бостон, Массачусетс: Биркхойзер, с. 42, 1999.
Rohde,U. и другие. (2012). Введение в дифференциальное исчисление: систематические исследования с инженерными приложениями для начинающих. Джон Уайли и сыновья.
Сохраб, Х. (2003). Базовый реальный анализ. Springer Science and Business Media.
Томсон, Б. и др., (2008). Элементарный реальный анализ, Том 1. ClassicalRealAnalysis.com.
Вайнман, А. и Раджагопал, К. (2000). Механическая реакция полимеров: введение. Издательство Кембриджского университета.
Калькулятор Desmos.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Типы разрывов / разрывных функций» Из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/calculus-definitions/types-of-discontinuity/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
ИсчислениеHowTo.com
Обзор исчисления AP: разрывы — Блог Magoosh
Шон Олт в 20 января 2018 г. в AP
Что такое разрыв? Любая точка, в которой функция не равна непрерывный называется прерывистым . На самом деле существуют различные типы разрывов, которые мы надеемся объяснить в этой обзорной статье.
Точки разрыва
Определение разрыва очень простое. Функция прерывиста в точке x = , если функция не непрерывна в точке .
Итак, давайте начнем с рассмотрения определения непрерывного .
Функция f является непрерывной в точке x = a , если верно следующее предельное уравнение.
Думайте об этом уравнении как о наборе трех условий.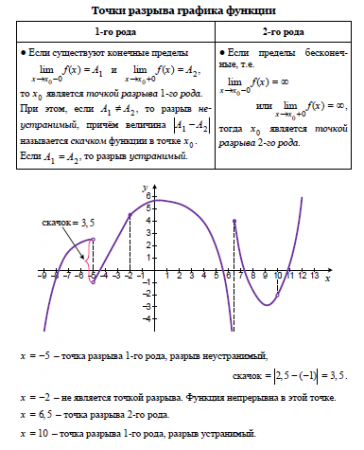
- Ограничение должно существовать. То есть для некоторого конечного числа L .
- Значение функции должно существовать. Другими словами, f ( a ) существует.
- Предел должен соответствовать значению функции. Итак, цифра L , которое вы получите, взяв лимит, должно быть таким же значением, как f ( a ).
Когда одно или несколько из этих условий не выполняются, функция имеет разрыв на x = a по определению.
Особенно интересно первое условие, что предел должен существовать. Лимит может не существовать по разным причинам. Если предел в виде x → a не существует, то можно сказать, что функция имеет неустранимый разрыв при x = a . Затем, в зависимости от того, почему предел не существует, мы далее классифицируем точку как скачок , бесконечное или бесконечное колебание разрыв.
Непрерывность перехода
Один из способов, при котором предел может не существовать в точке x = a , — это если левосторонний предел не совпадает с правым пределом.
На приведенном ниже графике наблюдается «несоответствие». Как x приближается к 1 слева, эта часть графика, кажется, приземляется на y = -1. С другой стороны, по мере того, как x приближается к 1 справа, значения y становятся все ближе и ближе к y = 3.
Функция f ( x ) с разрывом скачка при x = 1
В предельном обозначении мы бы написали:
Поскольку левый и правый пределы не совпадают, предел f ( x ) как x → 1 не существует .
Следовательно, по определению функция f разрывна при x = 1. Этот вид разрыва известен как скачок (по очевидным причинам).
Бесконечные разрывы (вертикальные асимптоты)
В некоторых функциях значения функции стремятся к ∞ или -∞, когда x приближается к некоторому конечному числу a . В этом случае говорят, что функция имеет бесконечный разрыв или вертикальная асимптота при x = a .
В этом случае говорят, что функция имеет бесконечный разрыв или вертикальная асимптота при x = a .
Вы можете думать о бесконечном разрыве как о крайнем случае скачкообразного разрыва.
Эта функция имеет бесконечный разрыв при x = 3.
Как правило, вы обнаружите такое поведение везде, где есть деление формы , отличное от нуля, над нулем .
Например, 3 x /( x + 12) имеет бесконечный разрыв в точке x = -12, потому что именно здесь знаменатель становится равным 0, а числитель отличен от нуля (3 × -12 = -36).
Пример
Найдите и классифицируйте разрывы f ( x ) = tan x на интервале [-2π, 2π].
Решение
Обратите внимание, что тангенс x = (sin x )/(cos x ), а знаменатель, cos x , равен нулю во всех точках формы π/2 + n π. Есть четыре x — значения в интервале [-2π, 2π], соответствующие: x = -3π/2, -π/2, π/2 и 3π/2.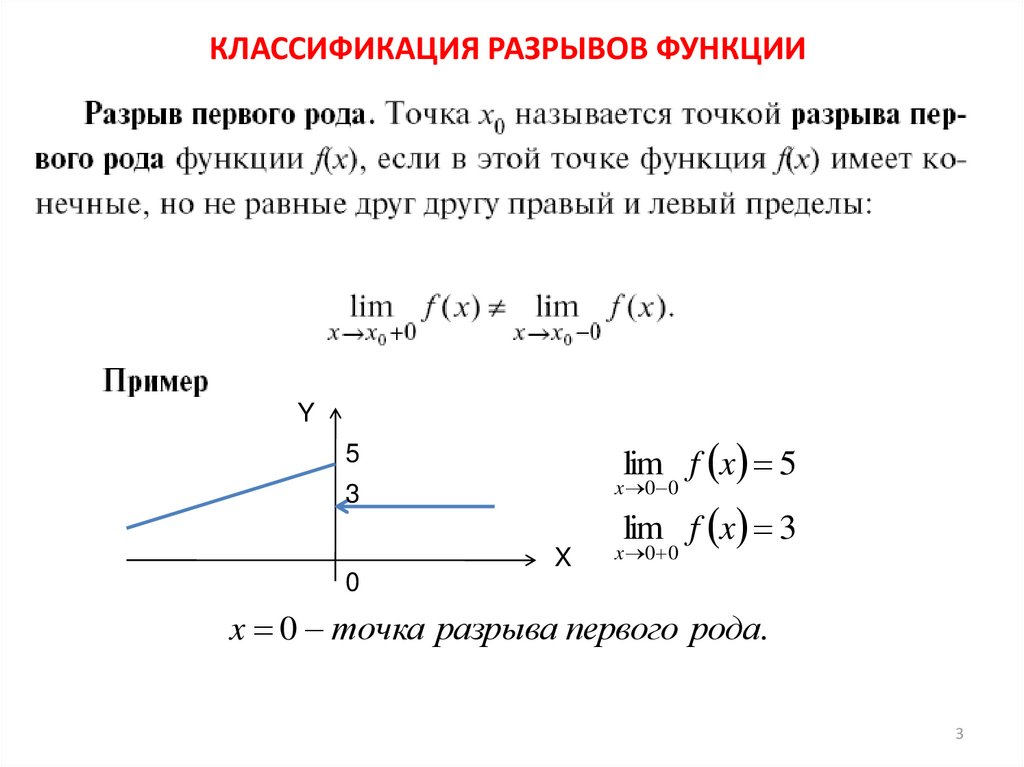 Подставив каждое из них в числитель sin x , мы убедимся, что верх не равен нулю, когда низ равен нулю. Таким образом, f имеет бесконечный разрыв в четырех точках: x = -3π/2, -π/2, π/2 и 3π/2 в интервале [-2π, 2π]
Подставив каждое из них в числитель sin x , мы убедимся, что верх не равен нулю, когда низ равен нулю. Таким образом, f имеет бесконечный разрыв в четырех точках: x = -3π/2, -π/2, π/2 и 3π/2 в интервале [-2π, 2π]
График может помочь нам визуализировать то, что происходит вблизи этих точек.
График тангенса x , показывающий бесконечное поведение при π/2 + п π.
Бесконечные разрывы колебаний
Большинство функций, которые вы встречаете, довольно скучны и предсказуемы. Даже при скачке или бесконечном разрыве можно что-то сказать о поведении значений функции. Однако, если ваша функция имеет бесконечных разрыва колебаний в точке x = a , тогда все становится диким!
Рассмотрим график f ( x ) = sin(1/ x ).
График sin(1/ x ) на [-5, 5]
Приближаясь к началу координат, кривая все чаще идет вверх и вниз. На самом деле, когда x → 0, как слева, так и справа, мы можем видеть, как колебания полностью выходят из-под контроля! Как будто кривая хочет убедиться, что она достигает через каждые точку в диапазоне от -1 до 1 при x = 0,
На самом деле, когда x → 0, как слева, так и справа, мы можем видеть, как колебания полностью выходят из-под контроля! Как будто кривая хочет убедиться, что она достигает через каждые точку в диапазоне от -1 до 1 при x = 0,
Как бы мы не увеличивали график, он становится все более и более диким.
График sin(1/ x ) на [-0,5, 0,5]
Причина такого странного поведения связана с тем, что сам sin x является периодическим. Тогда замена x на 1/ x в аргументе приводит к тому, что все эти бесконечно много периодических волн синусоидальной функции принимаются как x → ∞, а вместо этого сжимается рядом с началом координат.
Во всяком случае, поскольку нет единственного значения y , к которому кривая, кажется, движется как x → 0, предел не существует при x = 0,
Следовательно, f ( x ) = sin(1/ x ) имеет разрыв при x = 0 бесконечного разнообразия колебаний.
Съемные разрывы
Последняя категория разрыва отличается от остальных. В предыдущих случаях предела не существовало. Другими словами, условие 1 определения непрерывности не выполняется. Далее мы обсудим, что произойдет, если выполняется условие 1 (предел существует), но не выполняется условие 2 или 3.
A Function F имеет съемный разрыв на x = A , если предел F ( x ) как x → A Expars ) не существует, или значение f ( a ) не равно предельному значению.
Если предел существует, а f ( a ) не существует, то мы можем визуализировать график f как имеющий «дыру» на х = . Вы можете себе представить, что произойдет, если вы заполните эту дыру. Если это действительно устранимый разрыв , то заполнение дыры приводит к непрерывному графику!
Давайте посмотрим на график ниже.
На x = -2 есть дыра. На самом деле, график был бы непрерывным в этой точке, если бы дыра в (-2, 2) была заполнена.0050 х = -2.
Есть еще один случай для рассмотрения. Предположим, что оба условия 1 и 2 выполняются для функции в данной точке, но условие 3 не выполняется. То есть предел существует, значение функции существует, но это разных значений.
Эта ситуация происходит на графике, показанном ниже.
Сосредоточьтесь на том, что происходит вблизи x = 2.
Существует четко определенное предельное значение. Поскольку кривая приближается к y = 3 слева и справа, предел равен 3,9.0006
Но f (2) = 1 (исходя из расположения точки). Поскольку значение f не совпадает с предельным значением здесь, мы можем сказать, что f имеет устранимый разрыв при x = 2,
.Пример
Определите, где функция имеет устранимый разрыв, и определите значение функции, которое сделало бы ее непрерывной в этой точке.
Решение
Посмотрите на знаменатель. Мы знаем, что f будет неопределенным всякий раз, когда нижняя часть дроби равна 0. Это происходит, когда 2 x – 4 = 0, или после решения для x мы находим x = 2,
Итак, мы уже знаем, что в точке x = 2 имеется какая-то неоднородность (поскольку f (2) не существует — см. условие 2 определения непрерывности). Но разве съемный ? Это требует нахождения предела.
Поскольку предельное значение существует, теперь мы точно знаем, что на 9 существует устранимый разрыв.0050 х = 2,
Более того, сам предел говорит нам, каким должно быть значение, чтобы f стало непрерывным: -5/2.
Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Автор
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!
Нажмите сюда, чтобы узнать больше!
Расчет AP
← Предыдущий
Далее →
Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!
Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!
Как классифицировать разрывы
Краткий обзор
- На графиках открытые и закрытые кружки или вертикальные асимптоты, нарисованные в виде пунктирных линий, помогают нам идентифицировать разрывы.
- Как и прежде, графики и таблицы позволяют в лучшем случае оценить.
- При работе с формулами получение нуля в знаменателе указывает на точку разрыва.
- При работе с кусочно заданными функциями проверьте наличие разрывов в точках перехода, где заканчивается один кусок и начинается следующий.

Примеры
Пример 1
Используя график, показанный ниже, определите и классифицируйте каждую точку разрыва.
Шаг 1
В таблице ниже указано расположение (значение $$x$$) каждой несплошности и тип несплошности.
$$ \начать{массив}{с|л} {Икс} & {\mbox{Тип}}\\ \hline -7 & \mbox{Смешанный}\\ -3 & \mbox{Съемный}\\ 2 & \mbox{Прыжок}\\ 4 & \mbox{Бесконечно}\\ 6 & \mbox{Конечная точка} \конец{массив} $$
Обратите внимание, что разрыв при $$x=-7$$ является одновременно устранимым (значение функции отличается от одностороннего предельного значения) и конечной точкой (поскольку график не определен левее $$x= -7$$).
Пример 2
Используя приведенные ниже таблицы, определите, какой тип разрыва существует при $$x = 5$$?
$$ \begin{массив}{с|lcc|l} {Икс} & {е(х)}\\ \hline 4.9& 8.15\\ 4,99 и 8,015\\ 4,999 и 8,0015\\ 4,9999 и 8,00015\\ 4,99999 и 8,000015\\ \конец{массив} $$
$$ \begin{массив}{с|lcc|l} {Икс} & {е(х)}\\ \hline 5.1 и 2.4\\ 5.01 и 2.43\\ 5.001 и 2.403\\ 5,0001 и 2,4003\\ 5.00001 и 2.40003 \конец{массив} $$ 9+}f(x) \приблизительно 2,4$$
Отвечать
Таблицы заставляют нас полагать, что односторонние пределы различны, поэтому мы заключаем, что функция, вероятно, имеет разрыв скачка при $$x = 5$$.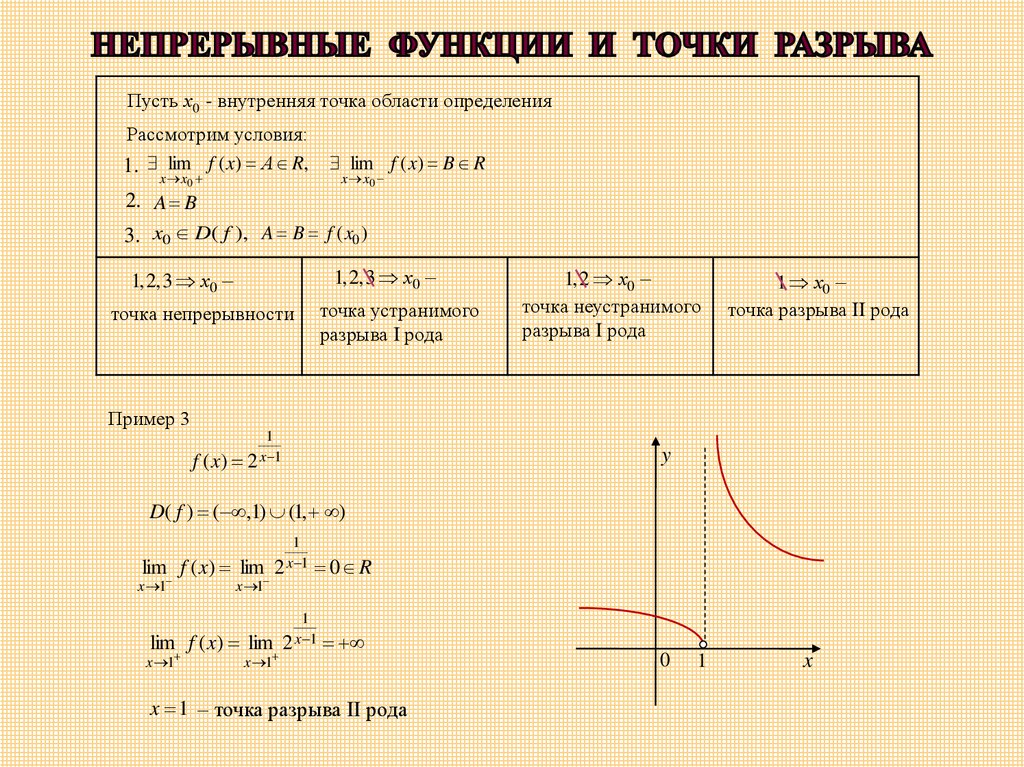
Реклама
Пример 3
Является ли приведенная ниже функция непрерывной в точке перехода? Если нет, определите тип разрыва, происходящего там. 92, & х\leq 1\\ х+3 и х > 1 \конец{массив} \Правильно. $$
Шаг 1
Определите точку (точки) перехода.
Точка перехода находится в $$x = 1$$, так как именно здесь функция переходит от одной формулы к другой.
Шаг 2 9+} (х+ 3) = 1 + 3 = 4 $$
Отвечать
Поскольку односторонние пределы различны, функция имеет скачкообразный разрыв при $$x = 1$$.
Пример 4
Является ли приведенная ниже функция непрерывной при x = 4? Если нет, определите тип разрыва, происходящего там. 9+} (6-х) = 6 -4 = 2 $$
Шаг 3
Определите значение функции.
$$ f(4) = 5 $$
Отвечать
Предел существует, и функция существует, но они имеют разные значения. Функция имеет устранимый разрыв в точке $$x = 4$$. 92-2(\синий{3})-3} = \ гидроразрыв {9 + 6 — 15} {9-6-3} = \ гидроразрыв 0 0 $$
Функция не определена при $$x = 3$$, поэтому в этой точке имеется разрыв. Чтобы определить тип, нам нужно будет оценить предел, когда $$x$$ приближается к 3.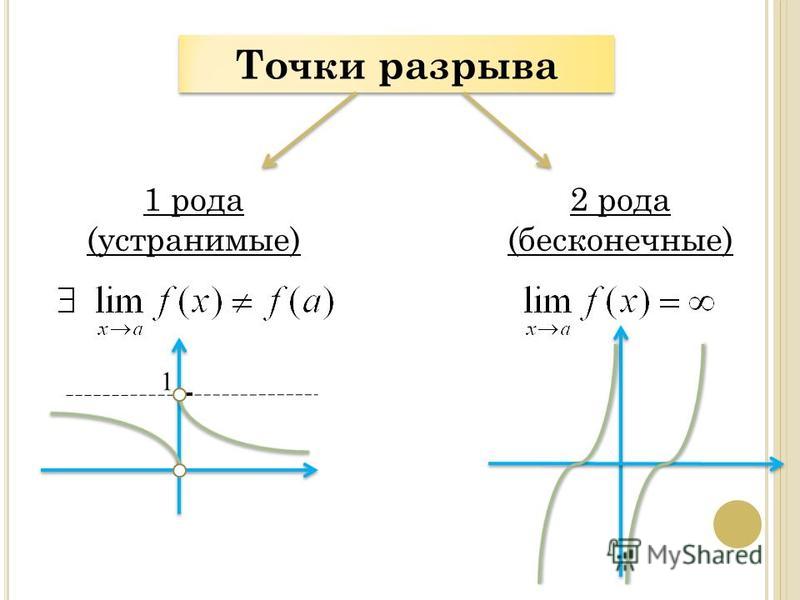
Шаг 2
Поскольку функция имеет вид $$\frac 0 0$$ при $$x = 3$$, необходимо найти и разделить общие множители в числителе и знаменателе. 92-2x-3} = \ frac {(x + 5) \ blue {(x-3)}} {\ blue {(x-3)} (x + 1)} = \ гидроразрыва {х+5} {х+1} $$
Шаг 3
Оценить предел более простой функции, когда $$x$$ приближается к 3.
$$ \displaystyle\lim_{\blue{x\to3}} \frac{x+5}{x+1} = \ гидроразрыв {\ синий 3 + 5} {\ синий 3 + 1} = \фракция 8 4 = 2 $$ 92-2(\синий{-1})-3} = \фракция{1 — 2 — 15}{1+2-3} = \фракция{-16} 0 $$
Поскольку у нас есть деление на ноль, функция не существует при $$x = -1$$.

 Разница первого и второго называется скачком.
Разница первого и второго называется скачком. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.

 Аналогично доказываются
Аналогично доказываются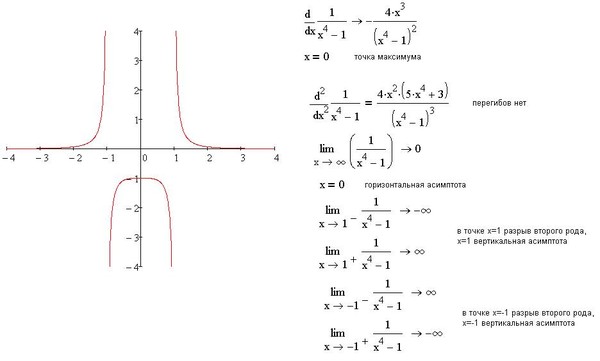 е.
е. 2.1.
2.1. 2.3.
2.3. 2.4.
2.4.