Транспонированная матрица.
Навигация по странице:
- Транспонированная матрица
- Свойства транспонированной матрицы
- Примеры задач на транспонирование матриц
Онлайн калькулятор. Транспонирование матриц.
Определение.
Транспонирование матрицы — это операция над матрицей, при которой ее строки и столбцы меняются местами:
aTij = aji
Свойства транспонированной матрицы
- Если матрица A имеет размер n×m, то транспонированная матрица AT имеет размер m×n;
- (AT)T = A;
- (k · A)T = k · AT;
- (A + B)T = AT + BT;
- (A · B)T = BT · AT.
Примеры задач на транспонирование матриц
Пример 1.
Найти транспонированную матрицу AT для матрицы
| A = | 4 | 2 | . | ||
| 9 | 0 |
Решение:
| AT = | 4 | 9 | ||
| 2 | 0 |
Пример 2
Найти транспонированную матрицу AT для матрицы
| A = | 2 | 1 | . | ||
| -3 | 0 | ||||
| 4 | -1 |
Решение:
| AT = | 2 | -3 | 4 | ||
| 1 | 0 | -1 |
Пример 3
Найти транспонированную матрицу A T для матрицы
| A = | 2 | -3 | 4 | . | ||
| 1 | 0 | -1 |
Решение:
| AT = | 2 | 1 | ||
| -3 | 0 | |||
| 4 | -1 |
Онлайн калькуляторы с матрицами.
Упражнения с матрицами.
Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Транспонированная матрица
Определение. Матрицу В называют транспонированной матрицей
А, а переход от А к В транспонированием,
если элементы каждой строки матрицы А
записать в том же порядке в столбцы
матрицы В.
А = ; В = АТ=;
другими словами, bji = aij.
В качестве следствия из предыдущего свойства (5) можно записать, что:
(ABC)T = CTBTAT,
при условии, что определено произведение матриц АВС.
Пример. Даны матрицы А = , В =, С =и число = 2. Найти АТВ+С.
AT = ; ATB = = = ;
C = ; АТВ+С = += .
Пример. Найти произведение матриц А = и В =.
АВ = =.
ВА = = 21 + 44 + 13 = 2 + 16 + 3 = 21.
Пример. Найти произведение матриц А=,
В =
Найти произведение матриц А=,
В =
АВ = ==.
3
Определители.( детерминанты)
Определение. Определителем квадратной матрицы А=называется число, которое может быть вычислено по элементам матрицы по формуле:
det A = , где
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det A =
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA
=
,
i
= 1,2,…,n.
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М 1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
4
Обратная матрица
Определим операцию деления матриц как операцию, обратную умножению.
Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е — единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.
Каждая
квадратная матрица с определителем, не
равным нулю имеет обратную матрицу и
притом только одну.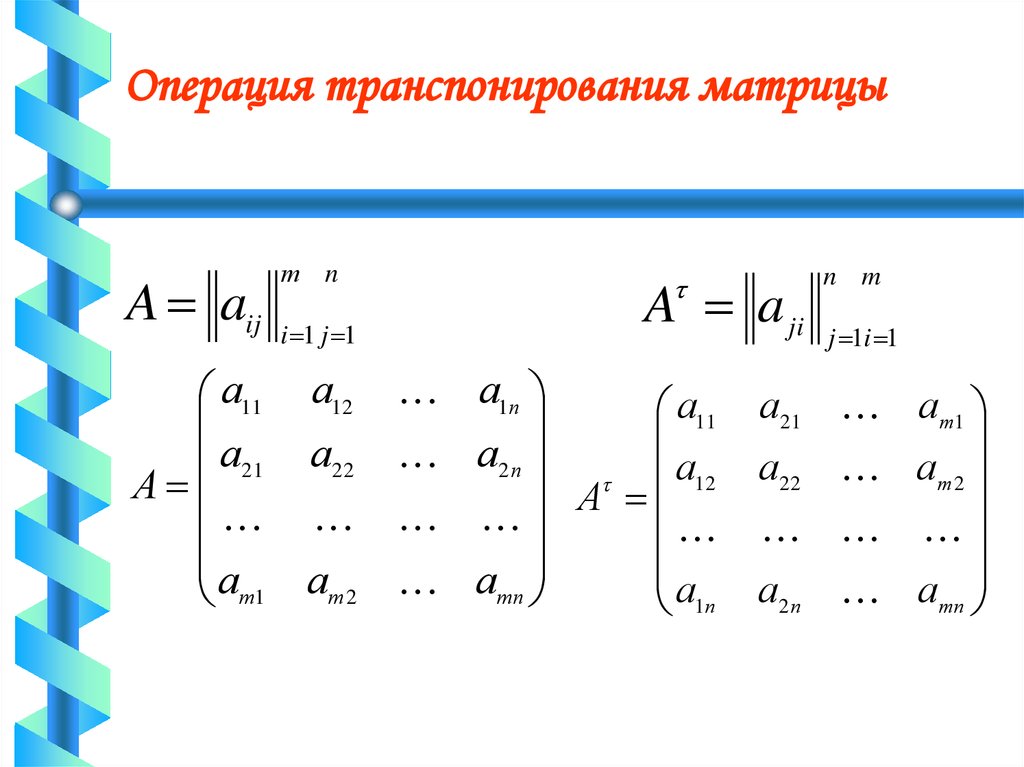
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E , i=(1,n), j=(1,n),
eij = 0, i j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
,
Решив эту систему, находим элементы матрицы Х.
Пример. Дана матрица А = , найти А-1.
Таким образом, А-1=.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
где Мji—
дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = , найти А-1.
det A = 4 — 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким образом, А-1=.
матричных транспозиций и симметричных матриц | by adam dhalla
Все, что вам нужно знать о транспонировании матриц и симметричных матрицах
Матричное транспонирование и симметричные матрицы связаны — фактически, определение симметричной матрицы состоит в том, что транспонирование симметричной матрицы A возвращает ту же матрицу A
Это продолжение моей серии по линейной алгебре, связанной с курсом Гилберта Стрэнга 18.06 MIT OCW по вводной линейной алгебре. Давайте сразу перейдем к основам транспонирования.
Давайте сразу перейдем к основам транспонирования.
Транспонирование матрицы
Мы транспонируем двумерную матрицу, используя ее строки в качестве столбцов или, наоборот, используя ее столбцы в качестве строк. Это все, что нужно для выполнения простой операции.
Точнее, запись в позиции a ij становится записью в позиции aji . Конкретно, посмотрите, как e меняется от позиции (3, 1) к позиции (1, 3). Это все хорошо, но как насчет транспонирования суммы или произведения матриц?
Транспонирование суммы матриц
Транспонирование суммы (и, соответственно, разности) матриц довольно просто. Мы можем просто «распределить» транспонирование на оба числа.
Это, опять же, имеет вполне логичный смысл и не требует доказательств, чтобы считать его правдой. В левой части мы добавляем две матрицы, а затем транспонируем сумму. Справа их дополнительно транспонируем и добавляем. Одни и те же числа по-прежнему добавляются друг к другу, поэтому конечный результат тот же. Конкретный пример:
Конкретный пример:
Оба способа добавления эквивалентны. Нам часто приходится упрощать транспонирование в матричных уравнениях, так что имейте это в виду.
Транспонирование произведения матриц
Интуитивно понять это труднее, чем суммирование. Давайте посмотрим, что происходит, когда мы транспонируем продукт AB.
Если вы знакомы с обратным произведением, мы факторизуем его идентично — мы транспонируем оба произведения, но обращаем порядок. Труднее взглянуть на это и понять, почему оно работает, поэтому давайте углубимся в детали умножения матриц, чтобы понять, почему это происходит.
Давайте рассмотрим ту же систему на конкретном примере.
Давайте посмотрим, откуда взялась первая строка нашей матрицы результатов. Возвращаясь назад с конца, мы видим, что эта строка на самом деле является столбцом до того, как она будет транспонирована. Этот столбец получается из первой и второй строк A, умноженных на первый столбец B. Можно сказать, что первая строка нашего результата есть произведение строк A на первый столбец B.
Скажем мы переставили A и B перед их умножением. Как нам найти способ сохранить тот же расчет (строки A по первому столбцу B)? Давайте сделаем это и посмотрим, как.
Выделены одни и те же строки A (теперь столбцы A) и первый столбец B (теперь первая строка B). Их нужно перемножить, чтобы получить первую строку B. В каком порядке мы должны умножить их в для того, чтобы получить первую строку продукта? Ну было бы, конечно:
Сохраняем идентичное умножение, и таким образом получаем точно такое же произведение для первой строки. Таким образом, наше правило, изложенное ранее, корректируется.
Симметричные матрицы
Симметричные матрицы, как было сказано ранее, это матрицы, которые после транспонирования становятся идентичными. Официально:
Согласно нашему предыдущему определению того, что такое транспонирование, при транспонировании некоторый элемент в строке i и столбце j (aij) становится элементом в строке j и столбце i (aij). Таким образом, в симметричной матрице aij должно = aji для всех aji. Глядя на пример симметричной матрицы, это очевидно.
Таким образом, в симметричной матрице aij должно = aji для всех aji. Глядя на пример симметричной матрицы, это очевидно.
Хороший прием для обнаружения симметричных матриц состоит в том, что они выглядят зеркально отраженными по диагонали. На самом деле симметричные матрицы появляются довольно часто. Они хороши и аккуратны для целого ряда вычислений. Давайте рассмотрим еще несколько свойств симметричных матриц.
Инверсия симметричной матрицы также является симметричной
Поначалу это свойство может показаться немного неожиданным, но мы можем очень, очень быстро доказать это, слегка изменив формулу для симметричной матрицы.
Если A уже симметрична, значит, A = A(T), их обратные стороны также должны быть симметричными, потому что: в основном говоря, транспонирование обратного равно обратному. Это свойство часто пригодится.
Произведение матрицы и ее транспонирования симметрично
Произведение любой матрицы (квадратной или прямоугольной) и ее транспонирования всегда симметрично. В более понятных обозначениях это:
В более понятных обозначениях это:
Это легко доказать, но трудно поверить, пока вы на самом деле не сделаете это, и тогда это становится совершенно очевидным. Давайте сначала рассмотрим конкретный случай, а затем докажем его с помощью матричных обозначений (легко).
Сделайте это умножение, чтобы действительно понять, почему мы получаем семь в углах. Проще говоря, для первых 7 мы умножаем (1, 2) на (3, 2), а для нижних 7 мы умножаем (3, 2) на (1, 2), что дает тот же продукт. Эту идею можно легко расширить до нескольких симметричных записей — мы просто умножаем некоторую строку в A, транспонируемую (a, b, c…. z) на столбец (z, y, z… a) в A, а затем позже, умножение некоторой строки в A, транспонированной (z, y, z…a) на некоторый столбец в A (a, b, c…. z), что дает два одинаковых ответа.
Давайте быстро докажем это с помощью изученного нами правила «перестановки продуктов». Помните, тест на симметрию состоит в том, чтобы взять транспонирование и посмотреть, дает ли оно то же самое.
Здесь, если мы возьмем транспонирование нашего продукта, мы получим тот же продукт, что означает, что наше транспонирование A * A симметрично.
Мы упомянули это как небольшую оговорку, но мы получим симметричную, но другую матрицу, если мы поменяем порядок транспонирования и оригинала. Например, с неквадратной матрицей:
Мы видим, что наши продукты разные — черт возьми, они разных размеров! Но они оба симметричны. Наш результат с одним элементом слева по-прежнему симметричен, поскольку транспонирование скаляра 10 равно 10.
Исключение по Гауссу Что, если A в A = LDU симметрично?
Если вы не знакомы с методом исключения Гаусса, можете пропустить эту часть. Если вы знакомы с исключением, но не знаете факторизации A = LU или A = LDU, ознакомьтесь с моей последней статьей в мини-сериале «Исключение по Гауссу».
[3/3] Полное руководство по исключению Гаусса
Часть 3 из 3: Факторизация исключения Гаусса; А = ЛУ; способ, которым компьютеры выполняют исключение
medium. com
com
Здесь мы имеем дело с вероятностью того, что наша матрица коэффициентов A симметрична. Есть ли способ быстрее найти нижнюю и верхнюю треугольные матрицы A = U в A = LDU?
Хорошо, если A симметрична или A(T) = A, то
Таким образом, найти нашу матрицу U еще проще, и нам не нужно беспокоиться о том, чтобы делать надоедливую операцию, когда мы делим U так, чтобы мы может иметь матрицу D, содержащую точки опоры, и матрицу U, состоящую только из единиц по диагонали. В качестве примера, давайте вычислим матрицу A 2 x 2 и разложим ее на LDL(T).
Итак, начнем — это все, что нужно знать о транспонировании и симметричных матрицах в базовом начальном курсе линейной алгебры.
Спасибо за внимание!
Адам Дхалла учится в старшей школе из Ванкувера, Британская Колумбия. Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды. Чтобы не отставать,
Подпишитесь на его I nstagram и его LinkedIn . Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.
Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.
Транспонирование — линейная алгебра
Все ресурсы по линейной алгебре
4 диагностических теста 108 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
Справка по линейной алгебре » Операции и свойства » Транспонировать
Найдите транспонированную матрицу .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти транспонирование, нам нужно превратить столбцы в строки. где 02
Нельзя транспонировать квадратную матрицу
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками транспонированной матрицы. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д. 2
Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д. 2
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками транспонированной матрицы. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками транспонированной матрицы. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками транспонированной матрицы.
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками транспонированной матрицы. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Объяснение:
Транспонирование матрицы просто означает преобразование столбцов исходной матрицы в строки транспонированной матрицы. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Что является транспонированием ?
Возможные ответы:
Правильный ответ:
Объяснение:
Поперечная матрица — это матрица, в которой столбцы теперь являются соответствующими строками — первый столбец теперь является первой строкой, второй столбец — второй строкой и т. д.
д.
Сообщить об ошибке
Найти транспонирование матрицы A.
Возможные ответы:
Ни один из других ответов
9000 5
Правильный ответ:
Объяснение:
Для матрицы A 3×2 транспонирование матрицы A является матрицей 2×3, где столбцы образованы из соответствующих строк A.
Сообщить об ошибке
Найти транспонирование матрицы A.
Возможные ответы:
Ни один из других ответов
Правильный ответ:
Объяснение:
Для матрицы 2 x 4 транспонированием матрицы A является матрица 4×2, где столбцы формируются из соответствующих строк матрицы A.
