Транспортна задача: Транспортная задача онлайн

Транспортная задача — решение методом потенциалов

Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.

Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы — затраты на перевозку 1 товара от каждого склада к каждому магазину.

Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.

Содержание:

• теоретический материал по транспортной задаче;
• общий план решения методом потенциалов;
• подробный пример решения транспортной задачи;
• практическое применение транспортной задачи.

Теоретический материал по транспортной задаче

Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.

Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.

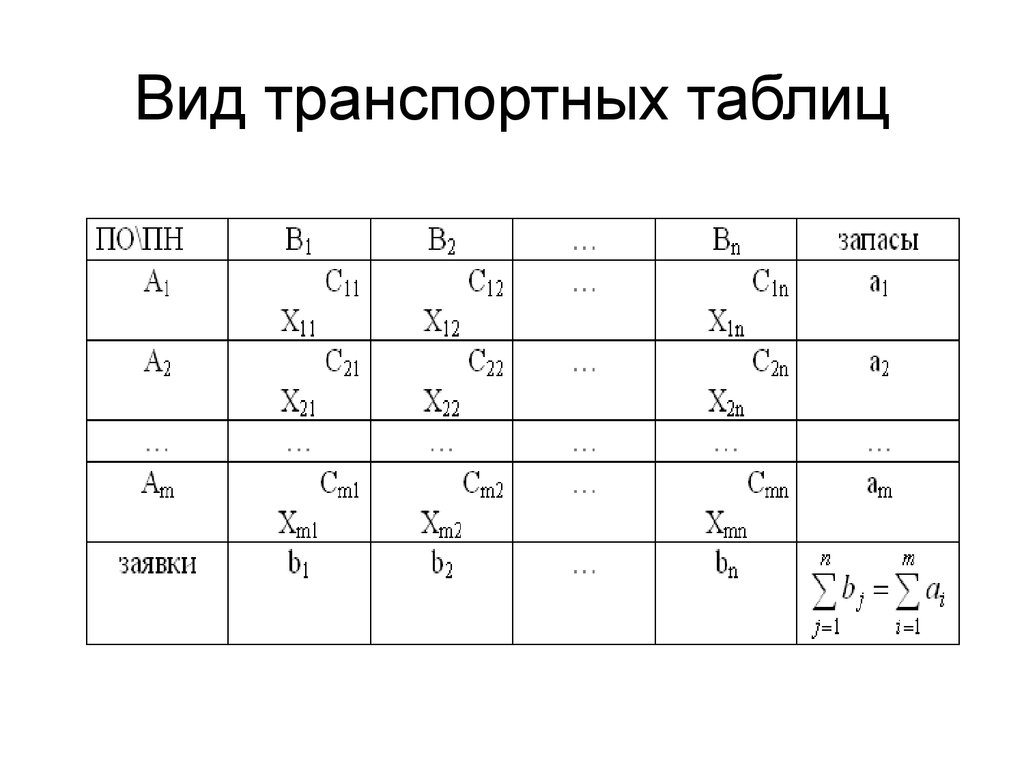
Математическая модель транспортной задачи имеет следующий вид:

где: Z — затраты на перевозку грузов;

X — объем груза;

C — стоимость (тариф) перевозки единицы груза;

A — запас поставщика;

B — запрос потребителя;

m — число поставщиков;

n — число потребителей.

Общий план решения транспортной задачи методом потенциалов

Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов — итерационное улучшение плана перевозок.

Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален — решение найдено. Если нет — улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.

Ниже приведен алгоритм решения транспортной задачи в самом общем виде:

1. Построение транспортной таблицы.
2. Проверка задачи на закрытость.
3. Составление опорного плана.
4. Проверка опорного плана на вырожденность.
5. Вычисление потенциалов для плана перевозки.
6. Проверка опорного плана на оптимальность.
7. Перераспределение поставок.
8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
9. Вычисление общих затрат на перевозку груза.
10. Построение графа перевозок.

Подробная инструкция по решению транспортной задачи

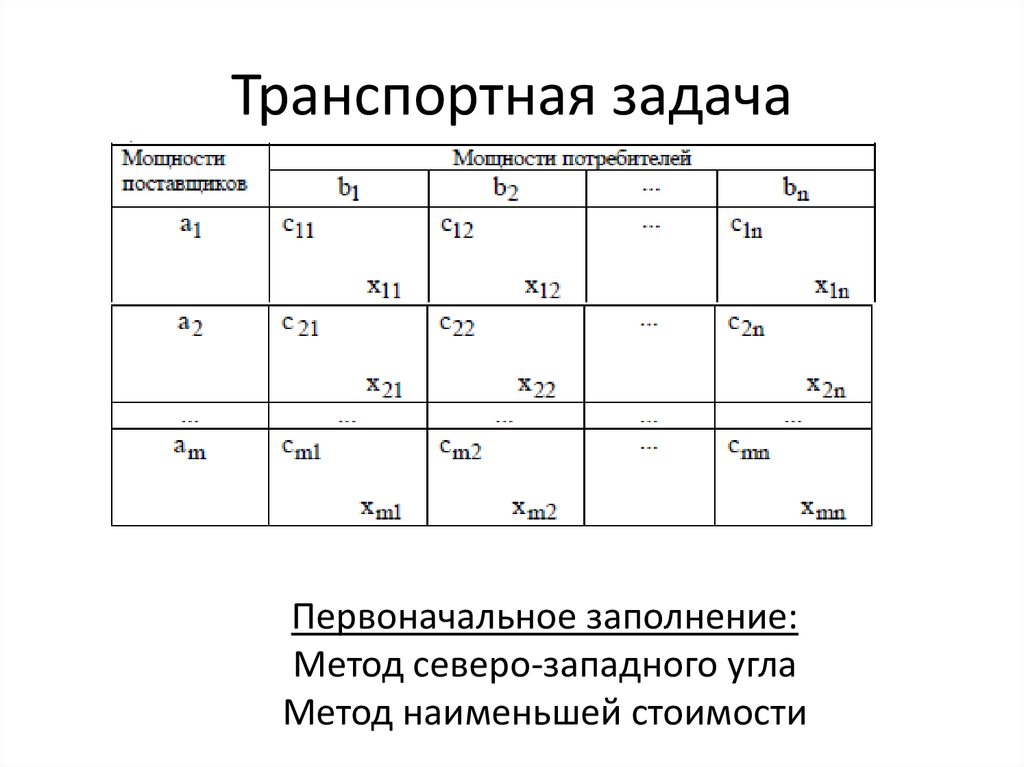
1. Построение транспортной таблицы

Заполняем транспортную таблицу с исходными данными, где указываем запасы материалов, имеющиеся на складах поставщиков (A_i), и потребности заводов (B_j) в этих материалах.

В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (C_ij).

2. Проверка задачи на закрытость

Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей — символом B.

Тогда:

Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой.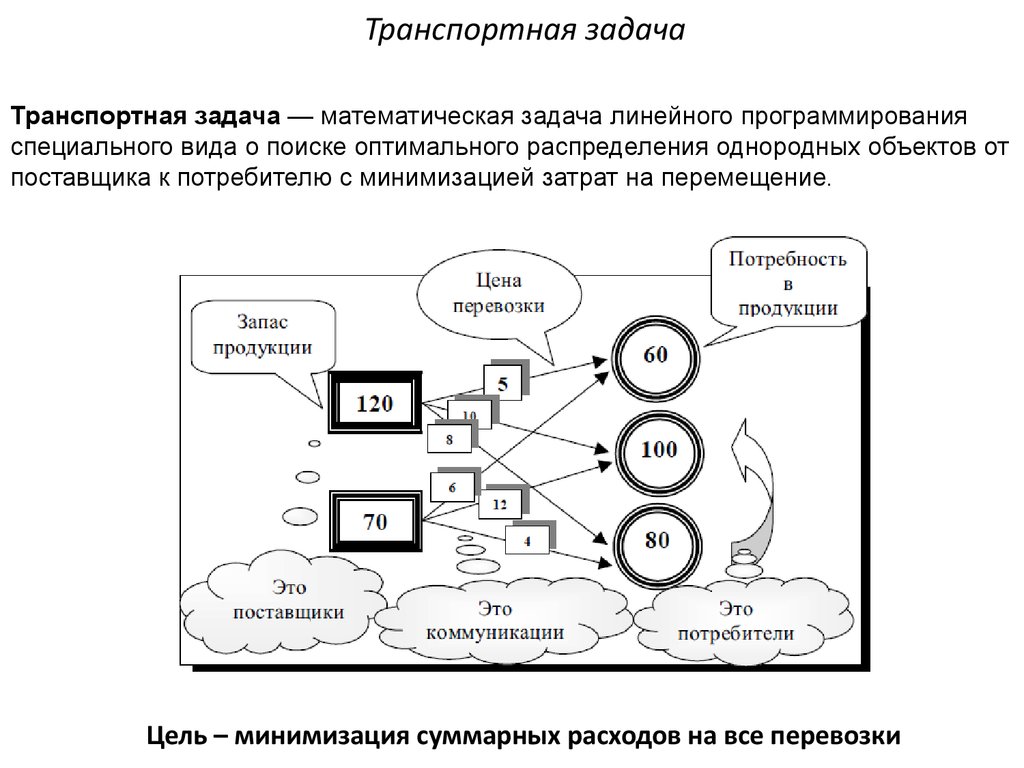 В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.

Проверим задачу на закрытость:

A = 10 + 20 + 30 = 60.

B = 15 + 20 + 25 = 60.

A = B, следовательно данная транспортная задача — закрытая.

3. Составление опорного плана

Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик» или «набросок», итерационно улучшая который мы постепенно придем к оптимальному плану.

Есть разные методы нахождения опорного плана. Наиболее распространены следующие:

а) Метод Северо-Западного угла

Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении

сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка («северо-западная» ячейка), потом следующая справа и т. д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.

Подробное описание метода и пример можно посмотреть здесь.

б) Метод минимального элемента

Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным тарифом. Затем выбирается следующая клетка с наименьшим значением тарифа и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).

Подробное описание метода и пример можно посмотреть здесь

в) Аппроксимация Фогеля

Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.

Подробное описание аппроксимации Фогеля и пример можно посмотреть здесь

г) Метод двойного предпочтения

Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.

Подробное описание метода и пример можно посмотреть здесь

Выберите один из методов и пройдите по ссылке в его описании, чтобы посмотреть как в данном примере был составлен опорный план и заполнена транспортная таблица.

4. Проверка опорного плана на вырожденность

Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n — 1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).

Проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!

План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:

Ломаная линия может иметь точки самопересечения, но не в клетках цикла.

В нашем примере количество базисных клеток = 5; m + n — 1 = 3 + 3 — 1 = 5.

Следовательно, первоначальный план перевозок — невырожденный (5 = 5).

5. Вычисление потенциалов для плана перевозки

Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.

Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.

Итак, сопоставим каждому поставщику A_i и каждому потребителю B_j соответствующие величины U_i и V_j так, чтобы для всех базисных клеток плана было выполнено следующее соотношение: U_i + V_j = C_ij.

Добавим к транспортной таблице дополнительную строку и столбец для U_i и V_j.

Предположим, что U₁ = 0.

Тогда мы сможем найти V₃ = C₁₃ — U₁ = 1 — 0 = 1.

Зная V₃, мы теперь можем найти U₃:

По аналогии вычисляем все оставшиеся потенциалы:

6. Проверка плана на оптимальность методом потенциалов

Для каждой свободной клетки плана вычислим разности ΔC_ij = C_ij — (U_i + V_j ), и запишем полученные значения в левых нижних углах соответствующих ячеек.

План является оптимальным, если все разности ΔC_ij ≥ 0.

В данном случае план — неоптимальный (ΔC₂₂ < 0), и его следует улучшить путем перераспределения поставок.

7. Перераспределение поставок

Найдем ячейку с наибольшей по абсолютной величине (т. е. без учета знака, по модулю) отрицательной разностью ΔC_ij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.

Отметим ячейку с отрицательной разностью ΔC_ij знаком «+», следующую знаком «—», и так далее, поочередно.

Затем находим минимальное значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).

Получим новый опорный план перевозок:

Так как базисных клеток стало больше, чем m + n — 1, то базисную клетку с нулевым значением делаем свободной:

Снова вычисляем значения потенциалов и разности ΔC_ij:

На этот раз все разности ΔC_ij ячеек положительные, следовательно, найдено оптимальное решение.

8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.

В нашем примере оптимальное решение найдено, поэтому переходим к пункту 9.

9. Вычисление общих затрат на перевозку груза

Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:

То есть нужно перемножить значения объемов грузоперевозок на соответствующие им тарифы.

Z_min = 10 ⋅ 1 + 15 ⋅ 3 + 5 ⋅ 2 + 15 ⋅ 1 + 15 ⋅ 2 = 110 ден. ед.

В результате общие затраты на доставку всей продукции для оптимального решения составляют 110 ден. ед.

10. Построение графа перевозок

Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.

В результате получится граф, аналогичный изображенному ниже:

Все, транспортная задача решена. Поздравляю!

Практическое применение транспортной задачи

Транспортная задача применяется во многих случаях. В частности:

• оптимизация поставок сырья и материалов на производственные предприятия;
• оптимизация доставок товаров со складов в розничные магазины;
• оптимизация пассажирских перевозок.

Это далеко не полный перечень возможностей прикладного использования транспортной задачи.

Галяутдинов Р.Р.

Источники

1. Галяутдинов Р. Р. Конспект лекций по логистике
2. Решение транспортной задачи в 1С: Предприятие 8. 2 // Волшебный форум (@romix). URL: http://kb.mista.ru/article.php?id=859 (дата обращения: 29.10.2013)
3. Транспортная задача // Википедия. URL: http://ru.wikipedia.org/wiki/Транспортная_задача (дата обращения: 29.10.2013)

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Транспортная задача и ее модификации

Линейное программирование применяется при расчете оптимальных режимов газопроводных магистралей, при выборе оптимальных зон тяготения потребителей к трубопроводам и нефтебазам, для выявления рациональных потоков нефти, нефтепродуктов и газа (различные модификации транспортной задачи) и др. Вопросы применения этих методов рассматриваются в специальной литературе [6, 27, 30, 33].  [c.79]
Возможны и другие усложнения транспортных задач. Конечно, все модификации, рассмотренные нами здесь, могут встречаться в транспортных моделях совместно, что не мешает сводить эти модели с помощью некоторых приемов к транспортной задаче замкнутого типа. Сейчас мы перейдем к рассмотрению одного вопроса также из области перевозок грузов, который, однако, к решению транспортной задачи уже не сводится.  [c.157]

Математическая постановка сводится к многопродуктовой многоэтапной транспортной задаче линейного программирования с учетом внутригодовой динамики потребления и сезонности работы автомобильного и речного транспорта [2]. Так как модель задачи является одной из модификаций транспортной задачи линейного программирования, то она может быть решена любым из алгоритмов решения транспортной задачи. Матрица такой задачи включает в себя Т блоков, каждый из которых моделирует условия многоэтапной, многопродуктовой транспортной задачи линейного программирования для одного временного отрезка года.  [c.77]

Транспортная задача и ее модификации  [c.131]

Классической транспортной задаче и различным ее модификациям и обобщениям посвящена обширная литература (см., например, библиографию к [81]). Стохастическая транспортная задача обсуждалась в (28, 66, 205, 311, 321, 325, 326, 341].

В приложениях значительный интерес представляет стохастическая постановка транспортной задачи, в которой предполагается, что спрос 6j — bj(ft>) в /-м пункте потребления случайная величина. Допустим вначале, что спрос bj непрерывно распределен с плотностью fpj(bj) [66, 326].  [c.35]

Классификация моделей. Статические однопродуктовые модели, сводящиеся к различным модификациям транспортной задачи. Специальные методы учета дополнительных ограничений. Производственные и производственно-транспортные модели. Многоэтапные и многопродуктовые модели. Динамические модели. Специальные методы реализации производственных и производственно-транспортных моделей. Экономико-математический анализ результатов решения задач оптимизации функционирования производственных систем.  [c.146]

Модификации стандартной транспортной задачи  [c.64]

Распределительные задачи решаются с помощью специальных вычислительных методов, представляющих собой модификацию методов решения транспортных задач. Частными видами таких задач являются  [c.29]

Для решения задач транспортного типа наиболее удобен метод потенциалов, Представляющий собой упрощенную модификацию симплексного метода. Алгоритм метода потенциалов рассматривается на следующем примере.  [c.138]

Небольшая модификация предложенных алгоритмов позволяет получить приближенную методику решения задачи с учетом фиксированных составляющих yij по маршруту г — > j. Для этого необходимо всякий раз сопоставлять выигрыш от уменьшения штрафов с транспортными расходами. В частности, для однородного случая это уменьшение штрафа за вычетом расходов, пропорциональных объему перевозки, составит  [c.226]

Возмоншы и другие усложнения задачи перевозки грузов. Конечно, все модификации, рассмотренные здесь, могут встречаться в транспортных моделях совместно, что, однако, не мешает сводить проблемы с помощью некоторых приемов к транспортной задаче исходного типа (4.2)—. (4.5).  [c.184]

Если же предположение о равенстве производителыюстей сделать нельзя, то приходится рассматривать Я-задачу. Алгоритмы решения А-задачи довольно эффективны, но все же с их помощью можно решать задачи меньшей размерности, чем для транспортных моделей. В обобщенной транспортной задаче возможны те же модификации, что и в обычной транспортной задаче.  [c.185]

РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ — упрощающая модификация более универсального симплексного метода линейного программирования, применимая для решения лишь нек-рого класса задач линейного программирования. Типичным примером задач этого класса являются т. и. транспортная задача линейного программирования (см. Перевозок план оптимальный) и задачи, формально-математически приводимые к той же модели.  [c.405]

Задачи математич. программирования делятся на задачи общего и спец. вида. Среди спец. задач в приложениях чаще других встречается т. н. транспортная задача — задача об оптимальной организации перевозок — п различные её модификации и обобщения. Методы, разработанные для решения задач трансн. типа, применяются также в системах СПУ (сетевого планирования и упрачлепия), обеспечивающих составление экономных текущих (оперативных) и перспективных планов в разных отраслях нар. х-ва. К математич. программированию относится теория двойственности, с помощью к-рой изучается связь между нарами т. н. двойственных или сопряжённых задач, характеризующих различные аспекты механизма оптимизации. Выводы теории двойственности позволяют сопоставить оптимальный план нронз-ва с системой оценок производственных факторов. Теория двойственности математич. программирования тесно связана с теорией игр.  [c.403]

Задача определения кратчайших маршрутов на заданной транспортной сети. Следует заметить, что для минимизации целевой функции ф( ж.. ) в транспортной задаче нужно, чтобы «стоимости» с.., входящие в выражение (2.3) для нее, уже были бы минимальны. Таким образом, возникает еще одна оптимизационная задача, связанная с отысканием «кратчайшего» маршрута LOT г-го склада до j-ro потребителя на заданной дорожной сети. Рассмотрим постановку этой задачи. Дана матрица dj длин участков дорожной сети, соединяющих узлы с номерами s и t. Если между какими-либо узлами дорожной сети нет прямого сообщения, то на соответствующем месте в матрице ничего не проставлено.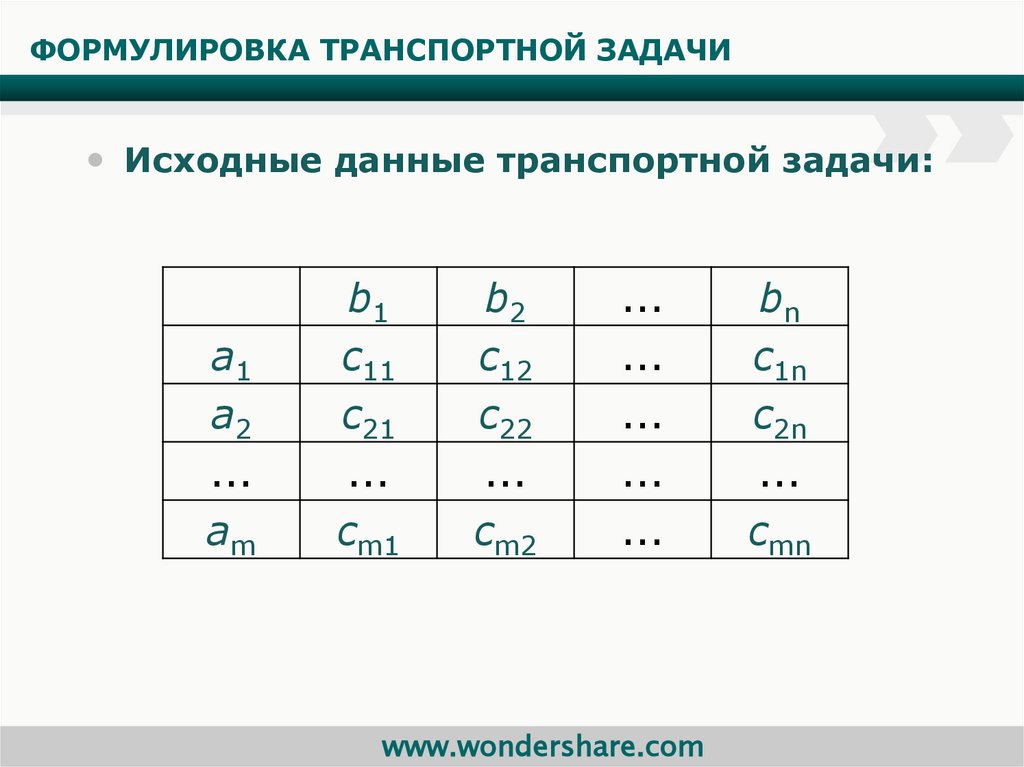 Заметим, что элемент ds( в общем случае может отличаться от элемента d(s в силу, например, одностороннего движения в том или ином направлении. Требуется определить кратчайший маршрут между узлом s и каким-либо другим узлом t. Для решения задачи исходные данные заносят в матрицу. Далее применяют или алгоритм Беллмана динамического программирования, или метод Дейкстры, который является его модификацией. Эти алгоритмы весьма просты, и справку по ним можно найти, например, в справочнике [39].  [c.161]

Модель задачи прогнозирования региональных транспортно-экономических связей по массовым светлым нефтепродуктам является одной из модификаций модели оптимального развития и размеще-ния нефтедобывающей и нефтеперерабатывающей промыцщен-ности, разработанной в ЦЭМИ АН СССР, и сводится к динамиче-  [c.92]

Решение возникающей задачи может быть осуществлено при помощи алгоритмов решения СТЗ ДО (однако их применение требует дополнительного обеспечения специальными приемами связности графа задачи) и алгоритмов, учитывающих блочный характер матрицы СТЗ.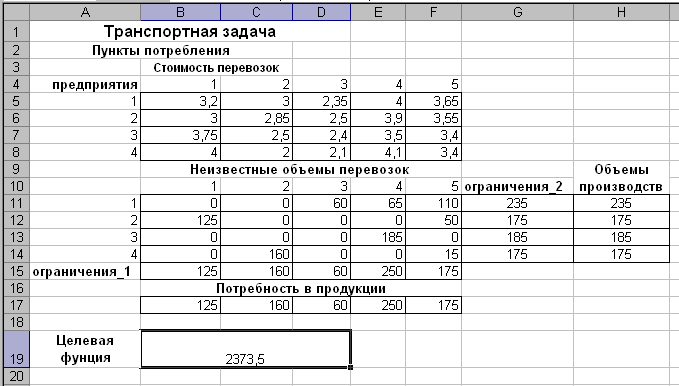 В статье [12] рассмотрены соответствующие модификации алгоритма К. В. Кима и известного метода декомпозиции. Вычислительные аспекты рассмотренных сетевых задач обсуждаются в статье [16]. В частности, соответствующие графы могут иметь большую размерность вследствие многократного дублирования (по числу продуктов) вершин и дуг исходной транспортной сети, однако на практике существует возможность существенного уменьшения этой размерности. В статье даются сравнительные оценки этих моделей для случая, когда возможно применение их обеих. Результаты весьма огра—ниченного эксперимента показали некоторую предпочтительность более частной модели.  [c.71]

TTF 2022

Hyatt Regency Sonoma Wine Country

Санта-Роза, Калифорния

5–8 апреля 2022 г.

Семинар TTF 2022 года будет совмещен с конференцией Sherwood Theory Conference 2022 года.

Повестка дня Шервуда доступна здесь.

Участники семинара могут получить доступ к презентациям и записям здесь

(пароль предоставлен, в случае его отсутствия свяжитесь с организаторами)

Даты проведения: 5-8 апреля 2022 г.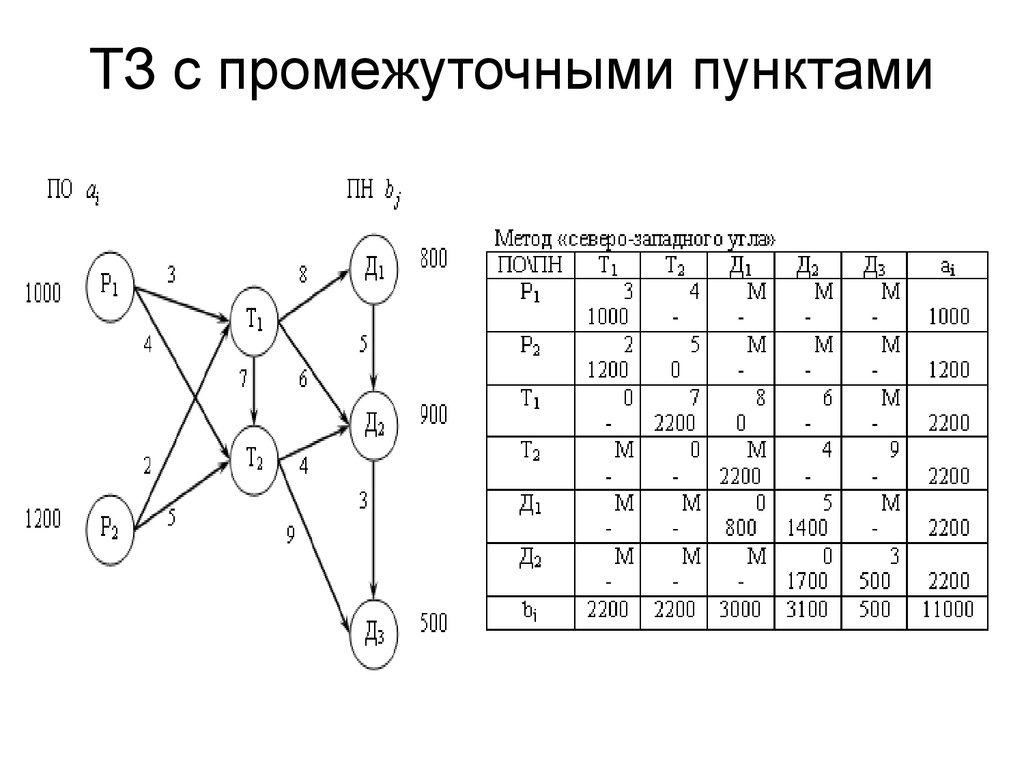

Осталось ограниченное количество бронирований отелей по нашей договорной цене: Пока нет

Пожалуйста, укажите здесь, если вы планируете посетить лично как можно скорее 18, 2022

Тезисы для стендовых докладов принимаются до 18 марта 2022 г.

Крайний срок подачи тезисов: 18 февраля 2022 г.

Крайний срок регистрации семинара по ценам раннего бронирования: 4 марта 2022 г.

Крайний срок бронирования мест в гостиницах: 4 марта 2022 г.

) заключается в разработке основанного на физике понимания переноса частиц, импульса и тепла в устройствах магнитного синтеза. Это понимание должно быть достаточно глубоким, чтобы оно позволяло разрабатывать прогностические модели переноса плазмы, которые можно было бы проверить экспериментально, а затем использовать для моделирования будущих характеристик сжигания плазмы в ИТЭР и термоядерных энергетических реакторах следующего шага. Чтобы добиться успеха в науке о переносе, важно охарактеризовать локальные флуктуации и перенос в термоядерной плазме, понять основные механизмы, ответственные за перенос, и, в конечном итоге, контролировать эти процессы переноса. Эти цели должны преследоваться в нескольких направлениях исследований, и основные темы семинара TTF развиваются, чтобы отражать новые достижения в понимании физики.

Predict First Initiative

Семинар 2022 года будет по-прежнему уделять особое внимание разработке и использованию транспортных средств для прогнозирования результатов экспериментов с современными исследовательскими установками термоядерной плазмы.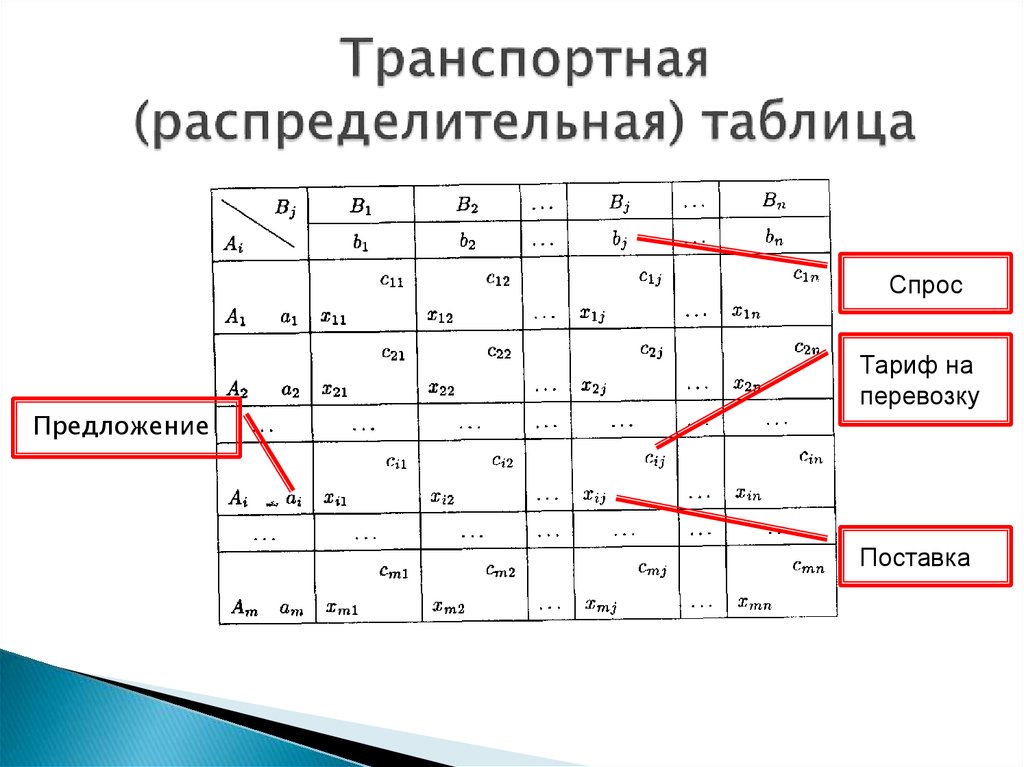 Эта инициатива Predict First повысит эффективность использования экспериментальной среды выполнения в ближайшем будущем и обеспечит более строгие проверочные тесты для теории, делающей следующий шаг к конечной цели TTF по созданию проверенных прогнозирующих транспортных моделей.

Мы намерены провести максимально возможное количество собраний лично. Однако мы понимаем, что ситуация с пандемией остается очень нестабильной и что не все участники будут чувствовать себя комфортно или смогут присутствовать лично. Встреча будет иметь значительный гибридный компонент: все выступления будут транслироваться в Zoom и виртуальная постерная сессия в дополнение к личным постерам. Обратите внимание, что стоимость регистрации будет одинаковой для очных и удаленных участников независимо от окончательного формата встречи.

Для тех, кто будет присутствовать на месте, мы будем принимать все разумные меры предосторожности, а также следовать указаниям Департамента общественного здравоохранения Калифорнии и Калифорнийского университета в Сан-Диего. В настоящее время правила не требуют подтверждения вакцинации или ношения маски в помещении (но это настоятельно рекомендуется), и поэтому мы также не будем требовать ни того, ни другого. Однако, учитывая, что это будет совместная встреча США и ЕС, а количество случаев заболевания в некоторых местах снова начинает расти, мы strongly encourage everyone to

1. Be fully vaccinated (including booster) if attending in-person

2. Wear a mask (ideally KN95 or better) while indoors

3. Пройдите тест на COVID-19 за 24–48 часов до поездки на встречу, даже если у вас нет симптомов

Хотя у многих работодателей есть правила, требующие вакцинации, помните, что она не защищает от инфекции , и что другие участники не могут быть вакцинированы сами или в их домохозяйстве есть непривитые лица (например, маленькие дети) или люди с ослабленным иммунитетом. Успешный семинар потребует особой осторожности и усердия со стороны участников, и мы просим всех быть внимательными и осторожными в отношении COVID. Обратите внимание, что все участники TTF (личные или виртуальные) должны соблюдать правила поведения на собраниях APS, доступные по адресу https://www.aps.org/meetings/policies/code-conduct.cfm. Это включает в себя уважение личного выбора других участников в отношении мер предосторожности COVID, вакцинации и ношения масок.

Поздняя регистрация Цена:

Студент: $200 | Общий: $400

Регистрация закрыта.

Хотите провести презентацию?

Прием тезисов завершен.

Министр транспорта приветствует окончательный отчет Национальной целевой группы по цепочке поставок

От: Transport Canada

Пресс-релиз

Крайне важно, чтобы канадцы своевременно получали доступные товары, особенно после последних 2,5 лет глобальной пандемии COVID-19. пандемия. Вот почему министр транспорта достопочтенный Омар Альгабра в начале этого года создал Национальную целевую группу по цепочке поставок для изучения ключевых вопросов, влияющих на работу цепочки поставок в Канаде. Задача Целевой группы заключалась в том, чтобы разработать рекомендации о том, как мы можем сделать нашу цепочку транспортных поставок более прочной, а жизнь канадцев — более доступной.

6 октября 2022 г.    Mississauga, Ontario    Transport Canada

Крайне важно, чтобы канадцы своевременно получали доступные товары, особенно после последних 2,5 лет глобальной пандемии COVID-19.пандемия. Вот почему министр транспорта достопочтенный Омар Альгабра в начале этого года создал Национальную целевую группу по цепочке поставок для изучения ключевых вопросов, влияющих на работу цепочки поставок в Канаде. Задача Целевой группы заключалась в том, чтобы разработать рекомендации о том, как мы можем сделать нашу цепочку транспортных поставок более прочной, а жизнь канадцев — более доступной.

Сегодня министр Альгабра приветствует окончательный отчет Целевой группы и с большим интересом изучает его. Заключительный отчет посвящен сферам деятельности, сотрудничеству и преобразованиям как всеобъемлющим темам для улучшения цепочки поставок в Канаде. Чтобы добиться реальных результатов для канадцев, было рекомендовано в общей сложности 21 действие.

Основные рекомендуемые действия в отчете включают:

• Снижение загруженности портов;
• Решение проблемы нехватки рабочей силы и удержания сотрудников;
• Создание федерального управления цепочки поставок для объединения соответствующей деятельности федерального правительства;
• Защита коридоров, пограничных переходов и шлюзов от разрушения;
• Разработка национальной стратегии цепочки поставок транспорта; и
• Привлечение Соединенных Штатов и провинций и территорий к взаимному признанию правил, политик и процессов.

Целевая группа провела обширные консультации, чтобы узнать мнение широкого круга заинтересованных сторон о приоритетных областях для краткосрочных и долгосрочных действий по уменьшению заторов, повышению надежности и повышению устойчивости в цепочке транспортных поставок Канады.

Укрепление нашей цепочки транспортных поставок в сотрудничестве с нашими провинциальными и территориальными партнерами является частью стратегии правительства Канады по реагированию на рост стоимости жизни и возвращению денег в карманы канадцев. Эффективная и устойчивая цепочка транспортных поставок является ключом к расширению экономического потенциала и производительности Канады и будет способствовать долгосрочному росту. Правительство Канады продолжит поддерживать канадцев посредством инвестиций в инфраструктуру и стратегии роста.

В будущем правительство Канады разработает Национальную стратегию цепочки поставок. Эта Стратегия будет основана на рекомендациях, включенных в окончательный отчет Целевой группы.

Котировки

«Обеспечение того, чтобы канадцы получали товары первой необходимости, было главным приоритетом для нашего правительства. За последние несколько месяцев я встречался с рядом партнеров по цепочке поставок и обсуждал проблемы и стратегии сотрудничества государственного и частного секторов, чтобы найти инновационные решения для уменьшения перегрузок по всей нашей цепочке поставок. Мы продолжаем работать над поиском ответов, чтобы цепочка поставок в Канаде оставалась эффективной и надежной. Я также хочу поблагодарить Национальную рабочую группу по цепочке поставок за их усилия в течение последних нескольких месяцев. Заключительный отчет Целевой группы окажется бесценным, поскольку Канада разрабатывает свою Национальную стратегию цепочки поставок» 9.0003

Достопочтенный Омар Альгабра
Министр транспорта

«Агентство пограничных служб Канады находится на переднем крае, содействуя торговле и поездкам в поддержку нашей экономики и канадского бизнеса. Мы продолжим работать с отраслевыми партнерами, чтобы обеспечить свободный поток законной торговли через границу, сохраняя при этом безопасность канадцев».

Достопочтенный Марко Э.Л. Мендичино
Министр общественной безопасности

«Пандемия вызвала массовые сбои на рынке труда, что привело к нехватке рабочих рук во многих отраслях, включая транспорт. По мере того, как наша экономика восстанавливается и растет, мы должны делать инвестиции и вносить изменения, которые не только устранят эти сбои, но и укрепят нашу рабочую силу в долгосрочной перспективе. Заключительный отчет Национальной целевой группы по цепочке поставок и ее рекомендации будут иметь решающее значение для этой работы, помогая нам принимать обоснованные стратегические решения».

Достопочтенная Карла Куалтроу
Министр занятости, развития рабочей силы и интеграции инвалидов Канады

«Мы благодарим министра транспорта за честь служить и предоставить нам возможность проконсультироваться с представителями отрасли со всей страны, чтобы получить всестороннее представление о приоритетах цепочки поставок Канады. Мы надеемся, что итоговый отчет Целевой группы по национальной цепочке поставок послужит ориентиром для обсуждений и сотрудничества, которые приведут к улучшению национальной цепочки поставок транспортных средств».

Жан Гаттузо и Луиза Яко
Сопредседатели, Целевая группа по национальной цепочке поставок

Краткие факты

• 31 января 2022 года министр транспорта провел национальный саммит по цепочке поставок. На саммите собрались федеральные министры, предприятия, лидеры отрасли и ассоциации, чтобы обсудить проблемы, стоящие перед нашей цепочкой поставок.

• Во время национального саммита по цепям поставок было объявлено о создании Национальной рабочей группы по цепям поставок.

• Целевой группе было поручено предоставить экспертные консультации и рекомендации в отношении действий, которые могут быть предприняты на всех уровнях правительства и промышленности для улучшения цепочки поставок Канады. Целевая группа опубликовала свой окончательный отчет 6 октября 2022 г.

• Правительство Канады через Национальный фонд торговых коридоров (NTCF) осуществляет инвестиции, которые будут поддерживать движение товаров по цепочкам поставок Канады.

• В бюджете

  на 2022 год было выделено 450 миллионов долларов в течение пяти лет, начиная с 2022–2023 годов, для поддержки проектов цепочки поставок через Национальный фонд торговых коридоров (NTCF), что поможет упростить перемещение товаров по транспортным сетям Канады. Благодаря этому дополнительному финансированию общий объем ассигнований на программу за 11 лет (2017–2028 годы) превысит 4,6 млрд долларов США.

• В 2021 году международная торговля товарами составила около 1,24 триллиона долларов, что на 16,8% больше, чем в 2020 году, и является самым высоким годовым объемом торговли за всю историю наблюдений.

• За последние два года спрос на потребительские товары в Северной Америке был выше, чем в среднем по миру, примерно на 5 процентных пунктов (8% против 3%), что оказывает большее давление, чем где-либо еще, на цепочки поставок транспортных средств.

• Транспортные расходы были основной движущей силой ускорения общего роста цен в 2021 году и выросли на 7,2% по сравнению с 2020 годом, опередив все основные категории инфляции. Действуя в соответствии с ключевыми рекомендациями, содержащимися в отчете Целевой группы, мы поможем снизить инфляционное давление и ускорить экономический рост».

Связанные ссылки

• Целевая группа по цепочке поставок
• Январь 2022 г.

  No related posts.