Транспортная задача: Транспортная задача онлайн

3. Практическая часть. Транспортная задача.

3.1.Поиск оптимальных решений с помощью линейных транспортных задач

Одной из главных задач макроэкономической науке является разработка различных методов наилучшего распределения ограниченных трудовых, материальных, финансовых, временных и других ресурсов для оптимального управления предприятиями. Наиболее подходящем инструментом решения проблем оптимизации является линейное программирование – один из разделов математического программирования.

«Линейное программирование – это метод поиска неотрицательных значений переменных, максимизирующих или минимизирующих значение линейной целевой функции при наличии ограничений, заданных в виде линейных неравенства.

Метод нахождения решения основной задачи линейного программирования, получивший название “симплексный метод” или “метод решения с помощью мультипликатора”, независимо друг от друга открыли в 1940г. советский учёный Л. В. Канторович и американский математик Дж. Данциг.

Разновидностью общей задачи линейного программирования является так называемая транспортная задача, применяемая как для оптимизации перевозки грузов, таки в ряде друг их приложений.

Формальным признаком транспортной задачи является то, что каждая переменная входит лишь в два ограничения, причем с коэффициентами, равными единице. Если при этом критерий оптимальности (сумма расходов, общий пробег) прямо пропорционален значениям переменных (транспортных потоков), возникает линейная транспортная задача. В других случаях рассматривается нелинейная транспортная задача, решаемая другими методами.

Транспортные задачи известны в двух постановках: матричной и сетевой»⁸.

3.2. Алгоритм решения транспортной задачи9

Постановка задачи: Пусть имеется m поставщиков и n потребителей. Мощность поставщиков и спросы потребителей, а так же затраты на перевозку груза для каждой пары «поставщик – потребитель» задаются таблицей.

поставщики	потребители	В1	В2	…	Вj	…	Bn	Мощность поставщиков
A1		С11	С12		С1j		С1n	a1
A2		С21	С22		С2j		С2n	a2
…		…	…		…		…
Ai		Сij	Сij		Сij		Сin	ai
…		…	…		…		…
Am		Cm1	Cm2		Cmj		Cmn	am
Спрос потребителей		b1	b2		bj		bn

Найти объемы перевозок каждой пары «поставщик – потребитель» так, чтобы: мощности всех поставщиков были реализованы; спросы всех потребителей были удовлетворены; суммарные затраты на перевозку были бы максимальны.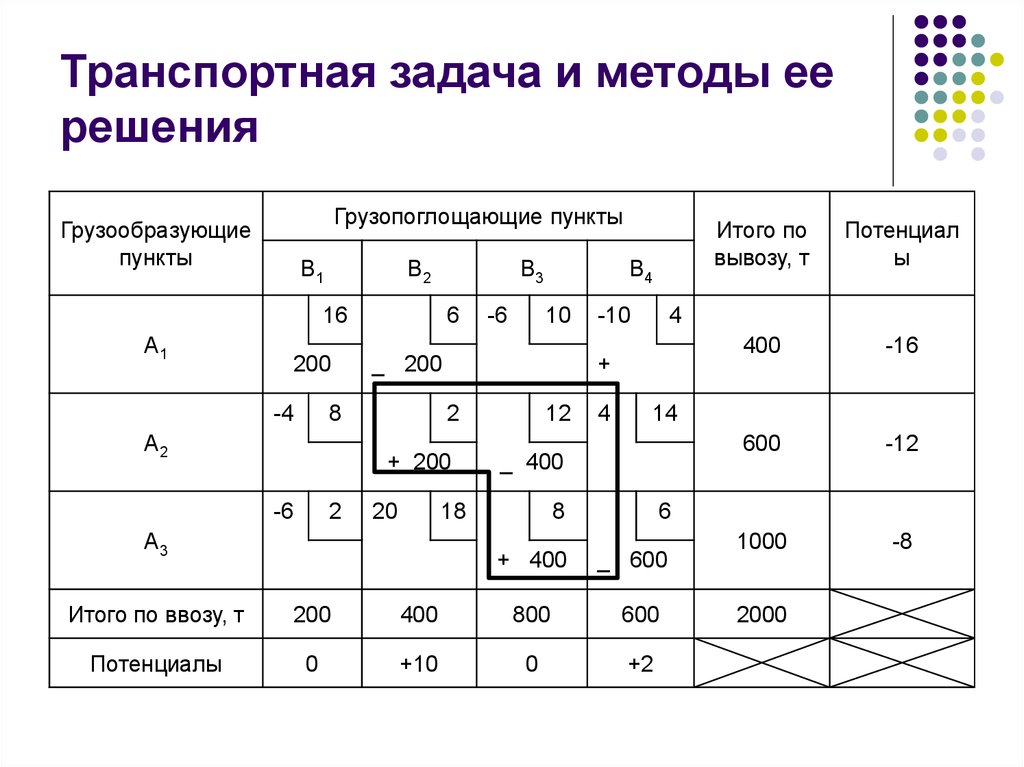

Особенности математической модели транспортной задачи:

• система ограничений есть система уравнений;

• коэффициенты при неизвестных системы ограничений равны единицы или нулю;

• каждая переменная входит в систему ограничений два раза: один раз в систему ограничений поставок, второй раз – в систему ограничений спроса.

Математическая модель транспортной задачи.

Пусть хij – количество груза, перевозимого с i-го в j-й пункт.

Целевая функция:

Система ограничений:

Для решения задачи составляется таблица. В клетки таблицы записывается стоимость соответствующих перевозок сij и в них же заносятся значения перевозок xij, удовлетворяющих поставленным ограничениям. Клетки с не нулевыми перевозками называются базисными, а с нулевыми – свободными.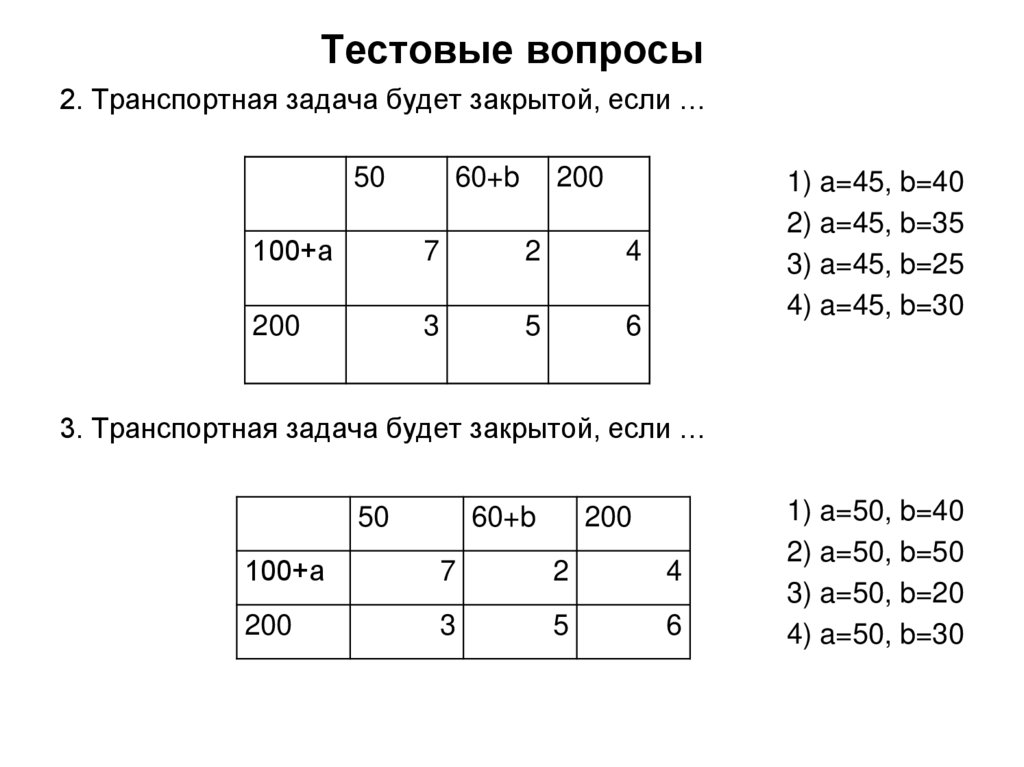

В зависимости от соотношения между запасами и заявками транспортная задача называется сбалансированной или несбалансированной.

Сбалансированная ТЗ:

Несбалансированная ТЗ:

Для сбалансированной ТЗ ограничения принимают вид равенств, то есть получаем m+n ограничений, в которых все переменные линейно зависимы. В результате допустимое решение сбалансированной ТЗ может быть получено, если заполнять клетки транспортной таблицы таким образом, чтобы сумма перевозок в каждой строке должна быть равна запасам ai, а сумма перевозок в каждом столбце равна соответствующей заявке вj. Вариантов заполнения транспортной таблицы множество, поэтому искомым решением является то из допустимых решений, для которых общая стоимость перевозок будет минимальной.

Методы решения транспортной задачи.

Транспортная задача может быть решена симплекс методом. Однако специфическая форма системы ограничений позволяет упростить симплекс метод.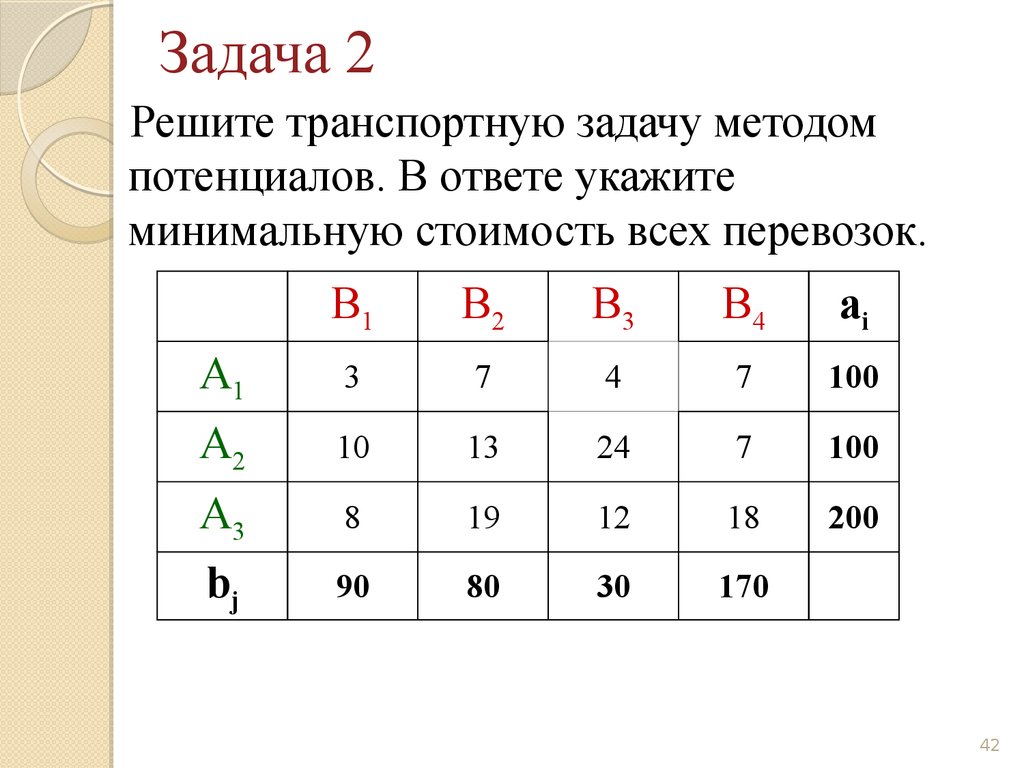

Метод северо-западного угла.

Заполнение клеток происходит последовательно по следующему алгоритму: сначала вывозится груз из пункта А1 и завозится в пункт В1, и этой перевозке х11 присваивается максимально возможное значение. Если заявка пункта В1 выполнена, а в пункте А1 еще остается груз, то он вывозится в пункт В2 и т.д. Если в пункте А1 недостаточно было груза для В1, то недостающий груз берется из А2 и т.д. После того как спрос потребителя А1 удовлетворен, он выпадает из рассмотрения и т.д.

Существенным недостатком метода северо-западного угла является то, что он построен без учета стоимости перевозок.

Метод минимального элемента.

Заполнение клеток транспортной таблицы начинается с той клетки, в которой значение минимально. В нее записывается максимально возможное значение перевозки хij, которое может быть равно либо запасу аi, либо заявке вj. Если заявка вj выполнена полностью, то j-й столбец больше не рассматривается. Если не вывезенный груз еще остался, то он вывозится в пункт с наименьшим тарифом.

Распеределенный метод улучшения плана перевозок.

Для улучшения плана используют цикл транспортной таблицы. Цикл – это несколько клеток, соединенных замкнутой ломанной с прямыми углами.

Изобразим два цикла: А1В1, А1В2, А2В2, А2В1; А1В3,А1В4, А2В4, А2В6, А1В5, А4В5, А4В3.

поставщики	потребители	В1	В2	В3	В4	В5	B6	Мощность поставщиков
A1		С11	С12	С13	С14	С15	С16	a1
A2		С21	С22	С23	С24	С25	С26	a2
A3		С31	С32	С33	С34	С35	С36	a3
А4		С41	С42	С43	С44	С45	С46	а4
A5		С51	С52	С53	С54	С55	С56	a5
Спрос потребителей		b1	b2	в3	b4	в5	b6

Каждый цикл имеет четное число вершин и ребер, то есть в таблице в каждой строке или столбце может находиться только четное число клеток, содержащих вершины.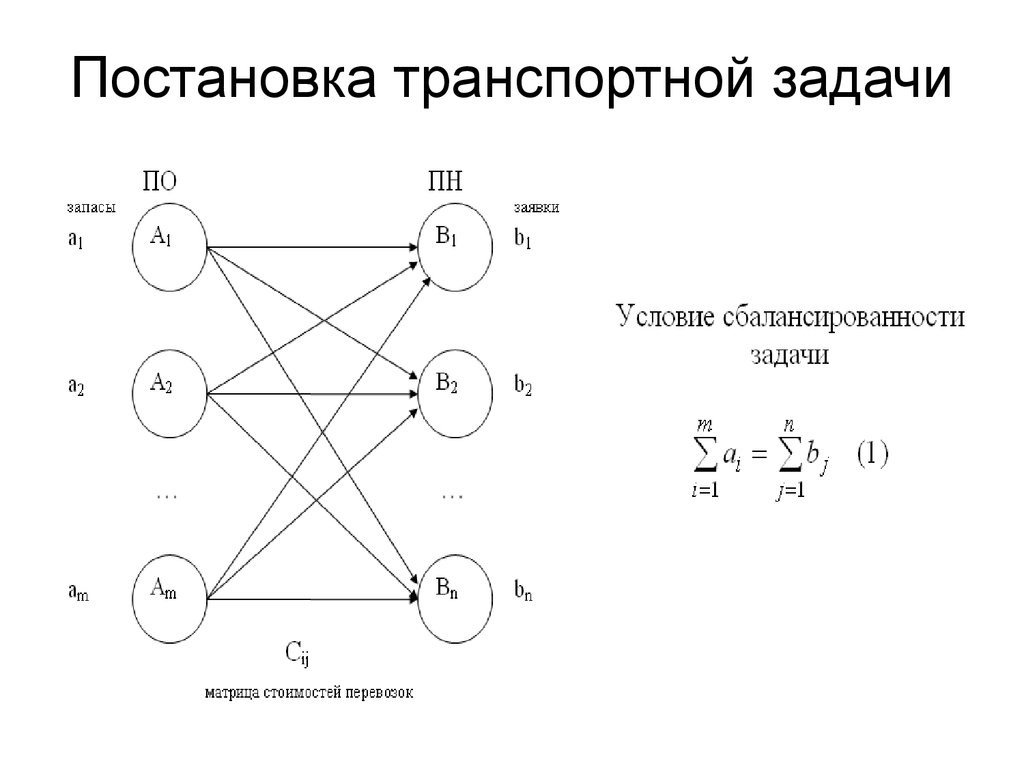 Поэтому в клетках-вершинах можно менять значения перевозки так, что в сумма по строкам и столбцам не изменяется. Вершины цикла, в которых увеличиваем перевозки «+», а в которых уменьшаем перевозки «-». Величину изменения обозначим ∆, ее будем перемещать по циклу. Максимальное значение ∆, на которое можно уменьшить перевозку, определяется условием неотрицательности перевозок.

Цена цикла q – это изменение стоимости перевозок при перемещении ∆ по циклу, которая равна разности между суммой стоимостей перевозок, соответствующих «+»-ым вершинам и суммой стоимостей «-» -ых вершин.

Q1= (с11+с22)-(с12+с21)

Q2 = (с13+с24+с16+с45)-(с14+с26+с15+с43)

При переносе по циклу к единиц груза, стоимость цикла и стоимость плана перевозок измениться на к единиц. Для улучшения плана перевозок нужно найти «-» цикл и переместить по нему максимально возможное количество груза, до тех пор пока таких циклов не останется. Количество груза, которое можно переместить определяется минимальным значением перевозок в «-» вершинах цикла.

Публикации по ключевому слову «транспортная задача»

---

Логистика, экономическая безопасность

Дата публикации: 19.10.2016 г.

Оцените материал Средняя оценка: 0 (Всего: 0)

Каравайцева Арина Андреевна , студентка
ФГБОУ ВО «Поволжский государственный технологический университет», Марий Эл Респ

«Решение транспортных задач с помощью теории графов»

В данной работе исследуется транспортная задача по составлению оптимального плана перевозки грузов с помощью теории графов, применяется принцип решения транспортных задач с помощью теории графов, рассматривается решение транспортной задачи на примере.

Экономические науки

Дата публикации: 28.09.2016 г.

Оцените материал Средняя оценка: 5 (Всего: 1)

Каравайцева Арина Андреевна , студентка
ФГБОУ ВО «Поволжский государственный технологический университет», Марий Эл Респ

«Применение дельта-метода при решении транспортных задач»

В данной статье исследуется транспортная задача по составлению оптимального плана перераспределения и перевозки продуктов с помощью дельта-метода.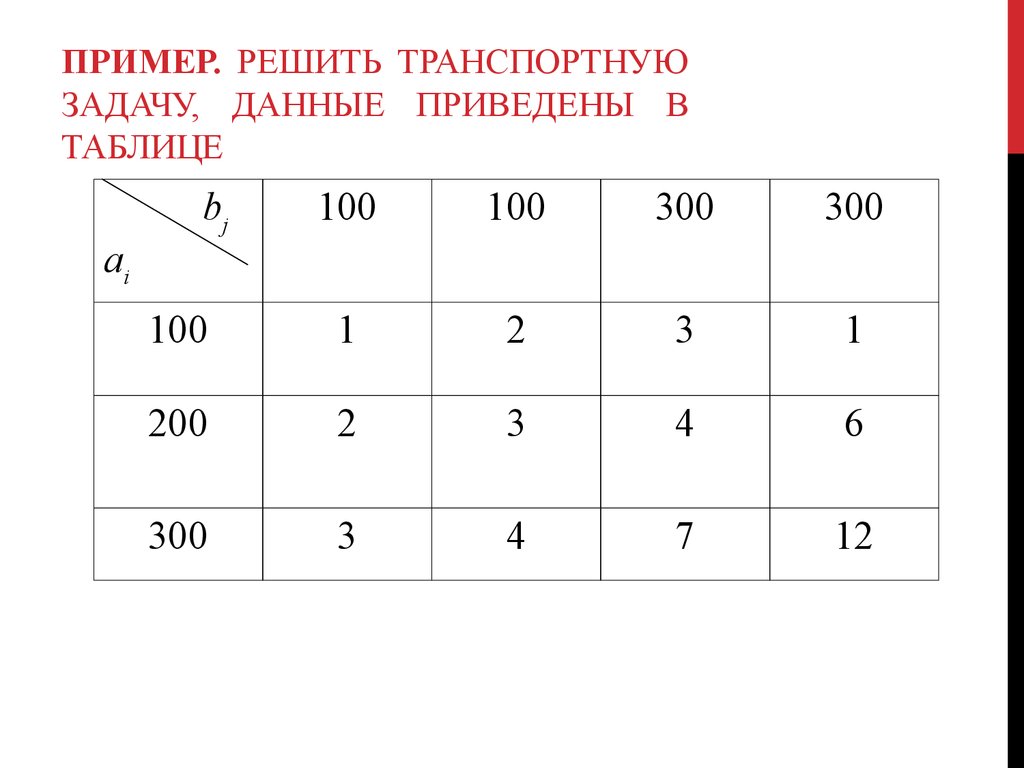

Технические науки

Дата публикации: 08.08.2016 г.

Оцените материал Средняя оценка: 3 (Всего: 2)

Лебедева Лариса Владимировна , канд. физ.-мат. наук , старший преподаватель
ФГАОУ ВО «Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского», Нижегородская обл

«О разработке учебных задач по теме «Транспортная задача линейного программирования»»

В работе предлагается способ выбора параметров математической модели закрытой транспортной задачи линейного программирования, оптимальное решение которой стандартным методом потенциалов определяется за малое количество шагов.

Математические методы и информационные технологии в экономике

Дата публикации: 15.03.2016 г.

Оцените материал Средняя оценка: 5 (Всего: 1)

Марданов Марат Вадимович , канд. пед. наук, доцент , доцент, преподаватель спецдисциплин
ГАПОУ «Казанский автотранспортный техникум им. А.П. Обыденнова», Татарстан Респ

«Оптимизация выпуска продукции в условиях волатильности рынка: модифицированная модель транспортной задачи»

В статье рассматривается применение математического моделирования для оптимизации производства продукции, основанном на модифицированной модели транспортной задачи. Автором приводится решение поставленной задачи средствами информационных технологий.

Экономика (экономическая теория, финансы, бухгалтерский учет, статистика и др.)

Дата публикации: 03.06.2015 г.

Оцените материал Средняя оценка: 5 (Всего: 1)

Золотарюк Анатолий Васильевич , канд. техн. наук , доцент
ФГОБУ ВО «Финансовый университет при Правительстве Российской Федерации», Москва г

«Математическая модель многокритериальной оптимизации транспортных перевозок»

В данной статье анализируются процессы транспортных перевозок и факторы, снижающие их эффективность. Формулируется математическая постановка транспортной многокритериальной оптимизационной задачи, и рассматриваются пути ее решения на основе парето‐оптимальных методов либо с помощью интеллектуального нейросетевого прогнозирования. Отмечаются направления и возможности использования результатов оптимизационной задачи транспортными компаниями и в учебном процессе вузов.

Логистика

Дата публикации: 28.09.2016 г.

Оцените материал Средняя оценка: 1 (Всего: 1)

Каравайцева Арина Андреевна , студентка
ФГБОУ ВО «Поволжский государственный технологический университет», Марий Эл Респ

«Применение дельта-метода при решении транспортных задач»

В работе исследуется транспортная задача по составлению оптимального плана перераспределения и перевозки продуктов с помощью дельта-метода.

IPEEC — Целевая группа по транспорту (TTG)

Главная страница > Целевая группа по транспорту (TTG)

Целевая группа по транспорту (TTG) была создана Группой двадцати с целью: энергетическое и экологическое воздействие автомобильного транспорта, особенно большегрузных транспортных средств (БТС).

Выявление и обмен передовым опытом среди стран G20 по внедрению экономически эффективных мер по повышению энергоэффективности и контролю выбросов в транспортном секторе.

Провести анализ и информационно-разъяснительную работу для оценки возможностей, барьеров, затрат и преимуществ действий по повышению энергоэффективности HDV, а затем рекомендовать курс действий для участвующих стран G20.

Почему транспорт важен для энергоэффективности?

Членство и управление

Ведущие члены: США.
Участники: Австралия, Бразилия, Канада, Китай, ЕС, Германия, Индия, Италия, Япония, Я, Россия и Великобритания. В число организаций-исполнителей входят Международный совет по чистому транспорту (ICCT) и Глобальная инициатива по экономии топлива (GFEI). ЕС, Италия и я являемся членами Руководящего комитета TTG.

Последние разработки

За последние несколько месяцев TTG достигла ряда важных результатов:

• Проведен опрос стран-участниц об их институциональных потребностях и технических проблемах для информирования разработки дорожных карт политики, в которых будут изложены будущие политические и программные улучшения для снижения энергопотребления и воздействия на окружающую среду автотранспортных средств, особенно тяжелых транспортных средств.
• Разработан отчет ( Удары Правил мирового класса по эффективности транспортных средств и выбросам в отдельных странах G20 ), в котором оценивается влияние внедрения стандартов эффективности и выбросов мирового класса в странах TTG в соответствии с Ведущей программой G20 по энергоэффективности.
• Возглавлял обмен опытом и передовой практикой по ключевым вопросам, включая соблюдение и правоприменение, устойчивые альтернативные виды топлива, глобальные усилия по внедрению топлива с низким содержанием серы, а также внутренний опыт в ЕС и Мексике.

Кроме того, TTG разработала и закрепила строгие формулировки в Ведущей программе энергоэффективности G20, которая включала первое в истории многостороннее признание и определение стандартов чистого топлива и транспортных средств «мирового класса». Определение стандартов «мирового класса» имеет важное значение для оценки возможного воздействия таких стандартов и принятия дальнейших политических мер. Анализ, проведенный одной из организаций-исполнителей TTG, ICCT, показал, что внедрение этих стандартов «мирового класса» только в странах TTG может обратить вспять рост транспортных выбросов и избежать выбросов CO2 в несколько гигатонн в год в 2040 году по сравнению с принятой в настоящее время политикой. сценарий.

Публикации

• Отчет G20 HDV (ICCT)
• Отчет G20 LDV (GFEI)

Последние публикации для этой целевой группы можно найти на странице Publications .

Дополнительная информация

• Международный совет по чистому транспорту
• Глобальная инициатива по экономии топливав результате Транспортного саммита штата Миссури, созванного Миссури с нарушениями развития 1 августа 2019 года в Колумбии, штат Миссури.

  Краткое изложение обсуждавшихся тем и тем, определенных 100 участниками саммита 1 августа, можно найти здесь: Отчет о транспортном саммите

  Миссия Целевой группы по транспорту штата Миссури: «обеспечивать лидерство, способствовать сотрудничеству , а также собрать передовой опыт для улучшения координации транспорта в штате Миссури, чтобы повысить качество жизни всех жителей штата Миссури за счет улучшения доступа к транспорту, доступности и доступности».

  Чтобы узнать больше о Целевой группе по транспорту или принять участие в будущих встречах, свяжитесь с Кэти Бингхэм по адресу [email protected] , чтобы добавить ее в список рассылки по электронной почте.

  Список заинтересованных сторон

  • • Список заинтересованных сторон
      • текущий список заинтересованных сторон
    Повестка дня саммита Целевой группы по транспорту
    • • Программа саммита
      • Флаер саммита виртуальной мобильности 2022 г., где вы можете найти информацию для регистрации на саммит 9.0008
      • События | ЗСТ (dot.gov)

  Повестка дня

  • • Повестка дня
    • Август 2022 г. Повестка дня
    • Апрель 2022 г. Повестка дня
    • Июль 2022 г. Повестка дня

  Презентации

  • • Мартовская презентация
    • Декабрь Презентация

   

   

   

   

   

   

   

  Заседания рабочей группы и материалы

  СИЗ и руководство по ресурсам финансирования для специализированных транспортных компаний

  2022

  • Сентябрь
    • Протокол встречи
  • апреля
    •  Протокол собрания
  • марта
    • Протокол собрания
  • февраля
    • Протокол собрания
  • 22 января 2022 г.
    • Протокол встречи

  2021

  • 21 декабря 2021 г.
    • Минуты
  • 21 ноября 2021 г.
    • Минуты
  • 5 октября 2021 г.
    • Минуты
  • 6 июля 2021 г.
    • Минуты
  • 1 июня 2021 г.
    • Минуты
  • 4 мая 2021 г.
    • Минуты
  • 2 февраля 2021 г.
    • Минуты
  • 13 января 2021 г.
    • Протокол исполнительного собрания

  2020

  • 1 декабря 2020 г.
    • Минуты
  • Руководство по финансированию средств индивидуальной защиты
  • 6 октября 2020 г.
    • Минуты
  • 4 августа 2020 г.
    • Минуты
    Презентация
    • «Распределение затрат для поставщиков транспортных услуг»
  • 2 июня 2020 г.
    • Минуты
  • 5 мая 2020 г.

    No related posts.