Уравнение с корнями как решить: Иррациональные уравнения — урок. Алгебра, 8 класс.

2+6} \approx 13 + \frac{6}{2 \cdot 13} \approx 13,23 $

Содержание

Уравнение и его корни: определения, примеры

После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.

Понятие уравнения

Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:

Определение 1

Уравнением называется равенство с неизвестным числом, которое нужно найти.

Принято обозначать неизвестные маленькими латинскими буквами, например, t, r, m др., но чаще всего используются x, y, z. Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.

Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x=5, y=6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x+7=38, z−4=2, 8·t=4, 6:x=3.

После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7·(x−1) =19, x+6·(x+6·(x−8))=3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x+2+4·x−2−x=10. Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x·(8+1)−7=8, 3−3=z+3 или 8·x−9=2·(x+17).

Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.

В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:

Определение 2

Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.

То есть, к примеру, выражение x+3=6·x+7 – это уравнение с переменной x, а 3·y−1+y=0 – уравнение с переменной y.

В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:

Определение 3

Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.

К примеру, равенство вида 3,7·x+0,6=1 является уравнением с одной переменной x, а x−z=5 – уравнением с двумя переменными x и z. Примером уравнения с тремя переменными может быть выражение x2+(y−6)2+(z+0,6)2=26.

Корень уравнения

Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.

Пример 1

Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a+1=5 мы заменим букву числом 2, то равенство станет неверным, а если 4, то получится верное равенство 4+1=5.

Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.

Определение 4

Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.

Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.

Пример 2

Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a+1=5. Согласно определению, корнем в данном случае будет 4, потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2+1=5.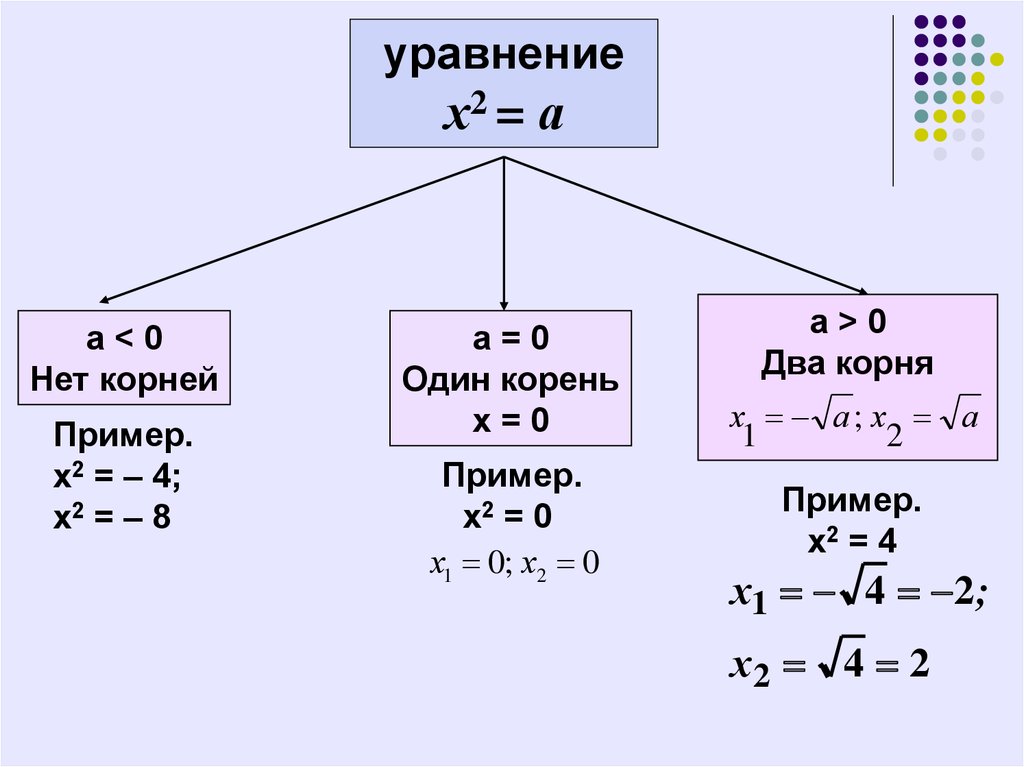

Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.

Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0·x=5. Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0.

Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.

Пример 3

Так, в уравнении x−2=4 есть только один корень – шесть, в x2=9 два корня – три и минус три, в x·(x−1)·(x−2)=0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.

Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅. Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня -2, 1 и 5, то пишем -2, 1, 5 или {-2, 1, 5}.

Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y, а корнями являются 2 и 7, то мы пишем y=2 и y=7. Иногда к буквам добавляются нижние индексы, например, x1=3, x2=5. Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N, целых – Z, действительных – R. Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x∈Z, а если любое действительное от единицы до девяти, то y∈1, 9.

Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.

Определение 5

Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.

Поясним определение на примерах.

Пример 4

Допустим, у нас есть выражение x+y=7, которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4, то равенство станет верным, значит, мы нашли решение.

Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как (3,4).

На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.

4.2: Решение уравнений с корнями

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 19645

Ларри Грин
Общественный колледж Лейк-Тахо

Результаты обучения

Решение уравнений, содержащих квадратные корни. 2 \nonnumber \]
Так как квадрат и квадратный корень сокращаются, мы получаем:
\[x-3=16 \нечисло \]
Наконец, прибавляя 3 к обеим сторонам, получаем:
\[x=19 \нечисло \]
Всегда полезно проверить свою работу. Мы делаем это, снова подключая ответ и проверяя, работает ли он. Подставляем $x=19$, чтобы получить
\[ \begin{align*}2+\sqrt{19-3} &=2+\sqrt{16} \\[4pt] &=2+4 \\[4pt] &= 6 \end{align*}\]
Да, решение верное.
Пример $\PageIndex{2}$
Стандартное отклонение $\sigma_\hat p$ выборочного распределения для пропорции следует формуле:
\[\sigma_\hat p=\sqrt {\ frac {p \ left (1-p \ right)} {n}} \ nonumber \]
Где $p$ — доля населения, а $n$ — размер выборки. Если доля генеральной совокупности составляет 0,24 и вам нужно, чтобы стандартное отклонение выборочного распределения было равно 0,03, то какой размер выборки вам нужен?
Раствор
Нам дано, что $p=0,24$ и $\sigma_{\hat p} = 0,03 $
Подставьте значение, чтобы получить:
\[0,03=\sqrt{\frac{0,24\left(1) -0.
24\right)}{n}} \nonumber \]
Мы хотим найти $n$, поэтому нам нужно $n$ в левой части уравнения. Просто переключитесь, чтобы получить:
\[\sqrt{\frac{0,24\left(1-0,24\right)}{n}}\:=\:0,03 \nonumber \]
Далее вычитаем:
\ [1-0,24\:=\:0,76\номер \]
И их умножить:
\[0,24\влево(0,76\вправо)=0,1824\номер\] 92 \nonumber \]
Квадрат отменяет квадратный корень, и возведение в квадрат правой части дает:
\[\frac{0.1824}{n}\:=\:0.0009 \nonumber \]
Мы можем написать:
\[\frac{0,1824}{n}\:=\frac{\:0,0009}{1} \nonumber \]
Перемножить, чтобы получить:
\[0,0009\:n\:=\:0,1824 \nonumber \]
Наконец, разделите обе части на 0,0009:
\[n\:=\frac{\:0,1824}{0,0009}=202,66667 \nonumber \]
Округлив, мы можем сделать вывод, что нам нужен размер выборки 203, чтобы получить стандартную ошибку 0,03. Мы можем проверить, разумно ли это, подставив $n = 203$ обратно в уравнение. С помощью калькулятора получаем:

\[\sqrt{\frac{0,24\left(1-0,24\right)}{203}}\:=\:0,029975 \nonumber \]
Поскольку это очень близко к 0,03, ответ разумен.
Упражнение
Стандартное отклонение $\sigma_\bar x$ выборочного распределения среднего значения определяется по формуле:
\[\sigma_\bar x=\frac{\sigma}{\sqrt{n }} \nonumber \]
Где $\sigma $ — стандартное отклонение генеральной совокупности, а $n$ — размер выборки. Если стандартное отклонение генеральной совокупности составляет 3,8, а стандартное отклонение выборочного распределения должно быть равно 0,5, то какой размер выборки вам нужен?
- Упражнение 1: Решение основного радикального уравнения — квадратные корни
- https://youtu.be/u1aGMkJIlMI
Эта страница под названием 4.2: Решение уравнений с корнями распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована Ларри Грином.
1. Наверх
- Была ли эта статья полезной?
1. Тип изделия
  Раздел или Страница
  Автор
  Ларри Грин
  Лицензия
  CC BY-NC-SA
  Показать страницу TOC
  нет
  Включено
  да
2. Теги
  92} члены в одной части уравнения, сохраняя константы в противоположной части. 2} в левой части, добавив обе части на + 1. Затем решите значения x, взяв квадратные корни из обеих частей уравнения. Как я упоминал ранее, нам нужно прикрепить символ плюс или минус к квадратному корню из константы. 92} слагаемых, по одному с каждой стороны уравнения. Мой подход состоит в том, чтобы собрать все квадраты x в левой части и объединить все константы в правой части. Затем найдите x как обычно, как в примерах 1 и 2.
  Решения этой квадратной формулы: x = 3 и x = — \,3.
  Пример 4 : Решите приведенное ниже квадратное уравнение, используя метод квадратного корня.
  Две скобки не должны вас беспокоить. Факт остается фактом: все переменные имеют квадратную форму, а это то, что нам нужно. Эта задача прекрасно решается методом квадратного корня. 92} термы слева и константы справа. Наконец, примените операцию извлечения квадратного корня с обеих сторон, и все готово!
  Не так уж и плохо, правда?
  Пример 5 : Решите приведенное ниже квадратное уравнение, используя метод квадратного корня.
  No related posts.