Трехмерные графики. Анимация — Решение математических задач в Maple
График поверхности, заданной явной функцией.
График функции z = f(x, y) можно нарисовать, используя команду plot3d(f(x,y), x=x1…x2, y=y1…y2, options). Параметры этой команды частично совпадают с параметрами команды plot. К часто используемым параметрам команды plot3d относится light=[angl1, angl2, c1, c2, c3] – задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами (angl1, angl2). Цвет определяется долями красного (c1), зеленого (c2) и синего (c3) цветов, которые находятся в интервале [0,1]. Параметр style=opt задает стиль рисунка: POINT –точки, LINE – линии, HIDDEN – сетка с удалением невидимых линий, PATCH – заполнитель (установлен по умолчанию), WIREFRAME – сетка с выводом невидимых линий,
 Параметр shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по
умолчанию, NONE – без раскраски.
Параметр shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по
умолчанию, NONE – без раскраски.В качестве примера построим график функции f=sin(x)+cos(y).
График поверхности, заданной параметрически.
Если требуется построить поверхность, заданную параметрически: x=x(u,v), y=y(u,v), z=z(u,v), то эти функции перечисляются в квадратных скобках в команде: plot3d([x(u,v), y(u,v), z(u,v)], u=u1..u2, v=v1..v2).
График поверхности, заданной неявно.
Трехмерный
график поверхности, заданной неявно уравнением F(x, y,z) =c, строится с помощью
команды пакета plot: implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1. 2=4.
2=4.
График пространственных кривых.
В пакете plot имеется команда spacecurve для построения пространственной кривой, заданной параметрически: x = x(t), y = y(t),z = z(t). Параметры команды:
> spacecurve([x(t),y(t),z(t)],t=t1..t2),
где переменная t изменяется от t1 до t2.
Построим график пространственной кривой х=sin(t), у=cos(t), z=exp(t).
Анимация.
Maple позволяет выводить на экран движущиеся изображения с помощью команд animate (двумерные) и animate3d (трехмерные) из пакета plot. Среди параметров команды animate3d есть
Что такое 3D графика?
Вступление
Вопрос о том, что же является двигателем всей компьютерной индустрии, давно заботит многих пользователей. То ли это фирма Intel, которая, не переставая, выпускает и выпускает новые процессоры. Но кто тогда заставляет их покупать? Может, во всем виноват Microsoft, который непрерывно делает свои окна больше и краше? Да нет, можно ведь довольствоваться старыми версиями программ — тем более спектр их возможностей практически не изменяется. Вывод напрашивается сам собой — во всем виноваты игры. Да, именно игры стремятся все более и более уподобиться реальному миру, создавая его виртуальную копию, хотят все более мощных ресурсов.
Вся история компьютерной графики на PC является тому подтверждением. Вспомните, в начале были тетрисы, диггеры, арканоиды. Вся графика заключалась в перерисовке небольших участков экрана, спрайтов, и нормально работала даже на XT. Но прошли те времена. Взошла звезда симуляторов.
С выходом таких игр, как F19, Formula 1 и т. п., в которых приходилось уже перерисовывать весь экран, предварительно заготавливая его в памяти, всем нам пришлось обзавестись, по крайней мере, 286 процессором. Но прогресс на этом не остановился. Желание уподобить виртуальный мир в игре реальному миру усилилось, и появился Wolf 3D.
п., в которых приходилось уже перерисовывать весь экран, предварительно заготавливая его в памяти, всем нам пришлось обзавестись, по крайней мере, 286 процессором. Но прогресс на этом не остановился. Желание уподобить виртуальный мир в игре реальному миру усилилось, и появился Wolf 3D.
Это, можно сказать, первая 3D-игра, в которой был смоделирован какой-никакой, но все же реалистичный мир. Для его реализации пришлось использовать верхнюю (более 640 Кб) память и загнать программу в защищенный режим. Для полноценной игры пришлось установить процессор 80386. Но и мир Wolf 3D страдал недостатками. Хотя стены и были не просто одноцветными прямоугольниками, но для их закраски использовались текстуры с небольшим разрешением, поэтому поверхности смотрелись прилично лишь на расстоянии. Конечно, можно было пойти по пути наращивания разрешения текстур, вспомним, например, DOOM. Тогда нам пришлось снова перейти на более новый процессор и увеличить количество памяти. Правда, все равно, хотя изображение и улучшилось, но ему были присущи все те же недостатки. Да и плоские объекты и монстры — кому это интересно. Тут то и взошла звезда Quake. В этой игре был применен революционный подход — z-буфер, позволивший придать объемность всем объектам. Однако вся игра все равно работала в невысоком разрешении и не отличалась высокой реалистичностью.
Да и плоские объекты и монстры — кому это интересно. Тут то и взошла звезда Quake. В этой игре был применен революционный подход — z-буфер, позволивший придать объемность всем объектам. Однако вся игра все равно работала в невысоком разрешении и не отличалась высокой реалистичностью.
Назревало новое аппаратное решение. И решение это оказалось, в общем-то, лежащим на поверхности. Раз пользователи хотят играть в трехмерном виртуальном мире, то процесс его создания (вспомним минуты ожидания, проведенные за 3D Studio перед появлением очередной картинки) надо кардинально ускорить. А раз центральный процессор с этой задачей справляется из рук вон плохо, было принято революционное решение — сделать специализированный.
Тут то и вылез производитель игровых автоматов 3Dfx, сделавший эту сказку былью с помощью своего графического процессора Voodoo. Человечество сделало еще один шаг в виртуальный мир.
А поскольку операционной системы на PC с текстурными окнами, уплывающими назад, в туман, пока нет, и не предвидится, весь аппарат трехмерной графики можно пока применить только к играм, что успешно делает все цивилизованное человечество.
Модель
Для изображения трехмерных объектов на экране монитора требуется проведение серии процессов (обычно называемых конвейером) с последующей трансляцией результата в двумерный вид. Первоначально, объект представляется в виде набора точек, или координат, в трехмерном пространстве. Трехмерная система координат определяется тремя осями: горизонтальной, вертикальной и глубины, обычно называемых, соответственно осями x, y и z. Объектом может быть дом, человек, машина, самолет или целый 3D мир и координаты определяют положение вершин (узловых точек), из которых состоит объект, в пространстве. Соединив вершины объекта линиями, мы получим каркасную модель, называемую так из-за того, что видимыми являются только края поверхностей трехмерного тела. Каркасная модель определяет области, составляющие поверхности объекта, которые могут быть заполнены цветом, текстурами и освещаться лучами света.
Рис. 1: Каркасная модель куба
Даже при таком упрощенном объяснении конвейера 3D графики становится ясно, как много требуется вычислений для прорисовки трехмерного объекта на двумерном экране. Можно представить, насколько увеличивается объем требуемых вычислений над системой координат, если объект движется.
Можно представить, насколько увеличивается объем требуемых вычислений над системой координат, если объект движется.
Рис. 2: Модель самолета с закрашенными поверхностями
Роль API
Программируемый интерфейс приложений (API) состоит из функций, управляющих 3D конвейером на программном уровне, но при этом может использовать преимущества аппаратной реализации 3D, в случае наличия этой возможности. Если имеется аппаратный ускоритель, API использует его преимущества, если нет, то API работает с оптимальными настройками, рассчитанными на самые обычные системы. Таким образом, благодаря применению API, любое количество программных средств может поддерживаться любым количеством аппаратных 3D ускорителей.
Для приложений общего и развлекательного направления, существуют следующие API:
- Microsoft Direct3D
- Criterion Renderware
- Argonaut BRender
- Intel 3DR

Для профессиональных приложений, работающих под управлением WindowsNT доминирует интерфейс OpenGL. Компания Autodesk, крупнейший производитель инженерных приложений, разработала свой собственный API, называемый Heidi.
Свои API разработали и такие компании, как Intergraph — RenderGL, и 3DFX — GLide.
Существование и доступность 3D интерфейсов, поддерживающих множество графических подсистем и приложений, увеличивает потребность в аппаратных ускорителях трехмерной графике, работающих в режиме реального времени. Развлекательные приложения, главный потребитель и заказчик таких ускорителей, но не стоит забывать и о прфессиональных приложениях для обработки 3D графики, работающих под управлением Windows NT, многие из которых переносятся с высокопроизводительных рабочих станций, типа Silicon Graphics, на PC платформу. Интернет приложения сильно выиграют от невероятной маневренности, интуитивности и гибкости, которые обеспечивает применение трехмерного графического интерфейса. Взаимодействие в World Wide Web будет гораздо проще и удобнее, если будет происходить в трехмерном пространстве.
Графический ускоритель
Рынок графических подсистем до появления понятия малтимедиа был относительно прост в развитии. Важной вехой в развитии был стандарт VGA (Video graphics Array), разработанный компанией IBM в 1987 году, благодаря чему производители видеоадаптеров получили возможность использовать более высокое разрешение (640х480) и большую глубину представления цвета на мониторе компьютера. С ростом популярности ОС Windows, появилась острая потребность в аппаратных ускорителях двумерной графики, чтобы разгрузить центральный процессор системы, вынужденный обрабатывать дополнительные события. Отвлечение CPU на обработку графики существенно влияет на общую производительность GUI (Graphical User Interface) — графического интерфеса пользователя, а так как ОС Windows и приложениям для нее требуется как можно больше ресурсов центрального процессора, обработка графики осуществлялась с более низким приоритетом, т.е. делалась очень медленно. Производители добавили в свои продукты функции обработки двумерной графики, такие, как прорисовка окон при открытии и свертовании, аппаратный курсор, постоянно видимый при перемещении указателя, закраска областей на экране при высокой частоте регенерации изображения. Итак, появился процессор, обеспечивающий ускорение VGA (Accelerated VGA — AVGA), также известный, как Windows или GUI ускоритель, который стал обязательным элементом в современных компьютерах.
Итак, появился процессор, обеспечивающий ускорение VGA (Accelerated VGA — AVGA), также известный, как Windows или GUI ускоритель, который стал обязательным элементом в современных компьютерах.
Внедрение малтимедиа создало новые проблемы, вызванные добавлением таких компонентов, как звук и цифровое видео к набору двумерных графических функций. Сегодня легко заметить, что многие продукты AVGA поддерживают на аппаратном уровне обработку цифрового видео. Следовательно, если на Вашем мониторе видео проигрывается в окне, размером с почтовую марку — пора установить в Вашей машине малтимедиа ускоритель. Малтимедиа ускоритель (multimedia accelerator) обычно имеет встроенные аппаратные функции, позволяющие масштабировать видеоизображение по осям x и y, а также аппаратно преобразовывать цифровой сигнал в аналоговый, для вывода его на монитор в формате RGB. Некоторые малтимедиа акселлераторы могут также иметь встроенные возможности декомпресси цифрового видео.
Разработчики графических подсистем должны исходить из требований, частично диктуемых размерами компьютерного монитора, частично под влиянием GUI, и частично под влиянием графического процессора. Первичный стандарт VGA с разрешением 640х480 пикселов был адекватен 14″ мониторам, наиболее распространенных в то время. Сегодня наиболее предпочтительны мониторы с размером диагонали трубки 17″, благодаря возможности выводить изображения с разрешением 1024х768 и более.
Первичный стандарт VGA с разрешением 640х480 пикселов был адекватен 14″ мониторам, наиболее распространенных в то время. Сегодня наиболее предпочтительны мониторы с размером диагонали трубки 17″, благодаря возможности выводить изображения с разрешением 1024х768 и более.
Основной тенденцией при переходе от VGA к малтимедиа ускорителям была возможность размещения как можно больше визуальной информации на мониторе компьютера. Использование 3D графики является логичным развитием этой тенденции. Огроммные объемы визуальной информации могут быть втиснуты в ограниченное пространство экрана монитора, если она представляется в трехмерном виде. Обработка трехмерной графики в режиме реального времени дает возможность пользователю легко оперировать представляемыми данными.
Игровые двигатели (Games engines)
Первое правило компьютерных игр — нет никаких правил. Традиционно, разработчики игр больше заинтересованы в крутой графике своих программ, чем следованию рекомендаций технарей. Не взирая на то, что в распоряжении разработчиков имеется множество трехмерных API, например — Direct3D, некоторые программисты идут по пути создания собственного 3D игрового интерфейса или двигателя. Собственные игровые двигатели — один из путей для разработчиков добиться невероятной реалистичности изображения, фактически на пределе возможностей графического программирования.
Не взирая на то, что в распоряжении разработчиков имеется множество трехмерных API, например — Direct3D, некоторые программисты идут по пути создания собственного 3D игрового интерфейса или двигателя. Собственные игровые двигатели — один из путей для разработчиков добиться невероятной реалистичности изображения, фактически на пределе возможностей графического программирования.
Нет ничего более желанного для разработчика, чем иметь прямой доступ к аппаратным функциям компонентов системы. Несколько известных разработчиков создали свои собственные игровые двигатели, работающие с оптимальным использованием аппаратных ускорителей графики, которые принесли им известность и деньги. Например, двигатели Interplay для Descent II и id Software для Quake, обеспечивают истинную трехмерность действия, используя наполную аппаратные функции 3D, если они доступны.
Графика без компромисов
Разговоры, ведущиеся уже довольно долгое время, о перспективах применения трехмерной графики в таких областях, как развлечения и бизнес, допредела подогрели интерес потенциальных пользователей, на рынке уже появился новый тип продуктов. Эти новые технологические решения, совмещают в себе великолепную поддержку 2D графики, соответствующую сегодняшним требованиям к Windows акселлераторам, аппаратную поддержку функций 3D графики и проигрывают цифровое видео с требуемой частотой смены кадров.
Эти новые технологические решения, совмещают в себе великолепную поддержку 2D графики, соответствующую сегодняшним требованиям к Windows акселлераторам, аппаратную поддержку функций 3D графики и проигрывают цифровое видео с требуемой частотой смены кадров.
В принципе, эти продукты можно смело отнести к новому поколению графических подсистем, обеспечивающих графику без компромиссов, занимающих достойное место стандартного оборудования в настольных вычислительных системах.
Среди представителей нового поколения можно назвать, в качестве примера, следующие продукты:
- процессор Ticket-To-Ride компании Number Nine Visual Technologies
- серия процессоров ViRGE компании S3 Inc.
- процессор RIVA128, разработанный совместно компаниями SGS Thomson и nVidia
Технология 3D-графики
Пусть нам все-таки удалось убедить Вас попробовать трехмерную графику в действии (если Вы до сих пор не сделали это), и Вы решили сыграть в одну из трехмерных игр, предназначенных для применения 3D-видеокарты.
Допустим, такой игрой оказался симулятор автомобильных гонок, и Ваша машина уже стоит на старте, готовая устремиться к покорению новых рекордов. Идет предстартовый обратный отсчет, и Вы замечаете, что вид из кабины, отображаемый на экране монитора, немного отличается от привычного.
Вы и прежде участвовали в подобных гонках, но впервые изображение поражает Вас исключительным реализмом, заставляя поверить в действительность происходящего. Горизонт, вместе с удаленными объектами, тонет в утренней дымке. Дорога выглядит необычайно ровно, асфальт представляет собой не набор грязно-серых квадратов, а однотонное покрытие с нанесенной дорожной разметкой. Деревья вдоль дороги действительно имеют лиственные кроны, в которых, кажется, можно различить отдельные листья. От всего экрана в целом складывается впечатление как от качественной фотографии с реальной перспективой, а не как от жалкой попытки смоделировать реальность.
Попробуем разобраться, какие же технические решения позволяют 3D-видеокартам передавать виртуальную действительность с такой реалистичностью. Каким образом изобразительным средствам PC удалось достигнуть уровня профессиональных студий, занимающихся трехмерной графикой.
Каким образом изобразительным средствам PC удалось достигнуть уровня профессиональных студий, занимающихся трехмерной графикой.
Часть вычислительных операций, связанных с отображением и моделированием трехмерного мира переложено теперь на 3D-акселератор, который является сердцем 3D-видеокарты. Центральный процессор теперь практически не занят вопросами отображения, образ экрана формирует видеокарта. В основе этого процесса лежит реализация на аппаратном уровне ряда эффектов, а также применение несложного математического аппарата. Попробуем разобраться, что же конкретно умеет графический 3D-процессор.
Возвращаясь к нашему примеру с симулятором гонок, задумаемся, каким образом достигается реалистичность отображения поверхностей дороги или зданий, стоящих на обочине. Для этого применяется распространенный метод, называемый текстурирование (texture mapping).
Это самый распространенный эффект для моделирования поверхностей. Например, фасад здания потребовал бы отображения множества граней для моделирования множества кирпичей, окон и дверей. Однако текстура (изображение, накладываемое на всю поверхность сразу) дает больше реализма, но требует меньше вычислительных ресурсов, так как позволяет оперировать со всем фасадом как с единой поверхностью. Перед тем, как поверхности попадают на экран, они текстурируются и затеняются. Все текстуры хранятся в памяти, обычно установленной на видеокарте. Кстати, здесь нельзя не заметить, что применение AGP делает возможным хранение текстур в системной памяти, а ее объем гораздо больше.
Однако текстура (изображение, накладываемое на всю поверхность сразу) дает больше реализма, но требует меньше вычислительных ресурсов, так как позволяет оперировать со всем фасадом как с единой поверхностью. Перед тем, как поверхности попадают на экран, они текстурируются и затеняются. Все текстуры хранятся в памяти, обычно установленной на видеокарте. Кстати, здесь нельзя не заметить, что применение AGP делает возможным хранение текстур в системной памяти, а ее объем гораздо больше.
Очевидно, что когда поверхности текстурируются, необходим учет перспективы, например, при отображении дороги с разделительной полосой, уходящей за горизонт. Перспективная коррекция необходима для того, чтобы текстурированные объекты выглядели правильно. Она гарантирует, что битмэп правильно наложится на разные части объекта — и те, которые ближе к наблюдателю, и на более далекие.
Коррекция с учетом перспективы очень трудоемкая операция, поэтому нередко можно встретить не совсем верную ее реализацию.
При наложении текстур, в принципе, также можно увидеть швы между двумя ближайшими битмэпами. Или, что бывает чаще, в некоторых играх при изображении дороги или длинных коридоров заметно мерцание во время движения. Для подавления этих трудностей применяется фильтрация (обычно Bi- или tri-линейная).
Билинейная фильтрация — метод устранения искажений изображения. При медленном вращении или движении объекта могут быть заметны перескакивания пикселов с одного места на другое, что и вызывает мерцание. Для снижения этого эффекта при билинейной фильтрации для отображения точки поверхности берется взвешенное среднее четырех смежных текстурных пикселов.
Трилинейная фильтрация несколько сложнее. Для получения каждого пиксела изображения берется взвешенное среднее значение результатов двух уровней билинейной фильтрации. Полученное изображение будет еще более четкое и менее мерцающее.
Текстуры, с помощью которых формируется поверхность объекта, изменяют свой вид в зависимости от изменения расстояния от объекта до положения глаз зрителя. При движущемся изображении, например, по мере того, как объект удаляется от зрителя, текстурный битмэп должен уменьшаться в размерах вместе с уменьшением размера отображаемого объекта. Для того чтобы выполнить это преобразование, графический процессор преобразует битмэпы текстур вплоть до соответствующего размера для покрытия поверхности объекта, но при этом изображение должно оставаться естественным, т.е. объект не должен деформироваться непредвиденным образом.
При движущемся изображении, например, по мере того, как объект удаляется от зрителя, текстурный битмэп должен уменьшаться в размерах вместе с уменьшением размера отображаемого объекта. Для того чтобы выполнить это преобразование, графический процессор преобразует битмэпы текстур вплоть до соответствующего размера для покрытия поверхности объекта, но при этом изображение должно оставаться естественным, т.е. объект не должен деформироваться непредвиденным образом.
Для того, чтобы избежать непредвиденных изменений, большинство управляющих графикой процессов создают серии предфильтрованных битмэпов текстур с уменьшенным разрешением, этот процесс называется mip mapping. Затем, графическая программа автоматически определяет, какую текстуру использовать, основываясь на деталях изображения, которое уже выведено на экран. Соответственно, если объект уменьшается в размерах, размер его текстурного битмэпа тоже уменьшается.
Но вернемся в наш гоночный автомобиль. Сама дорога уже выглядит реалистично, но проблемы наблюдаются с ее краями! Вспомните, как выглядит линия, проведенная на экране не параллельно его краю. Вот и у нашей дороги появляются «рваные края». И для борьбы с этим недостатком изображения применяется anti-aliasing.
Вот и у нашей дороги появляются «рваные края». И для борьбы с этим недостатком изображения применяется anti-aliasing.
| Рваные края | Ровные края |
|---|
Мы подходим к ключевому моменту функционирования всех 3D-алгоритмов. Предположим, что трек, по которому ездит наша гоночная машина, окружен большим количеством разнообразных объектов — строений, деревьев, людей.
Тут перед 3D-процессором встает главная проблема, как определить, какие из объектов находятся в области видимости, и как они освещены. Причем, знать, что видимо в данный момент, недостаточно. Необходимо иметь информацию и о взаимном расположении объектов. Для решения этой задачи применяется метод, называемый z-буферизация. Это самый надежный метод удаления скрытых поверхностей. В так называемом z-буфере хранятся значения глубины всех пикселей (z-координаты). Когда рассчитывается (рендерится) новый пиксел, его глубина сравнивается со значениями, хранимыми в z-буфере, а конкретнее с глубинами уже срендеренных пикселов с теми же координатами x и y. Если новый пиксел имеет значение глубины больше какого-либо значения в z-буфере, новый пиксел не записывается в буфер для отображения, если меньше — то записывается.
Необходимо иметь информацию и о взаимном расположении объектов. Для решения этой задачи применяется метод, называемый z-буферизация. Это самый надежный метод удаления скрытых поверхностей. В так называемом z-буфере хранятся значения глубины всех пикселей (z-координаты). Когда рассчитывается (рендерится) новый пиксел, его глубина сравнивается со значениями, хранимыми в z-буфере, а конкретнее с глубинами уже срендеренных пикселов с теми же координатами x и y. Если новый пиксел имеет значение глубины больше какого-либо значения в z-буфере, новый пиксел не записывается в буфер для отображения, если меньше — то записывается.
Z-буферизация при аппаратной реализации сильно увеличивает производительность. Тем не менее, z-буфер занимает большие объемы памяти: например даже при разрешении 640×480 24-разрядный z-буфер будет занимать около 900 Кб. Эта память должна быть также установлена на 3D-видеокарте.
Разрешающая способность z-буфера — самый главный его атрибут. Она критична для высококачественного отображения сцен с большой глубиной. Чем выше разрешающая способность, тем выше дискретность z-координат и точнее выполняется рендеринг удаленных объектов. Если при рендеринге разрешающей способности не хватает, то может случиться, что два перекрывающихся объекта получат одну и ту же координату z, в результате аппаратура не будет знать какой объект ближе к наблюдателю, что может вызвать искажение изображения.
Чем выше разрешающая способность, тем выше дискретность z-координат и точнее выполняется рендеринг удаленных объектов. Если при рендеринге разрешающей способности не хватает, то может случиться, что два перекрывающихся объекта получат одну и ту же координату z, в результате аппаратура не будет знать какой объект ближе к наблюдателю, что может вызвать искажение изображения.
Для избежания этих эффектов профессиональные платы имеют 32-разрядный z-буфер и оборудуются большими объемами памяти.
Кроме вышеперечисленных основ, трехмерные графические платы обычно имеют возможность воспроизведения некоторого количества дополнительных функций. Например, если бы Вы на своем гоночном автомобиле въехали бы в песок, то обзор бы затруднился поднявшейся пылью. Для реализации таких и подобных эффектов применяется fogging (затуманивание). Этот эффект образуется за счет комбинирования смешанных компьютерных цветовых пикселов с цветом тумана (fog) под управлением функции, определяющей глубину затуманивания. С помощью этого же алгоритма далеко отстоящие объекты погружаются в дымку, создавая иллюзию расстояния.
С помощью этого же алгоритма далеко отстоящие объекты погружаются в дымку, создавая иллюзию расстояния.
Реальный мир состоит из прозрачных, полупрозрачных и непрозрачных объектов. Для учета этого обстоятельства, применяется alpha blending — способ передачи информации о прозрачности полупрозрачных объектов. Эффект полупрозрачности создается путем объединения цвета исходного пиксела с пикселом, уже находящимся в буфере.
В результате цвет точки является комбинацией цветов переднего и заднего плана. Обычно, коэффициент alpha имеет нормализованное значение от 0 до 1 для каждого цветного пиксела. Новый пиксел = (alpha)(цвет пиксела А) + (1 — alpha)(цвет пиксела В).
Очевидно, что для создания реалистичной картины происходящего на экране необходимо частое обновление его содержимого. При формировании каждого следующего кадра, 3D-акселератор проходит весь путь подсчета заново, поэтому он должен обладать немалым быстродействием. Но в 3D-графике применяются и другие методы придания плавности движению. Ключевой — Double Buffering.
Ключевой — Double Buffering.
Представьте себе старый трюк аниматоров, рисовавших на уголках стопки бумаги персонаж мультика, со слегка изменяемым положением на каждом следующем листе. Пролистав всю стопку, отгибая уголок, мы увидим плавное движение нашего героя. Практически такой же принцип работы имеет и Double Buffering в 3D анимации, т.е. следующее положение персонажа уже нарисовано, до того, как текущая страница будет пролистана. Без применения двойной буферизации изображение не будет иметь требуемой плавности, т.е. будет прерывистым. Для двойной буферизации требуется наличие двух областей, зарезервированных в буфере кадров трехмерной графической платы; обе области должны соответствовать размеру изображения, выводимого на экран. Метод использует два буфера для получения изображения: один для отображения картинки, другой для рендеринга. В то время как отображается содержимое одного буфера, в другом происходит рендеринг. Когда очередной кадр обработан, буфера переключаются (меняются местами). Таким образом, играющий все время видит отличную картинку.
Таким образом, играющий все время видит отличную картинку.
В заключение обсуждения алгоритмов, применяемых в 3D-графических акселераторах, попробуем разобраться, каким же образом применение всех эффектов по отдельности позволяет получить целостную картину. 3D-графика реализуется с помощью многоступенчатого механизма, называемого конвейером рендеринга.
Применение конвейерной обработки позволяет еще ускорить выполнение расчетов за счет того, что вычисления для следующего объекта могут быть начаты до окончания вычислений предыдущего.
Конвейер рендеринга может быть разделен на 2 стадии: геометрическая обработка и растеризация.
На первой стадии геометрической обработки выполняется преобразование координат (вращение, перенос и масштабирование всех объектов), отсечение невидимых частей объектов, расчет освещения, определение цвета каждой вершины с учетом всех световых источников и процесс деления изображения на более мелкие формы. Для описания характера поверхности объекта она делится на всевозможные многоугольники.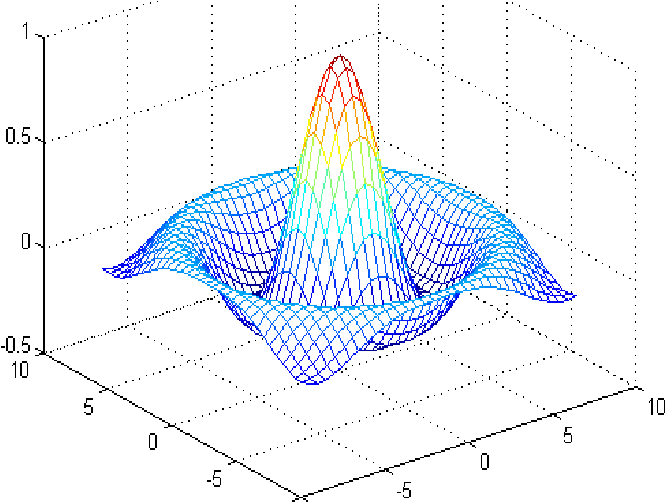
Наиболее часто при отображении графических объектов используется деление на треугольники и четырехугольники, так как они легче всего обсчитываются и ими легко манипулировать. При этом координаты объектов переводятся из вещественного в целочисленное представление для ускорения вычислений.
На второй стадии к изображению применяются все описанные эффекты в следующей последовательности: удаление скрытых поверхностей, наложение с учетом перспективы текстур (используя z-буфер), применение эффектов тумана и полупрозрачности, anti-aliasing. После этого очередная точка считается готовой к помещению в буфер со следующего кадра.
Из всего вышеуказанного можно понять, для каких целей используется память, установленная на плате 3D-акселератора. В ней хранятся текстуры, z-буфер и буфера следующего кадра. При использовании шины PCI, использовать для этих целей обычную оперативную память нельзя, так как быстродействие видеокарты существенно будет ограничено пропускной способностью шины. Именно по этому для развития 3D-графики особенно перспективно продвижение шины AGP, позволяющее соединить 3D-чип с процессором напрямую и тем самым организовать быстрый обмен данными с оперативной памятью. Это решение, к тому же, должно удешевить трехмерные акселераторы за счет того, что на борту платы останется лишь немного памяти собственно для кадрового буфера.
Именно по этому для развития 3D-графики особенно перспективно продвижение шины AGP, позволяющее соединить 3D-чип с процессором напрямую и тем самым организовать быстрый обмен данными с оперативной памятью. Это решение, к тому же, должно удешевить трехмерные акселераторы за счет того, что на борту платы останется лишь немного памяти собственно для кадрового буфера.
Заключение
Повсеместное внедрение 3D-графики вызвало увеличение мощности компьютеров без какого-либо существенного увеличения их цены. Пользователи ошеломлены открывающимися возможностями и стремятся попробовать их у себя на компьютерах. Множество новых 3D-карт позволяют пользователям видеть трехмерную графику в реальном времени на своих домашних компьютерах. Эти новые акселераторы позволяют добавлять реализм к изображениям и ускорять вывод графики в обход центрального процессора, опираясь на собственные аппаратные возможности.
Хотя в настоящее время трехмерные возможности используются только в играх, думается, деловые приложения также смогут впоследствии извлечь из них выгоду. Например, средства автоматизированного проектирования уже нуждаются в выводе трехмерных объектов. Теперь создание и проектирование будет возможно и на персональном компьютере благодаря открывающимся возможностям. Трехмерная графика, возможно, сможет также изменить способ взаимодействия человека с компьютером. Использование трехмерных интерфейсов программ должно сделать процесс общения с компьютером еще более простым, чем в настоящее время.
Например, средства автоматизированного проектирования уже нуждаются в выводе трехмерных объектов. Теперь создание и проектирование будет возможно и на персональном компьютере благодаря открывающимся возможностям. Трехмерная графика, возможно, сможет также изменить способ взаимодействия человека с компьютером. Использование трехмерных интерфейсов программ должно сделать процесс общения с компьютером еще более простым, чем в настоящее время.
Что такое 3D-графика – База знаний Timeweb Community
Под понятие 3D-графики можно отнести двухмерные изображения с элементами объема, который придается за счет работы с освещением и другими элементами, создающими на экране визуальную иллюзию. Еще к 3D-графике относятся полноценные трехмерные модели, создаваемые в специальных программах и применяемые в играх, кинематографе и мультипликации.
Далее я предлагаю детальнее остановиться на этом типе графики, разобраться во всех ее тонкостях, характеристиках и принципах создания при помощи современных технологий.
Что такое 3D-изображение
Для начала остановимся на 3D-изображениях и поймем, что вообще делает их трехмерными и какие типы картинок можно отнести к этой категории. Если при просмотре изображения вы можете описать ширину и высоту, но не наблюдаете глубины, значит, это двухмерная графика. Значки на рабочем столе и указатели на улицах – все это относится к 2D-графике (за некоторым исключением, когда художник использует тень или другие приемы, чтобы сделать картинку объемной). 3D-изображение обязательно обладает глубиной, то есть является объемным. Простой пример такой графики вы видите на следующем изображении:
Если нарисовать квадрат, представив только основные его четыре линии, это будет двухмерная модель. Но если немного повернуть квадрат, дорисовать грани и вершины, получится куб, являющийся объемным элементом, а значит, к нему относится характеристика 3D-модели.
История развития 3D
Полноценное представление 3D-элементов на экране мир увидел в короткометражном фильме «A Computer Animated Hand», вышедшем в 1972 году. На скриншоте ниже вы видите то, как аниматоры смогли спроектировать человеческую руку и анимировать ее на экране.
На скриншоте ниже вы видите то, как аниматоры смогли спроектировать человеческую руку и анимировать ее на экране.
Это дало сильный толчок в развитии анимационных технологий и применении подобных эффектов в кинематографе. Одним из первых фильмов, в котором зритель мог увидеть анимацию человеческого лица, считается «Futureworld», вышедший в 1976 году. Сразу после этого трехмерная графика начала прогрессировать очень быстро. Появились специальные программы, кинокомпании стали набирать сотрудников соответствующих должностей и реализовывали самые разные эффекты в своих проектах. Обладатели персональных компьютеров уже в начале 80-х годов могли скачать программу под названием 3D Art Graphics, которая включала в себя набор различных трехмерных объектов и эффектов.
Создание трехмерной графики
Как же работает трехмерная графика на компьютерах и на какие этапы делится ее создание?
-
3D-моделирование. На компьютере создается модель, в точности передающая форму объекта, который нужно представить.
 Это может быть любой предмет, животное или человек. В общем, все, что нас окружает. Существует несколько видов трехмерного моделирования, каждый из которых имеет свои особенности и принципы, но сейчас не будем вдаваться в эту тему. Если хотите, можете ознакомиться с такими программами, как Blender или 3Ds Max, чтобы узнать, как трехмерные объекты рисуются при помощи программ.
Это может быть любой предмет, животное или человек. В общем, все, что нас окружает. Существует несколько видов трехмерного моделирования, каждый из которых имеет свои особенности и принципы, но сейчас не будем вдаваться в эту тему. Если хотите, можете ознакомиться с такими программами, как Blender или 3Ds Max, чтобы узнать, как трехмерные объекты рисуются при помощи программ. -
Сценарий и анимация
. Модели всегда размещены на сцене и необходимы для выполнения определенного действия: перемещения, разрушения или передачи любого другого эффекта. Для расположения объектов на сцене и их анимирования может использоваться та же программа, которая применялась и для моделирования, но иногда разработчики обращаются к другому софту. Анимации тоже бывают разными, например, сейчас особо популярен захват движения (когда программа считывает движения человека и передает их на трехмерную фигуру). -
Рендеринг.
 Завершающий процесс работы над проектом. Подразумевает обработку цветов, типов поверхности, освещения и всех других параметров сцены. Для обработки необходим мощный компьютер, способный быстро считывать кадры и выдавать на экран необходимый результат.
Завершающий процесс работы над проектом. Подразумевает обработку цветов, типов поверхности, освещения и всех других параметров сцены. Для обработки необходим мощный компьютер, способный быстро считывать кадры и выдавать на экран необходимый результат.
3D-моделирование
В рамках этой статьи остановимся только на 3D-моделировании, поскольку именно этот процесс и является основной трехмерной графики. Вы уже знаете, что для выполнения данной операции используется специальный софт. Аниматор может взаимодействовать как с отдельными геометрическими фигурами и точками, преобразовывая их в необходимый объект, так и с одной болванкой, доводя ее до необходимой формы (как скульптор в реальной жизни).
Изначально модель имеет серый цвет, поэтому обязательным этапом является наложение текстур и материалов. В крупных компаниях этим занимается специально обученный человек, получивший заготовку от 3D-моделировщика. Он по эскизам или специальным шаблонам накладывает на модель различные элементы, имитирующие волосы, ткань или типы поверхностей. Это и делает 3D-модель похожей на настоящую.
Это и делает 3D-модель похожей на настоящую.
Тему можно развивать бесконечно, поскольку 3D-графика обладает огромным множеством интересных особенностей, которые делают индустрию такой сложной и высокооплачиваемой. Кинокомпании тратят миллионы долларов на создание моделей и эффектов, которые в реальной жизни повторить проблематично и еще более затратно. Сейчас при помощи 3D-графики создаются практически все современные игры и мультфильмы.
Построение графиков — Sage Tutorial in Russian v9.3
Sage может строить двумерные и трехмерные графики.
Двумерные графики
В двумерном пространстве Sage может отрисовывать круги, линии и
многоугольники; графики функций в декартовых координатах; также графики
в полярных координатах, контурные графики и изображения векторных полей.
Некоторые примеры будут показаны ниже. Для более исчерпывающей информации
по построению графиков см. Решение дифференциальных уравнений и Maxima,
а также документацию
Sage Constructions.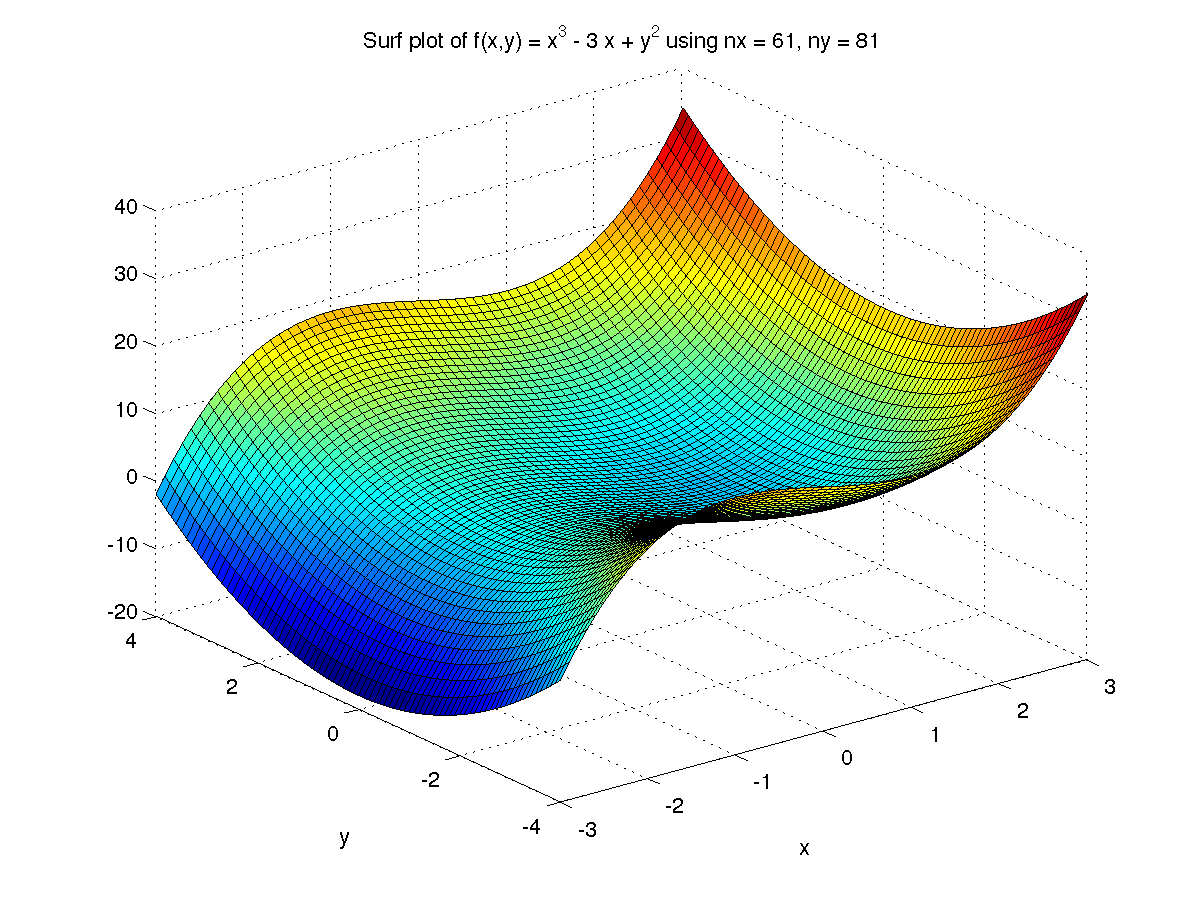
Данная команда построит желтую окружность радиуса 1 с центром в начале:
sage: circle((0,0), 1, rgbcolor=(1,1,0)) Graphics object consisting of 1 graphics primitive
Также можно построить круг:
sage: circle((0,0), 1, rgbcolor=(1,1,0), fill=True) Graphics object consisting of 1 graphics primitive
Можно создавать окружность и задавать ее какой-либо переменной. Данный пример не будет строить окружность:
sage: c = circle((0,0), 1, rgbcolor=(1,1,0))
Чтобы построить ее, используйте c.show() или show(c):
c.save('filename.png') сохранит график в файл.
Теперь эти „окружности“ больше похожи на эллипсы, так как оси имеют разный масштаб. Это можно исправить следующим образом:
sage: c.show(aspect_ratio=1)
Команда show(c, aspect_ratio=1) выполнит то же самое. Сохранить
картинку можно с помощью c.save('filename.png', aspect_ratio=1).
Строить графики базовых функций легко:
sage: plot(cos, (-5,5)) Graphics object consisting of 1 graphics primitive
Как только имя переменной определено, можно создать параметрический график:
sage: x = var('x')
sage: parametric_plot((cos(x),sin(x)^3),(x,0,2*pi),rgbcolor=hue(0. 3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
Хороший способ создания заполненных фигур — создание списка точек (L в следующем примере), а затем использование команды polygon для
построения фигуры с границами, образованными заданными точками. К
примеру, создадим зеленый дельтоид:
sage: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)), ....: 2*sin(pi*i/100)*(1-cos(pi*i/100))] for i in range(200)] sage: p = polygon(L, rgbcolor=(1/8,3/4,1/2)) sage: p Graphics object consisting of 1 graphics primitive
Напечатайте show(p, axes=false), чтобы не показывать осей на графике.
Можно добавить текст на график:
sage: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....: 6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,1/4,1/2))
sage: t = text("hypotrochoid", (5,4), rgbcolor=(1,0,0))
sage: show(p+t)
Учителя математики часто рисуют следующий график на доске: не одну
ветвь arcsin, а несколько, т. е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:
е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:
sage: v = [(sin(x),x) for x in srange(-2*float(pi),2*float(pi),0.1)] sage: line(v) Graphics object consisting of 1 graphics primitive
Так как функция тангенса имеет больший интервал, чем синус, при использовании той же техники для перевертывания тангенса требуется изменить минимальное и максимальное значения координат для оси x:
sage: v = [(tan(x),x) for x in srange(-2*float(pi),2*float(pi),0.01)] sage: show(line(v), xmin=-20, xmax=20)
Sage также может строить графики в полярных координатах, контурные построения и изображения векторных полей (для специальных видов функций). Далее следует пример контурного чертежа:
sage: f = lambda x,y: cos(x*y) sage: contour_plot(f, (-4, 4), (-4, 4)) Graphics object consisting of 1 graphics primitive
Трехмерные графики
Sage также может быть использован для создания трехмерных графиков. 2 — 1)
sage: implicit_plot3d(f, (x, -0.5, 0.5), (y, -1, 1), (z, -1, 1))
Graphics3d Object
2 — 1)
sage: implicit_plot3d(f, (x, -0.5, 0.5), (y, -1, 1), (z, -1, 1))
Graphics3d Object
3D графика — основа 3Д графики лежит геометрическая проекция отличием от 2Д
3D графика — разработка и создание 3д дизайна3D графика «трехмерная графика» — это особая разновидность компьютерной графики, предназначенная для созданий трехмерных моделей. В их основе лежит геометрическая проекция, которая выступает ключевым отличием между 3D и 2D. Создание геометрической проекции сопровождается использованием специализированного программного обеспечения. Конечным результатом выступает высокоточная копия реального объекта.
Наша компания предлагает комплексные услуги по разработке 3D графики и дизайну с использованием современного технического оснащения. Специалисты руководствуются полученным опытом и знаниями. Регулярное повышение квалификации позволяет справиться с задачами любой сложности.
Разработка 3D графики
Разработка 3D графики осуществляется в несколько последовательных этапов. От правильного соблюдения установленного алгоритма зависит качество конечного результата. Специалисты нашей компании проводят комплексную работу по разработке 3D графики в несколько этапов:
От правильного соблюдения установленного алгоритма зависит качество конечного результата. Специалисты нашей компании проводят комплексную работу по разработке 3D графики в несколько этапов:
- Оценка проекта — специалисты занимаются изучением предоставленного материала, объема работ
- Старт проекта — после согласования основных этапов, а также обсуждения финансовых вопросов, специалисты приступают к реализации проекта
- Выполнение работ — основная часть осуществляется в специальных программах, где дизайнер делает основные наброски. После утверждения подходящего варианта, он дорабатывается до совершенства
- Закрытие проекта — на данном этапе клиент получает готовый заказ
Специалисты компании «МирСео24» работают по-готовому техническому заданию «ТЗ», что исключает развитие непредвиденных ситуаций. Все этапы разработки с указанием общей стоимости содержаться в договоре, который подписывается между клиентом и исполнителем.
Технологии применения 3D графики
Технологии применения 3D графики необходимы во многих сферах жизни человека. Примечательно, что они доставляют визуальное наслаждение, и при этом приносят реальную прибыль. Встретить трехмерные изображения можно на телевидение, в кино, в играх, на рекламных щитах и т.д. Современная 3D графика, это:
Примечательно, что они доставляют визуальное наслаждение, и при этом приносят реальную прибыль. Встретить трехмерные изображения можно на телевидение, в кино, в играх, на рекламных щитах и т.д. Современная 3D графика, это:
- 3D графика в видеофильмах и мультфильмах — все персонажи, а также реалистичные спецэффекты создаются с помощью комплексной работы по разработке и созданию 3D графики в специальных 3D программных обеспечениях.
- 3D графика рекламных объектов — способности графики неисчерпаемы, благодаря уникальной модели можно создать рекламу продукта, и тем самым, побудить клиента к его приобретению
- 3D графический дизайн интерьеров — перед укладкой плитки или поклейкой обоев, клиент желает увидеть 3D модель и расставить все объекты согласно собственным предпочтениям. Сегодня, такая услуга предоставляется во всех строительных и мебельных магазинах
В скором времени, графика затронет и другие сферы жизни и станет неотъемлемой частью повседневной рутины. А пока, остается лишь заказывать качественный визуал и тем самым повышать узнаваемость бренда!
А пока, остается лишь заказывать качественный визуал и тем самым повышать узнаваемость бренда!
Образец 3D модели «Задвижка»
«Autodesk 3ds Max 2020»
Образец 3D модели «Музыкальный центр»
«Autodesk 3ds Max 2020»
Образец 3D модели «Червяк испанский»
«Autodesk 3ds Max 2020»
Создание 3D графики
Наша компания специализируется на создании 3D графики для любых сфер жизни. Веб дизайнеры проводят разработку по созданию 3D графики любого объекта с использованием современного технического оснащения. В основе создания уникальной модели лежат следующие этапы:
- 3D Моделирование — модель будущего объекта создается в специальном редакторе. Наиболее продвинутыми программами являются 3Ds Max и Adobe After Effects
- Текстурирование — на данном этапе осуществляется наложение текстур на ранее разработанную модель. Дополнением выступает настройка материалов и придание моделям реалистичности
- Освещение — на данном этапе создается и устанавливается направление и настройка источников освещения.
 Это действие осуществляется в графических редакторах, с использованием установленных источников света
Это действие осуществляется в графических редакторах, с использованием установленных источников света - 3D Анимация — движущие объекты подчеркивают реалистичность любой модели. Создание анимации осуществляется в современных редакторах, оснащенных множеством инструментов
- Рендеринг — на заключительном этапе трехмерная модель проходит через процесс преобразования. Итогом работы является «плоское» изображение
Описанные этапы разработки являются ключевыми, они следуют друг за другом в четко установленной последовательности.
Интересны услуги по созданию 3D графики Оформляйте заказ на официальной странице компании «МирСео24». Консультации и квалифицированная помощь предоставляются на бесплатной основе.
Видео пример 3D модели
«Задвижка»
Видео пример 3D модели
«Музыкальный центр»
Видео пример 3D модели
«Червяк испанский»
Виды 3D графики
Существует несколько разновидностей 3D моделирования.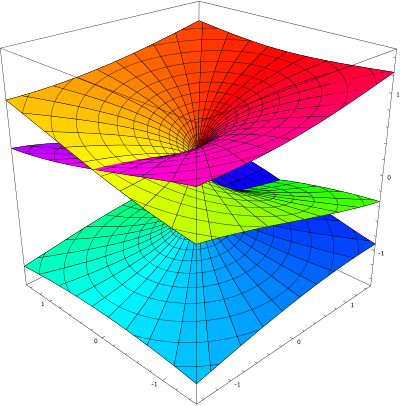 Наиболее востребованными вариантами выступают: полигональное и сплайновое.
Наиболее востребованными вариантами выступают: полигональное и сплайновое.
Полигональное моделирование — полигональный вид 3D графики появился несколько десятков лет назад. На тот момент для создания объемной модели приходилось вручную вводить координаты по осям. Это значительно увеличивало длительность работы и отражалось на корректности конечного результата.
В основе полигонального вида лежит использование трех или четырех вершин, в зависимости от требуемого результата. Большинство изображений созданы посредством трех вершин. Для каждого полигона характерен определенный оттенок и текстура. Все полигоны соединяются между собой, создавая тем самым полигональную сетку или объект. При необходимости дальнейшего увеличения объекта необходимо заранее создавать несколько полигонов.
Методика полигонального моделирования используется повсеместно, особенно для создания компьютерных игр.
Сплайновое моделирование — в основе сплайнового моделирования лежит использование специальных сплайнов. Их линии задаются посредством трехмерного набора контрольных точек, которые и определяют гладкость кривой. Все сплайны подводятся к сплайновому каркасу, на основе которого в дальнейшем создается огибающая трехмерная геометрическая поверхность.
Их линии задаются посредством трехмерного набора контрольных точек, которые и определяют гладкость кривой. Все сплайны подводятся к сплайновому каркасу, на основе которого в дальнейшем создается огибающая трехмерная геометрическая поверхность.
Указанная методика моделирования используется повсеместно, для создания персонажей игр, моделей для рекламных компаний, персонажей фильмов и мультфильмов.
Услуги по созданию и разработке 3D графики
Наша компания предоставляет комплексные услуги по созданию и разработке 3D графики. Специалисты оказывают качественный сервис по объемному моделированию для заказчиков из любой сферы деятельности. Полный спектр услуг по разработке 3D графики включает:
- Подготовка 3D модели, которая будет полностью оптимизирована под требования потенциального заказчика (с учетом конечной цели)
- Создание трехмерной модели с последующей печатью объекта
- Проведение консультаций относительно последующей реализации и процесса подготовки
Специалисты работают по установленному алгоритму, начиная с момента проектирования и заканчивая полной сдачей объекта. Услуги по моделированию решают ряд задач клиентов:
Услуги по моделированию решают ряд задач клиентов:
- демонстрация заказа в реалистичном виде (для застройщиков)
- наглядная презентация коммерческой недвижимости (для арендодателей)
- яркие презентации с целью реализации продукта/услуги (для маркетинга и рекламных компаний)
Виртуальная проекция позволяет увидеть ошибки и объективно оценить конечный результат. Это качественный инструмент, который является визуалом любого бизнеса. Для оформления услуг по 3D графике, звоните по указанным номерам телефонов или обращайтесь через форму обратной связи.
Программное обеспечение для создания 3D графики
Моделирование сопровождается использованием установленного программного обеспечения. Для получения броской трехмерной графики используются различные коммерческие продукты, в частности:
- Autodesk 3ds Max
- Autodesk Maya
- Autodesk Softimage
- Blender
Наша компания активно использует несколько программ среди которых две программы считаются самыми приоритетными: «Autodesk 3ds Max 2020» и специальный плагин «3D Element» для популярной программы по созданию видео и видео эффектов «Adobe After Effects». Программа 3Ds Max используется во многих сферах, в частности:
Программа 3Ds Max используется во многих сферах, в частности:
- визуализация объектов
- дизайн интерьера
- 3D моделирование
- Профильный 3Д дизайн
- Рекламная анимация
- 3D анимация
- 3D WEB-дизайн
- Компьютерная графика
Программа действительно многопрофильная, и указанными сферами использования не ограничивается. В 3Ds Max можно свободно создать фотореалистичную трехмерную модель. Разнообразный инструментарий позволяет разрабатывать уникальные объекты. Посредством анализа и настройки освещенности они обретают новые очертания и «оживают». Благодаря встроенному фотореалистичному визуализатору удалось добиться высокого уровня правдоподобности.
Ключевое достоинство программы – возможность установления дополнительных плагинов, что благотворно отражается на количестве инструментов и значительно расширяет стандартные возможности. 3Ds Max позволяет гибко управлять частицами, а также создавать разнообразные эффекты.
3D Element специальный плагин для Adobe After Effects – это универсальная программа (плагин — «plugin»), которая пользуется не меньшей популярностью. Главное достоинство – возможность редактирования любого видео, создание визуальных эффектов и анимации любой сложности. Программу часто используются в кинематографе для создания постпродакшна. Более того, она свободно функционирует как обычный редактор нелинейного типа, звуковой редактор и транскодер. Посредством программного обеспечения можно создавать модели с несколькими слоями в трехмерном пространстве.
Примечательно, что несмотря на расширенный функционал, программа очень простая в работе. Но при этом она позволяет создавать нереальные модели, подобий которым не существует.
Требуется качественный визуал? Планируете создание уникальных 3D моделей? Обращайтесь за помощью к специалистам компании «МирСео24».
Мы гарантируем комплексный подход и быстрое решение задач любой сложности.
Стоимость услуг по созданию 3D графики
Интересует стоимость услуг по созданию 3D графики? Фиксированный прайс-лист представлен на официальной странице компании «МирСео24».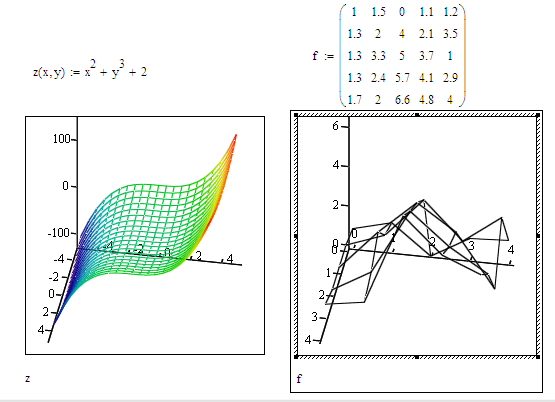 Но, стоимость способна варьироваться в зависимости от сложности графики и установленных сроков. На конечную цену влияют:
Но, стоимость способна варьироваться в зависимости от сложности графики и установленных сроков. На конечную цену влияют:
- Сложность объекта
- Наличие дополнительной анимации
- Наличие дополнительных спецэффектов
- Сроки выполнения
Проконсультироваться по любым вопросам вы можете по указанным номерам телефонов. Звоните прямо сейчас и получайте бесплатный расчет прямо сейчас!
Matplotlib. Урок 5. Построение 3D графиков. Работа с mplot3d Toolkit
До этого момента все графики, которые мы строили были двумерные, Matplotlib позволяет строить 3D графики. Этой теме посвящен данный урок.
Импортируем необходимые модули для работы с 3D:
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D
В библиотеке доступны инструменты для построения различных типов графиков. Рассмотрим некоторые из них более подробно.
Для построения линейного графика используется функция plot().
Axes3D.plot(self, xs, ys, *args, zdir=’z’, **kwargs)
- xs: 1D массив
- ys: 1D массив
- zs: скалярное значение или 1D массив
- z координаты. Если передан скаляр, то он будет присвоен всем точкам графика.
- zdir: {‘x’, ‘y’, ‘z’}
- Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’.
- **kwargs
- Дополнительные аргументы, аналогичные тем, что используются в функции plot() для построения двумерных графиков.
x = np.linspace(-np.pi, np.pi, 50) y = x z = np.cos(x) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot(x, y, z, label='parametric curve')Точечный график
Для построения точечного графика используется функция scatter().
Axes3D.scatter(self, xs, ys, zs=0, zdir=’z’, s=20, c=None, depthshade=True, *args, **kwargs)
- xs, ys: массив
- Координаты точек по осям x и y.
- zs: float или массив, optional
- Координаты точек по оси z. Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.
- zdir: {‘x’, ‘y’, ‘z’, ‘-x’, ‘-y’, ‘-z’}, optional
- Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’
- s: скаляр или массив, optional
- Размер маркера. Значение по умолчанию: 20.
- c: color, массив, массив значений цвета, optional
- Цвет маркера. Возможные значения:
- Строковое значение цвета для всех маркеров.
- Массив строковых значений цвета.
- Массив чисел, которые могут быть отображены в цвета через функции cmap и norm.

- 2D массив, элементами которого являются RGB или RGBA.
- Цвет маркера. Возможные значения:
- depthshade: bool, optional
- Затенение маркеров для придания эффекта глубины.
- **kwargs
- Дополнительные аргументы, аналогичные тем, что используются в функции scatter() для построения двумерных графиков.
np.random.seed(123) x = np.random.randint(-5, 5, 40) y = np.random.randint(0, 10, 40) z = np.random.randint(-5, 5, 40) s = np.random.randint(10, 100, 20) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.scatter(x, y, z, s=s)Каркасная поверхность
Для построения каркасной поверхности используется функция plot_wireframe().
plot_wireframe(self, X, Y, Z, *args, **kwargs)
- X, Y, Z: 2D массивы
- Данные для построения поверхности.
- rcount, ccount: int
- Максимальное количество элементов каркаса, которое будет использовано в каждом из направлений.
 Значение по умолчанию: 50.
Значение по умолчанию: 50.
- Максимальное количество элементов каркаса, которое будет использовано в каждом из направлений.
- rstride, cstride: int
- Параметры определяют величину шага, с которым будут браться элементы строки / столбца из переданных массивов. Параметры rstride, cstride и rcount, ccount являются взаимоисключающими.
- **kwargs
- Дополнительные аргументы, определяемые Line3DCollection.
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j] x = np.cos(u)*np.sin(v) y = np.sin(u)*np.sin(v) z = np.cos(v) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_wireframe(x, y, z) ax.legend()Поверхность
Для построения поверхности используйте функцию plot_surface().
plot_surface(self, X, Y, Z, *args, norm=None, vmin=None, vmax=None, lightsource=None, **kwargs)
- X, Y, Z : 2D массивы
- Данные для построения поверхности.
- rcount, ccount : int
- rstride, cstride : int
- color: color
- Цвет для элементов поверхности.

- Цвет для элементов поверхности.
- cmap: Colormap
- Colormap для элементов поверхности.
- facecolors: массив элементов color
- Индивидуальный цвет для каждого элемента поверхности.
- norm: Normalize
- Нормализация для colormap.
- vmin, vmax: float
- Границы нормализации.
- shade: bool
- Использование тени для facecolors. Значение по умолчанию: True.
- lightsource: LightSource
- Объект класса LightSource – определяет источник света, используется, только если shade = True.
- **kwargs
- Дополнительные аргументы, определяемые Poly3DCollection.
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j] x = np.cos(u)*np.sin(v) y = np.sin(u)*np.sin(v) z = np.cos(v) fig = plt.figure() ax = fig.P.S.add_subplot(111, projection='3d') ax.plot_surface(x, y, z, cmap='inferno') ax.legend()
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Использование 3D-графики в 2D-анимации — Кино и сериалы на DTF
В 2D мультипликации уже давно применяется 3D графика. Иногда это практически незаметно, иногда бьет по глазам. Знали ли вы, что диснеевская «Принцесса и лягушка» и короткометражка от этой же студии «Paperman» созданы с применением компьютерной графики? Даже в фильмах студии Гибли используются 3D-технологии!
1604 просмотров
3D технологии в Paperman
Для чего совмещать 2D и 3D
Есть ряд причин, прагматических и эстетических.
Во-первых, экономия. 2D-анимация — дорогостоящий и трудоемкий процесс. Анимировать некоторые сцены в 3D дешевле — например, сделать окружение или массовку.
Во-вторых, ускорение и упрощение процесса. Это связано с первой причиной: чем больше времени и сил аниматоров затрачено, тем дороже мультфильм. Многие рутинные операции можно автоматизировать. Например, морфинг, где программа сама отрисовывает промежуточные кадры.
В «Принцессе Мононоке» при помощи 3D были созданы некоторые бэкграунды. На CG модель местности «натянули» вручную нарисованные кадры.
Фон здесь создан при помощи 3D
CG позволяет создавать особо сложные сцены. 3D-анимация дает более точные ощущения пространства и объема. рисование разных углов конкретного объекта в 2D-областях может быть сложным и трудоемким по сравнению с 3D-моделями.
3D-анимация дает более точные ощущения пространства и объема. рисование разных углов конкретного объекта в 2D-областях может быть сложным и трудоемким по сравнению с 3D-моделями.
Освещение и перспективу, требующие сложных расчетов, тоже часто делают с применением 3D-технологий.
Освещение в «Клаусе» создано при помощи 3D
В каких сценах применяют 3D-графику
Окружение и задники. Нередко окружение моделируют в 3D, а персонажей в 2D. Это позволяет не рисовать огромное количество ракурсов одной локации, а просто перемещать по ней камеру.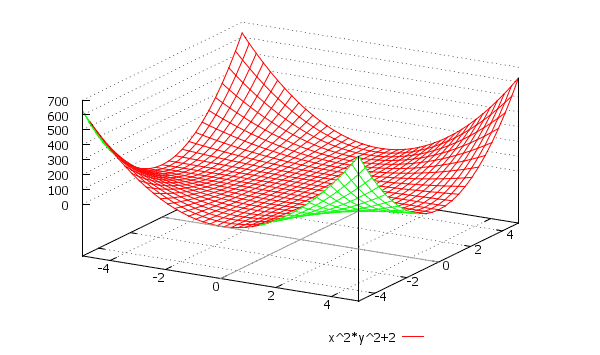
Пример 3D окружения
Миядзаки и сотрудники Studio Ghibli давно (начиная с «Принцессы Мононоке») экспериментируют с компьютерной анимацией. Они использовали Softimage 3D при создании задних планов, сцен с движущейся камерой в «Унесенных призраками» и «Ходячем замке». Компьютерная анимация в 2D-фильмах Гибли применяется с большой осторожностью, чтобы не разрушить магию традиционной анимации.
Работа с софтом при создании Ходячего замка
Динамичные сцены. Помните в диснеевском «Тарзане» сцену, где Тарзан скользит по лианам? Она выполнена при помощи технологии «виртуальной съемки». Аниматоры создавали виртуальную съемочную площадку, которую можно было крутить, как угодно. Камеры выписывали виражи, как в игровом кино, что придавало динамики. Эта сцена до сих пор выглядит впечатляюще.
Аниматоры создавали виртуальную съемочную площадку, которую можно было крутить, как угодно. Камеры выписывали виражи, как в игровом кино, что придавало динамики. Эта сцена до сих пор выглядит впечатляюще.
Транспорт и техника, фоновые объекты. Часто в 2D-анимации используют метод импорта 3D-объектов. Это помогает при рисовании автомобилей и сложной техники в перспективе. Модель рендерят (в программах типа Toon Boom это делается автоматически), и так она более органично вписывается в 2D-сцену. В «Ходячем замке» сам замок и некоторые его интерьеры были созданы в 3D и анимированы в Softimage.
Массовка. В сценах, где есть массовка, прорисовывать каждую фигуру в толпе — лишняя трата сил и средств. Во многих проектах массовку создают в 3D. Анимируют одну или несколько моделек и клонируют. Этим приемом пользовались, например, в диснеевском «Горбуне из Нотр-Дама», где многие сцены показывают толпу. Тем же методом сделана массовка в «Мулан».
Во многих проектах массовку создают в 3D. Анимируют одну или несколько моделек и клонируют. Этим приемом пользовались, например, в диснеевском «Горбуне из Нотр-Дама», где многие сцены показывают толпу. Тем же методом сделана массовка в «Мулан».
Присмотритесь к массовке: это 3D
Освещение. В мультфильме «Клаус» при помощи 3D-технологий выстроено освещение. Для этого был создан специальный инструмент под названием «Клаус Свет и Тень».
Движение камеры. Создав сцену в 3D, можно перемещать камеру по этой сцене и масштабировать, что существенно упрощает работу. В аниме «Волчьи дети Амэ и Юки» в отдельных сценах окружение было выполнено в 3D, чтобы эффектно показать движение героев при помощи пролета камеры, создать иллюзию живой съемки. 2D персонажи были нарисованы поверх.
2D персонажи были нарисованы поверх.
Лес смоделировали в компьютерной графике
Отрендерили и наложили анимацию 2D персонажа
Перспектива. В анимационном клипе «Freak of the Week» на песню группы Freak Kitchen сначала смоделировали персонажей в 3D, а потом отрисовали поверх моделек мимику и детали вручную. Это позволило играть с перспективой и масштабом, показывать сложные ракурсы.
Стилизация. В мультсериале «Удивительный мир Гамболла» комбинируются всевозможные виды анимации. Есть персонажи, созданные в 2D (Гамболл, Дарвин и др.), в технике фотомонтажа, в технике стоп-моушена. Есть здесь и 3D-персонажи: робот Боберт, воздушный шарик Алан и др. Такое разнообразие технологий позволяет создать уникальный, безумный мир, населенный разношерстными существами.
В мультсериале «Удивительный мир Гамболла» комбинируются всевозможные виды анимации. Есть персонажи, созданные в 2D (Гамболл, Дарвин и др.), в технике фотомонтажа, в технике стоп-моушена. Есть здесь и 3D-персонажи: робот Боберт, воздушный шарик Алан и др. Такое разнообразие технологий позволяет создать уникальный, безумный мир, населенный разношерстными существами.
Боберт создан в 3D
Сложные эффекты. Некоторые эффекты практически невозможно создать при помощи ручной анимации, и тут на помощь приходит 3D. В «Принцессе Мононоке» в сцене атаки разъяренного татаригами кабан был нарисован вручную, но каждый из червей, покрывающих его, был сделан при помощи 3D.
В «Ходячем замке», чтобы создать атмосферу военного патриотизма, Миядзаки показывает развевающиеся флаги. Это трехмерные каркасные модели, анимированные так, будто их толкает невидимая масса воздуха.
Это трехмерные каркасные модели, анимированные так, будто их толкает невидимая масса воздуха.
Эксперимент. В диснеевской короткометражке «Paperman» художники рисовали ключевую анимацию поверх CG рендера. По словам создателей, этот способ мог бы определить будущее 2D-анимации.
Disney для фильма «Paperman» разработали уникальную в своем роде программу под названием Meander. Эта программа — анимационный редактор, который представляет из себя гибрид между векторной и растровой графикой.
Почему 3D-графика в 2D-мультипликации часто плохо смотрится
Низкий бюджет и нехватка времени прямым образом влияет на качество анимации. Многие аниме-сериалы грешат халтурными 3D-сценами. Яркий пример — кривая массовка в аниме «Оверлорд». Сравните с 3D-толпой в диснеевских рисованных мультфильмах, о которых говорилось выше.
Многие аниме-сериалы грешат халтурными 3D-сценами. Яркий пример — кривая массовка в аниме «Оверлорд». Сравните с 3D-толпой в диснеевских рисованных мультфильмах, о которых говорилось выше.
Эта армия так и просит поскорее прикончить ее.
Не последнюю роль играет и развитие технологий. Например, в диснеевской «Планете сокровищ» 3D-объекты довольно заметно выделяются на фоне 2D, хотя все выполнено на высшем уровне для того времени (тем более, работали над мультфильмом лучшие профессионалы). Так, металлическая рука киборга Сильвера анимирована в 3D.
Один из лучших современных примеров совмещения 2D и 3D анимации — мультфильм «Человек-паук: через вселенные». Здесь на компьютерные модели накладывали изображение, выполненное вручную. В результате получился уникальный визуальный стиль, приближенный к комиксу.
Здесь на компьютерные модели накладывали изображение, выполненное вручную. В результате получился уникальный визуальный стиль, приближенный к комиксу.
Какие трудности возникают при совмещении 3D и 2D
Если в 3D сделано окружение, сложно бывает показать, как 2D-персонаж с ним взаимодействует. В таких случаях окружение и анимацию персонажа делают в разных программах. Потом изображение из одной программы импортируют в другую. Иногда 2D анимацию делают поверх 3D-окружения. Чтобы лучше показать взаимодействие, аниматор на черновом этапе работы намечает в 3D-окружении линии, по которым должен двигаться 2D-персонаж.
Вспомогательные линии
Объекты, выполненные в 2D и 3D должны быть похожи друг на друга, не выбиваться из общего визуального стиля. Во многом это зависит от уровня детализации и того, как деталь ведет себя на движущейся поверхности.
Во многом это зависит от уровня детализации и того, как деталь ведет себя на движущейся поверхности.
Кроме того, между 2D и 3D не должно быть разрыва в частоте кадров в секунду. Их должно быть не менее 24 в секунду.
Применение компьютерной графики в 2D-анимации — это прием, который может сделать сцену глубже и красивее, облегчить работу аниматору. Но этим приемом надо пользоваться грамотно и не злоупотреблять, иначе можно испортить сцену.
Создать 3D-график Трехмерные графики находят широкое применение в науке, технике и финансах.
Типы трехмерных графиковТипы графиков перечислены ниже вместе с форматами данных, которые можно использовать для создания каждого типа. Для определения виртуальной матрицы см. Создание трехмерных и контурных графиков на основе виртуальной матрицы.
Как создавать и настраивать 3D-графикиЧтобы создать трехмерный график из данных матрицы или рабочего листа, вы выбираете данные и нажимаете соответствующую кнопку графика на панели инструментов 3D и Контурные графики .В качестве альтернативы вы можете выбрать график в меню Plot . Чтобы создать график из виртуальной матрицы, вы должны нажать кнопку графика на панели инструментов 3D и Contour Graphs , чтобы открыть диалоговое окно, которое поможет вам указать данные X, Y, Z и создать график. Дополнительные сведения о создании графиков из виртуальных матриц см. В Создание трехмерных и контурных графиков из виртуальных матриц . Мы подробно представили каждый тип трехмерных графиков в Приложение 2 — Типы графиков , вы можете обратиться к нему для получения более подробной информации. Настройка трехмерных графиков в основном выполняется в диалоговых окнах Axis и Plot Details . Вы можете узнать больше о диалоговом окне Axis и узнать, как настроить оси графика в Graph Axes . Для получения дополнительной информации о диалоговом окне Plot Details см. Customizing Your Graph . |
3D-график в Excel | Как создать трехмерный график поверхности (диаграмму) в Excel?
3D-графики также известны как графики поверхностей в Excel, которые используются для представления трехмерных данных. Чтобы создать трехмерный график в Excel, нам необходимо иметь трехмерный диапазон данных, что означает, что у нас есть трехмерные данные. x, y и z, трехмерные графики или графики поверхности можно использовать на вкладке вставки в Excel.
Excel Трехмерная диаграмма
Прежде чем мы начнем создавать 3D-график в Excel, мы должны знать, что такое сюжет. Графики — это диаграммы в Excel, которые визуально представляют заданные данные. В Excel есть различные типы диаграмм, которые используются для описания данных. Но в основном данные представлены в виде 2D-диаграмм, что означает, что данные или таблица находятся в двух сериях, то есть по оси X и оси Y. Но как насчет того, чтобы построить эту диаграмму, если у нас есть три переменные X, Y и Z. Это то, что мы узнаем об этом 3D-графике в теме Excel.
У нас есть постановка задачи, что у нас есть данные по трем осям последовательностей, то есть X, Y и Z. Как нам нанести эти данные на диаграммы. Диаграмма, которую мы используем для представления этих данных, в Excel называется трехмерным графиком или графиком поверхности. 3D-графики представляют трехмерные данные; здесь есть три переменные. Одна переменная зависит от двух других, а две другие переменные не зависят. Двумерные диаграммы полезны для представления данных, а трехмерные данные полезны при анализе данных.Такие как CO-отношение и регресс. Диаграмма этого типа строится по осям X, Y и Z, где две оси горизонтальны, а одна — вертикальна. Какая ось должна оставаться основной осью, зависит от пользователя диаграммы. Какие данные, независимые или одна из двух зависимых, могут быть первичной осью.
Где в Excel можно найти трехмерный график или поверхностную диаграмму? На вкладке «Вставка» в разделе диаграмм мы можем найти вариант для поверхностных диаграмм.
Выделенные диаграммы являются поверхностными или трехмерными графиками в Excel.
Как создать трехмерный график в Excel?
А теперь сделаем поверхность, то есть трехмерные графики в excel, с помощью пары примеров.
Пример # 1
Давайте сначала выберем несколько случайных данных, как показано ниже,
У нас есть несколько случайных чисел, сгенерированных в столбцах Excel X, Y и Z, и мы построим эти данные на трехмерных графиках.
- Выберите данные, в которых мы хотим построить трехмерную диаграмму.
- Теперь на вкладке «Вставка» в разделе диаграмм щелкните поверхностную диаграмму.
- Типичный трехмерный график поверхности в Excel показан ниже, но на данный момент мы не можем многое прочитать из этого графика.
- Как видим, работа поверхностной карты осуществляется в цветах. Диапазоны показаны цветами.
- В настоящее время эта диаграмма не так удобна для чтения, поэтому щелкните карту правой кнопкой мыши и выберите «Форматировать область диаграммы».
- Появится панель инструментов форматирования диаграммы, затем нажмите «Эффекты».В «Эффектах» нажмите «Поворот 3D-изображения», как показано ниже.
- Измените значения для поворота X и Y и перспективы, что изменит диаграмму, и ее будет легче читать.
- Вот так теперь выглядит диаграмма после изменения поворота по умолчанию.
- Теперь мы должны назвать ось. Мы можем дать название оси, нажав на кнопку, предоставленную Excel.
Приведенная выше поверхностная диаграмма представляет собой трехмерный график для случайных данных, выбранных выше.Давайте использовать 3D-графики поверхности в Excel для некоторых сложных ситуаций.
Пример # 2
Предположим, у нас есть данные по региону, продажи которого осуществляются за шесть месяцев, и мы хотим отобразить эти данные в виде диаграммы. Взгляните на данные ниже,
Теперь мы хотим показать это на трехмерной диаграмме, поскольку у нас есть три переменные, с которыми нужно определить. Один — это месяц, другой — прибыль или убыток, понесенные компанией, а третий — общий объем продаж, выполненных за этот период месяца.Выполните следующие шаги:
- Выберите данные, в которых мы хотим построить трехмерную диаграмму.
- На вкладке «Вставка» под диаграммами в разделе щелкните поверхностную диаграмму.
- В настоящее время трехмерная диаграмма выглядит так, как показано ниже:
- Цвета показывают диапазоны значений на диаграмме, и они находятся в диапазоне от -20000 до 60000, но наши данные в прибылях / убытках находятся только в диапазоне от 7000 до -5000 и от 30000 до 40000, поэтому нам нужно изменить их.Щелкните диаграмму правой кнопкой мыши и выберите область чата «Форматировать».
- Появится панель инструментов форматирования диаграммы. Щелкните эффекты, а в нижней части эффектов снимите флажок автомасштабирования.
- Параметр «Проверки» на панели инструментов диаграммы в Excel изменяет перспективу до точки, в которой мы можем правильно просматривать диаграмму.
- В настоящее время наш график выглядит следующим образом:
- Теперь на вкладке «Дизайн» есть различные другие параметры форматирования диаграмм, например, для добавления элемента диаграммы.
Добавьте заголовок к диаграмме как «Данные о продажах».
Почему мы используем 3D Plot в Excel? Чтобы ответить на этот вопрос, мы можем обратиться к примеру два. Данные были в трех сериях, т.е. мы должны были представить данные в трех осях.
Это было невозможно с двухмерными диаграммами, поскольку двухмерные диаграммы могут представлять данные только по двум осям. Поверхность 3D-графиков в Excel работает с цветовым кодированием. Цвет представляет диапазоны данных, в которых они определены.
Например, посмотрите на снимок экрана ниже из примера 2:
Каждый диапазон значений представлен разным набором цветов.
Что нужно помнить
- 3D-графики поверхности в Excel полезны, но их очень сложно использовать, поэтому они используются не очень часто.
- Из трех осей на трехмерном графике одна расположена вертикально, а две другие — горизонтально.
- На трехмерном поверхностном графике в Excel необходимо отрегулировать трехмерное вращение в соответствии с диапазоном данных, так как может быть сложно читать с графика, если перспектива неправильная.
- Ось должна быть названа, чтобы избежать путаницы, какая ось является осью X, Y или Z для пользователя.
Рекомендуемые статьи
Это руководство по 3D-графику в Excel. Здесь мы обсудим, как создать трехмерный поверхностный график (диаграмму) в Excel, а также практические примеры и загружаемый шаблон Excel. Вы можете узнать больше об Excel из следующих статей —
Пакет All in One Excel VBA (35 курсов с проектами)- 35+ курсов
- 120+ часов
- Полный пожизненный доступ
- Свидетельство о завершении
Основы визуализации данных
Трехмерные графики довольно популярны, в частности, в бизнес-презентациях, а также среди ученых.Они также почти всегда используются ненадлежащим образом. Я редко вижу трехмерный график, который нельзя улучшить, превратив его в обычную двухмерную фигуру. В этой главе я объясню, почему у трехмерных графиков возникают проблемы, почему они обычно не нужны и в каких ограниченных обстоятельствах трехмерные графики могут быть подходящими.
Избегайте беспричинного 3D
Многие программы для визуализации позволяют украсить графики, превращая графические элементы графиков в трехмерные объекты. Чаще всего мы видим, как круговые диаграммы превращаются в диски, повернутые в пространстве, столбчатые диаграммы превращаются в столбцы, а линейные диаграммы — в полосы.Примечательно, что ни в одном из этих случаев третье измерение не передает никаких реальных данных. 3D используется просто для украшения и украшения сюжета. Я считаю такое использование 3D неоправданным. Это однозначно плохо, и его следует стереть из визуального словаря специалистов по данным.
Проблема с беспричинным 3D заключается в том, что проекция 3D-объектов в двух измерениях для печати или отображения на мониторе искажает данные. Человеческая зрительная система пытается исправить это искажение, отображая двумерную проекцию трехмерного изображения обратно в трехмерное пространство.Однако это исправление может быть только частичным. В качестве примера возьмем простую круговую диаграмму с двумя срезами, один из которых представляет 25% данных, а другой — 75%, и повернем эту круговую диаграмму в пространстве (рисунок 26.1). По мере того как мы меняем угол, под которым смотрим на круговую диаграмму, кажется, что изменяется и размер ломтиков. В частности, 25% -ный срез, расположенный в передней части пирога, выглядит намного больше, чем 25%, когда мы смотрим на пирог под прямым углом (рис. 26.1a).
Рисунок 26.1: Та же трехмерная круговая диаграмма, показанная под четырьмя разными углами.Вращение пирога в третьем измерении заставляет кусочки пирога спереди казаться больше, чем они есть на самом деле, а кусочки пирога сзади — меньше. Здесь, в частях (a), (b) и (c), синий срез, соответствующий 25% данных, визуально занимает более 25% площади, представляющей круговую диаграмму. Только часть (d) является точным представлением данных.
Подобные проблемы возникают и для других типов трехмерных графиков. На рис. 26.2 показано распределение пассажиров «Титаника» по классам и полу с использованием трехмерных полос.Из-за того, как стержни расположены относительно осей, все стержни выглядят короче, чем они есть на самом деле. Например, всего 322 пассажира путешествовали в 1-м классе, однако рисунок 26.2 предполагает, что их было меньше 300. Эта иллюзия возникает из-за того, что столбцы, представляющие данные, расположены на расстоянии от двух задних поверхностей, на которых серые горизонтальные линии нарисованы. Чтобы увидеть этот эффект, рассмотрите возможность расширения любого из нижних краев одного из столбцов, пока он не достигнет самой нижней серой линии, которая представляет собой 0.Затем представьте, что вы проделываете то же самое с любым верхним краем, и вы увидите, что все столбцы выше, чем кажется на первый взгляд. (См. Рисунок 6.10 в главе 6, где представлена более разумная двухмерная версия этого рисунка.)
Рисунок 26.2: Количество пассажиров-мужчин и женщин на Титанике, путешествующих 1-м, 2-м и 3-м классами, показано в виде трехмерной гистограммы. Общее количество пассажиров 1-го, 2-го и 3-го классов составляет 322, 279 и 711 соответственно (см. Рис. 6.10). Однако на этом графике полоса 1-го класса, по-видимому, представляет менее 300 пассажиров, полоса 3-го класса, кажется, представляет менее 700 пассажиров, а полоса 2-го класса кажется ближе к 210–220 пассажирам, чем фактические 279 пассажиров.Кроме того, планка 3-го класса визуально доминирует над фигурой и заставляет количество пассажиров 3-го класса казаться больше, чем оно есть на самом деле.
Избегайте трехмерных шкал положения
В то время как визуализации с беспричинным 3D можно легко отклонить как плохие, менее ясно, что думать о визуализациях, использующих три подлинных шкалы положения ( x , y и z ) для представления данных. В этом случае использование третьего измерения служит реальной цели.Тем не менее, полученные графики часто трудно интерпретировать, и, на мой взгляд, их следует избегать.
Рассмотрим трехмерный график разброса топливной эффективности в зависимости от рабочего объема и мощности для 32 автомобилей. Мы видели этот набор данных ранее в главе 2, рисунок 2.5. Здесь мы наносим смещение по оси x , мощность по оси y и топливную экономичность по оси z и представляем каждую машину точкой (рис. 26.3). Несмотря на то, что эта трехмерная визуализация показана с четырех разных точек зрения, трудно представить, как именно точки распределяются в пространстве.Я нахожу часть (d) рисунка 26.3 особенно запутанной. Кажется, что это почти другой набор данных, хотя ничего не изменилось, кроме угла, под которым мы смотрим на точки.
Рисунок 26.3: Топливная эффективность в зависимости от рабочего объема и мощности для 32 автомобилей (модели 1973–74). Каждая точка представляет одну машину, а цвет точки представляет количество цилиндров машины. На четырех панелях (a) — (d) показаны одни и те же данные, но используются разные точки зрения. Источник данных: Motor Trend, 1974.
Основная проблема таких 3D-визуализаций заключается в том, что они требуют двух отдельных последовательных преобразований данных. Первое преобразование отображает данные из пространства данных в пространство трехмерной визуализации, как обсуждалось в главах 2 и 3 в контексте шкал положения. Второй отображает данные из пространства 3D-визуализации в 2D-пространство окончательной фигуры. (Это второе преобразование, очевидно, не происходит для визуализаций, показанных в истинной трехмерной среде, например, когда они показаны как физические скульптуры или объекты, напечатанные на 3D-принтере.Мое основное возражение здесь — против 3D-визуализаций, отображаемых на 2D-дисплеях.) Второе преобразование необратимо, потому что каждая точка на 2D-дисплее соответствует строке точек в пространстве 3D-визуализации. Следовательно, мы не можем однозначно определить, где в трехмерном пространстве находится какая-либо конкретная точка данных.
Наша визуальная система, тем не менее, пытается преобразовать 3D в 2D. Однако этот процесс ненадежен, чреват ошибками и сильно зависит от соответствующих реплик в изображении, которые передают некоторое ощущение трехмерности.Когда мы убираем эти реплики, инверсия становится совершенно невозможной. Это можно увидеть на рисунке 26.4, который идентичен рисунку 26.3, за исключением того, что все признаки глубины удалены. В результате получается четыре случайных расположения точек, которые мы вообще не можем интерпретировать и которые даже нелегко связать друг с другом. Не могли бы вы сказать, какие точки в части (а) соответствуют точкам в части (б)? Я, конечно, не могу.
Рисунок 26.4: Топливная эффективность в зависимости от рабочего объема и мощности для 32 автомобилей (модели 1973–74).Четыре панели (a) — (d) соответствуют тем же панелям на рисунке 26.3, только все линии сетки, обеспечивающие глубину, были удалены. Источник данных: Motor Trend, 1974.
Вместо применения двух отдельных преобразований данных, одно из которых необратимо, я думаю, что обычно лучше просто применить одно подходящее обратимое преобразование и отобразить данные непосредственно в 2D-пространство. Редко бывает необходимо добавлять третье измерение в качестве шкалы положения, поскольку переменные также могут быть отображены на шкале цвета, размера или формы.Например, в главе 2 я построил сразу пять переменных набора данных о топливной эффективности, но при этом использовал только две шкалы положения (рис. 2.5).
Здесь я хочу показать два альтернативных способа построения графиков именно тех переменных, которые показаны на рис. 26.3. Во-первых, если мы в первую очередь заботимся о топливной эффективности как переменной отклика, мы можем построить ее дважды: один раз в зависимости от рабочего объема, а второй — от мощности (рисунок 26.5). Во-вторых, если нас больше интересует, как рабочий объем двигателя и мощность соотносятся друг с другом, а топливная эффективность является второстепенной переменной, представляющей интерес, мы можем построить график зависимости мощности от рабочего объема и сопоставить топливную эффективность с размером точек (рис.6). Оба рисунка более полезны и менее запутаны, чем рисунок 26.3.
Рисунок 26.5: Топливная эффективность в зависимости от рабочего объема (а) и мощности (б). Источник данных: Motor Trend, 1974.
Рисунок 26.6: Зависимость мощности от рабочего объема для 32 автомобилей, топливная эффективность представлена размером точки. Источник данных: Motor Trend, 1974.
Вы можете задаться вопросом, заключается ли проблема с трехмерными диаграммами рассеяния в том, что фактическое представление данных, точки, сами по себе не передают никакой трехмерной информации.Что произойдет, например, если вместо этого мы будем использовать трехмерные стержни? На рис. 26.7 показан типичный набор данных, который можно визуализировать с помощью трехмерных столбцов, уровней смертности в Вирджинии 1940 года, стратифицированных по возрастным группам, полу и местоположению жилья. Мы видим, что трехмерные полосы действительно помогают нам интерпретировать график. Маловероятно, что можно принять полосу на переднем плане за полосу на заднем плане или наоборот. Тем не менее проблемы, обсуждаемые в контексте рисунка 26.2, существуют и здесь. Трудно точно судить о высоте отдельных столбиков, а также трудно проводить прямые сравнения.Например, был ли уровень смертности городских женщин в возрастной группе 65–69 лет выше или ниже, чем у городских мужчин в возрастной группе 60–64 лет?
Рисунок 26.7: Показатели смертности в Вирджинии в 1940 году, визуализированные в виде трехмерной гистограммы. Показатели смертности показаны для четырех групп населения (городских и сельских женщин и мужчин) и пяти возрастных категорий (50–54, 55–59, 60–64, 65–69, 70–74), и они указаны в единицах смертей на 1000 человек. Этот рисунок отмечен как «плохой», потому что трехмерная перспектива затрудняет чтение сюжета.Источник данных: Молино, Гиллиам и Флоран (1947).
В общем, лучше использовать графики Trellis (Глава 21) вместо трехмерных визуализаций. Для набора данных о смертности в Вирджинии требуется только четыре панели, если они представлены в виде решетки (рис. 26.8). Считаю эту цифру понятной и легко интерпретируемой. Сразу становится очевидным, что уровень смертности среди мужчин был выше, чем среди женщин, а также что у городских мужчин уровень смертности был выше, чем у сельских мужчин, тогда как среди городских и сельских женщин такой тенденции не наблюдается.
Рисунок 26.8: Показатели смертности в Вирджинии в 1940 году, представленные в виде графика Trellis. Показатели смертности показаны для четырех групп населения (городских и сельских женщин и мужчин) и пяти возрастных категорий (50–54, 55–59, 60–64, 65–69, 70–74), и они указаны в единицах смертей на 1000 человек. Источник данных: Молино, Гиллиам и Флоран (1947).
Надлежащее использование 3D-визуализаций
Однако иногда могут быть уместны визуализациис использованием трехмерных координатных шкал.Во-первых, проблемы, описанные в предыдущем разделе, вызывают меньшее беспокойство, если визуализация является интерактивной и может вращаться зрителем, или, альтернативно, если она отображается в среде виртуальной реальности или дополненной реальности, где ее можно рассматривать с разных сторон. Во-вторых, даже если визуализация не интерактивна, отображение ее медленно вращающегося, а не статического изображения с одной точки зрения, позволит зрителю различить, где в трехмерном пространстве находятся различные графические элементы. Человеческий мозг очень хорошо восстанавливает трехмерную сцену из серии изображений, снятых под разными углами, и медленное вращение графики обеспечивает именно эти изображения.
Наконец, имеет смысл использовать 3D-визуализацию, когда мы хотим показать реальные 3D-объекты и / или данные, отображенные на них. Например, отображение топографического рельефа гористого острова — разумный выбор (рис. 26.9). Точно так же, если мы хотим визуализировать сохранение эволюционной последовательности белка, нанесенного на его структуру, имеет смысл показать эту структуру как трехмерный объект (рис. 26.10). Однако в любом случае эти визуализации все равно было бы легче интерпретировать, если бы они отображались как вращающиеся анимации.Хотя это невозможно в традиционных печатных публикациях, это можно легко сделать при размещении рисунков в Интернете или при проведении презентаций.
Рисунок 26.9: Рельеф острова Корсика в Средиземном море. Источник данных: Служба мониторинга земель Коперник.
Рисунок 26.10: Паттерны эволюционной изменчивости белка. Цветная трубка представляет собой остов протеина экзонуклеазы III из бактерии Escherichia coli (идентификатор банка данных протеина: 1AKO).Окраска указывает на эволюционную консервацию отдельных участков в этом белке, при этом темная окраска указывает на консервативные аминокислоты, а светлая окраска указывает на вариабельные аминокислоты. Источник данных: Marcos and Echave (2015).
3D-график
Трехмерный график в общем записывается: z = f ( x , y ). То есть значение z- находится путем подстановки как значения x- , так и значения y- .
Первый пример, который мы видим ниже, — это график z = sin ( x ) + sin ( y ). Это функция x и y .
Вы можете использовать следующий апплет, чтобы исследовать трехмерные графики и даже создавать свои собственные, используя переменные x и y . Вы также можете переключаться между режимом 3D Grapher и контурным режимом.
Развлечения
1. Выберите любой из предустановленных трехмерных графиков в раскрывающемся списке вверху.
2. Вы можете ввести свою собственную функцию из x и y , используя простые математические выражения (допустимый синтаксис см. Ниже на графике).
3. Выберите режим Contour с помощью флажка. В этом режиме вы смотрите на трехмерный график сверху, а цветные линии представляют собой равные высоты (это похоже на контурную карту в географии). Синие линии самые низкие, а красные — самые высокие.
4. Вы можете изменить нижний и верхний пределы x- и y- , используя ползунки под графиком.
5. Вы можете изменять , масштаб z- (изменяя высоту каждого пика) и количество сегментов (которое изменяет частоту дискретизации) с помощью ползунков под графиком.
6. Увеличивайте и уменьшайте масштаб с помощью колесика мыши (или сжимания двумя пальцами, если на мобильном устройстве). Также используйте ползунок z-Scale , чтобы увидеть основные характеристики графика
7. Переместите весь график влево и вправо с помощью правой кнопки мыши и перетаскивания (или смахивания тремя пальцами на мобильном устройстве)
Этот апплет должен нормально работать на мобильных устройствах.y ) и логарифм ( ln (x + y) для натурального логарифма и log (x + y) для логарифма с основанием 10)
абс (x + y) sign (sin (x)) Фактически, вы можете использовать большинство математических функций JavaScript, включая
- потолок:
потолок (x)и круглый :круглый (x) - квадратный корень:
sqrt (y)
Вы также можете использовать любые комбинации вышеперечисленного, например ln (abs (x-y)) .
Если ваш график не работает: Попробуйте использовать скобки! Например, «загар 2x» не сработает. Надо поставить tan (2x) .
Дополнительная информация
Кредит: Вышеупомянутый 3D-график основан на примерах Ли Стемкоски Three.js.
3D-графики
3D-графики создаются на основе данных, определенных как Z = f (X, Y). Что касается 2D-графиков, есть два способа получить 3D-график в зависимости от способа определения значений (X, Y, Z):
Вы можете иметь свои Z-значения в матрице.SciDAVis будет считать, что все данные, представленные в матрице, являются значениями Z, а значения X и Y могут быть определены как функция номеров столбцов и строк.
Данные в матрицу можно вводить несколькими способами:
по одному с клавиатуры,
путем чтения файла ascii в таблице и преобразования таблицы в матрицу,
по установка значений с помощью функции.
Если вы хотите построить график функции, матрица не нужна.Вы можете использовать непосредственно команду New -> New Surface 3D Plot . Это откроет соответствующее диалоговое окно, и вы сможете определить математическое выражение вашей функции.
Можно выбрать несколько видов трехмерных графиков. Список доступных графиков см. В разделе меню Plot3d в справочной главе.
Рисунок 2-8. Пример 3D-графиков.
3D-графики используют OpenGL, поэтому вы можете легко вращать, масштабировать и сдвигать их с помощью мыши.В диалоговом окне настроек 3D-графика или с помощью панели инструментов Surface 3D вы можете изменить все предопределенные настройки трехмерного графика: сетки, масштабы, оси, заголовок, легенду и цвета для различных элементов.
Есть несколько типов графиков, которые можно построить из матрицы. Они представлены в меню Plot3d.
Это самый простой способ получить трехмерный график. Это делается с помощью команды New -> New Surface 3D Plot из меню File или напрямую с помощью Ctrl-Alt-Z.Откроется следующее диалоговое окно:
Рисунок 2-9. Определение нового трехмерного графика поверхности
Вы можете ввести функцию z = f (x, y) и диапазоны для X, Y и Z. Затем SciDAVis создаст трехмерный график по умолчанию:
Рисунок 2-10. 3D-график поверхности, созданный по умолчанию
Затем вы можете настроить этот график, открыв диалоговое окно «Параметры графика поверхности». Вы можете изменить диапазоны и параметры оси, добавить заголовок, изменить цвета различных элементов и изменить соотношение сторон графика.Кроме того, вы можете использовать различные команды панели инструментов 3D-графика, чтобы добавить сетки на стены или изменить стиль графика. После некоторых изменений вы можете получить следующий график:
Рисунок 2-11. Трехмерный график поверхности после настроек
Если вы хотите изменить саму функцию, вы можете использовать команду поверхность … , которую можно активировать из контекстного меню, щелкнув правой кнопкой мыши на трехмерном графике. Это повторно откроет диалоговое окно определения функции поверхности.
Второй способ получить трехмерный график — использовать матрицу. Поэтому первым делом нужно заполнить матрицу, задав функцию.
Команда New -> New Matrix создает пустую матрицу по умолчанию с ячейками 32×32. Затем используйте команду Set Dimensions … , чтобы изменить количество строк и столбцов матрицы. Это диалоговое окно также используется для определения диапазонов X и Y.
Затем используйте команду Set Values … , чтобы заполнить ячейки числами.Диапазоны X и Y, определенные на предыдущем шаге, не известны этому диалоговому окну, тогда функция определяется с номерами строки и столбца (i и j) в качестве параметров ввода (подробности см. В разделе «Установочные значения»).
Другой способ получить матрицу — импортировать файл ASCII в таблицу с помощью команды Импорт ASCII -> Один файл … из меню Файл. Затем таблица может быть преобразована в матрицу с помощью команды Convert to Matrix command из меню Table.
Затем эту матрицу можно использовать для построения трехмерного графика с помощью одной из команд меню «График».
3D-график> Настройки виджета> Дизайн дисплея> Измерение
График Dewesoft 3D показывает трехмерные массивы или массивы с историей. С помощью этого графика мы можем показать историю БПФ, порядок и водопад БПФ из математики отслеживания порядка, подсчет дождевых потоков из модуля анализа усталости и даже данные тепловизионного зрения.
При выборе 3D-графика в левой и правой части экрана появятся следующие настройки:
- Свойства элемента управления — для получения подробной информации о свойствах элемента управления: группировка, количество столбцов, добавление / удаление, прозрачность.
- Параметры чертежа — выбирает, какие параметры будут отображаться на графике.
- Селектор каналов
Входные данные для 3D-графика могут быть:
- Математика БПФ на основе блоков (история БПФ во времени)
- STFT математика
- Математика CPB на основе блоков (CPB со временем)
- Каскад заказов и БПФ из модуля отслеживания заказов
- Зависимость водопада заказов от времени
- 3D дождь и счет Маркова
- Тепловизор FLIR (требуется специальный модуль).
Обратите внимание, что 3D-просмотр может быть недоступен на компьютерах, на которых не установлен DirectX или графическая карта не поддерживает 3D-функции, требуемые для графика.
Недвижимость
- Автоматическое масштабирование автоматически масштабирует ось z.
- Тип оси Z может быть установлен на линейный, логарифмический, 0 дБ, уровень звука в дБ от Ref.dB. Минимум и максимум каждой шкалы можно определить, щелкнув минимальное и максимальное значение, как на любом графике. Это также работает для шкалы z, которая находится в левой части дисплея. Палитра оси Z
- может быть как в цвете радуги, так и в оттенках серого.
- Проекцию оси можно изменить. Первый (2D (X, Y)) представляет собой планарный вид и в основном используется, когда данные, основанные на времени, отображаются, например, как история БПФ. Второй (2D (Y, X)) полезен при отображении матричных каналов, таких как количество дождевых потоков или тепловизионное изображение. Отслеживание заказов находится посередине, некоторые пользователи предпочитают первый, а другие — второй вариант. Также есть трехмерный вид (3D (X, Y)).
- Трехмерный вид можно повернуть, нажав и удерживая левую кнопку мыши, чтобы повернуть его. Прокрутка колеса мыши или нажатие клавиши Shift и левой кнопки увеличивает или уменьшает масштаб изображения при перемещении мыши вверх и вниз. Щелкните правой кнопкой мыши и перемещайте мышь, чтобы вращать график вокруг плоскости отображения.
Маркеры
Перемещение кнопки мыши по графику поместит курсор в виде перекрестия в ближайшую точку на графике.
Нажав на точку правой кнопкой мыши, вы можете добавить маркер в направлении X или Y.В приведенном ниже примере канал, назначенный трехмерному графику, — это водопад заказов из математики отслеживания заказов. Канал в направлении X — это заказы, а канал по оси Y — это скорость. Имя оси X и оси Y читается из имени канала. Все курсоры можно удалить, щелкнув правой кнопкой мыши и выбрав «Удалить маркер».
Когда курсор будет добавлен, вы увидите плоскость, указывающую на «Снятие заказов». Маркер «Срез по порядку» создает канал, который можно отобразить на 2D-графике.
При щелчке по кнопке «Вырезать заказы» появится стрелка.С помощью этой опции вы можете вручную перемещать маркер в спектре.
При ручном перемещении маркера обновляется также канал «Отрезка заказов», отображаемый на 2D графике — отсечение рассчитывается и обновляется автоматически.
Те же свойства применяются также для добавления маркера в направлении Y (Speed cut).
Когда на 2D-графике отображается разрез в направлении Y, на этом же 2D-графике также виден маркер в направлении X. Разрез в направлении X виден в виде линии в положении маркеров, что указывает на разрез Одерса.
Добавление нескольких маркеров
На трехмерный график можно добавить несколько маркеров в обоих направлениях. Каждый из них создаст канал, который можно отобразить на 2D-графике.
При наличии нескольких маркеров на одном трехмерном графике вы можете изменить их цвет для облегчения идентификации.
Идентификатор, тип, цвет, положение по оси X и положение по оси Y могут отображаться в таблице маркеров.
| linkLabel ([ str or fn ]) | Ссылка на функцию доступа к объекту или атрибут для имени (показано на этикетке).Поддерживает простой текст или HTML-контент. Обратите внимание, что этот метод внутренне использует innerHTML , поэтому не забудьте предварительно очистить любой вводимый пользователем контент, чтобы предотвратить уязвимости XSS. | наименование |
| linkVisibility ([ boolean , str or fn ]) | Функция доступа к объекту ссылки, атрибут или логическая константа для отображения строки ссылки. Значение false поддерживает силу ссылки без ее рендеринга. | правда |
| linkColor ([ str or fn ]) | Ссылка на функцию доступа к объекту или атрибут для цвета линии. | цвет |
| linkAutoColorBy ([ str or fn ]) | Свяжите функцию доступа к объекту ( fn (ссылка) ) или атрибут (например, 'type' ) для автоматической группировки цветов. Влияет только на ссылки без атрибута цвета. | |
| linkOpacity ([ num ]) | Получатель / установщик для непрозрачности строк ссылок между [0,1]. | 0,2 |
| linkWidth ([ num , str or fn ]) | Функция доступа к объекту ссылки, атрибут или числовая константа для ширины линии ссылки. При нулевом значении будет отображаться линия ThreeJS с постоянной шириной ( 1px ) независимо от расстояния. Для индексации значения округляются до ближайшего десятичного знака. | 0 |
| ссылка Разрешение ([ число ]) | Получатель / установщик геометрического разрешения каждого звена, выраженного в количестве радиальных сегментов, на которые нужно разделить цилиндр. Более высокие значения дают более гладкие цилиндры. Применимо только к ссылкам с положительной шириной. | 6 |
| linkCurvature ([ num , str or fn ]) | Функция доступа к объекту ссылки, атрибут или числовая константа для радиуса кривизны линии связи.Изогнутые линии представлены как трехмерные кривые Безье, и допускается любое числовое значение. Значение 0 отображает прямую линию. 1 указывает радиус, равный половине длины линии, в результате чего кривая приближается к полукругу. Для саморегулирующихся ссылок ( исходный равен целевой ) кривая представлена в виде петли вокруг узла с длиной, пропорциональной значению кривизны. Линии изогнуты по часовой стрелке для положительных значений и против часовой стрелки для отрицательных значений.Обратите внимание, что визуализация изогнутых линий является чисто визуальным эффектом и не влияет на поведение основных сил. | 0 |
| linkCurveRotation ([ num , str or fn ]) | Свяжите функцию доступа к объекту, атрибут или числовую константу для поворота вдоль оси линии, применяемого к кривой. Не влияет на прямые линии. При повороте на 0 кривая ориентирована в направлении пересечения с плоскостью XY .Угол поворота (в радианах) будет вращать изогнутую линию по часовой стрелке вокруг оси «от начала до конца» от этой исходной ориентации. | 0 |
| linkMaterial ([ Material , str or fn ]) | Функция или атрибут доступа к объекту ссылки для указания настраиваемого материала для стилизации ссылок графа. Должен возвращать экземпляр ThreeJS Material. Если возвращается значение falsy , для этой ссылки будет использоваться материал по умолчанию. | Материал ссылки по умолчанию — MeshLambertMaterial, стилизованный в соответствии с цветом и непрозрачностью . |
| linkThreeObject ([ Object3d , str or fn ]) | Функция или атрибут доступа к объекту ссылки для создания пользовательского 3D-объекта для визуализации в виде ссылок на график. Должен возвращать экземпляр ThreeJS Object3d. Если возвращается значение falsy , для этой ссылки будет использоваться тип трехмерного объекта по умолчанию. | Объект ссылки по умолчанию представляет собой линию или цилиндр, размер которого соответствует ширине и оформлен в соответствии с материалом . |
| linkThreeObjectExtend ([ bool , str or fn ]) | Функция доступа к объекту ссылки, атрибут или логическое значение, указывающее, следует ли заменить ссылку по умолчанию при использовании настраиваемого объекта linkThreeObject ( false ) или расширить его ( true ). | ложный |
| linkPositionUpdate ([ fn (linkObject, {start, end}, link) ]) | Получатель / установщик для пользовательской функции, вызывающей обновление позиции ссылок на каждой итерации рендеринга. Он получает соответствующую ссылку ThreeJS Object3d , координаты начала и конца ссылки ( {x, y, z} каждая) и данные ссылки . Если функция возвращает истинное значение, обычная функция обновления позиции не будет запускаться для этой ссылки. | |
| linkDirectionalArrowLength ([ num , str or fn ]) | Функция доступа к объекту ссылки, атрибут или числовая константа для длины стрелки, указывающей направление ссылки. Стрелка отображается непосредственно над линией связи и указывает в направлении источник > цель . Значение 0 скрывает стрелку. | 0 |
| linkDirectionalArrowColor ([ str or fn ]) | Ссылка на функцию доступа к объекту или атрибут цвета стрелки. | цвет |
| linkDirectionalArrowRelPos ([ num , str or fn ]) | Функция доступа к объекту ссылки, атрибут или числовая константа для продольного положения наконечника стрелки вдоль линии связи, выраженная как отношение между 0 и 1 , где 0 указывает непосредственно рядом с узлом источника , 1 рядом с целевым узлом и 0.5 прямо посередине. | 0,5 |
| linkDirectionalArrowResolution ([ число ]) | Геттер / сеттер для геометрического разрешения острия стрелки, выраженного в количестве сегментов среза, чтобы разделить окружность основания конуса. Более высокие значения дают более гладкие стрелки. | 8 |
| linkDirectionalParticles ([ num , str or fn ]) | Функция доступа к объекту ссылки, атрибут или числовая константа для количества частиц (маленьких сфер), отображаемых над линией связи.Частицы распределяются с равным интервалом вдоль линии, движутся в направлении источник > цель и могут использоваться для указания направленности линии связи. | 0 |
| linkDirectionalParticleSpeed ([ num , str or fn ]) | Функция доступа к объекту Link, атрибут или числовая константа для скорости направленных частиц, выраженная как отношение длины ссылки к перемещению за кадр.Значения выше 0,5 не приветствуются. | 0,01 |
| linkDirectionalParticleWidth ([ num , str or fn ]) | Ссылка на функцию доступа к объекту, атрибут или числовую константу для ширины направленных частиц. Для индексации значения округляются до ближайшего десятичного знака. | 0,5 |
| linkDirectionalParticleColor ([ str or fn ]) | Ссылка на функцию доступа к объекту или атрибут для цвета направленных частиц. | цвет |
| linkDirectionalParticleResolution ([ число ]) | Геттер / сеттер для геометрического разрешения каждой направленной частицы, выраженного в количестве сегментов среза, чтобы разделить окружность. Более высокие значения дают более гладкие частицы. | 4 |
| emitParticle ( ссылка ) | Альтернативный механизм для генерации частиц, этот метод испускает нециклическую одиночную частицу в пределах определенного звена.Испускаемая частица имеет тот же стиль (скорость, ширина, цвет), что и обычные свойства частицы. Допустимый объект link , который включен в graphData , должен быть передан как единственный параметр. |

 Это может быть любой предмет, животное или человек. В общем, все, что нас окружает. Существует несколько видов трехмерного моделирования, каждый из которых имеет свои особенности и принципы, но сейчас не будем вдаваться в эту тему. Если хотите, можете ознакомиться с такими программами, как Blender или 3Ds Max, чтобы узнать, как трехмерные объекты рисуются при помощи программ.
Это может быть любой предмет, животное или человек. В общем, все, что нас окружает. Существует несколько видов трехмерного моделирования, каждый из которых имеет свои особенности и принципы, но сейчас не будем вдаваться в эту тему. Если хотите, можете ознакомиться с такими программами, как Blender или 3Ds Max, чтобы узнать, как трехмерные объекты рисуются при помощи программ.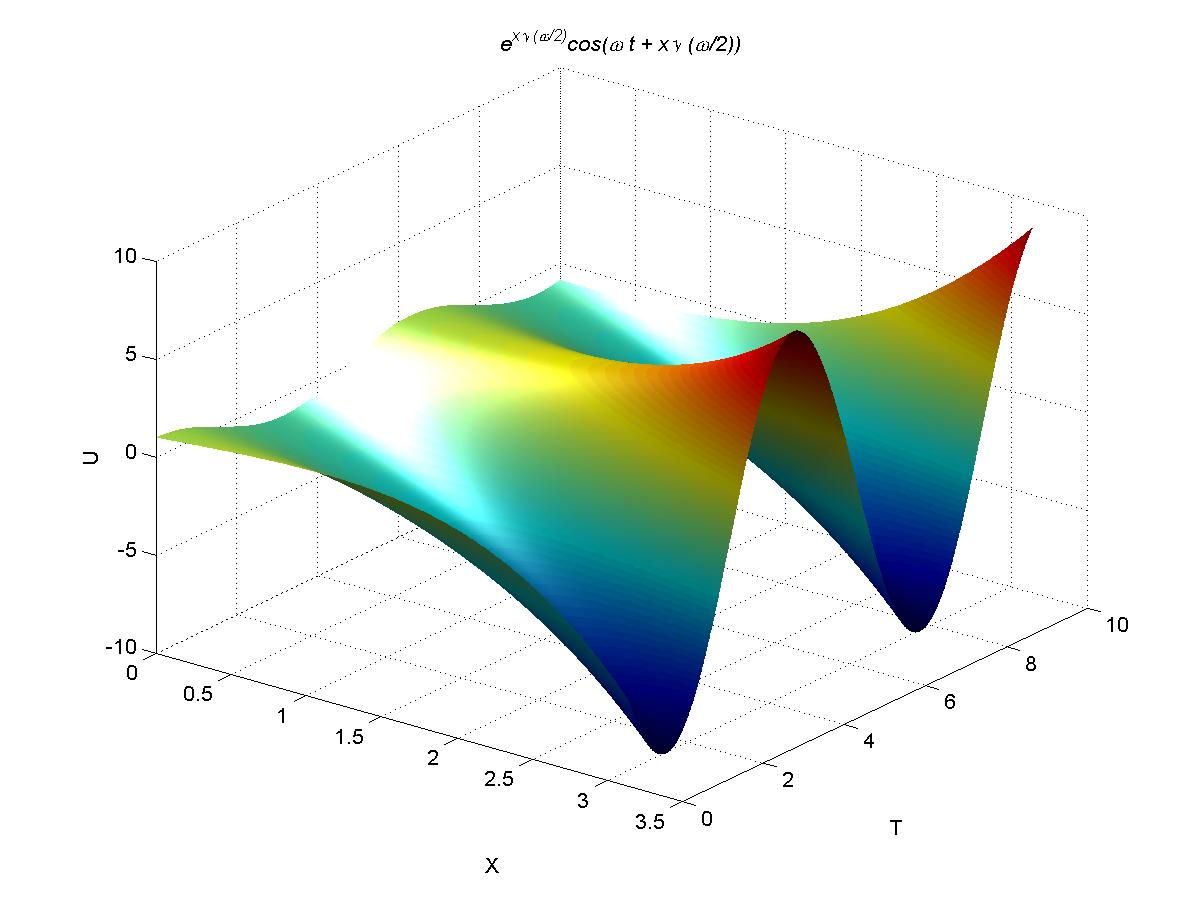 Завершающий процесс работы над проектом. Подразумевает обработку цветов, типов поверхности, освещения и всех других параметров сцены. Для обработки необходим мощный компьютер, способный быстро считывать кадры и выдавать на экран необходимый результат.
Завершающий процесс работы над проектом. Подразумевает обработку цветов, типов поверхности, освещения и всех других параметров сцены. Для обработки необходим мощный компьютер, способный быстро считывать кадры и выдавать на экран необходимый результат. 3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
 Это действие осуществляется в графических редакторах, с использованием установленных источников света
Это действие осуществляется в графических редакторах, с использованием установленных источников света
 Значение по умолчанию: 50.
Значение по умолчанию: 50.
 add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='inferno')
ax.legend()
add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='inferno')
ax.legend() Origin включает в себя широкий спектр типов трехмерных графиков, в том числе трехмерный разброс, трехмерные полосы и трехмерные поверхности. Создание этих графиков в Origin выполняется быстро и легко: вы можете просто выбрать данные и щелкнуть нужную кнопку графика или команду меню, чтобы создать график. После создания вы можете изменять и манипулировать графиком различными способами, включая вращение, изменение размера, построение пересечения нескольких поверхностей, изменение отображения метки оси и т. Д.Вы можете вращать и изменять размер 3D-графиков графически или вводя точные числа в текстовые поля. Как правило, вы можете изменить внешний вид любого элемента графика, дважды щелкнув по нему, открыв диалоговое окно и изменив настройки. Здесь мы видим три примера трехмерных графиков:
Origin включает в себя широкий спектр типов трехмерных графиков, в том числе трехмерный разброс, трехмерные полосы и трехмерные поверхности. Создание этих графиков в Origin выполняется быстро и легко: вы можете просто выбрать данные и щелкнуть нужную кнопку графика или команду меню, чтобы создать график. После создания вы можете изменять и манипулировать графиком различными способами, включая вращение, изменение размера, построение пересечения нескольких поверхностей, изменение отображения метки оси и т. Д.Вы можете вращать и изменять размер 3D-графиков графически или вводя точные числа в текстовые поля. Как правило, вы можете изменить внешний вид любого элемента графика, дважды щелкнув по нему, открыв диалоговое окно и изменив настройки. Здесь мы видим три примера трехмерных графиков: Ниже приведены минимальные системные требования для Origin 9.0 для построения графиков OpenGL, особенно требования к видеокарте и драйверам:
Ниже приведены минимальные системные требования для Origin 9.0 для построения графиков OpenGL, особенно требования к видеокарте и драйверам: Предыдущие версии выполняли некоторую нормализацию данных X и Y перед построением графика. Таким образом, контурные и трехмерные поверхностные графики данных рабочего листа XYZ, созданные в версии 2016 и выше, могут отличаться от графиков тех же данных, созданных в более ранних версиях. Это изменение будет наиболее заметно, если между значениями X и Y имеются большие различия в диапазоне шкалы. См. FAQ-822 для получения дополнительной информации.
Предыдущие версии выполняли некоторую нормализацию данных X и Y перед построением графика. Таким образом, контурные и трехмерные поверхностные графики данных рабочего листа XYZ, созданные в версии 2016 и выше, могут отличаться от графиков тех же данных, созданных в более ранних версиях. Это изменение будет наиболее заметно, если между значениями X и Y имеются большие различия в диапазоне шкалы. См. FAQ-822 для получения дополнительной информации.