Треугольник геометрия: Треугольники — геометрия и искусство

Содержание

Треугольники — геометрия и искусство

Многоугольник
Треугольники
Треугольники в искусстве
Четырехугольники
Правильные многоугольники
Построение

Плоские фигуры > Многоульники

Треуго́льник (в евклидовом пространстве) — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.
Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.
Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла.

Вершины — три точки А, В и С. Стороны — отрезки АВ, ВС и СА.
Углы — ∟ ВАС, ∟ СВА и ∟ АСВ.

Периметр треугольника — сумма длин трех сторон треугольника.

Медиана треугольника (m)— отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

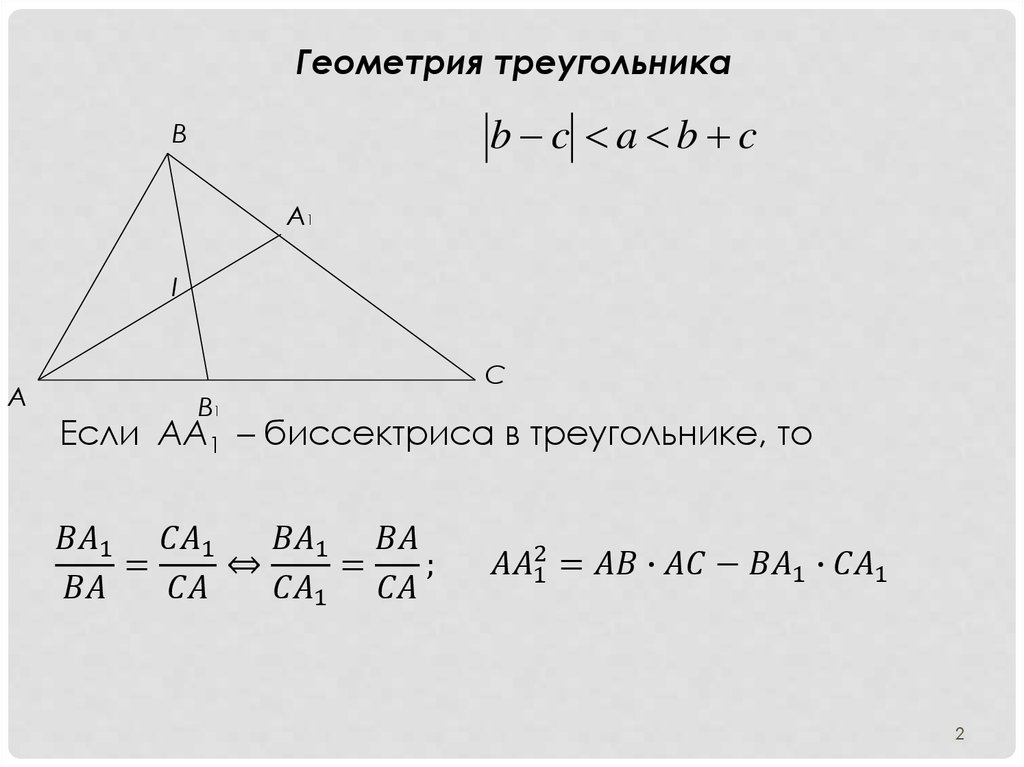
Биссектриса треугольника (b) — отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника (h)— перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

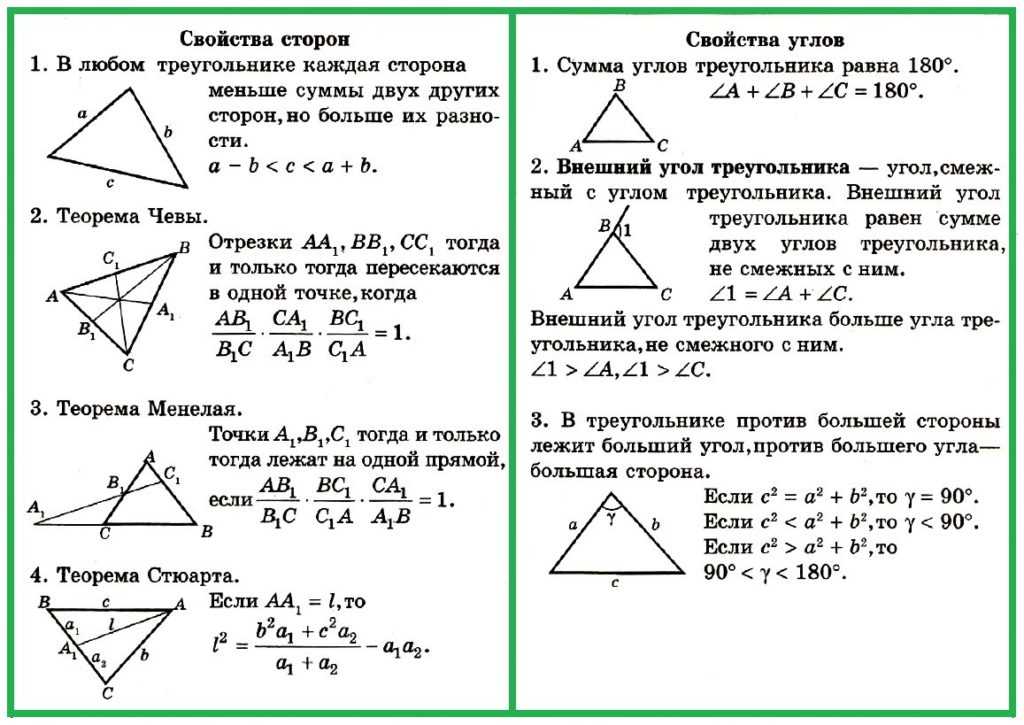
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.

Теорема. Сумма углов треугольника 180°

Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон.

АВ <АС + СВ.
АС <AB + BC.

BC <ВА + АС.

В треугольнике:
1) против большей стороны лежит больший угол
2) против большего угла лежит большая сторона

В прямоугольном треугольнике гипотенуза больше катета

Классификация треугольников
По углам

В треугольнике может быть только один тупой угол

В треугольнике может быть только один прямой угол

По сторонам

Треугольник называется равнобедренным, если две его стороны равны.
Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

Теорема
В равнобедренном треугольнике углы при основании равны.
Теорема
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Равносторонний треугольник — все стороны и углы равны

Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.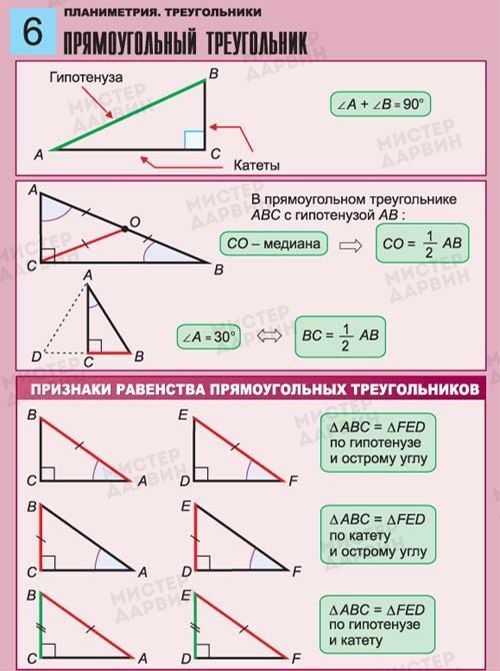

В равных треугольниках против соответственно равных сторон лежат равные углы.

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Теорема. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Прямоугольный треугольник

ГИПОТЕНУЗА — сторона прямоугольного треугольника, лежащая прготив прямого угла. (греческое «гипо» — под, снизу, внизу, «тейнейн» — натягивать (тетеву лука)).

КАТЕТ — одна из двух сторон прямоугольного треугольника, образующих прямой угол.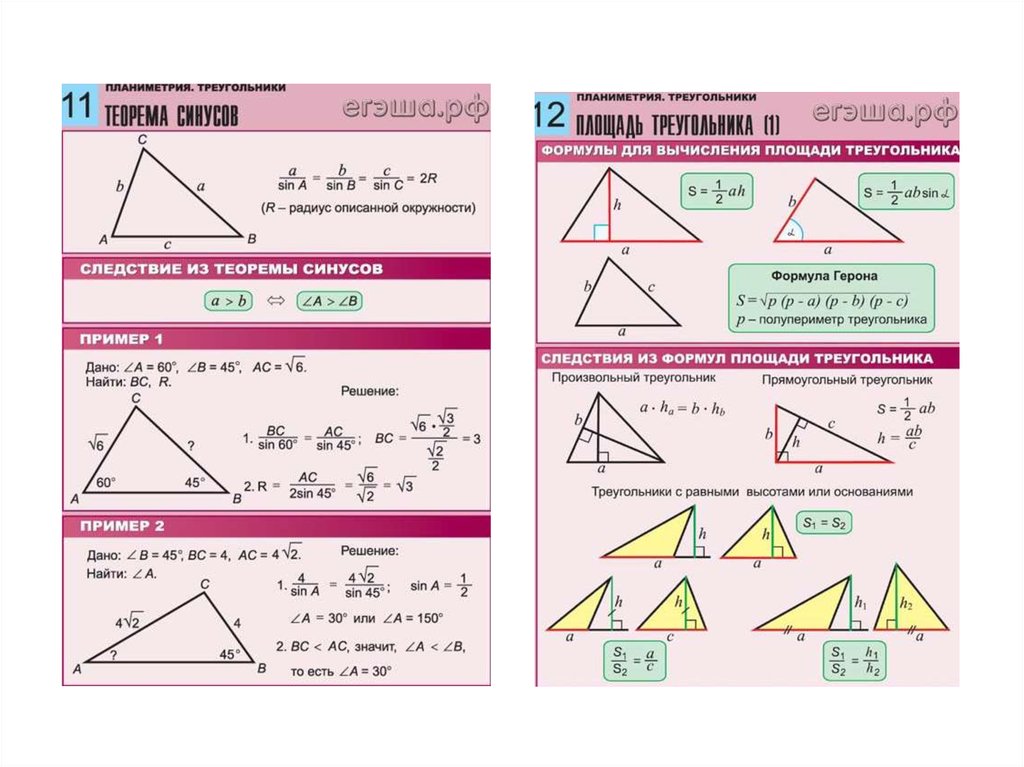 Название «катет» происходит от греческого káthetos — перпендикуляр, опущенный, отвесный. Название также встречается в архитектуре и означает отвес через средину задка ионической капители.

СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
• Сумма двух острых углов прямоугольного треугольника равна 90°.
• Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.

ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету

Треугольник — это простейшая фигура: три стороны и три вершины. Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы.

Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).

Через 2000 лет в Древней Греции изучение свойств треугольника ведется очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны; становится известным, что биссектрисы, как меридианы и высоты, пересекаются в одной точке.

Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения, лежат, на одной окружности». Эта окружность получила название «окружности девяти точек». Ее центр оказался в се-редине отрезка, соединяющего точку пересечения высот с центром описанной окружности.

Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывает такую красивую, с теорему: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник называется внешним треугольником Наполеона. » Аналогично строится и внутренний треугольник Наполеона.

Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.

Тем удивительнее было открытие, сделанное американским математиком Франком Морли. Он доказал, что если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника (1899).

Энц. «Я познаю мир. Математика», 2006

Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского.

Геометрия. Урок 3. Треугольники — ЁП

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение треугольника

Виды треугольников

Отрезки в треугольнике

Биссектриса
Медиана
Высота
Средняя линия

Площадь треугольника

Равнобедренный треугольник

Свойства р/б треугольника

Равносторонний треугольник

Площадь
Высота

Прямоугольный треугольник

Свойства п/у треугольника
Теорема Пифагора
Площадь п/у треугольника

Примеры решений заданий из ОГЭ

Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠A – угол, образованный сторонами AB и AC и противолежащий стороне BC.

Угол ∠B – угол, образованный сторонами BA и BC и противолежащий стороне AC.

Угол ∠C – угол, образованный сторонами CB и CA и противолежащий стороне AB.

Треугольник остроугольный, если все три угла в треугольнике острые.

Треугольник прямоугольный, если у него один из углов прямой (=90°).

Треугольник тупоугольный, если у него один из углов тупой.

Примеры:

Основные свойства треугольника:

Против большей стороны лежит больший угол.
Против равных сторон лежат равные углы.
Сумма углов в треугольнике равна 180°.
Если продолжить одну из сторон треугольника, например, AC, и взять на продолжении стороны точку D, образуется внешний угол ∠BCD к исходному углу ∠ACB.

Внешний угол равен сумме двух внутренних углов, не смежных с ним. ∠BCD=180°−∠ACB∠BCD=∠A+∠B
Неравенство треугольника: любая из сторон треугольника меньше суммы двух других сторон и больше их разности.

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

ab=mn
Биссектрисы пересекаются в одной точке. Точка пересечения биссектрис – центр вписанной в треугольник окружности.

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
Три медианы, проведенные в одном треугольнике, разбивают его на шесть равновеликих треугольников.

S1=S2=S3=S4=S5=S6

Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Пример:

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

m=a2

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Площадь произвольного треугольника можно найти следующими способами:

Полупроизведение стороны на высоту, проведенную к этой стороне.
S=12a⋅ha
Полупроизведение двух сторон на синус угла между ними.
S=12a⋅b⋅sinα
По формуле Герона.
S=p(p−a)(p−b)(p−c)p=a+b+c2

Равнобедренным называется треугольник, у которого две стороны равны.

Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:

В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.

Равносторонним называется треугольник, у которого все стороны и все углы равны.

Площадь равностороннего треугольника находится по формуле S=a234

Высота равностороннего треугольника находится по формуле h=a32

Треугольник называется прямоугольным, если у него один из углов равен 90°.

Свойства прямоугольного треугольника:

Сумма двух острых углов треугольника равна 90°.
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
Если катет равен половине гипотенузы, он лежит напротив угла в 30°.
a=c2c=2⋅a
Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
m=c2
Пропорциональные отрезки в прямоугольном треугольнике a=m⋅cb=n⋅ch=m⋅n

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

c2=a2+b2

У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:

S=12a⋅b

Модуль геометрия: задания, связанные с треугольниками

Скачать домашнее задание к уроку 3.

Треугольник и его виды / Геометрия / Справочник по математике 5-9 класс

Главная
Справочники
Справочник по математике 5-9 класс
Геометрия
Треугольник и его виды

Треугольник — это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки — сторонами.

Данная фигура является треугольником (произносят: треугольник АВС, пишут: ∆ АВС). Точки А, В, С — вершины треугольника, а отрезки АВ, ВС, АС ‒ стороны.

Периметр треугольника — это сумма длин всех его сторон.

Виды треугольников

По виду углов:

Остроугольный треугольник — это треугольник, у которого все три угла острые.

Тупоугольный треугольник — это треугольник, у которого один из углов тупой.

Прямоугольный треугольник — это треугольник, у которого один из углов прямой.

Сумма углов любого треугольника равна 180⁰.

По количеству равных сторон:

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

∆OXP — равнобедренный: XO = XP. Равные стороны на рисунке отмечают равным количеством чёрточек (в нашем случае одной чёрточкой). В равнобедренном треугольники равные стороны

называют боковыми сторонами, а третью сторону — основанием, т.е. в ∆OXP: XO и XP — боковые стороны, а OP — основание.

Равносторонний треугольник — это треугольник, у которого все стороны равны.

∆WYZ — равносторонний: WY = YZ = ZW. Равносторонний треугольник также называют правильным. Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле:

P = 3

Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Прямая

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Измерение углов. Транспортир. Виды углов

Окружность, круг, шар

Цилиндр, конус

Отрезок-xx

Геометрия

Правило встречается в следующих упражнениях:

5 класс

Задание 209, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 367, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 718, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1704, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 7, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Номер 9, Мерзляк, Полонский, Якир, Учебник

Номер 2, Мерзляк, Полонский, Якир, Учебник

Номер 507, Мерзляк, Полонский, Якир, Учебник

Номер 888, Мерзляк, Полонский, Якир, Учебник

Номер 1178, Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 382, Мерзляк, Полонский, Якир, Учебник

Номер 685, Мерзляк, Полонский, Якир, Учебник

Номер 713, Мерзляк, Полонский, Якир, Учебник

Номер 1184, Мерзляк, Полонский, Якир, Учебник

Номер 1257, Мерзляк, Полонский, Якир, Учебник

Номер 1263, Мерзляк, Полонский, Якир, Учебник

Номер 1267, Мерзляк, Полонский, Якир, Учебник

Задание 365, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1372, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1595, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 753, Мерзляк, Полонский, Якир, Учебник

Номер 980, Мерзляк, Полонский, Якир, Учебник

Треугольники — базовая геометрия

Все ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 9 … 54 55 Следующая →

Справка по базовой геометрии » Плоская геометрия » Треугольники

Какова длина диагонали квадрата со сторонами ?

Возможные ответы:

Правильный ответ:

Пояснение:

Диагональ делит квадрат на два прямоугольных треугольника, катетами которых являются стороны квадрата, а гипотенуза — диагональю треугольника.

Используя теорему Пифагора, получаем:

или

Сообщить об ошибке

Возможные ответы:

5 Правильный ответ:

0005

Объяснение:

Сообщить об ошибке

Прямоугольный треугольник имеет две стороны длины ; какова правильная формула для нахождения длины гипотенузы ?

Возможные ответы:

Правильный ответ:

Объяснение:

Теорема Пифагора утверждает, что сумма квадратов сторон треугольника равна квадрату гипотенузы, суммируемой как но для случая прямоугольных равнобедренных треугольников, где a и b равны, это может быть переписано как:

, что упрощается до

Сообщить об ошибке

это треугольник.

Используя теорему Пифагора, вычислите длину гипотенузы .

Возможные ответы:

Недостаточно информации для ответа на этот вопрос.

Правильный ответ:

Объяснение:

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. То есть

, где — гипотенуза, а — две другие стороны.

Здесь соответствует , и, поскольку это треугольник, длина равна длине , поэтому мы это знаем.

Применить теорему Пифагора.

Значит, длина гипотенузы равна .

Сообщить об ошибке

Следующее изображение не в масштабе.

Найдите длину гипотенузы прямоугольного треугольника:

Возможные ответы:

Правильный ответ:

5 Объяснение:

Поскольку задача утверждает, что этот треугольник является прямоугольным, и дает длину двух катетов, третью сторону (гипотенузу) можно вычислить с помощью теоремы Пифагора.

, где a и b могут быть произвольно выбраны для любой длины катета, а c представляет собой длину гипотенузы.

но поскольку вопрос требует найти длину гипотенузы, с не может быть отрицательным числом. Следовательно, окончательный ответ +13,9.

Сообщить об ошибке

Следующее изображение не в масштабе.

Найдите длину гипотенузы прямоугольного треугольника.

Возможные ответы:

Правильный ответ:

Пояснение:

Треугольники 45/45/90 всегда равнобедренные. Это означает, что две стороны треугольника равны. На рисунке это указывает, какие две стороны конгруэнтны.

Отсюда мы можем найти длину гипотенузы по теореме Пифагора. Мы можем подтвердить это, потому что задача не дала нам мер углов для выполнения триггерных функций.

c также равно -2√2, но поскольку гипотенуза является физической длиной, значение не может быть отрицательным расстоянием.

Сообщить об ошибке

Квадрат имеет длину стороны . Какова длина его диагонали?

Возможные ответы:

Невозможно определить из предоставленной информации0016

Объяснение:

Ответ можно найти двумя разными способами. Первый шаг — осознать, что на самом деле это вопрос треугольника, хотя он начинается с квадрата. Нарисовав квадрат и добавив диагональ, вы можете увидеть, что вы формируете два прямоугольных треугольника. Кроме того, диагональ делит пополам два угла в девяносто градусов, в результате чего треугольники становятся треугольниками.

Отсюда можно пойти одним из двух путей: с помощью теоремы Пифагора найти диагональ или признать треугольник треугольником.

1) Использование теоремы Пифагора

Как только вы распознаете прямоугольный треугольник в этом вопросе, вы можете начать использовать теорему Пифагора. Помните формулу: , где и – длины катетов треугольника, .

В этом случае . Мы можем подставить эти значения в уравнение, а затем найти гипотенузу треугольника и диагональ квадрата:

Длина диагонали .

2) Использование свойств треугольников

Второй подход основан на распознавании треугольника. Хотя это можно довольно легко решить с помощью теоремы Пифагора, следующий метод может быть быстрее.

треугольников имеют отношения длин сторон , где представляет длины сторон катетов треугольника, а представляет собой длину гипотенузы.

В данном случае потому что это длина стороны нашего квадрата и треугольников, образованных диагональю квадрата.

Следовательно, используя соотношения треугольников, мы получаем гипотенузу нашего треугольника, которая также является диагональю нашего квадрата.

Сообщить об ошибке

Какова длина гипотенузы равнобедренного прямоугольного треугольника с площадью ?

Возможные ответы:

Правильный ответ:

Объяснение:

Напомним, что равнобедренный прямоугольный треугольник также является треугольником. Его стороны выглядят следующим образом:

Следовательно, площадь треугольника равна:

, так как основание и высота одинаковы.

Для наших данных это означает:

Решая для , вы получаете:

Итак, ваш треугольник выглядит так:

Теперь вы можете легко найти это с отношением Это . Вы также можете использовать теорему Пифагора. Чтобы сделать последнее, это:

Теперь просто посчитайте внимательно:

Это странный вид факторинга, но он имеет смысл, если вы распределяете обратно в группу. Это означает, что вы можете упростить:

Сообщить об ошибке

Когда солнце светит на столб, оно оставляет на земле тень, которая также . Каково расстояние от вершины столба до конца его тени?

Возможные ответы:

Правильный ответ:

Пояснение:

Столб и его тень составляют прямой угол. Поскольку они имеют одинаковую длину, они образуют равнобедренный прямоугольный треугольник (45/45/90). Мы можем использовать теорему Пифагора, чтобы найти гипотенузу. . В таком случае, . Поэтому мы делаем. Так .

Сообщить об ошибке

Найдите длину гипотенузы.

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы найти гипотенузу треугольника, можно воспользоваться теоремой Пифагора. Для любого прямоугольного треугольника с длинами катетов и и гипотенузой ,

Теперь подставьте значения и из вопроса.

Решить.

Упрощение.

Сообщить об ошибке

← Предыдущий 1 2 3 4 5 6 7 8 9 … 54 55 Следующий →

Уведомление об авторских правах

Все ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции

Геометрические свойства треугольников

Ключевые термины

o Треугольник

O Vertex

O Равносторонний треугольник

O Scalen0005

o Тупой треугольник

o Правый треугольник

O Pythagorean Теорема

o Гипотеназа

O LEG

O Высота

O BASE

Цели

O Идентифицируйте различные тиры

. использовать теорему Пифагора, чтобы найти длины сторон прямоугольного треугольника

o Определить высоту(и) и основание(я) треугольника

o Вычислите площадь треугольника

Треугольник назван удачно: он состоит из трех ( tri ) углов, образованных тремя несовпадающими непараллельными прямыми. То, что линии не совпадают, означает, что они не перекрываются, а то, что они не параллельны, означает, что каждая линия пересекается с любой другой линией. Соответственно, треугольник также имеет три стороны. Попробуйте нарисовать любые три несовпадающие непересекающиеся линии; если вы расширите их достаточно далеко, они все пересекутся и образуют треугольник, такой как показанный ниже.

Конечно, для образования треугольника достаточно трех пересекающихся отрезков; в любом случае точки пересечения могут обозначаться или не обозначаться помеченными (или не помеченными) точками. Эти точки пересечения называются вершинами (что является формой множественного числа вершины ).

Используя то, что мы уже узнали о геометрии, мы можем доказать хорошо известное свойство треугольников: сумма мер углов треугольника равна 180°. Начнем с произвольного треугольника ABC, который показан ниже. Обратите внимание, что рисунок не обязательно выполнен в масштабе.

Теперь продолжим отрезок AB (который мы можем записать как ), образуя линию p , и добавим линию q , параллельную p и пересекающую точку C. Теперь мы используем метки вершин как метки углов (выделены курсивом), чтобы не загромождать диаграмму.

Обратите внимание, что два отрезка являются просто секущими: они пересекают две параллельные прямые. Поэтому мы можем использовать свойства параллельных прямых, пересекаемых секущими, чтобы делать выводы об углах, показанных на диаграмме. По правилам соответствующих углов мы можем вывести следующее:

Но обратите внимание, что три угла A , B и C , образованные линией q , являются дополнительными углами. (Хотя мы узнали о дополнительных углах в контексте только двух углов, тот же принцип применим и к трем или более углам.) Таким образом,

Хотите узнать больше? Почему бы не пройти онлайн-курс по геометрии?

А + В + С = 180°

В результате мы доказали, что сумма углов треугольника равна 180°. Обратите внимание, что мы не делали никаких предположений ни об одном из углов, и наш рисунок не предполагался в масштабе. Этот результат является общим и относится ко всем треугольникам.

Практическая задача: Какова мера угла a ниже?

Решение : Три линии на диаграмме образуют треугольник. Поскольку вертикальные (противоположные) углы равны по размеру, мы можем добавить к диаграмме следующую информацию.

Наконец, потому что углы треугольной суммы до 180 °,

39 ° + 47 ° + A = 180 °

A = 180 ° — 39 ° — 47 ° = 94 °

= 180 ° — 39 ° — 47 ° = 940005 = 180 ° — 39 °. Таким образом, угол a равен 94°.
Типы треугольников
Полезно указать несколько классов треугольников с уникальными свойствами, которые могут помочь в геометрическом анализе. Один конкретный тип треугольника — это равносторонний треугольник ; определяющим свойством этого треугольника является то, что все его стороны имеют одинаковую длину. Кроме того, его углы также равны. Ниже показан равносторонний треугольник; обратите внимание, что стороны одинаковой длины отмечены одним и тем же символом косой черты.

Другой тип треугольника — это равнобедренный треугольник , у которого две стороны одинаковой длины. (Если равнобедренный треугольник не определяется как имеющий ровно двух сторон одинаковой длины, равносторонний треугольник также является равнобедренным треугольником, но не наоборот.) Два угла, прилежащие к третьей (неравной) стороне, также равны. Ниже показан равнобедренный треугольник. (Разные меры углов обозначаются разными метками, как и разные длины сторон.)
Разносторонний треугольник имеет три стороны разной длины. Кроме того, если все три угла в треугольнике меньше 90°, то этот треугольник соответственно называется остроугольным треугольником . Если угол больше 90°, то треугольник называется тупоугольным . (Обратите внимание, что только один угол в треугольнике может быть больше 90°, так как сумма всех углов равна только 180°.) Если треугольник имеет угол 90°, то он называется прямоугольным треугольником . Прямоугольные треугольники обладают различными особыми свойствами, одно из которых заключается в том, что длины сторон связаны соотношением 9.0015 Теорема Пифагора . Рассмотрим прямоугольный треугольник, подобный показанному ниже.

Сторона c , противоположная прямому углу, называется гипотенузой . Две другие стороны называются ногами . Мы можем связать длины сторон с помощью следующей формулы (теорема Пифагора):

Эта теорема применима только к прямоугольным треугольникам. Если мы знаем длины двух сторон прямоугольного треугольника, мы можем вычислить длину третьей стороны.
Практическая задача: Сколько градусов в каждом углу равностороннего треугольника?
Решение: Напомним из определения, что все углы равностороннего треугольника имеют одинаковую меру. Назовем эту меру α . Объедините это с тем фактом, что сумма всех углов треугольника равна 180°; мы можем тогда написать

Таким образом, каждый угол в равностороннем треугольнике имеет меру 60°.
Практическая задача : Найдите длину неизвестной стороны в треугольнике ниже.
Решение : Поскольку этот треугольник прямоугольный, мы можем использовать теорему Пифагора.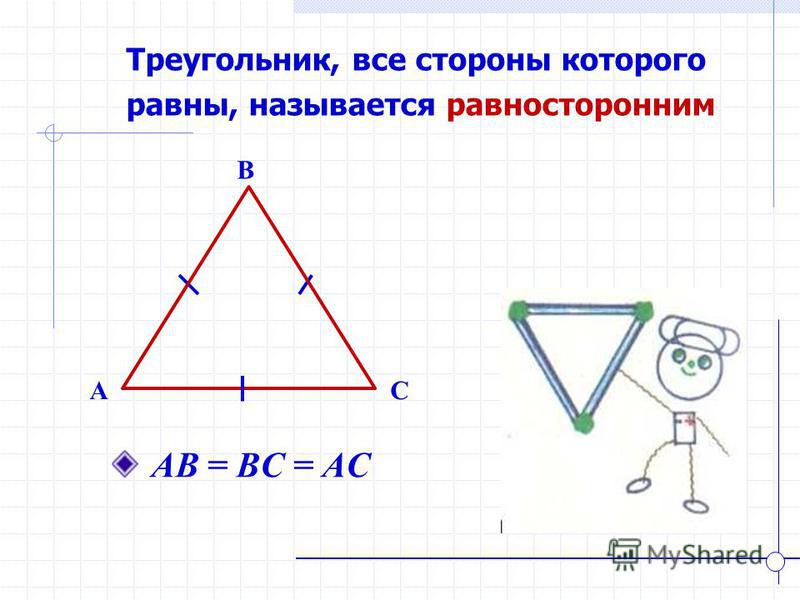 Неизвестная сторона — это катет, который мы можем назвать x , а сторона длины 5 — это гипотенуза. Тогда

Таким образом, неизвестная сторона имеет длину 4 (технически длина составляет «4 единицы», но единицы измерения не указаны и поэтому иногда не упоминаются). Обратите внимание, что мы используем положительный квадратный корень в приведенном выше расчете; отрицательный результат не будет иметь никакого значения в этом контексте.

Другие аспекты треугольников
При анализе треугольников иногда полезно определить высоту треугольника. Высота — это отрезок прямой, проходящий через вершину и перпендикулярный стороне, противоположной этой вершине. Эта противоположная сторона в данном случае называется основанием треугольника. Высота показана пунктирной линией в треугольнике ниже.

В некоторых случаях нам может понадобиться вычислить площадь треугольника. Возможно, вы уже хорошо знаете, что площадь прямоугольника — это просто произведение его длины и ширины (), но площадь треугольника может показаться менее понятной. Однако мы можем связать треугольник с прямоугольником следующим образом. Давайте воспользуемся типовой диаграммой треугольника, приведенной выше, и сделаем копию треугольника, как показано ниже. Мы также определяем несколько длин в треугольнике.

Теперь мы можем разрезать второй треугольник пополам по пунктирной линии высоты, а затем соединить одинаковые части.

Обратите внимание, что теперь мы образовали прямоугольник длиной b + c (длина основания треугольника) и шириной a (высота или высота треугольника). , треугольника). Но мы знаем, что площадь прямоугольника — это просто произведение длины на ширину. В этом случае мы объединили два равноценных треугольника, чтобы сформировать прямоугольник. Таким образом, площадь один из треугольников равен половине площади прямоугольника. Таким образом, мы показали, что площадь треугольника равна половине произведения длин основания и высоты (или высоты). Если длина основания равна B (которое выше равно b + c ), а высота равна H , то площадь A равна

9004. треугольник, как показано выше, тот же процесс можно повторить для любого треугольника; принципы одинаковы, даже если конкретный пример может отличаться. Кроме того, вы можете выбрать любую из трех комбинаций высота-база в треугольнике; вычисление площади приведет к одному и тому же результату в каждом случае.
Практическая задача : Найдите площадь треугольника.

Решение: Площадь треугольника равна половине произведения основания и высоты (или высоты). На схеме показан треугольник с высотой 4 единицы и основанием 7+2=9 единиц. Таким образом, площадь равна

Площадь треугольника равна 18 квадратных единиц.
Руководство по геометрии и практические задачи
Если вы думали, что ACT был большим поклонником кругов, то приготовьтесь к его абсолютно бесстыдной любви к треугольникам. На одном дыхании вы можете найти различные размеры тупоугольного треугольника, а на следующем — равнобедренного прямоугольного треугольника. Задач треугольника ACT будет так же много, как и разнообразно, поэтому убедитесь, что вы ознакомились со всеми различными типами перед днем теста.
Это будет вашим полным руководством по треугольникам ACT — типы треугольников, которые появятся в ACT, формулы, которые вам нужно знать, чтобы решить их, и стратегии, которые вам нужно будет применять при подходе к вопросу о треугольнике. Мы также разберем настоящие математические задачи ACT и дадим вам пошаговые инструкции о том, как наиболее эффективно решать любые задачи с треугольниками, с которыми вы сталкиваетесь.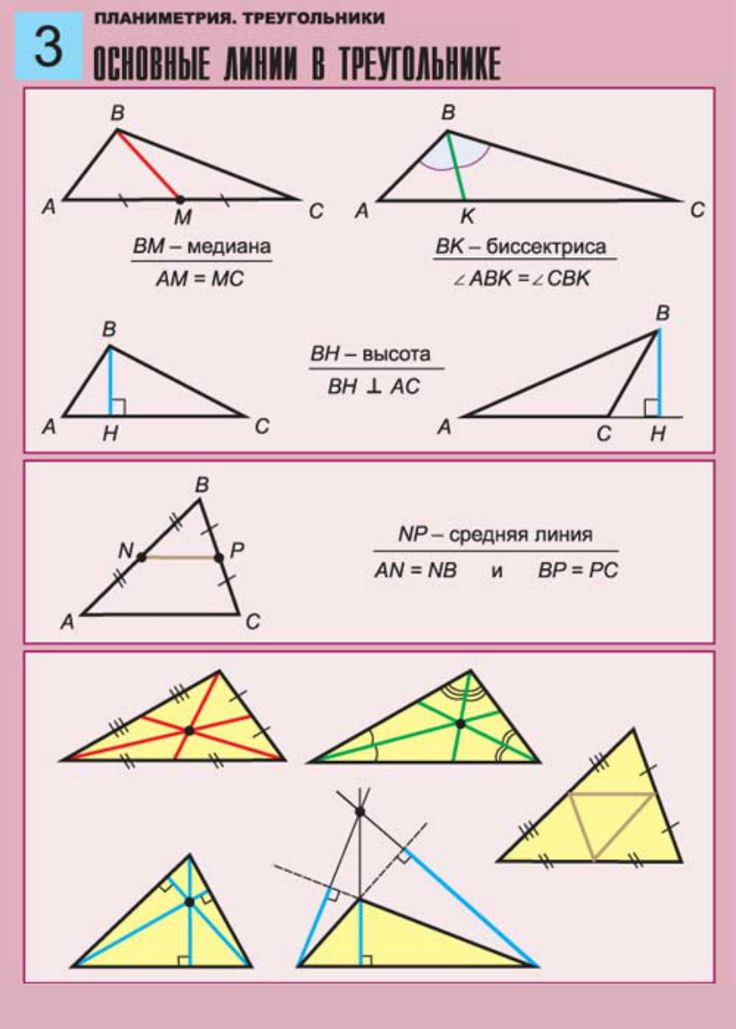

Что такое треугольники?
Прежде чем перейти к решению задачи о треугольнике, давайте обсудим основы. Треугольник — это плоская фигура, состоящая из трех прямых линий, которые соединяются под тремя углами. Сумма этих углов равна 180°.
Каждая из трех сторон треугольника называется катетом треугольника, а самый большой (самый длинный) катет называется гипотенузой. Угол, противолежащий гипотенузе, всегда будет наибольшим из трех углов.
Сумма любых двух катетов треугольника всегда должна быть больше, чем мера третьей стороны. Почему? Потому что, когда сумма двух линий меньше, чем мера третьей линии, они не могут все соединиться в треугольник.
Треугольники, у которых сумма катетов лишь немногим больше, чем гипотенуза, довольно длинные и узкие, но они все же образуют «выпуклость» треугольника, потому что в сумме они длиннее третьей стороны.
Но если ноги слишком короткие, они никогда не сойдутся, каким бы пологим ни был угол.
И если линии имеют длину точной длины гипотенузы, то они выровняются в идеально прямую линию, точно перекрывающую гипотенузу.
Давайте рассмотрим пример такой задачи ACT:
Длина сторон треугольника равна 6 дюймам и 9 дюймам. Если третья сторона — целое число, каков наименьший возможный периметр треугольника в дюймах?
4
15
18
19
29
На основании наших правил для длин сторон треугольников мы знаем, что сумма двух сторон должна быть больше третьей. Поскольку мы пытаемся найти наименьший периметр, мы должны найти недостающую сторону, взяв разность длин двух наших сторон:
9 долларов США — 6 = 3 доллара
Учитывая, что сумма двух сторон должна быть больше, чем третья сторона, наша недостающая сторона должна быть больше 3. (Почему? Потому что 6 долларов + 3 = 9$ и нам нужно, чтобы сумма была больше 9.)
Если наша недостающая сторона является целым числом (которое, как нам говорят, верно), и мы пытаемся найти минимальное значение периметра, то наша недостающая сторона должна быть наименьшее целое число больше 3.
Это означает, что наша недостающая сторона равна 4.
Чтобы найти наш периметр, мы должны сложить все наши стороны вместе:
$4 + 6 + 9 = 19 $
Наш окончательный ответ D , 19.
(Примечание: всегда обращайте внимание на точный вопрос, который вам задают, и не попадайтесь на приманку ответов! Если вы проходили тест слишком быстро, у вас мог возникнуть соблазн выбрать ответ на выбор A, 4, что было значением недостающей длины стороны.Но, так как нас попросили найти периметр , это был бы неверный ответ.)

Готовы войти в царство особых треугольников (и стать безумно крутыми)?

Особые треугольники
Существует несколько различных видов особых треугольников, каждый из которых обычно появляется в ACT.
В этом разделе мы определим и опишем все виды треугольников, которые вы увидите в тесте. В следующем разделе мы рассмотрим все формулы, которые вам нужно знать для решения задач с треугольником ACT, а также способы их использования.

Равнобедренные треугольники
Равносторонний треугольник — это треугольник, у которого три равные стороны и три равных угла. Хотя размеры ног могут быть любыми (при условии, что все они равны), все измерения углов должны равняться 60°. Почему? Потому что углы треугольника всегда должны составлять 180°, а 180/3 = 60$.

a

Равнобедренные треугольники
Равнобедренный треугольник — это треугольник, у которого две стороны и два угла равны.
Стороны, противоположные равным углам, всегда будут равны, а углы, лежащие напротив равных сторон, всегда будут равны. Это знание часто приведет вас к правильным ответам на многие вопросы ACT, в которых, как вам кажется, вам дается очень мало информации.
(Мы рассмотрим, как решить эту проблему позже в руководстве, а пока обратите внимание, как кажется, что вам дано недостаточно информации. Но, если вы помните, что углы, лежащие напротив равных прямых, также равны, то вы увидите, что теперь у вас ровно столько, чтобы решить задачу)

Прямоугольные треугольники
Прямоугольный треугольник — это треугольник, в котором один из углов равен 90° (90° — прямой угол). Это означает, что сумма двух других углов также должна быть 90°, так как сумма углов треугольника всегда равна 90°.
Катет, противолежащий углу 90°, всегда будет гипотенузой треугольника. Это связано с тем, что угол 90° всегда будет самым большим углом в прямоугольном треугольнике. (Почему? Потому что два угла в 90° образуют прямую линию, а не треугольник.)
Особые прямоугольные треугольники
Существует много различных видов прямоугольных треугольников, и некоторые из них считаются «особыми». Это треугольники, у которых есть заданные углы или длины сторон и соответствующие им формулы. Понимание этих типов треугольников (и их формул) сэкономит вам значительное количество времени при прохождении теста.
Мы рассмотрим формулы, соответствующие этим типам треугольников, в следующем разделе, а пока давайте рассмотрим их определения.
Равнобедренный прямоугольный треугольник
Равнобедренный прямоугольный треугольник — это именно то, на что он похож — прямоугольный треугольник, в котором две стороны и два угла равны.
Хотя размеры сторон могут меняться, в равнобедренном треугольнике всегда будет один угол по 90° и два угла по 45°. (Почему? Потому что в прямоугольном треугольнике по определению должен быть один угол 90°, а сумма двух других углов должна составлять 90°. Таким образом, 90/2 = 45$.)
30-60-90 Треугольники
Треугольник 30-60-90 — это особый прямоугольный треугольник, определяемый своими углами. Это прямоугольный треугольник из-за угла 90°, а два других угла должны быть равны 30° и 60°.
Прямоугольные треугольники 3-4-5 и 5-12-13
Треугольники 3-4-5 и 5-12-13 являются особыми прямоугольными треугольниками, определяемыми длинами сторон. Числа 3-4-5 и 5-12-13 описывают длины сторон треугольника, а это означает, что если у вас есть прямоугольный треугольник с двумя длинами сторон 4 и 5, то вы автоматически знаете, что третья сторона равна 3. Любые непротиворечивые множители этих чисел также будут работать одинаково. Таким образом, прямоугольный треугольник может иметь катеты:
3(1)-4(1)-5(1) => 3-4-5
3(2)-4(2)-5(2) => 6-8-10
3( 3)-4(3)-5(3) => 9-12-15
И так далее.
Такие треугольники считаются особыми прямоугольными, поскольку все их стороны являются целыми числами.
a
a
Теперь пришло время формулы треугольника!

Формулы треугольников
Теперь, когда вы знаете, как будут выглядеть все ваши треугольники, давайте рассмотрим, как найти недостающие переменные и информацию о них.
Никаких формул на АСТ вам не дадут, поэтому вы должны знать все эти формулы наизусть. (Для получения дополнительной информации о формулах, которые вам понадобятся для раздела математики ACT, ознакомьтесь с нашим руководством по 31 формуле, которую вы должны знать перед днем экзамена.)
-как они работают и когда. Все механические заучивания в мире не помогут вам, если вы не знаете, когда и как их применять при решении ваших проблем.

Все треугольники
Площадь
$a = {1/2}bh$
$b$ — основание треугольника, т. е. длина любой из сторон треугольника.
$h$ — высота треугольника, полученная путем проведения прямой линии (под углом 90°) от основания треугольника до угла, противоположного от основания.
Это означает, что в прямоугольном треугольнике высота равна длине катета, сходящегося под углом 90° к основанию. В непрямоугольном треугольнике вы должны создать новую линию для своего роста. 92 + 16}$
Треугольники 3-4-5 и 5-12-13 (и их кратные) особенные, потому что вам не нужно работать с теоремой Пифагора, чтобы найти меры сторон третьей длины . Помните, если две стороны прямоугольного треугольника равны 12 и 15, то вы автоматически знаете, что третья сторона равна 9 (потому что 3(3)-4(3)-5(3) = 9-12-15$).
Хотя мы можем найти длину BC, используя теорему Пифагора, мы также можем просто знать, что она равна 5. (Почему? Потому что это гипотенуза прямоугольного треугольника с длинами катетов 3 и 4).
Теперь мы можем составить пропорцию, чтобы найти меру стороны AE. Длина AE до его гипотенузы будет пропорциональна длине BD до его гипотенузы.
${AE}/20 = 3/5$
$5AE = 60$
$12$
Наш окончательный ответ: B , 12.
Равнобедренный прямоугольный треугольник x x√2$
Хотя недостающие длины сторон равнобедренного треугольника можно найти с помощью теоремы Пифагора, можно также сократить путь и сказать, что равные длины сторон равны $x$, а гипотенуза равна $x√2$. 92$
$c = √200$
$c = √100 * √2$ (Почему мы смогли разделить наш корень таким образом? Ознакомьтесь с нашим руководством по расширенным целым числам ACT и его разделом о корнях, если этот процесс вам это незнакомо.)
$c = 10√2$
Итак, у нас остались длины сторон 10, 10 и 10√2. Или, другими словами, длины наших сторон равны $x, x$ и $x√2$.
Итак, наш окончательный ответ: E , $10√2$
30-60-90 Треугольник
$x, x√3, 2x$
Как и в случае с равнобедренным прямоугольным треугольником, длина сторон треугольника 30-60-90 определяется набором правил.
Опять же, вы можете найти эти длины по теореме Пифагора, но вы также всегда можете найти их по правилу: $x, x√3, 2x$, где $x$ — сторона, противоположная 30°, $x√3 $ — сторона, противоположная 60°, а $2x$ — сторона, противоположная 90°.
a
a
Запишите все незнакомые вам формулы. Вам нужно будет знать их к экзаменационному дню, поэтому небольшая практика и систематизация сейчас будут иметь большое значение для того, чтобы держать их прямо в голове.

Типичные вопросы-треугольники
Большинство вопросов-треугольников в ACT связаны с диаграммой, хотя некоторые из них представляют собой чисто словесные задачи. Давайте рассмотрим некоторые стандартные типы вопросов в каждой категории.
Задачи со словами
Большинство задач со словами на треугольники довольно просты, если их нарисовать. На самом деле, часто причина, по которой они дают вам задачу в виде словесной задачи вместо того, чтобы предоставить вам диаграмму, заключается в том, что создатели теста думали, что задачу будет слишком легко решить с помощью изображения.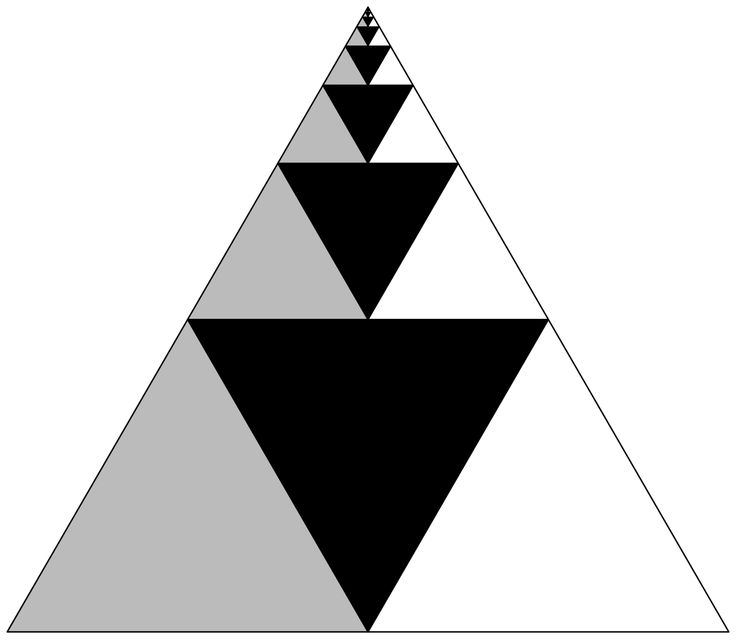
По возможности рисуйте свою собственную диаграмму, когда вам дают задачу на треугольник без таковой. Это не займет у вас много времени, и вам будет намного проще визуализировать вопрос.
Это должна быть простая фигура, но никогда не помешает быстро набросать ее, чтобы все детали были в порядке.
Нам говорят, что это прямоугольный треугольник и нам нужно найти длину одной недостающей стороны, поэтому нам нужно будет использовать теорему Пифагора.
92$
$c = √85$
Наш окончательный ответ: G , $√85$
Задачи с диаграммами
Существует несколько различных типов задач на треугольники, в которых используются диаграммы. Давайте разобьем их на категории и обсудим стратегии для каждой из них.
Тип диаграммы 1 — поиск пропущенных значений
Большинство задач с треугольниками относятся к этой категории — вас попросят найти недостающий угол, площадь, периметр или длину стороны (среди прочего) на основе предоставленная информация.
Некоторые из этих вопросов будут более сложными, чем другие, но ACT всегда предоставит вам достаточно информации для решения проблемы, так что вам решать, как собрать подсказки вместе.
Давайте пройдемся по некоторым реальным математическим примерам этого типа в ACT: Во-первых, давайте заполним предоставленную нам информацию, чтобы не потерять след того, какие углы что измеряют.
Мы знаем, что сумма внутренних углов треугольника равна 180 градусам, поэтому мы можем найти ACB, вычитая наши данные из 180.
$180 — 30 — 110$
$40$
Мы также знаем, что длина любой прямой составляет 180 градусов. BCD коллинеарны, а это значит, что они лежат на одной прямой. Таким образом, мы можем найти угол ACD, вычитая нашу меру ACB из 180.
Пример 2,
Подобные треугольники пропорциональны друг другу, поэтому мы можем найти длины сторон треугольника BAC, установив пропорции с треугольником LKM.
${BA}/{AC} = {LK}/{KM}$
${BA}/3 = 12,5/7,5$
$7,5BA = 37,5$
$BA = 5$
вторая пропорция будет следовать той же модели.
${AC}/{BC} = {KM}/{LM}$
$3/{BC} = 7,5/15$
$7,5BC = 45$
$BC = 6$
Теперь мы есть все меры сторон треугольника BAC, значит, мы можем найти его периметр.
5$ + 3 + 6$
14$
Наш окончательный ответ B , 14.
Тип диаграммы 2 – Отношения и (не)равенства
Обычно в таких вопросах вас просят либо найти отношения между частями различных треугольников, либо вас спрашивают, являются ли определенные стороны или углы треугольников равны или не равны.
Нам говорят, что AD равен ВС, значит, их соответствующие углы тоже будут равны. Это означает, что углы CAB и DBA равны (следовательно, углы EAB и EBA равны). Таким образом, мы можем исключить вариант ответа K.
Теперь, если углы CAB и DBA равны, то углы CBA и DAB ТАКЖЕ должны быть равны. Почему? Итак, мы знаем, что каждый треугольник имеет угол 90 градусов и один угол, равный некоторому неизвестному измерению (которое мы могли бы назвать $x$). Это означает, что третий оставшийся угол (назовем его $y$) ТАКЖЕ должен быть одинаковым для каждого треугольника.
Тогда каждый треугольник будет состоять из:
180$ = 90 + x + y$
Это означает, что мы можем исключить вариант ответа J.
По тем же соображениям, если угол DAB = углу CBA, то стороны, противоположные этим углам, также должны быть равны. Это означает, что AC = BD, что означает, что вариант ответа F можно исключить.
Поскольку AD и CB равны и оба являются частью треугольника с гипотенузой AB, катеты CA и DB пересекутся таким образом, что каждая половина катета будет равна соответствующей половине катета другого треугольник. Другими словами, AE = EB и DE = EC. Это означает, что мы можем исключить вариант ответа H.
Единственный вариант ответа, который у нас остался, это G. AD НЕ МОЖЕТ равняться AE. Почему? AD — катет треугольника ADE, а AE — гипотенуза того же треугольника. Из наших определений мы знаем, что гипотенуза всегда должна быть наибольшей стороной треугольника и поэтому не может быть равна ни одному из катетов.
Наш окончательный ответ — G.
Тип диаграммы 3 — Несколько фигур или фигур внутри фигур
Как видно из предыдущих примеров, некоторые задачи на треугольники в ACT будут включать несколько треугольников ( или другие геометрические фигуры), объединенные вместе. Этот метод представления задач предназначен для проверки вашего понимания линий и углов, а также треугольников.
Для задач такого типа вы должны использовать предоставленную вам информацию и решать для получения дополнительной информации в дальнейшем, пока не найдете именно то, что ищете.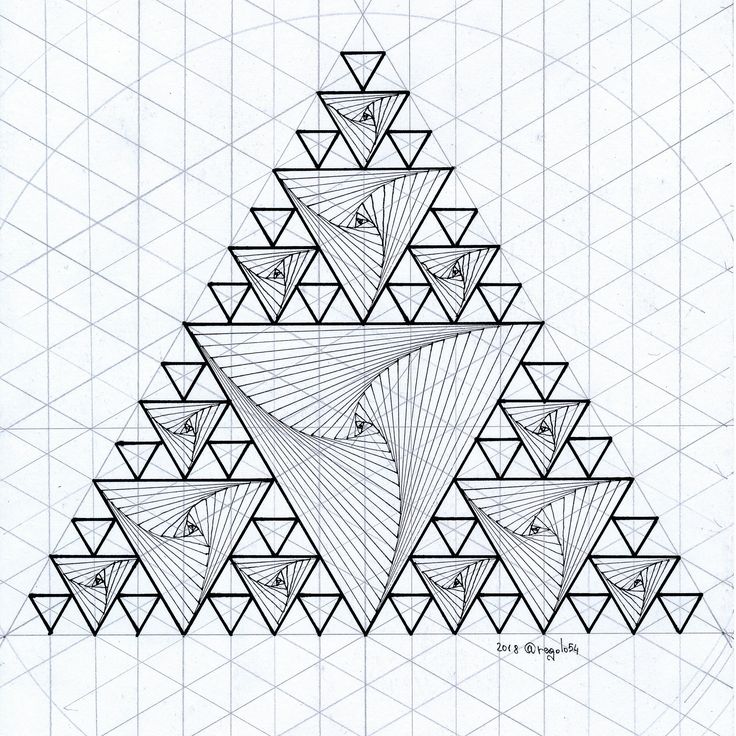 По сути, это эффект домино при решении проблем.
Поскольку в этой задаче используются переменные, самый простой способ решить ее — подставить собственные числа. Итак, давайте сделаем это.
Нам говорят, что каждый незаштрихованный треугольник является конгруэнтным прямоугольным треугольником. Поскольку с переменными может быть сложно работать, давайте заменим $x$ на 4. (Почему 4? Почему бы и нет!) 92$
$80$
Теперь мы должны просто разделить наш заштрихованный квадрат на незаштрихованный квадрат ABCD, чтобы определить, какую долю он составляет от большего квадрата.
$80/144$
$80 ÷ 16 = 5$ и $144 ÷ 16 = 9$
$5/9$
стратегии — беспроигрышные!

Стратегии решения вопроса о треугольнике
Поскольку существует так много различных типов задач на треугольники, трудно выделить один точный путь их решения.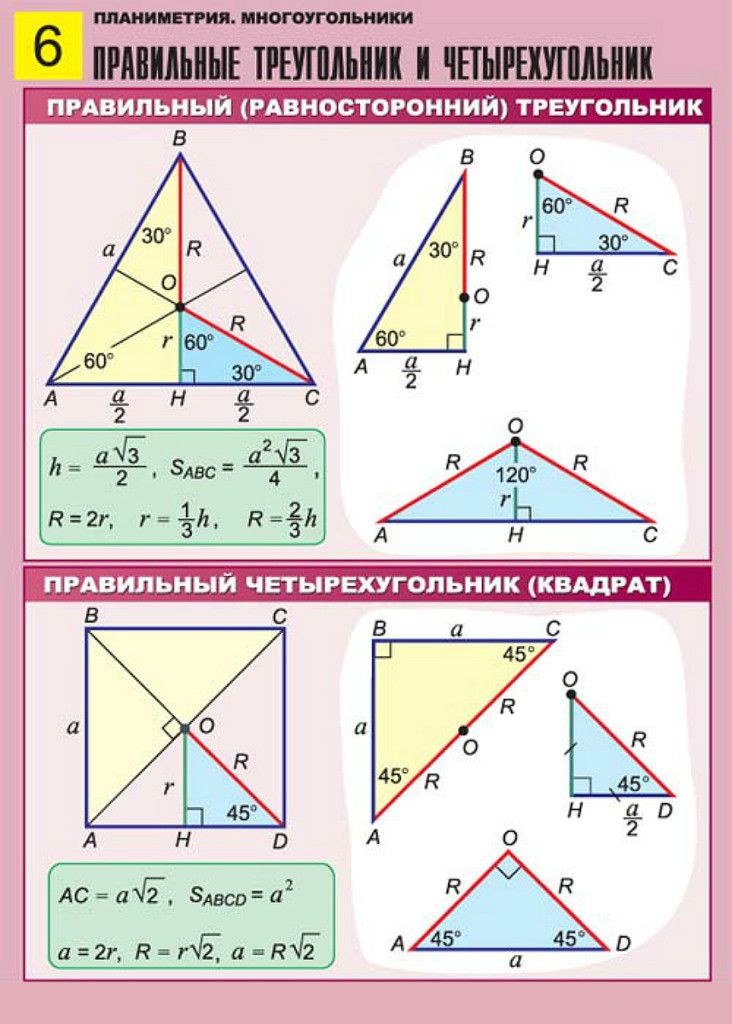
Тем не менее, ваши самые большие преимущества и стратегии при решении задач треугольника будут заключаться в следующем:
1) Запишите свои формулы
Поскольку вам не дано никаких формул, вы должны держать их в голове и в своем сердце. Хорошая новость заключается в том, что чем больше вы практикуетесь, тем лучше у вас будет получаться вычислять площади треугольников или длины сторон треугольников 30-60-90 или что-то еще, что вам нужно.
Но если вы чувствуете, что забудете свои формулы во время прохождения теста, потратьте несколько секунд и запишите их, прежде чем приступать к решению своих вопросов. Как только вы это сделаете, они навсегда останутся с вами, чтобы вы могли работать до конца математического раздела, и вам не придется беспокоиться о том, что вы их забудете.
2) Используйте свои формулы (и используйте короткие пути)
Как только вы убедитесь, что запомнили свои формулы, их использование является самым важным шагом для любой задачи треугольника. И, учитывая, что большинство ваших формул, по сути, действуют как короткие пути (зачем решать с помощью теоремы Пифагора, если вы знаете, что катеты треугольника 30-60-90 равны $x, x√3, 2x$?), вы сэкономит вам много времени и энергии, если вы сможете держать свои формулы под рукой и в порядке.
3) При работе с многофигурными фигурами разбивайте их на маленькие шаги
Помните, что решение задачи многофигурного треугольника похоже на работу с домино. Каждая последующая часть информации уступает место для поиска следующей части информации.
Не пугайтесь, что у вас недостаточно информации или слишком много фигур или линий, с которыми нужно иметь дело. У вас всегда будет достаточно данных, чтобы двигаться дальше — просто сосредоточьтесь на поиске одной формы и одной части информации за раз, и костяшки домино встанут на свои места.
4) Нарисуйте
Нарисуйте свои собственные диаграммы, если они вам не даны.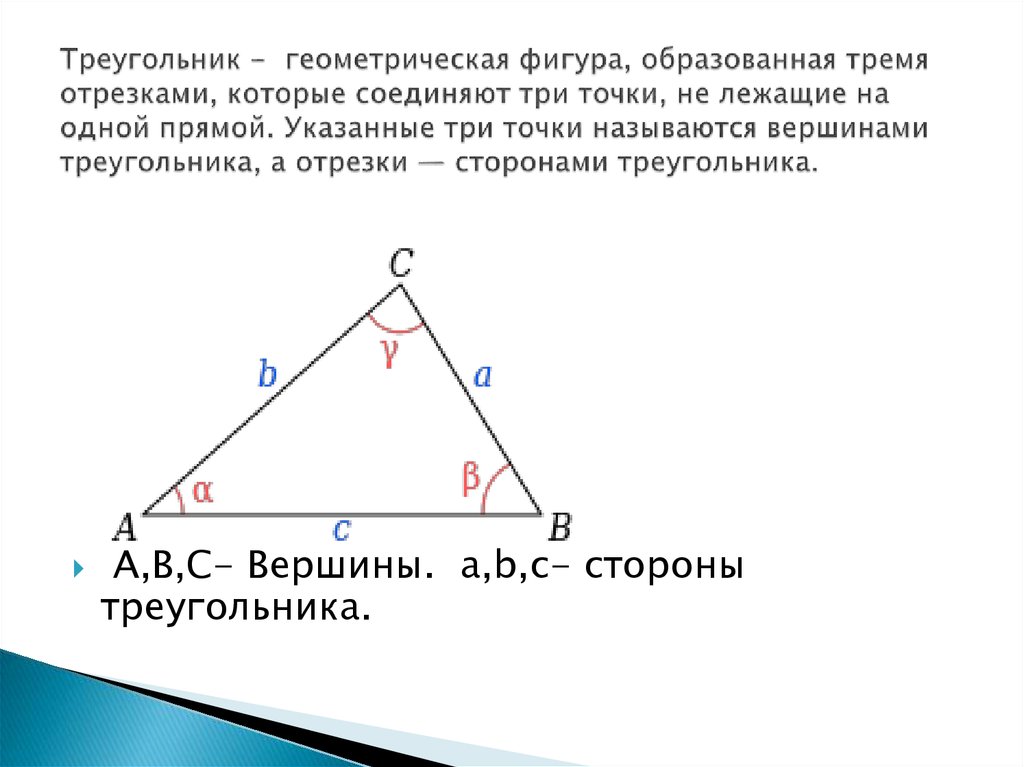 Нарисуйте сверху ваших диаграмм, когда вы — это заданных картинок. Запишите свои данные и все измерения, которые вы найдете на пути к вашей отсутствующей переменной (или переменным), отметьте конгруэнтные линии и углы.
Чем больше вы сможете прояснить свои диаграммы, тем меньше вероятность того, что вы сделаете ошибки по невнимательности, перепутав числа и равенства.

Готовы проверить свои знания?

Проверь свои знания
Теперь давайте проверим свои знания о треугольниках на более реальных математических задачах ACT.
1)

2)
3)

4)
Answers: B, F, E, H
Объяснение ответа:
1) Поскольку нам сказали, что это равнобедренная трапеция, мы знаем, что все непараллельные стороны должны быть равны. Это означает, что углы, опирающиеся на эти стороны (углы BDC и ACD), также должны быть равны.
Мы также знаем, что сумма внутренних градусов треугольника всегда равна 180 градусам, поэтому мы можем найти меру DXC, вычитая два наших известных угла из 180.
Итак, DB — прямая линия, а это значит, что углы, образующие линию, должны составлять 180 градусов. Это означает, что мы можем найти угол BXC, вычитая известный угол из 180.
$180 — 130$
$50$
Наконец, мы снова знаем, что сумма внутренних углов треугольника будет равна 180, поэтому мы можем найти DBC, вычитая наши известные углы из 180.
$180 — 50 — 35
$95$
Наш окончательный ответ: B , 95°.

2) Из наших определений треугольника мы знаем, что чем больше сторона, противоположная углу, тем больше будет угол. (Если вы когда-нибудь почувствуете неуверенность в отношениях между углами и сторонами треугольника, вы также можете обратиться к своим правилам и определениям тригонометрии.)
Итак, если мы нарисуем некоторые случайные измерения сторон для XZ и YZ (при условии, что они следуют правилу XZ > YZ), мы ясно увидим, что угол Y будет больше, чем угол X.
Наш окончательный вариант ответ F, угол X < угол Y.

3) Нам сказали, что треугольник является прямоугольным треугольником с гипотенузой, а это означает, что мы можем использовать наши сокращения, чтобы найти длины двух других сторон.
Мы знаем, что длины сторон равнобедренного прямоугольного треугольника равны $x, x$ и $x√2$. Поскольку мы уже знаем, что гипотенуза равна $8√2$, мы можем сказать, что две другие стороны равны 8.
Теперь мы можем сложить стороны, чтобы найти периметр.
$8 + 8 + 8√2$
$16 +8√2$
Наш окончательный ответ: E, $16 + 8√2$

16, 900 заполните предоставленную нами информацию.
Теперь мы можем знать, что треугольники и внешний угол лежат на одной прямой, а это означает, что сумма углов, образующих линию, равна 180°. Это означает, что мы можем найти угол CBD, вычитая наш внешний угол из 180.
$180 — 140$
$40$
Теперь, когда у нас есть две меры внутренних углов в треугольнике DCB, мы можем найти меру третьего (поскольку внутренние углы в треугольнике всегда будут составлять в сумме 180).
$180 — 40 — 47$
$93$
[Примечание: вы можете заметить, что сумма двух углов, не касающихся внешнего угла, равна сумме внешнего угла — $47 + 93 = 140$. Это не совпадение. Всегда будет так, что сумма двух несоединенных углов будет равна внешнему углу треугольника любого типа.)
Теперь у нас снова есть два угла, которые образуют прямую линию, а это значит, что мы можем найти меру угла CDA, вычитая из 180° наш известный угол.
$180 — 93$
$87$
И, наконец, CAD образует треугольник, а это означает, что сумма его внутренних углов будет равна 180. Мы можем найти угол ACD, вычитая два наших известных значения из 180°.
$180 — 76 — 87$
$17$
Наш окончательный ответ: H, 17°.

О, да. Вы заслужили этот сон.

Выводы
Будь то задача по тригонометрии или задача по геометрии, вы будете видеть треугольники несколько раз на любом заданном ACT. Хотя большинство задач с треугольниками довольно просты, вам необходимо знать основные строительные блоки треугольников и геометрии, чтобы понять, как их решать.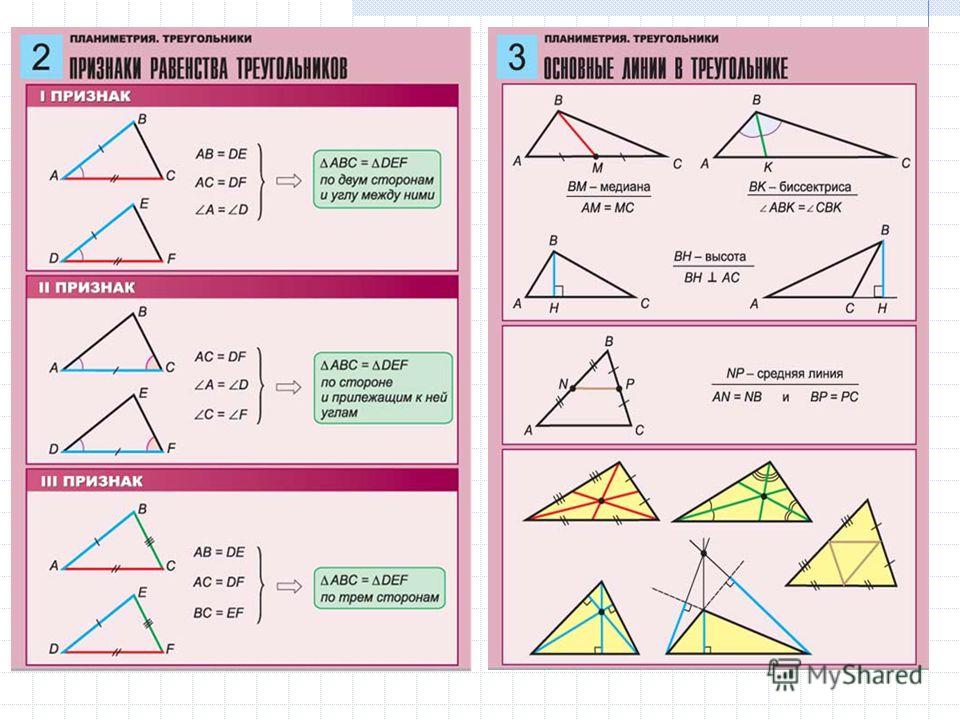
Знайте свои определения, запоминайте формулы и делайте все возможное, чтобы сохранять ясность ума во время прохождения теста. И, как всегда, практика, практика, практика! Чем больше опыта вы приобретете в решении разнообразных треугольных вопросов, которые ACT может поставить перед вами, тем лучше для вас будет.

Что дальше?
Ого! Вы взяли треугольники и выиграли (аплодисменты себе)! Хотите больше геометрии? Перейдите к нашим руководствам по кругам, многоугольникам и объемной геометрии ACT и завершите все свои исследования геометрии за один раз.
Не знаете, какую тему обсудить дальше? Убедитесь, что у вас есть четкое представление обо всех математических темах, по которым вы будете тестироваться, и ознакомьтесь со всеми нашими математическими руководствами ACT для справки и практики. Каждое руководство содержит определения, формулы и реальные практические вопросы ACT и шаг за шагом разбивает процесс решения.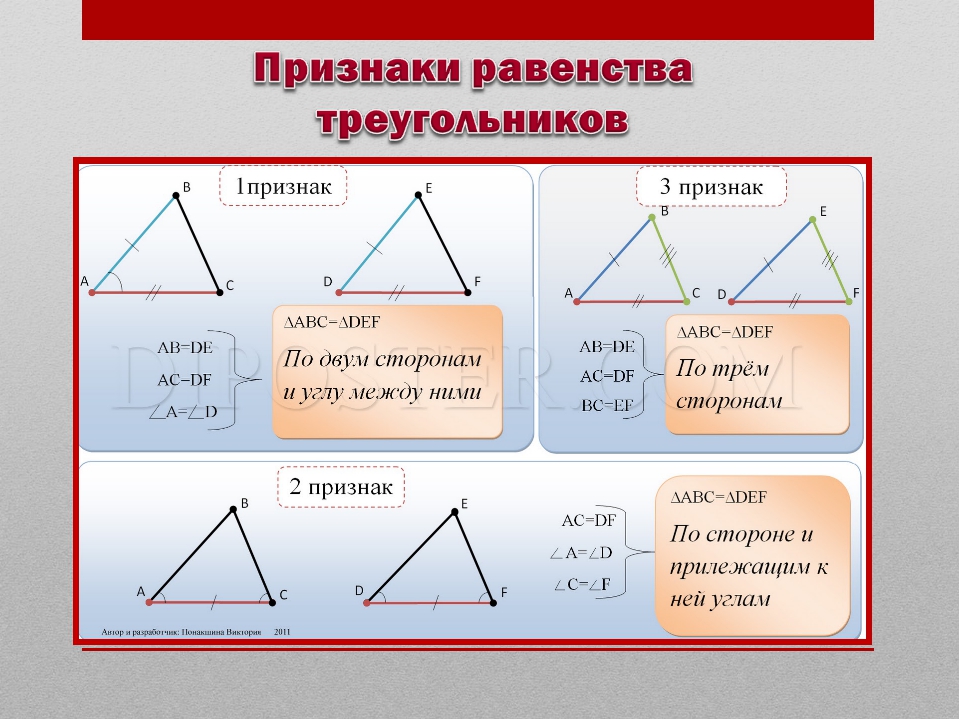
Откладывали? Ознакомьтесь с нашим руководством о том, как вернуть время учебы и победить демонов прокрастинации.
Хотите получить высший балл? Наше руководство по математике на 36 баллов (написанное отличником!) поможет вам достичь цели.
Хотите улучшить свой результат ACT на 4 балла?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к ACT. Мы гарантируем возврат ваших денег , если вы не улучшите свой балл ACT на 4 балла или более.
Наша программа полностью онлайн, и она настраивает то, что вы изучаете, в соответствии с вашими сильными и слабыми сторонами. Если вам понравился этот урок математики, вам понравится и наша программа. Вместе с более подробными уроками вы получите тысячи практических задач, организованных по отдельным навыкам, чтобы вы могли учиться наиболее эффективно. Мы также дадим вам пошаговую программу, чтобы вы никогда не запутались в том, что изучать дальше.
No related posts.