Все формулы треугольника. Формулы биссектрисы. Основные формулы треугольника.
- Альфашкола
- Статьи
- Основные формулы треугольника
Дарим в подарок бесплатный вводный урок!
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Подготовка к ОГЭ по математике
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по грамматике русского языка
- Репетитор по английскому языку для подготовки к ОГЭ
- Репетитор по грамматике английского языка
- Репетитор по английскому для взрослых
- Репетитор по биологии для подготовки к ОГЭ
- Программирование Pascal
- Scratch
Основные формулы треугольника
В этой статье вы найдете все формулы площадей треугольника:
6 формул площади треугольника
Теорема косинусов
\(a^2=b^2+c^2-2bc* cos α\)
\(b^2=a^2+c^2-2ac* cos β\)
\(a^2=a^2+b^2-2ab* cos γ\)
Медианные формулы
\(m^2_a=14(2b^2+2c^2-a^2)\)
\(m^2_b=14(2a^2+2c^2-b^2)\)
\(m^2_c=14(2a^2+2b^2-c^2)\)
Формулы биссектрисы
\(\frac{a}{b}=\frac{n}{m}\)
\(l^2=ab-nm\)
Прямоугольный треугольник
\(c^2=a^2+b^2\)
\(S=\frac{1}{2}ab=\frac{1}{2}ch\)
\(a^2=n⋅с\)
\(b^2=mc\)
\(h^2=m*n\)
\( r=\frac{a+b−c}{2}\)- радиус вписанной окружности
\( sin α=a/c\)
\( tan α=a/b\)
\( cot α=b/a\)
Формулы площади
полупериметр \(p=\frac{a+b+c}{2}\)
Площадь треугольника
\(S=\frac{ ch_c}{2}\)
\(S=\frac{ab sin γ}{2}\)
\(S=\sqrt{p(p−a)(p−b)(p−c)}\)
\(S=pr \)
где \(r\) радиус треугольника вписанной окружности
\(S=\frac{abc}{ 4R}\)
где — R-радиус описанной окружности
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Вадим Вадимович Козлов
Репетитор по математике
Стаж (лет)
Образование:
Брянский государственный технический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ксения Анатольевна Астапенко
Репетитор по математике
Стаж (лет)
Образование:
Филиал МГЛУ «Лингвогуманитарный колледж»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Наталья Николаевна Шарапова
Репетитор по математике
Стаж (лет)
Образование:
Челябинский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Все, что нужно знать об олимпиаде «Кенгуру»
- Периметр треугольника
- Задачи «на части»
- ЕГЭ по математике, профильный уровень.
 Неравенства
Неравенства - ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
- Как по координатам вершин треугольника записать уравнения сторон и уравнение биссектрисы
- Задачи на оптимизацию. Задание №17 из ЕГЭ
- 5 способов быстро запомнить таблицу умножения
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
- Определение треугольника
- Классификация треугольников
- Свойства треугольников
- Медианы треугольника
- Биссектриссы треугольника
- Высоты треугольника
Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.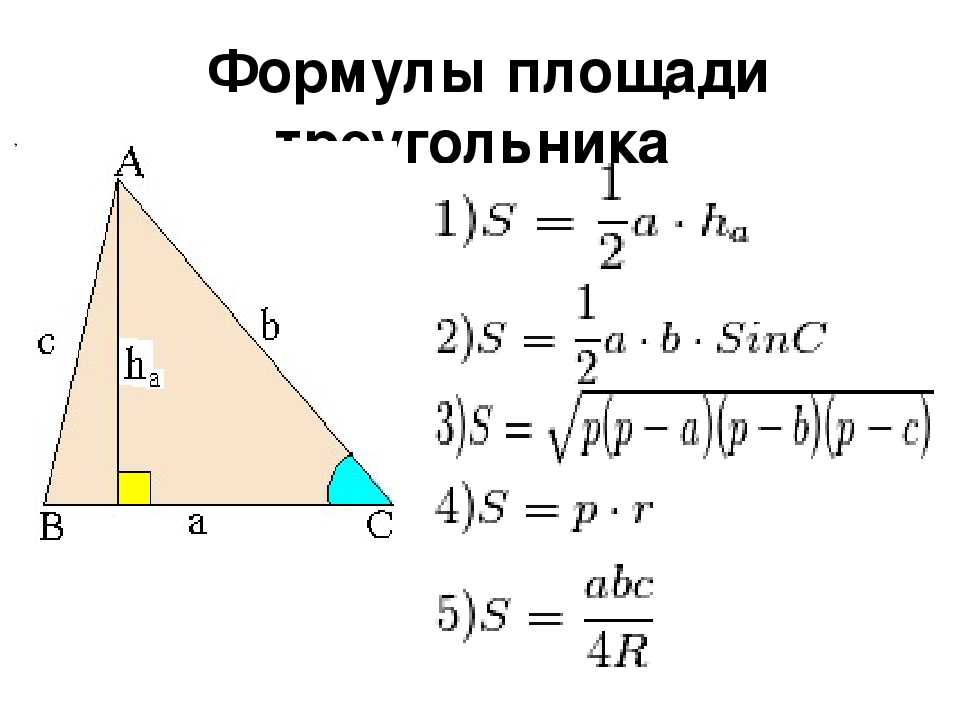 Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке.
- угол α — ∠ВСА или ∠ACB;
- угол β — ∠ВАC или ∠CAB;
- угол γ — ∠АBC или ∠CBA;
Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.
Разносторонний – треугольник, у которого все стороны имеют разную длину.a ≠ b ≠ c
∠ α ≠ ∠ β ≠ ∠ γ
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
a = b
∠ α=∠ β
3
.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.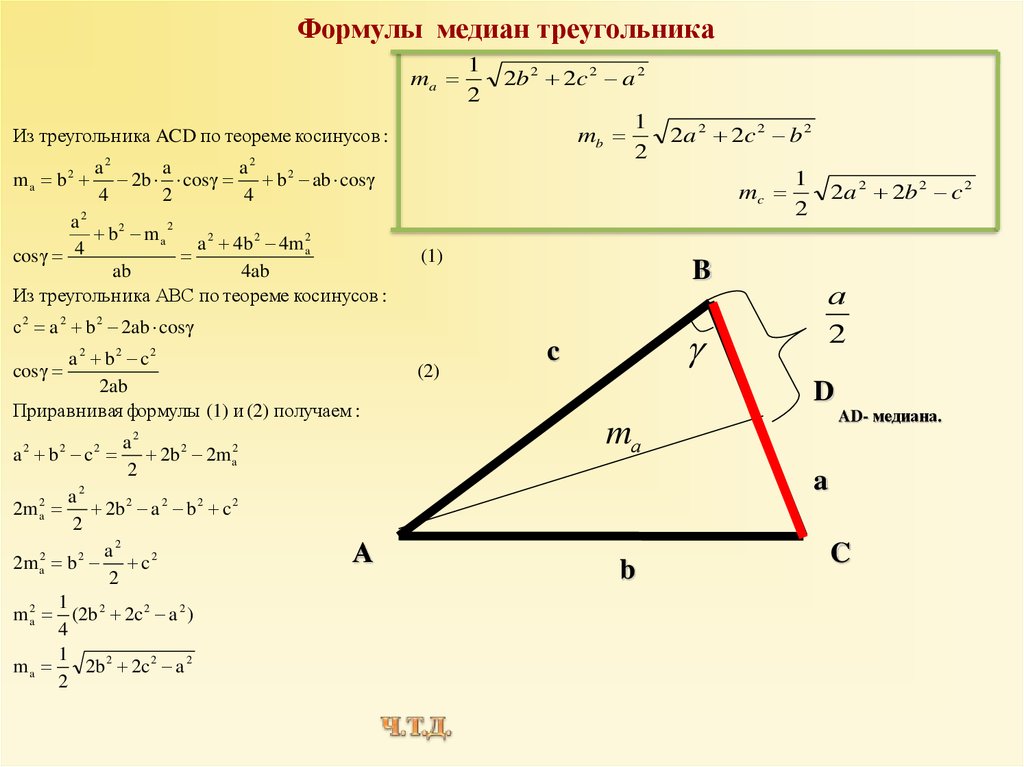
a = b = c
∠ α = ∠ β = ∠ γ = 60°
4.
Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°∠ α < 90°
∠ β < 90°
∠ γ < 90°
5.
Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.∠ α < 90°
∠ β < 90°
∠ γ > 90°
6.
Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).∠ α < 90°
∠ β < 90°
∠ γ = 90°
Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
α + β + γ = 180°
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
- В треугольнике против большей стороны лежит больший угол, и обратно.
 Против равных сторон лежат равные углы:
Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b 2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
4. Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.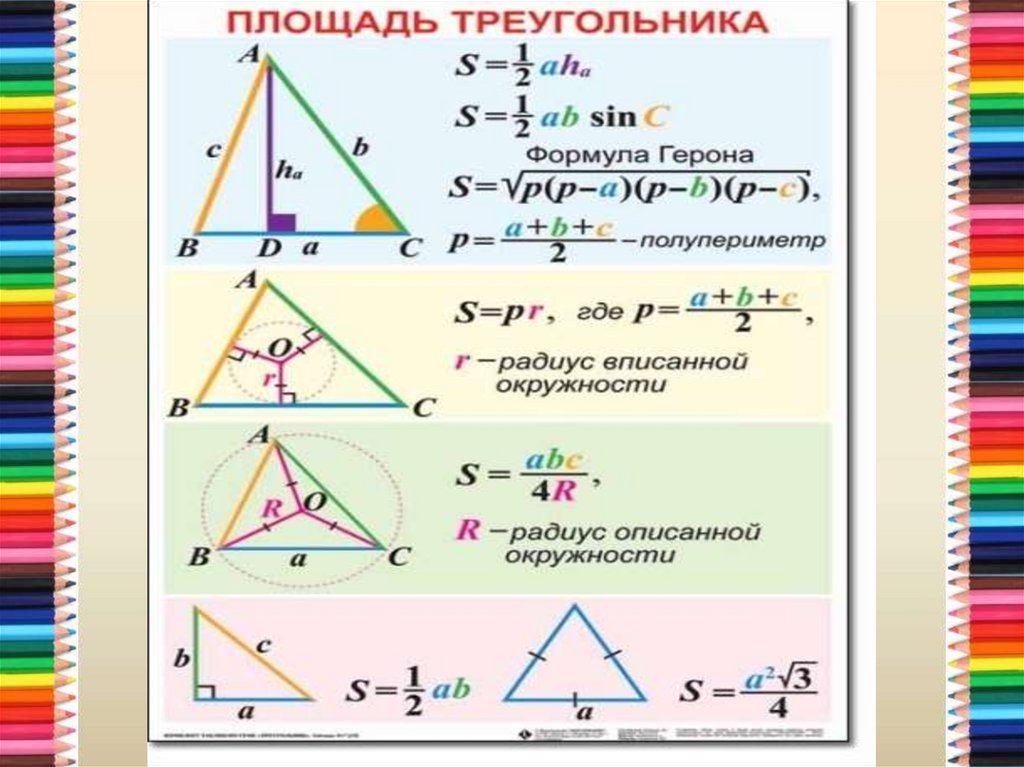
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 | |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF =
= S∆BOD = S∆COD = S∆COE
5. Из векторов, образующих медианы, можно составить треугольник.
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Формулы сторон через медианы
a =
√2(mb2+mc2)-m a2
b =
√2(mb2+mc2)-mb2
c =
√2(mb2+mc2)-mc2
Биссектриссы треугольника
Биссектриса угла треугольника— луч с началом в вершине угла, делящий угол на два равных угла.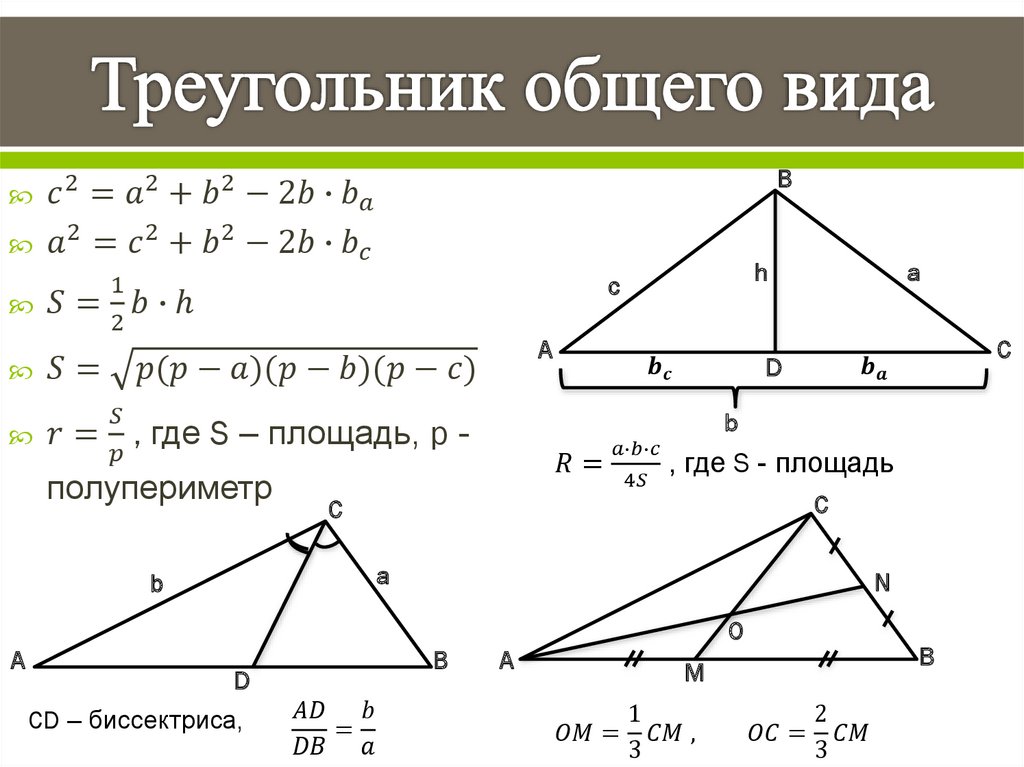
Свойства биссектрис треугольника:
1. Биссектрисы треугольника пересекаются в одной точке О,которая называется ИНЦЕНТР. Инцентр равноудален от трех сторон треугольника, следовательно инцентр — центр вписанной окружности.
2. Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
| AE | = | EC |
| AB | BC |
3. Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между La и La’ = 90°
4. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
5. Если в треугольнике три биссектрисы равны, то треугольник — равносторонний.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
La =
√bcp(p-a)
b+c
Lb =
√bcp(p-b)
a+c
Lc =
√bcp(p-c)
a+b
p =
a + b + c
2
Формулы биссектрис треугольника через две стороны и угол:
La =
2bc·cos
a+b
Lb =
2ac·cos
a+c
Lc =
2ab·cos
b+c
Высоты треугольника
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
В зависимости от типа треугольника высота может содержаться
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
1. Высоты треугольника пересекаются в одной точке O, называемой ортоцентром треугольника.
2. Если в треугольнике две высоты равны, то треугольник — равнобедренный.
3. Если в треугольнике все высоты равны, то треугольник — равносторонний.
Формулы высот треугольника
ha = b sin γ= c sin β
hb= c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:
ha =
hb =
hc =
Формула треугольника — Типы треугольников
Примечание: Оставшиеся два угла прямоугольного треугольника всегда острые.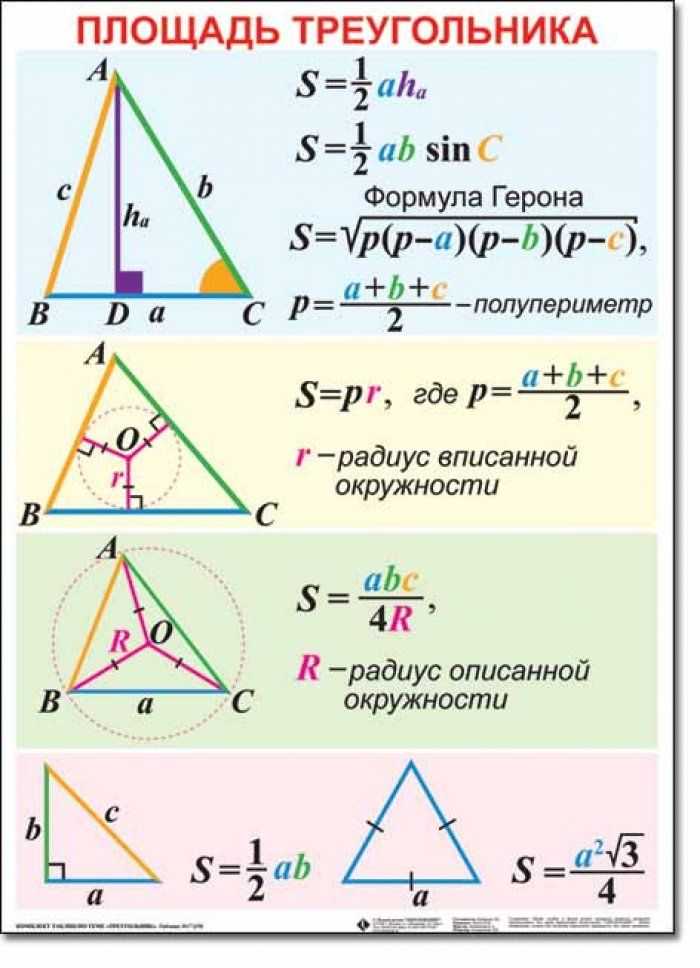 Важным свойством прямоугольных треугольников является Теорема Пифагора. Он утверждает, что в прямоугольном треугольнике, сумма квадратов основания и перпендикуляра равна квадрату гипотенузы треугольника.
Важным свойством прямоугольных треугольников является Теорема Пифагора. Он утверждает, что в прямоугольном треугольнике, сумма квадратов основания и перпендикуляра равна квадрату гипотенузы треугольника.
На рисунке выше DABC — прямоугольный треугольник, поэтому (AB) 2 + (АС) 2 = (ВС) 2 . Здесь AB = 6 и AC = 8, поэтому BC = 10, поскольку 6 2 + 8 2 = 36 + 64 = 100 = (BC) 2 и BC = &redic;100.
Любой треугольник, в котором длины сторон относятся как 3:4, всегда является прямоугольным.
В общем случае, если x, by и z — длины сторон треугольника, в котором x 2 + y 2 = z 2 , то такой треугольник называется прямоугольным.
Есть несколько пифагорейских троек, которые часто используются в вопросах. Лучше запомнить эти тройки.
- 3, 4 и 5
- 5, 12 и 13
- 7, 24 и 25
- 8, 15 и 17
- 9, 40 и 41
- 11, 60 и 61
- 12, 35 и 37
- 16, 63 и 65
- 20, 21 и 29
- 28, 45 и 53.

Любое кратное этих пифагорейских троек также будет пифагорейской тройкой, т. е. когда мы говорим, что это тройка 5, 12, 13, если мы умножим все эти числа на 3, это также будет тройкой, т. е. 15, 36, 39также будет пифагорейской тройкой.
(iv) 45 ° — 45 ° — 90 ° Треугольник : Особые треугольники: Если три угла треугольника равны 45°, 45° и 90°, то перпендикулярная сторона этого прямоугольного треугольника в 1 / &редик; 2 раза больше гипотенузы треугольника. В треугольнике с углами 45°-45°-90° длины трех сторон этого треугольника относятся как 1:1: &redic;2.
Например, в ∆PQR, если PR = 2 см, то PQ = &redic;2 см и QR = &redic;2 см.
(в) 30 ° — 60 ° — 90 ° Треугольник : В треугольнике 30°-60°-90° длины трех стороны этого треугольника находятся в отношении 1: &redic;3 : 2.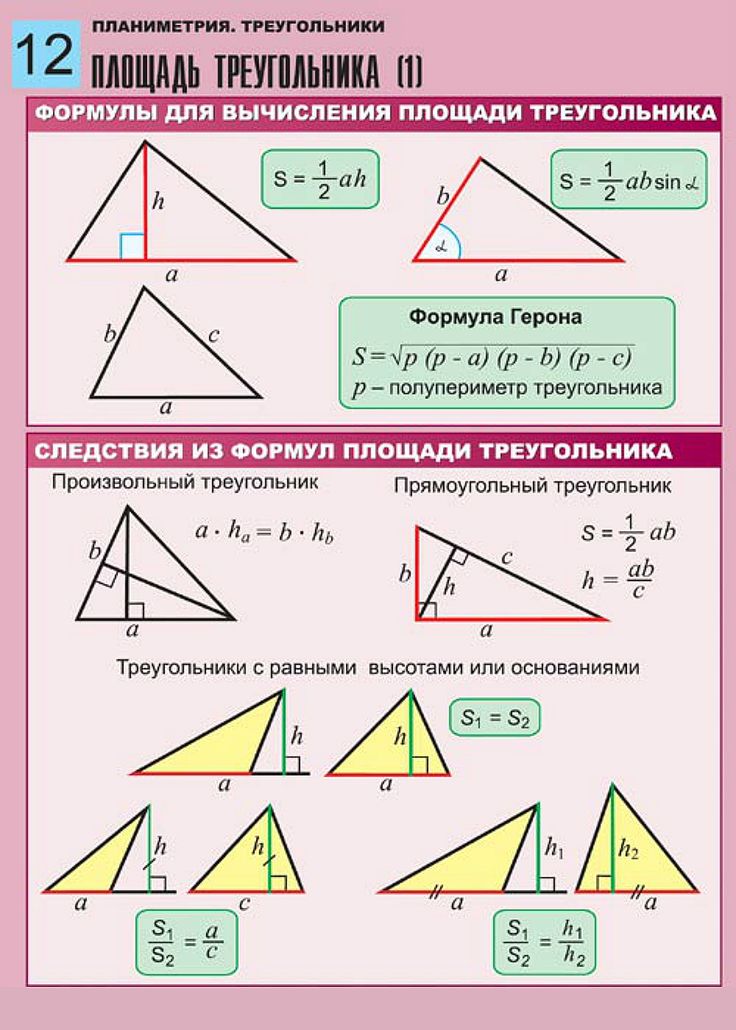 Например, в ∆ABC, если AC = 3, то AB = 3&redic;3 и BC = 6. Подводя итог, приведенные ниже формулы могут быть применены к вычислить две другие стороны 30°-60°-9Треугольник 0°, когда дана одна из трех сторон.
Например, в ∆ABC, если AC = 3, то AB = 3&redic;3 и BC = 6. Подводя итог, приведенные ниже формулы могут быть применены к вычислить две другие стороны 30°-60°-9Треугольник 0°, когда дана одна из трех сторон.
Сторона, противоположная 30 ° = ½ гипотенузы.
Сторона, противоположная 60 ° = &redic;3/2 гипотенузы.
Некоторые важные свойства треугольников
(i) Сумма трех внутренних углов треугольника равна 180°.
In ∆ABC, ∠ABC + ∠BAC + ∠ACB = 180°
(ii) Сумма внутреннего угла и прилежащего к нему внешнего угла равна 180°.
На рисунке на предыдущей странице ∠ABC + ∠ABH = 180°
∠ABC + ∠CBI = 180°
(iii) Два внешних угла, имеющих одну и ту же вершину, конгруэнтны.
(iv) Мера внешнего угла равна сумме мер двух внутренних углов (называемых удаленными внутренними углами) треугольника, не смежного с ним.
(vi) Сумма любых двух сторон треугольника всегда больше третьей стороны.
В ∆ABC AB + BC > AC, а также AB + AC > BC и AC + BC > AB.
(vii) Разность любых двух сторон всегда меньше, чем разность третьей стороны.
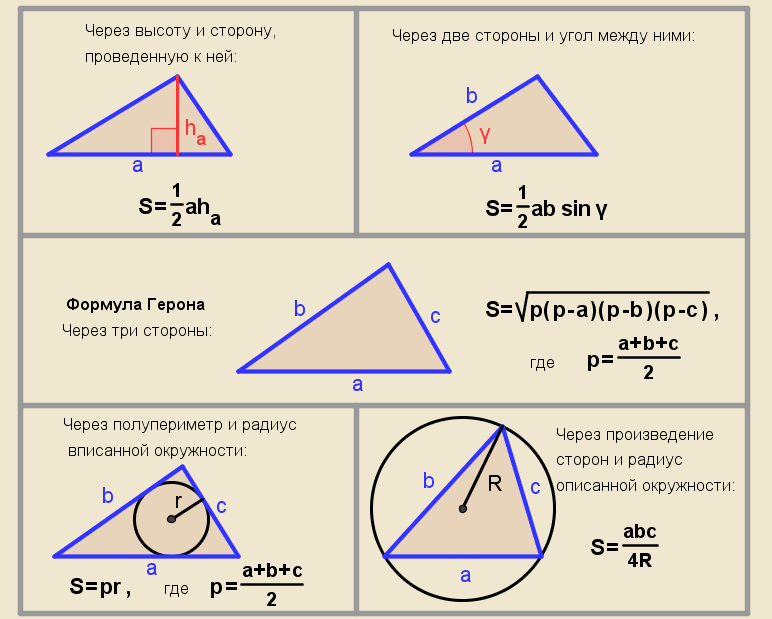
Высота: Высота треугольника — это отрезок, проведенный из вершины перпендикулярно стороне, противоположной этой вершине. Относительно этой вершины и высоты противоположная сторона называется основанием.
Площадь треугольника равна: (длина высоты) × (длина основания) / 2,
BD = 5
В ∆ABC BD — высота до основания AC, а AE — высота до основания BC.
Формула треугольника : Площадь треугольника ∆ABC равна ½ × BD × AC = ½ × 5 × 8 = 20.
Площадь треугольника также равна (AE × BC) / 2. Если DABC вверху равнобедренный и AB = BC, то высота BD делит основание пополам; то есть AD = DC = 4. Точно так же любая высота равностороннего треугольника делит пополам сторону, к которой он обращен.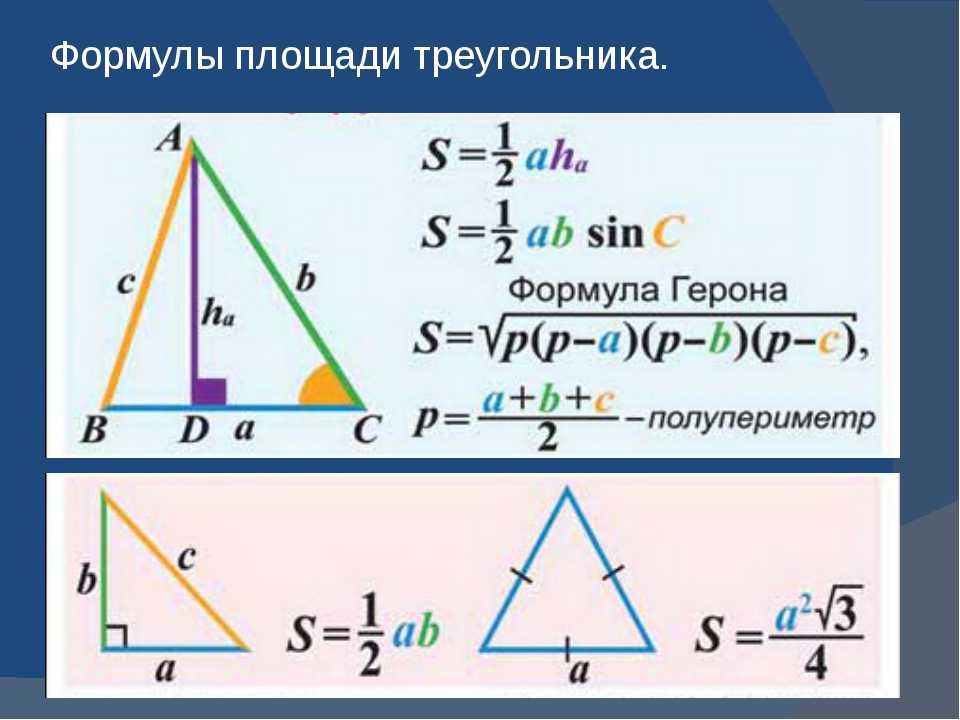
Конгруэнтность треугольников : Если стороны и углы одного треугольника равны соответствующим сторонам и углам другого треугольника, то говорят, что эти два треугольника равны.
Два треугольника конгруэнтны, если
- Две стороны и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника (SAS).
- 2 угла и 1 сторона треугольника соответственно равны двум углам и соответствующей стороне другого треугольника (AAS).
- Три стороны треугольника соответственно конгруэнтны трем сторонам другого треугольника (SSS).
- 1 сторона и гипотенуза прямоугольного треугольника соответственно конгруэнтны 1 стороне и гипотенузе другого прямоугольного треугольника. треугольник (правая сторона).
Подобие треугольников:
Говорят, что два треугольника подобны друг другу, если они похожи только по форме. Соответствующие углы этих треугольников равны, а соответствующие стороны только пропорциональны. Все конгруэнтные треугольники подобны, но не обязательно все подобные треугольники конгруэнтны.
Все конгруэнтные треугольники подобны, но не обязательно все подобные треугольники конгруэнтны.
Два треугольника подобны, если
- Три стороны одного треугольника пропорциональны трем сторонам другого треугольника (SSS).
- Два угла треугольника соответственно равны двум углам другого треугольника (AA).
- Две стороны треугольника пропорциональны двум сторонам другого треугольника, а прилежащие к ним углы равны (SAS).
Рекомендуемое действие:
Начните подготовку с БЕСПЛАТНОГО доступа к 25+ макетам, 75+ видео и 100+ тестам по главам. Зарегистрируйтесь сейчас
Свойства треугольников :
- Если два треугольника подобны, отношение сторон = отношение высот = отношение медиан = отношение биссектрис угла = отношение внутренних радиусов = отношение радиусов описанной окружности.
- Отношение площадей = b 1 h 1 /b 2 h 2 = (s 1 ) 2 /(s 2 9023 1 ) 2 , где б 1 и ч 1 — основание и высота первого треугольника, а b 2 и h 2 — основание и высота второго треугольника.
 s 1 и s 2 — соответствующие стороны первого и второго треугольника соответственно.
s 1 и s 2 — соответствующие стороны первого и второго треугольника соответственно. - Два треугольника на каждой стороне перпендикуляра, проведенного из вершины прямого угла к наибольшей стороне, т. е. гипотенузе, подобны друг другу, а также подобны большему треугольнику.
∆ DBA аналогичен ∆ DCB, который аналогичен ∆ BCA.
- Высота от вершины прямого угла до гипотенузы – это среднее геометрическое отрезков, на которые делится гипотенуза.
т. е. (DB) 2 = AD * DC
Центр окружности : Центр окружности — это центр описанной окружности треугольника. Его можно найти пересечением серединных перпендикуляров.
Incenter : Incenter — это точка, представляющая центр вписанной окружности многоугольника. Соответствующий радиус вписанной окружности известен как внутренний радиус вписанной окружности.
Формула треугольников для класса 10
Трехсторонняя замкнутая фигура, образованная прямыми линиями, называется треугольником, а многоугольник из трех сторон называется треугольником.
Треугольник ABC состоит из шести элементов, а именно угла ABC (или ∠B), угла ACB (или ∠C), угла BAC (∠A) и трех сторон AB, BC и CA.
Типы треугольников:
- На основании сторон:
- Треугольник, у которого нет равных сторон, называется разносторонним треугольником.
- Треугольник, у которого две стороны равны, называется равнобедренным треугольником.
- Треугольник, у которого все стороны равны, называется равносторонним треугольником.
- На базе Углов:
- Треугольник, у которого все углы острые, называется остроугольным треугольником.
- Треугольник, у которого угол при вершине прямой, называется прямоугольным.
- Треугольник, у которого один угол тупой, называется тупоугольным треугольником.
Подобие треугольников
Две фигуры подобны, если они имеют одинаковую форму, но не обязательно одного размера, тогда как две конгруэнтные фигуры имеют «одинаковую форму» и «один и тот же размер».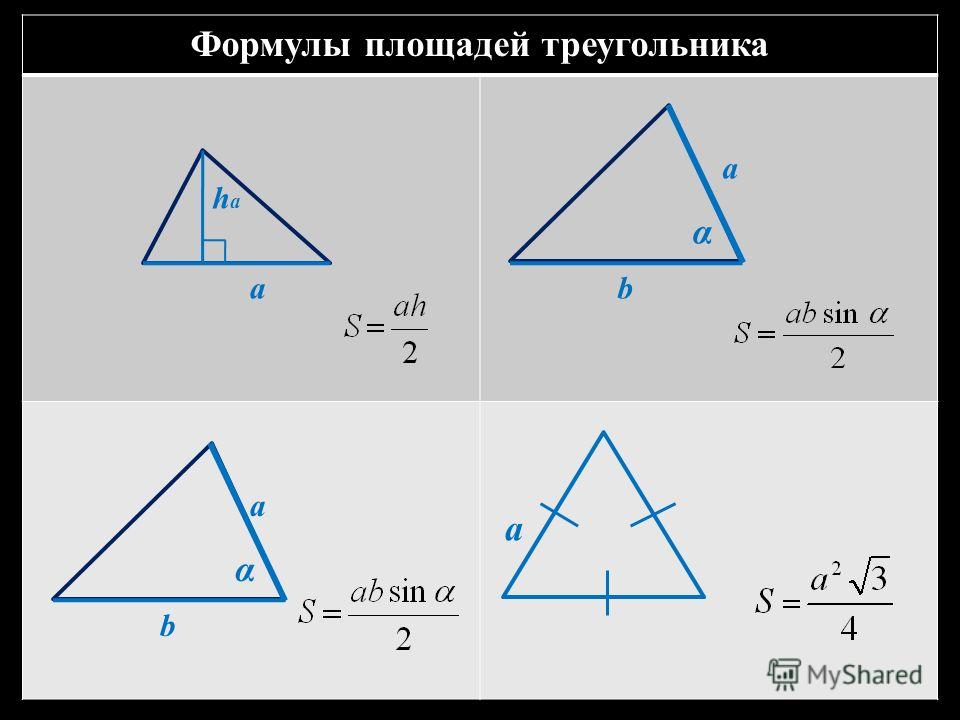 Следовательно, две конгруэнтные фигуры подобны, но обратное не обязательно верно.
Следовательно, две конгруэнтные фигуры подобны, но обратное не обязательно верно.
Все правильные многоугольники с одинаковым числом сторон, такие как равносторонние треугольники, квадраты, шестиугольники и т. д., подобны. В частности, все окружности также подобны.
Два треугольника называются подобными, если
- Их соответствующие углы равны
- Их соответствующие стороны находятся в одинаковом отношении
Основная теорема пропорциональности (теорема Фалеса):
Если провести прямую, параллельную одной стороне треугольника, чтобы пересечь две другие стороны в разных точках, то две другие стороны делятся в том же отношении.
Обратная основная теорема пропорциональности:
Если прямая делит любые две стороны треугольника в одинаковом отношении, то эта прямая параллельна третьей стороне.
Критерии подобия двух треугольников
- AAA Правило подобия: Если в двух треугольниках соответствующие углы равны, то их соответствующие стороны пропорциональны и, следовательно, треугольники подобны.

Следствие: Если два угла треугольника равны двум углам другого треугольника, то эти два треугольника подобны. Это называется критерием подобия AA для двух треугольников.
- SSS Правило подобия: Если соответствующие стороны двух треугольников пропорциональны, то их соответствующие углы равны и, следовательно, треугольники подобны.
Бесплатная загрузка в формате pdf для Математическая формула для главы 10 класса – Треугольники. Этот PDF-файл состоит из всех важных форм главы «Треугольники», подготовленных экспертом по физике Уоллахом.
Решения NCERT подготовлены экспертами, решают все вопросы по математике из учебника NCERT с помощью Решения NCERT для 10 класса по математике. Если каким-либо учащимся необходимо пройти онлайн-тест, чтобы проверить свои понятия или понимание, они могут посетить Викторина по треугольникам .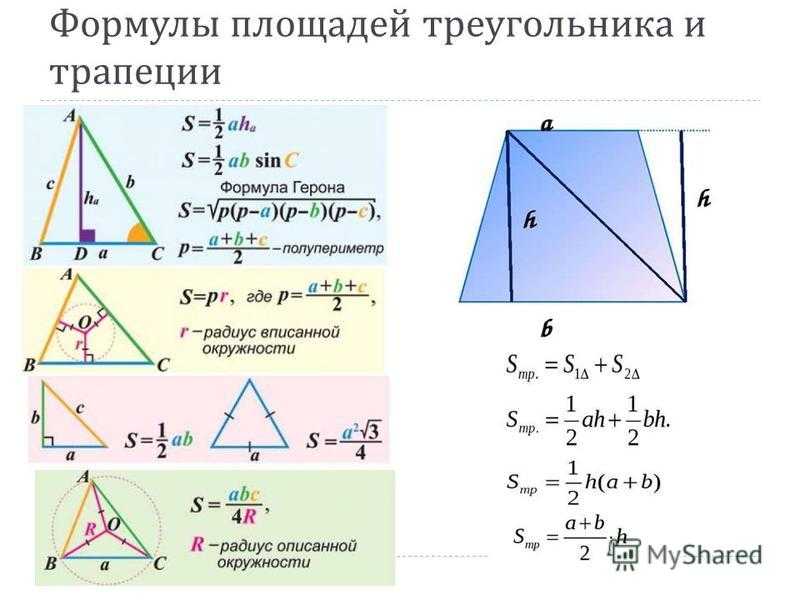
Часто задаваемые вопросы (FAQ)
Q1. Какие есть формулы для треугольников?
Ответ. Формулы треугольника могут быть математически выражены следующим образом;
Площадь треугольника, A = [(½) b × h] ; где «b» — основание треугольника, а «h» — высота треугольника.
Периметр треугольника P = (a + b + c) , где a, b и c — три стороны треугольника.
Q2. Какие теоремы треугольника в 10 классе?
Ответ. Некоторые важные теоремы о треугольниках и окружностях для 10-го стандарта приведены ниже.
- Теорема Пифагора
- Теорема о средней точке
- Теорема об остатках
- Основная теорема арифметики
- Теорема о биссектрисе угла
- Теорема о вписанном угле
- Теорема Чевы
- Теорема Байеса
Q3. Какая формула площади треугольника?
Ответ.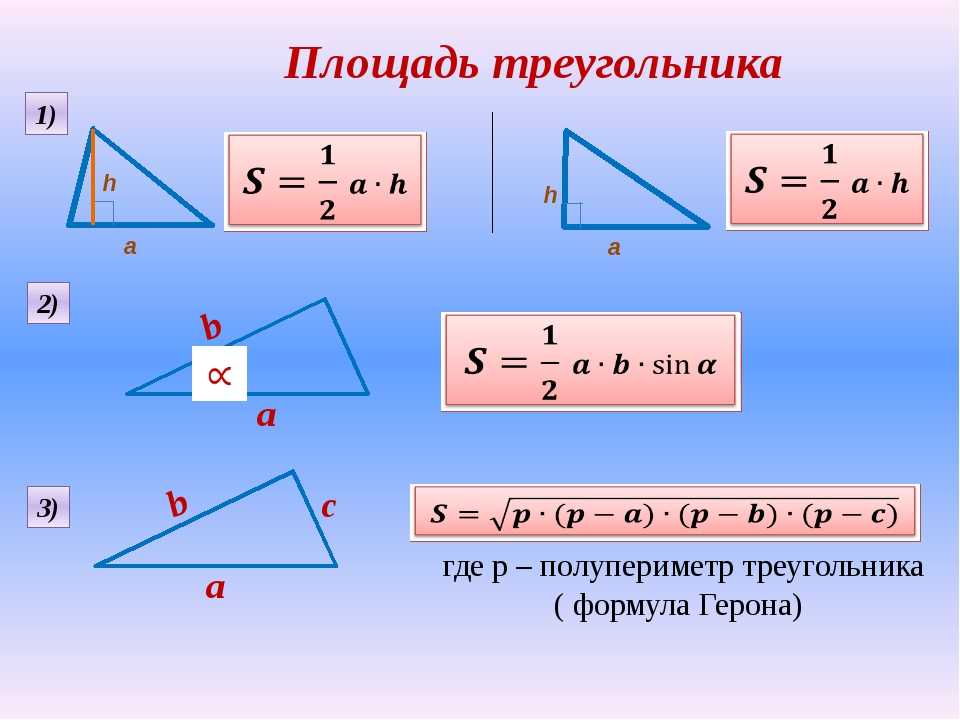

 Неравенства
Неравенства Против равных сторон лежат равные углы:
Против равных сторон лежат равные углы:
 s 1 и s 2 — соответствующие стороны первого и второго треугольника соответственно.
s 1 и s 2 — соответствующие стороны первого и второго треугольника соответственно.