3 Признака равенства треугольника
Первый признак равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых: AC = A1C1, AB = A1B1, ∠A = ∠A1.
Докажите равенство треугольников △ABC = △A1B1C1.
Доказательство:
△A1B1C1 = △ABC, если при наложение вершина A1 совмещается с вершиной A, и сторона A
A1B1 = AB, вершина B совпадает с вершиной B1
A1C1 = AC, поскольку ∠A = ∠A1, вершина C совпадает с вершиной C1.
B1C1 = BC,
△ABC = △A1B1C1.
Теорема доказана.
Важно!
Первый признак используют при доказательстве второго и третьего признаков равенства треугольников.
Познавайте математику вместе с нашими лучшими преподавателями, на занятиях по математике для учеников с 1 до 11 класса!
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых:
AC = A1C1, ∠A = ∠A1, ∠C = ∠C1.
Докажите, что △ABC = △A1B1C1.
Доказательство:
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1.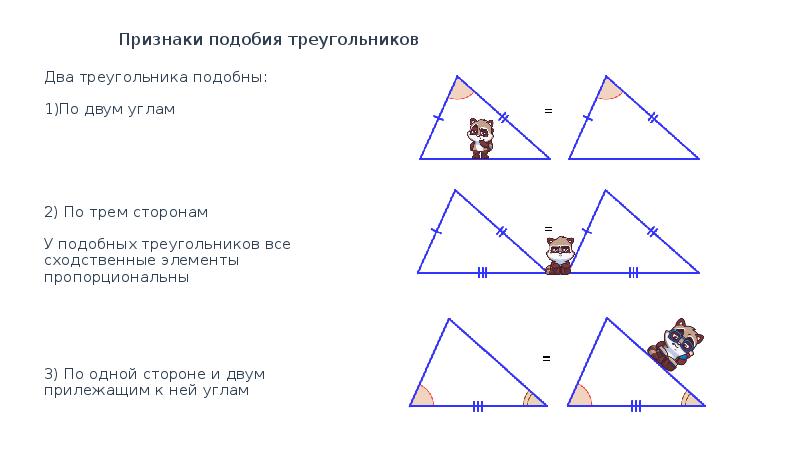
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB = A1B1, поскольку мы знаем, что ∠A = ∠A1,
CB = C1B1, поскольку мы знаем, что ∠C = ∠C1.
B совпадает с B1, △ABC △A1B1C1
Теорема доказана.
Третий признак равенства треугольников
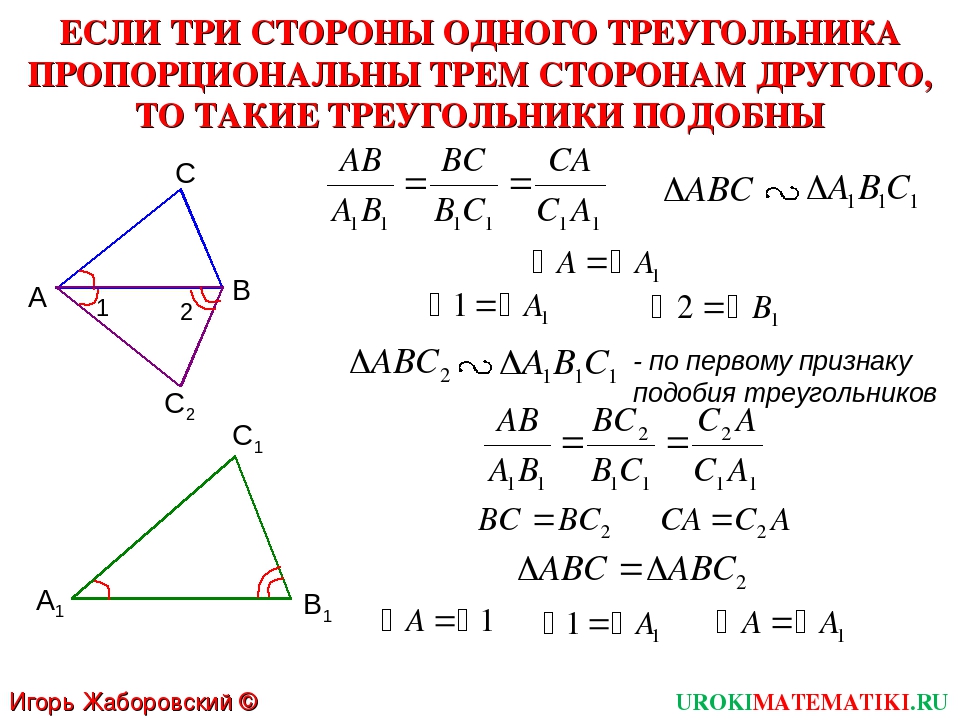
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Даны два треугольника △ABC и △A1B1C1, у которых:
AC = A1C1,
AB = A1B1,
CB = C1B1.
Докажите, что △ABC = △A1B1C1.
Доказательство 3 признака равенства треугольников:
Наложим △ABC на △A1B1C1, таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C — с вершиной C1.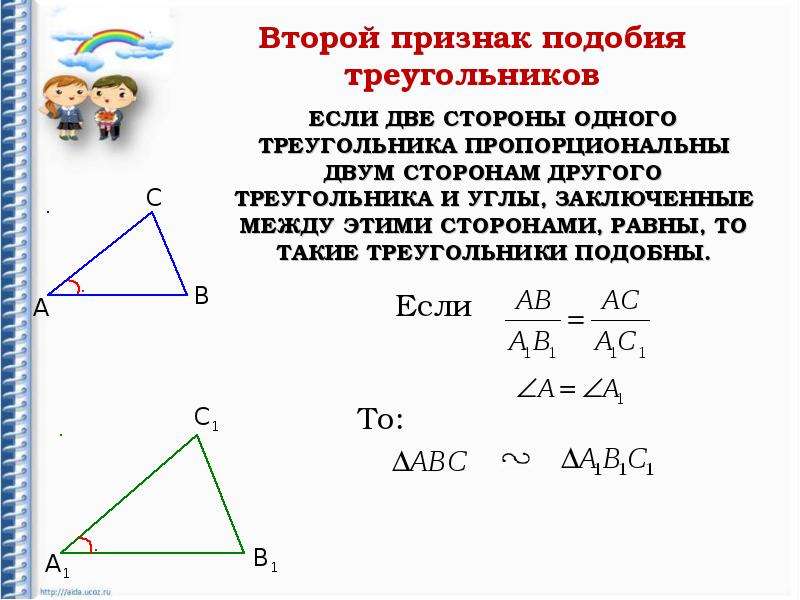
AC = A1C1, BC = B1C1, то △A1C1
С и △B1C1С — равнобедренные.∠1=∠2, ∠3=∠4 (по свойству равнобедренного треугольника),
∠A1СB1 = ∠A1C1B1.
AC = A1C1, BC = B1C1.
∠C = ∠C1, тогда △ABC = △A1B1C1.
Теорема доказана.
Кроме трех основных теорем, запомните еще несколько свойств равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
- Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
- Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.

- Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
- Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
- Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способом. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
В онлайн-школе Skysmart ваш ребенок научится доказывать любые теоремы и справляться с даже самыми сложными задачками на контрольных.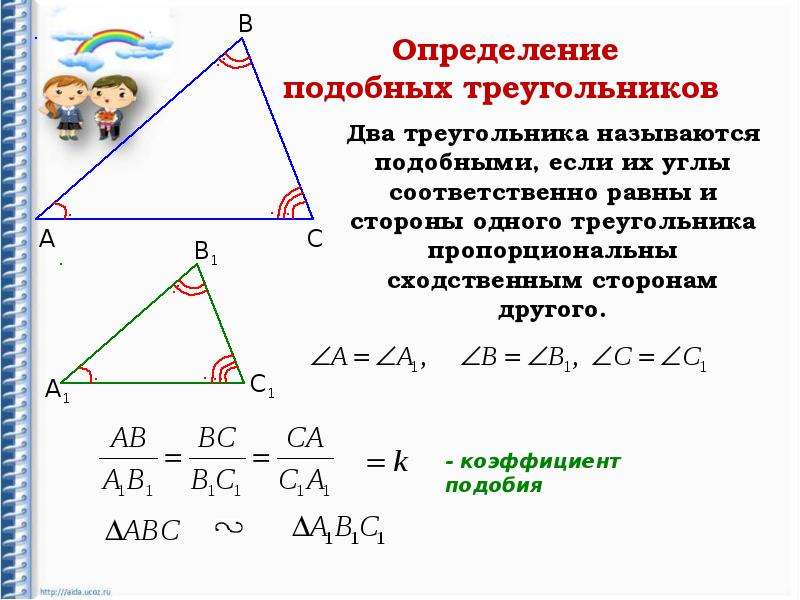
Записывайтесь на бесплатный вводный урок по математике и начните заниматься в удовольствие уже завтра!
Признаки подобия треугольников [wiki.eduVdom.com]
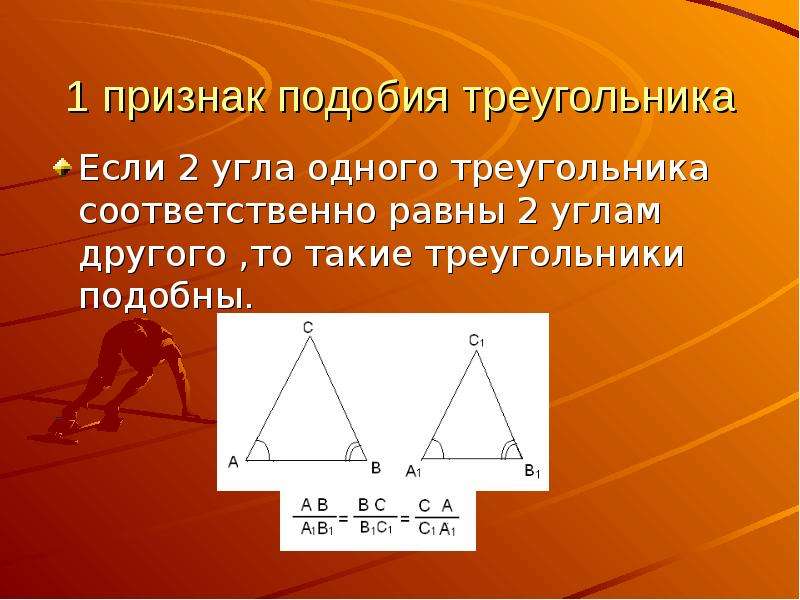
Теорема 1. Первый признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то такие
треугольники подобны.
Доказательство. Пусть ABC и $А_1В_1С_1$ — треугольники, у которых $\angle A = \angle A_1 ; \angle B = \angle B_1$ , и, следовательно, $\angle C = \angle C_1$ . Докажем, что $\triangle ABC \sim \triangle A_1B_1C_1$ (рис.1).
Рис.1
Отложим на ВА от точки В отрезок $ВА_2$, равный отрезку $A_1B_1$ , и через точку $А_2$ проведем прямую, параллельную прямой АС. Эта прямая пересечет ВС в некоторой точке $С_2$ .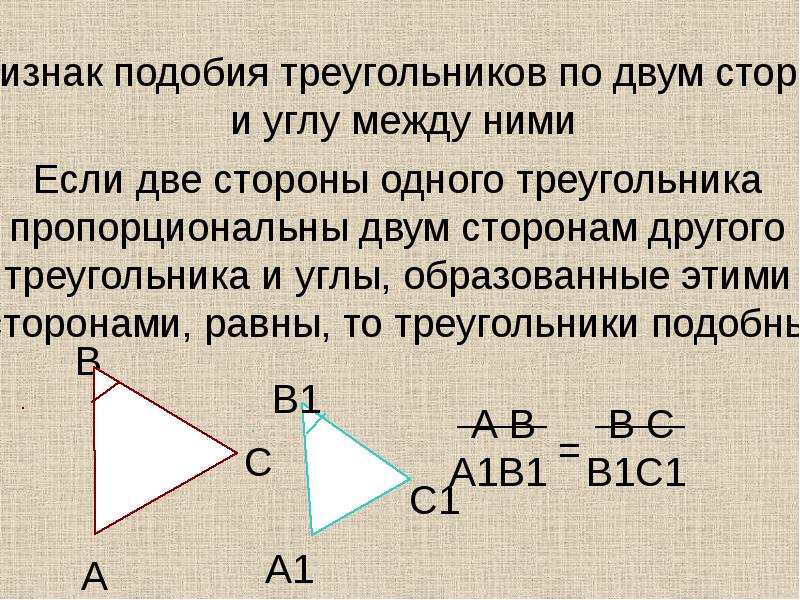
По аналогичной схеме устанавливаются теоремы 2 и 3.
Теорема 2. Второй признак подобия треугольников. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами
равны, то треугольники подобны.
Теорема 3. Третий признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Из теоремы 1 вытекает следующее.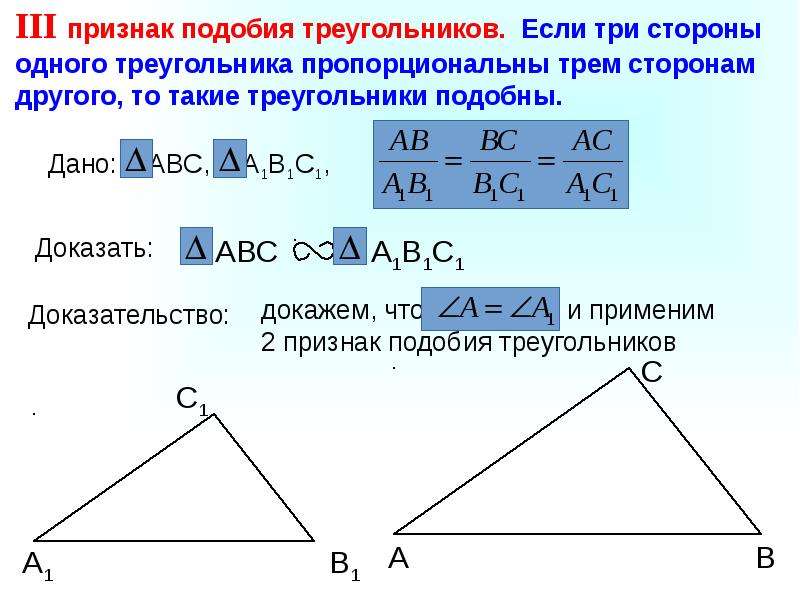
Следствие 1. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам, т. е. тем высотам, которые опущены на сходственные стороны.
Пример 1. Подобны ли два равносторонних треугольника?
Решение. Так как в равностороннем треугольнике каждый внутренний угол равен 60° (следствие 3), то два равносторонних треугольника подобны по первому признаку.
Пример 2. В треугольниках ABC и $А_1В_1С_1$ известно, что $\angle A = \angle A_1 ; \angle B = \angle B_1 ; АВ = 5 м, ВС = 7 м, А_1В_1 = 10 м, А_1С_1 = 8 м.$ Найти неизвестные стороны треугольников.
Решение. Треугольники, определенные условием задачи, подобны по первому признаку подобия.
Из подобия треугольников следует:
$$ \frac{AB}{A_1B_1} = \frac{BC}{B_1C_1} = \frac{AC}{A_1C_1} \,\,\, (1) $$
Подставив в равенство (1) данные из условия задачи, получим:
$$ \frac{5}{10} = \frac{7}{B_1C_1} = \frac{AC}{8} \,\,\, (2) $$
Из равенства (2) составим две пропорции
$$ \frac{5}{10} = \frac{7}{B_1C_1}
\\ \frac{5}{10} = \frac{AC}{8}
\\ \text{ откуда }В_1С_1 = 14 (м), АС = 4 (м). $$
$$
Пример 3. Углы В и $В_1$ треугольников ABC и $А_1В_1С_1$ равны. Стороны АВ и ВС треугольника ABC в 2,5 раза больше сторон $A_1B_1$ и $B_1C_1$ треугольника $A_1B_1C_1$. Найти АС и $A_1C_1$ , если их сумма равна 4,2 м.
Решение. Пусть условию задачи отвечает рисунок 2.
Рис.2
Из условия задачи: $$ 1) \angle B = \angle B_1 ; \\ 2) \frac{AB}{A_1B_1} = \frac{BC}{B_1C_1} = 2,5 \\ 3) AC + A_1C_1 = 4,2 м. $$ Следовательно, $\triangle ABC \sim \triangle А_1В_1С_1$. Из подобия этих треугольников следует $$ \frac{AC}{A_1C_1} = 2,5\text{ , или }АС = 2,5\bullet А_1С_1 $$ Так как АС = 2,5 • А1С1, то АС + А1C1 = 2,5 • А1С1 + A1C1 = 4,2, откуда A1C1 = 1,2 (м), АС = 3 (м).
Пример 4. Подобны ли треугольники ABC и А1В1С1, если АВ = 3 см, ВС = 5 см, АС = 7 см, А1В1 = 4,5 см, B1C1 = 7,5 см, A1C1 = 10,5 см?
Решение.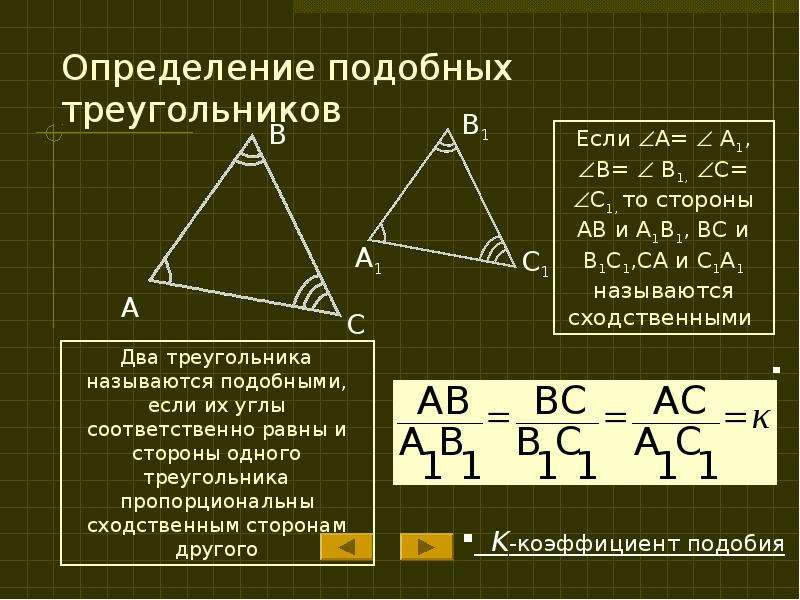
Пример 5. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Решение. Рассмотрим произвольный треугольник ABC. Обозначим буквой О точку пересечения его медиан $АА_1\text{ и }ВВ_1$ и проведем среднюю линию $A_1B_1$ этого треугольника (рис.3).
Рис.3
Отрезок $A_1B_1$ параллелен стороне АВ, поэтому $\angle 1 = \angle2 \text{ и } \angle 3 = \angle 4 $. Следовательно, треугольники АОВ и $A_1OB_1$ подобны по двум углам, и, значит, их стороны пропорциональны: $$ \frac{AO}{A_1O} = \frac{BO}{B_1O} = \frac{AB}{A_1B_1} $$
Но $AB = 2A_1B_1$ , поэтому $AO = 2A_1O$ и $BO = 2B_1O$ .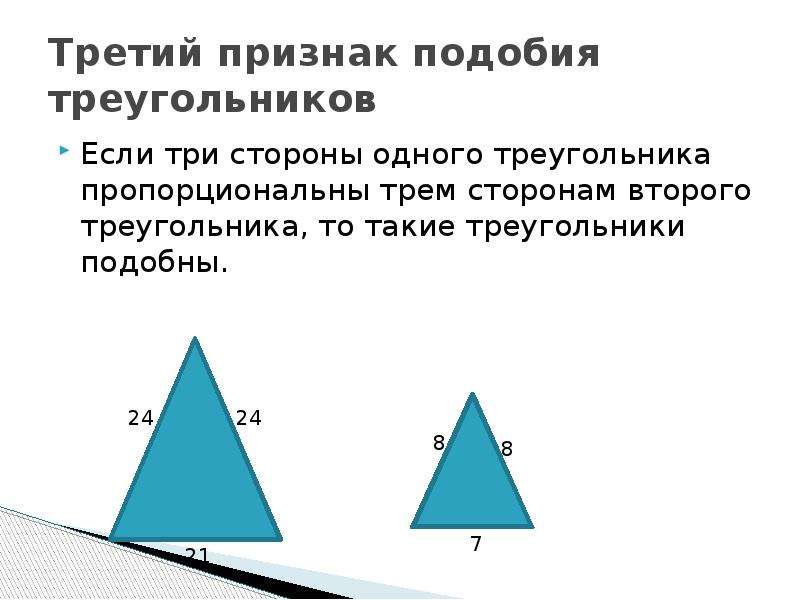
Аналогично доказывается, что точка пересечения медиан $BB_1\text{ и }CC_1} делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.
Итак, все три медианы треугольника ABC пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.
Замечание. Ранее отмечалось, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. На основе последнего утверждения устанавливается, что и высоты треугольника (или их продолжения) пересекаются в одной точке. Эти три точки и точка пересечения медиан называются замечательными точками треугольника.
Пример 6. Проектор полностью освещает экран А высотой 90 см, расположенный на расстоянии 240 см. На каком наименьшем расстоянии в см. от проектора нужно расположить экран Б, высотой 150 см, так, что бы он был полностью освещён, если настройки проектора остаются неизменными.
Видео-решение.
Презентация на тему: «2,3 признаки подобия треугольников».
библиотека
материалов
Содержание слайдов
Номер слайда 1
Номер слайда 2
A B С BC II AD. Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Запишите равенство отношений соответствующих сторон. COB AOD по 1 признаку подобия D BC AD = BO OD OC OA = O 4 12 21 21 4 12 x x x 21 = 4 12
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Запишите равенство отношений соответствующих сторон. COB AOD по 1 признаку подобия D BC AD = BO OD OC OA = O 4 12 21 21 4 12 x x x 21 = 4 12
Номер слайда 3
A B P Трапеция АDPC. Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Запишите равенство отношений соответствующих сторон. BDP BAC по 1 признаку C DP AC = BP BC BD BA = D 8 21 8 4 x x x 21 = 8 12 12 12 21
Номер слайда 4
A B P Найдите пары подобных треугольников и докажите их подобие.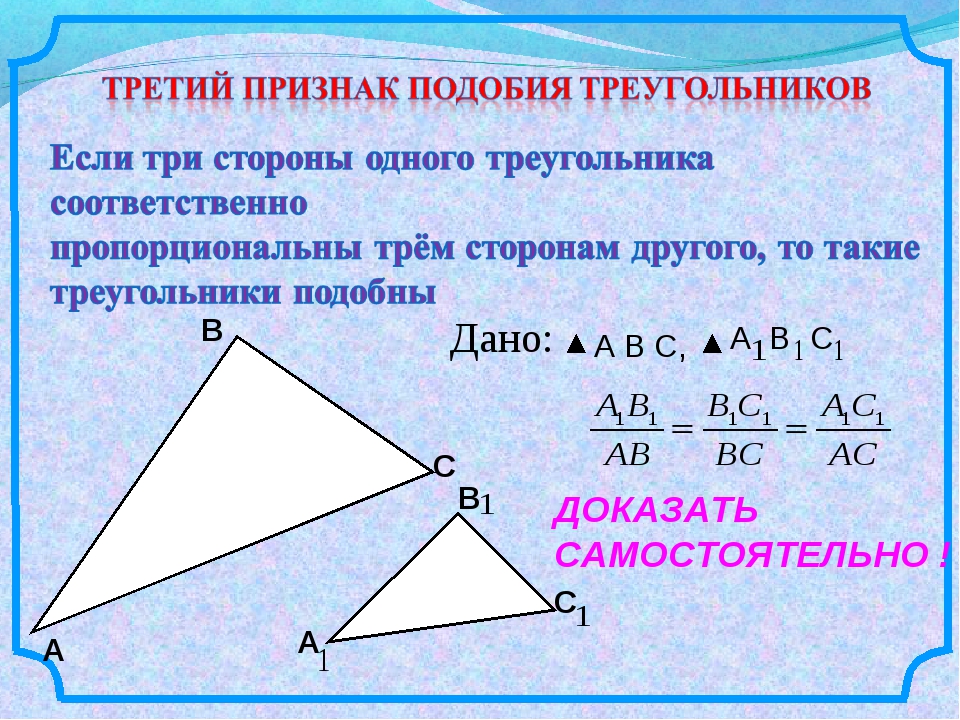 Найдите АВ и РС. Блиц-опрос BDP BAC по 1 признаку C D 6 10 4 5 8 8 12 2 Справимся без пропорции
Найдите АВ и РС. Блиц-опрос BDP BAC по 1 признаку C D 6 10 4 5 8 8 12 2 Справимся без пропорции
Номер слайда 5
докажем, что и применим 1 признак подобия треугольников А С В В1 С1 А1 II признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. ABC А1В1С1 Доказать: Доказательство: Дано: ABC, А1В1С1,
Номер слайда 6
А С В В1 С1 А1 С2 2 1 Рассмотрим у которого 1= А1, 2= В1. ABC2, ABC2 А1В1С1 по двум углам Тогда по условию АС = АС2 1).
ABC2, ABC2 А1В1С1 по двум углам Тогда по условию АС = АС2 1).
Номер слайда 7
А С В В1 С1 А1 С2 2 1 2). ABC = АВС2 по двум сторонам и углу между ними В = 2, 2= В1 = В1 В
Номер слайда 8
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B С 7см Е К F 400 400 8см 3,5см 4см 4 8 = 3,5 7 Верно FEK AВС по 2 признаку
Блиц-опрос A B С 7см Е К F 400 400 8см 3,5см 4см 4 8 = 3,5 7 Верно FEK AВС по 2 признаку
Номер слайда 9
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос Р Q R 3см В С А 400 400 3см 5см 5см 5 3 = 5 3 Верно ABC PQR по 2 признаку
Номер слайда 10
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B C 10см M L K 700 400 10см 5см 5см 5 10 = 5 10 Верно KML ABC по 2 признаку 400
Блиц-опрос A B C 10см M L K 700 400 10см 5см 5см 5 10 = 5 10 Верно KML ABC по 2 признаку 400
Номер слайда 11
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B C 8см M L K 10см 4см 3см 6 3 = 8 4 Верно KML ABC по 2 признаку 6см
Номер слайда 12
Найдите пары подобных треугольников и докажите их подобие. A B C 92см 3 69 = 4 92 Верно KML ABC по 2 признаку M L K 69 115см 5см 4см 3
A B C 92см 3 69 = 4 92 Верно KML ABC по 2 признаку M L K 69 115см 5см 4см 3
Номер слайда 13
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос AВС РВD по 2 признаку 3 12 = 5 20 Верно A B P C D 5 3 12 20 Найти
Номер слайда 14
A B С Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос AОD COD по 2 признаку D O 4 5 15 12 4 12 = 5 15 Верно 21 ? 7
Блиц-опрос AОD COD по 2 признаку D O 4 5 15 12 4 12 = 5 15 Верно 21 ? 7
Номер слайда 15
Площадь треугольника МОС на 8 см2 меньше площади треугольника КОР. Найти площадь треугольника ОКР, если КО=15см, ОР=12см, ОМ=5см, ОС=4см. C M О K P 5 x x-8 4 12 15 4 12 = 5 15 Верно MCO PKO по 2 признаку Запишите теорему об отношении площадей подобных треугольников SMCO SKPO = k2 x-8 x = 1 9 MO OK SMCO SKPO = 2 x x-8 5 15
Номер слайда 16
докажем, что и применим 2 признак подобия треугольников А С В В1 С1 А1 III признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. ABC А1В1С1 Доказать: Доказательство: Дано: ABC, А1В1С1,
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. ABC А1В1С1 Доказать: Доказательство: Дано: ABC, А1В1С1,
Номер слайда 17
А С В В1 С1 А1 С2 2 1 Рассмотрим у которого 1= А1, 2= В1. ABC2, ABC2 А1В1С1 по двум углам Тогда по условию АС = АС2 1). ВС = ВС2
Номер слайда 18
1= А1 А1 А А С В В1 С1 А1 С2 2 1 2).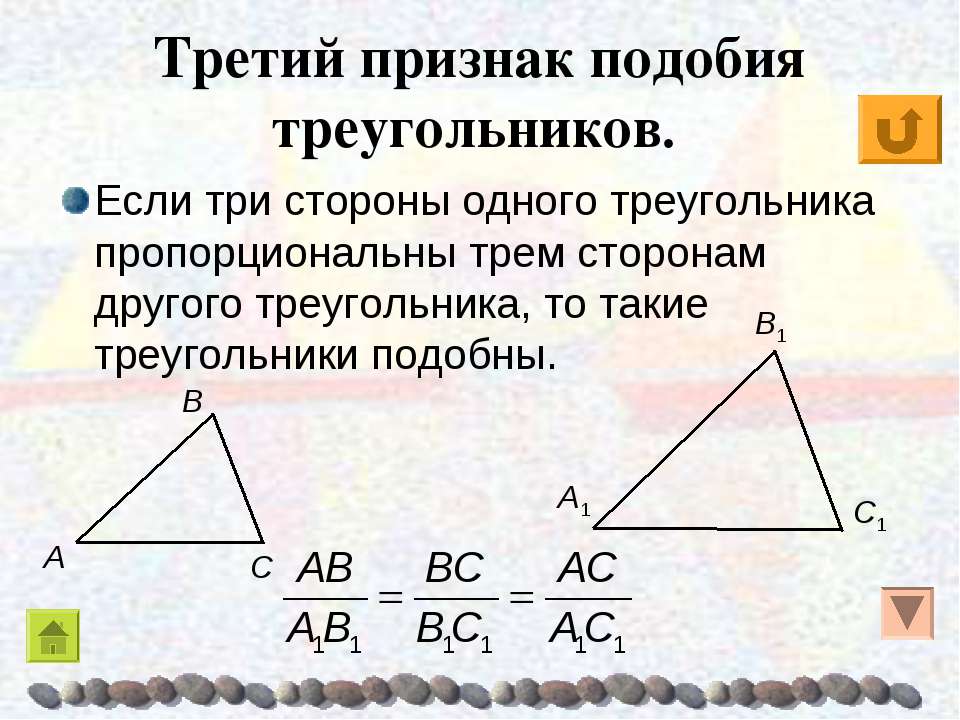 ABC = АВС2 по трем сторонам А = 1, =
ABC = АВС2 по трем сторонам А = 1, =
Номер слайда 19
A B C Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос D E F 3см 3см 3см 5см 5см 5см 3 5 = 3 5 Верно DEF ABC по 3 признаку = 3 5 Докажите по 1 признаку подобия, по 2 признаку.
Номер слайда 20
A B C Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос D E F 4см 8см 6см 6см 9см 12см 6 4 = 9 6 Верно DEF ABC по 3 признаку = 12 8
Блиц-опрос D E F 4см 8см 6см 6см 9см 12см 6 4 = 9 6 Верно DEF ABC по 3 признаку = 12 8
Номер слайда 21
Найдите пары подобных треугольников и докажите их подобие. Блиц-опрос A B C 6см M L K 8см 3см 4см 4 8 = 4 8 Верно KML ABC по 3 признаку 4см 8см = 3 6
Номер слайда 22
Доказать: КМ II BL Блиц-опрос A B C 6 M L K 10 7 3 7 14 = 5 10 Верно KMA LBC по 3 признаку 5 14 = 3 6 Найти
Номер слайда 23
A B С Найдите пары подобных треугольников и докажите их подобие.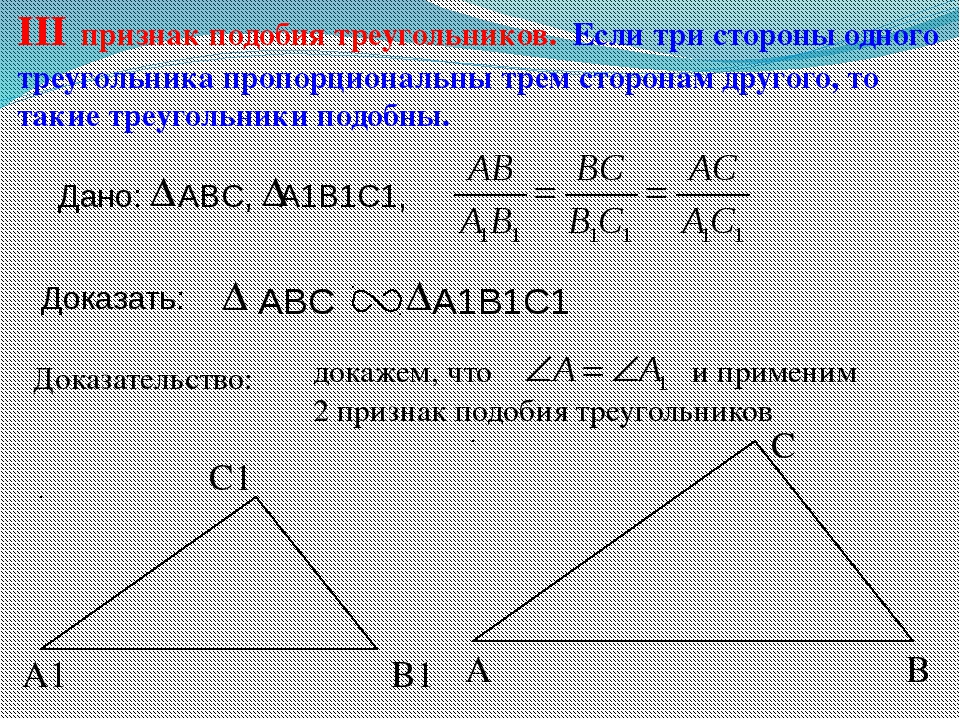 Найдите угол ВАD. D 15 14 550 21 10 9 1 3 800 10 15 = 14 21 Верно АСD ABC по 3 признаку = 14 9 1 3 800 550
Найдите угол ВАD. D 15 14 550 21 10 9 1 3 800 10 15 = 14 21 Верно АСD ABC по 3 признаку = 14 9 1 3 800 550
Номер слайда 24
9 6 D N К 18см С В А 13,5см 6см 6 9 = 12 18 Верно DNK ABC по 3 признаку 12см = 9 13,5 В треугольниках АВС и DNK известны стороны. SDNK=36cм2. Найдите площадь треугольника АВС. 9см 9см Запишите теорему об отношении площадей подобных треугольников SABC SDNK = k2 x 36 = 4 9 AB DN SABC SDNK = 2 36 x x
Номер слайда 25
2 2 ADСD – параллелограмм.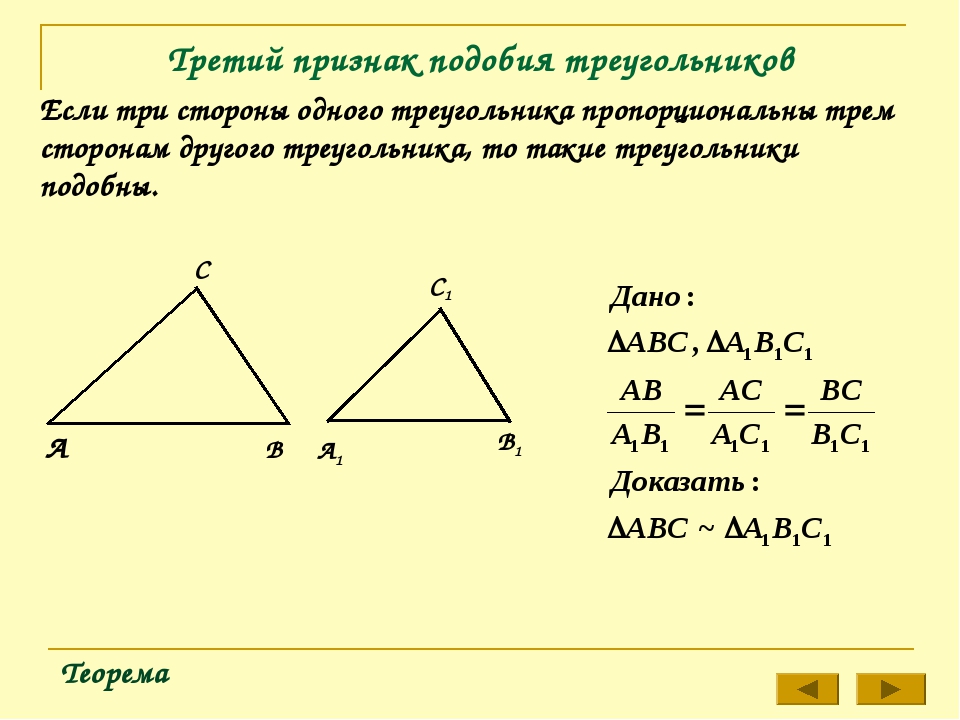 OF BC AB = 2см, BF = 5см, ВС = 9см. Найдите BЕ. B ЕFB NFA по 1 признаку A F N С D 9 BE AN = BF AF FE FN = 5 x 7 Е 7 O 9-x x 5 9-x 9-x x 9-x = 5 7
OF BC AB = 2см, BF = 5см, ВС = 9см. Найдите BЕ. B ЕFB NFA по 1 признаку A F N С D 9 BE AN = BF AF FE FN = 5 x 7 Е 7 O 9-x x 5 9-x 9-x x 9-x = 5 7
Номер слайда 26
A B С АВСD – параллелограмм. РАВСD=45см, ВN AD, BF CD, BN : BF = 2 : 3 Найти AB и AD. Запишите равенство отношений соответствующих сторон. ABN CBF по 1 признаку N BA CB = BN BF AN CF = F D 22,5-x x 22,5-x = 2 3 2 3 x x 22,5-x pАВСD=45:2=22,5(см)
Номер слайда 27
В треугольнике АВС DF II BC, AD = 3 cм, DB = 1см. SADF=27cм2. Найдите площадь треугольника АВС. 4 4 В А F Запишите теорему об отношении площадей подобных треугольников АDF ABC по 1 признаку C SADF SABC = k2 D 1 27 x = 9 16 3 3 AD AB SADF SABC = 2 27 х х
SADF=27cм2. Найдите площадь треугольника АВС. 4 4 В А F Запишите теорему об отношении площадей подобных треугольников АDF ABC по 1 признаку C SADF SABC = k2 D 1 27 x = 9 16 3 3 AD AB SADF SABC = 2 27 х х
Третий признак подобия треугольников
Прежде, чем познакомиться с третьим признаком подобия треугольников, вспомним известные нам первый и второй.
Итак, первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
Ну а теперь сформулируем третий признак подобия треугольников.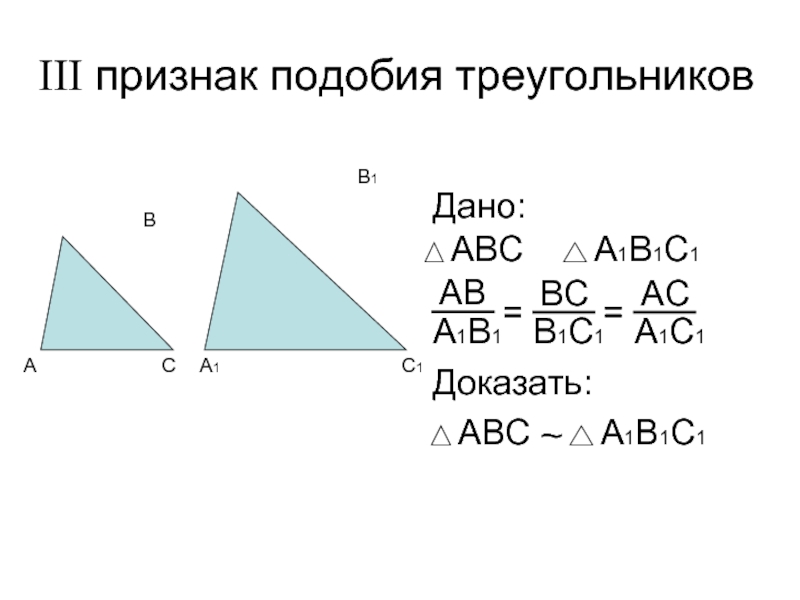
Теорема (3-й признак подобия треугольников). Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Доказательство.
.
, , тогда по 1-му признаку.
.
Получаем, что , .
Тогда по 3-му признаку.
Следовательно, .
Так как , то .
Следовательно, .
Что и требовалось доказать.
Давайте найдём среди следующих треугольников подобные.
У каждого из треугольников известны длин трёх его сторон, а тогда воспользуемся только что доказанным третьим признаком подобия треугольников.
Посмотрим внимательно на значения их длин и заметим, что стороны треугольника а пропорциональны сторонам треугольника в, а значит, эти треугольники подобны. При этом коэффициент подобия равен 2.
Задача. Подобны ли треугольники и , если см, см, см, см, см, см?
Решение.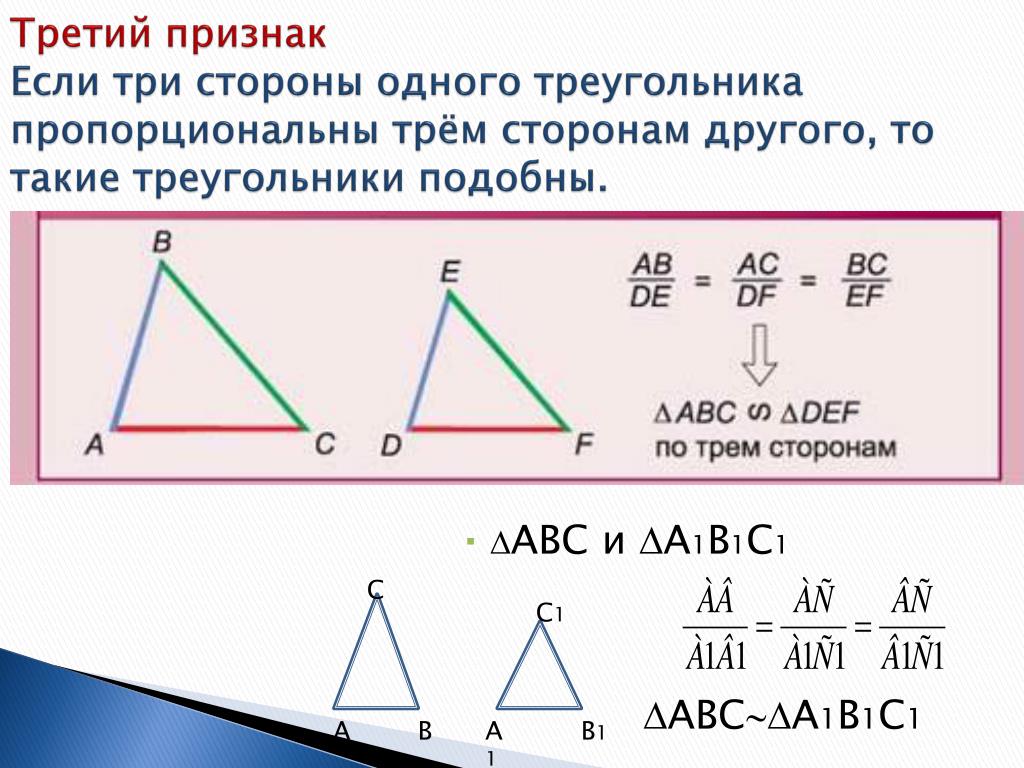
,
,
.
Значит, .
Следовательно, .
Ответ: .
Задача. Докажите, что прямоугольные треугольники и подобны, если стороны и треугольника соответственно равны см и см, а стороны и треугольника соответственно равны см и см.
Решение.
,,
(см).
, ,
(см).
; ; .
Значит, .
Следовательно, по 3-му признаку.
Что и требовалось доказать.
Итак, сегодня на уроке мы познакомились с ещё одним признаком подобия треугольников: если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Также мы закрепили материал на практике.
Первый признак подобия треугольников 8 класс онлайн-подготовка на Ростелеком Лицей
Первый признак подобия треугольников.
Докажем подобие треугольников по двум углам.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Дано: ΔABC, ΔA1B1C1,
∠A = ∠A1, ∠B = ∠B1,
Доказать: ΔABC∼ΔA1B1C1
Доказательство:
-
По теореме о сумме углов треугольника
∠C = 180°-(∠A+∠B), ∠C1 = 180°-(∠A1+∠B1).
Так как ∠A = ∠A1и ∠B = ∠B1, то и ∠C = ∠C1.
-
Пусть AB<A1B1. На луче A1B1 отложим отрезок A1B2 такой, что A1B2 = AB.
-
Через точку B2 проведем прямую B2C2, параллельную прямой B1C1.

-
∠A1B2C2 = ∠A1B1C1 (как соответственные при B2C2∥ B1C1 и секущей A1B1).
Значит, ∠A1B2C2 = ∠B.
-
В треугольниках A1B2C2и ABC:
∠A1 = ∠A,
∠A1B2C2 = ∠B,
A1B2 = AB.
Значит, ΔA1B2C2= ΔABC (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: A1C2 = AC.
-
По теореме о пропорциональных отрезках А1С2:А1С1 = А1В2:А1В1.

Так как A1B2= AB и A1C2 = AC, то АС:А1С1 = АВ:А1В1.
-
Аналогично доказывается, что АВ:А1В1 = ВС:В1С1.
-
Таким образом, в треугольниках ABC и A1B1C1:
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1,
АВ:А1В1 = ВС:В1С1 = АС:А1С1.
Значит, ΔABC∼ΔA1B1C1 по определению подобных треугольников, что и требовалось доказать.
При решении задач чаще других используется именно 1-й признак подобия треугольников.
Задача 1. Доказать, что любые два равнобедренных треугольника, у которых углы между равными сторонами равны, являются подобными.
Решение. Пусть даны равнобедренные треугольники ABC и A1B1C1 с ∠A = ∠A1 (углы А и А1 лежат против оснований ВС и В1С1 соответственно). Так как треугольник ABC равнобедренный, то ∠B = ∠C = (180−∠A):2. Так как треугольник A1B1C1 равнобедренный, то ∠B1 = ∠C1 = (180−A1):2 = (180−∠A):2 = ∠B = ∠C.
То есть ∠B = ∠B1, ∠C = ∠C1. По первому признаку подобия получаем, что треугольники ABC и A1B1C1 подобны.
Задача 2.
Дано:
∠А = ∠В
СО:DO = 7:2
AC = 21 см
Найти: ВD
Решение: рассмотрим ∆АОС и ∆ВОD.
Так как ∠А = ∠В (по условию задачи), ∠АОС = ∠ВОD (как вертикальные углы), то по первому признаку подобия треугольников ∆АОС ~ ∆ВОD.
Следовательно, сходственные стороны треугольников пропорциональны:
АО:ВО = АС:BD = CO:DO
Подставив данные, получим 21:BD = 7:2
Ответ: BD = 6см.
Контрольная работа по геометрии
а) АВ = 10 см, ВС = 5 см, АС = 7 см, = 15 см, = 7,5 см, = 9,5 см? б) угол А = 37°, угол В = 48°, угол = 95°, угол = 48°? в) АВ = 10 см, ВС = 8 см, = 5 см, = 3 см, угол С = углу = 90°? | Контрольная работа по геометрии
а) АВ = 10 см, ВС = 5 см, АС = 7 см, = 15 см, = 7,5 см, = 9,5 см? б) угол А = 37°, угол В = 48°, угол = 95°, угол = 48°? в) АВ = 10 см, ВС = 8 см, = 5 см, = 3 см, угол С = углу = 90°? | Контрольная работа по геометрии
а) АВ = 10 см, ВС = 5 см, АС = 7 см, = 15 см, = 7,5 см, = 9,5 см? б) угол А = 37°, угол В = 48°, угол = 95°, угол = 48°? в) АВ = 10 см, ВС = 8 см, = 5 см, = 3 см, угол С = углу = 90°? | Контрольная работа по геометрии
а) АВ = 10 см, ВС = 5 см, АС = 7 см, = 15 см, = 7,5 см, = 9,5 см? б) угол А = 37°, угол В = 48°, угол = 95°, угол = 48°? в) АВ = 10 см, ВС = 8 см, = 5 см, = 3 см, угол С = углу = 90°? |
Признаки подобия треугольников
Автор mednik На чтение 4 мин Просмотров 5 Опубликовано
При изучении геометрии вы непременно обращали внимание, что часть фигур очень похожа на другие. Отличаются только размеры. Но геометрия — наука точная и слово «похожие» не всегда определяет реальное положение вещей. Например, прямоугольный треугольник похож на равносторонний, но при ближайшем рассмотрении легко обнаружить различия, — отличаются углы, длины сторон, конфигурация.
Отличаются только размеры. Но геометрия — наука точная и слово «похожие» не всегда определяет реальное положение вещей. Например, прямоугольный треугольник похож на равносторонний, но при ближайшем рассмотрении легко обнаружить различия, — отличаются углы, длины сторон, конфигурация.
В геометрии применяется другое понятие — «подобие». Это более узкий термин, который определяет фигуры, которые идентичны по всем параметрам, кроме размера. Если увеличить, или уменьшить одну из фигур, то получится другая, с полным соответствием. Знак подобия в геометрии «~» имеет очень большой смысл. Это не просто обозначение «похожести», а специальный термин. Он говорит о том, что из одной фигуры можно получить другую, если преобразовать ее особым образом.
Самый простой способ — увеличение размеров. Но не простое увеличение, а пропорциональное. То есть, каждая сторона фигуры увеличивается на строго определенную величину. Соотношение новой длины и исходной называется коэффициентом подобия.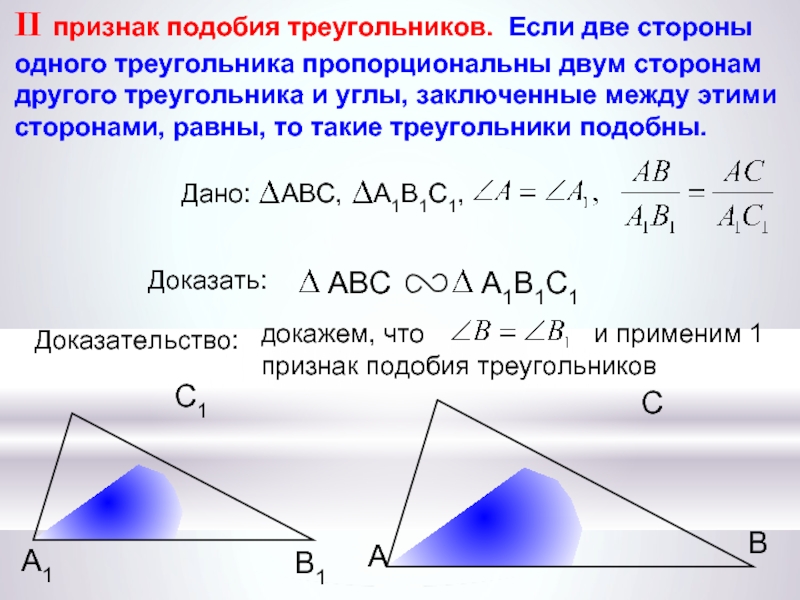 Согласно правилам математики К≠ 0. Смысл ясен, на ноль делить нельзя. В остальном значение К может принимать любое значение, в том числе, и дробное. Если в десятичном исчислении коэффициент находится в диапазоне от ноля до единицы, то фигура уменьшается при проецировании, если К ≥ 1, то фигура получится больше, или идентичной исходной.
Согласно правилам математики К≠ 0. Смысл ясен, на ноль делить нельзя. В остальном значение К может принимать любое значение, в том числе, и дробное. Если в десятичном исчислении коэффициент находится в диапазоне от ноля до единицы, то фигура уменьшается при проецировании, если К ≥ 1, то фигура получится больше, или идентичной исходной.
Каждая из геометрических фигур имеет ряд признаков, по которым ее можно сравнить с другой и определить, подобные фигуры, или просто похожие. У треугольников таких признаков три. Рассмотрим их более подробно. В идеале, треугольники называются подобными, если у них три угла одинаковые, а три стороны пропорциональны, согласно коэффициенту К. Но не всегда есть возможность измерить углы и стороны. Есть ряд признаков, требующих меньшего числа измерений, по которым легко определить, подобные треугольники, или нет.
Первый признак подобия
Если два угла произвольного треугольника равны двум углам другого, значит, фигуры подобные. В геометрической графике это записывается так:
ΔАВС ~ΔА1В1С1 А=∠А1, ∠В=∠В1, ∠С=∠С1.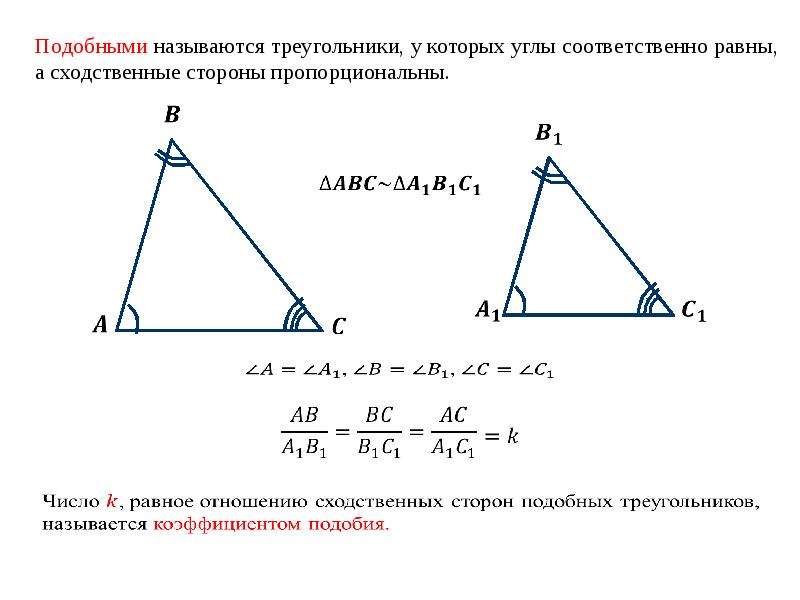
Доказательство первого признака подобия приводить не будем, ввиду того, что признак проверен и доказан, информация об этом есть в любом учебнике. Намного важнее, что из этого признака вытекает следствие, которое не менее важно, чем сам признак. Во многих задачах на ЕГЭ и в учебниках упор делается именно на знание этого правила. «Если три стороны одного треугольника попарно параллельны трем сторонам другого, то эти фигуры подобны».
Утверждение не менее очевидно, чем первый признак подобия. Формулируется оно так:
Если две соответствующие стороны треугольников пропорциональны, а углы между ними равные, то фигуры подобные.
Это правило называется признаком подобия по двум сторонам и углу между ними. Геометрическая запись выглядит так:
ΔАВС ~ΔА1В1С1 ↔ ∠ А=∠А1, АВ/А1В1 = АС/А1С1.
Самый простой и наиболее понятный признак подобия: если три стороны одной фигуры пропорциональны трем сторонам другой с одинаковым коэффициентом К, то треугольники подобные. Записывается такое утверждение таким образом:
Записывается такое утверждение таким образом:
ΔАВС ~ΔА1В1С1↔АВ/А1В1 = АС/А1С1= ВС/В1С1..
Доказательство этого утверждения опять же приводить не будем вследствие дефицита размера статьи. Лучше остановимся на следствиях, которые вытекают из этих утверждений. Многие из параметров геометрических фигур можно определить, пользуясь названными правилами.
Один из способов применения признаков подобия демонстрирует теорема об отношении периметров подобных треугольников. В формулировке говорится о том, что отношение периметров подобных треугольников равно коэффициенту пропорциональности сторон. На практике это выглядит так — вам нужно найти периметр треугольника со сторонами в несколько километров, что часто требуется в строительстве, агротехнике и геодезии. Если нарисовать подобный треугольник на бумаге, со сторонами в несколько сантиметров и вычислить периметр, то он будет ровно настолько же меньше, как и стороны треугольников. То есть, коэффициент К работает и в случае с периметром.
То есть, коэффициент К работает и в случае с периметром.
Вторая задача — найти соотношение площадей подобных треугольников. Здесь тоже существует определенная пропорция, но уже квадратичная. То есть, соотношение площадей фигур равно квадрату К.
S1/S = k2.
При решении задач поможет также лемма о подобных треугольниках, говорящая о том, что любая прямая, пересекающая треугольник параллельно одной из сторон, отсекает от него подобную фигуру.
Пользуясь полученной информацией, несложно решить любую задачу по определению параметров подобных треугольников.
похожих треугольников
Два треугольники как говорят похожий если их соответствующие углы равны конгруэнтный и соответствующие стороны лежат в пропорция . Другими словами, похожие треугольники имеют одинаковую форму, но не обязательно одного размера.
Треугольники
конгруэнтный
если к тому же их соответствующие стороны имеют одинаковую длину.
Длины сторон двух одинаковых треугольников пропорциональны.То есть, если Δ U V W похоже на Δ Икс Y Z , то имеет место следующее уравнение:
U V Икс Y знак равно U W Икс Z знак равно V W Y Z
Это обычное отношение называется масштаб .
Символ ∼ используется для обозначения сходства.
Пример:
Δ
U
V
W
∼
Δ
Икс
Y
Z
. Если
U
V
знак равно
3
,
V
W
знак равно
4
,
U
W
знак равно
5
а также
Икс
Y
знак равно
12
, найти
Икс
Z
а также
Y
Z
.
Нарисуйте фигуру, чтобы облегчить себе визуализацию.
Запишите пропорцию. Убедитесь, что соответствующие стороны указаны правильно.
3 12 знак равно 5 Икс Z знак равно 4 Y Z
Коэффициент масштабирования здесь 3 12 знак равно 1 4 .
Решение этих уравнений дает Икс Z знак равно 20 а также Y Z знак равно 16 .
Понятия подобия и масштабного коэффициента могут быть распространены не только на треугольники, но и на другие фигуры.
похожих треугольников — объяснения и примеры
Теперь, когда мы закончили с конгруэнтными треугольниками, мы можем перейти к другой концепции, называемой подобных треугольников.
В этой статье мы узнаем о похожих треугольниках, особенностях подобных треугольников, о том, как использовать постулаты и теоремы для определения похожих треугольников, и, наконец, как решать похожие задачи о треугольниках.
Что такое похожие треугольники?
Понятия похожих треугольников и конгруэнтных треугольников — это два разных термина, которые тесно связаны. Подобные треугольники — это два или более треугольника одинаковой формы, равных пар соответствующих углов и одинакового отношения соответствующих сторон.
Иллюстрация подобных треугольников:
Рассмотрим три треугольника ниже. Если:
- Соотношение соответствующих сторон равно.
AB / PQ = AC / PR = BC = QR, AB / XY = AC / XZ = BC / YZ
- ∠ A = ∠ P = ∠X, ∠B = ∠Q = ∠Y, ∠C = ∠R = ∠Z
Следовательно, ΔABC ~ ΔPQR ~ ΔXYZ
Сравнение подобных треугольников и конгруэнтных треугольников
| Характеристики | Конгруэнтных треугольников | похожих треугольников размер | одинаковый размер и форма | Та же форма, но другой размер |
| Символ | ≅ | ~ | ||
| Соответствующие длины сторон | Отношение соответствующих сторон конгруэнтных треугольников всегда равно постоянное число 1.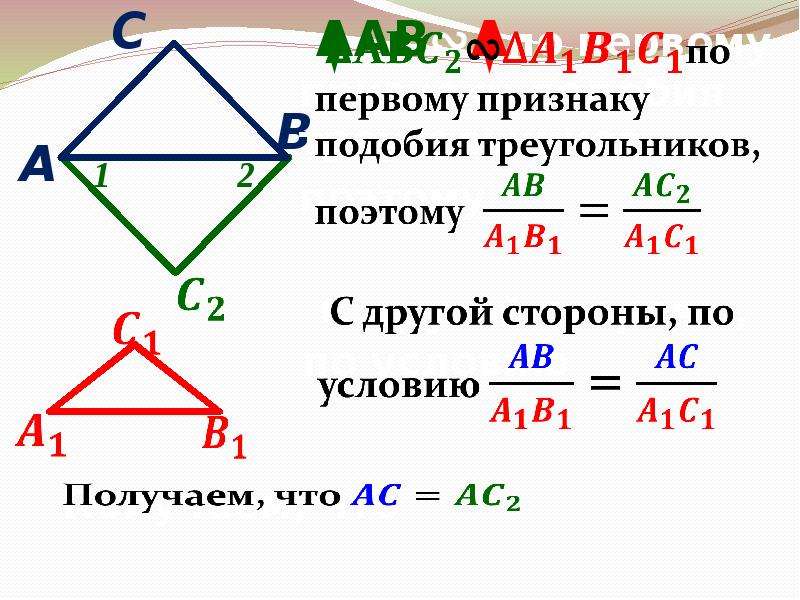 | Соотношение всех соответствующих сторон в подобных треугольниках согласовано. | ||
| Соответствующие углы | Все соответствующие углы равны. | Каждая пара соответствующих углов равна. |
Как определить похожие треугольники?
Мы можем доказать сходство в треугольниках, применяя аналогичные теоремы о треугольниках. Это постулаты или правила, используемые для проверки похожих треугольников.
Существует трех правил для проверки похожих треугольников: правило AA , правило SAS или правило SSS.
Правило угла-угла (AA):
Согласно правилу AA два треугольника считаются подобными, если два угла в одном конкретном треугольнике равны двум углам другого треугольника.
Правило стороны-угла-стороны (SAS):
Правило SAS гласит, что два треугольника подобны, если соотношение их соответствующих двух сторон равно, а также угол, образованный двумя сторонами, равен.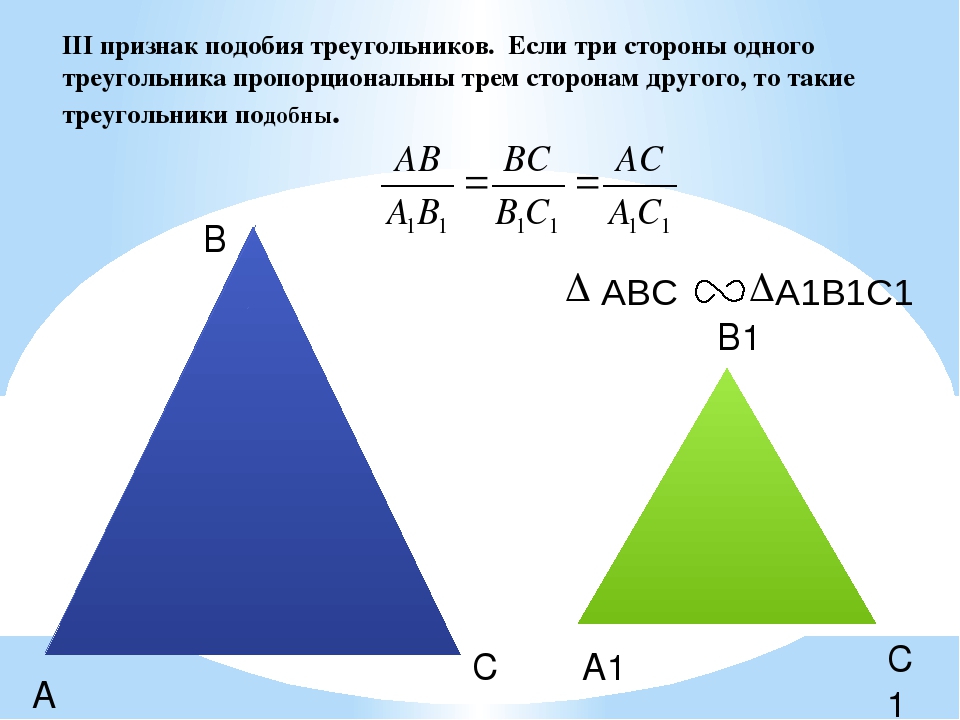
Правило стороны-стороны-стороны (SSS):
Два треугольника подобны, если все соответствующие три стороны данных треугольников находятся в одинаковой пропорции.
Как решать подобные треугольники?
Существует двух типов одинаковых задач треугольника ; это задачи, которые требуют от вас доказательства того, что данный набор треугольников подобен, и те, которые требуют, чтобы вы вычислили недостающие углы и длины сторон подобных треугольников.
Давайте посмотрим на следующие примеры:
Пример 1
Проверьте, похожи ли следующие треугольники
Решение
Сумма внутренних углов в треугольнике = 180 °
Следовательно, учитывая Δ PQR
P + ∠Q + ∠R = 180 °
60 ° + 70 ° + ∠R = 180 °
130 ° + ∠R = 180 °
Вычтем обе стороны на 130 °.
∠ R = 50 °
Рассмотрим Δ XYZ
∠X + ∠Y + ∠Z = 180 °
∠60 ° + ∠Y + ∠50 ° = 180 °
∠ 110 ° + ∠Y = 180 °
Вычтем обе стороны на 110 °
∠ Y = 70 °
Отсюда;
- По правилу угла-угла (AA) ΔPQR ~ ΔXYZ.

- ∠Q = ∠ Y = 70 ° и ∠Z = ∠ R = 50 °
Пример 2
Найдите значение x в следующих треугольниках, если ΔWXY ~ ΔPOR.
Решение
Учитывая, что два треугольника подобны, тогда;
WY / QR = WX / PR
30/15 = 36 / x
Перекрестное умножение
30x = 15 * 36
Разделите обе стороны на 30.
x = (15 * 36) / 30
x = 18
Следовательно, PR = 18
Давайте проверим, равны ли пропорции соответствующих двух сторон треугольников.
WY / QR = WX / PR
30/15 = 36/18
2 = 2 (RHS = LHS)
Пример 3
Проверьте, похожи ли два треугольника, показанные ниже, и рассчитайте значение k.
Решение
По правилу SAS, два треугольника подобны.
Доказательство:
8/4 = 20/10 (LHS = RHS)
2 = 2
Теперь вычислите значение k
12 / k = 8/4
12 / k = 2
Умножьте оба стороны на k.
12 = 2k
Разделите обе части на 2
12/2 = 2k / 2
k = 6.
Пример 4
Определите значение x на следующей диаграмме.
Решение
Пусть треугольник ABD и ECD подобны треугольникам.
Примените правило стороны-угла-стороны (SAS), где A = 90 градусов.
AE / EC = BD / CD
x / 1,8 = (24 + 12) / 12
x / 1,8 = 36/12
Перекрестное умножение
12x = 36 * 1,8
Разделите обе стороны на 12.
x = (36 * 1,8) / 12
= 5,4
Следовательно, значение x равно 5,4 мм.
Предыдущий урок | Главная страница | Следующий урокТеоремы подобия треугольника
Прежде чем пытаться понять подобие треугольников, очень важно понять концепцию пропорций и соотношений, потому что подобие полностью основано на этих принципах.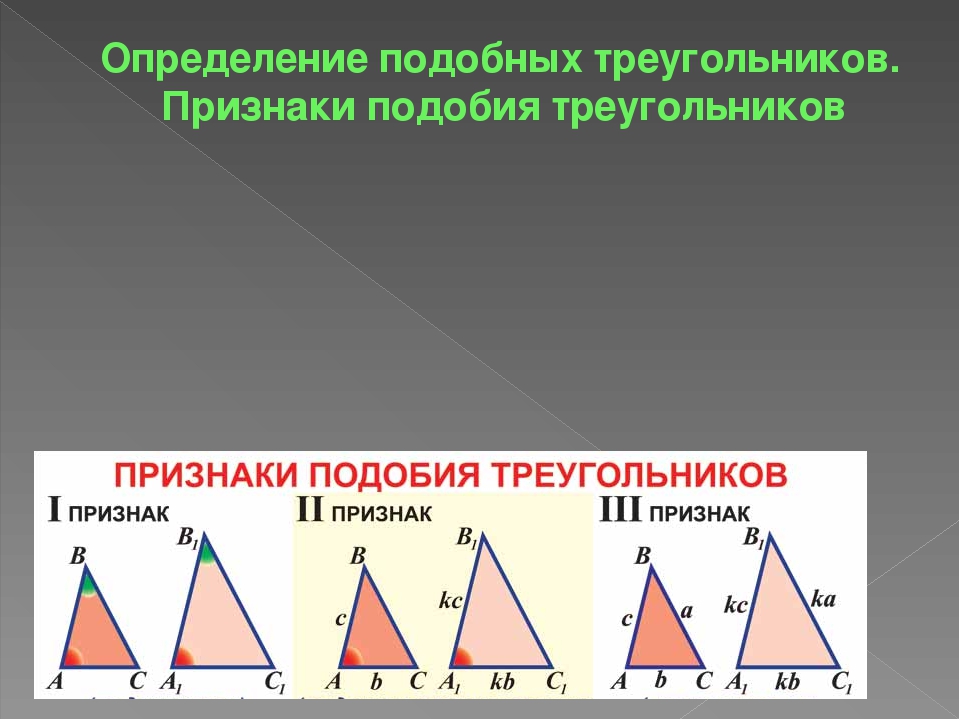
Сходство треугольников — это еще одна связь, которую могут иметь два треугольника. Мы уже узнали о конгруэнтности, где все стороны должны быть одинаковой длины. Точно так же углы должны быть равными со всеми сторонами пропорциональными. Сходство — это отношение эквивалентности.
Два треугольника $ ABC $ и $ DEF $ похожи, поэтому мы пишем: $ \ bigtriangleup ABC \ sim \ bigtriangleup DEF $.
Есть четыре теоремы, которые мы можем использовать, чтобы определить, похожи ли два треугольника.
Теорема AA
Два треугольника подобны, если их два соответствующих угла совпадают.
Пусть $ ABC $ — заданный треугольник. Итак, как мы можем построить подобный треугольник?
Мы расширим отрезки $ \ overline {AB} $ и $ \ overline {AC} $ на вершины $ B $ и $ C $ соответственно. На прямой $ AC $ выбираем точку $ D $ и строим прямую, параллельную прямой $ BC $ и проходящую через точку $ D $. Пересечение ранее построенной прямой и прямой $ AB $ составляет точку $ E $.
Получившийся треугольник $ AFD $ подобен данному треугольнику $ ABC $, как показано ниже.
$ \ beta = \ beta ’, \ gamma = \ gamma’ \ Rightarrow \ alpha = \ alpha ’$ (если два соответствующих угла имеют равную меру, то третий также равен и соответствует).
Верны также следующие пропорции:
$ \ frac {\ mid AB \ mid} {\ mid AF \ mid} = \ frac {\ mid AC \ mid} {\ mid AD \ mid} = \ frac {\ mid CB \ mid} {\ mid DF \ mid} $.
Теорема SSS
Два треугольника подобны, если длины всех соответствующих сторон пропорциональны.
Треугольники $ ABC $ и $ DEF $ являются аналогичными треугольниками, если:
Пример 1 .
Это следующие треугольники
$$ \ треугольник {ABC}: \ quad a = 2, \ quad b = 4, \ quad c = 5, $$
$$ \ треугольник {DEF}: \ quad d = 4, \ quad e = 8, \ quad f = 10 $$
похоже?
Решение :
У нас:
$$ \ frac {a} {d} = \ frac {b} {e} = \ frac {c} {f} \ Rightarrow \ frac {2} {4} = \ frac {4} {8} = \ frac {5} {10} \ Rightarrow \ frac {1} {2} = \ frac {1} {2} = \ frac {1} {2}.
Следовательно, треугольники $ ABC $ и $ DEF $ подобны по теореме SSS.
Если мы нашли другое значение в какой-либо части, треугольники не похожи.
Теорема SAS
Два треугольника подобны, если соответствующие длины двух сторон пропорциональны, а включенные углы совпадают.
Треугольники $ ABC $ и $ DEF $ похожи, если $ \ alpha = \ alpha ‘$ и $ \ frac {\ mid DE \ mid} {\ mid AB \ mid} = \ frac {\ mid AC \ mid} {\ mid DF \ mid} $.{\ circ} $
похоже?
Решение :
Это должно быть: $ \ frac {a} {w} = \ frac {b} {e} $.
У нас:
$$ \ frac {20} {10} = \ frac {5} {2.5} \ Rightarrow 2 = 2. $$
Эти две соответствующие стороны пропорциональны, и включенные углы равны. Следовательно, треугольники $ ABC $ и $ WER $ являются подобными треугольниками согласно теореме SAS.
Теорема SSA
Два треугольника подобны, если длины двух соответствующих сторон пропорциональны и их соответствующие углы на большем из этих двух совпадают.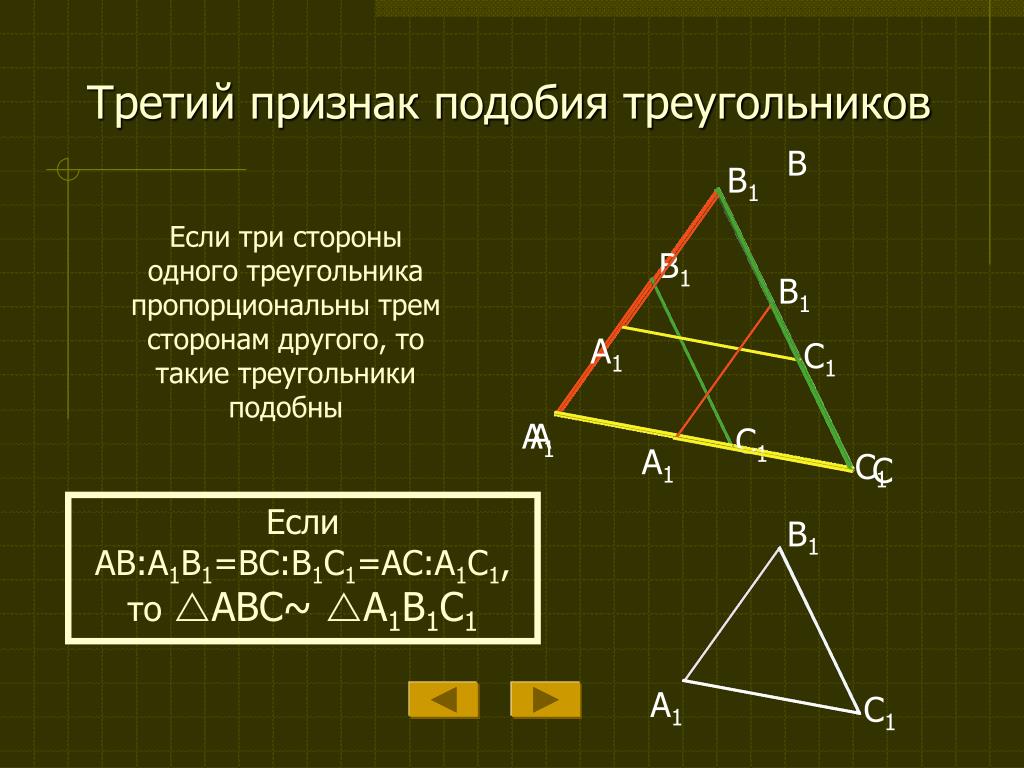 {\ circ} $
{\ circ} $
похоже?
Решение :
Надо сравнить все стороны по длине.
В данном случае
$$ \ frac {a} {b ‘} = \ frac {b} {a’} \ Rightarrow \ frac {6} {12} = \ frac {3} {6} \ Rightarrow \ frac {1} {2 } = \ frac {1} {2}, $$
, что верно. Противоположный угол к стороне наибольшей длины в треугольнике $ ABC $ равен $ \ alpha $, а угол, противоположный к самой длинной стороне треугольника $ GHJ $, равен $ \ beta $.
Отсюда следует, что $ \ alpha = \ beta $, что означает, что треугольники $ ABC $ и $ GHJ $ подобны по теореме SSA.
Листы схожести треугольников
Подобные треугольники (740,4 КБ, 2183 обращений)
Подобные прямоугольные треугольники (179,2 КБ, 1250 обращений)
Как определять похожие треугольники — стенограмма видео и урока
Теоремы подобия треугольника
Хорошо. Теперь, когда мы пополнились словарным запасом, давайте подробнее рассмотрим каждую из теорем подобия.
Теперь, когда мы пополнились словарным запасом, давайте подробнее рассмотрим каждую из теорем подобия.
Начнем с Угол — Угол (AA). Чтобы два треугольника были подобны по углу — углу (AA), два угла одного треугольника совпадают с двумя углами другого треугольника. Посмотрите на треугольник JKL ниже. Угол J равен 52 градусам, а угол K равен 60 градусам. Если мы вычтем 52 и 60 из 180 (общее количество градусов, на которое должны складываться все углы в треугольнике), мы увидим, что угол L равен 68 градусам.
Теперь посмотрим на треугольник MNO ниже. Если угол M конгруэнтен углу J, а угол N конгруэнтен углу K, что мы можем сказать об углах L и O? Можно сказать, что они тоже конгруэнтны. С тремя парами совпадающих углов треугольники имеют одинаковую форму, но разные размеры, что означает, что их стороны пропорциональны, а треугольники похожи.
Для «Сторона — угол — сторона» (SAS) угол одного треугольника должен быть конгруэнтен соответствующему углу другого треугольника, а длины сторон, включая эти углы, пропорциональны.С конгруэнтными включенными углами пропорциональные стороны не могут колебаться, а третья сторона в обоих треугольниках должна иметь определенную длину. Таким образом, если две стороны уже пропорциональны, длины третьих сторон также должны быть пропорциональными, что доказывает сходство треугольника.
Последняя теорема — Сторона — Сторона — Сторона (SSS), что означает, что три набора соответствующих сторон двух треугольников пропорциональны. Если соотношения всех соответствующих сторон равны, то стороны аналогичны, как и треугольники.
При определении, какая теорема доказывает сходство, не задумывайтесь над этим; просто посмотрите на буквы в каждой теореме. Для того, чтобы треугольники были подобны Угол — Угол (AA), будут предусмотрены измерения двух углов в каждом треугольнике. Если аналогично «Сторона — Угол — Сторона» (SAS), тогда у вас будут размеры двух сторон и углы обоих треугольников. Для «Сторона — Сторона — Сторона» (SSS) у вас будут все три длины сторон для обоих треугольников. Давай попрактикуемся.
Для того, чтобы треугольники были подобны Угол — Угол (AA), будут предусмотрены измерения двух углов в каждом треугольнике. Если аналогично «Сторона — Угол — Сторона» (SAS), тогда у вас будут размеры двух сторон и углы обоих треугольников. Для «Сторона — Сторона — Сторона» (SSS) у вас будут все три длины сторон для обоих треугольников. Давай попрактикуемся.
Они похожи?
Треугольник ABC подобен треугольнику DEF?
Рассмотрим данную информацию.У нас есть длины двух сторон в обоих треугольниках и размеры включенных углов. Это звучит как Сторона — Угол — Сторона (SAS). Но, прежде чем заключить подобие по этой теореме, мы должны проверить конгруэнтность углов и пропорциональных сторон.
Угол B и угол E составляют 63 градуса, поэтому указанные углы совпадают. Чтобы задать пропорции сторон, всегда сравнивайте две самые маленькие стороны вместе и две самые большие стороны вместе, в том же порядке между треугольниками. В этом примере наши отношения 3/6 и 5/8. Если преобразовать в десятичные числа, 3/6 = 0,5 и 5/8 = 0,625. Поскольку эти соотношения не равны, треугольник ABC не похож на треугольник DEF.
В этом примере наши отношения 3/6 и 5/8. Если преобразовать в десятичные числа, 3/6 = 0,5 и 5/8 = 0,625. Поскольку эти соотношения не равны, треугольник ABC не похож на треугольник DEF.
Для нашего следующего примера определите, похож ли треугольник RST на треугольник WXY.
Поскольку нам даны длины всех трех сторон в обоих треугольниках, Сторона — Сторона — Сторона (SSS) — единственная теорема, которая может доказать сходство.Настройте наши пропорции. Две меньшие стороны имеют отношение 6/3, самые большие стороны имеют отношение 10/5, а остальные стороны имеют отношение 8/4. Для упрощения все отношения равны двум. Следовательно, треугольник RST подобен треугольнику WXY по теореме подобия Сторона — Сторона — Сторона (SSS).
Давай сделаем еще один. Треугольник CRE похож на треугольник PHB?
На основании предоставленной информации эти треугольники могут совпадать только по углу — углу (AA). Но оказывается, что только одна пара углов конгруэнтна. Итак, вы можете подумать, что треугольники не похожи. Прежде чем делать вывод, давайте вычислим величину угла E. Вычитая 180-40-95, мы находим, что угол E составляет 45 градусов. С этой информацией мы теперь видим, что угол R и угол H совпадают, а также угол E и угол B. Следовательно, треугольник CRE подобен треугольнику PHB по теореме подобия угол-угол (AA).
Но оказывается, что только одна пара углов конгруэнтна. Итак, вы можете подумать, что треугольники не похожи. Прежде чем делать вывод, давайте вычислим величину угла E. Вычитая 180-40-95, мы находим, что угол E составляет 45 градусов. С этой информацией мы теперь видим, что угол R и угол H совпадают, а также угол E и угол B. Следовательно, треугольник CRE подобен треугольнику PHB по теореме подобия угол-угол (AA).
Краткое содержание урока
Подобные треугольники обладают теми же характеристиками, что и другие подобные фигуры: совпадающие соответствующие углы и пропорциональные соответствующие стороны.Теоремы подобия треугольников, а именно: Угол — Угол (AA), Сторона — Угол — Сторона (SAS) и Сторона — Сторона — Сторона (SSS), служат в качестве ярлыков для идентификации похожих треугольников. При оценке сходства всегда начинайте с изучения предоставленной информации, которая поможет вам выяснить, какую теорему использовать при определении, похожи ли треугольники или нет.
Результат обучения
По завершении этого урока вы сможете:
- Определить аналогичные цифры
- Опишите характеристики, необходимые для того, чтобы треугольники были похожими
- Объясните три теоремы подобия треугольников
- Определите, похожи ли два треугольника, используя теоремы Угол — Угол, Сторона — Угол — Сторона или Сторона — Сторона — Сторона
треугольников (предварительная алгебра, введение в геометрию) — Mathplanet
Треугольник состоит из трех отрезков.Сегменты линии пересекаются в своих конечных точках. Чтобы назвать треугольник, мы часто используем его вершины (название конечных точек). Треугольник ниже называется ABC.
У треугольника три угла. Сумма углов всегда равна 180 ° в треугольнике.
У нас есть разные типы треугольников. Треугольник классифицируется по углам и количеству совпадающих сторон.
Треугольник с тремя острыми ангелами называется острым треугольником.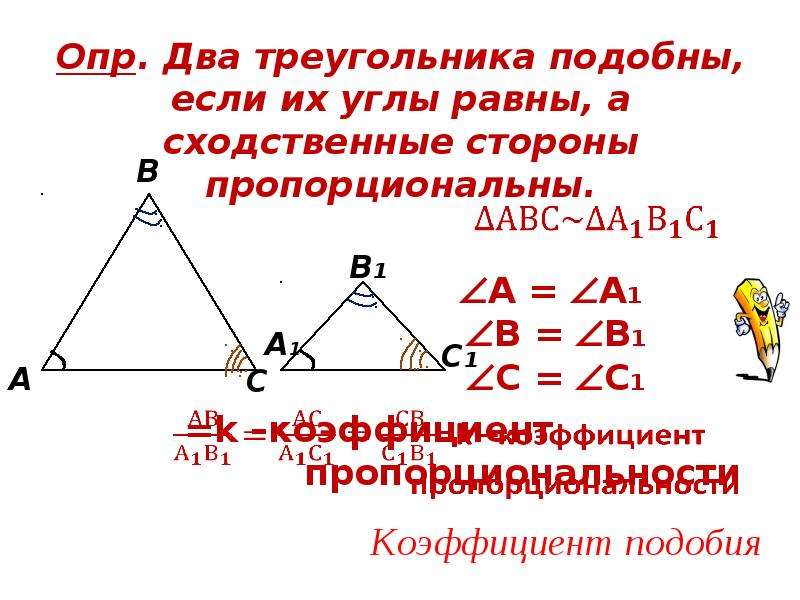
Треугольник с одним прямым углом называется прямоугольным.
Треугольник с одним тупым углом называется тупым треугольником.
Когда треугольник имеет три равные стороны, мы называем его равносторонним треугольником. Отметим совпадающие стороны косой чертой. Углы в равностороннем треугольнике всегда равны 60 °.
Если у треугольника две равные стороны, он называется равнобедренным треугольником. Углы, противоположные двум сторонам одинаковой длины, совпадают.
Треугольник без равных сторон или углов называется разносторонним треугольником.
Когда два треугольника совпадают, это означает, что они имеют одинаковый размер и форму. Это означает, что у них одинаковые углы. Красные косые черты показывают нам, какие стороны и углы совпадают. Конгруэнтность показана этим символом
.$$ \ cong $$
$$ \ begin {matrix} A \ cong X & & AB \ cong XY \\ B \ cong Y & & BC \ cong YZ \\ C \ cong Z & & AC \ cong XZ \ end {matrix} $$
Треугольники с одинаковыми углами, но не одинакового размера, называются подобными. Подобные треугольники имеют пропорциональные стороны. Сходство показано этим символом
Подобные треугольники имеют пропорциональные стороны. Сходство показано этим символом
$$ \ sim $$
$$ \ bigtriangleup ABC \ sim \ bigtriangleup XYZ $$
$$ A = X, \: \: B = Y, \: \: C = Z $$
$$ \ frac {a} {x} = \ frac {b} {y} = \ frac {c} {z} $$
Пример
Найдите x в подобных треугольниках.
Мы знаем, что, поскольку треугольники похожи, стороны пропорциональны, что означает, что
$$ \ frac {x} {14} = \ frac {3} {21} \ Rightarrow $$
$$ x = \ frac {14 \ cdot 3} {21} = \ frac {42} {21} = 2 $$
$$ x = 2 $$
Видеоурок
Определите, какие треугольники прямые, равнобедренные, острые, разносторонние, тупые или равносторонние
Соответствие и сходство
Обзор
В области математики и, в частности, геометрии, соответствие и сходство являются взаимосвязанными терминами.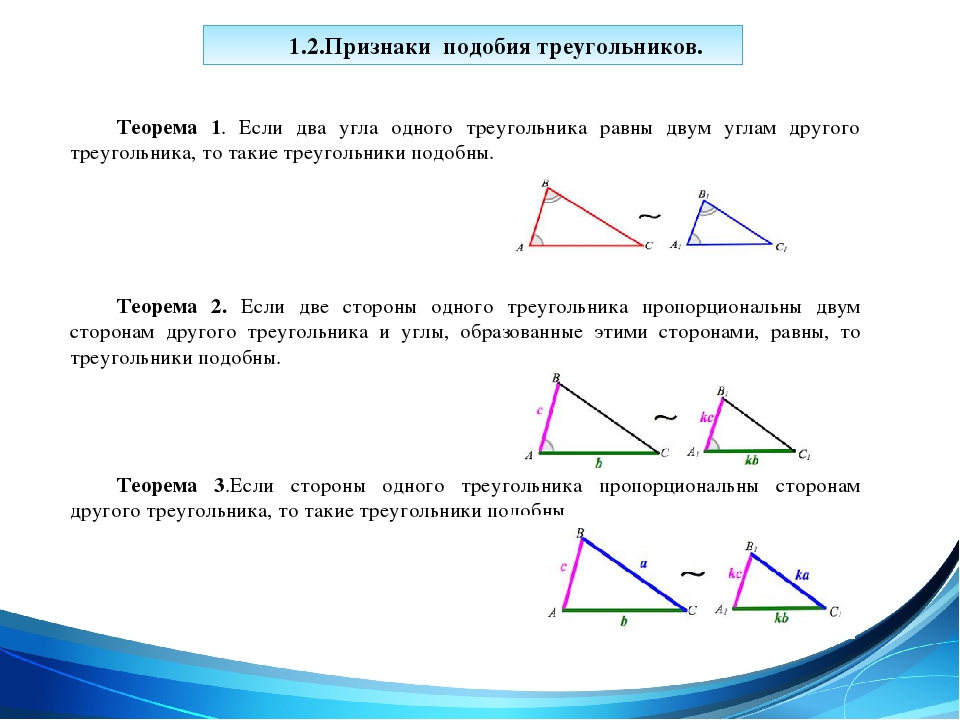 Сравнение по существу означает, что две фигуры или предметы имеют одинаковую форму и размер. Хотя конгруэнтные объекты идентичны, их ориентация относительно друг друга и их физические координаты в плоскости или трехмерном пространстве часто будут различаться. Например, два показанных ниже треугольника являются равносторонними треугольниками и имеют стороны одинаковой длины. Таким образом, они совпадают, несмотря на то, что треугольник справа перевернут.
Сравнение по существу означает, что две фигуры или предметы имеют одинаковую форму и размер. Хотя конгруэнтные объекты идентичны, их ориентация относительно друг друга и их физические координаты в плоскости или трехмерном пространстве часто будут различаться. Например, два показанных ниже треугольника являются равносторонними треугольниками и имеют стороны одинаковой длины. Таким образом, они совпадают, несмотря на то, что треугольник справа перевернут.
Треугольники совпадают, потому что имеют одинаковую форму и размеры.
Сходство означает, что две фигуры или предметы имеют одинаковую форму, но обычно не одного и того же размера.Два круга всегда будут похожи, например, потому что по определению имеют одинаковую форму. Однако, если окружности имеют разную длину радиусов, они не будут совпадать.
Два круга всегда похожи, потому что имеют одинаковую форму
Конгруэнтность
Слово конгруэнтность происходит от латинского слова congruo , что по сути означает , я согласен, . В геометрии, если два объекта описываются как конгруэнтные, подразумевается, что один может быть точно сопоставлен с другим. Другими словами, они имеют одинаковую форму и размер, но часто не имеют одинакового расположения или ориентации. Например, две конгруэнтные двумерные формы могут сосуществовать в одной и той же плоскости или находиться в разных плоскостях. Две конгруэнтные трехмерные формы могут сосуществовать в одном и том же трехмерном пространстве, но иметь разные пространственные координаты и могут быть по-разному ориентированы вокруг осей x , y и z .
В геометрии, если два объекта описываются как конгруэнтные, подразумевается, что один может быть точно сопоставлен с другим. Другими словами, они имеют одинаковую форму и размер, но часто не имеют одинакового расположения или ориентации. Например, две конгруэнтные двумерные формы могут сосуществовать в одной и той же плоскости или находиться в разных плоскостях. Две конгруэнтные трехмерные формы могут сосуществовать в одном и том же трехмерном пространстве, но иметь разные пространственные координаты и могут быть по-разному ориентированы вокруг осей x , y и z .
Любая простая двух- или трехмерная форма может быть указана в терминах координат точек x , y и (для трехмерных форм) z точек, определяющих ее границы. Круг, например, представляет собой двумерную форму, которая имеет определенный центр (или исходную точку , ) и периметр, состоящий из всех точек, находящихся на заданном расстоянии (радиус ) от центра в той же плоскости.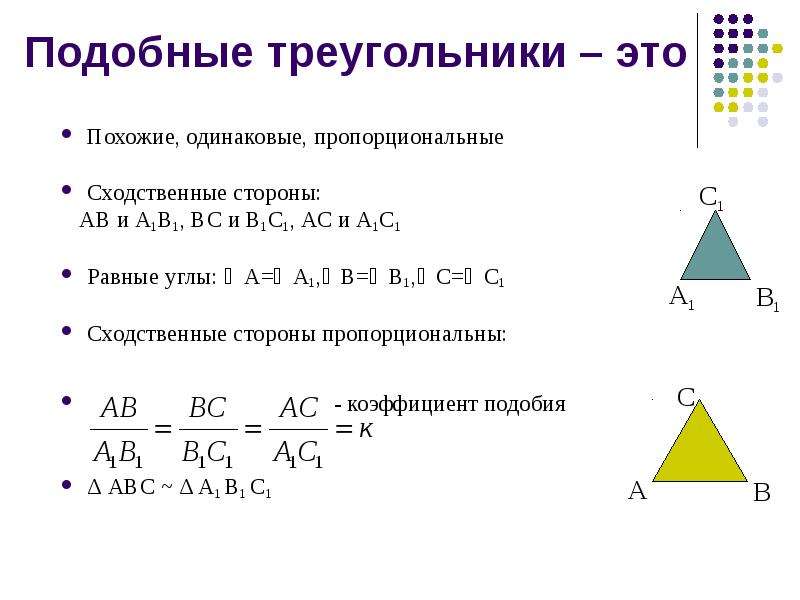 .Точно так же треугольник — это двухмерная форма, которая определяется тремя точками на плоскости. Фактически, любые три точки на плоскости могут определять треугольник, при условии, что все они не лежат на одной линии. Куб определяется восемью точками в трехмерном пространстве, а сфера определяется одной точкой в трехмерном пространстве и всеми точками, которые лежат на заданном расстоянии от этой точки в любом направлении.
.Точно так же треугольник — это двухмерная форма, которая определяется тремя точками на плоскости. Фактически, любые три точки на плоскости могут определять треугольник, при условии, что все они не лежат на одной линии. Куб определяется восемью точками в трехмерном пространстве, а сфера определяется одной точкой в трехмерном пространстве и всеми точками, которые лежат на заданном расстоянии от этой точки в любом направлении.
В оставшейся части этого обсуждения мы будем интересоваться только двумерными формами, хотя те же принципы могут быть одинаково хорошо применены к трехмерным объектам.Для любой двумерной формы точки, которые определяют эту форму, можно рассматривать как отображение , потому что они могут быть заданы как набор координат x и y . Чтобы две формы были конгруэнтными, должна быть возможность точно отобразить одну форму на другую, используя последовательность перемещений , вращений и отражений .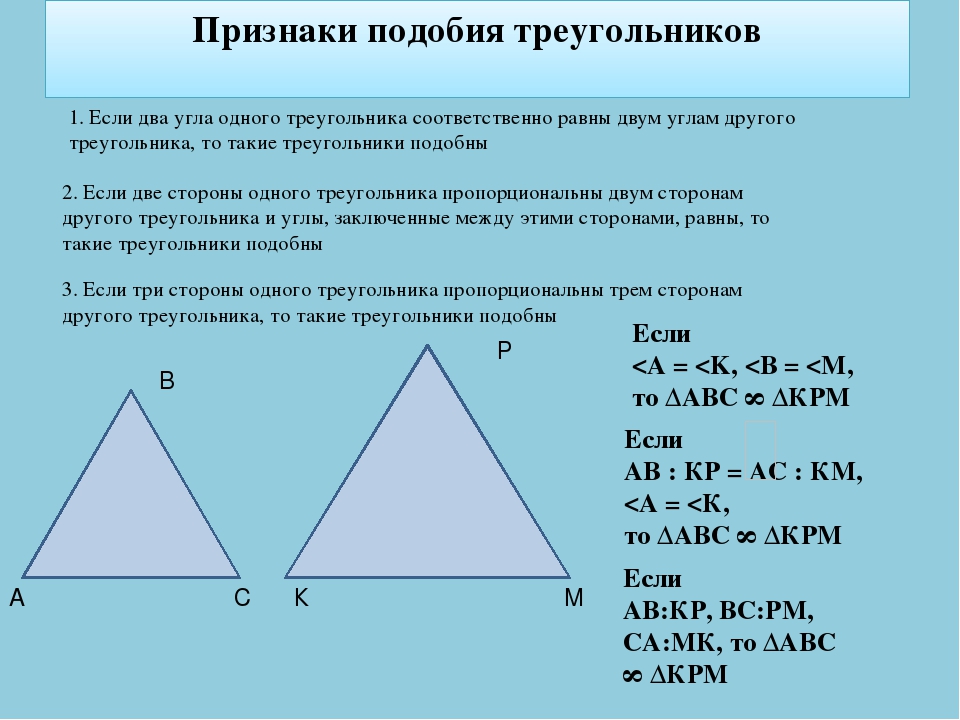 Каждый из этих терминов представляет собой действие, которое можно применить к форме, чтобы изменить ее положение или ориентацию, и они будут подробно обсуждаться в другом месте.На данный момент, вероятно, проще всего сказать, что мы должны иметь возможность перемещать одну фигуру и, если необходимо, повернуть ее на угол или перевернуть так, чтобы она лежала точно над другой фигурой, при этом все соответствующие точки имеют одинаковое значение x и y координаты.
Каждый из этих терминов представляет собой действие, которое можно применить к форме, чтобы изменить ее положение или ориентацию, и они будут подробно обсуждаться в другом месте.На данный момент, вероятно, проще всего сказать, что мы должны иметь возможность перемещать одну фигуру и, если необходимо, повернуть ее на угол или перевернуть так, чтобы она лежала точно над другой фигурой, при этом все соответствующие точки имеют одинаковое значение x и y координаты.
Конгруэнтные треугольники с разными координатами и ориентацией
Две фигуры, нарисованные в разных местах на одной плоскости, возможно, с разной ориентацией, очевидно, будут иметь разные сопоставления.Как же тогда мы можем доказать соответствие? На самом деле это относительно просто. Два отображения совпадают, если и , только если , расстояние между любыми двумя точками в одном отображении такое же, как расстояние между соответствующими двумя точками в другом отображении.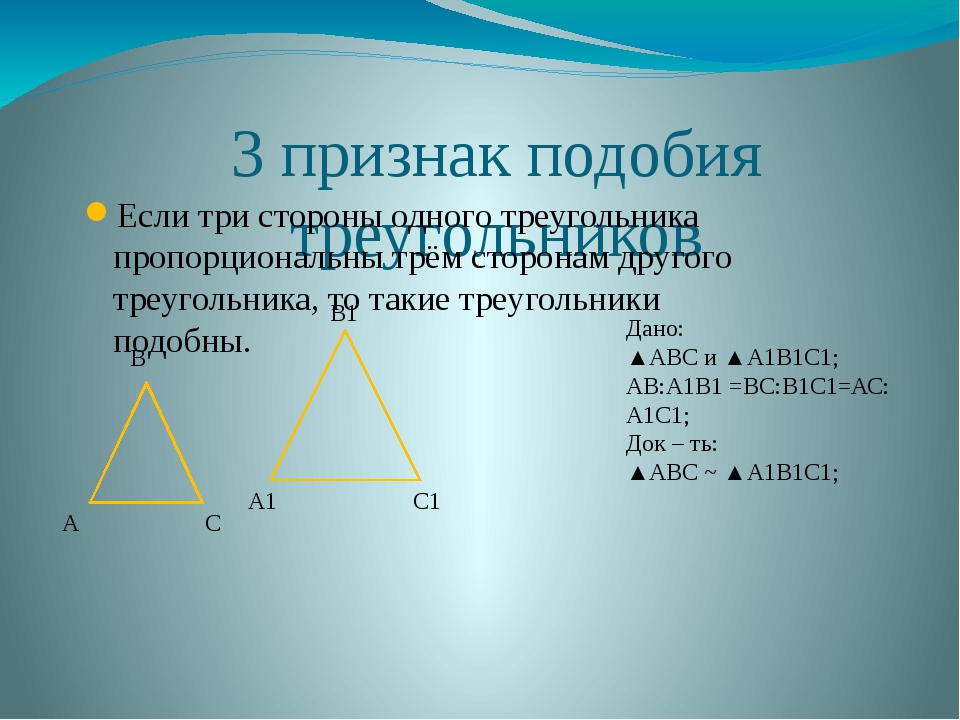 Это определение конгруэнтности работает для любой двумерной формы.
Это определение конгруэнтности работает для любой двумерной формы.
На рисунке ниже два неправильных многоугольника ABCD и A’B’C’D ‘совпадают. Если вы внимательно изучите изображение, вы сможете увидеть, что если многоугольник ABCD повернуть по часовой стрелке на угол девяноста градусов (90 °) вокруг точки C, а затем сдвинуть его по горизонтали вправо на три квадрата на сетке, то его точки точно совпадут с таковыми многоугольника A’B’C’D ‘.Чтобы доказать соответствие, необходимо показать, что расстояние между любыми двумя точками для многоугольника A’B’C’D ‘такое же, как расстояние между соответствующими двумя точками для многоугольника ABCD. Сюда входят пары несмежных точек, такие как A и C и A ‘и C’. Опять же, внимательное изучение изображения должно показать, что это действительно так (посмотрите на расстояние между двумя точками с точки зрения количества квадратов между ними на сетке как в горизонтальном, так и в вертикальном направлениях).
Два неправильных многоугольника совпадают
Как вы можете видеть из вышеизложенного, если мы возьмем точную копию двухмерной формы и поместим ее в другое место на той же (или в другой) двумерной плоскости, и даже если мы изменим ориентацию форма (например, перевернуть ее вверх дном или набок, или повернуть на произвольный угол) форма остается той же самой.То же самое применимо, если мы возьмем копию некоторой трехмерной формы и поместим ее в другое место в трехмерном пространстве, даже если мы повернем ее на разные произвольно выбранные углы для всех трех осей. Размеры и форма объекта остаются неизменными. Эти свойства часто называют инвариантами . Примеры инвариантов в конгруэнтных объектах включают соответствующие углы и длины сторон треугольника, длину и высоту прямоугольника и радиус круга или сферы.
Для некоторых двумерных форм существуют другие тесты, которые можно применить, чтобы доказать соответствие./918870b1bc4a305.s.siteapi.org/img/bb22326010622f7f3181a71f4177d938d9c92517.jpg) Одна из таких форм — треугольник. Два треугольника конгруэнтны, если можно показать, что соответствующие стороны имеют одинаковую длину, а соответствующие углы имеют одинаковую величину. Это включает в себя сравнение шести атрибутов (три стороны и три угла), но обычно мы можем доказать соответствие, используя меньшее количество атрибутов.Соответствие часто можно доказать, если мы сможем показать, что длины двух сторон и величина одного угла или длина одной стороны и величина двух углов одинаковы для обоих треугольников. Это не работает для всех возможных комбинаций сторон и углов, но комбинации, для которых это работает, описаны на странице, озаглавленной «Треугольники». Если два треугольника, ΔABC и ΔDEF, совпадают, мы можем выразить это с помощью символа сравнения (≅):
Одна из таких форм — треугольник. Два треугольника конгруэнтны, если можно показать, что соответствующие стороны имеют одинаковую длину, а соответствующие углы имеют одинаковую величину. Это включает в себя сравнение шести атрибутов (три стороны и три угла), но обычно мы можем доказать соответствие, используя меньшее количество атрибутов.Соответствие часто можно доказать, если мы сможем показать, что длины двух сторон и величина одного угла или длина одной стороны и величина двух углов одинаковы для обоих треугольников. Это не работает для всех возможных комбинаций сторон и углов, но комбинации, для которых это работает, описаны на странице, озаглавленной «Треугольники». Если два треугольника, ΔABC и ΔDEF, совпадают, мы можем выразить это с помощью символа сравнения (≅):
ΔABC ≅ ΔDEF
Сходство
Сходство , как и конгруэнтность, требует, чтобы два объекта имели абсолютно одинаковую форму.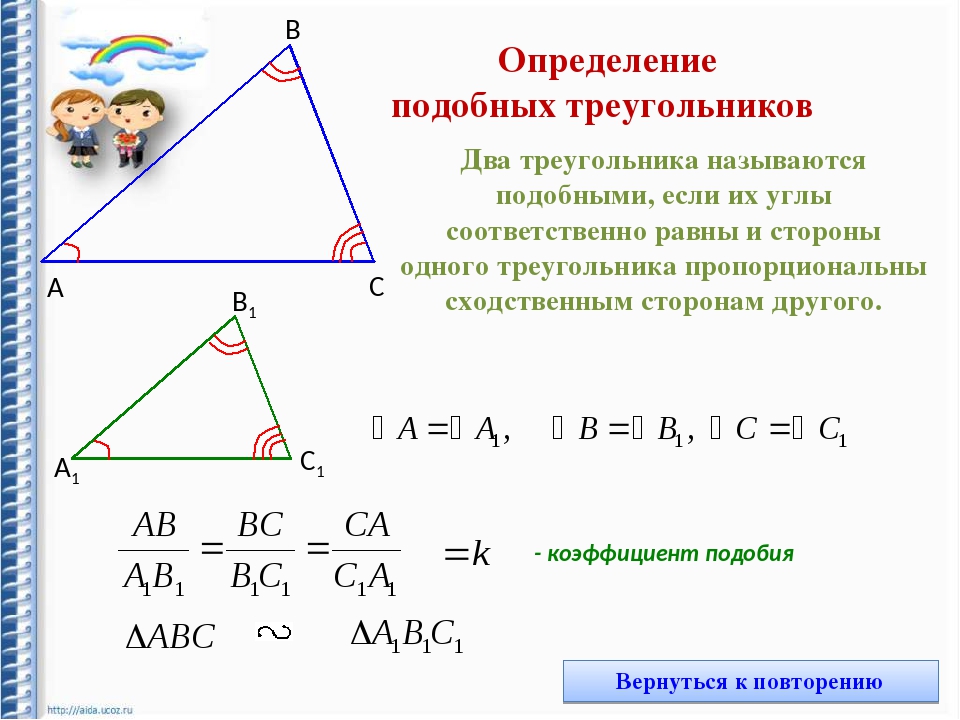 Однако для существования подобия размеры не должны быть одинаковыми. Здесь есть несколько выводов. Во-первых, в то время как два конгруэнтных объекта также должны быть подобными по определению, два подобных объекта не обязательно должны быть конгруэнтными. Во-вторых, если два объекта похожи, то второй объект является либо увеличенной, либо уменьшенной версией первого (или, возможно, даже того же размера, и в этом случае объекты также совпадают). Ориентация и расположение двух объектов часто различаются, но это не имеет никакого отношения к тому, похожи они или нет.Ранее мы говорили, что все круги похожи. Также должно быть довольно легко увидеть, что все правильные многоугольники одного и того же типа всегда будут одинаковыми.
Однако для существования подобия размеры не должны быть одинаковыми. Здесь есть несколько выводов. Во-первых, в то время как два конгруэнтных объекта также должны быть подобными по определению, два подобных объекта не обязательно должны быть конгруэнтными. Во-вторых, если два объекта похожи, то второй объект является либо увеличенной, либо уменьшенной версией первого (или, возможно, даже того же размера, и в этом случае объекты также совпадают). Ориентация и расположение двух объектов часто различаются, но это не имеет никакого отношения к тому, похожи они или нет.Ранее мы говорили, что все круги похожи. Также должно быть довольно легко увидеть, что все правильные многоугольники одного и того же типа всегда будут одинаковыми.
Все правильные многоугольники одного типа похожи
Чтобы два неправильных многоугольника были похожими, все соответствующие стороны должны иметь одинаковую длину, а все соответствующие внутренние углы должны иметь одинаковую величину. Мы видели, что можем взять два конгруэнтных объекта и сопоставить один с другим с помощью процесса вращения и перемещения (т.е.поворачивая один объект и перемещая его так, чтобы все его точки лежали над соответствующими точками другого объекта). Мы можем сделать то же самое с двумя похожими объектами, если мы включим дополнительный шаг масштабирования одного из объектов, чтобы его размеры совпадали с размерами другого объекта (это должно произойти до любого поворота и перемещения, которые могут потребоваться). На изображении ниже показаны два похожих неравносторонних треугольника.
Мы видели, что можем взять два конгруэнтных объекта и сопоставить один с другим с помощью процесса вращения и перемещения (т.е.поворачивая один объект и перемещая его так, чтобы все его точки лежали над соответствующими точками другого объекта). Мы можем сделать то же самое с двумя похожими объектами, если мы включим дополнительный шаг масштабирования одного из объектов, чтобы его размеры совпадали с размерами другого объекта (это должно произойти до любого поворота и перемещения, которые могут потребоваться). На изображении ниже показаны два похожих неравносторонних треугольника.
Два одинаковых неравносторонних треугольника
Показанные выше треугольники на самом деле являются разносторонними треугольниками (то есть треугольниками, в которых нет двух углов и двух сторон, не равных). Два треугольника (фактически любые два треугольника) можно назвать подобными, если длины соответствующих сторон изменяются в той же пропорции. Применительно к треугольникам ABC и DEF это можно выразить как:
Применительно к треугольникам ABC и DEF это можно выразить как:
| AB | = | BC | = | CA |
| DE | EF | FD |
Два треугольника также можно назвать подобными, если можно показать, что любые два соответствующих угла равны по величине (что автоматически потребовало бы, чтобы третья пара соответствующих углов была равной по величине, поскольку внутренние углы треугольника всегда равна ста восьмидесяти градусам):
∠ ABC = ∠ DEF и ∠ BCA = ∠ EFD
или же:
∠ ABC = ∠ DEF и ∠ CAB = ∠ FDE
или же:
∠ BCA = ∠ EFD и ∠ CAB = ∠ FDE
Дополнительно можно показать, что два треугольника подобны, если любые две соответствующие пары сторон различаются по длине в одинаковой пропорции, а включенные углы равны. Например:
Например:
| AB | = | BC | и ∠ ABC = ∠ DEF |
| DE | EF |
или же:
| BC | = | CA | и ∠ BCA = ∠ EFD |
| EF | FD |
или же:
| CA | = | AB | и ∠ CAB = ∠ FDE |
| FD | DE |
Если треугольники ABC и DEF похожи, мы можем выразить это с помощью символа подобия (~):
ΔABC ~ ΔDEF
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov. | |



 Найдите ВО и отношение площадей треугольников ВОС и АОД, АД = 5 см, ВС = 2 см, АО = 25 см.
Найдите ВО и отношение площадей треугольников ВОС и АОД, АД = 5 см, ВС = 2 см, АО = 25 см.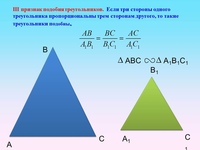 Найдите соотношения: а) , б) ; в) .
Найдите соотношения: а) , б) ; в) .
 Si le problème persiste,
veuillez communiquer avec le service de soutien Technique de Alberta Education (доступный
en anglais seulement).
Si le problème persiste,
veuillez communiquer avec le service de soutien Technique de Alberta Education (доступный
en anglais seulement).