Тригонометрия. Радианная мера угла. Тригонометрический круг. Формулы приведения
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
УРОК 1
Радианная мера угла
Единичной окружностью
называется окружность с центром в начале
координат и радиусом, равным единице.
Центральный угол, опирающийся
на дугу, длина которой равна радиусу
окружности, называется углом в один
радиан.
В
R
R
0
R
А
1 рад
1 радиан =
АОВ
П
1
радиан
180
Длина
АВ = ОА =R
180 0
1 радиан
57 0
П
Положительные и отрицательные углы в окружности
Начало отсчета углов — в точке (1;0)
У
+
I
0
III
R=1
+
—
(a >0)
Ро х
0Ро
IV
Рa (a >0)
0Рa
(a >0)
повернули на угол a
против часовой стрелки
—
II
Рa
ОРо
ОРa
повернули на угол
по часовой стрелки
(a >0)
Угол поворота радиуса ОРо против часовой
стрелки считается положительным,
а по часовой — отрицательным
Определение косинуса и синуса
Косинусом угла a называется ордината
точки единичной окружности, полученной
при повороте точки (1;0) на угол a радиан
вокруг начала координат.

У
А
sin a
0
a
cos a
(1;0)
Х
Синусом угла a называется абсцисса
точки единичной окружности,
полученной при повороте точки (1;0) на
угол a радиан вокруг начала координат
Тригонометрические функции угла и числового аргумента
Определение тригонометрических функций
Через единичную
Через произвольную
окружность (радиус равен 1) окружность
Рa (х;у)
у
0
В
Рa (х;у)
у
a
Через прямоугольный
треугольник (для острых
углов
c
a
х
0
a
х
А
a
b
Sin a = y — ордината точки Р
Соs a = х — абсцисса точки Р
у sin a
х cos a
х cos a
ctga
у sin a
tga
у
R
х
cos a
R
у
tga
х
х
ctga
у
sin a
а
с
b
cos a
c
a
tga
b
b
ctga
a
sin a
С
Представление тангенса в единичной окружности
А(1;уА )
у
АР0 — ось тангенсов
А Р0
a
Р0
х
1
ОУ
sin a
tga
cos a
Тангенсом угла a называется отношение
синуса угла a к его косинусу
По общему определению
уA
tga У A
1
—
ордината соответствующей точки оси
Представление котангенса в единичной окружности
У
В (хВ;1)
С
a
0
Х
СВ — ось котангенсов
СВ
Ох
cos a
ctgx
sin aa
Котангенсом угла a называется
отношение косинуса угла a к его синусу
По общему определению ctga
xB
X B — абсцисса соответствующей точки оси
1
котангенсов
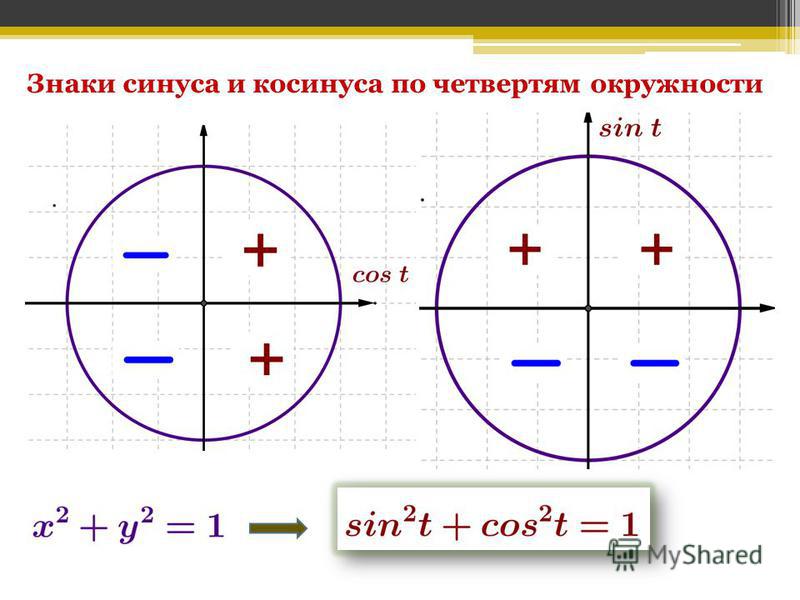
Знаки тригонометрических функций
cosa
Sina
II
I
+
_
+
I
+
+
_
_
_
II
III
IV
II
III
III
_
+
+
IV
I
Сtg a
_
IV
tg a
Тригонометрический круг
Значения тригонометрических функций некоторых углов
Единичная окружность соответствует 2p радиан
(1800 = p радиан)
=>
1 радиан = 180 0 /p ~ 57 0
Тригонометрические функции противоположного аргумента
cos( a ) cos a
sin( a ) sin a
tg ( a ) tga
ctg ( a ) ctga
Формулы приведения
Аргумент x
Приводимая
функция
2п+α
п/2+α
п +α
3/2п+α
2п-α
Sinx
Cosx
Tgx
Ctgx
мнемоническое правило:
п/2
п
Если аргумент изменяется на
угол, кратный p ,
название функции не меняется.
Если аргумент изменяется на
угол , кратный p/2 (но не кратный
p) , название функции меняется
на противоположное.
Знак новой функции
определяется знаком исходной,
считая , что a ( 0 , p/2).
0
3п/2
Формулы приведения
Аргумент x
Приводимая
функция
2п+α
п/2+α
п +α
3/2п+α
2п-α
Sinx
Cosx
Tgx
Ctgx
+sint
+cost
+tgt
+ctgt
+cost
— sint
— ctgt
— tgt
-sint
-cost
+tgt
+ctgt
— cost
+sint
-ctgt
-tgt
-sint
cost
-tgt
-ctgt
мнемоническое правило:
п/2
п
Если аргумент изменяется на
угол, кратный p ,
название функции не меняется.
угол , кратный p/2,
название функции меняется на
противоположное.
Знак новой функции
определяется знаком исходной,
считая , что a ( 0 , p/2).
0
3п/2
Домашнее задание 1
УРОК 2
Тригономе
трические
формулы
Упражнения (д.
 з. – чётные номера)
з. – чётные номера)English Русский Правила
Урок 1. Градусное измерение угловых величин
В некоторой плоскости фиксируют положение луча ОА и называют его начальной стороной угла, а второй луч, исходящий из той же точки, вращают в этой плоскости от положения ОА до положения ОВ и его называют подвижным лучом, а его конечное положение ОВ – конечной стороной ∠ АОВ, т. е. ∠ АОВ рассматривают как результат вращения луча в плоскости от положения ОА до положения ОВ.
При таком определении угла его величина является мерой вращения конечной его стороны относительно начальной.
Для непосредственного измерения дуг и углов, как и отрезков, принимают некоторую определённую дугу (угол) за единицу измерения и при помощи этой единицы измеряют остальные дуги и углы.
Существуют различные единицы измерения дуг и углов: градус, радиан, большое
и малое деления, полный оборот, румб т.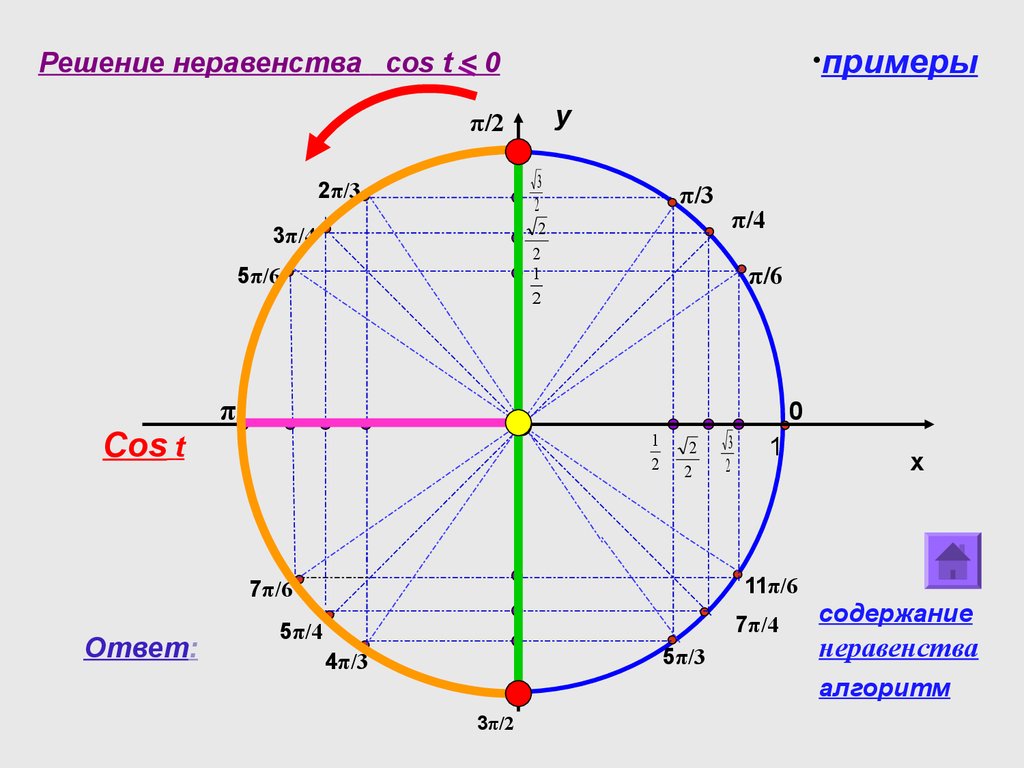 д..
д..
Дугу, длина которой равна
части длины её окружности, называют дугой в один градус, а угол, равный центральному углу, опирающемуся на дугу в один градус, называют углом в один градус (1°).
Градусы придумали в
Древнем Вавилоне. Взяли и разбили окружность на
1 градус – это 1/360 часть окружности.
Могли разбить на 100 частей. Или на 1000. Но разбили на 360.
Тригонометрический круг.
Тригонометрия пришла людям на помощь, когда выяснилось, что для многих расчётов недостаточно тех углов, которые определялись обычной геометрией. В геометрии мы не встретим углы больше, чем 360°. Поэтому тригонометрия – это раздел математики, посвящённый углам.
Нарисуем тригонометрический круг. Круг это аналог числовой прямой в геометрии.
Круг это аналог числовой прямой в геометрии.
1. Рисуем систему координат.
2. Изображаем круг. Центр совпадает с центром системы координат. Рекомендуется выбирать за длину радиуса 4, 6 или 8 клеточек в зависимости от того, какого размера надо нарисовать круг.
3. Ставим точку отсчёта 0 для измерения углов.
4. Затем изобразим угол: одну сторону зафиксируем на горизонтальной оси, а другая останется свободной и сможет крутиться, куда вздумает, как на шарнире.
5. Теперь мысленно вращаем незакреплённую сторону. Пусть она вращается против часовой стрелки. Вот она совершила полный оборот и вернулась на своё место. Визуально угол остался прежним, но на самом деле к нему добавился полный оборот, то есть 360°.
6. Учитывая полные обороты, каждый угол можно представить, как
α + 360° ∙ n,
где n – целое число.
Вращение против часовой стрелки – это положительное
направление, а по часовой – отрицательное.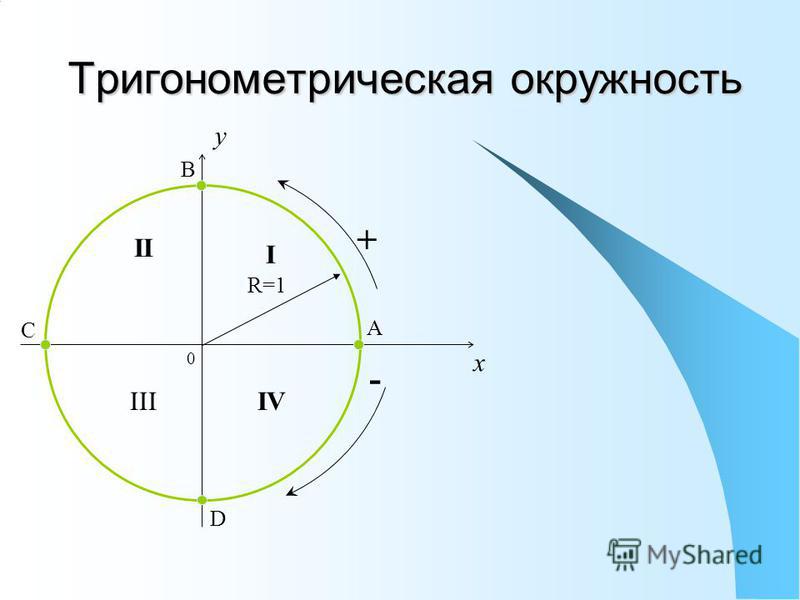
Как отсчитываются углы на круге
Сначала нарисуем тригонометрический круг.
На данном рисунке отмечены номера четвертей (или квадрантов)
I, II, III, IV.
Четверти всегда нумеруются против часовой стрелки. Также добавлены цифры
0°, 90°, 180°, 270°, 360°
на осях. Это значения углов, отсчитанные от неподвижной стороны, которые попадают на координатные оси.
Из рисунка видно, что:
– если угол от 0° до 90°, то он принадлежит I четверти;
– если угол от 90° до 180°, то он принадлежит II четверти;
– если угол от 180° до 270°, то он принадлежит III четверти;
– если угол от 270° до 360°, то он принадлежит IV четверти.
Это для положительных углов.
Неподвижная сторона угла всегда привязана к положительной полуоси Ох. Любой угол в тригонометрии отсчитывается от этой
полуоси. Это базовое начало отсчёта углов.
Также на рисунке добавлена красная стрелочка с плюсом. Что же означает эта стрелочка ?
Если угол мы будем крутить по стрелочки с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным.
ПРИМЕР:
На рисунке показан угол +45°
Обратите внимание, что осевые углы
0°, 90°, 180°, 270°, 360°
также отмотаны именно в “плюс”, по красной стрелочке.
А теперь посмотрим на другую картинку.
Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак “минус”.
Из рисунка видно, что:
– если угол от 0° до –90°, то он принадлежит IV четверти;
– если угол от –90° до –180°, то он принадлежит III четверти;
– если угол от –180° до –270°, то он принадлежит II четверти;
– если угол от –270° до –360°, то он
принадлежит I четверти.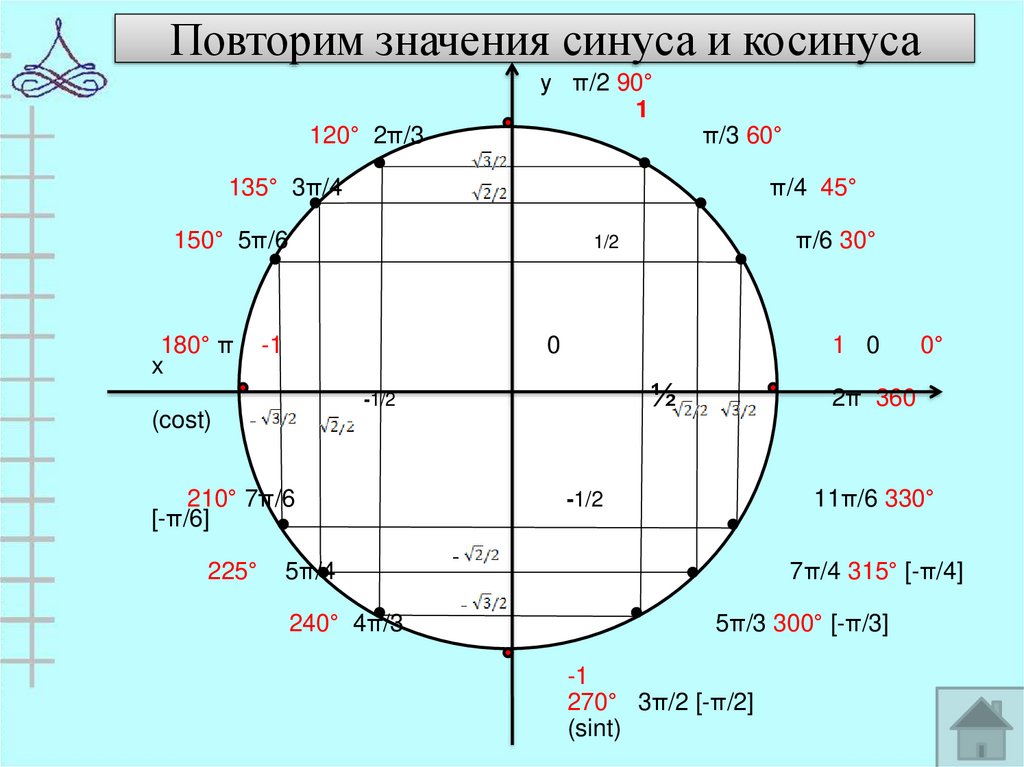
Это для отрицательных углов.
Отсчёт угла ведётся строго от нуля против часовой стрелки, если угол положительный, и по часовой стрелке – если угол отрицательный.
Ещё нарисована синяя стрелочка. Также с минусом. Это стрелочка – направление отрицательного отсчёта углов на круге. Она показывает, что, если мы будем откладывать угол по ходу часовой стрелки, то угол будет считаться отрицательным.
ПРИМЕР:
На рисунке показан угол –45°.
Помните, что нумерация четвертей никогда не меняется. Неважно, в плюс или минус мы отсчитываем углы. Всегда строго против часовой стрелки.
Начало отсчёта углов – от положительной полуоси Ох. По часовой стрелке – “минус”, против часовой стрелки – “плюс”.
Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Величины углов, лежащих на осях координат
(0°, 90°, 180°, 270°, 360°),
надо запомнить.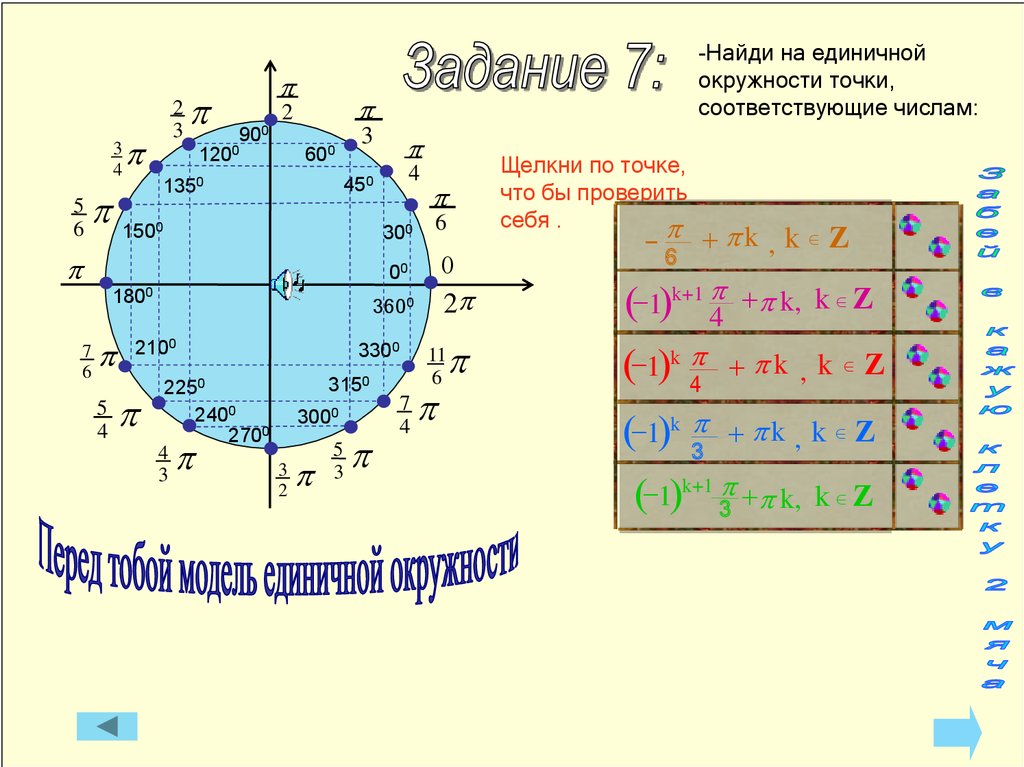 Причём как в плюс, так и в минус.
Причём как в плюс, так и в минус.
Одну и туже точку на круге можно обозначить как положительным углом, так и отрицательным.
ПРИМЕР:
Положительный угол +270° занимает на круге то же самое положение, что и отрицательный угол –90°.
Положительный угол +45° занимает на круге то же самое положение, что и отрицательный угол –315°.
Положительный угол +150° занимает на круге то же самое положение, что и отрицательный угол –210°.
Положительный угол +230° занимает на круге то же самое положение, что и отрицательный угол –130°.
Любую точку на круге можно обозначить как положительным, так и отрицательным углом.
Выбор конкретного направления зависит исключительно от задания.
Из примера мы выяснили, что угол 45° в точности
совпадает с углом –315°. Так как полный
оборот равен 360°, а у нас есть
угол 45°, то определяем,
сколько не хватает до полного оборота.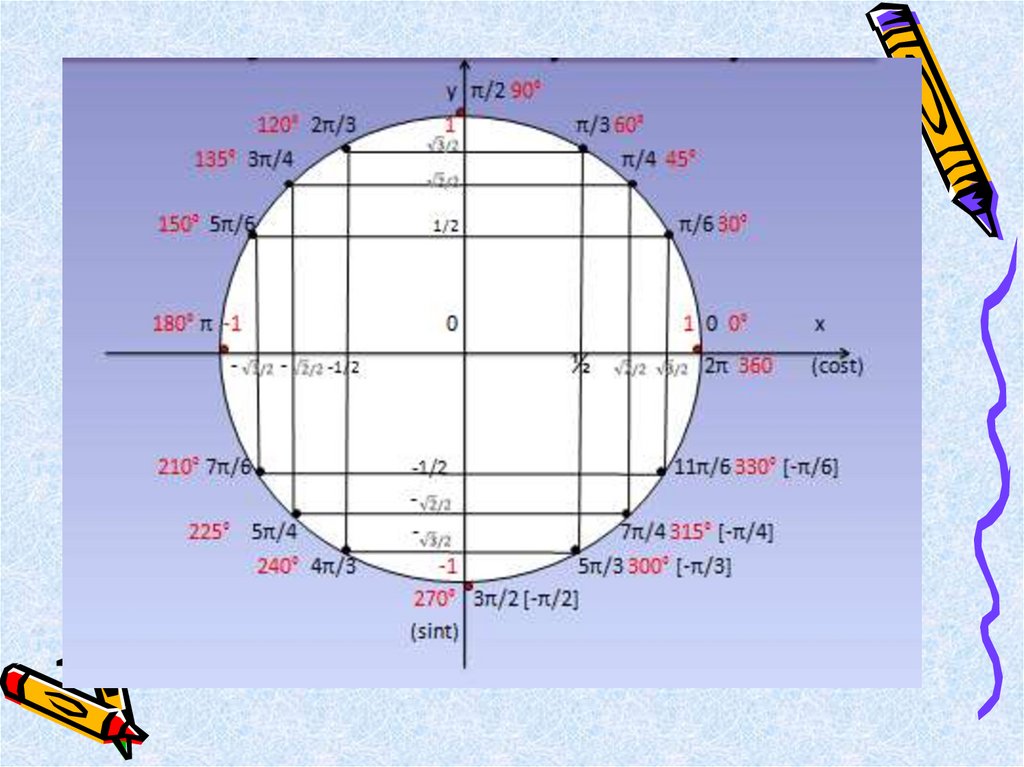 Отнимаем 45° от 360° – вот и получили 315°. Отсчитываем в
отрицательную сторону – и получаем угол –315°.
Отнимаем 45° от 360° – вот и получили 315°. Отсчитываем в
отрицательную сторону – и получаем угол –315°.
Построение углов в пределах одного оборота (между 0° и 360°).
ПРИМЕР:
Нарисуем угол 60°.
РЕШЕНИЕ:
Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично. Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часовой стрелки.
Теперь проводим вторую (подвижную) сторону угла в первой четверти, так как 60° – это строго между 0° и 90°. Рисуем под углом примерно 60° к неподвижной стороне. Как отсчитать примерно 60° без транспортира ? Это две трети от прямого угла.
Делим мысленно первую четверть круга на три
части, забираем себе две трети, и рисуем прямую.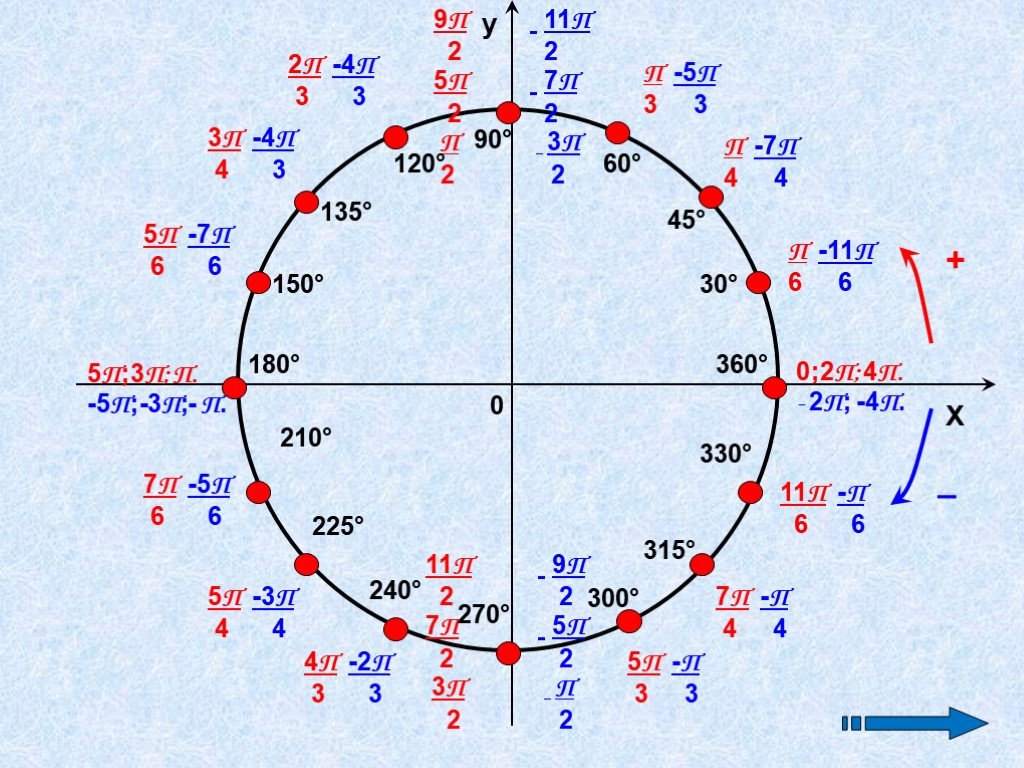 ПРИМЕР:
ПРИМЕР:
Нарисуем угол 265°.
РЕШЕНИЕ:
Прикидываем, где он может располагаться ? Понятно, что не в первой четверти и даже не во второй, так как они на 90° и на 180° оканчиваются. И не в четвёртой четверти, так как она начинается с 270°. Значит угол 265° будет находиться в третьей четверти. Рисуем:
Абсолютная точность здесь не требуется. Пускай в реальности этот угол получится, скажем 263°. Но на самый главный вопрос (какая четверть ?) ответ получили безошибочно.
Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает это угол.
Как нарисовать угол большим за 360° ?
Для правильного рисования таких углов на круге необходимо всё то же самое –
выяснить, в какую четверть попадает интересующий нас угол. Здесь умение
безошибочно определять четверть куда более важно, чем для углов от 0° до 360°.
Здесь умение
безошибочно определять четверть куда более важно, чем для углов от 0° до 360°.
ПРИМЕР:
Надо выяснить в какую четверть попадает угол 444°.
РЕШЕНИЕ:
Так как задан положительный угол, то начинаем двигаться против часовой стрелки от оси Ох. Сделали один оборот – дошли до 360°. Находим сколько градусов осталось до 444°. Считаем оставшийся хвостик:
444° – 360° = 84°.
Итак, 444° – это один полный оборот (360°) плюс ещё 84°. Очевидно это первая четверть. Значит, угол 444° попадает в первую четверть.
Осталось теперь изобразить этот угол. Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.Здесь спиралью показано, как именно складывается угол 444° из углов 360° и 84°.
Пунктирная красная линия – это
один полный оборот, к которому дополнительно присоединяется угол 84° (сплошная
линия).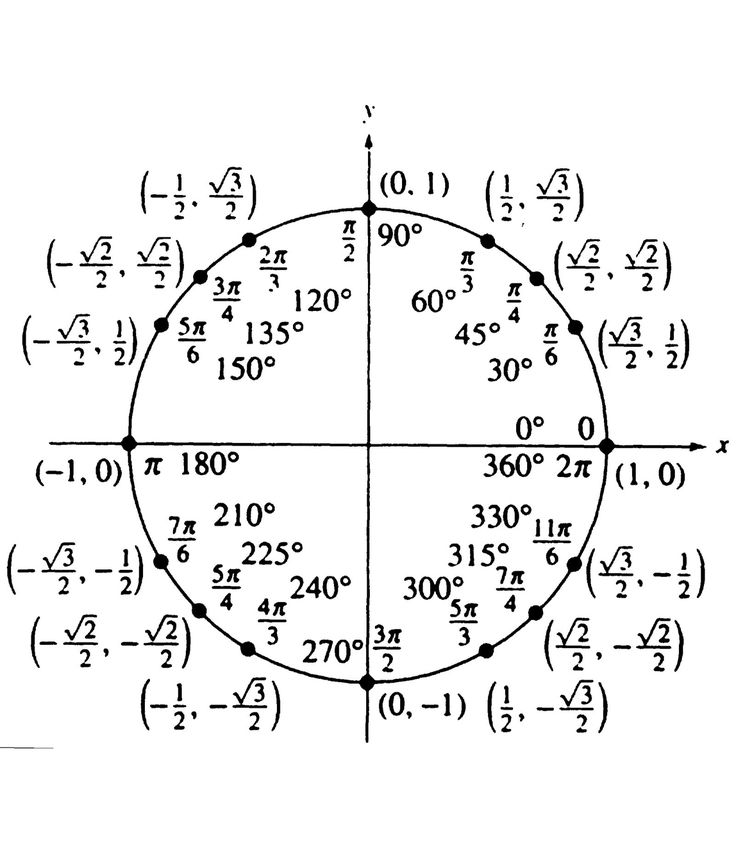 Положение угла 444° полностью совпадает с положением угла 84°.
Положение угла 444° полностью совпадает с положением угла 84°.
Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге не изменится.
ПРИМЕР:
В какую четверть попадает угол 1000° ?
РЕШЕНИЕ:
Считаем, сколько полных оборотов находится в тысяче градусов. Один оборот – это 360°, ещё один – уже 720°, третий – 1080° … Стоп! Перебор! Значит, в угле 1000° находится два полных оборота. Отнимаем их из 1000° и считаем остаток:
1000° – 2 ∙ 360° = 280°.
Значит, положение угла 1000° на круге то же самое, что и у угла 280°. Угол попадает в четвёртую четверть.
Рисуем:
Для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов находится в
заданном большом угле.
ПРИМЕР:
В какую четверть попадает угол 31240° ?
РЕШЕНИЕ:
Поделим угол 31240° на 360°. Получим:
31240° : 360° = 86,777 …
То, что число получилось дробным – не страшно. Нас интересуют только целые обороты.
В угле 31240° находится 86 полных оборотов.
В градусах это будет:
86 ∙ 360° = 30960°.
Производим вычитание и получаем:
31240° – 30960° = 280°.
Угол попадает в четвёртую четверть.
Если задан угол, больше чем 360°, то:
Сначала нужно определить, сколько полных оборотов находится в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.
Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.
Отнимаем эти обороты от исходного угла и работаем с
привычным углом в пределах от 0° до 360°.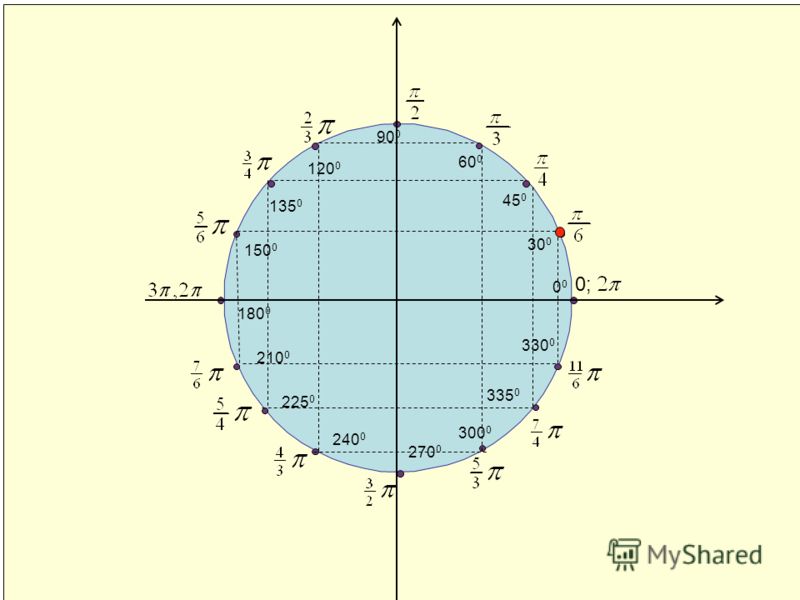
Как работать с отрицательными углами ?
Точно так же, как и с положительными углами, только с одним единственным отличием. Поворачивать углы надо в обратную сторону, в минус. По ходу часовой стрелки.
ПРИМЕР:
Надо нарисовать угол –200°.
РЕШЕНИЕ:
Сначала всё как обычно для положительных углов – оси, круг. Ещё синюю стрелочку с минусом изобразим, да углы на осях по-другому подпишем. Их придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус:
0°, –90°, –180°, –270°, –360°.
Рисунок получится следующий:
Теперь нарисовать правильно
угол –200° никакого труда не составляет. Это –180° и минус ещё 20°. Начинаем вращать от нуля в минус: четвёртую
четверть проходим, третью тоже, доходим до –180°. Дальше продолжаем отсчитывать –20° во второй
четверти по часовой стрелке.
Дальше продолжаем отсчитывать –20° во второй
четверти по часовой стрелке.
Итого: угол –200° попадает
во вторую четверть. Углы на осях координат
(0°, –90°, –180°, –270°, –360°)
надо помнить для того, чтобы безошибочно определять четверть, куда попадает угол.
ПРИМЕР:
В какую четверть попадает угол –2000° ?
РЕШЕНИЕ:
Для начала считаем, сколько полных оборотов находится в этом угле. Поделим 2000 на 360. Получим 5 с остатком. Остаток пока нам не нужен, его позже сосчитаем, когда будем рисовать угол. Считаем пять полных оборотов в градусах:
5 ∙ 360° = 1800°.
Считаем остаток:
2000° – 1800° = 200°.
Остаток будет со знаком минус, так как нам задан отрицательный угол.
Рисуем угол, только уже без лишних оборотов:
Из рисунка видно, что заданный
угол попадает во вторую четверть.
Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак минус на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Мы рассматривали положительные углы, отрицательные углы, большие углы, маленькие углы. Также выяснили, что любую точку на тригонометрическом круге можно обозвать положительным или отрицательным углом, отбрасывали полные обороты. Но какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов, больших и не очень, положительных и отрицательных – всяких. И разница между этими углами будет составлять целое число полных оборотов.
Повороты.
Назовём углом произвольный поворот луча вокруг точки. Разумеется, начальное и
конечное положение луча при повороте образуют как раз ту геометрическую фигуру,
которую мы и раньше называли углом. В этом заключается связь между старым и
новым определениями. Однако, одно и тоже взаимное расположение лучей может быть
достигнуто бесконечным множеством различных поворотов. На чертеже
В этом заключается связь между старым и
новым определениями. Однако, одно и тоже взаимное расположение лучей может быть
достигнуто бесконечным множеством различных поворотов. На чертеже
Отмечено несколько таких поворотов:
I, II, III и IV.
Для того чтобы задать угол, надо задать его вершину О, его стороны ОА и ОВ и отметить тот поворот, который переводит ОА в ОВ.
Таким образом, разные углы могут иметь общими и вершину и стороны. На чертеже
отмечены четыре разных угла I, II, III и IV с общими сторонами ОА, ОВ и общей
вершиной О.
Отметим, что поворот от
первой стороны ОА угла ко второй ОВ может
быть совершен в двух противоположных направлениях. Повороты, производимые в
одном из направлений, совершенно безразлично в каком, условимся называть положительными углами, а тогда повороты,
проводимые в противоположном направлении, – отрицательными
углами. Обычно на чертежах положительными считаются повороты,
совершаемые против часовой стрелки, а отрицательными – повороты, совершаемые по
часовой стрелке.
Обычно на чертежах положительными считаются повороты,
совершаемые против часовой стрелки, а отрицательными – повороты, совершаемые по
часовой стрелке.
Поворот определяется:
а) его центром О,
б) углом поворота α,
в) направлением поворота.
При этом считается, что угол поворота α лежит в границах
0° ≤ α ≤ 180°.
Поворот на 0° – это тоже отображение плоскости:
Е (Х) = Х.
Для любого центра О повороты на 180° в обоих направлениях совпадают и будут центрально симметричными (относительно центра поворота О).
Познакомимся с другой системой задания поворотов, преимущества которой выяснятся постепенно.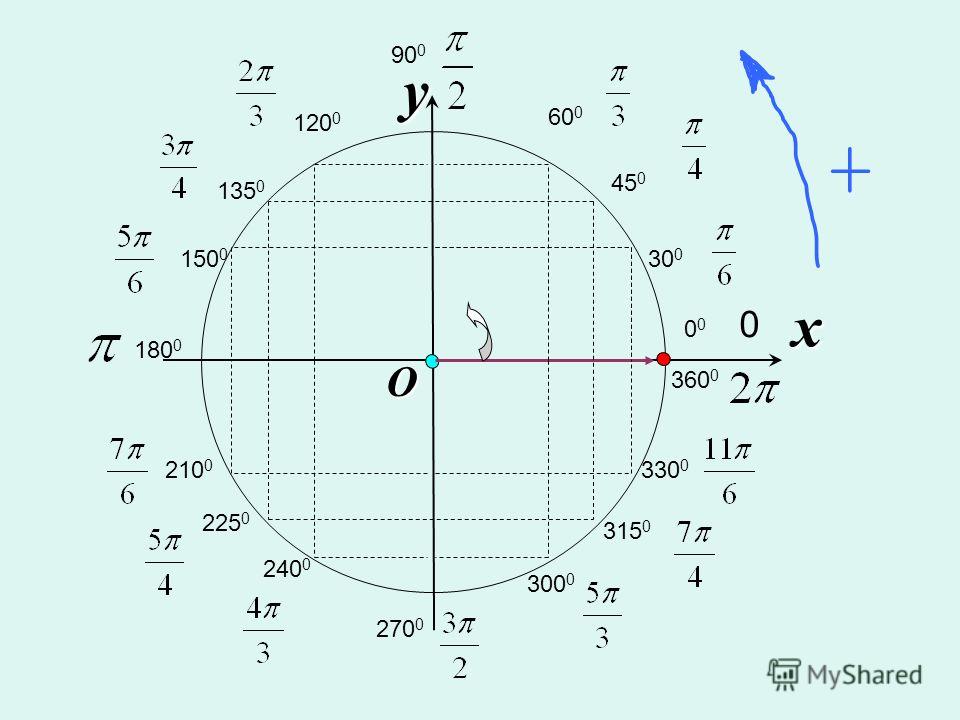
Выберем произвольное направление поворота как положительное, а отрицательным будем считать противоположное ему направление. Положительным обычно считают направление поворота против часовой стрелки.
ПРИМЕР:
Поворот на 70° против часовой стрелки называть будем просто поворотом на 70°, а поворот на 70° по часовой стрелки – поворотом на минус 70°.
При таком условии поворот полностью определяется:
а) его центром О,
б) углом поворота α.
Угол поворота теперь считается направленной величиной, числовое значение которой может быть как положительным, так и отрицательным. Поворот с центром О на угол α обозначают
ПРИМЕР:
Повороты, показанные стрелками на рисунке
обозначаются
Любой поворот можно задать его центром О и углом поворота α, который лежит в границах
–180° ≤ α ≤ 180°.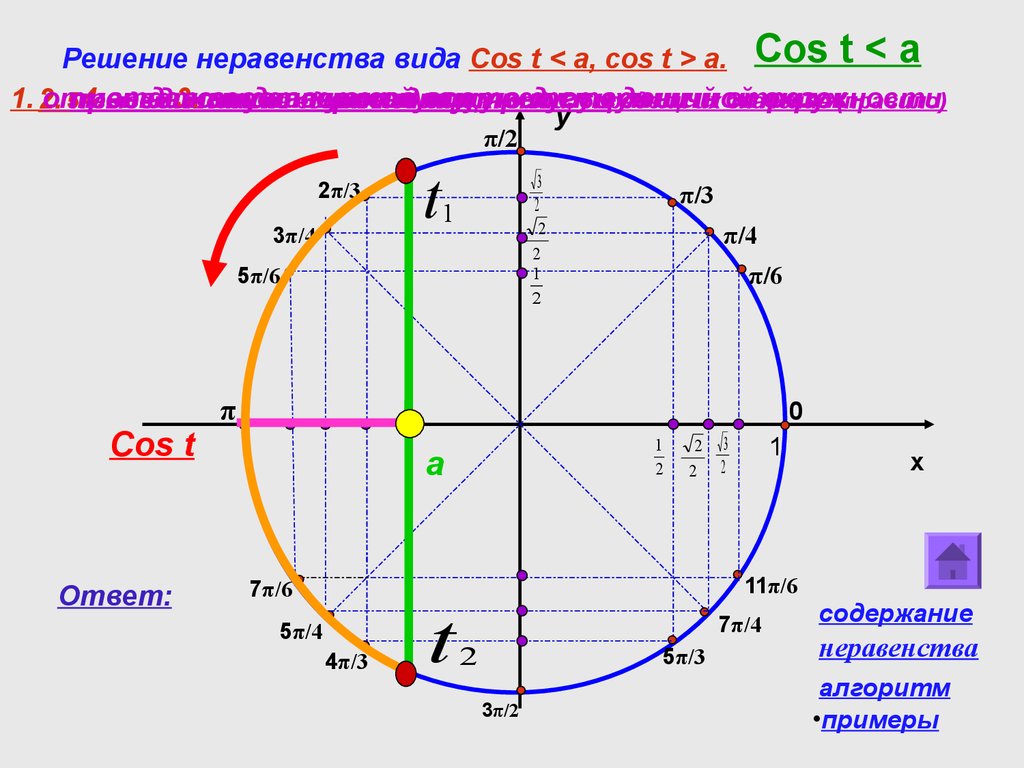
Иногда необходимо рассматривать повороты на углы, которые не лежат в границах
–180° ≤ α ≤ 180°.
ПРИМЕР:
Рисунок объясняет, почему поворот на –90° совпадает с поворотом на +270°.
Рассматривая повороты с каким-нибудь заданным центром, пишем вместо
опуская букву О. Поворот мы представляем как результат вращения. Чтобы наглядно представить себе вращение, положите на лист бумаги лист кальки и проколите оба два листа шпилькою в некоторой точке О. Точка О останется неподвижной, любая другая обозначенная на кальке точка Х будет двигаться по окружности. Если сначала она занимала положение Хо, то после поворота на 270° против часовой стрелки она займёт положение Х1.
Тот же самый результат получим и в случае вращения по часовой стрелке на 90°. Поэтому мы считаем, что записи
Поэтому мы считаем, что записи
будут просто разными обозначения одного и того же самого поворота. Тот же самый поворот можно получить с помощью вращения другими разными способами. В результате вращения на 360° по часовой стрелкой или против часовой стрелки все нанесённые на кальку точки возвращаются на первоначальные места, поэтому поворот
можно получить в результате вращения на такие углы:
–90°; –90° + 360° = 270°;
–90° + 360° × 2 = 630°; … ;
–90° – 360° = –450°;
–90° – 360° × 2 = –810°; … .
Вообще, поворот получается не только вращением на угол α, а и на угол
α + 360° × n,
где n – любое целое число.
Отже, якщо
β = α + 360° × n,
где n целое и
–180° ≤ α ≤ 180°,
то поворотом на угол β называется поворот Rα.
(Повороты на угол α, который лежит в границах
–180° ≤ α ≤ 180°,
были определены раньше).
ПРИМЕР:
R1200⁰ = R120⁰ + 360⁰×3 = R120⁰,
R720⁰ = R360⁰×2 = R0⁰ = Е,
R-1200⁰ = R-120⁰ — 360⁰×3 = R-120⁰.
Задания к уроку 1
Единичный круг — Уроки Wyzant
Автор: ShuJen W.
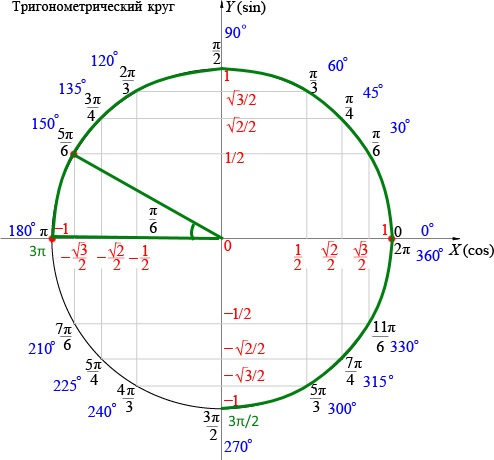
На приведенном выше рисунке представлен график единичного круга на координатной оси X–Y.
Из графика видно, что Единичная окружность определяется как имеющая Радиус ( r ) = 1.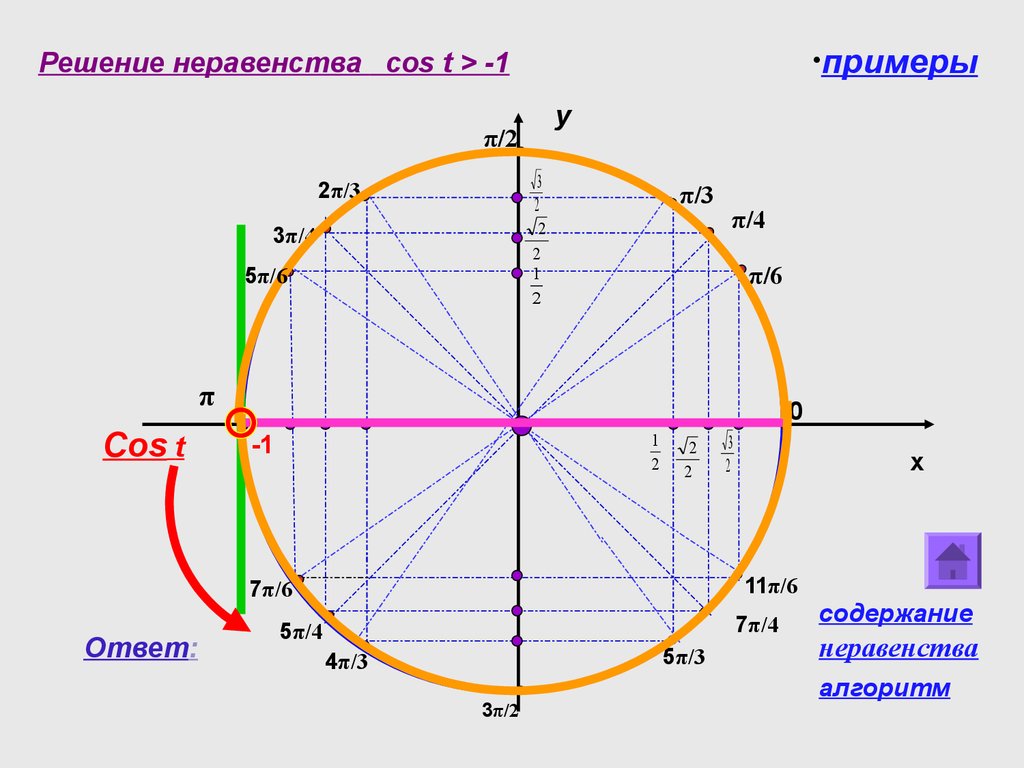
Переходя из квадранта I в квадрант IV против часовой стрелки, координатные точки на оси единичной окружности:
(1, 0), (0, 1), (-1, 0) и (0, -1)
Это важно помнить, когда мы определяем координаты X и Y вокруг единичного круга. Единичный круг имеет 360°. На приведенном выше графике единичный круг разделен на 4 квадранта, которые делят единичный круг на 4 равные части. Каждая часть ровно 90°.
Вопрос: Почему каждая секция/квадрант равна 90°?
Также можно показать, что единичный круг состоит из четырех углов по 90°, что в сумме составляет 360°:
Теперь мы собираемся разделить единичный круг на 30°, 45° и 60°. углы. Это особые углы, и их очень важно помнить.
Начнем с квадранта I, так как это основа, а координаты X и Y положительны. См. ниже.
Затем мы переходим к Квадранту II, который начинается с 90° и продолжается до 180°. На приведенной ниже диаграмме каждый угол в квадранте II составляет 30°, 45° и 60° в пределах этого квадранта. Однако, поскольку точки отсчета углов находятся на отметке 0° в квадранте I, они обозначаются в соответствии с углом, который они образуют из квадранта I в квадрант II. Например, 45° в квадранте II обозначено как 135°, потому что это угол, который он составляет от 0° в квадранте I до угла 45° в квадранте II. Кроме того, из графика видно, что угол 45° в квадранте II находится между 90° и 180° на единичной окружности. Это делается для углов 30°, 45° и 60° в каждом квадранте. См. ниже.
Однако, поскольку точки отсчета углов находятся на отметке 0° в квадранте I, они обозначаются в соответствии с углом, который они образуют из квадранта I в квадрант II. Например, 45° в квадранте II обозначено как 135°, потому что это угол, который он составляет от 0° в квадранте I до угла 45° в квадранте II. Кроме того, из графика видно, что угол 45° в квадранте II находится между 90° и 180° на единичной окружности. Это делается для углов 30°, 45° и 60° в каждом квадранте. См. ниже.
На приведенном ниже графике показаны градусы единичного круга во всех 4 квадрантах от 0° до 360°.
Теперь мы добавим радианы к единичному кругу. Радианы — стандартная единица измерения угла.
Формула для расчета радианов:
Мы рассчитаем радианы для каждого градуса на единичном круге, отмеченном выше.
| Градусов | Формула | Радиан (упрощенный) |
| 0° | (0°)*( π / 180° ) | 0 |
| 30° | (30°)*( π / 180° ) = 30π / 180° радиан | № / 6 |
| 45° | (45°)*( π / 180° ) = 45π / 180° радиан | № / 4 |
| 60° | (60°)*( π / 180° ) = 60π / 180° радиан | № / 3 |
| 90° | (90°)*( π / 180° ) = 90π / 180° радиан | № / 2 |
| 120° | (120°)*( π / 180° ) = 120π / 180° радиан | 2π / 3 |
| 135° | (135°)*( π / 180° ) = 135π / 180° радиан | 3π / 4 |
| 150° | (150°)*( π / 180° ) = 150π / 180° радиан | 5π / 6 |
| 180° | (180°)*( π / 180° ) = 180π / 180° радиан | № / 1 |
| 210° | (210°)*( π / 180° ) = 210π / 180° радиан | 7π / 6 |
| 225° | (225°)*( π / 180° ) = 225π / 180° радиан | 5π / 4 |
| 240° | (240°)*( π / 180° ) = 240π / 180° радиан | 4π / 3 |
| 270° | (270°)*( π / 180° ) = 270π / 180° радиан | 3π / 2 |
| 300° | (300°)*( π / 180° ) = 300π / 180° радиан | 5π / 3 |
| 315° | (315°)*( π / 180° ) = 315π / 180° радиан | 7π / 4 |
| 330° | (330°)*( π / 180° ) = 330π / 180° радиан | 11π / 6 |
| 360° | (360°)*( π / 180° ) = 360π / 180° радиан | 2π / 1 |
На приведенном ниже графике показаны радианы во всех 4 квадрантах с соответствующими углами.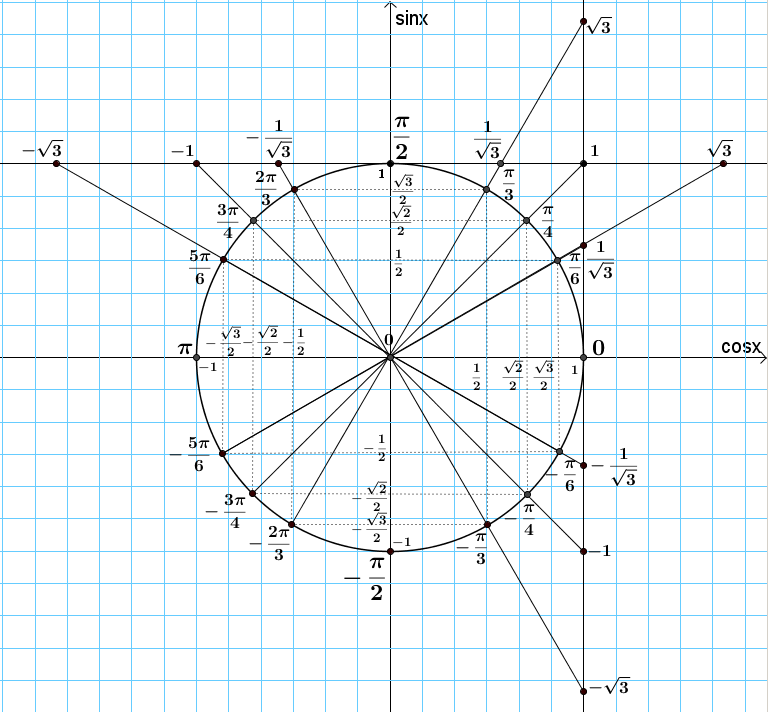 В этой статье объясняется простой способ запоминания точек на единичной окружности.
В этой статье объясняется простой способ запоминания точек на единичной окружности.
Далее мы определим координаты X и Y на единичном круге. Чтобы сделать это, нам нужно понять взаимосвязь Особых Правильных Треугольников 30 – 60 – 9.0 и 45 – 45 – 90 градусов к координатной плоскости. Эти прямоугольные треугольники очень важно помнить, потому что они обладают определенными свойствами, которые пригодятся при решении тригонометрических функций.
Ниже показаны прямоугольные треугольники 30-60-90 и 45-45-90 градусов в квадранте I. Квадрант. Например, на приведенном ниже графике показан прямоугольный треугольник 45-45-90 градусов во всех 4 квадрантах. Обратите внимание, что углы треугольников по-прежнему равны 45° независимо от того, в каком квадранте они находятся, но координаты X и Y меняют знак. Например, обратите внимание, что квадрант III, как X, так и Y отрицательный. Также обратите внимание, что r = радиус окружности = гипотенуза треугольника . Эта информация используется для определения координат X и Y на единичном круге.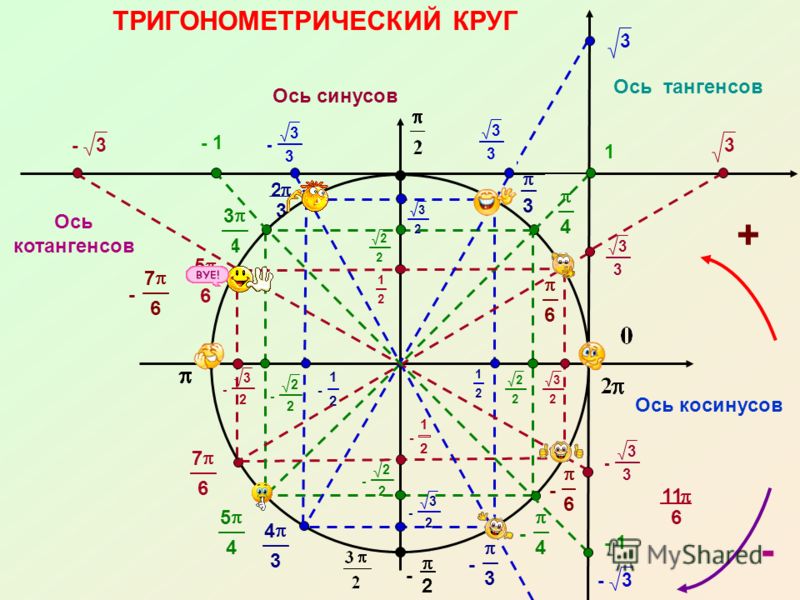
При решении для X, Y или r в треугольнике 90 ° мы можем использовать теорему Пифагора.
X 2 + Y 2 = r 2 (Теорема Пифагора)
Справа теорема Пифагора используется для определения радиуса угла 45°.
Итак, для угла 45° имеем X = 1, Y = 1, и r = √2
Кроме того, X и Y через радиус и угол можно записать как:
X = r*cosΘ и Y = r*sinΘ
Если заданы r и Θ, то можно найти координату X.
Далее мы определим тригонометрические функции:
COSθ ° = x / R = Примыкание / Hipotenus| sinΘ° = Y / r = Напротив / Гипотенуза | tanΘ° = Y / X = Напротив / Смежно | |
| сек°° = r / X = Гипотенуза / Смежный | cscΘ° = r / Y = Гипотенуза / Противоположная | раскладушка Θ° = X / Y = Смежный / Противоположный |
Давайте решаем тригонометрические функции для треугольника 45-45-90 градусов и определить координаты x:
| cosθ ° = X / | ° = X / | ° = x / | ° = x / | . | sinΘ° = Y / r | tanΘ° = Y / X |
| cos45° = 1 / √2 = √2 / 2 | sin45° = 1 / √2 = √2 / 2 | tan45° = Y / X = 1 / 1 = 1 |
После решения для cos45° и sin45° давайте определим точки координат X и Y для единичного круга.
Поскольку X = r*cosΘ, Y = r*sinΘ, и r = 1
Для Θ = 45° , имеем X = 1*cos45° = √2 / 2 и Y = 1*sin45° = √2 / 2
Ниже приведен график для координат X4 и Y ° Угол:
Давайте решаем тригонометрические функции для треугольника 30-60-90 градусов и определить координаты X-Y:
Cosθ ° = x / Cosθ ° = x / R 1 x / R 1 . sinΘ° = Y / r | tanΘ° = Y / X | |
| cos30° = √3 / 2 | sin30° = 1 / 2 | tan30° = 1 / √3 = √3 / 3 |
| cos60° = 1 / 2 | sin60° = √3 / 2 | загар60° = √3 / 1 |
Ниже приведены графики координат X и Y для углов 30° и 60°:
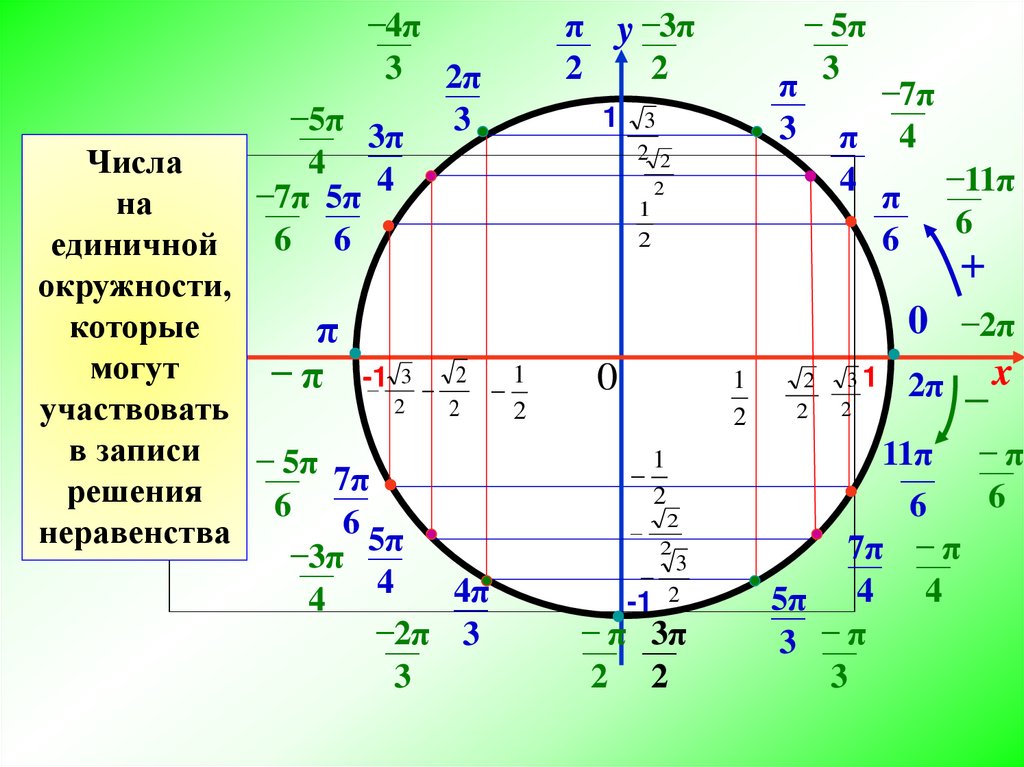
В таблице ниже показаны точки координат X,Y, связанные с градусами на единичной окружности.
| Градусы = Θ | (X,Y) координата | градусов = Θ | (X,Y) координата |
| 0° | (1, 0) | 210° | (- √3 / 2 , – 1 / 2 ) |
| 30° | ( √3 / 2 , 1 / 2 ) | 225° | (- √2 / 2 , – √2 / 2 ) |
| 45° | ( √2 / 2 , √2 / 2 ) | 240° | (- 1 / 2 , – √3 / 2 ) |
| 60° | ( 1 / 2 , √3 / 2 ) | 270° | (0, -1) |
| 90° | (0, 1) | 300° | ( 1 / 2 , – √3 / 2 ) |
| 120° | (- 1 / 2 , √3 / 2 ) | 315° | (- √2 / 2 , – √2 / 2 ) |
| 135° | (- √2 / 2 , √2 / 2 ) | 330° | ( √3 / 2 , – 1 / 2 ) |
| 150° | (- √3 / 2 , 1 / 2 ) | 360° | (1, 0) |
| 180° | (-1, 0) |
Ключевые формулы для запоминания:
x = r*cosθ
y = r*sinθ
на круге единицы, радиус (R) = 1
Pythagorean Theorem: x 2 9007 + y. 2 = r 2
2 = r 2
Особые прямоугольные треугольники:
На приведенном ниже графике показаны координаты X и Y на единичной окружности. Обратите внимание, что в квадранте I обе точки координат X и Y положительны. Однако в квадранте II координата X отрицательна, а координата Y положительна. В квадранте III и X, и Y отрицательны, а в квадранте IV X положителен, но Y отрицательна.
Каков радиус единичной окружности?
A.
√2 / 2
B.
1
C.
√3 / 2
D.
1 / 2
Правильный ответ здесь будет B .
Сколько градусов в единичном круге?
А.
360°
Б.
180°
C.
270°
D.
90°
Правильный ответ здесь будет A .
В каком квадранте находится 135°?
A.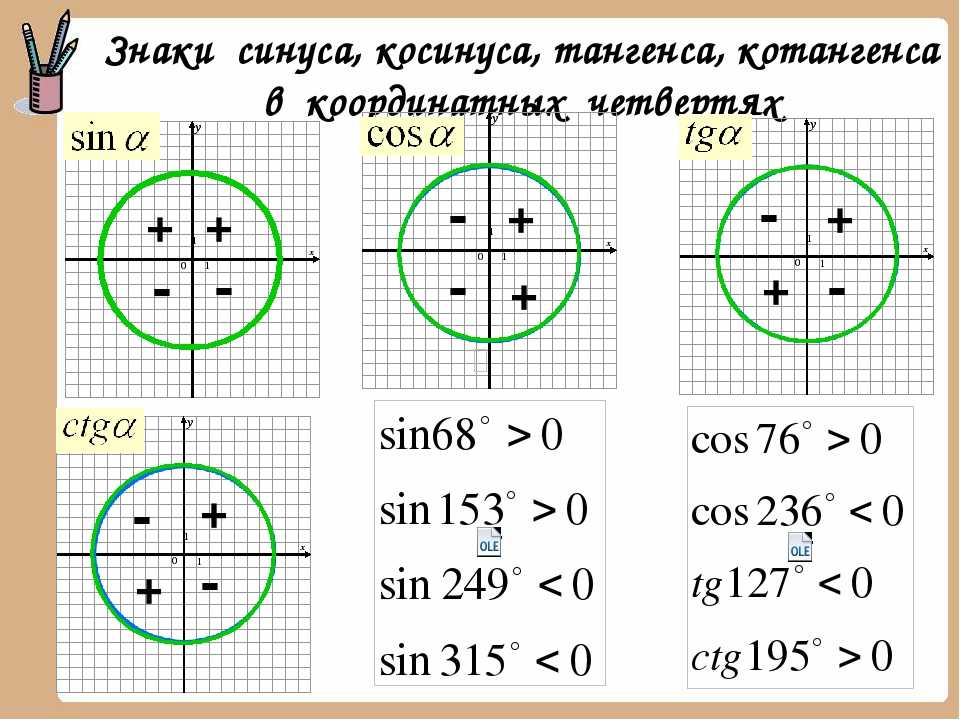
I
B.
II
C.
III
D.
IV
. Правильный ответ здесь будет B .
В каком квадранте находится число 315°?
А.
I
B.
II
C.
III
D.
IV
Правильный ответ здесь будет D .
Чему равен 150° в радианах?
A.
2π / 3
B.
π
C.
5π / 6
D.
3π / 4
Правильный ответ здесь будет С .
Чему равен 240° в радианах?
A.
2π / 3
B.
π
C.
5π / 6
D.
4π / 3
Здесь правильным ответом будет D .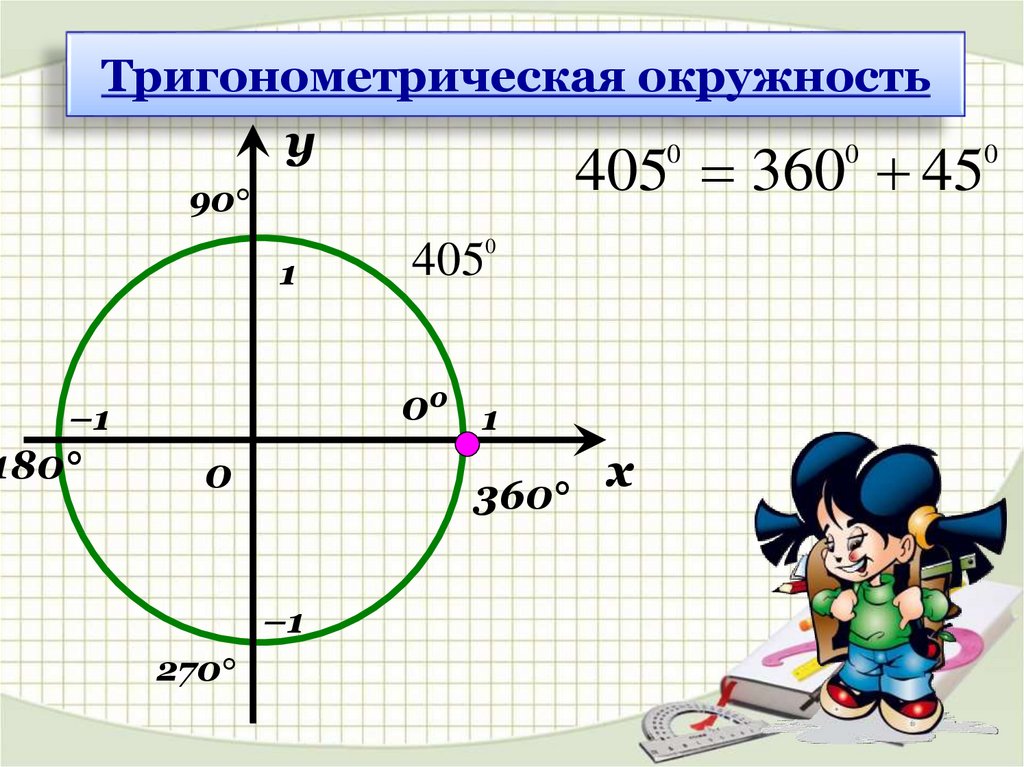
Чему равен 180° в радианах?
А.
2π / 3
B.
π
C.
5π / 6
D.
4π / 3
. Правильный ответ здесь будет 1.
Каковы координаты X, Y угла 45° на единичной окружности?
A.
( √2 / 2 , √2 / 2 )
B.
(- √2 / 2 , 666666666666666667 /667 /667 /667 /67 /67 /67 /7 /67 /67 /67 /67 /67 /7 /7 ( √2 / 2 9009, ( √2 / 2 9009, .0068 2 )
C.
( √2 / 2 , — √2 / 2 )
D.
(0, 1)
. быть А .
Каковы координаты X, Y угла 150° на единичной окружности?
A.
( √3 / 2 , 1 / 2 )
B.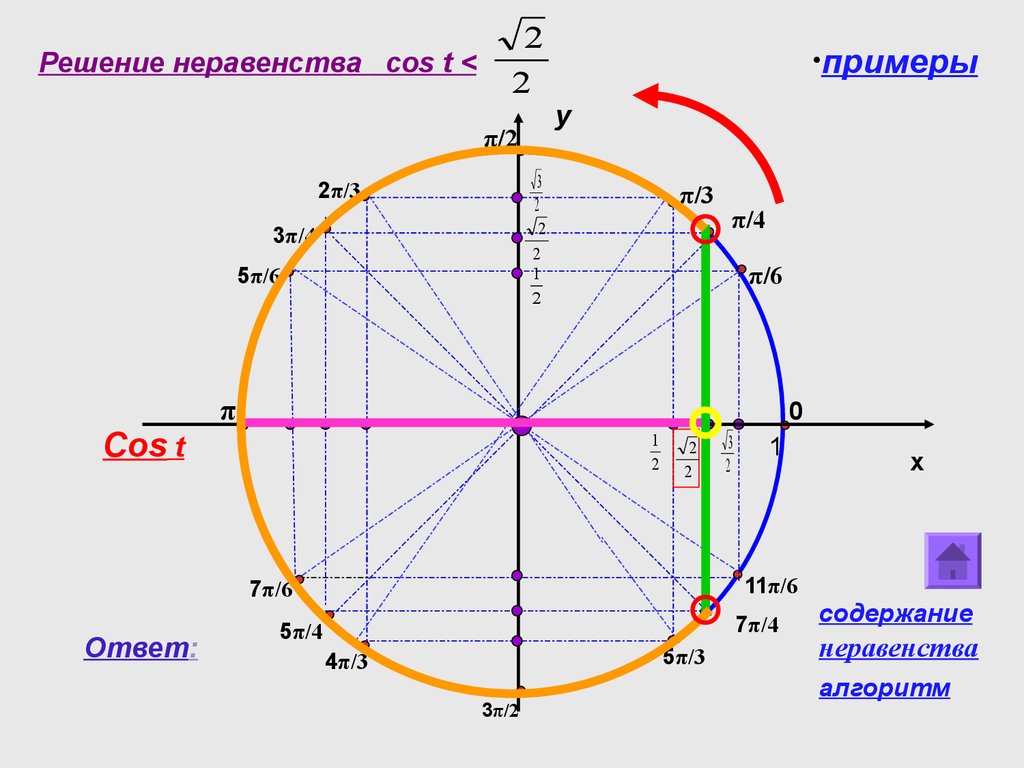
(- a0068 2 )
C.
(- 1 / 2 , √3 / 2 )
D.
(0, 1)
Здесь Б .
Обзор скачка Cuemath | Обучение математике
Cuemath.com Отзывы
Cuemath помогает наладить связь между различными областями математики и реальной жизнью. Это повышает способность ребенка работать и преодолевать все препятствия. Он имеет автономный темп
Определить математическую задачу
Математика — это способ определения взаимосвязей между числами, фигурами и другими математическими объектами.
Скачать полное решение
Наша команда экспертов может предоставить вам комплексное решение, которое поможет вам добиться успеха.

Определить математические уравнения
Чтобы определить математические уравнения, можно использовать различные методы, такие как пробы и ошибки, поиск закономерностей или использование алгебры.
Разберитесь с математическими задачами
Математика — это способ решения задач, требующих точного и точного решения.
Решить математические задачи
Чтобы определить, в чем заключается математическая задача, вам нужно будет внимательно изучить предоставленную информацию и использовать свои навыки решения задач.
 Как только вы определили, в чем проблема, вы можете начать работать над поиском решения.
Как только вы определили, в чем проблема, вы можете начать работать над поиском решения.Выяснить математическое уравнение
Решение математических уравнений может быть интересным и сложным способом провести время.
Обзор продукта Cue Math
Программа Cuemath следует принципу обучения на практике. В Cuemath дети изучают математику, практикуясь самостоятельно. В большинстве школ ваш
Читать отзывы о службе поддержки клиентов cuemath.com
Cue Math не что иное, как афера. Учитель может быть хорошим, это индивидуальный опыт, но сама компания, ее торговые и рекомендательные представители — большие мошенники. Они
831 Специалисты по математике
4,7 Уровень удовлетворенности
61738 Счастливые студенты
Отзывы клиентов
Это действительно помогает, когда я запутался, и объясняет шаги, и с макетом действительно легко работать. Полностью бесплатный, без рекламы и действительно потрясающий продукт. Нет рекламы нет пополнений. Он точен в 100% случаев, если вы используете его правильно.
Полностью бесплатный, без рекламы и действительно потрясающий продукт. Нет рекламы нет пополнений. Он точен в 100% случаев, если вы используете его правильно.
Джордж Бак
Обзор Куэмата
Пробный урок, который мы посетили, был веселым и увлекательным с космической темой и миссиями, которые нужно было выполнить с наклейками, которые хвалили за хорошую работу. После
НЕМЕДЛЕННАЯ ПОМОЩЬ
Если вы чувствуете себя подавленным, помощь доступна круглосуточно и без выходных. Просто протяни руку, и кто-то будет рядом, чтобы поддержать тебя.
Уточнение математических уравнений
Математическое уравнение простое, но все равно сбивает с толку.
Хронометраж
Я всегда засекаю время.
Решить математическое уравнение
Я не могу решать математические уравнения.

 Как только вы определили, в чем проблема, вы можете начать работать над поиском решения.
Как только вы определили, в чем проблема, вы можете начать работать над поиском решения.