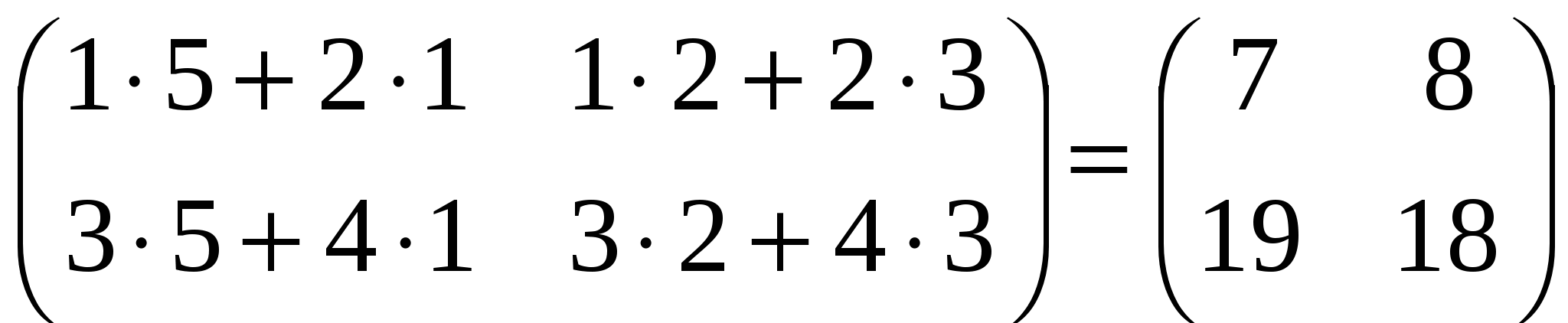Решение модуля 4.7 Поколение Python: для продвинутых
Главная » Ответы на Stepik » Поколение Python: курс для продвинутых
Опубликовано: Рубрика: Поколение Python: курс для продвинутыхАвтор: admin
Представляю вам ответы и решения урока 4.7(Операции над матрицами в математике) на курс «Поколение Python: курс для продвинутых»
Модуль 4.6
Все модули
Модуль 6.1
Найти сумму матриц
2 3 4 6 7 8 10 11 12
Найти произведение матрицы
3 6 9 12 15 18 21 24 27
Одну матрицу можно умножать на другую только тогда, когда
количество столбцов в первой матрице совпадает с количеством строк во второй матрице
Результат умножения матрицы размера Am×n на матрицу размером Bn×k – матрица C с размером
Cm×k
Найти произведение матриц
Примечание.Мы умножаем строку первой матрицы на столбец второй матрицы. Чтобы найти элемент c_{ij}cij результирующей матрицы C = A \times BC=A×B мы умножаем каждый элемент ii-ой строки матрицы AA на соответствующий ему элемент jj-ого столбца матрицы BB и суммируем произведения.
Мы умножаем строку первой матрицы на столбец второй матрицы. Чтобы найти элемент c_{ij}cij результирующей матрицы C = A \times BC=A×B мы умножаем каждый элемент ii-ой строки матрицы AA на соответствующий ему элемент jj-ого столбца матрицы BB и суммируем произведения.12 15 18 24 30 36 36 45 54
Найти произведение матриц
Примечание. Мы умножаем строку первой матрицы на столбец второй матрицы. Чтобы найти элемент c_{ij}cij результирующей матрицы C = A \times BC=A×B мы умножаем каждый элемент ii-ой строки матрицы AA на соответствующий ему элемент jj-ого столбца матрицы BB и суммируем произведения.
-2 -2 1 2
Для матрицы
1 0 100 1
Напишите программу для вычисления суммы двух матриц.
Формат входных данных
Напишите программу для вычисления суммы двух матриц.На вход программе подаются два натуральных числа nn и mm — количество строк и столбцов в матрицах, затем элементы первой матрицы, затем пустая строка, далее следуют элементы второй матрицы.
n, m = [int(i) for i in input().split()]
matrix1 = [[int(i) for i in input().split()] for _ in range(n)]
a = input()
matrix2 = [[int(i) for i in input().split()] for _ in range(n)]
matrix3 = [[0] * m for _ in range(n)]
for i in range(n):
for j in range(m):
matrix3[i][j] += matrix1[i][j] + matrix2[i][j]
for row in matrix3:
print(*row)Напишите программу, которая перемножает две матрицы.
Формат входных данных
На вход программе подаются два натуральных числа nn и mm — количество строк и столбцов в первой матрице, затем элементы первой матрицы, затем пустая строка. Далее следуют числа mm и kk — количество строк и столбцов второй матрицы затем элементы второй матрицы.
n, m = [int(i) for i in input().split()]
a = [[int(j) for j in input().split()] for _ in range(n)]
input()
m, k = [int(i) for i in input().split()]
b = [[int(j) for j in input().split()] for _ in range(m)]
c = [[0] * k for i in range(n)]
for i in range(n):
for j in range(k):
el = 0
for r in range(m):
el += a[i][r] * b[r][j]
c[i][j] = el
for row in c:
print(*row) Напишите программу, которая возводит квадратную матрицу в m-ую степень.
Формат входных данных
На вход программе подаётся натуральное число n — количество строк и столбцов в матрице, затем элементы матрицы, затем натуральное число mm.
n = int(input())
a = [list(map(int, list(input().split()))) for _ in range(n)]
m = int(input())
def multi(a, b):
n = len(a)
b = list(zip(*b))
return [[sum([a[i][r] * b[j][r] for r in range(n)]) for j in range(n)] for i in range(n)]
def expo(a, m):
c = list(a)
for _ in range(m-1):
c = multi(c, a)
return c
result = expo(a, m)
[print(*row) for row in result]7 10 902 просмотров
Понравилась статья? Поделиться с друзьями:
Возведение тензора в дробную степень
mmutic
1
Здравствуйте, мне нужно возвести матрицу в степень -1/2, но я полагаю, что при использовании только **(-1/2) вычисления будут поэлементными.
Например, если я делаю
m = torch.tensor([[.5,.5],[.7,.9]]) напечатать (м ** (-1/2))
я получаю
тензор([[1.4142, 1.4142],
[1.1952, 1.0541]])
9(-1/2). К сожалению, torch.matrix_power() принимает только целые числа, а torch.pow() также выполняет вычисления поэлементно. Спасибо!
математика
(Раджан Паудель)
2
Хотя это и не лучшее решение, но оно будет работать.
scipy будет работать без изменения тензора факела на numpy, например.
импорт scipy.linalg
m = torch.tensor([[.5,.5],[.7,.9]])
print(scipy.linalg.fractional_matrix_power(m, (-1/2)))
массив([[ 2.69776664, -1.10907208],
[-1.55270001, 1.81051025]])
К. Франк
(К. Франк)
3
Привет, ммутик!
ммутик:
Мне нужно возвести матрицу в степень -1/2, но я полагаю, что использование только **(-1/2) делает вычисление поэлементным.
Стандартный подход к возведению матрицы в степень состоит в том, чтобы вычислить ее
собственное разложение, а затем возвести в степень собственные значения. Вот сценарий pytorch версии 0.3.0, который иллюстрирует это:
import torch
печать (факел. __версия__)
m = torch.FloatTensor([[.5,.5],[.7,.9]]) # исходная матрица
# желаемый результат
mres = torch.FloatTensor ([[ 2.69776664, -1.10907208], [-1.55270001, 1.81051025]])
evals, evecs = torch.eig (m, eigenvectors = True) # получить собственное разложение
evals = evals[:, 0] # получить действительную часть (действительных) собственных значений
# восстановить исходную матрицу
mchk = torch.matmul (evecs, torch.matmul (torch.diag (evals), torch.inverse (evecs)))
mchk -m # проверить разложение
evpow = evals**(-1/2) # возведение собственных значений в дробную степень
# построить возведенную в степень матрицу из возведенных в степень собственных значений
mpow = torch.matmul (evecs, torch.matmul (torch.diag (evpow), torch.inverse (evecs)))
mpow - mres # результат проверки
Вот результат:
>>> Импорт факела
>>> распечатать (факел.__версия__)
0.3.0b0+591e73e
>>>
>>> m = torch.FloatTensor([[.5,.5],[.7,.9]]) # исходная матрица
>>>
>>> # желаемый результат
... mres = torch. FloatTensor ([[ 2.69776664, -1.10907208], [-1.55270001, 1.81051025]])
>>>
>>> evals, evecs = torch.eig (m, eigenvectors = True) # получить собственное разложение
>>> evals = evals[:, 0] # получить действительную часть (действительных) собственных значений
>>>
>>> # перестроить исходную матрицу
... mchk = torch.matmul (evecs, torch.matmul (torch.diag (evals), torch.inverse (evecs)))
>>>
>>> mchk - m # проверка разложения
1.00000e-07 *
-0,5960 0,0000
-0,5960 1,1921
[torch.FloatTensor размером 2x2]
>>>
>>> evpow = evals**(-1/2) # возведение собственных значений в дробную степень
> >>
>>> # построить возведенную в степень матрицу из возведенных в степень собственных значений
... mpow = torch.matmul (evecs, torch.matmul (torch.diag (evpow), torch.inverse (evecs)))
>>>
>>> mpow - mres # результат проверки
1.00000e-07 *
4,7684 7,1526
-2,3842 -7,1526
[torch.FloatTensor размером 2x2]
Вы можете видеть, что эта схема восстанавливает ваш результат Matlab (на самом деле
результат scipy мистера математики, потому что он распечатал его с большей точностью
).
Математически это будет работать для положительных полуопределенных (квадратных) матриц
(хотя численно вы, вероятно, захотите, чтобы ваше наименьшее
собственное значение было достаточно больше нуля, чтобы его вычисление не
давало отрицательное значение из-за числовой ошибки).
математика: scipy будет работать без изменения тензора факела на numpy
Однако, если вы хотите использовать autograd для расчета градиентов (например, для обратного распространения
), выполнение вычисления в scipy не будет работать
(если вы не напишете свою собственную функцию .backward() ).
Поскольку подход torch.eig() полностью работает с функциями pytorch tensor
, вы получаете автоградацию/градиенты «бесплатно».
Удачи.
К. Франк
3 лайков
байтСамурай
(Альфред Фельдмейер)
4
Это старый, так что извините, если мой вопрос может быть наивным, но разве это не подходит для вычисления матрицы?
Итак, если я запущу это, я получу тот же результат, что и с scipy:
X.inverse().sqrt()
Я полагаю, это также поддерживает градиенты?
КФранк
(К. Франк)
5
Привет, Альфред!
байтСамурай:
X.inverse().sqrt()
Это неверно. torch.sqrt() вычисляет квадратные корни из
отдельных элементов тензора (не матричный квадратный корень).
( torch.inverse() , однако вычисляет обратную матрицу,
, а не обратные величины отдельных элементов.
__версия__)
m = torch.FloatTensor([[.5,.5],[.7,.9]]) # исходная матрица
# желаемый результат
mres = torch.FloatTensor ([[ 2.69776664, -1.10907208], [-1.55270001, 1.81051025]])
evals, evecs = torch.eig (m, eigenvectors = True) # получить собственное разложение
evals = evals[:, 0] # получить действительную часть (действительных) собственных значений
# восстановить исходную матрицу
mchk = torch.matmul (evecs, torch.matmul (torch.diag (evals), torch.inverse (evecs)))
mchk -m # проверить разложение
evpow = evals**(-1/2) # возведение собственных значений в дробную степень
# построить возведенную в степень матрицу из возведенных в степень собственных значений
mpow = torch.matmul (evecs, torch.matmul (torch.diag (evpow), torch.inverse (evecs)))
mpow - mres # результат проверки
FloatTensor ([[ 2.69776664, -1.10907208], [-1.55270001, 1.81051025]])
>>>
>>> evals, evecs = torch.eig (m, eigenvectors = True) # получить собственное разложение
>>> evals = evals[:, 0] # получить действительную часть (действительных) собственных значений
>>>
>>> # перестроить исходную матрицу
... mchk = torch.matmul (evecs, torch.matmul (torch.diag (evals), torch.inverse (evecs)))
>>>
>>> mchk - m # проверка разложения
1.00000e-07 *
-0,5960 0,0000
-0,5960 1,1921
[torch.FloatTensor размером 2x2]
>>>
>>> evpow = evals**(-1/2) # возведение собственных значений в дробную степень
>
