Тригонометрические уравнения. Задания ЕГЭ по математике (профильный уровень)
Лучшие репетиторы для сдачи ЕГЭ
Математика
Русский язык
История
Тип задания: 13
Тема:
Область допустимых значений (ОДЗ)
Условие
а) Решите уравнение 2(\sin x-\cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку \left[ \frac{3\pi }2;\,3\pi \right].
Показать решение
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 \sin x-2 \cos x-tg x=0. Учитывая, что \cos x \neq 0, слагаемое 2 \sin x можно заменить на 2 tg x \cos x, получим уравнение 1+2 tg x \cos x-2 \cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 \cos x)=0.
1) 1-tg x=0, tg x=1, x=\frac\pi 4+\pi n, n \in \mathbb Z;
2) 1-2 \cos x=0, \cos x=\frac12, x=\pm \frac\pi 3+2\pi n, n \in \mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку \left[ \frac{3\pi }2;\, 3\pi \right].
2+3t-2=0,
t_1=\frac12, t_2=-2, t_2\notin [-1; 1].
\cos 4x=\frac12,
4x=\pm \frac\pi 3+2\pi n,
x=\pm \frac\pi {12}+\frac{\pi n}2, n \in \mathbb Z.
Решим второе уравнение.
tg x=0,\, x=\pi k, k \in \mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1-я и 3-я четверти, в которых tg x>0.
Получим: x=\pi k, k \in \mathbb Z; x=\frac\pi {12}+\pi n, n \in \mathbb Z; x=\frac{5\pi }{12}+\pi m, m \in \mathbb Z.
б) Найдём корни, принадлежащие промежутку \left( 0;\,\frac{3\pi }2\right].
x=\frac\pi {12}, x=\frac{5\pi }{12}; x=\pi ; x=\frac{13\pi }{12}; x=\frac{17\pi }{12}.
Ответ
а) \pi k, k \in \mathbb Z; \frac\pi {12}+\pi n, n \in \mathbb Z; \frac{5\pi }{12}+\pi m, m \in \mathbb Z.
б) \pi; \frac\pi {12}; \frac{5\pi }{12}; \frac{13\pi }{12}; \frac{17\pi }{12}.
Источник: «Математика. Подготовка к ЕГЭ-2017.
2 x+\cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно \cos x, получаем:
(\cos x)_{1,2}=\frac{1\pm\sqrt 9}4=\frac{1\pm3}4. Поэтому либо \cos x=1, либо \cos x=-\frac12. Если \cos x=1, то x=2k\pi , k \in \mathbb Z. Если \cos x=-\frac12, то x=\pm \frac{2\pi }3+2s\pi , s \in \mathbb Z.
Аналогично, решая второе уравнение, получаем либо \cos x=-1, либо \cos x=\frac12.Если \cos x=-1, то корни x=\pi +2m\pi , m \in \mathbb Z. Если \cos x=\frac12, то x=\pm \frac\pi 3+2n\pi , n \in \mathbb Z.
Объединим полученные решения:
x=m\pi , m \in \mathbb Z; x=\pm \frac\pi 3 +s\pi , s \in \mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =\frac{11\pi }3, x_2=4\pi , x_3 =\frac{13\pi }3.
Ответ
а) m\pi, m \in \mathbb Z; \pm \frac\pi 3 +s\pi , s \in \mathbb Z;
б) \frac{11\pi }3, 4\pi , \frac{13\pi }3.
Источник: «Математика.
2 \frac x2=1+\cos x. Получим уравнение: 5(1+\cos x) =\frac{11+5tgx}{1+tgx}.
Заметим, что \frac{11+5tgx}{1+tgx}= \frac{5(1+tgx)+6}{1+tgx}= 5+\frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 \cos x=5 +\frac{6}{1+tgx}. Отсюда \cos x =\frac{\dfrac65}{1+tgx}, \cos x+\sin x =\frac65.
2. Преобразуем \sin x+\cos x по формуле приведения и формуле суммы косинусов: \sin x=\cos \left(\frac\pi 2-x\right), \cos x+\sin x= \cos x+\cos \left(\frac\pi 2-x\right)= 2\cos \frac\pi 4\cos \left(x-\frac\pi 4\right)= \sqrt 2\cos \left( x-\frac\pi 4\right) = \frac65.
Отсюда \cos \left(x-\frac\pi 4\right) =\frac{3\sqrt 2}5. Значит, x-\frac\pi 4= arc\cos \frac{3\sqrt 2}5+2\pi k, k \in \mathbb Z,
или x-\frac\pi 4= -arc\cos \frac{3\sqrt 2}5+2\pi t, t \in \mathbb Z.
Поэтому x=\frac\pi 4+arc\cos \frac{3\sqrt 2}5+2\pi k,k \in \mathbb Z,
или x =\frac\pi 4-arc\cos \frac{3\sqrt 2}5+2\pi t,t \in \mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0.
2=1, значит \frac{3\sqrt 2}5<1.
2. Из неравенств (1) по свойству арккосинуса получаем:
arccos 1<arc\cos \frac{3\sqrt 2}5<arc\cos \frac{\sqrt 2}2,
0<arccos\frac{3\sqrt2}{5}<\frac{\pi}{4}.
Отсюда \frac\pi 4+0<\frac\pi 4+arc\cos \frac{3\sqrt 2}5<\frac\pi 4+\frac\pi 4,
0<\frac\pi 4+arccos \frac{3\sqrt 2}5<\frac\pi 2,
0<a<\frac\pi 2.
Аналогично, -\frac\pi 4<arccos\frac{3\sqrt2}{5}<0,
0=\frac\pi 4-\frac\pi 4<\frac\pi 4-arccos \frac{3\sqrt 2}5< \frac\pi 4<\frac\pi 2,
0<b<\frac\pi 2.
При k=-1 и t=-1 получаем корни уравнения a-2\pi и b-2\pi.
\Bigg( a-2\pi =-\frac74\pi +arccos \frac{3\sqrt 2}5,\, b-2\pi =-\frac74\pi -arccos \frac{3\sqrt 2}5\Bigg). При этом -2\pi <a-2\pi <-\frac{3\pi }2,
-2\pi <b-2\pi <-\frac{3\pi }2. Значит, эти корни принадлежат заданному промежутку \left( -2\pi , -\frac{3\pi }2\right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если k\geqslant 1 и t\geqslant 1, то корни больше 2\pi. Если k\leqslant -2 и t\leqslant -2, то корни меньше -\frac{7\pi }2.
Ответ
а) \frac\pi4\pm arccos\frac{3\sqrt2}5+2\pi k, k\in\mathbb Z;
б) -\frac{7\pi}4\pm arccos\frac{3\sqrt2}5.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 13
Тема:
Область допустимых значений (ОДЗ)
Условие
а) Решите уравнение \sin \left( \frac\pi 2+x\right) =\sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; \pi ];
Показать решение
Решение
а) Преобразуем уравнение:
\cos x =-\sin 2x,
\cos x+2 \sin x \cos x=0,
\cos x(1+2 \sin x)=0,
\cos x=0,
x =\frac\pi 2+\pi n, n \in \mathbb Z;
1+2 \sin x=0,
\sin x=-\frac12,
x=(-1)^{k+1}\cdot \frac\pi 6+\pi k, k \in \mathbb Z.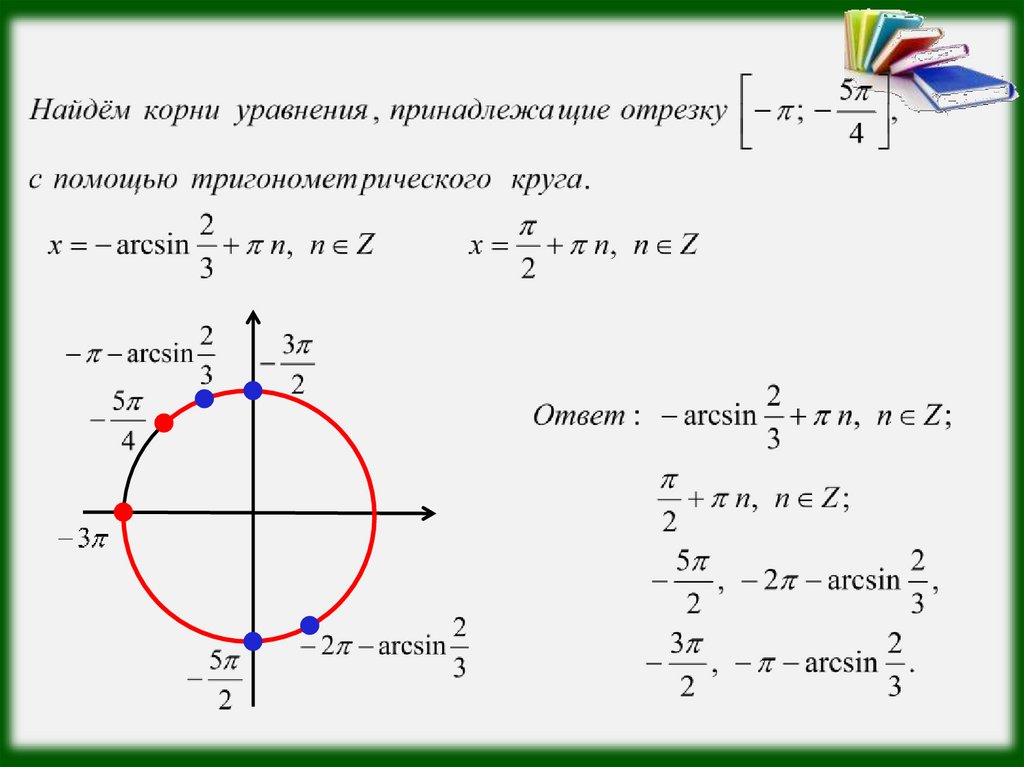
{k+1}\cdot \frac\pi 6+\pi k, k \in \mathbb Z;
б) \frac\pi 2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 13
Тема:
Область допустимых значений (ОДЗ)
Условие
а) Решите уравнение \frac{\sin x-1}{1+\cos 2x}=\frac{\sin x-1}{1+\cos (\pi +x)}.
б) Найдите все корни этого уравнения, принадлежащие отрезку \left[ -\frac{3\pi }{2}; -\frac{\pi }2 \right].
Показать решение
Решение
а) Найдём ОДЗ уравнения: \cos 2x \neq -1, \cos (\pi +x) \neq -1; Отсюда ОДЗ: x \neq \frac \pi 2+\pi k,
k \in \mathbb Z, x \neq 2\pi n, n \in \mathbb Z. Заметим, что при \sin x=1, x=\frac \pi 2+2\pi k, k \in \mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, \sin x \neq 1.
Разделим обе части уравнения на множитель (\sin x-1), отличный от нуля.
2+t-1=0, корни которого t_1=-1 и t_2=\frac12. Возвращаясь к переменной x, получим \cos x = \frac12 или \cos x=-1, откуда x=\frac \pi 3+2\pi m, m \in \mathbb Z, x=-\frac \pi 3+2\pi n, n \in \mathbb Z, x=\pi +2\pi k, k \in \mathbb Z.
б) Решим неравенства
1) -\frac{3\pi }2 \leqslant \frac{\pi }3+2\pi m \leqslant -\frac \pi 2 ,
2) -\frac{3\pi }2 \leqslant -\frac \pi 3+2\pi n \leqslant -\frac \pi {2,}
3) -\frac{3\pi }2 \leqslant \pi+2\pi k \leqslant -\frac \pi 2 , m, n, k \in \mathbb Z.
Решение:
1) -\frac{3\pi }2 \leqslant \frac{\pi }3+2\pi m \leqslant -\frac \pi 2 , -\frac32 \leqslant \frac13+2m \leqslant -\frac12 -\frac{11}6 \leqslant 2m \leqslant -\frac56 , -\frac{11}{12} \leqslant m \leqslant -\frac5{12}.
Нет целых чисел, принадлежащих промежутку \left [-\frac{11}{12};-\frac5{12}\right].
2) -\frac {3\pi} 2 \leqslant -\frac{\pi }3+2\pi n \leqslant -\frac{\pi }{2}, -\frac32 \leqslant -\frac13 +2n \leqslant -\frac12 , -\frac76 \leqslant 2n \leqslant -\frac1{6}, -\frac7{12} \leqslant n \leqslant -\frac1{12}.
2 x-\sin x-1=0.
Решим первое уравнение как квадратное относительно \sin x,
(\sin x)_{1,2}=\frac{-1 \pm \sqrt 9}4=\frac{-1 \pm 3}4. Поэтому либо \sin x=-1, либо \sin x=\frac12. Если \sin x=-1, то x=\frac{3\pi }2+ 2k\pi , k \in \mathbb Z. Если \sin x=\frac12, то либо x=\frac\pi 6 +2s\pi , s \in \mathbb Z, либо x=\frac{5\pi }6+2t\pi , t \in \mathbb Z.
Аналогично, решая второе уравнение, получаем либо \sin x=1, либо \sin x=-\frac12. Тогда x =\frac\pi 2+2m\pi , m \in \mathbb Z, либо x=\frac{-\pi }6 +2n\pi , n \in \mathbb Z, либо x=\frac{-5\pi }6+2p\pi , p \in \mathbb Z.
Объединим полученные решения:
x=\frac\pi 2+m\pi,m\in\mathbb Z; x=\pm\frac\pi 6+s\pi,s \in \mathbb Z.
б) Выберем корни, которые попали в заданный промежуток с помощью числовой окружности.
Получим: x_1 =\frac{7\pi }2, x_2 =\frac{23\pi }6, x_3 =\frac{25\pi }6.
Ответ
а) \frac\pi 2+ m\pi , m \in \mathbb Z; \pm \frac\pi 6 +s\pi , s \in \mathbb Z;
б) \frac{7\pi }2;\,\,\frac{23\pi }6;\,\,\frac{25\pi }6.
{2x}=25, x=1.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку [\log_5 4; \log_5 11]. Заметим, что \log_5 3<\log_5 4<1<\log_5 11, значит, указанному отрезку принадлежит корень x=1.
Ответ
а) 1; \log_5 3;
б) 1.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Тип задания: 13
Тема:
Область допустимых значений (ОДЗ)
Условие
а) Решите уравнение 2\cos x\left( \cos x+\cos \frac{5\pi }4\right) + \cos x+\cos \frac{3\pi }4=0.
б) Найдите все корни этого уравнения, принадлежащие промежутку \left[ \pi ;\,\frac{5\pi }2\right).
Показать решение
Решение
а) Так как \cos \frac{5\pi }4= \cos \left( \pi +\frac\pi 4\right) = -\cos \frac\pi 4= -\frac{\sqrt 2}2 и \cos \frac{3\pi }4= \cos \left( \pi -\frac\pi 4\right) = -\cos \frac\pi 4= -\frac{\sqrt 2}2, то уравнение примет вид: 2\cos x\left( \cos x-\frac{\sqrt 2}2\right) +\cos x-\frac{\sqrt 2}2=0.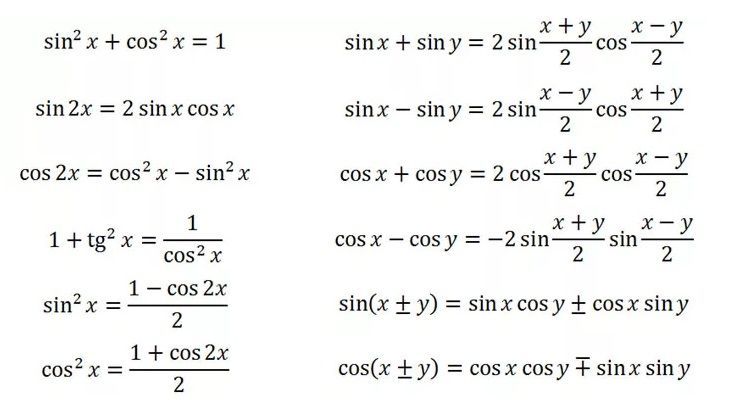
Отсюда (2\cos x+1)\left( \cos x-\frac{\sqrt 2}2\right) =0.
Тогда \cos x=-\frac12; x=\pm\frac{2\pi }3+2\pi n или \cos x=\frac{\sqrt 2}2;\, x=\pm\frac\pi 4+2\pi n, где n \in \mathbb Z.
б) Корни, принадлежащие промежутку \left[ \pi ;\,\frac{5\pi }2\right), найдём с помощью числовой окружности: \frac{4\pi }3;\,\, \frac{7\pi }4;\,\, \frac{9\pi }4.
Ответ
а) \pm\frac{2\pi }3+2\pi n;\,\, \pm\frac\pi 4=2\pi n, n \in \mathbb Z.
б) \frac{4\pi }3;\, \frac{7\pi }4;\, \frac{9\pi }4.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
МатематикаРусский язык
История
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928Структура ЕГЭ-2023 по математике: профильный уровень
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
В первой вас ждут задания с кратким ответом, который вы впоследствии занесете в бланк. Во второй — развернутое решение каждого задания.
ЕГЭ по математике по заданиям
Часть 1
№
Сложность
Формат
Перв. балл
Тема (проверяемые элементы содержания и виды деятельности)
Задание 1
Уровень сложности: низкая
Формат ответа: Краткий
Первич. балл: 1
Геометрические фигуры, координаты и векторы
Задание 2
Уровень сложности: низкая
Формат ответа: Краткий
Первич. балл: 1
Геометрические фигуры, координаты и векторы
Задание 3
Уровень сложности: низкая
Формат ответа: Краткий
Первич. балл: 1
Простейшие математические модели
Задание 4
Уровень сложности: повышенная
Формат ответа: Краткий
Первич.
балл: 1
Использование приобретённых знаний и умений в практической деятельности и повседневной жизни
Задание 5
Уровень сложности: низкая
Формат ответа: Краткий
Первич. балл: 1
Уравнения и неравенства
Задание 6
Уровень сложности: низкая
Формат ответа: Краткий
Первич. балл: 1
Выполнение вычислений и преобразований
Задание 7
Уровень сложности: низкая
Формат ответа: Краткий
Первич. балл: 1
Действия с функциями
Задание 8
Уровень сложности: повышенная
Формат ответа: Краткий
Первич. балл: 1
Использование приобретённых знаний и умений в практической деятельности и повседневной жизни
Задание 9
Уровень сложности: повышенная
Формат ответа: Краткий
Первич.
балл: 1
Построение и исследование простейших математических моделей
Задание 10
Уровень сложности: повышенная
Формат ответа: Краткий
Первич. балл: 1
Действия с функциями
Задание 11
Уровень сложности: повышенная
Формат ответа: Краткий
Первич. балл: 1
Действия с функциями
Часть 2
№
Сложность
Формат
Перв. балл
Тема
Задание 12
Уровень сложности: повышенная
Формат ответа: Развернутый
Первич. балл: 2
Уравнения, неравенства
Задание 13
Уровень сложности: повышенная
Формат ответа: Развернутый
Первич. балл: 3
Действия с геометрическими фигурами, координатами и векторами
Задание 14
Уровень сложности: повышенная
Формат ответа: Развернутый
Первич.
балл: 2
Уравнения, неравенства
Задание 15
Уровень сложности: повышенная
Формат ответа: Развернутый
Первич. балл: 2
Использование приобретённых знаний и умений в практической деятельности и повседневной жизни
Задание 16
Формат ответа: Развернутый
Первич. балл: 3
Действия с геометрическими фигурами, координатами и векторами
Задание 17
Уровень сложности: высокая
Формат ответа: Развернутый
Первич. балл: 4
Уравнения, неравенства
Задание 18
Уровень сложности: высокая
Формат ответа: Развернутый
Первич. балл: 4
Построение и исследование математических моделей
Примите участие в моем онлайн-классе по тригонометрии | Экзамен
ПРОЙДИТЕ МОЙ ОНЛАЙН-КЛАСС ПО ТРИГОНОМЕТРИИ ДЛЯ МЕНЯ
Тригонометрия является разделом математики .
Все дело в треугольниках. Тригонометрия, без сомнения, является одним из худших предметов, которые могут найти студенты. Но изучение тригонометрии важно для того, чтобы закончить различные курсы и продвинуться в жизни, если вы хотите стать математиком. Студентам-математикам предстоит много работы. Они регулярно получают много домашних заданий.
Вы ищете «Могу ли я заплатить кому-нибудь за мой онлайн-урок по тригонометрии»? , если да, то вы попали в нужное место, так как вы только что нашли одного из самых проверенных и надежных экспертов для работы. Online Class Hero поможет вам в вашем классе тригонометрии.
ЗАПЛАТИТЕ КОМУ-ТО, ЧТОБЫ СДЕЛАЛ ЗА МЕНЯ ЗАДАНИЕ ПО ТРИГОНОМЕТРИИ
Вы застряли между углом и длиной треугольника? Боитесь потерять оценки за задание по тригонометрии?
Герой онлайн-класса — ваш спаситель. Мы можем сделать вашу домашнюю работу по тригонометрии до крайнего срока.
Вы хотите заплатить кому-нибудь за домашнее задание по тригонометрии? Если да, Online Class Hero выполнит домашнее задание по тригонометрии нашими ведущими университетскими экспертами.
ЗАПЛАТИТЕ КОМУ-ТО, ЧТОБЫ СДЕЛАЛ ДЛЯ МЕНЯ МОЁ ТРИГОНОМЕТРИЧЕСКОЕ ЭССЕ
Как можно написать эссе на такую тему, как тригонометрия? Вы должны хорошо знать все концепции тригонометрии. Но студенты часто имеют ограниченные знания. Могу ли я заплатить кому-нибудь, чтобы он сделал за меня эссе по тригонометрии ? Да, ты можешь!
Герой онлайн-класса спас тысячи отстающих учеников, которые буквально ненавидят тригонометрию. Online Class Hero находится на поле уже много лет. У нас есть квалифицированные писатели, которые могут написать для вас эссе по тригонометрии. Просто заплатите, и ваше эссе готово.
ОНЛАЙН-КЛАСС ПО ТРИГОНОМЕТРИИ
ОНЛАЙН-ТРИГОНОМЕТРИЯ ДОМАШНЕЕ ЗАДАНИЕ
ОНЛАЙН-ЭКЗАМЕН ПО ТРИГОНОМЕТРИИ
ПРОЙДИТЕ ДЛЯ МЕНЯ МОЙ ОНЛАЙН-ТЕСТ ПО ТРИГОНОМЕТРИИ
Очень сложно получить полный балл в контрольной по математике. С этим согласны все! Тригонометрия — один из тех предметов, по которым учащимся не хватает знаний, но теперь вы можете получить высшие баллы за тест по тригонометрии.
Вы можете подумать, как это возможно? Могу ли я нанять кого-нибудь для прохождения теста по тригонометрии? Да, можно!
Онлайн-класс Hero имеет лучший преподавательский состав. Мы наняли квалифицированную команду, которая может пройти ваш тест по тригонометрии за вас, и успех гарантирован.
ПРОЙДИТЕ МОЙ ОНЛАЙН ТЕСТ ИЛИ ЭКЗАМЕН ПО ТРИГОНОМЕТРИИ
Вы знаете, что экзамены — одна из самых важных вещей, с которыми приходится сталкиваться студенту в своей жизни, но для многих студентов это неприятно. Когда мы говорим о предмете Тригонометрия, многие находят его чрезвычайно трудным и испытывают давление, чтобы сдать тест или экзамен по этому предмету.
Не волнуйтесь, у Online Class Hero есть отличное качество решений, которые можно рассмотреть с подлинным «Сдайте мой онлайн-экзамен или тест по тригонометрии» услуги онлайн.
Герой онлайн-класса даст вам уверенность в опыте и успешных оценках от дипломированных специалистов.
ЗАПЛАТИТЕ КОМУ-ТО, ЧТОБЫ ВЫПОЛНИЛ МОЮ ТРИГОНОМЕТРИЮ ДИСКУССИИ ДЛЯ МЕНЯ
Учащиеся, которым нужно выполнить разные задания, у которых есть много предметов для изучения и работы в офисе, у них нет времени, чтобы быть в курсе событий на доске обсуждений по тригонометрии . Темы форума по тригонометрии обычно слишком скучны, чтобы не привлекать внимание студентов и не заставлять их участвовать в научных дискуссиях.
Чтобы отслеживать все ваши тематические доски для обсуждения тригонометрии, а также эффективные сеансы связи для них, Online Class Hero может предоставить вам эффективные онлайн-услуги «Заплатите кому-нибудь за использование моих онлайн-досок для обсуждения тригонометрии» .
ЗАПЛАТИТЕ КОМУ-ТО, ЧТОБЫ СДЕЛАЛ МОЙ ЭКЗАМЕН ПО ТРИГОНОМЕТРИИ ДЛЯ МЕНЯ
Каждый студент тригонометрии хочет, чтобы кто-нибудь сдал его экзамен под наблюдением, чтобы они могли хорошо попрактиковаться. Онлайн-класс Герой всегда здесь, чтобы помочь студентам .
Вы ищете кого-то, кто мог бы сдать экзамен по тригонометрии вместо вас? Вы в правильном месте.
Если вам нужен высокоэффективный онлайн-экзамен Proctored от любого поставщика профессиональных услуг на рынке, не забудьте имя Online Class Hero. У них есть надежное программное обеспечение и системы для решения ваших проблем с гарантированным и эффективным экзаменом под наблюдением для вас со 100% результатами.
Блок 8 — Тригонометрия прямоугольного треугольника
Геометрия (период 6) > Раздел 8 — Тригонометрия прямоугольного треугольникаПонедельник 03.06.опубликовано 4 июня 2013 г., 12:01 Гарретом Шорром [ обновлено 4 июня 2013 г., 19:43 ]
Четверг, 23 маяопубликовано 27 мая 2013 г., 12:26 Гарретом Шорром [ обновлено 27 мая 2013 г., 12:31 ]
|
D 
, 10:55 Гарретом Шорром
[
обновлено 14 мая 2013 г., 10:56
]
, 14:12
]
05.