Тригонометрические выражения
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-10-06
Тригонометрические выражения. Друзья! Для вас очередная статья с примерами на вычисление тригонометрических выражений. Примеры довольно простые, большинство из них, при определённом навыке, можно решить устно. Если вы основательно изучили тригонометрию и уяснили все важные и необходимые основы, то с решением не будет никаких трудностей.
Что используется в ходе решения данных выражений: формулы приведения, свойства периодичности тригонометрических функций, свойство чётности нечётности, формулы – синуса и косинуса двойного аргумента и, конечно же, основное тригонометрическое тождество.
Рекомендации:
— если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента;
— если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения.
Последнюю статью с выражениями можно посмотреть здесь (там также использовались формулы функций двойного аргумента).
Формулы периодичности, чётности-нечётности здесь.
Основное тригонометрическое тождество здесь.
Рассмотрим задачи:
17289. Найдите значение выражения
Используем формулу синуса двойного аргумента:
Выражение в числителе «сворачиваем»:
*Второй путь: можно было использовать эту же формулу преобразовав знаменатель.
Ответ: 18
63139. Найдите значение выражения
Для решения этого примера достаточно знать формулу косинуса двойного аргумента:
Преобразуем знаменатель:
Ответ: –22
63229. Найдите значение выражения
В данном случае 63 градуса представляем как разность 900 – 270
Ответ: 33
63763. Найдите значение выражения
Представим 1000 как разность 3600 – 2600, применим свойство периодичности нечётности синуса:
Ответ: –34
63819. Найдите значение выражения
Найдите значение выражения
Используем формулу приведения косинуса. Представим 1530 как разность 1800 – 270:
Ответ: –38
63875. Найдите значение выражения
Используем формулу приведения для тангенса. Представим 1480 как разность 1800 – 320:
Ответ: 22
63929. Найдите значение выражения
Представим 3730 как сумму 3600 + 130, используем свойство периодичности:
Ответ: –20
63985. Найдите значение выражения
Используем формулы приведения:
*Применили формулу тригонометрии:
Ответ: –5
97369. Найдите значение выражения
Применяем формулу синуса двойного аргумента в числителе, и формулу приведения в знаменателе:
Ответ: –40
97967. Найдите значение выражения
Применяем формулу синуса двойного аргумента:
Ответ: –7
64097. Найдите значение выражения
Найдите значение выражения
Используем формулы приведения и основное тригонометрическое тождество:
Ответ: 37
64149. Найдите значение выражения
Используем формулы приведения и основное тригонометрическое тождество:
*Подробнее:
Ответ: –30
64205. Найдите значение выражения
Используем формулу приведения и основное тригонометрическое тождество:
Ответ: 21
63519. Найдите значение выражения
Косинус функция чётная, то есть
Её период равен 2Пn, то есть
Значит
Используем формулу приведения для косинуса:
Ответ: 6
63587. Найдите значение выражения
Период тангенса равен 180 градусам (Пи радиан), функция тангенса нечётная:
Ответ: 132
63651. Найдите значение выражения
Применяем свойство нечётности синуса, выделяем период и используем формулу приведения:
Ответ: 6
26755. Найдите значение выражения
Найдите значение выражения
Посмотреть решение
26756. Найдите значение выражения
Посмотреть решение
26757. Найдите значение выражения
Посмотреть решение
26765. Найдите значение выражения
Посмотреть решение
26766. Найдите значение выражения
Посмотреть решение
26767. Найдите значение выражения
Посмотреть решение
27769. Найдите значение выражения
Посмотреть решение
26770. Найдите значение выражения
Посмотреть решение
77412. Найдите значение выражения
Посмотреть решение
77414. Найдите значение выражения
Посмотреть решение
26772. Найдите значение выражения
Посмотреть решение
26773. Найдите значение выражения
Посмотреть решение
26774. Найдите значение выражения
Найдите значение выражения
Посмотреть решение
26761. Найдите значение выражения
Посмотреть решение
26762. Найдите значение выражения
Посмотреть решение
26763. Найдите значение выражения
Посмотреть решение
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Выражения | ЕГЭ-№6Тригонометрия
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Тест по теме: «Преобразования тригонометрических выражений»
Материал опубликовал
4
#9 класс #Алгебра #Учебно-дидактические материалы #Тест (специальный формат) #Учитель-предметник #Школьное образование
ТЕСТ
по алгебре (9 класс)
Тема: «Преобразования тригонометрических выражений»
Пояснительная записка:
Тестовые задания по теме «Преобразования тригонометрических выражений» предназначены для учащихся 9 класса. Тест можно использовать как КИМ после изучения данной темы, так и при подготовке выпускников основной школы к итоговой аттестации. Тест составлен в двух вариантах. Ключи правильных ответов прикладываются.
Тест можно использовать как КИМ после изучения данной темы, так и при подготовке выпускников основной школы к итоговой аттестации. Тест составлен в двух вариантах. Ключи правильных ответов прикладываются.
Тема: «Преобразования тригонометрических выражений»
Вариант 1
Упростите выражение
cos В) sin2 С) -tg2 D) ctg2 Е) –cos2
Преобразуйте выражение
tg(-)∙cos+sin
-sin В) cos С) -tg D) 1 Е) 0
Упростите выражение
A) B) C) D) E)
Найдите значение выражения
(sin — cos)2+2sin∙cos
A) 1 B) 0 C)-1 E)2 D)1,5
5. Упростите выражение
2; B) 0; C) 1; D) -1; E)
6. Упростите выражение и найдите его значение
, если
A) 0,11; B) 0,49; C) 1; D) 0; E) -0,7
7. Упростите выражение
Упростите выражение
2; B) 0; C) 1; D) -1; E) 4
8. Найти значение выражения
, если
A) 3; B) 5; C) ; D) E)
9. Упростите
A) B) C) D) E)
10. Упростите
A) B) C) D) E)
Тема: «Преобразования тригонометрических выражений»
Вариант 2
1 Упростите выражение
А) cos В) sin С) ctg2 D) tg Е) –ctg2
Преобразуйте выражение
Cos2 *tg2 (-)-1
А) 0 В) cos2 С) sin D) cos Е) -cos2
Упростите выражение
A) B) C) D) E)
Найдите значение выражения
Sin4+ cos 4+2sin2*cos2
A) 1 B)-1 C)2 D) 1.5 Е)-2
5. Упростите выражение
A) — B) 1. 5 C) 1 D) -1 Е) -2
5 C) 1 D) -1 Е) -2
6. Упростите выражение и найдите его значение
, если
A) 0,11; B) 0,49; C) 1; D) 0; E) -0,7
7. Упростите выражение
A) 1; B) 0; C) -1; D) 1; E) 2
8. Найти значение выражения
, если
A) ; B) ; C)1; D) -2 E)
9. Упростите
A) B) C) D) E)
10. Упростите
A) B) C) D) E)
Тест | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
вар 1 | C | E | B | A | C | B | B | E | C | B |
вар 2 | C | B | A | C | B | B | E | C | B |
Опубликовано в группе «В помощь учителю»
Чтобы написать комментарий необходимо авторизоваться.
Упрощение триггерных выражений — Все это
Следующий пост Предыдущий пост
1 ноября 2022 г., 9:43, Dr. Drang
При использовании любой системы компьютерной алгебры наступает момент, когда вы задаетесь вопросом, почему результат, полученный программой, не так прост, как вы могли бы его сделать. рукой. Чтобы научиться пользоваться такой системой, вы должны изучить ее приемы замещения и упрощения.
Довольно часто результаты кажутся более сложными, чем должны быть, потому что вы держите в голове определенные базовые предположения о природе переменных, о которых вы не сообщили программе. 92}\]
, что кажется странным, пока вы не поймете, что оно не знает, что \(r\) является положительным или, по крайней мере, неотрицательным числом. Но если я добавлю это вверху блокнота,
Но если я добавлю это вверху блокнота,
$предположений = r ≥ 0
Mathematica делает то, что я ожидаю, и упрощает корень до \(r\).
Как только я узнал о $Предположениях
Предположения и опции Предположения , я получил больше результатов, чем ожидал от Mathematica. Но я все еще борюсь с тригонометрическими упрощениями. На выходных я вычислял определенный интеграл и получил результат, включающий этот член:ArcTan[Cot[θ]]
Во-первых, я был немного удивлен, увидев котангенс — функцию, которой я не пользовался со времен средней школы (или, может быть, даже средней школы). По какой-то причине математические выводы, которые я видел со времен колледжа, отказались от перевернутых тригонометрических функций — секанса, косеканса и котангенса — в пользу деления на их «обычные» аналоги. Единственное исключение, которое я могу придумать, это формула секущей для эксцентрично нагруженных колонн.
Во всяком случае, должен быть более простой способ выражения арктангенса котангенса угла. Я попробовал первую линию обороны всех, Simplify , и только что получил ArcTan[Cot[θ]] обратно. Затем я попробовал TrigExpand , TrigReduce и TrigFactor без особой надежды на успех, поскольку они направлены на переписывание возможностей триггерных функций и триггерных функций, применяемых к нескольким углам. Я получил то, что ожидал: всего лишь ArcTan[Cot[θ]] .
Мне не пришлось долго думать, чтобы получить упрощенный ответ, который я искал: дополнение \(\theta\). Рассмотрим этот график тангенса (синий) и котангенса (красный) в первом квадранте. 9{-1}(\cot \theta) = \frac{\pi}{2} — \theta\]
Конечно, я не получил этот результат через Mathematica, я получил его путем размышлений.
Я смог использовать Mathematica, чтобы подтвердить этот результат, но это было окольным путем. Я нанес ArcTan[Cot[θ]] на первый квадрант и получил то, что выглядело как красивая прямая линия.
Если это прямая линия, то наклон везде должен быть -1. Для проверки я взял производную:
Да ладно, Mathematica, ты можешь лучше. Я применил к результату TrigFactor и (наконец) получил –1. Точка пересечения с y выглядит так, как будто она находится на π/2, что я подтвердил через
. Я не мог просто подставить 0 вместо θ, потому что котангенс 0 не определен. И мне пришлось использовать ограничение по направлению, потому что ограничение снизу идет к –π/2.
Хотя я попросил Mathematica подтвердить, что ArcTan[Cot[θ]] равно π/2 – θ, я так и не получил от нее самого ответа. Может быть, это потому, что Mathematica думает ArcTan[Cot[θ]] — лучший ответ; скорее всего, это потому, что я не использовал его достаточно долго, чтобы знать его приемы.
-
Физическая проблема, с которой я имел дело, заключалась в том, что угол всегда должен был находиться в первом квадранте — между 0 и π/2 радиана или от 0° до 90°.
 И если вам интересно, да, я включил это ограничение в свою декларацию
И если вам интересно, да, я включил это ограничение в свою декларацию $Assumptions; но это не помогло. ↩
Следующий пост Предыдущий пост
Упрощение тригонометрических выражений с использованием тождеств, пример 1
Упрощение тригонометрических выражений с использованием тождеств, пример 1 | Pearson+ ChannelsRecent Channels
- Trigonometry
Chemistry
- General Chemistry
- Organic Chemistry
- Analytical Chemistry
- Biochemistry
Biology
- General Biology
- Microbiology
- Anatomy & Physiology
- Genetics
- Cell Biology
Math
- College Algebra
- Trigonometry
- Precalculus
Physics
- Physics
Business
- Microeconomics
- Macroeconomics
- Financial Accounting
Социальные науки
- Психология
Начните печатать, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.
Колледж ТригонометрияТригонометрические тождества и уравненияПроверка тригонометрических тождествФундаментальные тригонометрические тождества для проверки тождеств
patrickJMT
61views
Было ли это полезно?
Связанные видео
Сумма и разности идентификации для синуса и косинуса, пример 3
Patrickjmt
153views
Доказание личности — другие примеры, пример 1
Patrickjmt
126Views
0002 Использование идентификаторов с двойным углом для решения уравнений, пример 2
Patrickjmt
139Views
Сумма и разности для синуса и косинуса, пример 2
Patrickjmt
74views
Сумма и дифференцированные идентификаторы, чтобы упростить выражение, пример 1
.patrickJMT
77views
Подтверждение личности, пример 2
patrickJMT
121views
Тригонометрические тождества: как их получить/запомнить – часть 3 из 3
patrickJMT
59views
Using the Sum and Difference Identities for Sine, Cosine and Tangent, Ex 1
patrickJMT
109views
Identities for Sum and Differences of Sine and Cosine, Example 3
patrickJMT
68views
Использование тождеств двойного угла для решения уравнений, пример 30003
94Views
Сумма и разности идентификации для синуса и косинуса, пример 1
Patrickjmt
110views
Полуглатые идентификаторы для оценки тригонометрических выражений, пример 1
Patrickjmt
47wiews
TRIGOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMOMTRITIRITRITRIS. Они — Часть 1 из 30003
Они — Часть 1 из 3000338Views
Сумма и различия.
Полуугольные тождества для вычисления тригонометрических выражений, пример 3
patrickJMT
68views
Доказательство тождества, пример 1
Patrickjmt
41views
Упрощающие тригонометрические выражения с использованием идентификаторов, пример 1
Patrickjmt
61views
Использование двойного угла для уравнений.
85просмотров
Проверка тригонометрических тождеств
Профессор Дэйв объясняет
77просмотров
Проверка тригонометрических идентичностей: фундаментальные идентичности
Mathispower4u
35Views
SUM и DINITION для упрощения выражения, пример 2
Patrickjmt
71views
Упрощающие тригонометрические выражения с использованием идентификационных идентификаторов 3
9000.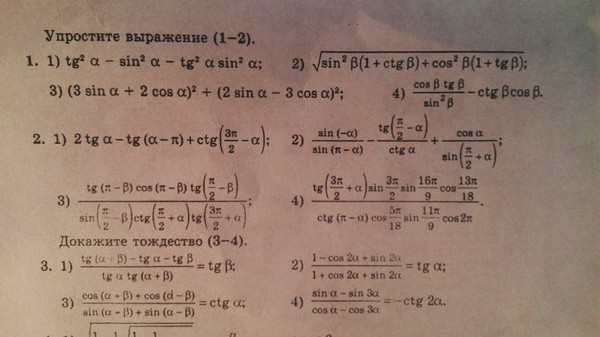


 И если вам интересно, да, я включил это ограничение в свою декларацию
И если вам интересно, да, я включил это ограничение в свою декларацию