Решение задач по механике с использованием тригонометрии, 10 класс
Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа № 34 города Томска
Конспект интегрированного урока по алгебре и физики в 10 классе
«Решение задач по механике с использованием тригонометрии»
Подготовили:
учитель математики
Пихтовникова Светлана Александровна,
Учитель физики
Бурлаков Алексей Дмитриевич
Томск 2010
«Решение задач по механике с использованием тригонометрии»
Интегрированный урок для профильного физико-математического класса.
10 класс.
Пихтовникова Светлана Александровна,
учитель математики
высшей категории,
Бурлаков Алексей Дмитриевич,
Учитель физики
МОУ СОШ № 34 города Томска
Наука начинается тогда,
когда начинают считать.
Д.И.Менделеев
Слеп физик без математики.
М.В.Ломоносов
Рано или поздно всякая
правильная математическая идея
находит применение в том
или ином деле.
А.Н.Крылов
Цель урока:
Закрепление и актуализация, и интеграция знаний по физике и математики.
Задачи урока:
Образовательные задачи:
Закрепить знания обучающихся по теме: «Механика», тригонометрические формулы и решение тригонометрических уравнений;
Продолжить формирования навыков решения задач, формировать умение решать нестандартные задачи
Показать на наглядном примере связь тригонометрии и механики.
Развивающие задачи:
Воспитание учащихся на уроке:
НОТ: обучение умению ставить цель, выделять существенное, главное, планировать работу, осуществлять самоконтроль, подводить итоги, работать в оптимальном темпе, беречь время.

Тип урока: интегрированный урок – практикум.
Оборудование: мультимедийный проектор, ватман, чертежные инструменты, математическая энциклопедия, раздаточный материал.
План урока:
Организационный момент. Вступительное слово учителя
Устная разминка
Работа по группам
Защита работ
Историческая справка
Практическая работа
Итог урока. Заключительное слово учителя.
Ход урока:
1. Вступительное слово учителя. Слайды: 2,3,4
Начало тригонометрии 10 класса.
2. Устно:
1. Вспомним формулы (Слайд 5)
Уравнение скорости:
Найдите сторону х прямоугольного треугольника, изображенных на данных рисунках (Слайды7,8,9,10)
Выберите тригонометрическое уравнение, решения которого включают обе точки, отмеченные на единичной окружности.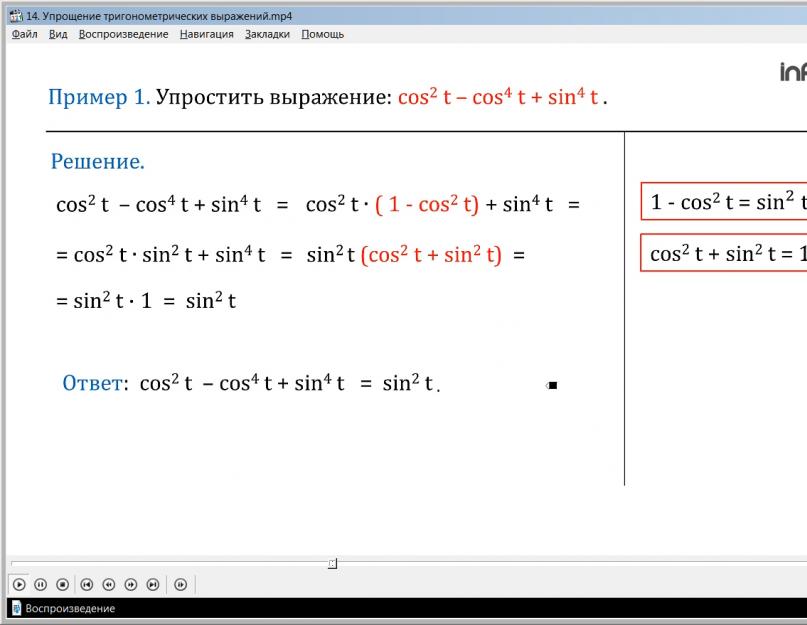 (Слайд 11)
(Слайд 11)
Выберите тригонометрическое уравнение, решения которого включают обе точки, отмеченные на единичной окружности. (Слайд 12)
Выберите тригонометрическое уравнение, решения которого включают обе точки, отмеченные на единичной окружности. (Слайд 13)
3. Работа по группам.
Каждой группе выдаются ватманы, задания, фломастеры, математическая энциклопедия.
Свой отчет о работе учащиеся оформляют на листах ватмана
1 группа (Слайд 14)
1.Под каким углом нужно бросить мяч , чтобы он улетел как можно дальше?
2. в справочнике найдите, что означает тригонометрия
2 группа (Слайд 15)
1. Летящая пуля ударяет в шар висящий на невесомой, нерастяжимой нити, ударяет и застревает в нем.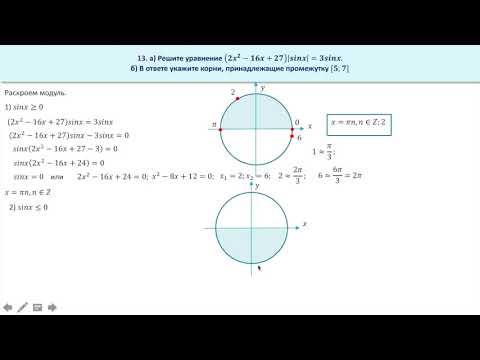 Длина нити 1 м, mпули =9г, mшара= 9 кг, угол на который отклоняется шар с пулей 100. Найти скорость летящей пули.
Длина нити 1 м, mпули =9г, mшара= 9 кг, угол на который отклоняется шар с пулей 100. Найти скорость летящей пули.
2. в справочнике найдите, что означает синус
3 группа (Слайд 16)
1. Найдите коэффициент трения между шариковой ручкой и бумагой.
Оборудование: линейка.
Силой тяжести ручки можно пренебречь.
2. в справочнике найдите, что означает косинус
4 группа.
1. Решите уравнение:
2. в справочнике найдите, что означает тангенс
5 группа.
1. Решите уравнение с параметром а:
2. в справочнике найдите, что означает котангенс
4. Отчет групп сопровождается показом рисунков на экране (слайды 14-17)
Задача 1.
Под каким углом к горизонту нужно бросить мяч, чтобы он упал максимально далеко?
Y
_
А υ
_
υ0 _
g
h
α
O X
l
Движение мяча можно описать в двухмерной системе координат, где движение вдоль оси ОХ – равномерное, а вдоль оси ОY – равноускоренное с ускорением g = 9,8м/с2, tп – время полета,
l — υ0 cos α • tп , дальность полета — максимальная высота полета
в точке А
так как 2 sinα cosα = sin2α l max когда sin 2α = 1 sin 2α = 1; 2α = 90; α = 45, то есть мяч надо бросить под углом 45 к горизонту и дальность полета будет
Задача 2. (Слайд 15)
(Слайд 15)
С какой скоростью υ1 должна лететь пуля, чтобы после абсолютно неупругого удара она отклонила шар, подвешенный на нити, на угол α? Масса пули m1 , масса шара m2, длина нити l ,угол отклонения α.
Закон сохранения импульса для пули и шара в проекциях m1 υ1= (m1 + m2)υ где υ – скорость пули и шара после удара, (1)
Закон сохранения энергии для пули и шара, отклонившихся на угол α после удара, где h – высота подъема пули и шара после удара
h = l – l cosα = l (1—cosα) υ2=2gl(1—cosα) подставляя формулу (1) получаем, используя , получаем
Задача 3.(Слайд 16)
Найдите коэффициент трения между ручкой и бумагой (массой ручки пренебрегите). Укрепитесь в бумагу вертикально поставленной ручкой, а затем постепенно наклоняйте ее, продолжая нажимать на верхний конец. При некотором угле наклона α ручка начнет скользить по бумаге. Это произойдет в тот момент, когда горизонтальная составляющая силы F станет больше максимальной силы трения покоя между ручкой и бумагой.
Укрепитесь в бумагу вертикально поставленной ручкой, а затем постепенно наклоняйте ее, продолжая нажимать на верхний конец. При некотором угле наклона α ручка начнет скользить по бумаге. Это произойдет в тот момент, когда горизонтальная составляющая силы F станет больше максимальной силы трения покоя между ручкой и бумагой.
В момент начала скольжения Fcosα = (mg + Fsinα) где m – масса ручки. = Fcosα /(mg + Fsinα)
Масса ручки невелика, сила F ограничена только возможностями экспериментатора и прочностью ручки, поэтому массой ручки можно пренебречь
5. Немного истории:
«Кто впервые придумал рассматривать изучаемое математическое понятие и зачем?».
Впервые тригонометрические соотношения вводятся в курсе геометрии следующим образом. Рассматривается прямоугольный треугольник (рис. 1), и на уровне определений утверждается: (Слайд18)
В первую очередь нас будут интересовать вопросы: «Откуда появилась необходимость рассматривать представленные выше соотношения сторон прямоугольного треугольника?» и «Как появилась символика, используемая в определениях (*)?».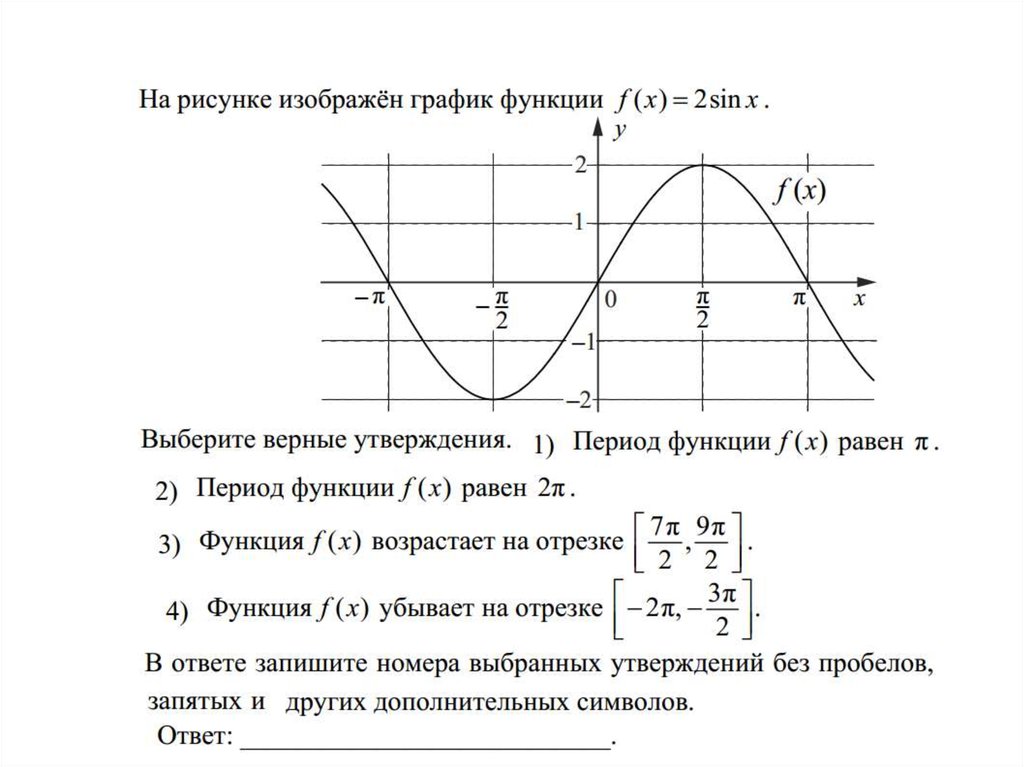
Ключ к отгадке надо искать в практической деятельности людей, причем речь идет о временах настолько далеких (может второе тысячелетие до н.э., а может и ранее), что никакими письменными свидетельствами, позволяющими дать однозначный ответ, мы не располагаем. Поэтому позволим себе высказать некоторые догадки.
В древние времена строительство сооружений велось примерно таким образом и такими средствами, как и сегодня строят небольшие дома и подсобные помещения. При этом строители используют нехитрые инструменты: веревку, отвес, колышки и пр. Между прочим, в Древнем Египте существовали люди специальной профессии, которых называли гарпедонапты, что значит, натягиватели веревки. С них начиналось любое строительство. А зачем нужна веревка строителям? Чтобы ровно в линию выкладывать кирпичи или камни.
Предложим учащимся вслушаться в слова «линия» и «лен». Действительно, откроем этимологический словарь:
Линия. Через посредство немецкого языка заимствовано в начале XVIII в. из латыни. Лат. linea —«нитка» — производное от linum — «лен». Еще веревка нужна для того, чтобы получить прямой угол, например в целях строительства привычного нам четырехугольного дома. Ведь такой дом построить легче всего. А строительство домов иных форм и сейчас является трудной архитектурной задачей.
Через посредство немецкого языка заимствовано в начале XVIII в. из латыни. Лат. linea —«нитка» — производное от linum — «лен». Еще веревка нужна для того, чтобы получить прямой угол, например в целях строительства привычного нам четырехугольного дома. Ведь такой дом построить легче всего. А строительство домов иных форм и сейчас является трудной архитектурной задачей.
Учащиеся уже знают, что одним из важнейших изобретений человечества было изобретение колеса. А почему? Да потому, что в природе колеса нет. Колесо — это именно человеческое изобретение. Теперь другой вопрос: а есть ли в природе прямой угол? Примеры привести можно (ветка, растущая перпендикулярно стволу дерева; само дерево, растущее перпендикулярно к земле и т.п.), но вряд ли перечисленное годится для того, чтобы создать шаблон прямого угла. Издавна строители научились получать прямой угол с помощью веревки. В Древнем Египте заметили, что если на веревке завязать узелки на равном расстоянии друг от друга, и натянуть веревку так, чтобы, говоря современным языком, получался треугольник со сторонами 3, 4, 5, то угол, лежащий против наибольшей стороны, окажется прямым. С тех пор треугольник со сторонами 3, 4, 5 называется египетским.
С тех пор треугольник со сторонами 3, 4, 5 называется египетским.
Треугольник с черными кружками, обозначающими узлы, показан на рис. 2. Этот чертеж лучше всего поясняет суть дела. В вершинах треугольника мы видим древние египетские изображения жрецов. У них в руках — инструменты, напоминающие измерители расстояний, какими пользуются и сейчас. В Древнем Египте измерения были священным делом — уделом немногих образованных людей — жрецов.
Историю с натягиванием веревки продолжают еще несколько древних терминов: катет — значит «отвес», гипотенуза — «натянутая», а другой катет прямоугольного треугольника не назывался катетом (т.е. отвесом), о нем говорили как об основании (рис. 3). (Слайд 19)
По натянутой веревке (другими словами, по гипотенузе) можно проводить стачивание боковой грани строящейся пирамиды.
Теперь мы подошли к главному вопросу: «Как объяснить строителям, по какому углу стачивать грань пирамиды?» (В Древнем Египте пирамиду выкладывали из грубых крупных камней, и надо было ее отшлифовать или иным образом подкорректировать. ) Один из способов: задать отношение высоты пирамиды к апофеме, или, если говорить о плоскости, задать отношение катета-отвеса к гипотенузе. Вот и получается прообраз косинуса угла стачивания (рис. 4). А когда задавались другие отношения — отношение катета-основания к катету-отвесу или отношение катета-основания к гипотенузе — это были прообразы понятий тангенса и синуса угла.
) Один из способов: задать отношение высоты пирамиды к апофеме, или, если говорить о плоскости, задать отношение катета-отвеса к гипотенузе. Вот и получается прообраз косинуса угла стачивания (рис. 4). А когда задавались другие отношения — отношение катета-основания к катету-отвесу или отношение катета-основания к гипотенузе — это были прообразы понятий тангенса и синуса угла.
(Слайд 20)
В самом деле, задавать указанные отношения сторон прямоугольного треугольника очень удобно. Так, если на макете пирамиды (рис. 5, а) определить отношение высоты пирамиды к ее апофеме как 2:3, то и для самой пирамиды (рис. 5, 6) это отношение сохранится, ведь большая пирамида есть подобие маленькой (макета пирамиды). (Слайд 21)
Теперь мы понимаем: рассматривать отношения длин строи прямоугольного треугольника очень удобно, так как для всех подобных прямоугольных треугольников эти отношения сохраняются (все правильно, как потом узнают учащиеся, у подобных треугольников углы равны, а, значит, равны и тригонометрические функции углов).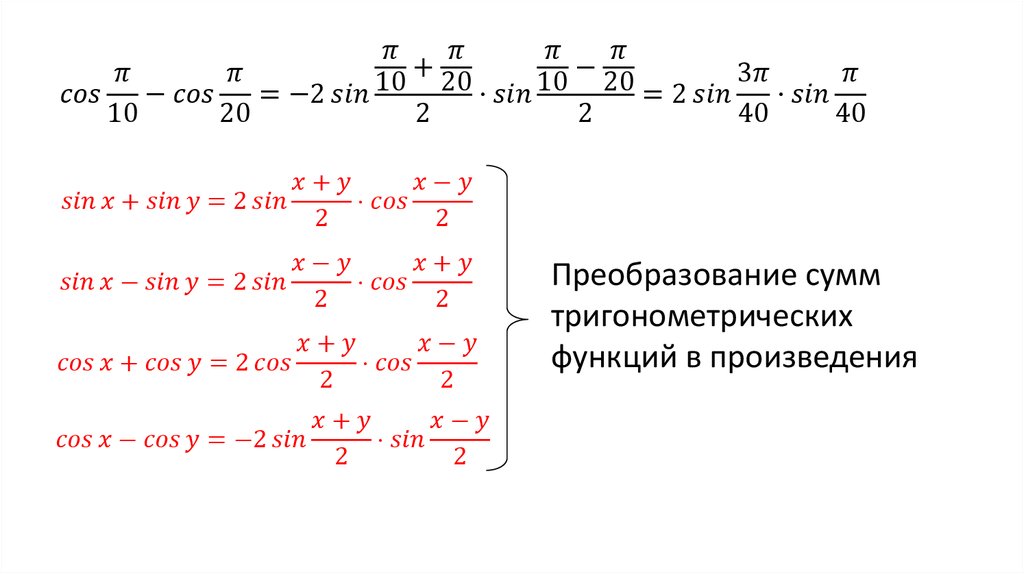
Судя по всему, на идею подобных фигур люди обратили внимание достаточно давно. Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров (своего рода «палетка»).
В дальнейшем геометрические знания накапливались, а тригонометрические соотношения в прямоугольных треугольниках стали все чаще использоваться для решения таких задач практики, как нахождение расстояний до недоступных объектов. Приведем несколько примеров.
Легенда гласит, что Фалес (философ и математик, имя которого уже известно учащимся) привел в изумление египетского царя Амазиса, измерив высоту одной из пирамид по величине отбрасываемой ею тени. Догадка Фалеса заключалась в том, что в течение дня бывает момент, когда длина тени каждого предмета равна высоте самого этого предмета. Он дождался момента, когда длина его тени стала равна его росту, и тогда, измерив тень пирамиды, вычислил ее высоту. Сформулируем другую не менее известную задачу:
Он дождался момента, когда длина его тени стала равна его росту, и тогда, измерив тень пирамиды, вычислил ее высоту. Сформулируем другую не менее известную задачу:
Задача 1. Определить расстояние от корабля, находящегося в море, до берега (Слайд 22)
Решение. Пусть корабль находится в точке К, а наблюдатель — в точке А (рис. 6). Построим прямой угол с вершиной в точке А, откладываем на берегу отрезок АС и делим его пополам точкой В. Затем из точки С передвигаемся по прямой т, перпендикулярной ВС, до тех пор, пока не дойдем до точки D, из которой точки К и В видны лежащими на одной прямой. Отметим полученную точку как D. Прямоугольные треугольники BCD и ВАК равны, следовательно, АК = CD, а длину отрезка CD можно непосредственно измерить.
Решение задач о нахождении расстояний до недоступных объектов, а также задач на вычисление недоступных высот было одним из источников развития тригонометрического знания. К сожалению, на момент рассказа об этом учитель почти ничего не может показать учащимся, так как они еще не изучали подобие треугольников, теоремы синусов и косинусов и пр. Однако позже к этим задачам можно вернуться. Поэтому мы приведем дополнительно еще одну очень известную задачу. Ее текст можно найти в трактате китайского математика III в. Лю Хуэя «Математика морского острова». Несколько странное название трактата объясняется тем, что в нем решены различные задачи на определение расстояний до недоступных объектов, расположенных на острове, причем точка наблюдения находится вне его.
К сожалению, на момент рассказа об этом учитель почти ничего не может показать учащимся, так как они еще не изучали подобие треугольников, теоремы синусов и косинусов и пр. Однако позже к этим задачам можно вернуться. Поэтому мы приведем дополнительно еще одну очень известную задачу. Ее текст можно найти в трактате китайского математика III в. Лю Хуэя «Математика морского острова». Несколько странное название трактата объясняется тем, что в нем решены различные задачи на определение расстояний до недоступных объектов, расположенных на острове, причем точка наблюдения находится вне его.
Задача Лю Хуэя.
Задача 2. Наблюдают недоступный морской остров (рис.).(Слайд 23)
Для этого установили пару шестов MN и KL одинаковой высоты в 6 бу (6 шагов). Предыдущий шест от последующего удален на 1000 бу (Л/А). Пусть последующий шест (АХ) вместе с предыдущим (А/УУ) находится на одной прямой с островом. Если отойти от предыдущего шеста по прямой на 123 бу (МР), то глаз человека, лежащего на земле, будет наблюдать верхний конец шеста совпадающим с вершиной острова
Если отойти от предыдущего шеста по прямой на 123 бу (МР), то глаз человека, лежащего на земле, будет наблюдать верхний конец шеста совпадающим с вершиной острова
Если отойти по прямой от последующего шеста на 127 бу (KQ), то глаз человека, лежащего на земле, будет наблюдать верхний конец шеста также совпадающим с вершиной острова
Какова высота острова (АВ) и его удаленность от первого шеста (AM).
Решение. Рассмотрим две пары подобных треугольников АВР, MNP и ABQ, KLQ. В современных обозначениях запишем:
(*)
где х = AM.
Приравнивая выражения для АВ, найдем
х = 30750 (бу), АВ= 1506 (бу). Заметим, что в выражениях (*) отношение
есть значения тангенсов углов NPM и
LQK, так что в манипулировании с подобными треугольниками уже содержатся предпосылки к переходу к тригонометрическим понятиям.
До сих пор мы рассматривали самую глубинную предысторию зарождения тригонометрического знания, но именно она отразилась в самом слове «тригонометрия», которое буквально означает «измерение треугольника». Действительно, термин тригонометрия состоит из двух греческих слов: тригоном, что означает «треугольник» и метрейн, что означает «измерять». Кроме того, данный первичный исторический рассказ помогает объединить в сознании учащихся такие темы, как знакомство с прямоугольным треугольником, теорема Пифагора, подобие треугольников, тригонометрические соотношения в прямоугольном треугольнике. И главное, у учащихся возникает желание посмотреть на эти темы как с исторической, так и с современной точек зрения, т.е. повышается интерес к изучению геометрии.
Теперь мы перейдем собственно к моменту, когда мы можем обратиться непосредственно к истории тригонометрии. Итак, тригонометрия, как и всякая наука, вырастала из потребностей человеческой практики, поэтому потребности не ограничивались, как мы упоминали выше, только лишь потребностями строительства или нахождения расстояний до недоступных объектов. Задачи мореплавания, требовавшие по звездам определять правильный курс корабля, задачи определения по звездам пути при движении караванов в пустыне, задачи земледелия, требовавшие введения точного календаря, и многие другие обусловили развитие астрономии, а с ней и тригонометрии. Причем сферическая тригонометрия развивалась наряду с плоской.
Задачи мореплавания, требовавшие по звездам определять правильный курс корабля, задачи определения по звездам пути при движении караванов в пустыне, задачи земледелия, требовавшие введения точного календаря, и многие другие обусловили развитие астрономии, а с ней и тригонометрии. Причем сферическая тригонометрия развивалась наряду с плоской.
По сути, тригонометрия появилась в древности как один из разделов астрономии. Дело в том, что преобладающей гипотезой о строении Вселенной была геоцентрическая, согласно которой Земля есть шар, расположенный в центре небесной сферы, которая равномерно вращается вокруг своей оси. Светила считаются расположенными на этой сфере. При изучении их движения большое значение приобретают задачи о расположении точек и фигур на сфере. Работы, в которых подобные задачи решаются, получили название сферики. Плоская тригонометрия при таких условиях отнюдь не играла лишь второстепенную роль по сравнению со сферической тригонометрией.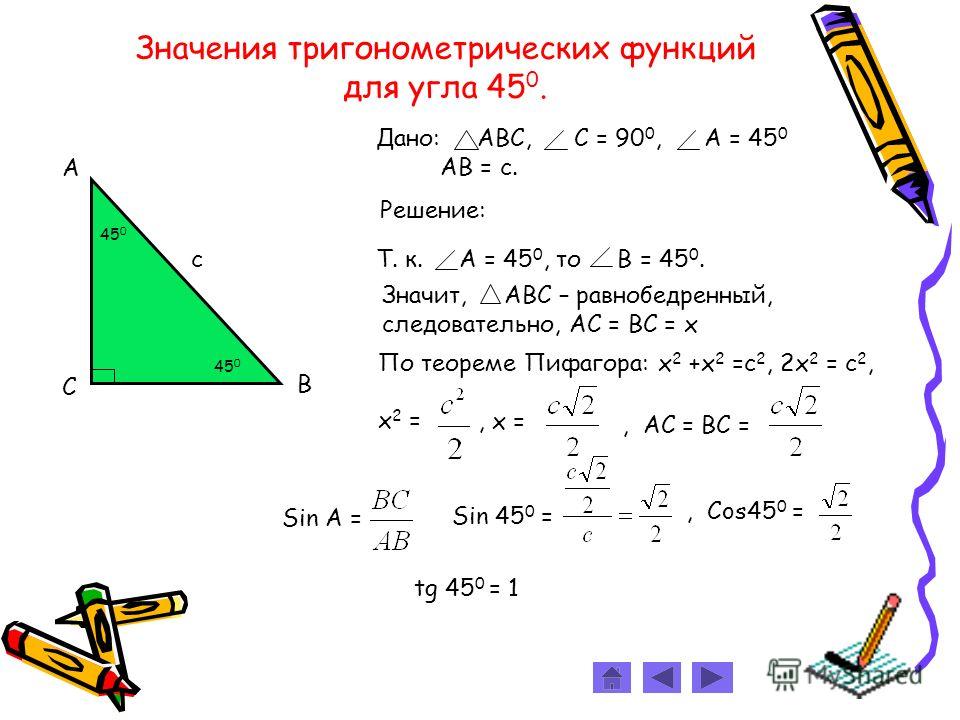 У нее была своя область приложений: помимо решения задач на определение расстояний до недоступных объектов, она являлась частью практической астрономии — фигуры на сфере проектировались на плоскость горизонта, меридиана и т.д., и таким образом многие задачи сводились к плоским случаям.
У нее была своя область приложений: помимо решения задач на определение расстояний до недоступных объектов, она являлась частью практической астрономии — фигуры на сфере проектировались на плоскость горизонта, меридиана и т.д., и таким образом многие задачи сводились к плоским случаям.
Отдельные вопросы из тригонометрии уже успешно решали древнегреческие астрономы, однако они рассматривали хорды, а не синусы, косинусы и другие, как говорили в древности, линии. Если говорить точнее, то греческие астрономы рассматривали по сути только синус, вместо которого использовали хорду, равную удвоенной линии синуса половинной дуги.
Метод составления тригонометрических таблиц состоял в следующем. В основе всех построений астрономов древности находится круг заданного диаметра. На нем рассматривалась единственная тригонометрическая характеристика: длина хорды, стягивающей дугу, соответстствующую данному центральному углу (рис. 8). Задача состояла в составлении таблицы значений этой функции с наибольшей, по возможности, точностью и высокой частотой в последовательности значений аргумента. По существу таблицы хорд являются таблицами синусов.
По существу таблицы хорд являются таблицами синусов.
Первые тригонометрические таблицы (таблицы хорд), которые положили начало вычислительной тригонометрии, составил еще во II в. до н.э. древнегреческий астроном Гиппарх. Венцом же развития астрономии и тригонометрии в Древней Греции можно считать работу «Большое математическое построение астрономии в 13 книгах» («Альмагест») знаменитого астронома Клавдия Птолемея (II в. н.э.). Сведения по прямолинейной и сферической тригонометрии изложены в первой книге «Альмагеста». Показывая, как вычислять хорды, Птолемей делил окружность на 360 частей (градусов). Он составил такую таблицу синусов (хорд), которая много веков была единственным пособием при решении задач о треугольниках.
Начало учению о тригонометрических величинах было положено в Индии, начиная с IV-VI вв. Индийские ученые впервые в науке стали употреблять линию синуса как половину хорды, и составили первые тригонометрические таблицы синусов (полухорд). Им были известны также основное тригонометрическое тождество, формулы приведения, формула синуса половинного угла.
Им были известны также основное тригонометрическое тождество, формулы приведения, формула синуса половинного угла.
Заметим, что греческое слово хорде, от которого происходит наш термин «хорда», буквально означает «тетива лука», «струна». Индийские ученые впервые предложили рассматривать величину полухорды (синуса), которую называли архаджива, что буквально означает «половина тетивы лука», но потом стали называть джива, что значит «тетива лука».
Как по примеру индийских математиков не увидеть на рис. 9 лук с натянутой стрелой?
Арабские математики, которые позже (начиная с VIII в.) осваивали накопленные математические знания, писали слово джива в арабской транскрипции как джиба, что созвучно арабскому слову джайб, которое дословно означает «пазуха».
Вместе с военными завоеваниями арабов слово «пазуха» для обозначения полухорды в тригонометрии попало в Европу (X—XII вв. ), где европейские ученые перевели его на латынь как «синус». Поскольку латинский язык считался общепризнанным научным языком в Европе, то термин «синус» нашел там широкое распостранение и сохранился до настоящего времени. Кстати, этот термин применяется не только в математике: сейчас в медицине заболевание пазух носа называют синуситом. Индийские ученые рассматривали линии синуса BD и косинуса OD (рис. 10) только для острого угла.
), где европейские ученые перевели его на латынь как «синус». Поскольку латинский язык считался общепризнанным научным языком в Европе, то термин «синус» нашел там широкое распостранение и сохранился до настоящего времени. Кстати, этот термин применяется не только в математике: сейчас в медицине заболевание пазух носа называют синуситом. Индийские ученые рассматривали линии синуса BD и косинуса OD (рис. 10) только для острого угла.
Интересно заметить, что европейские математики XII—XVI вв. часто называли синус sinus rectus (прямой синус), а радиус тригонометрической окружности sinus totus, т.е. весь (полный) синус. Слово «косинус» — это сокращение латинского выражения complementy sinus, т.е. «дополнительный синус» или, иначе, «синус дополнительной дуги»; вспомните: cos a = sin (90° — а).
В IX-X вв. центр математических исследований, значит, и центр развития тригонометрического знания, переместился в Среднюю Азию, где трудами арабских математиков тригонометрия впервые выделилась из астрономии как самостоятельная наука. В частности, ученые стран ислама ввели новые тригонометричекие величины: тангенс и котангенс. В трактате «Плоские четырехсторонники» ученого-энциклопедиста и государственного деятеля XIII в. Насирэддина Туей плоская и сферическая тригонометрия выступают как самостоятельные предметы. Для сравнения, в Европе тригонометрия достигла ‘этого уровня, стала успешно развиваться и трактоваться как самостоятельная наука лишь в XV в., и начало этому было положено трудами немецкого астронома и математика, профессора Региомонтана.
В частности, ученые стран ислама ввели новые тригонометричекие величины: тангенс и котангенс. В трактате «Плоские четырехсторонники» ученого-энциклопедиста и государственного деятеля XIII в. Насирэддина Туей плоская и сферическая тригонометрия выступают как самостоятельные предметы. Для сравнения, в Европе тригонометрия достигла ‘этого уровня, стала успешно развиваться и трактоваться как самостоятельная наука лишь в XV в., и начало этому было положено трудами немецкого астронома и математика, профессора Региомонтана.
Понятия «тангенс» и «котангенс», как и первые таблицы этих новых тригонометрических величин, родились не из рассмотрения тригонометрической окружности, а из учения о солнечных часах — гномоники. Солнечные часы первоначально представляли собой шест, вертикально воткнутый в землю (греческое слово гномон — название этого шеста — означает «распознаватель»). Время отсчитывалось подлине и направлению тени, отбрасываемой шестом (рис. 1П.
1П.
Один из современников ал-Хорезми (IX в.)’ математик и астроном Ахмед ал-Мазави, названный «Вычислитель» (ал-Хабаш, ал-Хасиб), занимаясь гномоникой, констатировал, что отношение длины тени и к постоянной длине / гномона солнечных часов меняется в зависимости от высоты Солнца, измеряемой углом (и), соответствующих значениям углов т.е. (в современной символике) u = /ctgq>, или (если учесть, что Эта таблица дала возможность определять высоту Солнца по длине тени. Отношение длины тени к длине шеста определяет высоту солнца над горизонтом (рис. 12, а).
Для случая горизонтального гномона, перпендикулярного к вертикальной стене (рис. 12, ff), ал-Хабаш составил таблицу обращенных теней:
Живший в конце X в. в Багдаде Абу-ль-Вафа в своей «Совершенной книге» — своем «Альмагесте»2 — вводил тригонометрические линии не через прямоугольный треугольник, а с помощью окружности, определяя, например, тангенс как отрезок касательной к окружности. В некоторых местах Абу-ль-Вафа принимал радиус окружности за единицу.
В некоторых местах Абу-ль-Вафа принимал радиус окружности за единицу.
Начиная с XIV—XV вв. центр математических исследований перемещается в Европу. В XIII— XIV вв. при переводе арабских произведений на латинский язык новые тригонометрические функции котангенс и тангенс были названы umbra recta —прямая тень, и umbra versa — обратная тень. Известно, что линию тангенсов уже использовал в своих работах английский математик Томас Брадвар-дин (1290-1349).
Термин tangens (от лат. касающийся [отрезок касательной]) был введен только в 1583 г. датским математиком Томасом Финком в связи с ролью этой линии на тригонометрической окружности. Термин «котангенс» образован по аналогии с термином «косинус», и встречается впервые в 1620 г. у английского ученого Эдмунта Гутера.
В Европе первое сочинение, в котором тригонометрия рассматривалась как самостоятельная математическая дисциплина, написал в 1462—1464 гг. немецкий математик и астроном Региомонтан. Он называл свой труд «Пять книг о треугольниках всех видов». В это время тригонометрия no-прежнему продолжала формироваться и развиваться под определяющим влиянием астрономии. В XV—XVI вв. усовершенствовались таблицы тригонометрических функций, которые были необходимы астрономам, разрабатывались все новые вычислительные приемы3, рассматривались все более сложные задачи решения плоских и сферических треугольников, оттачивалась техника работы с тригонометрическими линиями.
немецкий математик и астроном Региомонтан. Он называл свой труд «Пять книг о треугольниках всех видов». В это время тригонометрия no-прежнему продолжала формироваться и развиваться под определяющим влиянием астрономии. В XV—XVI вв. усовершенствовались таблицы тригонометрических функций, которые были необходимы астрономам, разрабатывались все новые вычислительные приемы3, рассматривались все более сложные задачи решения плоских и сферических треугольников, оттачивалась техника работы с тригонометрическими линиями.
В XVI в. французский математик Франсуа Виет (1540—1603) использовал тригонометрию для решения кубического уравнения. В некоторых его результатах устанавливалась связь между тригонометрией и алгеброй. Кроме того, он положил начало буквенным обозначениям в тригонометрии. Таким образом, на пороге XVII в. в развитии тригонометрии наметилось новое направление — аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур, а учение о тригонометрических функциях строилось на геометрической основе, то развитие нового (аналитического) направления привело к тому, что тригонометрия постепенно стала одной из глав математического анализа. Начало этого преображения тригонометрии связано с именем знаменитого ученого много лет работавшего в Петербурге Леонарда Эйлера (1707—1783). Эйлер усовершенствовал как символику, так и содержание тригонометрии. Перечислим некоторые его нововведения в этой области.
Начало этого преображения тригонометрии связано с именем знаменитого ученого много лет работавшего в Петербурге Леонарда Эйлера (1707—1783). Эйлер усовершенствовал как символику, так и содержание тригонометрии. Перечислим некоторые его нововведения в этой области.
1. До Эйлера совсем редко рассматривались тригонометрические функции дуг, превышающих л. Лишь в его трудах разрабатывается учение о тригонометрических функциях любого аргумента и впервые ясно изложен вопрос о знаках тригонометрических функций в каждом квадранте.
2. В отличие от своих предшественников Эйлер исключил из своих формул R — целый синус (sinus totus), принимая R = 1 и упрощая, таким образом, записи и вычисления.
3. Понимая аргумент тригонометрической функции не только как угол или дугу, а как любую числовую величину, Эйлер впервые стал систематически излагать тригонометрию аналитическим путем. До него каждая тригонометрическая теорема доказывалась отдельно на основании соответствующего каждому случаю геометрического чертежа. Эйлер же выводил теоремы, исходя из небольшого числа основных соотношений.
Эйлер же выводил теоремы, исходя из небольшого числа основных соотношений.
4. Для обозначения тригонометрических функций Эйлер использовал символы sinx, cosx, tangx, cotjf и т.д., а также ввел употребляемые поныне обозначения а, Ь, с для сторон и А, В, С для соответствующих противоположных углов треугольника ABC, что способствовало появлению единой символики в тригонометрии.
5. Эйлер стал рассматривать тригонометрию как науку о тригонометрических функциях и придал ей современный вид.
Таким образом, именно имя Эйлера должен помнить учащийся, который учится работать с тригонометрической окружностью, выводит формулы тригонометрии, учится решать тригонометрические уравнения и неравенства, изучает свойства тригонометрических функций.
В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометрических функциях — является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе. Другая же часть — решение треугольников — рассматривается как глава геометрии.
Другая же часть — решение треугольников — рассматривается как глава геометрии.
Третья часть-это широкое применение в других областях, например, в физике.
6. Практическая работа.
Н айдите коэффициент трения между вашей ручкой и бумагой
7. Итог урока. Задание на дом:
Это хорошо решить!
Решите уравнение:
а) (2х-3)│sin x│=sin x;
б)
2. Как влияет разбег на дальность полета мяча брошенного под углом к горизонту?
Домашнее задание.
Как влияет разбег на дальность полета мяча, брошенного под углом к горизонту? Пусть Δl –увеличение дальности полета за счет разбега. Полагая, что за счет разбега мячу сообщается дополнительная горизонтальная скорость, а вертикальная составляющая практически не меняется, получаем где υ0 – начальная скорость броска, l дальность полета без разбега вся дальность полета будет l+Δl.
Используемая литература:
1. Власова И.Н., Малых А. Е. Очерки по истории элементарной геометрии. (Материалы для спецкурса по геометрии.) — Пермь, 1998.
2. Глейзер Г.И. История математики в школе: VII-VUI кл. — М: Просвещение, 1982.
3. Глейзер Г.И. История математики в школе: IX— X кл. — М.: Просвещение, 1983.
4. Рыбников К.А. История математики: Учебник. — М.: Изд-во МГУ, 1994.
5. Чистяков В.Д. Материалы по истории математики в Китае и Индии. — М.: Учпедгиз, 1960.
6. Мордкович А.Г., П.В. Семенов Алгебра и начала анализа 10 класс (профильный уровень)М: Мнемозина 2005
7. Б.И. Вершинин, С.Н. Постников. Сборник задач по физике .Томск. Пеленг,1997
8. В.А. Касьянов . Физика 10 (профильный уровень)
Список использованной литературы
1. Иванов Б.А., Петров В.И. Литература. 10-11 класс. Ч.2.- М.: ООО «Обучение», 2006
Иванов Б.А., Петров В.И. Литература. 10-11 класс. Ч.2.- М.: ООО «Обучение», 2006
2. Григорьев М.И. Анализ стихотворного текста – М.: «Ученик», 2003.
Использованные материалы и Интернет-ресурсы
1. Видеокассета «Культура России. Серебряный век», 2006 г.
2. Иванов И.С. «Великая Россия», CD, 2007 г.
3. Петров Т.И., песня «Россия»
4. http://sitename.ru
Тригонометрия
ТРИГОНОМЕТРИЯ – раздел математики, изучающий тригонометрические функции и их применение в решении задач, главным образом геометрических. Слово «тригонометрия» дословно с греческого языка переводится как «треугольник+измерение»..
Задачи тригонометрии
Основная задача тригонометрии – решение треугольников, то есть нахождение неизвестных величин треугольника через известные его величины. Любую геометрическую задача можно свести к решению с помощью треугольников, поэтому тригонометрия применима и в планиметрии (изучении плоских геометрических фигур), и в стереометрии (изучении пространственных геометрических фигур).
Любая тригонометрическая величина есть функция угла (изменяется с изменением угла), поэтому и появилось название «тригонометрические функции».
Тригонометрические функции – функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec).
Обратные тригонометрические функции, или круговые функции, — арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).
Прямые функции угла используют, когда по угла находят функцию, а обратные – когда по функции находят угол.
История тригонометрииРешение треугольников было долгое время одним из разделов астрономии. Но зачатки науки можно найти в математических рукописях Древнего Египта, Китая и Вавилона. Считается, что измерение углов в градусах, минутах и секундах пришло к нам от вавилонских математиков.
Способы решения сферических треугольников впервые были письменно изложены греческим астрономом Гиппархом в середины II века до н. э.
э.
Решения треугольников Гиппархом и Птолемеем (создателем геоцентрической системы мира, господствовавшей до Коперника) не знали синусов, косинусов и тангенсов. Линии синусов и косинусов начали использовать индийские астрономы (IV-V в.в.). В дальнейшем тригонометрия развивалась арабоязычными учеными (Муххамед из Буджана, Насир эд-Дина из Туса).
Европейцы познакомились с тригонометрией в XII в. Выдающийся немецкий астроном Региомонтан составил таблицы синусов с точностью до седьмой значащей цифры с интервалом 1´.
Термин «тригонометрия» впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613).
Буквенные обозначения появились в тригонометрии лишь в середине XVIII в., ввели х русский академик Эйлер, именно он придал тригонометрии такой вид, который присущ ей до сих пор. Он же ввел и обратные тригонометрические функция.
 также полезные материалы по тригонометрии:
также полезные материалы по тригонометрии:
Таблица значений тригонометрических функций часто встречающихся углов
Тригонометрические тождества и преобразования
Таблица производных тригонометрических функций
Как вычисляются значения тригонометрических функций
Содержание главы:
- Синус
- Теорема синусов
- Задачи на решение с помощью теоремы синусов
- Теорема синусов (часть 2)
- Косинус
- Основное свойство функции косинуса
- Теорема косинусов и ее доказательство.
- Теорема косинусов. Пример решения задачи
- Тангенс и его свойства
- Тригонометрические соотношения в прямоугольном треугольнике
- Тригонометрический круг
- Радианы и градусы.
 Радiани i градуси
Радiани i градуси
- Таблица значений тригонометрических функций
- Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15)
- Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) — таблица значений
- Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
- Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60)
- Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105)
- Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120)
- Тригонометрические тождества и преобразования
- Пояснение (доказательство) простейших тригонометрических тождеств
- Преобразования тригонометрических функций вида (α + a/bπ) и доказательство
- Тригонометрические формулы понижения степени sin cos tg
- Косинус двойного угла
0
Периметр и площадь прямоугольника | Описание курса | Синус
Практические задачи с применением тригонометрии
Занятие по математике на тему «Практические задачи с применением тригонометрии»
группа МС-16-1
Преподаватель: Пересыпкина Е. А.
А.
Практические задачи с применением тригонометрии
ТРИГОНОМЕТРИЯ В НАШЕЙ ЖИЗНИ
Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия,
в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике,
в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии,
в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках,
в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве,
в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.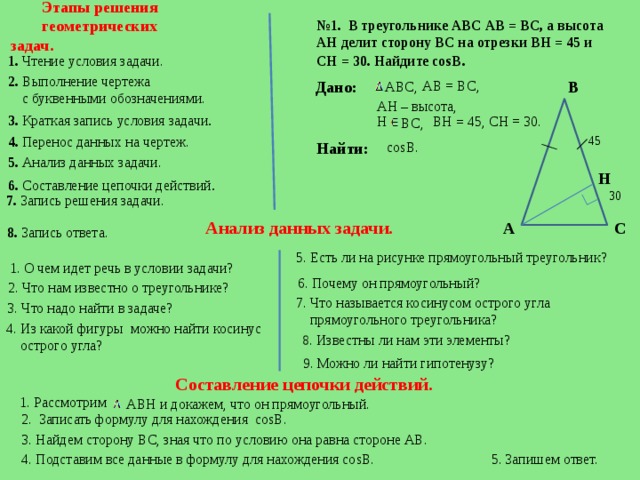
Восход и заход солнца
Изменение фаз Луны
Чередование времен года
Затмение и движение планет
Вращение колеса
Морские приливы и отливы
Эпидемии гриппа
Модель биоритмов
- Модель биоритмов можно построить с помощью тригонометрических функций
- Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Тригонометрия в медицине
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Тригонометрия в физике
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений, например:
Механические колебания
Гармонические колебания
Механические колебания
Механическими колебаниями
Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Теория радуги
- Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
- sin α / sin β = n 1 / n 2
n 1 показатель преломления первой среды
n 2 показатель преломления второй среды
α -угол падения, β -угол преломления
Северное сияние
- Оно возникает при проникновении в верхние слои атмосферы планет заряженных частиц солнечного ветра, и определяется взаимодействием магнитного поля планеты с солнечным ветром.

- Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца.
Fл = q·V·B·sin a
q- величина заряда движущегося во внешнем магнитном поле
V- модуль скорости движущегося заряда B- модуль вектора индукции внешнего магнитного поля a- угол между вектором скорости заряда и вектором магнитной индукции.
Тригонометрия в архитектуре
- Детская школа Гауди в Барселоне
- Страховая корпорация Swiss Re в Лондоне
Взмах крыльев птицы при полете напоминает синусоиду
Какой четверти принадлежит угол(у доски):
1. 185°
6 . 590°
2. 102°
7. 746°
3. -102°
8. -15°
4. 250°
9. 312°
5. -250°
10. -192°
 сos315°2. cos212° 0 7. tg15° 0 3. tg365° 0 8. sin470°4. ctg290° 0 9. ctg143°5. sin94° 10. соs56° «
сos315°2. cos212° 0 7. tg15° 0 3. tg365° 0 8. sin470°4. ctg290° 0 9. ctg143°5. sin94° 10. соs56° «
Найдитe ошибки(устно):
1. sin128° 0
6. сos315°
2. cos212° 0
7. tg15° 0
3. tg365° 0
8. sin470°
4. ctg290° 0
9. ctg143°
5. sin94°
10. соs56°
Определите знак выражения(у доски):
1. sin213°tg46°cos389°
2. cos819°sin119°tg512°
3 . tg212°cos200°sin89°
4. cos72°sin179°cos600°
Найдите значение выражения(у доски):
- 2cos0° — 4sin90° + 5tg180°
- 2ctg90° — 3cos270° + 5sin180°
- 6tg30° + 4sin60° — ctg30°
- 4sin90° — 3cos180°
- 8cos90° + 7sin360° + 12tg180°
Основные тригонометрические формулы(самостоятельно)
.
Вариант 1
Вариант 2
Найдите :
Найдите:
sinα, tgα, ctgα,
sinα, cosα, сtgα,
если
если
tgα= 2
cosα= — 5/13
π
π/2
Упростите выражение(самостоятельно):
вариант 1 вариант 2
1. 1 – sin²α 1. 1 — cos²α
1 – sin²α 1. 1 — cos²α
2. sin²α + cos²α + tg²α 2. sin²α + cos²α +сtg²α
3. tgαctgα + ctg²α 3. tgαctgα + tg²α
4. 1 – cos²α — sin²α 4. -1 + cos²α + sin²α
5. sin²α – tgαctgα 5. cos ²α – tgαctgα
6. sinαctgα 6. cosαtgα
Замените функцией угла α :
- sin(π/2 – α) 6. sin(270° — α)
- cos(3π/2 –α) 7. tg(360°+α)
- tg(π + α) 8. cos(π – α)
- cos(2π –α) 9. ctg(90°- α)
- ctg(π/2 + α) 10. sin(180°+α)
Задачи на косвенное измерение величин.
Знание тригонометрических функций позволяет нам решать такие задачи с большей точностью.
1.Определить высоту предмета, к основанию которого подойти нельзя.
Например, нужно определить высоту телевизионной антенны, которая отделена от нас рекой.
Астролябия
Астролябия – инструмент используется для измерения
небесной высоты. Небесная высота относительная «высота»
Небесная высота относительная «высота»
звезды, планеты или другого небесного объекта над горизонтом.
2.Определить расстояние между пунктами А и В, разделенными
препятствиями.
а ) Пусть требуется найти расстояние от пункта А до пункта В, находящегося за рекой.
б) Пусть нужно определить расстояние от пункта А до пункта В, между которыми находится водное пространство .
3.Определить значение величин в задачах, в которых непосредственное измерение произвести невозможно
в )На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью показанном на рис .
г )На рис. показаны два вектора напряжения, V 1 =50В и V 2 =90В . Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V 1 .
Определить величину результирующего вектора. (т.е. длину СА) и угол между результирующим вектором и V 1 .
Тригонометрия в нашей специальности
Примеры минимальных уклонов канализации
Разметка и резка труб под углом круглого сечения
Пример лекала для трубы диаметром 630мм, угол среза 10 град.
Резка трубы под углом
производится по бумажным лекалам, обернутым вокруг заготовки.
Какой бы способ резки труб не был выбран, необходимо следить за точностью нанесения разметки. От этого зависит точность реза.
Поэтому изготовим лекала с помощью миллиметровой бумаги.
Цилиндр, пересеченный наклонной плоскостью. Формула для построения развертки.
y=R· tgα· sinx,
где α-угол среза трубы,R-радиус трубы
Пример цилиндрической трубы с коленом, угол 45 ͦ. развертка
развертка
Пример цилиндрической трубы с коленом, угол 60 ͦ. развертка
Задание по вариантам(выполняется на миллиметровой бумаге)
- 1й вариант — построить лекало трубы диаметром 40мм, угол среза 30 ͦ.
- 2й вариант — построить лекало трубы диаметром 50мм, угол среза 60 .
- 3й вариант — — построить лекало трубы диаметром 30мм, угол среза 45 ͦ
Рефлексия
1. На уроке я работал активно / пассивно
2. Своей работой на уроке я доволен / не доволен
3. Урок для меня показался коротким / длинным
4. За урок я не устал / устал
5. Мое настроение стало лучше / стало хуже
6. Материал урока мне был понятен / не понятен, полезен / бесполезен
Решение разноуровневых задач по тригонометрии
Решение разноуровневых задач по тригонометрии — Общеобразовательные программы 16 ч. заочная с применением дистанционных технологий
заочная с применением дистанционных технологийОбратная связь
Поле ФИО некорректно заполнено
Поле Телефон некорректно заполнено
Некорректный E-mail
Данный email уже был зарегистрирован в системе.
Пожалуйста, авторизуйтесь!
Некорректный Ваш вопрос
Я даю своё согласие РУДН на обработку моих персональных данных на следующих условиях. Не отмечено
Не отмечено
Регистрация
Некорректный пароль. Минимум 6 символов
Пароли не совпадают
Сектор дополнительного профессионального образования института гостиничного бизнеса и туризма (СДПО ИГБиТ)
Институт повышения квалификации и переподготовки кадров (ИППК)
Институт мировой экономики и бизнеса (ИМЭБ)
Международная академия телевидения и информационного бизнеса (МАТИБ)
Факультет непрерывного медицинского образования (ФНМО)
Межфакультетский центр дополнительного профессионального образования «Перспектива»
Учебно-научный центр радиационного и экологического контроля «РАДЭКО»
Автошкола РУДН
Центр коллективного пользования (Научно-образовательный центр) (ЦКП НОЦ)
Центр дополнительного профессионального образования Юридического института (ЦДПО Юр. инст.)
инст.)
Центр дополнительного профессионального образования Экономического факультета (ЦДПО Эконом. ф-та)
Центр дополнительного профессионального образования Факультета Гуманитарных и социальных наук (ФГСН)
Центр дополнительного профессионального образования института экологии (ЦДПО Эколог. и-та)
Центр дополнительного профессионального образования Филологического факультета (ЦДПО Фил. ф-та)
Центр дополнительного профессионального образования Аграрно-технологического института (ЦДПО АТИ)
ЦДО Института иностранных языков (ИИЯ)
Институт медико-биологических технологий (ИМБТ)
Институт восточной медицины (ИВМ)
Центр дополнительного образования Инженерной академии
Учебно-научный информационный библиотечный центр (Научная библиотека) (УНИБЦ НБ)
Институт биохимической технологии и нанотехнологии (ИБХТН)
Институт непрерывного педагогического образования РУДН (ИНПО)
Международный институт стратегического развития отраслевых экономик (МИСРОЭ)
Международный центр непрерывного образования (МЦНО) РУДН
Институт русского языка РУДН (ИРЯ)
Центр дополнительного образования Медицинского института (Центр ДО МИ)
Высшая школа промышленной политики и предпринимательства (ВШППиП)
Сектор дополнительного профессионального образования института гостиничного бизнеса и туризма (СДПО ИГБиТ)Институт повышения квалификации и переподготовки кадров (ИППК)Институт мировой экономики и бизнеса (ИМЭБ)Международная академия телевидения и информационного бизнеса (МАТИБ)Факультет непрерывного медицинского образования (ФНМО)Межфакультетский центр дополнительного профессионального образования «Перспектива»Учебно-научный центр радиационного и экологического контроля «РАДЭКО»Автошкола РУДНЦентр коллективного пользования (Научно-образовательный центр) (ЦКП НОЦ)Центр дополнительного профессионального образования Юридического института (ЦДПО Юр. инст.)Центр дополнительного профессионального образования Экономического факультета (ЦДПО Эконом. ф-та)Центр дополнительного профессионального образования Факультета Гуманитарных и социальных наук (ФГСН)Центр дополнительного профессионального образования института экологии (ЦДПО Эколог. и-та)Центр дополнительного профессионального образования Филологического факультета (ЦДПО Фил. ф-та)Центр дополнительного профессионального образования Аграрно-технологического института (ЦДПО АТИ)ЦДО Института иностранных языков (ИИЯ)Институт медико-биологических технологий (ИМБТ)Институт восточной медицины (ИВМ)Центр дополнительного образования Инженерной академииУчебно-научный информационный библиотечный центр (Научная библиотека) (УНИБЦ НБ)Институт биохимической технологии и нанотехнологии (ИБХТН)Институт непрерывного педагогического образования РУДН (ИНПО)Международный институт стратегического развития отраслевых экономик (МИСРОЭ)Международный центр непрерывного образования (МЦНО) РУДНИнститут русского языка РУДН (ИРЯ)Центр дополнительного образования Медицинского института (Центр ДО МИ)Высшая школа промышленной политики и предпринимательства (ВШППиП)
инст.)Центр дополнительного профессионального образования Экономического факультета (ЦДПО Эконом. ф-та)Центр дополнительного профессионального образования Факультета Гуманитарных и социальных наук (ФГСН)Центр дополнительного профессионального образования института экологии (ЦДПО Эколог. и-та)Центр дополнительного профессионального образования Филологического факультета (ЦДПО Фил. ф-та)Центр дополнительного профессионального образования Аграрно-технологического института (ЦДПО АТИ)ЦДО Института иностранных языков (ИИЯ)Институт медико-биологических технологий (ИМБТ)Институт восточной медицины (ИВМ)Центр дополнительного образования Инженерной академииУчебно-научный информационный библиотечный центр (Научная библиотека) (УНИБЦ НБ)Институт биохимической технологии и нанотехнологии (ИБХТН)Институт непрерывного педагогического образования РУДН (ИНПО)Международный институт стратегического развития отраслевых экономик (МИСРОЭ)Международный центр непрерывного образования (МЦНО) РУДНИнститут русского языка РУДН (ИРЯ)Центр дополнительного образования Медицинского института (Центр ДО МИ)Высшая школа промышленной политики и предпринимательства (ВШППиП)
Я даю своё согласие РУДН на обработку моих персональных данных на следующих условиях.
Не дано согласие на обработку персональных данных
Авторизация
Неверный логин и/или пароль
Восстановить пароль | Регистрация
Служба дополнительного образования РУДН https://www.dpo.rudn.ru Москва +7 499 936-85-94 Служба дополнительного образования РУДН https://www.dpo.rudn.ru Москва +7 499 936-85-94Формат обучения: Общеобразовательные программы
Формы обучения:
- заочная с применением дистанционных технологий
Объем: 16 ак. ч.
ч.
Центр ДПО: Межфакультетский центр дополнительного профессионального образования «Перспектива»
Направления обучения:
- Инженерные науки
БЕСПЛАТНО
записаться на курс
Вид аттестации: Тестовый контроль
Выдаваемый документ: Электронный сертификат
Поделиться
Отзывы
На данный курс отзывов нет, вы можете первым оставить свой отзыв Все отзывы Оставить отзыв
Курс разработан таким образом, что сначала даётся теоретический материал и объясняются сложные для понимания элементы теории. Темы охватывают практические проблемы. После окончания темы лектор решает задачи на виртуальной доске. Задачи составлены таким образом, чтобы студент хорошо усваивал материал. Сперва мы рассматриваем простые задачи, а затем, шаг за шагом переходим на более сложные уровни.
Темы охватывают практические проблемы. После окончания темы лектор решает задачи на виртуальной доске. Задачи составлены таким образом, чтобы студент хорошо усваивал материал. Сперва мы рассматриваем простые задачи, а затем, шаг за шагом переходим на более сложные уровни.
Язык курса: английский
Содержание программы:
- Тема 1
Тригонометрические функции числового аргумента. Формулы приведения.
- Тема 2
Соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения.
- Тема 3
Формулы двойного и половинного аргумента.

- Тема 4
Методика решения тригонометрических уравнений.
Для кого?
студентов, поступающих в высшие учебные заведения, а также для студентов, изучающих математику в университетах.
Цель:
углубить знания по теме «Тригонометрия».
Руководитель
Рекач Фёдор Владимирович
Записаться на курс
«Решение разноуровневых задач по тригонометрии»
Поле Фамилия некорректно заполнено
Поле Имя некорректно заполнено
Поле Отчество некорректно заполнено
Некорректный E-mail
Данный email уже был зарегистрирован в системе.
Пожалуйста, авторизуйтесь!
Я даю своё согласие РУДН на обработку моих персональных данных на следующих условиях. Не отмечено
Похожие курсы
Современные технологии мониторинга земель сельскохозяйственного назначения
Объем:36 ак. ч.
Продолжительность:
- 2 недели
Формат обучения:Общеобразовательные программы
15 000 ₽ $310 подробнее
Базовый курс механики – физика для всех специальностей (на арабском языке)
Объем:16 ак. ч.
ч.
Формат обучения:Общеобразовательные программы
ПО ЗАПРОСУ
подробнее
Основы электричества и магнетизма
Объем:16 ак. ч.
Формат обучения:Общеобразовательные программы
БЕСПЛАТНО
подробнее
Методика решения задач по геометрии с применением тригонометрии
Введение
Математика является неотъемлемой и существенной частью общечеловеческой культуры. Изучение данной дисциплины оказывает значительное воздействие на развитие и формирование личности, совершенствует мышление, помогает выработке мировоззрения, качественно влияет на нравственное и духовное воспитание учащихся. Эффективность обучения во многом зависит от подбора задач, от их систематизации. В современной методике обучения математике все больше внимания уделяется использованию совокупностей, систем задач.
Тригонометрия традиционно является одной из важнейших составных частей школьного курса математики, представляет собой его целостный и самостоятельный раздел. Даже при первоначальном знакомстве с тригонометрией обращает на себя внимание тот факт, что этот предмет тесно связан с геометрией, а значит и с решением задач, что всегда вызывают особые трудности у учащихся. Решение же задач с применением тригонометрии еще более усиливает эти трудности.
Сейчас все большее распространение получает прогрессивный метод обучения через задачи как реализация системы проблемного обучения. Задачи становятся не только и не столь целью, сколько средством обучения. Умение решать задачи — показатель обученности и развития учащихся. Умение решать задачи с помощью тригонометрии показатель высокой культуры ученика.
Несмотря на то, что задачи в 8 классе курса геометрии решаются в большом количестве, затем тригонометрия используется и при решении задач в курсе алгебры, это остается проблемой для всех учащихся. Они часто заменяют простой тригонометрический метод решения задач более сложным геометрическим или алгебраическим.
Они часто заменяют простой тригонометрический метод решения задач более сложным геометрическим или алгебраическим.
Подобная тенденция, к сожалению, сохраняется и в последние годы. Необходимы поиски путей устранения данной проблемы, что свидетельствует об актуальности темы нашего исследования.
Объект исследования: задачи по геометрии с применением тригонометрии в курсе математики 8 класса.
Предмет исследования: методика решения задач по геометрии с применением тригонометрии в 8 классе.
Цель исследования: изучить различные методические подходы к решению задач по геометрии с применением тригонометрии в курсе математики 8 класса.
Гипотеза исследования: оптимальный подход к решению задач по геометрии с применением тригонометрии будет способствовать развитию аналитического, логического, конструктивного мышления учащихся и формированию их математической зоркости.
Методы исследования: наблюдение, анализ, сравнение, репродуктивный и частично — поисковый.
Задачи исследования:
Глубоко изучить тригонометрический материал в курсе геометрии основной школы;
— Рассмотреть различные методы решения текстовых задач, предлагаемых альтернативных учебниках;
— Решить наиболее интересные задачи из курса геометрии 8 класса;
— Рассмотреть нестандартные задачи, предлагаемые в альтернативных учебниках геометрии;
— Проверить гипотезу.
Глава 1. Соотношение между сторонами и углами прямоугольного треугольника в курсе геометрии 8 класса
1.1История развития вопроса
История тригонометрии, как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур, охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобились ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц.
Историки полагают, что тригонометрию создали древние астрономы, немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, в наши дни она охватывает практически все естественные науки, технику и ряд других областей деятельности.
Со временем область применения тригонометрии постоянно расширялась, в наши дни она охватывает практически все естественные науки, технику и ряд других областей деятельности.
Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году. Его «Трактат о полном «четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам. Сочинение ат-Туси стало широко известно в Европе и существенно повлияло на развитие тригонометрии.
Таким образом, к концу XIII века были открыты базовые теоремы, составляющие содержание тригонометрии:
Выражение любой тригонометрической функции через любую другую;
Формулы для синусов и косинусов кратных и половинных углов, а также для суммы и разности углов;
Теоремы синусов и косинусов;
Решение плоских и сферических треугольников.
Современный вид тригонометрии придал Леонард Эйлер. В трактате «Введение в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций, эквивалентное современному, и соответственно определил обратные функции. Если его предшественники понимали синус и прочие понятия геометрически, то есть как линии в круге или треугольнике, то после работ Эйлера, стали рассматриваться как безразмерные аналитические функции действительного и комплексного переменного. Для комплексного случая он установил связь тригонометрических функций с показательной функцией (формула Эйлера). Подход Эйлера с этих пор стал общепризнанным и вошёл в учебники.
В России первые сведение о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей», опубликованном при участии Л.Ф. Магницкого в 1703 году.
В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии. Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М.Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М.Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
1.2 Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
Рассмотрим прямоугольный треугольник АВС с прямым углом С (рис. 1).
А
В
С
Рис.1
Катет ВС этого треугольника является противолежащим углу А, а катет АС — прилежащим к этому углу.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Синус, косинус и тангенс угла ? обозначаются символами sin ?, cos ?, tg ? (читаются: «синус альфа», «косинус альфа» и «тангенс альфа». На рисунке 1
На рисунке 1
sin А = , (1)
cos А = (2)
tg А = . (3)
Из формул (1) и (2) получаем:
= * =
Сравнивая с формулой (3), находим:
tg А=(4),
то есть тангенс угла равен отношению синуса к косинусу этого угла.
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны. В самом деле, пусть АВС и А1В1С — два прямоугольных треугольника с прямым углами С и С1 и равными острыми углами А и А1. Треугольники АВС и А1В1С1 подобны по первому признаку подобия треугольников, поэтому = = . Из этих равенств следует, что = , то есть sin А = sin А1. Аналогично = , то есть cos А = cos А1, и = , то есть tg А = tg А1.
А
В
С
Рис. 2
Рассмотрим прямоугольный треугольник АВС с прямым углом С (рис. 2). Докажем, что в прямоугольном треугольнике АВС sin А = cos В и cos А = sin В.
sin А = cos В, так как ?А + ?В = 90?, то ?А = 90? — ?В,
sin А = sin ( 90? — ?В ) = cos В, sin ( 90? — ?В ) = cos В.
cos А = sin В, так как ?А + ?В = 90?, то ?А = 90? — ?В,
cos А = cos ( 90? — ?В ) = sin В, cos ( 90? — ?В ) = sin В.
1.3 Основное тригонометрическое тождество в курсе геометрии 8 класса
Докажем теперь справедливость равенства
+ = 1
Возьмем любой прямоугольный треугольник АВС с углом при вершине А, равным ? (рис. 3).
В
А
С
Рис. 3
По теореме Пифагора + = . Разделим обе части равенства на . Получим:
+ = 1, sin А = , cos А = .
Таким образом, ? + ? = 1 (1).
Это равенство есть тождество. Оно верно для любого острого угла ?.
? + ? = 1
называется основным тригонометрическим тождеством.
Из основного тригонометрического тождества можно получить два тождества:
1 +? = (2) и 1 +? = (3).
Чтобы получить второе тождество, разделим обе части полученного равенства на ?. Получим:
+ 1 = , или 1 +? = (4)
Если обе части тождества ? + ? = 1 разделить на ?, то получим третье тождество:
1 +? = (5).
Значение этих тождеств заключается в том, что они позволяют, зная одну из величин ? или ?, найти две другие.
Примером применения этих тождеств может служить такая задача:
Вычислите значения sin ? и ?, если ? = , где ? — острый угол.
Решение:
Так так ? + ? = 1, то sin ? = = =,
= =
Ответ: sin ? = , = .
1.4 Значения синуса, косинуса и тангенса для углов 30?, 45? и 60?
Найдем сначала значение синуса, косинуса и тангенса для углов 30? и 60?. Для этого рассмотрим прямоугольный треугольник АВС с прямым углом С (рис. 4), у которого ?А=30?, ?В =60?.
В
А
С
Рис.4
Так как катет, лежащий против угла в 30?, равен половине гипотенузы, то = . Но = sin А = sin 30?. С другой стороны, = В = 60?. Итак, -sin 30? = , 60? = . Из основного тригонометрического тождества получаем:
30? = = = ,
= = = .
По формуле (4) находим:
tg 30? = = = , tg 60? = =
Найдем теперь sin 45?, 45? и tg 45?. Для этого рассмотрим равнобедренный прямоугольный треугольник АВС с прямым углом С (рис. 5).
Для этого рассмотрим равнобедренный прямоугольный треугольник АВС с прямым углом С (рис. 5).
А
В
С
Рис. 5
В этом треугольнике АС = ВС, ?А=?В= 45?. По теореме Пифагора
= + = 2 = 2, откуда АС = ВС = .
Следовательно,
sin 45? = = = = , 45?= = = = ,
tg 45?= tg = = 1.
Составим таблицу значений sin ?, ? и для углов ?, равных 30?, 45? и 60?:
30?45?60?tg ?1
Для любого острого угла ? справедливы равенства:
(90? — ?) = ?
(90? — ?) = ?
Пусть АВС — прямоугольный треугольник с острым углом ? при вершине А (рис. 6). Тогда острый угол при вершине В равен 90? — ?. По определению
sin А = , cos А = ,
(90? — ?) =, (90? — ?) = .
Из этого следует, что (90? — ?) = ? и (90? — ?) = ?.
В
А
С
Рис.6
аналитический математический геометрия тригонометрия
Глава 2. Задачи по геометрии с применением тригонометрии в курсе геометрии 8 класса
.1 Задачи на вычисление
Роль задач по тригонометрии в геометрии очень велика, так как решение задач с конкретным содержанием помогает осуществлять постепенный переход к дедуктивным доказательствам. Систематическое решение задач способствует сознательному и прочному усвоению теории, помогает увидеть ее практическую ценность, в то же время решение задач развивает логическое мышление ученика, творческую инициативу, сообразительность и дает ему ряд нужных практических умений и навыков. Самое главное, что знание тригонометрии способствует экономии рабочего времени ученика во многих ситуациях.
Систематическое решение задач способствует сознательному и прочному усвоению теории, помогает увидеть ее практическую ценность, в то же время решение задач развивает логическое мышление ученика, творческую инициативу, сообразительность и дает ему ряд нужных практических умений и навыков. Самое главное, что знание тригонометрии способствует экономии рабочего времени ученика во многих ситуациях.
Рассмотрим задачи на вычисление.
Задача 1
Найти синус, косинус и тангенс угла А треугольника АВС с прямым углом С, если ВС = 8, АВ = 17.
A
В
С
Дано: ? ABC, ?С = 90?.
Найти: sin А, cos А, tg А.
Решение:
Так как ? АВС прямоугольный, то теореме Пифагора АС =- ,
АС = = 15
sin А = , sin А = ,
cos А = , cos А = ,
tg А = , tg А =
Ответ: sin А = , cos А = , tg А = .
Такие задачи способствуют осознанному восприятию определения синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Задача 2
Найти площадь равнобедренной трапеции с основаниями 2 см и 6 см, если угол при большем основании равен ?.
АD
В
В1С1С
Дано: ABCD — трапеция, АВ = СD, ВС = 2 см, АD = 6 см, ?А = ?.
Найти: SАВСD.
Решение:
)Рассмотрим прямоугольные треугольники АВВ1 и DСС1.
? АВВ1 = ? ДСС1 по катету и гипотенузе ( АВ = СD по условию, ВВ1 = СС1 как расстояния между параллельными прямыми ВС и АD ), из этого следует, что АВ1 = С1D как соответственные элементы равных треугольников. А В1 = С1 D = ( 6 — 2): 2 = 2 см.
) Рассмотрим ? АВВ1:
ВВ1 = А В1 * tg ?А, ВВ1 = 2 * tg ?.
3) SАВСD = (АД + ВD) * ВВ1
SАВСD = ( 6 + 2) * 2 tg ? = 8 tg ? .
Ответ: SАВСD = 8 tg ? .
Задача 3
Найти диагонали ромба, если его диагонали равны 2 и 2.
АВ
DС
Дано: АВСD — ромб, АС = 2, ВD = 2.
Найти: ?А, ?В.
Решение:
)Рассмотрим ? АОВ, АО = АС, ВО = ВD по свойству диагоналей ромба,
АО = * 2 = 1, ВО = * 2 =
2)? АОВ — прямоугольный, ?О = 90?.
tg?ВАО = , tg?ВАО = = , значит, ?ВАО = 60?,
?АВО = 90? — 60?= 30?
)?А = 60? * 2 = 120?, ?В = 30? * 2 = 60? по свойству ромба,
?С = 180? — 60? = 120?, ?D = 180? — 120? = 60?,
так как сумма односторонних углов равна 180?
Ответ: ?А = ?В =120?, ?В = ?D = 60?.
Решение таких задач способствует не только осознанному закреплению определений синуса, косинуса и тангенса острого угла прямоугольного треугольника, но и развитию математической зоркости учащихся.
Задача 4
В параллелограмме АВСD сторона равна 12 см, а угол ВАD равен 47?50?. Найти площадь параллелограмма, если его диагональ ВD перпендикулярна к стороне АВ.
DС
АВ
Дано: АВСD — параллелограмм, АD = 12, ?ВАD = 47?50?, ВD АВ.
Найти: SАВСD.
Решение:
)Рассмотрим ? АВD, он прямоугольный, ?= 90?
2) = cos? А, АВ = АD * cos? А
АВ = 12 * cos 47?50? = 12 * 0, 6712 ? 8,06
= sin ? А, ВD = АD * sin ? А
ВD = 12 * sin 47?50? = 12 * 0, 7412 ? 8,89
)SАВСД = АВ * ВD, SАВСD = 8,06 * 8,89 ? 71,76 ? 72
Ответ: 72
Решение подобных задач способствует формированию у учащихся умений рассуждать, связывать воедино вопросы алгебры, геометрии, тригонометрии.
Задача 5
Стороны прямоугольника равны 3 см и см. Найти углы, которые образует диагональ со стороной прямоугольника.
ВС
АD
Дано: АВСD — прямоугольник, АВ = , АD = 3.
Найти: ?АВD, ?АDВ.
Решение:
)Рассмотрим ? АВD — прямоугольный, так как ?А = 90?,
tg ? АВD = , tg ? АВD = = , ? АВD = 60?,
?АDВ = 90? — 60? = 30?
Ответ: ? АВD = 60?, ?АDВ = 30?.
Решение такой задачи способствует развитию исследовательских навыков у учащихся. Например, при решении этой задачи ученик должен увидеть прямоугольный треугольник, выяснить какими углами являются ?АВД и ?АДВ, вспомнить определение синуса, косинуса, тангенса, выбрать необходимые определения. Еще более глубокие исследования проводит ученик, решая следующую задачу:
Задача 6
В равнобедренный треугольник РМК с основанием МК вписана окружность с радиусом 2. Высота PH делится точкой пересечения с окружностью в отношении 1: 2, считая от вершины Р. Найти периметр треугольника РМК и установить его вид.
N
Р
МНК
Дано: ? РМК — равнобедренный, МК — основание, окр. (О; r) — вписана, РН — высота, РА: АН = 1: 2, r = 2.
Найти: РРМК.
Решение:
)Так как РА: АН = 1: 2, тот НА = 2РА, то есть РН = 3ОА = 3 ОН = 3РА, так как ОА = 2, то РН = 6.
2)Рассмотрим ? МРН: ?РНМ = 90?, так как РН — высота,
sin ?М = , отсюда РМ = , РН = 6.
? ОРМ — прямоугольный, так как ОN РМ, где N — точка касания по свойству касательных к окружности.
Значит, sin ? NРО = , sin ? NРО = = , ? NРО = 30?, значит, ?М = 60?.
Следовательно,
РМ = = = 12
3)Так как ? МРК — равнобедренный, ?М = 60? (угол при основании), то ? МРК — равносторонний.
Значит, МР = РК = МК = 12.
)РРМК = 36.
Ответ: 36, треугольник равносторонний.
Интересной задачей для учеников 8 класса является задача на вычисление высоты и площади правильного треугольника.
Задача 7
Найти высоту и площадь правильного треугольника со стороной а и высотой h.
Дано: ? АВС — правильный, АВ = ВС = АС = а, BD = h — высота.
Найти: SАВС, h.
А
В
DС
Решение:
)Рассмотрим прямоугольный треугольник АВD (так как BD — высота). Из прямоугольного треугольника АВD находим BD = АВ * sin 60?.
Из прямоугольного треугольника АВD находим BD = АВ * sin 60?.
BD = h = а * =
2)SАВС = , SАВС = =
Ответ: h =, SАВС = .
Как видим, задача очень легко и быстро решается с помощью тригонометрии.
При этом развивается не только аналитическое, логическое мышление учащихся, их математическая зоркость, но и умение рационально мыслить, экономить свое рабочее время, находить оптимальные пути решения задач.
Для сравнения покажем, как задача решалась до изучения вопросов тригонометрии.
Дано: ? АВС — правильный, АВ = ВС = АС = а, BD = h — высота.
Найти: SАВС, h.
Решение:
1)Проводим высоту BD.
2)? АВD: ?ВАD = 60?, тогда ?АВD = 30?, а против угла в 30? лежит
АD = АВ, АD = .
3)BD = h = , BD = h = = =
4)SАВС = , SАВС = =
Ответ: h =, SАВС = .
Затруднения, которые испытывают при решении подобных задач ученики, вызываются не геометрическим содержанием, а скорее непривычкой учащихся применять в геометрии свои знания по тригонометрии.
Задачи, для решения которых должны быть использованы многие геометрические предложения, требующие умения разобраться в чертежах, установить связь между данными и искомыми элементами, провести ряд умозаключений для обоснования своих догадок. Такие задачи расширяют геометрические представления учащихся, их пространственное воображение, развивают логическое мышление, способствуют межпредметной интеграции.
2.2 Задачи на построение
Задача на построение состоит в том, что требуется построить наперед указанными инструментами некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры.
Каждая фигура, удовлетворяющая задаче, называется решением этой задачи. Найти решение задачи на построение — значит свести ее к конечному числу основных построений, то есть указать конечную последовательность основных построений.
Задача 1
Построить угол ? в прямоугольном треугольнике АВС, если известно, что tg ? = .
Эта задача, как и любая другая на построение, требует глубокого анализа.
Учитель должен приучить учеников задавать себе вопросы следующего характера:
Что должно выполняться в этом треугольнике, если tg ? = ?
(Так как tg А = , то на ВС приходится три единицы, а на АС — пять единиц).
Дано: tg ? = .
Построить: ??.
Решение:
Задача решается путем построения прямоугольного треугольника по двум катетам, тангенс ? — это отношение противолежащего катета к прилежащему катету. Из условия следует, что противолежащий катет равен 3, а прилежащий равен 5. Строим прямоугольный треугольник с катетами три единицы и пять единиц:
А
В
С
Задача 2
Построить в прямоугольном треугольнике угол, синус которого в два раза больше его косинуса.
Дано: sin ? = 2 cos ?.
Построить: угол ?.
Решение: Пусть ? — искомый угол. По условию sin ? = 2 cos ?, отсюда tg ? = 2.Поэтому необходимо построить прямоугольный треугольник с прямым углом С, у которого = . Тогда ?А будет искомым.
Тогда ?А будет искомым.
ВС
Систематическое изучение геометрических построений необходимо в школьном курсе, так как в процессе изучения задач они концентрируют в себе знания из других областей математики, развивают навыки практической графики, формируют поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, способствуют выработке конкретных геометрических представлений, а также к более тщательной обработке умений и навыков.
2.3Задачи на доказательство
В задачах на доказательство требуется обосновать некоторые утверждение относительно геометрической фигуры, которое высказано заранее. Решение задач на доказательство имеет большое значение в развитии логической мысли учащихся. Именно при выполнении доказательств оттачивается логическое мышление учеников, разрабатываются логические схемы решения задач, возникает потребность учащихся в обосновании математических фактов. Это можно увидеть при решении следующей задачи:
Задача 1
В прямоугольном треугольнике синус угла А равен . Доказать, что косинус угла В равен , ? С = 90?.
Доказать, что косинус угла В равен , ? С = 90?.
Решение: Рассмотрим прямоугольный треугольник АВС (?С = 90?):
А
ВС
На основе определения sin А = , а cos А = .
sin A = cos B, так как ?А + ?В = 90?, то ?В = 90? — ?А,
cos B = cos( 90? — ?А) = sin A, sin A = 30?, B = cos( 90? — 30?) = cos 60? = , что и требовалось доказать.
Задача 2
В прямоугольном треугольнике тангенс угла А равен . Доказать, что синус угла А равен .
Решение:
Рассмотрим прямоугольный треугольник АВС (?С = 90?):
В
А
С
tg ?A = , tg A = 60?, значит, ?A = 60?, sin A = 60? = , что и требовалось доказать.
Такие задачи способствуют осознанному восприятию определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, а также закреплению формул приведения.
Задача 3
Доказать, что в прямоугольном треугольнике 55? + 55? = 1.
Решение:
? + ? = 1 — основное тригонометрическое тождество, которое выполняется при любых значениях ?, таким образом оно будет выполняться и при ? = 55?, то есть 55? + 55? = 1.
Задача 4
Доказать, что в прямоугольном треугольнике sin 35? = cos 65?.
Решение:
Рассмотрим прямоугольный треугольник АВС (?С = 90?):
Сначала докажем, что sin A = sin (90? — ?В),
sin A = cos B, так как ?А + ?В = 90?, то ?А = 90? — ?В,
sin A = sin (90? — ?В) = cos B, 35? = cos 65?, что и требовалось доказать
Такие задачи способствуют закреплению формул приведения и основного тригонометрического тождества, развитию логического и аналитического мышления.
Заключение
В ходе работы над проблемой — решение задач по геометрии с применением тригонометрии в курсе математики 8 класса, были изучены объект и, предмет исследования, которые показали необходимость осознанности работы над такими задачами.
В ходе исследования выяснено, что рациональное решение геометрических задач по тригонометрии является одной из самых актуальных в современной методике. Так как тригонометрия традиционно является одной из важнейших составных частей школьного курса математики, представляет собой его целостный и самостоятельный раздел.
Установлено, что решение задач по геометрии с применением тригонометрии способствует более рациональной работе с задачами.
Решение задач на вычисление способствует развитию аналитического и логического мышления, что необходимо в современной жизни.
Решение задач на построение способствует развитию конструктивного мышления и эстетического вкуса учащихся.
Решение задач на доказательство способствует формированию аналитического, логического и пространственного мышления учащихся.
Установлено, что систематическая работа по формированию навыков решения задач по геометрии с применением тригонометрии способствует развитию общего интеллектуального развития учащихся, их творческих способностей, потенциала школьника, умению разбираться в создавшейся ситуации, делать нужные умозаключения. Основным средством развития творческих способностей ученика является решение задачи, при этом главная цель — не получение результата решения задачи, а само решение задачи, как совокупность логических шагов, приводящих к получению ответа. Очень важно научить ученика использовать оптимальные методы решения задач, среди которых тригонометрический метод является наиболее простейшим.
Очень важно научить ученика использовать оптимальные методы решения задач, среди которых тригонометрический метод является наиболее простейшим.
Цель курсовой работы достигнута: изучены различные методические подходы к решению задач по геометрии с применением тригонометрии в курсе математики 8 класса.
Таким образом, подтвердилась выдвинутая гипотеза, оптимальный подход к решению задач по геометрии с применением тригонометрии будет способствовать развитию аналитического, логического, конструктивного мышления учащихся и формированию их математической зоркости.
Теги:
Методика решения задач по геометрии с применением тригонометрии
Курсовая работа (теория)
Математика
Просмотров: 13224
Найти в Wikkipedia статьи с фразой: Методика решения задач по геометрии с применением тригонометрии
Тригонометрические формулы примеры решения. Решение тригонометрических уравнений. Задачи для самостоятельного решения
Тригонометрические уравнения — тема не самая простая. Уж больно они разнообразные.) Например, такие:
Уж больно они разнообразные.) Например, такие:
sin 2 x + cos3x = ctg5x
sin(5x+π /4) = ctg(2x-π /3)
sinx + cos2x + tg3x = ctg4x
И тому подобное…
Но у этих (и всех остальных) тригонометрических монстров есть два общих и обязательных признака. Первый — вы не поверите — в уравнениях присутствуют тригонометрические функции.) Второй: все выражения с иксом находятся внутри этих самых функций. И только там! Если икс появится где-нибудь снаружи, например, sin2x + 3x = 3, это уже будет уравнение смешанного типа. Такие уравнения требуют индивидуального подхода. Здесь мы их рассматривать не будем.
Злые уравнения в этом уроке мы тоже решать не будем.) Здесь мы будем разбираться с самыми простыми тригонометрическими уравнениями. Почему? Да потому, что решение любых тригонометрических уравнений состоит из двух этапов. На первом этапе злое уравнение путём самых различных преобразований сводится к простому. На втором — решается это самое простое уравнение. Иначе — никак.
Иначе — никак.
Так что, если на втором этапе у вас проблемы — первый этап особого смысла не имеет.)
Как выглядят элементарные тригонометрические уравнения?
sinx = а
cosx = а
tgx = а
ctgx = а
Здесь а обозначает любое число. Любое.
Кстати, внутри функции может находиться не чистый икс, а какое-то выражение, типа:
cos(3x+π /3) = 1/2
и тому подобное. Это усложняет жизнь, но на методе решения тригонометрического уравнения никак не сказывается.
Как решать тригонометрические уравнения?
Тригонометрические уравнения можно решать двумя путями. Первый путь: с использованием логики и тригонометрического круга. Этот путь мы рассмотрим здесь. Второй путь — с использованием памяти и формул — рассмотрим в следующем уроке.
Первый путь понятен, надёжен, и его трудно забыть.) Он хорош для решения и тригонометрических уравнений, и неравенств, и всяких хитрых нестандартных примеров. Логика сильнее памяти!)
Логика сильнее памяти!)
Решаем уравнения с помощью тригонометрического круга.
Включаем элементарную логику и умение пользоваться тригонометрическим кругом. Не умеете!? Однако… Трудно же вам в тригонометрии придётся…) Но не беда. Загляните в уроки «Тригонометрический круг…… Что это такое?» и «Отсчёт углов на тригонометрическом круге». Там всё просто. В отличие от учебников…)
Ах, вы в курсе!? И даже освоили «Практическую работу с тригонометрическим кругом» !? Примите поздравления. Эта тема будет вам близка и понятна.) Что особо радует, тригонометрическому кругу безразлично, какое уравнение вы решаете. Синус, косинус, тангенс, котангенс — ему всё едино. Принцип решения один.
Вот и берём любое элементарное тригонометрическое уравнение. Хотя бы это:
cosx = 0,5
Надо найти икс. Если говорить человеческим языком, нужно найти угол (икс), косинус которого равен 0,5.
Как мы ранее использовали круг? Мы рисовали на нём угол. В градусах или радианах. И сразу видели тригонометрические функции этого угла. Сейчас поступим наоборот. Нарисуем на круге косинус, равный 0,5 и сразу увидим угол. Останется только записать ответ.) Да-да!
И сразу видели тригонометрические функции этого угла. Сейчас поступим наоборот. Нарисуем на круге косинус, равный 0,5 и сразу увидим угол. Останется только записать ответ.) Да-да!
Рисуем круг и отмечаем косинус, равный 0,5. На оси косинусов, разумеется. Вот так:
Теперь нарисуем угол, который даёт нам этот косинус. Наведите курсор мышки на рисунок (или коснитесь картинки на планшете), и увидите этот самый угол х.
Косинус какого угла равен 0,5?
х = π /3
cos60° = cos(π /3 ) = 0,5
Кое-кто скептически хмыкнет, да… Мол, стоило ли круг городить, когда и так всё ясно… Можно, конечно, хмыкать…) Но дело в том, что это — ошибочный ответ. Вернее, недостаточный. Знатоки круга понимают, что здесь ещё целая куча углов, которые тоже дают косинус, равный 0,5.
Если провернуть подвижную сторону ОА на полный оборот , точка А попадёт в исходное положение. С тем же косинусом, равным 0,5. Т.е. угол изменится на 360° или 2π
радиан, а косинус — нет. Новый угол 60° + 360° = 420° тоже будет решением нашего уравнения, т.к.
Т.е. угол изменится на 360° или 2π
радиан, а косинус — нет. Новый угол 60° + 360° = 420° тоже будет решением нашего уравнения, т.к.
Таких полных оборотов можно накрутить бесконечное множество… И все эти новые углы будут решениями нашего тригонометрического уравнения. И их все надо как-то записать в ответ. Все. Иначе решение не считается, да…)
Математика умеет это делать просто и элегантно. В одном кратком ответе записывать бесконечное множество решений. Вот как это выглядит для нашего уравнения:
х = π /3 + 2π n, n ∈ Z
Расшифрую. Всё-таки писать осмысленно приятнее, чем тупо рисовать какие-то загадочные буковки, правда?)
π /3 — это тот самый угол, который мы увидели на круге и определили по таблице косинусов.
2π — это один полный оборот в радианах.
n — это количество полных, т.е. целых оборотов. Понятно, что n может быть равно 0, ±1, ±2, ±3. … и так далее. Что и указано краткой записью:
… и так далее. Что и указано краткой записью:
n ∈ Z
n принадлежит (∈ ) множеству целых чисел (Z ). Кстати, вместо буквы n вполне могут употребляться буквы k, m, t и т.д.
Эта запись означает, что вы можете взять любое целое n . Хоть -3, хоть 0, хоть +55. Какое хотите. Если подставите это число в запись ответа, получите конкретный угол, который обязательно будет решением нашего сурового уравнения.)
Или, другими словами, х = π /3 — это единственный корень из бесконечного множества. Чтобы получить все остальные корни, достаточно к π /3 прибавить любое количество полных оборотов (n ) в радианах. Т.е. 2π n радиан.
Всё? Нет. Я специально удовольствие растягиваю. Чтобы запомнилось получше.) Мы получили только часть ответов к нашему уравнению. Эту первую часть решения я запишу вот как:
х 1 = π /3 + 2π n, n ∈ Z
х 1 — не один корень, это целая серия корней, записанная в краткой форме.
Но есть ещё углы, которые тоже дают косинус, равный 0,5!
Вернёмся к нашей картинке, по которой записывали ответ. Вот она:
Наводим мышку на картинку и видим ещё один угол, который тоже даёт косинус 0,5. Как вы думаете, чему он равен? Треугольнички одинаковые… Да! Он равен углу х , только отложен в отрицательном направлении. Это угол -х. Но икс-то мы уже вычислили. π /3 или 60°. Стало быть, можно смело записать:
х 2 = — π /3
Ну и, разумеется, добавляем все углы, которые получаются через полные обороты:
х 2 = — π /3 + 2π n, n ∈ Z
Вот теперь всё.) По тригонометрическому кругу мы увидели (кто понимает, конечно)) все углы, дающие косинус, равный 0,5. И записали эти углы в краткой математической форме. В ответе получились две бесконечные серии корней:
х 1 = π /3 + 2π n, n ∈ Z
х 2 = — π /3 + 2π n, n ∈ Z
Это правильный ответ.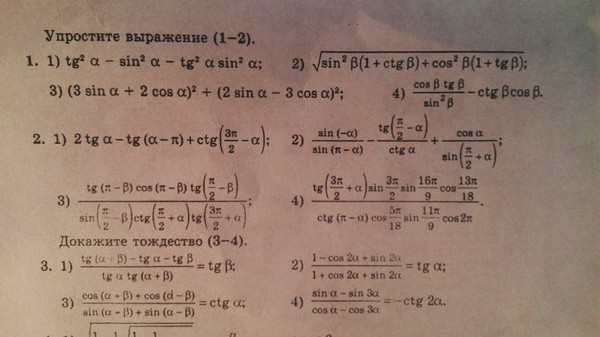
Надеюсь, общий принцип решения тригонометрических уравнений с помощью круга понятен. Отмечаем на круге косинус (синус, тангенс, котангенс) из заданного уравнения, рисуем соответствующие ему углы и записываем ответ. Конечно, нужно сообразить, что за углы мы увидели на круге. Иногда это не так очевидно. Ну так я и говорил, что здесь логика требуется.)
Для примера разберём ещё одно тригонометрическое уравнение:
Прошу учесть, что число 0,5 — это не единственно возможное число в уравнениях!) Просто мне его писать удобнее, чем корни и дроби.
Работаем по общему принципу. Рисуем круг, отмечаем (на оси синусов, разумеется!) 0,5. Рисуем сразу все углы, соответствующие этому синусу. Получим вот такую картину:
Сначала разбираемся с углом х в первой четверти. Вспоминаем таблицу синусов и определяем величину этого угла. Дело нехитрое:
х = π /6
Вспоминаем про полные обороты и, с чистой совестью, записываем первую серию ответов:
х 1 = π /6 + 2π n, n ∈ Z
Половина дела сделана. А вот теперь надо определить второй угол… Это похитрее, чем в косинусах, да… Но логика нас спасёт! Как определить второй угол через х? Да легко! Треугольнички на картинке одинаковые, и красный угол х равен углу х . Только отсчитан он от угла π
в отрицательном направлении. Потому и красный.) А нам для ответа нужен угол, отсчитанный правильно, от положительной полуоси ОХ, т.е. от угла 0 градусов.
А вот теперь надо определить второй угол… Это похитрее, чем в косинусах, да… Но логика нас спасёт! Как определить второй угол через х? Да легко! Треугольнички на картинке одинаковые, и красный угол х равен углу х . Только отсчитан он от угла π
в отрицательном направлении. Потому и красный.) А нам для ответа нужен угол, отсчитанный правильно, от положительной полуоси ОХ, т.е. от угла 0 градусов.
Наводим курсор на рисунок и всё видим. Первый угол я убрал, чтобы не усложнял картинку. Интересующий нас угол (нарисован зелёным) будет равен:
π — х
Икс мы знаем, это π /6 . Стало быть, второй угол будет:
π — π /6 = 5π /6
Снова вспоминаем про добавку полных оборотов и записываем вторую серию ответов:
х 2 = 5π /6 + 2π n, n ∈ Z
Вот и всё. Полноценный ответ состоит из двух серий корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Уравнения с тангенсом и котангенсом можно легко решать по тому же общему принципу решения тригонометрических уравнений. Если, конечно, знаете, как нарисовать тангенс и котангенс на тригонометрическом круге.
Если, конечно, знаете, как нарисовать тангенс и котангенс на тригонометрическом круге.
В приведённых выше примерах я использовал табличное значение синуса и косинуса: 0,5. Т.е. одно из тех значений, которые ученик знать обязан. А теперь расширим наши возможности на все остальные значения. Решать, так решать!)
Итак, пусть нам надо решить вот такое тригонометрическое уравнение:
Такого значения косинуса в кратких таблицах нет. Хладнокровно игнорируем этот жуткий факт. Рисуем круг, отмечаем на оси косинусов 2/3 и рисуем соответствующие углы. Получаем вот такую картинку.
Разбираемся, для начала, с углом в первой четверти. Знать бы, чему равен икс, сразу бы ответ записали! Не знаем… Провал!? Спокойствие! Математика своих в беде не бросает! Она на этот случай придумала арккосинусы. Не в курсе? Зря. Выясните, Это много проще, чем вы думаете. По этой ссылке ни одного мудрёного заклинания насчёт «обратных тригонометрических функций» нету… Лишнее это в данной теме.
Если вы в курсе, достаточно сказать себе: «Икс — это угол, косинус которого равен 2/3». И сразу, чисто по определению арккосинуса, можно записать:
Вспоминаем про дополнительные обороты и спокойно записываем первую серию корней нашего тригонометрического уравнения:
х 1 = arccos 2/3 + 2π n, n ∈ Z
Практически автоматом записывается и вторая серия корней, для второго угла. Всё то же самое, только икс (arccos 2/3) будет с минусом:
х 2 = — arccos 2/3 + 2π n, n ∈ Z
И все дела! Это правильный ответ. Даже проще, чем с табличными значениями. Ничего вспоминать не надо.) Кстати, самые внимательные заметят, что эта картинка с решением через арккосинус ничем, в сущности, не отличается от картинки для уравнения cosx = 0,5.
Именно так! Общий принцип на то и общий! Я специально нарисовал две почти одинаковые картинки. Круг нам показывает угол х по его косинусу. Табличный это косинус, или нет — кругу неведомо. Что это за угол, π
/3, или арккосинус какой — это уж нам решать.
Что это за угол, π
/3, или арккосинус какой — это уж нам решать.
С синусом та же песня. Например:
Вновь рисуем круг, отмечаем синус, равный 1/3, рисуем углы. Получается вот такая картина:
И опять картинка почти та же, что и для уравнения sinx = 0,5. Опять начинаем с угла в первой четверти. Чему равен икс, если его синус равен 1/3 ? Не вопрос!
Вот и готова первая пачка корней:
х 1 = arcsin 1/3 + 2π n, n ∈ Z
Разбираемся со вторым углом. В примере с табличным значением 0,5 он был равен:
π — х
Так и здесь он будет точно такой же! Только икс другой, arcsin 1/3. Ну и что!? Можно смело записывать вторую пачку корней:
х 2 = π — arcsin 1/3 + 2π n, n ∈ Z
Это совершенно правильный ответ. Хотя и выглядит не очень привычно. Зато понятно, надеюсь.)
Вот так решаются тригонометрические уравнения с помощью круга. Этот путь нагляден и понятен. Именно он спасает в тригонометрических уравнениях с отбором корней на заданном интервале, в тригонометрических неравенствах — те вообще решаются практически всегда по кругу. Короче, в любых заданиях, которые чуть сложнее стандартных.
Короче, в любых заданиях, которые чуть сложнее стандартных.
Применим знания на практике?)
Решить тригонометрические уравнения:
Сначала попроще, прямо по этому уроку.
Теперь посложнее.
Подсказка: здесь придётся поразмышлять над кругом. Лично.)
А теперь внешне простенькие… Их ещё частными случаями называют.
sinx = 0
sinx = 1
cosx = 0
cosx = -1
Подсказка: здесь надо сообразить по кругу, где две серии ответов, а где одна… И как вместо двух серий ответов записать одну. Да так, чтобы ни один корень из бесконечного количества не потерялся!)
Ну и совсем простые):
sinx = 0,3
cosx = π
tgx = 1,2
ctgx = 3,7
Подсказка: здесь надо знать, что такое арксинус, арккосинус? Что такое арктангенс, арккотангенс? Самые простые определения. Зато вспоминать никаких табличных значений не надо!)
Ответы, разумеется, в беспорядке):
х 1 = arcsin0,3 + 2π
n, n ∈ Z
х 2 = π
— arcsin0,3 + 2
Не всё получается? Бывает. Прочтите урок ещё раз. Только вдумчиво (есть такое устаревшее слово…) И по ссылкам походите. Главные ссылки — про круг. Без него в тригонометрии — как дорогу переходить с завязанными глазами. Иногда получается.)
Прочтите урок ещё раз. Только вдумчиво (есть такое устаревшее слово…) И по ссылкам походите. Главные ссылки — про круг. Без него в тригонометрии — как дорогу переходить с завязанными глазами. Иногда получается.)
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Урок и презентация на тему: «Решение простейших тригонометрических уравнений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Программная среда «1С: Математический конструктор 6. 1″
1″
Что будем изучать:
1. Что такое тригонометрические уравнения?
3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.
Что такое тригонометрические уравнения?
Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.
Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции.
Повторим вид решения простейших тригонометрических уравнений:
1)Если |а|≤ 1, то уравнение cos(x) = a имеет решение:
X= ± arccos(a) + 2πk
2) Если |а|≤ 1, то уравнение sin(x) = a имеет решение:
3) Если |а| > 1, то уравнение sin(x) = a и cos(x) = a не имеют решений 4) Уравнение tg(x)=a имеет решение: x=arctg(a)+ πk
5) Уравнение ctg(x)=a имеет решение: x=arcctg(a)+ πk
Для всех формул k- целое число
Простейшие тригонометрические уравнения имеют вид: Т(kx+m)=a, T- какая либо тригонометрическая функция.
 n – минус один в степени n.
n – минус один в степени n.Ещё примеры тригонометрических уравнений.
Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3
Решение:
А) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:
X/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk
Ответ: x=5πk, где k – целое число.
Б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Ответ: x=2π/9 + πk/3, где k – целое число.
Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке .
Решение:
Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
X= ± π/16+ πk/2;
Теперь давайте посмотрим какие корни попадут на наш отрезок. При k
При k=0, x= π/16, мы попали в заданный отрезок .
При к=1, x= π/16+ π/2=9π/16, опять попали.
При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.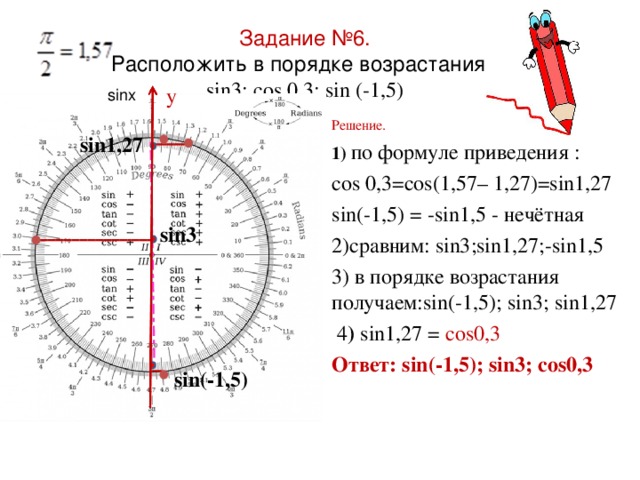
Ответ: x= π/16, x= 9π/16
Два основных метода решения.
Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.
Решим уравнение:
Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).
В результате замены получим: t 2 + 2t -1 = 0
Найдем корни квадратного уравнения: t=-1 и t=1/3
Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.
X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Ответ: x= -π/4+πk; x=arctg(1/3) + πk.
Пример решения уравнения
Решить уравнений: 2sin 2 (x) + 3 cos(x) = 0
Решение:
Воспользуемся тождеством: sin 2 (x) + cos 2 (x)=1
Наше уравнение примет вид:2-2cos 2 (x) + 3 cos (x) = 0
2 cos 2 (x) — 3 cos(x) -2 = 0
Введем замену t=cos(x): 2t 2 -3t — 2 = 0
Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2
Тогда cos(x)=2 и cos(x)=-1/2.
Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.
Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Ответ: x= ±2π/3 + 2πk
Однородные тригонометрические уравнения.
Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.
Уравнения вида
однородными тригонометрическими уравнениями второй степени.
Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.
Решить уравнение:
Пример: cos 2 (x) + sin(x) cos(x) = 0
Решение:
Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0
Тогда нам надо решить два уравнения:
Cos(x)=0 и cos(x)+sin(x)=0
Cos(x)=0 при x= π/2 + πk;
Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Ответ: x= π/2 + πk и x= -π/4+πk
Как решать однородные тригонометрические уравнения второй степени?
Ребята, придерживайтесь этих правил всегда!
1. Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:
Делаем замену переменной t=tg(x) получаем уравнение:
Решить пример №:3
Решить уравнение:
Решение:
Разделим обе части уравнения на косинус квадрат:
Делаем замену переменной t=tg(x): t 2 + 2 t — 3 = 0
Найдем корни квадратного уравнения: t=-3 и t=1
Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
Tg(x)=1 => x= π/4+ πk
Ответ: x=-arctg(3) + πk и x= π/4+ πk
Решить пример №:4
Решить уравнение:
Решение:
Преобразуем наше выражение:
Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk
Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk
Решить пример №:5
Решить уравнение:
Решение:
Преобразуем наше выражение:
Введем замену tg(2x)=t:2 2 — 5t + 2 = 0
Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2
Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2
2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2
Задачи для самостоятельного решения.

1) Решить уравнение
А) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7
2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].
3) Решить уравнение: ctg 2 (x) + 2ctg(x) + 1 =0
4) Решить уравнение: 3 sin 2 (x) + √3sin (x) cos(x) = 0
5) Решить уравнение:3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0
6)Решить уравнение:cos 2 (2x) -1 — cos(x) =√3/2 -sin 2 (2x)
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Универсальная тригонометрическая подстановка
Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.
 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3. - Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ. ) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
) Ученик обязан знать, что arcsin 0,5 = π
/6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т. п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Тригонометрические задачи с решениями
Задача 1 :
Угол подъема верха здания на расстоянии 50 м от его подножия в горизонтальной плоскости равен 60°. Найдите высоту здания.
Решение :
Нарисуйте эскиз.
Здесь AB представляет собой высоту здания, BC представляет собой расстояние от здания до точки наблюдения.
В прямоугольном треугольнике ABC сторона, лежащая против угла 60°, известна как противоположная сторона (AB), сторона, лежащая против угла 90° называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (BC).
Теперь нам нужно найти длину стороны АВ.
Tanθ = противоположная сторона/соседняя сторона
TAN60 ° = AB/BC
√3 = AB/50
√3 x 50 = AB
AB = 50√3
Приблизительное значение √3 — 1,732
AB = 50 (1,732)
AB = 86,6 м
Итак, высота здания 86,6 м.
Задача 2 :
Лестница, приставленная к стене так, что она достигает вершины стены высотой 6 м, и лестница наклонена под углом 60°. Найдите, на каком расстоянии лестница от подножия стены.
Решение :
Нарисуйте эскиз.
Здесь AB представляет собой высоту стены, BC представляет собой расстояние между стеной и основанием лестницы, а AC представляет собой длину лестницы.
В прямоугольном треугольнике ABC сторона, лежащая против угла 60°, называется противоположной стороной (AB), сторона, лежащая против угла 90°, называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной ( ДО Н.Э).
Теперь нам нужно найти расстояние между подошвой лестницы и стеной. То есть нам надо найти длину BC.
То есть нам надо найти длину BC.
tanθ = противоположная сторона/прилегающая сторона
tan60° = AB/BC
√3 = 6/BC
BC = 6/√3
BC = (6/√3) x (√3/√ 3)
ВС = (6√3)/3
ВС = 2√3
Приблизительное значение √3 равно 1,732.
BC = 2 (1,732)
BC = 3,464 м
Итак, расстояние между подошвой лестницы и стеной равно 3,464 м.
Задача 3 :
Веревка воздушного змея имеет длину 100 метров и наклон веревки относительно земли составляет 60°. Найдите высоту воздушного змея, считая, что тетива не имеет провисания.
Решение:
Нарисуйте эскиз.
Здесь AB представляет высоту воздушного змея от земли, BC представляет собой расстояние воздушного змея от точки наблюдения.
В прямоугольном треугольнике ABC сторона, лежащая против угла 60°, называется противолежащей стороной (AB), сторона, лежащая против угла 90°, называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (BC) .
Теперь нам нужно найти высоту стороны AB.
sinθ = противолежащая сторона/сторона гипотенузы
sinθ = AB/AC
sin60° = AB/100
√3/2 = AB/100
(√3/2) x 100 = AB
AB = 50√3 м
3 9 высота кайта от земли 50√3 м.
Задача 4 :
С вершины башни высотой 30 м мужчина наблюдает за основанием дерева под углом падения 30°. Найдите расстояние между деревом и башней.
Решение:
Нарисуйте эскиз.
Здесь AB представляет высоту башни, BC представляет собой расстояние между подошвой башни и подошвой дерева.
Теперь нам нужно найти расстояние между подошвой башни и подошвой дерева (ВС).
tanθ = противоположная сторона/прилегающая сторона
tan30° = AB/BC
1/√3 = 30/BC
BC = 30√3
Приблизительное значение √3 равно 1,7.
BC = 30(1,732)
BC = 51,96 м
Итак, расстояние между деревом и башней равно 51,96 м.
Задача 5 :
Мужчина хочет определить высоту маяка. Он измерил угол в точке А и обнаружил, что тангенс А = 3/4. Какова высота маяка, если А находится на расстоянии 40 м от основания?
Он измерил угол в точке А и обнаружил, что тангенс А = 3/4. Какова высота маяка, если А находится на расстоянии 40 м от основания?
Решение:
Нарисуйте эскиз.
Здесь BC представляет собой высоту маяка, AB представляет собой расстояние между маяком и точкой наблюдения.
В прямоугольном треугольнике ABC сторона, лежащая против угла A, называется противоположной стороной (BC), сторона, лежащая против угла 90°, называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (AB). ).
Теперь нам нужно найти высоту маяка (ВС).
tanA = противоположная сторона/прилегающая сторона
tanA = BC/AB
Дано: tanA = 3/4.
3/4 = БК/40
Умножьте каждую сторону на 40.
30 = БК
Итак, высота маяка 30 м.
Задача 6 :
Лестница, прислоненная к вертикальной стене, образует с землей угол 20°. Нижняя часть лестницы находится на расстоянии 3 м от стены. Найдите длину лестницы.
Найдите длину лестницы.
Решение:
Нарисовать эскиз.
Здесь AB представляет собой высоту стены, BC представляет собой расстояние от стены до основания лестницы.
В прямоугольном треугольнике ABC сторона, лежащая против угла 20°, называется противолежащей стороной (AB), сторона, лежащая против угла 90°, называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной ( ДО Н.Э).
Теперь нам нужно найти длину лестницы (AC).
cosθ = смежная сторона/сторона гипотенузы
Cosθ = BC/AC
Cos 20° = 3/AC
0,9397 = 3/AC
AC = 3/0,9396
AC = 3,192
Итак, длина лестницы составляет около 3,193 м.
Задача 7 :
Воздушный змей летит на высоте 65 м, привязанный к веревке. Если наклон струны относительно земли составляет 31°, найдите длину струны.
Решение:
Нарисуйте эскиз.
Здесь AB обозначает высоту воздушного змея. В прямоугольном треугольнике ABC сторона, лежащая против угла 31°, называется противоположной стороной (AB), а сторона, лежащая против угла 90° называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (BC).
В прямоугольном треугольнике ABC сторона, лежащая против угла 31°, называется противоположной стороной (AB), а сторона, лежащая против угла 90° называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (BC).
Теперь нам нужно найти длину строки AC.
sinθ = противоположная сторона/сторона гипотенузы
sinθ = ab/ac
sin31 ° = ab/ac
0,5150 = 65/AC
Ac = 65/0,5150
AC = 126,2 м
в округе, в энтузиаре, тот длина струны 126,2 м.
Задача 8 :
Длина нити между воздушным змеем и точкой на земле равна 90 м. Если нить образует угол θ с уровнем земли, так что тангенс θ = 15/8, какой высоты будет воздушный змей?
Решение:
Нарисуйте эскиз.
Здесь AB представляет высоту шара от земли. В прямоугольном треугольнике ABC сторона, лежащая против угла θ, называется противоположной стороной (AB), сторона, лежащая против угла 90°, называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (BC).
Теперь нам нужно найти длину стороны АВ.
tanθ = 15/8 —-> cotθ = 8/15
cscθ = √(1+ cot 2 θ)
cscθ = √(1 + 64/225)
cscθ2 = 5(2 + 64/225) + 64)/225
cscθ = √289/225
cscθ = 17/15 —-> sinθ = 15/17
Но, sinθ = противоположная сторона/сторона гипотенузы = AB/AC.
AB/AC = 15/17
AB/90 = 15/17
AB = 79,41
Итак, высота башни 79,41 м.
Задача 9 :
Наблюдается самолет, приближающийся к точке, которая находится на расстоянии 12 км от точки наблюдения и имеет угол места 50°. Найдите высоту самолета над землей.
Решение :
Нарисуйте эскиз.
Здесь AB обозначает высоту самолета от земли. В прямоугольном треугольнике ABC сторона, лежащая против угла 50°, называется противолежащей стороной (AB), сторона, лежащая против угла 90°, называется стороной гипотенузы (AC), а оставшаяся сторона называется прилежащей стороной (BC).
Теперь нам нужно найти длину стороны АВ.
На приведенном выше рисунке АВ обозначает высоту самолета над землей.
sinθ = противоположная сторона/гипотеновая сторона
sin50 ° = ab/ac
0,7660 = H/12
0,7660 x 12 = H
H = 9,192
SO, Высокая Высокая Высокая аэропорта выше. земля 9,192 км.
Задача 10 :
Воздушный шар соединен с метеорологической станцией кабелем длиной 200 м, наклоненным под углом 60° к земле. Найдите высоту шара от земли. (Представьте, что трос не провисает)
Решение :
Нарисуйте эскиз.
Здесь AB представляет высоту шара от земли. В прямоугольном треугольнике ABC сторона, лежащая против угла 60°, называется противолежащей стороной (AB), сторона, лежащая против угла 90°, называется гипотенузой (AC), а оставшаяся сторона называется прилежащей стороной (BC).
Теперь нам нужно найти длину стороны АВ.
На приведенном выше рисунке AB обозначает высоту воздушного шара над землей.
sinθ = противоположная сторона/сторона гипотенузы
AB = 100√3
AB = 100(1,732)
AB = 173,2 м
Итак, высота воздушного шара от земли 173,2 м.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. онлайнmath5all.com
Решение текстовых задач с помощью тригонометрии
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Тригонометрия Помощь » Треугольники » Прямоугольные треугольники » Решение словесных задач с помощью тригонометрии
Ожидая, пока ваша сестра закончит прыжок с тарзанки, вы решаете выяснить, какой высоты платформа, с которой она прыгает. Вы стоите в футах от основания платформы, а угол подъема от вашего положения до вершины платформы составляет градусы. Сколько футов высота платформы?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете нарисовать следующий прямоугольный треугольник, используя информацию, полученную в вопросе:
Поскольку вы хотите найти высоту платформы, вам нужно будет использовать касательную.
Обязательно округляйте до десятичных знаков.
Сообщить об ошибке
Когда угол подъема солнца составляет градусы, флагшток отбрасывает тень длиной фут. В футах, какая высота флагштока?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете нарисовать следующий прямоугольный треугольник из информации, полученной в вопросе.
Чтобы найти высоту флагштока, вам нужно будет использовать тангенс.
Обязательно округляйте до десятичных знаков.
Высота флагштока футов.
Сообщить об ошибке
Лестница длиной в фут опирается на стену дома под углом в градусы. В футах, как далеко до стены дома доходит лестница?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете нарисовать следующий прямоугольный треугольник из информации, данной в вопросе:
Чтобы узнать, как далеко поднимается лестница, вам нужно будет использовать синус.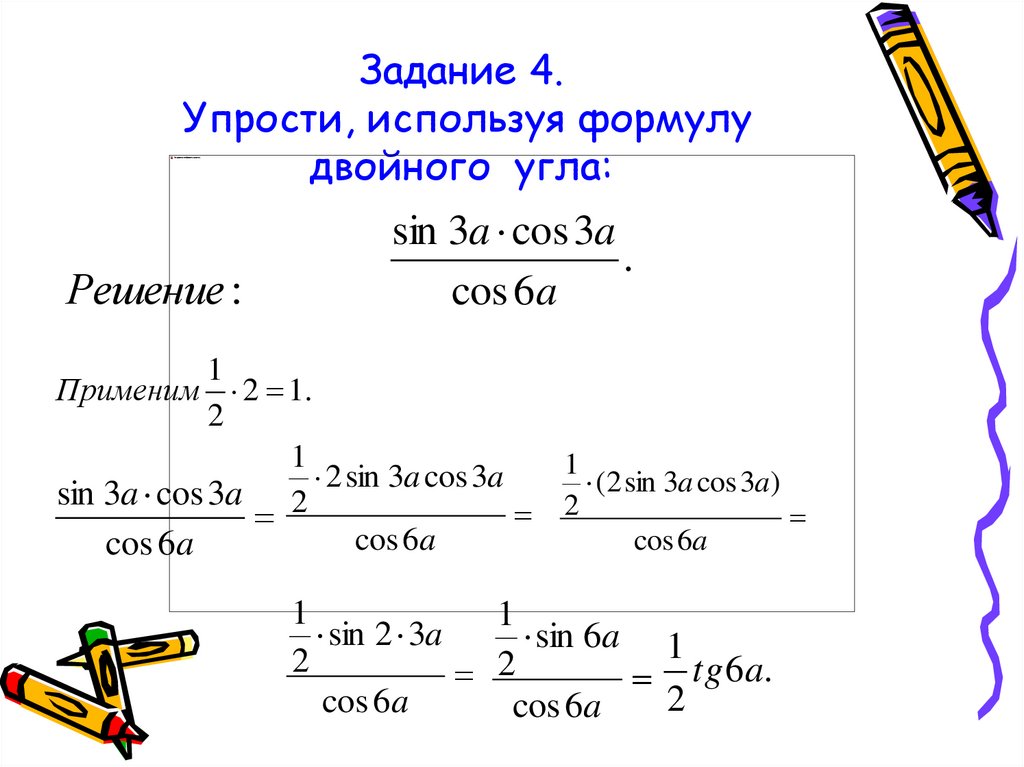
Сообщить об ошибке
В прямоугольном треугольнике ABC, где угол A равен 90 градусам, сторона AB равна 15 , а сторона AC равна 36 , какова длина стороны BC?
Возможные ответы:
Этот треугольник не может существовать.
Правильный ответ:
Пояснение:
Этот треугольник может существовать. Так как угол прямой, мы можем использовать теорему Пифагора, где это гипотенуза:
Сообщить об ошибке. Какой длины провод, w? Округлите ответ до двух знаков после запятой.
Возможные ответы:
21,83 метра
23,81 метра
25 метров
28,31 метра
6 9:035823,81 метра
Объяснение:
Чтобы разобраться в задаче, начните с рисования диаграммы. Обозначьте угол возвышения как 25 o , высоту между землей и местом, где провод касается флагштока, как 10 метров, и нашу неизвестную длину провода как w.
Обозначьте угол возвышения как 25 o , высоту между землей и местом, где провод касается флагштока, как 10 метров, и нашу неизвестную длину провода как w.
Теперь нам просто нужно найти w, используя информацию, приведенную на диаграмме. Нам нужно спросить себя, какие части треугольника 10 и w относятся к нашему известному углу 25 или . 10 противоположно этому углу, а w — гипотенуза. Теперь спросите себя, какие триггерные функции связывают противоположность и гипотенузу. Есть два правильных варианта: синус и косеканс. Использование синуса, вероятно, является наиболее распространенным, но оба варианта подробно описаны ниже.
Мы знаем, что синус данного угла равен гипотенузе, деленной на гипотенузу, а косеканс угла равен гипотенузе, деленной на противоположность (обратное значение функции синуса). Следовательно:
(Используйте калькулятор в режиме градусов, чтобы найти это значение после округления до двух знаков после запятой)
метры
Чтобы решить эту задачу вместо использования функции косеканса, мы получим:
калькулятор в режиме градусов, чтобы найти это после округления до двух знаков после запятой)
метров
Причина, по которой мы получили 23,7 здесь и 23,81 выше, связана с различиями в округлении в середине задачи.
Обратите внимание, что выбор ответа правильный на основе теоремы Пифагора, но не использует всю предоставленную информацию для поиска точного решения с округлением до двух знаков после запятой.
Сообщить об ошибке
Когда солнце находится на высоте 22 o над горизонтом, какова длина тени здания высотой 60 метров?
Возможные ответы:
65 метров
24 метра
82 метра
150 метров
162 метра
Правильный ответ:
150 метров
Объяснение:
Чтобы решить эту проблему, сначала настройте диаграмму, которая показывает всю информацию, указанную в задаче.
Далее нам нужно интерпретировать, какая длина стороны соответствует тени здания, что и просит нас найти задача. Гипотенуза или основание треугольника? Подумайте о том, когда вы смотрите на тень. Когда вы видите тень, вы видите ее на чем-то другом, например, на земле, тротуаре или другом объекте. Мы видим тень на земле, которая соответствует основанию нашего треугольника, так что это то, что мы будем решать. Мы назовем эту базу b.
Когда вы видите тень, вы видите ее на чем-то другом, например, на земле, тротуаре или другом объекте. Мы видим тень на земле, которая соответствует основанию нашего треугольника, так что это то, что мы будем решать. Мы назовем эту базу b.
Затем подумайте, какие триггерные функции связывают наш известный угол 22 o с основанием (или смежными) и противоположными сторонами треугольника. Если вы подумали о касательной (или котангенсе), вы правы! Мы это знаем и . Для простоты мы будем использовать тангенс для решения этой задачи. У нас есть:
(Используйте калькулятор и округлите до двух, чтобы найти это)
метров
Следовательно, длина тени, отбрасываемой зданием, составляет 150 метров.
Если вы получили один из неправильных ответов, возможно, вы использовали синус или косинус вместо тангенса, или вы могли использовать функцию тангенса, но инвертировали дробь (соседняя над противоположной вместо противоположной над соседней).
Сообщить об ошибке
С вершины маяка, который находится на высоте 105 метров над уровнем моря, угол погружения лодки составляет 19 o . На каком расстоянии от лодки находится вершина маяка?
Возможные ответы:
36,15 метра
318,18 метра
423,18 метра
110,53 метра
Правильный ответ:
318,18 метра 3
3 Объяснение: Чтобы решить эту проблему, нам нужно создать диаграмму, но для того, чтобы создать эту диаграмму, нам нужно понять словарный запас, который используется в этом вопросе. Следующая диаграмма поясняет разницу между углом наклона (угол, направленный вниз; относится к нашей задаче) и углом подъема (угол, направленный вверх; относится к другим задачам, но не к этой конкретной). Представьте, что вершина синей линии высоты — это вершина маяка, зеленая линия с надписью GroundHorizon — это уровень моря, а точка B — это место, где находится лодка.
Объединяя данную информацию и эту диаграмму, мы знаем, что угол падения составляет 19 o и высота (синяя линия) составляет 105 метров. Хотя синяя линия нарисована слева на диаграмме, мы можем предположить, что она такая же, как и справа. Затем нам нужно подумать о триггерной функции, которая связывает данный угол, данную сторону и сторону, для которой мы хотим найти. Высота или синяя линия находится напротив известного угла, и мы хотим найти расстояние между лодкой (точка B) и вершиной маяка. Это означает, что мы хотим определить длину гипотенузы или красной линии с надписью SlantRange. Функция синуса связывает противоположность и гипотенузу, поэтому мы будем использовать ее здесь. Получаем:
(где d – расстояние между верхушкой маяка и лодкой)
(используя калькулятор в режиме градусов и округляя до двух цифр, получаем это )
метры
Сообщить об ошибке
Ангелина только что получила новую машину, и она хочет покататься на ней на вершине горы и посетить смотровую площадку. Если она проедет 4000 м по дороге, наклоненной под углом 22 90 246 o 90 247 к горизонтали, то на какой высоте над отправной точкой она окажется, когда доберется до смотровой площадки?
Если она проедет 4000 м по дороге, наклоненной под углом 22 90 246 o 90 247 к горизонтали, то на какой высоте над отправной точкой она окажется, когда доберется до смотровой площадки?
Possible Answers:
3708.74 meters
9.37 meters
1480 meters
10677.87 meters
1616.1 meters
Correct answer:
1480 meters
Объяснение:
Как и в случае с другими задачами на триггеры, начните с наброска диаграммы имеющейся и запрашиваемой информации.
Анджелина и ее машина начинаются в левом нижнем углу диаграммы. Дорога, по которой она едет, является гипотенузой нашего треугольника, а угол дороги относительно плоской поверхности равен 22 9 .0246 или . Поскольку мы хотим найти изменение высоты (также называемое возвышением), мы хотим определить разницу между ее конечной и начальной высотой, которая на диаграмме обозначена x. Затем рассмотрим, какая тригонометрическая функция связывает вместе угол, противоположные стороны и гипотенузу относительно него; правильный — синус. Затем настройте:
Затем рассмотрим, какая тригонометрическая функция связывает вместе угол, противоположные стороны и гипотенузу относительно него; правильный — синус. Затем настройте:
(используя калькулятор в режиме градусов и округлив до двух знаков после запятой, мы получаем это )
Следовательно, разница в высоте между начальной и конечной точками Анджелины составляет 1480 метров.
Сообщить об ошибке
Два здания с плоскими крышами находятся на расстоянии 50 футов друг от друга. Более короткое здание имеет высоту 40 футов. Угол возвышения от крыши более короткого здания до края более высокого здания составляет 48 o . Какова высота более высокого здания?
Возможные ответы:
95,5 футов
73,5 футов
55,5 футов
40 футов
77,2 фута
Правильный ответ:
95,5 футов . Пояснение: Чтобы решить эту задачу, давайте начнем с рисования схемы двух зданий, расстояния между ними и угла между вершинами двух зданий. Затем отметьте данные длины и угол. Нас просят найти высоту более высокого здания, но на этой диаграмме нет треугольника, одна из сторон которого равна всей высоте большего (самого правого и синего) здания. Однако вместо этого мы можем найти расстояние , а затем прибавить его к 40-футовой высоте более короткого здания, чтобы найти полную высоту более высокого здания. Начните с поиска : Помните, что это не полная высота большого здания. Чтобы найти это, нам нужно добавить футы. Следовательно, более высокое здание имеет высоту 95,5 футов. Сообщить об ошибке Два здания с плоскими крышами находятся на расстоянии 80 футов друг от друга. Более короткое здание имеет высоту 55 футов. Угол возвышения от крыши более короткого здания до края более высокого здания составляет 32 o . Possible Answers: 104.6 feet 49.6 feet 97.4 feet 129.6 feet 122.8 feet Correct answer: 104.6 feet Пояснение: Чтобы решить эту задачу, давайте начнем с рисования схемы двух зданий, расстояния между ними и угла между вершинами двух зданий. Затем отметьте данные длины и угол. Нас просят найти высоту более высокого здания, но на этой диаграмме нет треугольника, одна из сторон которого равна всей высоте большего (крайнего справа и синего) здания. Однако вместо этого мы можем найти расстояние , а затем прибавить его к 40-футовой высоте более короткого здания, чтобы найти полную высоту более высокого здания. Начните с поиска : Помните, что это не полная высота большого здания. Сообщить об ошибке ← Назад 1 2 Далее → Уведомление об авторских правах 6 Диагностические тесты
155 практических тестов
Вопрос дня
Карточки
Learn by Concept Решение треугольников – термин для решения основной тригонометрической задачи нахождения параметров треугольника, включающих угол и длину сторон. Треугольник может располагаться либо на плоскости, либо на сфере. На рисунке 1 показан треугольник со сторонами a, b и c и углами A, B и C соответственно. Треугольник общей формы имеет 6 основных компонентов. Вся тема посвящена поиску этих компонентов треугольника. Рисунок 1: Треугольник При решении треугольника может быть несколько сценариев, иногда отсутствует определенная сторона, а иногда отсутствуют углы. Если даны два угла, то можно найти третий угол. Рассмотрим следующую фигуру, где нам известны только угол A и угол B, и нас интересует нахождение третьего угла C. Мы знаем, что сумма всех углов треугольника равна 180 o , т.е. ∠A Рис.0003 На приведенном выше рисунке, если ∠A = 89 o и ∠C = 56 o , найдите значение ∠B. Решение: Мы знаем, что сумма всех углов треугольника равна 180 o . ↑B = 180 O — (секрет + ♂) См. Рисунок 3: Даны два угла и одна сторона Для этого сценария мы можем использовать закон синуса, который можно использовать для нахождения остальных сторон этого треугольника. Третий угол можно найти методом, рассмотренным в предыдущей теме относительно суммы всех углов треугольника равной 180 o . Закон синусов или правило синусов — это уравнение, связывающее длину сторон произвольного треугольника с синусом его угла. Это один из двух законов тригонометрии, который обычно используется для нахождения длин и углов в общем треугольнике. Рассмотрим снова фигуру 1. Закон синусов гласит, что если разделить сторону «а» на синус угла «А», она будет равна стороне «b», деленной на синус угла «В», а также равна стороне «с». деленная на синус угла ‘С’. Математически это можно записать так: Где a, b и c — стороны, а A, B и C — противоположные углы этих сторон соответственно. В некоторых ссылках вы увидите, что некоторые авторы установили правило синусов как обратное отношение вышеприведенных соотношений. Следовательно, обе формы верны, т. е. Из приведенных выше уравнений ясно, что при любых двух углах и любой стороне (за исключением угла между двумя сторонами, который мы обсудим в следующем разделе), мы можем найти остальные компоненты треугольника. Этот метод также называется триангуляцией. Например, не обязательно, чтобы два заданных угла были такими, противоположные стороны которых нам известны. Мы можем найти третий угол, используя закон: сумма всех углов треугольника = 180 или . Найдя этот третий угол, мы можем применить правило синусов, чтобы найти другие параметры. Пример : Найдите длину «а» на рисунке 1, если ∠A = 40 o , ∠C = 70 o и сторона c = 5 см. Решение : Используя правило синусов, мы можем решить этот треугольник. Посмотрите на параметры и затем примените соответствующее уравнение, чтобы найти длину a. Крест умножить. a = 3,42 см Правило синусов в этом случае не работает, потому что отсутствуют углы, противоположные данным сторонам. Также отсутствует противоположная сторона, к которой дан угол. Рассмотрим следующий рисунок треугольника, в котором даны две стороны и угол между ними. Из этих данных мы должны решить треугольник. Существует еще одно правило, называемое правилом косинуса, согласно которому мы должны знать длины двух сторон, скажем, здесь b и c, и угол A между этими двумя сторонами. Сторону а можно определить по закону косинусов: То же верно и для других сторон: После нахождения всех трех сторон вы можете найти и угол, перестроив приведенные выше уравнения или применив правило синусов. Пример : Если длина b = 10 футов, c = 12 футов и угол A = 70 o на рисунке 1, найдите длину a. Решение : Имея две стороны и угол между ними, мы должны обязательно применить здесь правило косинусов. Подключите значения, b = 10 футов, C = 12 футов и угол A = 70 O A = 12,7 FT Посмотрим, какое правило здесь работает. Нам даны только три стороны, и мы хотим решить треугольник, т.е. нужно найти остальные 3 угла. На рис. 6 показан этот сценарий. Давайте посмотрим, можем ли мы применить здесь правило синусов. Рисунок 5: Три стороны и угол не указан Предположим, мы хотим найти угол B (см. рис. 1) и нам известны стороны a, b и c. Правило синусов: Мы можем видеть, что, подставив все заданные стороны в отношения выше, мы не можем найти значение углов. Мы даже можем получить три уравнения, но у нас недостаточно данных, чтобы вычислить значение любого угла. Следовательно, правило синусов здесь не работает, поскольку ни один из углов нам не известен. Правило косинуса равно 92$ Разделите обе части на 2ac. Возьмем обратные косинусы с обеих сторон. Пример: Даны три стороны треугольника: a = 10см, b = 8см, c = 7см Найдите угол C. Мы можем изменить эту формулу косинуса, чтобы получить ответ . Выберите подходящее уравнение из приведенных выше уравнений. Нам нужно найти угол C, поэтому мы выберем: Вставьте заданные значения. C = 52,62 o Если вам нужно найти другие углы этого треугольника, используйте закон синусов. Обратите внимание, что мы используем закон синусов в тех случаях, когда искомый угол меньше по сравнению с другими углами, потому что функция обратного синуса дает ответы меньше 90 o даже для углов больше 90 o . Следовательно, закон косинусов более надежен, чем закон синусов для определения угла. Думайте о тригонометрии как о наборе инструментов. В нем есть ряд полезных законов и геометрических методов для решения конкретного треугольника для любых неизвестных. Правило синусов и правило косинусов являются наиболее важными правилами. Существуют определенные шаги, необходимые для решения треугольника: Вопрос 1: Если один угол треугольника равен 50 o , а другой угол в два раза больше третьего, найдите два неизвестных угла. Вопрос 2: Решите следующий треугольник для стороны a и углов A и B. Вопрос 3: Дан треугольник ABC с углом ABC = θ. Найдите по теореме косинусов значение стороны CA, если длина AB = 7 см, длина BC = 9см и угол θ = 60 o . Вопрос 4: Дан вам равнобедренный треугольник (у которого две стороны равны) с длиной двух сторон, равных x, а между ними 80 o . Найдите третью сторону, если она в два раза больше первых двух сторон. Вопрос 5: Учитывая, что треугольники ABD и CBD подобны. Вопрос 6: Поврежденная башня огорожена из соображений безопасности. Чтобы найти расстояние до ближайшего дома, человек становится в точке Р и измеряет угол возвышения как 25 или . Затем он проходит 15 метров прямо от дома к основанию башни до точки Q, где угол возвышения становится равным 45 o . Рассчитать расстояние от дома до башни. Вопрос 7: Учитывая, что котангенс угла θ равен 0,57. Если начальная и конечная стороны угла θ равны 20 футам и 30 футам, найдите сторону, противоположную углу θ. Уравнение, включающее тригонометрические функции, называется 9\circ k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(. Это наиболее общее решение уравнения. Часто часть, которая говорит «for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)» опускается, так как обычно понял, что \(k \) варьируется для всех целых чисел.Общее решение в радианах будет: \[ А ~=~ 0,6435 \;+\; \pi k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)} 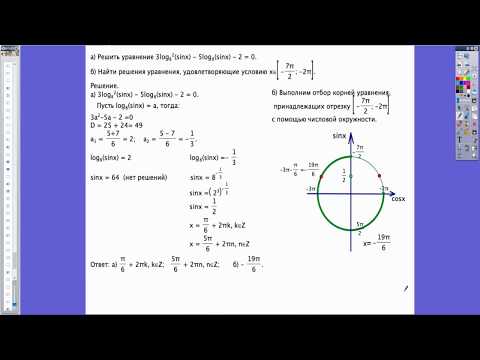 0003
0003 Какова высота более высокого здания?
Какова высота более высокого здания?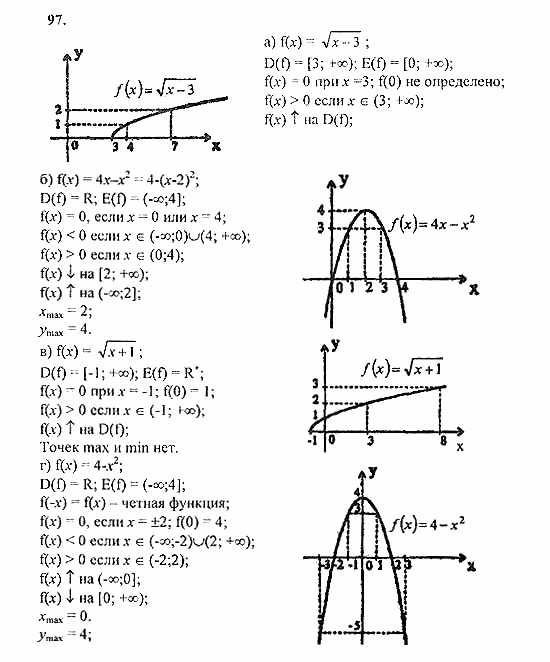 Чтобы найти это, нам нужно добавить футы. Следовательно, более высокое здание имеет высоту 104,6 фута.
Чтобы найти это, нам нужно добавить футы. Следовательно, более высокое здание имеет высоту 104,6 фута. Все ресурсы по тригонометрии
Тригонометрические решения треугольников Примеры – MathsTips.com
 Существуют разные методы решения каждого из этих треугольников с помощью тригонометрических функций. Мы обсудим каждый из этих примеров.
Существуют разные методы решения каждого из этих треугольников с помощью тригонометрических функций. Мы обсудим каждый из этих примеров. 1. Два угла и сторона не указана
♂ = 180 O — (89 O + 56 O )
Ϫb = 180 O — 145444444444444444444444444444444444444444447447 402447)
♂ = 180 O — 140247) . )
∠B = 35 o 2. Два угла и одна сторона / один угол и две стороны (без учета угла)
 рисунок 3, для двух углов A и B и стороны b стандартный метод решения такого рода задач требует от нас использования фундаментальных соотношений.
рисунок 3, для двух углов A и B и стороны b стандартный метод решения такого рода задач требует от нас использования фундаментальных соотношений. Закон синусов (или правило синусов)
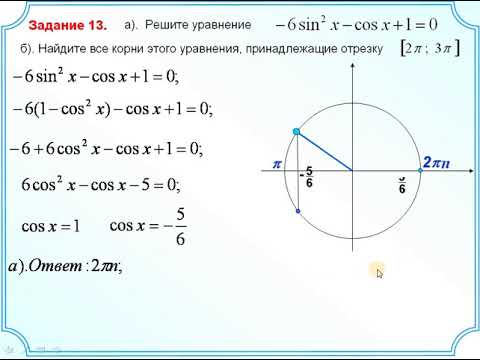

3. Две стороны и угол между ними
Правило косинуса

4. Три стороны и угла
 Применим к этой задаче правило косинусов.
Применим к этой задаче правило косинусов. Также обратите внимание, что меньший угол — это тот, который противоположен более короткой стороне.
Также обратите внимание, что меньший угол — это тот, который противоположен более короткой стороне. Резюме
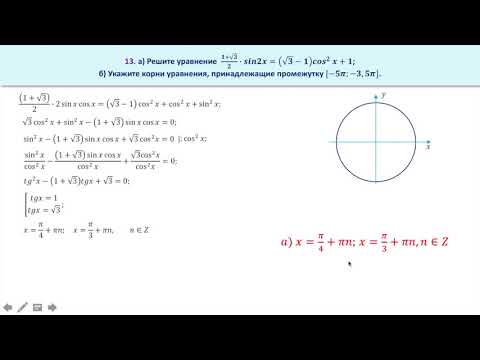 Углы можно проверить, сложив все 3 из них, и их сумма должна быть равна 180 o . Если вы нашли стороны по правилу косинусов, то стороны можно проверить, применив к ним правило синусов. Если ответы по обоим правилам совпадают, то вы проделали хорошую работу.
Углы можно проверить, сложив все 3 из них, и их сумма должна быть равна 180 o . Если вы нашли стороны по правилу косинусов, то стороны можно проверить, применив к ним правило синусов. Если ответы по обоим правилам совпадают, то вы проделали хорошую работу. Упражнение
 Найдите угол θ, если длина AB = BD = 10 см и угол CBD = 45 o .
Найдите угол θ, если длина AB = BD = 10 см и угол CBD = 45 o . 6.1: Решение тригонометрических уравнений — Математика LibreTexts
 ..\)}
..\)}
\nonumber \]
\nonumber \] Пример 6.1
92 \;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \pm\,\frac{1}{\sqrt{2}}
\quad \Rightarrow\quad \theta ~=~ \frac{\pi}{4}\;,~\frac{3\pi}{4}\;,~\frac{5\pi}{4}\;,~
\frac{7\pi}{4}~,
\nonumber \]
и, поскольку период косинуса равен \(2\pi \), мы должны добавить \(2\pi k \) к каждому из этих углы, чтобы получить общее решение. Но обратите внимание, что приведенные выше углы отличаются кратно \(\frac{\pi}{2} \). Итак, поскольку каждое кратное \(2\pi \) также кратно \(\frac{\pi}{2} \), мы можем объединить эти четыре отдельных ответа в один:
\[ \boxed{\theta ~=~ \frac{\pi}{4} \;+\; \frac{\pi}{2}\,k}
\qquad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \( . ..\)}
..\)}
\номер\]
Пример 6.3
Решите уравнение \(\;2\,\сек\;\тета ~=~ 1 \).
Решение:
Изоляция \(\;\sec\;\theta \) дает нам
\[ \sec\;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \frac{1}{\sec\;\theta} ~=~ 2~,
\nonumber \]
что невозможно. Таким образом, существует \(\fbox{нет решения}\). 92 \;+\; Икс \;-\; 1 ~=~ 0 \quad\Rightarrow\quad x ~=~ \frac{-1 \;\pm\; \sqrt{1 — (4)\,(-1)}}{
2\,(1)} ~=~ \frac{-1 \;\pm\; \sqrt{5}}{2} ~=~ -1,618\;,~0,618
\nonumber \]
по квадратичной формуле элементарной алгебры. Но \(-1,618 < -1 \), поэтому невозможно, чтобы \(\;\sin\theta = x = -1,618 \). Таким образом, мы должны иметь \(\;\sin\;\theta = x = 0,618 \). Следовательно, возможны два решения: \(\theta = 0,666\) рад в QI и его отражение \(\pi - \theta = 2,475\) рад вокруг оси \(y\) в QII. Добавление к ним кратных \(2\pi \) дает нам общее решение:
\[ \boxed{\theta ~=~ 0,666 \;+\; 2\pi k \quad\text{and}\quad 2,475 \;+\; 2\pi k}
\qquad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(. ..\)}
..\)}
\ nonumber \]
Пример 6.5
Решите уравнение \(\;\sin\;\theta ~=~ \tan\;\theta \).
Решение:
Попробовав тот же метод, что и в предыдущем примере, мы получим
\[\nonumber \begin{align*}
\sin\;\theta ~&=~ \tan\;\theta\ \\nonumber
\sin\;\theta ~&=~ \frac{\sin\;\theta}{\cos\;\theta}\\ \nonumber
\sin\;\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~\cos\;\theta \;-\; \sin\;\theta ~&=~ 0\\ \nonumber
\sin\;\theta~(\cos\;\theta \;-\; 1) ~&=~ 0\\ \nonumber
&\Rightarrow \quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ 1\\ \nonumber
&\Стрелка вправо\quad \theta ~=~ 0\;, ~\pi \quad\text{or}\quad \theta ~=~ 0\\ \nonumber
&\Стрелка вправо\quad \theta ~=~ 0\;,~\pi~,
\end{align*} \ нечисло \]
плюс кратные \(2\pi \). Итак, поскольку приведенные выше углы кратны \(\pi \), а каждое кратное \(2\pi \) кратно \(\pi \), мы можем объединить два ответа в один для общего решения: 9{-1} \frac{1}{2} = \frac{\pi}{3} \), есть два возможных решения для \(3\theta\): \(3\theta = \frac{\pi {3} \) в QI и его отражение \(-3\theta = -\frac{\pi}{3} \) вокруг оси \(x\) в QIV. Добавление к ним кратных \(2\pi \) дает нам:
Добавление к ним кратных \(2\pi \) дает нам:
\[ 3\theta ~=~ \pm\,\frac{\pi}{3} \;+\; 2\pi k \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\nonumber \ ]
Таким образом, разделив все на \(3 \), мы получим общее решение для \(\theta\):
\[ \boxed{\theta ~=~ \pm\,\frac{\pi}{9} \;+\; \frac{2\pi}{3} k}
\qquad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(. ..\)}
\nonumber \]
Пример 6.7
Решите уравнение \(\;\sin\;2\theta ~=~ \sin\;\theta \).
Решение:
Здесь мы используем формулу двойного угла для синуса:
\[\nonumber \begin{align*}
\sin\;2\theta ~&=~ \sin\;\theta\ \\nonumber
2\,\sin\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~(2\,\cos\;\theta \;-\;1) ~&=~ 0\\ \номер
&\Rightarrow\quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ \frac{1}{2}\\ \nonumber
&\Rightarrow \quad \theta ~=~ 0\;,~\pi \quad\text{or}\quad \theta ~=~ \pm\,\frac{\pi}{3}\\ \nonumber
&\Rightarrow\ quad \ boxed {\ theta ~ = ~ \ pi k \ quad \ text {and} \ quad \ pm \, \ frac {\ pi} {3} \; + \; 2\pi k}
\qquad\text{для \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(. ..\)}
..\)}
\ end{align*}
\nonumber \]
Пример 6.8
Решить уравнение \(\;2\,\sin\;\theta \;-\; 3\,\cos\;\theta ~=~ 1 \).
Рисунок 6.1.1: Скопируйте и вставьте заголовок сюда. (Авторское право; автор через источник)Решение
Мы будем использовать технику, которую обсуждали в главе 5, для нахождения амплитуды комбинации функций синуса и косинуса. Возьмите коэффициенты \(2\) и \(3\) при \(\;\sin\;\theta\) и \(\;-\cos\;\theta\) соответственно в приведенном выше уравнении и сделайте на них стороны прямоугольного треугольника, как на рис. 6.1.1. Пусть \(\phi \) будет углом, показанным в прямоугольном треугольнике. Участок длины \(3 >0 \) означает, что угол \(\phi \) находится над осью \(x\), а участок длины \(2>0 \) означает, что \(\phi \) находится справа от оси \(y\). Следовательно, \(\phi \) должен быть в QI. Гипотенуза имеет длину \(\sqrt{13} \) по теореме Пифагора, и, следовательно, \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) и \(\; \sin\;\theta = \frac{3}{\sqrt{13}} \). Мы можем использовать это, чтобы преобразовать уравнение, чтобы решить его следующим образом:
Мы можем использовать это, чтобы преобразовать уравнение, чтобы решить его следующим образом:
\[\nonumber \begin{align*}
2\,\sin\;\theta \;-\; 3\,\cos\;\theta ~&=~ 1\\ \nonumber
\sqrt{13}\,\left( \tfrac{2}{\sqrt{13}}\,\sin\;\theta \ ;-\; \tfrac{3}{\sqrt{13}}\,\cos\;\theta
\right) ~&=~ 1\\ \nonumber
\sqrt{13}\,( \cos\; \phi\;\sin\;\theta \;-\;\sin\;\phi\;\cos\;\theta ) ~&=~ 1\\ \nonumber
\sqrt{13}\,\sin\ ;(\theta — \phi) ~&=~ 1\quad\text{(по формуле вычитания синусов)}\\ \nonumber
\sin\;(\theta — \phi) ~&=~ \tfrac{1 }{\sqrt{13}}\\ \номер
&\Rightarrow\quad \theta — \phi ~=~ 0,281 \quad\text{or}\quad \theta — \phi ~=~ \pi — 0,281 = 2,861\\ \nonumber
&\Rightarrow\quad \theta ~=~ \фи \;+\; 0,281 \quad\text{or}\quad \theta ~=~ \phi \;+\; 2.861
\end{align*} \nonumber \]
Теперь, поскольку \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) и \(\phi \) в QI наиболее общим решением для \(\phi\) является \(\phi = 0,983 + 2\pi k \) для \(k=0 \), \(\pm\,1 \), \(\ ч\,2 \), \(. .. \). Итак, поскольку нам нужно было добавить кратные \(2\pi \) к решениям \(0,281 \) и \(2,861 \) в любом случае, наиболее общее решение для \(\theta \):
.. \). Итак, поскольку нам нужно было добавить кратные \(2\pi \) к решениям \(0,281 \) и \(2,861 \) в любом случае, наиболее общее решение для \(\theta \):
\[\begin{align*}
\тета ~&=~ 0,983 \;+\; 0,281 \;+\; 2\pi k\quad\text{and}\quad 0,983 \;+\; 2,861 \;+\; 2\pi k\\
&\Стрелка вправо\четверка \boxed{\theta ~=~ 1,264 \;+\; 2\pi k\quad\text{and}\quad 3.844 \;+\; 2\pi k}
\quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(…\)}
\ end{align*} \nonumber \]
Примечание: в примере 6.8, если уравнение было \(\;2\,\sin\;\theta \;+\; 3\,\cos\;\theta ~= ~ 1 \), то мы все равно использовали бы прямоугольный треугольник с длинами сторон \(2\) и \(3\), но вместо формулы вычитания использовали бы формулу сложения синусов.
Эта страница под названием 6.1: Решение тригонометрических уравнений распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Майклом Корралом посредством исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Майкл Коррал
- Лицензия
- ГНУ ФДЛ
- Версия лицензии
- 1,3
- Показать страницу Оглавление
- нет
- Теги
- источник@http://www.mecmath.net/trig/index.html
- тригонометрическое уравнение
Обучение решению задач по тригонометрии, включающих навыки алгебраического преобразования посредством обучения по аналогии и обучения по сравнению
Введение
Тема тригонометрии является частью школьной программы по математике средней школы. Тригонометрия является необходимым условием для изучения исчисления в старших классах математики и имеет важное значение для студентов, которые хотят изучать курсы естественных наук, технологий, инженерии и математики (STEM). Изучение задач по тригонометрии требует понимания нескольких взаимосвязанных математических понятий, таких как навыки алгебраического преобразования , знания геометрии и рассуждения о графическом представлении понятий . Из-за необходимости изучения нескольких взаимосвязанных понятий учащиеся испытывают большие трудности при изучении задач по тригонометрии (Блэкетт и Талл, 1991; Кендал и Стейси, 1998). Наша цель в этой концептуальной аналитической статье — подчеркнуть важность формирования навыков алгебраического преобразования для облегчения начального этапа изучения задач тригонометрии. Основное внимание здесь уделяется вычислению неизвестной стороны прямоугольного треугольника по известной стороне и углу, что может представлять проблему для многих учащихся.
Тригонометрия является необходимым условием для изучения исчисления в старших классах математики и имеет важное значение для студентов, которые хотят изучать курсы естественных наук, технологий, инженерии и математики (STEM). Изучение задач по тригонометрии требует понимания нескольких взаимосвязанных математических понятий, таких как навыки алгебраического преобразования , знания геометрии и рассуждения о графическом представлении понятий . Из-за необходимости изучения нескольких взаимосвязанных понятий учащиеся испытывают большие трудности при изучении задач по тригонометрии (Блэкетт и Талл, 1991; Кендал и Стейси, 1998). Наша цель в этой концептуальной аналитической статье — подчеркнуть важность формирования навыков алгебраического преобразования для облегчения начального этапа изучения задач тригонометрии. Основное внимание здесь уделяется вычислению неизвестной стороны прямоугольного треугольника по известной стороне и углу, что может представлять проблему для многих учащихся. В частности, мы утверждаем, что у некоторых учащихся могут возникнуть трудности при решении sin30° = 9.1398 x /5, скажем, несмотря на то, что научились решать аналогичную задачу, например, x /4 = 3. Для более сложных тригонометрических задач, таких как sin30° = 12/ x , где прочислительное является знаменателем , студентов учили «заменять» x на sin30°, а затем вычислять x (Источник: личное сообщение).
В частности, мы утверждаем, что у некоторых учащихся могут возникнуть трудности при решении sin30° = 9.1398 x /5, скажем, несмотря на то, что научились решать аналогичную задачу, например, x /4 = 3. Для более сложных тригонометрических задач, таких как sin30° = 12/ x , где прочислительное является знаменателем , студентов учили «заменять» x на sin30°, а затем вычислять x (Источник: личное сообщение).
Мы утверждаем, что такая стратегия обучения, описанная для задач тригонометрии, не соответствует навыкам алгебраического преобразования, которые необходимы для решения задач тригонометрии. Например, он не пытается связать предшествующие знания учащегося о решении 9 задач.1398 линейных уравнений с дробью к решению задач тригонометрии. Помимо этого, учащиеся могут испытывать большие трудности, когда пытаются различить два типа задач по тригонометрии, которые выглядят похожими, но все же концептуально отличаются друг от друга, следовательно, из-за относительного положения местоимения (т.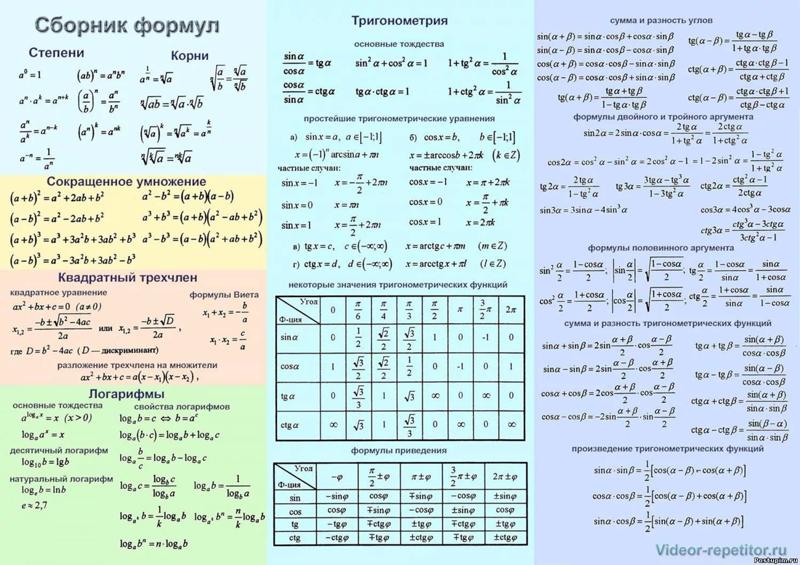 е. числитель против знаменатель) (Кендал и Стейси, 1998). Исходя из этого, преподавателям важно рассмотреть различные теоретические подходы, педагогические стратегии и/или образовательные программы, которые могли бы помочь учащимся приобрести соответствующие навыки для решения тригонометрических задач, различающихся расположением местоимения (т. знаменатель). Одна из возможностей, например, связана с использованием разных, но сопоставимых теорий обучения, которые могли бы способствовать эффективному обучению и способствовать осмысленному пониманию. Таким образом, цель этой статьи, расположенной в контексте актуальной темы тригонометрии, состоит в том, чтобы мы рассмотрели эффективность двух теорий обучения: обучение по аналогии и обучение по сравнению . Мы утверждаем, что этот анализ может стать основой для дальнейшего развития исследований, теоретических, эмпирических, концептуальных и/или методологических, в области эффективного применения различных теорий обучения.
е. числитель против знаменатель) (Кендал и Стейси, 1998). Исходя из этого, преподавателям важно рассмотреть различные теоретические подходы, педагогические стратегии и/или образовательные программы, которые могли бы помочь учащимся приобрести соответствующие навыки для решения тригонометрических задач, различающихся расположением местоимения (т. знаменатель). Одна из возможностей, например, связана с использованием разных, но сопоставимых теорий обучения, которые могли бы способствовать эффективному обучению и способствовать осмысленному пониманию. Таким образом, цель этой статьи, расположенной в контексте актуальной темы тригонометрии, состоит в том, чтобы мы рассмотрели эффективность двух теорий обучения: обучение по аналогии и обучение по сравнению . Мы утверждаем, что этот анализ может стать основой для дальнейшего развития исследований, теоретических, эмпирических, концептуальных и/или методологических, в области эффективного применения различных теорий обучения.
Концепция обучения по аналогии
Обучение по аналогии , подкрепленная теорией отображения структур (Gentner, 1983), обеспечила теоретическую основу для развития исследований в области изучения текстовых задач (Reed et al., 1985, 2012; Рид, 1987; Росс и Кеннеди, 1990 г.; Камминс, 1992). Теория структурного отображения подчеркивает построение «относительных общностей» между исходным примером (выученной проблемой) и целевой проблемой (новой проблемой) с точки зрения структуры проблемы. Задачи с двумя словами могут иметь разный контекст, но иметь схожую структуру проблемы, например: (i) «Если 20 % моих сбережений составляют 300 долларов, сколько у меня сбережений?» против (ii) «Джошуа платит 260 долларов в неделю за аренду, что составляет 25% его недельной зарплаты. Сколько Джошуа зарабатывает в неделю?» Использование Алгебра приближается к , мы можем составить два уравнения, например 20% x = 300 долларов и 25% x = 260 долларов соответственно, и решить для x . Поскольку эти два уравнения имеют общие реляционные элементы, они используют одну и ту же процедуру решения. Аналоговый перенос, вероятно, произойдет, если учащиеся смогут успешно сопоставить реляционные элементы между исходным примером и целевой проблемой. Действительно, аналогичное рассуждение изученной проблемы и новой проблемы позволяет учащимся восстановить схему изученной проблемы, которая применима для решения новой проблемы.
Поскольку эти два уравнения имеют общие реляционные элементы, они используют одну и ту же процедуру решения. Аналоговый перенос, вероятно, произойдет, если учащиеся смогут успешно сопоставить реляционные элементы между исходным примером и целевой проблемой. Действительно, аналогичное рассуждение изученной проблемы и новой проблемы позволяет учащимся восстановить схему изученной проблемы, которая применима для решения новой проблемы.
Холиок (1984) и Холиоак и Кох (1987) выделили четыре задачи для облегчения обучения по аналогии: построить мысленное представление исходного примера и целевой проблемы (Задание 1), найти исходный пример как аналог целевой задачи ( Задача 2), сопоставьте реляционные элементы исходного примера и целевой проблемы (Задача 3) и расширьте отображение для решения целевой проблемы (Задача 4). Авторы не предложили определенной последовательности для выполнения этих четырех задач и не указали, какая задача или задачи имеют решающее значение для стимулирования обучения по аналогии.
В исследованиях сообщалось о пользе включения вспомогательных сигналов , таких как подсказка (Novick and Holyoak, 1991) или напоминание (Ross, 1984) для доступа к исходному примеру. Таким образом, предоставление подсказки относится к Задаче 2. В исследовании, проведенном Cummins (1992), практика извлечения сходных понятий между исходным примером и целевой проблемой привела к аналогичному переносу. Мы можем приписать извлечение сходных понятий деятельности по картированию, что относится к Задаче 3. Другие исследователи также подчеркивали важность процесса картирования для достижения аналогичного переноса (Gentner et al., 2003). Участники, которые заполнили диаграмму, выделив элементы отношений между двумя сценариями переговоров, превзошли тех участников, которые просто изучали два сценария переговоров. Однако, в противоположность этому, Рид (1989) не смог найти доказательств аналогового переноса для текстовых задач, несмотря на то, что выполнил задания 2 и 3: (1) предоставил учащимся подсказку для доступа к исходному примеру, (2) потребовал, чтобы учащиеся построили задачи сопоставления понятий между исходным примером и целевая проблема.
Исследование, проведенное одним из нас несколько лет назад (Ngu and Yeung, 2012), показало, что наличие нескольких компонентов в исходном примере (т. е. символические уравнения, категоризация) или целевой задаче (т. е. подсказка, категоризация), или и то, и другое, фактически облегчили отображение символических уравнений в исходном примере на целевую задачу, что привело к эффективности аналогового переноса. Мы утверждаем, что полученные данные дали новое теоретическое представление об обучении по аналогии, подчеркнув важность наличия нескольких компонентов, а не одного компонента, для стимулирования аналогового переноса для текстовых задач.
В свете предшествующих исследований обучения по аналогии использование подсказок для доступа к исходному примеру представляется важной задачей по аналогии для облегчения переноса. Тем не менее, использование подсказки для доступа к источнику станет излишним, если исходный пример остается видимым, в то время как учащиеся участвуют в сопоставлении исходного примера и целевой проблемы (Richland et al.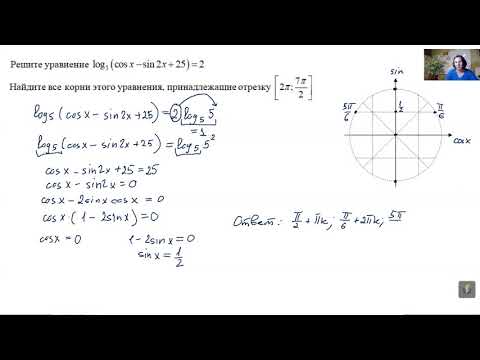 , 2007). Ряд исследователей (Gentner et al., 2003; Rittle-Johnson and Star, 2007; Richland and McDonough, 2010) отмечают преимущество одновременного представления двух примеров, а не последовательного. Одновременное представление двух примеров в этом случае устраняет необходимость предоставления учащимся подсказки для доступа к исходному примеру. Представление примеров в последовательной манере, напротив, требует возможной необходимости предоставления соответствующих подсказок, чтобы напомнить учащимся об исходном примере.
, 2007). Ряд исследователей (Gentner et al., 2003; Rittle-Johnson and Star, 2007; Richland and McDonough, 2010) отмечают преимущество одновременного представления двух примеров, а не последовательного. Одновременное представление двух примеров в этом случае устраняет необходимость предоставления учащимся подсказки для доступа к исходному примеру. Представление примеров в последовательной манере, напротив, требует возможной необходимости предоставления соответствующих подсказок, чтобы напомнить учащимся об исходном примере.
Действительно, сопоставление двух обработанных примеров не только делает ненужным поиск исходного примера, но также дает учащимся возможность провести сравнение, требующее усилий. В своем исследовании Kurtz et al. (2001) выступал за реализацию взаимного согласования, чтобы способствовать абстрагированию лежащей в основе общей структуры в двух частично понятых сценариях. Участники, которые совместно интерпретировали два сценария в сочетании с перечислением конкретных соответствий, продемонстрировали большее взаимное соответствие, чем те участники, которые совместно или по отдельности интерпретировали два сценария. Кроме того, взаимное согласование двух частично понятых текстовых примеров способствовало передаче по аналогии сложной научной концепции (Orton et al., 2012).
Кроме того, взаимное согласование двух частично понятых текстовых примеров способствовало передаче по аналогии сложной научной концепции (Orton et al., 2012).
Как видно из предыдущих разделов, исследования поддержали использование сопоставления двух примеров для содействия обучению по аналогии. Тем не менее, эффективность выполнения операций взаимного сопоставления зависит от ориентации двух изображений (Kurtz and Gentner, 2013) или объектов в двух примерах (Matlen et al., 2020). Выравнивание двух примеров в одной и той же ориентации, а не в разных ориентациях, в этом случае облегчает прямое согласование процесса сопоставления, что повышает эффективность рассуждений по аналогии.
Концепция обучения путем сравнения
Опираясь на теорию структурного картирования (Gentner, 1983) для поощрения переноса по аналогии, ряд исследований недавно выявил положительные эффекты обучения путем сравнения (Alfieri et al., 2013; Ziegler и Стерн, 2014; Риттл-Джонсон и др. , 2017). Например, Дуркин и Риттл-Джонсон (2012) исследовали влияние сравнения правильных и неправильных примеров на изучение десятичных чисел. Одновременное отображение правильных и неправильных десятичных понятий помогло учащимся исправить свои неправильные представления о величине десятичных чисел. Аналогичное направление исследований включало в себя просьбу студентов обосновать, почему конкретный шаг решения был хорошим шагом (например, 1 = 2·9).1398 x — 5, 6 = 2 x ) или неверный шаг (например, 3 = 6 x — 2, 3 = 3 x ) помогли учащимся закрепить и уточнить свое понимание концептуальных знаний, которые занимался решением линейных уравнений (Booth et al., 2013). Более того, Große and Renkl (2007) продемонстрировали положительный эффект от использования правильного и неправильного проработанного примера в области вероятностных задач. Они утверждали, что обучение на правильных и неправильных примерах дает учащимся возможность различать сходства и различия между двумя типами проработанных примеров.
, 2017). Например, Дуркин и Риттл-Джонсон (2012) исследовали влияние сравнения правильных и неправильных примеров на изучение десятичных чисел. Одновременное отображение правильных и неправильных десятичных понятий помогло учащимся исправить свои неправильные представления о величине десятичных чисел. Аналогичное направление исследований включало в себя просьбу студентов обосновать, почему конкретный шаг решения был хорошим шагом (например, 1 = 2·9).1398 x — 5, 6 = 2 x ) или неверный шаг (например, 3 = 6 x — 2, 3 = 3 x ) помогли учащимся закрепить и уточнить свое понимание концептуальных знаний, которые занимался решением линейных уравнений (Booth et al., 2013). Более того, Große and Renkl (2007) продемонстрировали положительный эффект от использования правильного и неправильного проработанного примера в области вероятностных задач. Они утверждали, что обучение на правильных и неправильных примерах дает учащимся возможность различать сходства и различия между двумя типами проработанных примеров.
Вместо сравнения правильных и неправильных примеров для облегчения математического обучения, сравнивая два контрастных выражения алгебры (например, Y 3 + Y 3 = 2 Y 3 3 3 3 3 3 3 3 3 3 3 3 3 3 . 3 × y 3 = y 6 ) рядом друг с другом также помогло учащимся различать внешне похожие (например, буквы, числа), но концептуально разные понятия (например, сложение и умножение) в пределах два контрастирующих рабочих примера (Ziegler and Stern, 2014). Студенты, изучавшие одновременно противоположные выражения алгебры, превзошли тех студентов, которые изучали выражения алгебры последовательно. Таким образом, в целом развитие исследований на сегодняшний день подтвердило преимущество использования обучения по сравнению с повышением эффективности обучения математике.
Обучение по аналогии и обучение по сравнению в классе математики
Помимо проведения лабораторных испытаний, исследователи также изучили межнациональные различия при использовании обучения по аналогии на уроках математики для восьмиклассников (Richland et al. , 2007). Учителя в странах с высокими показателями в области математики (например, в Гонконге, Японии), например, склонны использовать гораздо больше визуально-пространственных опор и связующих жестов, чтобы подчеркнуть аналогичные сравнения, чем их коллеги в США. Частое использование визуально-пространственной поддержки и связывающих жестов, которые направляют внимание учащихся на аналог источника, может помочь снизить требования к когнитивной обработке, поскольку устраняет необходимость искать аналог источника (Richland et al., 2017).
, 2007). Учителя в странах с высокими показателями в области математики (например, в Гонконге, Японии), например, склонны использовать гораздо больше визуально-пространственных опор и связующих жестов, чтобы подчеркнуть аналогичные сравнения, чем их коллеги в США. Частое использование визуально-пространственной поддержки и связывающих жестов, которые направляют внимание учащихся на аналог источника, может помочь снизить требования к когнитивной обработке, поскольку устраняет необходимость искать аналог источника (Richland et al., 2017).
Вместо проведения обучения путем сравнения в нетронутых классах, продолжавшегося несколько дней, Star et al. (2015), напротив, осуществили годичное вмешательство между «сравненной» учебной программой и «обычной» учебной программой. Учебная программа сравнения была включена в обычную учебную программу в качестве дополнительных материалов. Более широкое использование сравнительных материалов коррелировало с более высоким приобретением процедурных знаний. Тем не менее, было непросто побудить учителей постоянно использовать сравнительные материалы в течение года.
Тем не менее, было непросто побудить учителей постоянно использовать сравнительные материалы в течение года.
Действительно, исходя из вышеизложенного, рассуждение по аналогии облегчается использованием вспомогательных сигналов (например, подсказки), чтобы привлечь внимание учащихся к соответствующему исходному примеру, который разделяет процедуру решения, аналогичную целевой задаче. Тем не менее, мы можем исключить намек на доступ к исходному примеру, если поместим исходный пример и целевую проблему рядом (например, Риттл-Джонсон и Стар, 2007). Отображение реляционных общностей между исходным примером и целевой проблемой является еще одной важной задачей по аналогии, которая облегчает перенос по аналогии. Однако успешный перенос по аналогии зависит от активного процесса сравнения (например, совместной интерпретации плюс соответствия конкретных списков) (например, Kurtz et al., 2001) и прямого сопоставления примеров (например, Matlen et al., 2020). Тем не менее, из нашего изучения литературы интересно отметить, что построение мысленной репрезентации исходного примера на начальном этапе обучения по аналогии (Holyoak and Koh, 1987) уделяется минимальное внимание с точки зрения исследований и/или развития обучения.
Важным моментом обучения путем сравнения, напротив, является одновременное отображение двух проработанных примеров рядом друг с другом, что затем позволяет учащимся определить сходства и различия между двумя процедурами решения двух проработанных примеров (Rittle-Johnson). и др., 2017). Следовательно, обучение путем сравнения может улучшить понимание учащимся математических понятий (или неправильных представлений), а также конкретных процедур, относящихся к двум рабочим примерам (например, Booth et al., 2013).
Интересно отметить, что методологически обучение по аналогии и обучение по сравнению состояли из использования различных типов вмешательств. Что касается обучения по аналогии, исследователи внедрили вмешательства в лабораторных и классных условиях (Alfieri et al., 2013) и также включили использование визуально-пространственной поддержки и связывающих жестов (Richland et al., 2007). Аналогичным образом, для обучения посредством сравнения исследователи проводили как краткосрочные вмешательства (например, Rittle-Johnson and Star, 2007), так и долгосрочные вмешательства (например, один календарный год) для улучшения изучения алгебры (Star и др. , 2015). Таким образом, в целом мы утверждаем, что педагогические практики, включающие использование как обучения по аналогии, так и обучения по сравнению, эффективны, помогая учащимся изучать математику. Какой подход является более подходящим и/или эффективным? С нашей точки зрения, мы признаем, что два педагогических подхода дополняют друг друга — сила одного подхода может противостоять слабости другого подхода, и как таковой этот «дополнительный баланс» может отражать целостную позицию, когда человек узнает, как решать задачи по тригонометрии.
, 2015). Таким образом, в целом мы утверждаем, что педагогические практики, включающие использование как обучения по аналогии, так и обучения по сравнению, эффективны, помогая учащимся изучать математику. Какой подход является более подходящим и/или эффективным? С нашей точки зрения, мы признаем, что два педагогических подхода дополняют друг друга — сила одного подхода может противостоять слабости другого подхода, и как таковой этот «дополнительный баланс» может отражать целостную позицию, когда человек узнает, как решать задачи по тригонометрии.
Задачи по тригонометрии
Наша цель для обсуждения — предложить эффективную инструкцию, которая могла бы облегчить изучение двух разных типов задач по тригонометрии, которые различаются из-за относительного положения прочислительного — например, cos60° = x /2 , где прочислитель — числитель, а sin30° = 8/ x , где прочислитель — знаменатель. Как отмечалось ранее, задачи тригонометрии аналогичны линейным уравнениям с дробью. В ходе нашего исследования мы обнаружили, что решать линейные уравнения с дробью сложнее, особенно если прочислитель является знаменателем, а не числителем, поскольку в первом случае требуется больше шагов решения (Нгу и Фан, 2016).
В ходе нашего исследования мы обнаружили, что решать линейные уравнения с дробью сложнее, особенно если прочислитель является знаменателем, а не числителем, поскольку в первом случае требуется больше шагов решения (Нгу и Фан, 2016).
Несмотря на важность задач по тригонометрии в школьной программе по математике, исследований, касающихся эффективного преподавания и изучения этого типа задач, относительно мало (Kendal and Stacey, 1998; Weber, 2005; Weber et al., 2008). Исследования показали, что учащиеся испытывали большие трудности, когда им приходилось учиться решать оба типа тригонометрических задач (например, sin30° = 8/ x против cos60° = x /2) (Кендал и Стейси, 1998 г.) . Чтобы решить эту проблему, Кендал и Стейси (1998) сравнил метод единиц круга и метод отношения , уделив особое внимание решению проблем учащихся в применении навыков алгебраического преобразования для решения задач тригонометрии с прочислительными в качестве знаменателей. Для метода единичного круга авторы создали прямоугольный треугольник, который имел те же свойства, что и данный прямоугольный треугольник. Требовалось несколько навыков, чтобы создать масштабный коэффициент, который позволил бы решать задачи тригонометрии с прочислительными в качестве знаменателей (например, выровнять два прямоугольных треугольника с точки зрения сходных свойств). Для метода отношений, напротив, на основе информации, представленной в прямоугольном треугольнике, студенты должны были выразить тригонометрическое отношение в уравнении (например, cos60 ° = x /2), а затем найти x . Результаты посттеста показали, что метод единичного круга уступает методу отношений, независимо от типа задач тригонометрии (например, sin30° = 8/ x или cos60° = x /2).
Требовалось несколько навыков, чтобы создать масштабный коэффициент, который позволил бы решать задачи тригонометрии с прочислительными в качестве знаменателей (например, выровнять два прямоугольных треугольника с точки зрения сходных свойств). Для метода отношений, напротив, на основе информации, представленной в прямоугольном треугольнике, студенты должны были выразить тригонометрическое отношение в уравнении (например, cos60 ° = x /2), а затем найти x . Результаты посттеста показали, что метод единичного круга уступает методу отношений, независимо от типа задач тригонометрии (например, sin30° = 8/ x или cos60° = x /2).
Хорошо известно, что обучение решению задач тригонометрии, требующих навыков алгебраического преобразования, является широко распространенной проблемой, которая по-прежнему актуальна для многих учащихся средних школ (Weber, 2005). Эта трудность, возможно, усугубляется существующими учебными материалами, которые описаны и рекомендованы в учебниках (например, Vincent et al. , 2012). Например, Винсент и др. (2012) подробно описал процедуру решения задач тригонометрии, в которых прочислительные используются в качестве числителей (например, cos50° = x /8): умножьте обе стороны на 8, что включает одну операцию. Когда прочислитель является знаменателем (например, sin30° = 12/ x ), напротив, авторы рекомендуют две операции: (i) умножить обе части на x и (ii) разделить обе стороны на sin30°. Мы утверждаем, что изложение процедуры решения для обоих типов задач тригонометрии логично. Сказав это, однако, мы отмечаем, что Vincent et al. (2012) не пытались связать два типа задач тригонометрии с предварительными знаниями учащихся о линейных уравнениях с дробью.
, 2012). Например, Винсент и др. (2012) подробно описал процедуру решения задач тригонометрии, в которых прочислительные используются в качестве числителей (например, cos50° = x /8): умножьте обе стороны на 8, что включает одну операцию. Когда прочислитель является знаменателем (например, sin30° = 12/ x ), напротив, авторы рекомендуют две операции: (i) умножить обе части на x и (ii) разделить обе стороны на sin30°. Мы утверждаем, что изложение процедуры решения для обоих типов задач тригонометрии логично. Сказав это, однако, мы отмечаем, что Vincent et al. (2012) не пытались связать два типа задач тригонометрии с предварительными знаниями учащихся о линейных уравнениях с дробью.
Мы утверждаем, что важно учитывать, в какой степени обучение по аналогии, которое может опираться на предварительные знания учащегося о решении линейных уравнений с дробью, может способствовать эффективному решению задач тригонометрии, требующих навыков алгебраического преобразования. В то же время мы также рассматриваем потенциал обучения путем сравнения, чтобы различать различные процедуры решения задач тригонометрии, которые имеют прочислительные в качестве знаменателей (например, sin30° = 8/ x 9).1399 ) или как числители (например, cos60° = x /2). Мы обсудим процедуру решения линейных уравнений с дробью в следующем разделе, учитывая, что они связаны с задачами тригонометрии.
В то же время мы также рассматриваем потенциал обучения путем сравнения, чтобы различать различные процедуры решения задач тригонометрии, которые имеют прочислительные в качестве знаменателей (например, sin30° = 8/ x 9).1399 ) или как числители (например, cos60° = x /2). Мы обсудим процедуру решения линейных уравнений с дробью в следующем разделе, учитывая, что они связаны с задачами тригонометрии.
Процедура решения линейных уравнений
В соответствии с предыдущими исследованиями (например, Ngu et al., 2015; Ngu and Phan, 2016) мы используем реляционных и операционных строк для описания процедуры решения линейного уравнения . Линия отношения относится к «количественному отношению, в котором левая часть уравнения равна правой части уравнения». Оперативная линия, напротив, относится к использованию «операции, которая изменяет состояние уравнения и, следовательно, такой процедурный шаг сохранит равенство уравнения». Например, ссылаясь на уравнение 1 на рисунке 1, строки 1 и 3 являются реляционными линиями, тогда как, напротив, строка 2 является операционной линией. Кроме того, для этого примера мы используем обратный метод для иллюстрации процедуры решения уравнений, имеющих дробь (рис. 1). Наше предыдущее исследование подтвердило использование обратного метода, а не балансового метода для решения линейных уравнений, особенно тех уравнений, которые включают несколько шагов решения (Ngu et al., 2015, 2018). Основное различие между обратным методом и балансовым методом в этом смысле заключается в рабочей линии (например, × 4 с обеих сторон вместо ÷ 2 становится × 2) (см. Рисунок 1 для обратного метода). Центральное место в природе обратного метода занимает сама обратная операция. Концептуализация операции, обратной делению, в данном случае — это операция умножения (т. е. ÷ 2 становится × 2). Согласно Ding (2016), интересно, что понимание обратной операции в начальной школе, вероятно, поможет в изучении математики в старших классах (например, дифференцирование и интегрирование в исчислении). Обратный метод, как мы обнаружили из наших существующих исследований, вероятно, будет создавать меньшую когнитивную нагрузку, чем метод баланса, особенно для линейных уравнений, которые имеют несколько шагов решения.
Кроме того, для этого примера мы используем обратный метод для иллюстрации процедуры решения уравнений, имеющих дробь (рис. 1). Наше предыдущее исследование подтвердило использование обратного метода, а не балансового метода для решения линейных уравнений, особенно тех уравнений, которые включают несколько шагов решения (Ngu et al., 2015, 2018). Основное различие между обратным методом и балансовым методом в этом смысле заключается в рабочей линии (например, × 4 с обеих сторон вместо ÷ 2 становится × 2) (см. Рисунок 1 для обратного метода). Центральное место в природе обратного метода занимает сама обратная операция. Концептуализация операции, обратной делению, в данном случае — это операция умножения (т. е. ÷ 2 становится × 2). Согласно Ding (2016), интересно, что понимание обратной операции в начальной школе, вероятно, поможет в изучении математики в старших классах (например, дифференцирование и интегрирование в исчислении). Обратный метод, как мы обнаружили из наших существующих исследований, вероятно, будет создавать меньшую когнитивную нагрузку, чем метод баланса, особенно для линейных уравнений, которые имеют несколько шагов решения.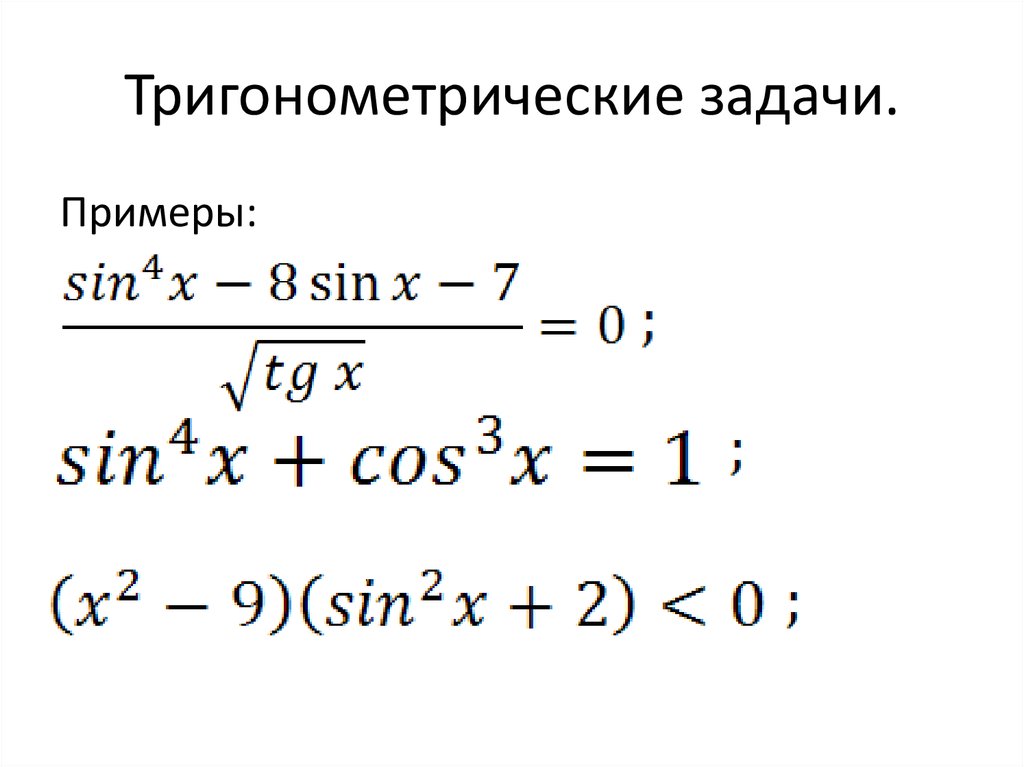
Рисунок 1. Три варианта исходных примеров.
Задачи тригонометрии с прочислителем в качестве числителя
В этом разделе статьи подробно излагается наша фундаментальная предпосылка, которая «приравнивает» задачу тригонометрии, в которой в качестве числителя используется прочислитель (например, sin30° = x /6), с этой линейного уравнения с дробью (например, x /4 = 3). Использование результатов существующих научных исследований (Холиоак, 1984; Холиоак и Кох, 1987; Курц и др., 2001; Нгу и Йеунг, 2012; Альфиери и др., 2013; Риттл-Джонсон и др., 2017; Матлен и др., 2020) мы предлагаем два основных этапа для облегчения обучения по аналогии задачам тригонометрии, требующим навыков алгебраического преобразования. Теперь мы подробно обсудим каждый из этапов ниже.
Первый этап: три варианта исходных примеров
Согласно разработке учебного плана и расписанию, мы предполагаем, что учащиеся должны были изучить линейные уравнения с дробью, прежде чем они изучат тему тригонометрии (Vincent et al. , 2012). Эта последовательность полезна, поскольку позволяет преподавателям проводить параллель между выученной задачей, такой как линейное уравнение с дробью, x /4 = 3 (исходный пример), и новой задачей, такой как задача тригонометрии, sin30° = x /6 (целевая проблема). Однако начинающие учащиеся могут не обязательно распознать сходство между исходным примером и целевой проблемой без помощи учителя. Для облегчения обучения по аналогии на первом этапе происходит мысленное представление трех вариантов исходных примеров в терминах процедуры решения (рис. 1). Цель в этом случае состоит в том, чтобы помочь учащимся выбрать соответствующий исходный пример из трех различных вариантов исходных примеров, который затем может служить руководством для решения целевой проблемы.
, 2012). Эта последовательность полезна, поскольку позволяет преподавателям проводить параллель между выученной задачей, такой как линейное уравнение с дробью, x /4 = 3 (исходный пример), и новой задачей, такой как задача тригонометрии, sin30° = x /6 (целевая проблема). Однако начинающие учащиеся могут не обязательно распознать сходство между исходным примером и целевой проблемой без помощи учителя. Для облегчения обучения по аналогии на первом этапе происходит мысленное представление трех вариантов исходных примеров в терминах процедуры решения (рис. 1). Цель в этом случае состоит в том, чтобы помочь учащимся выбрать соответствующий исходный пример из трех различных вариантов исходных примеров, который затем может служить руководством для решения целевой проблемы.
Все три варианта исходных примеров представляют собой одношаговые уравнения, которые имеют одну операционную линию и две относительные линии (Нгу и Фан, 2016, 2017). Мы помещаем три уравнения рядом, чтобы облегчить процесс картирования (Курц и др.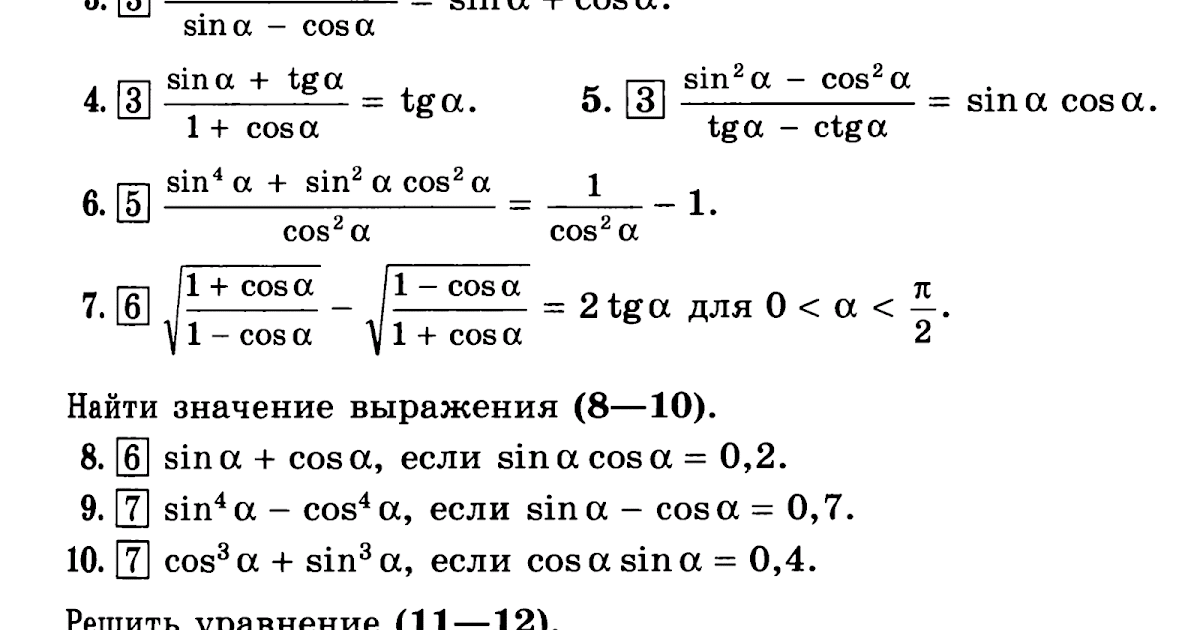 , 2001; Риттл-Джонсон и Стар, 2009; Матлен и др., 2020). Кроме того, мы помечаем шаги решения, например, строки 1, 2 и 3 в уравнении. 1 (Нгу и Фан, 2016, 2017), чтобы дать явную подсказку (Ричланд и др., 2017), которая будет поощрять и облегчать активное сравнение. По сути, уравнение 1 является основным исходным примером, тогда как уравнения. 2 и 3 являются производными уравнения. 1. Уровень сложности трех вариантов увеличивается по сравнению с уравнениями 1–3. уравнение 1 отличается от уравнения. 2 с точки зрения относительного положения пронумерации (т.е. левая сторона по сравнению с правой стороной). Различная ориентация прочислительного препятствовала бы прямому выравниванию реляционных элементов (Курц и Гентнер, 2013; Матлен и др., 2020), и, следовательно, это отрицательно сказалось бы на эффективности сравнения по аналогии. Напротив, отображение уравнений. 2 и 3 в той же ориентации, в которой пронумерал расположен в правой части уравнения, позволит напрямую выровнять реляционные элементы и, таким образом, облегчит процесс сопоставления (Курц и Гентнер, 2013).
, 2001; Риттл-Джонсон и Стар, 2009; Матлен и др., 2020). Кроме того, мы помечаем шаги решения, например, строки 1, 2 и 3 в уравнении. 1 (Нгу и Фан, 2016, 2017), чтобы дать явную подсказку (Ричланд и др., 2017), которая будет поощрять и облегчать активное сравнение. По сути, уравнение 1 является основным исходным примером, тогда как уравнения. 2 и 3 являются производными уравнения. 1. Уровень сложности трех вариантов увеличивается по сравнению с уравнениями 1–3. уравнение 1 отличается от уравнения. 2 с точки зрения относительного положения пронумерации (т.е. левая сторона по сравнению с правой стороной). Различная ориентация прочислительного препятствовала бы прямому выравниванию реляционных элементов (Курц и Гентнер, 2013; Матлен и др., 2020), и, следовательно, это отрицательно сказалось бы на эффективности сравнения по аналогии. Напротив, отображение уравнений. 2 и 3 в той же ориентации, в которой пронумерал расположен в правой части уравнения, позволит напрямую выровнять реляционные элементы и, таким образом, облегчит процесс сопоставления (Курц и Гентнер, 2013). Следует отметить, что уравнение. 2 (например, 2 = x /5) соответствует целевой задаче (например, sin30° = x /6), учитывая, что обе задачи имеют процифры, расположенные в правой части уравнения. Уравнение 3, напротив, отличается от уравнения 2, потому что первое имеет десятичное число. Расположение прочислительного в правой части уравнения и наличие десятичного числа рассматриваются как особенности одношаговых уравнений; мы утверждаем, что эти особенности создают серьезные проблемы для многих учащихся (Ngu and Phan, 2017).
Следует отметить, что уравнение. 2 (например, 2 = x /5) соответствует целевой задаче (например, sin30° = x /6), учитывая, что обе задачи имеют процифры, расположенные в правой части уравнения. Уравнение 3, напротив, отличается от уравнения 2, потому что первое имеет десятичное число. Расположение прочислительного в правой части уравнения и наличие десятичного числа рассматриваются как особенности одношаговых уравнений; мы утверждаем, что эти особенности создают серьезные проблемы для многих учащихся (Ngu and Phan, 2017).
В соответствии с рекомендацией Kurtz et al. (2001), чтобы облегчить рассуждения по аналогии, наша концепция требует, чтобы учащиеся выполнили три задания (см. рис. 1). Наша цель состоит в том, чтобы побудить учащихся к глубокому анализу трех исходных примеров. В первом задании учащиеся должны сравнить и описать сходства и различия между тремя уравнениями по отношению к строке 1. Цель состоит в том, чтобы помочь учащимся участвовать в глубоких рассуждениях по аналогии, ведущих к выявлению общей реляционной структуры во всех уравнениях. три уравнения. Сравнивая уравнения. 1 и 2, например, раскрыли бы различное расположение пронумерации (то есть, левая сторона против правой стороны). Сравнивая уравнения. 2 и 3, напротив, показало бы, что эти уравнения не демонстрируют однозначного соответствия с точки зрения атрибута элементов из-за наличия десятичного числа в уравнении. 3. Следует отметить, что уравнение. 3 (1,2 = x /3) согласуется с целевой задачей (sin30° = x /6), учитывая, что обе задачи имеют процифры, расположенные в правой части уравнения, и что sin30° можно выразить в виде десятичной дроби. Кроме того, как мы видим, математическая операция для строки 1 (например, ÷ 2 становится × 2 в уравнении 1) одинакова для всех трех уравнений. Таким образом, сравнив строку 1 трех уравнений, мы ожидаем, что учащиеся поймут, что эти три уравнения принадлежат к одной и той же категории линейных уравнений, что требует использования одной и той же математической операции для решения.
три уравнения. Сравнивая уравнения. 1 и 2, например, раскрыли бы различное расположение пронумерации (то есть, левая сторона против правой стороны). Сравнивая уравнения. 2 и 3, напротив, показало бы, что эти уравнения не демонстрируют однозначного соответствия с точки зрения атрибута элементов из-за наличия десятичного числа в уравнении. 3. Следует отметить, что уравнение. 3 (1,2 = x /3) согласуется с целевой задачей (sin30° = x /6), учитывая, что обе задачи имеют процифры, расположенные в правой части уравнения, и что sin30° можно выразить в виде десятичной дроби. Кроме того, как мы видим, математическая операция для строки 1 (например, ÷ 2 становится × 2 в уравнении 1) одинакова для всех трех уравнений. Таким образом, сравнив строку 1 трех уравнений, мы ожидаем, что учащиеся поймут, что эти три уравнения принадлежат к одной и той же категории линейных уравнений, что требует использования одной и той же математической операции для решения.
Что касается второй задачи, учащиеся должны создать параллельные шаги решения, такие как строки 2 и 3 уравнения. 2 и 3, которые совпадают с линиями 2 и 3 в уравнении. 1 (Курц и др., 2001). Создание параллельных шагов решения для уравнений. 2 и 3 привлекут внимание учащихся к однозначному соответствию относительно элементов отношения между тремя уравнениями. Третье задание, напротив, требует, чтобы учащиеся ответили на наводящий вопрос, например: «Почему может быть полезно сравнить уравнения? 1–3?» Мы ожидаем, что такая задача укрепит понимание учащимися сходства между тремя уравнениями с точки зрения схемы процедуры совместного решения. Короче говоря, выполнив три задания, мы ожидаем, что учащиеся сделают вывод и поймут, что три уравнения используют одинаковую процедуру решения, несмотря на относительное положение прочислительного (т. е. правая сторона против левой) и разницу в формате. числа (например, 2 против 1,2). После того как учащиеся мысленно представили три варианта исходных примеров и сделали вывод о схеме процедуры совместного решения, мы ожидаем, что они выберут соответствующий исходный пример (1,2 = 9).
2 и 3, которые совпадают с линиями 2 и 3 в уравнении. 1 (Курц и др., 2001). Создание параллельных шагов решения для уравнений. 2 и 3 привлекут внимание учащихся к однозначному соответствию относительно элементов отношения между тремя уравнениями. Третье задание, напротив, требует, чтобы учащиеся ответили на наводящий вопрос, например: «Почему может быть полезно сравнить уравнения? 1–3?» Мы ожидаем, что такая задача укрепит понимание учащимися сходства между тремя уравнениями с точки зрения схемы процедуры совместного решения. Короче говоря, выполнив три задания, мы ожидаем, что учащиеся сделают вывод и поймут, что три уравнения используют одинаковую процедуру решения, несмотря на относительное положение прочислительного (т. е. правая сторона против левой) и разницу в формате. числа (например, 2 против 1,2). После того как учащиеся мысленно представили три варианта исходных примеров и сделали вывод о схеме процедуры совместного решения, мы ожидаем, что они выберут соответствующий исходный пример (1,2 = 9). 1398 x /3) и впоследствии использовать это для решения целевой задачи тригонометрии (sin30° = x /6). Это составляет вторую стадию аналогичного процесса обучения.
1398 x /3) и впоследствии использовать это для решения целевой задачи тригонометрии (sin30° = x /6). Это составляет вторую стадию аналогичного процесса обучения.
Второй этап: сопоставьте соответствующий исходный пример и целевую задачу
Мы предполагаем, что учащиеся должны изучить определение тригонометрических отношений до того, как они научатся решать задачи тригонометрии, требующие навыков алгебраического преобразования. Каждое тригонометрическое отношение представляет собой число (то есть дробь или десятичное число), которое определяется как одна сторона над другой стороной в прямоугольном треугольнике.
Как показано на рис. 2, если разместить рядом соответствующий исходный пример (1,2 = x /3) и целевую задачу (sin30° = x /6), нет необходимости предоставлять подсказка для доступа к соответствующему исходному примеру (Rittle-Johnson and Star, 2009; Matlen et al., 2020). И снова мы предоставляем явную подсказку (Richland et al., 2017), в которой мы используем строки 1, 2, 3 и так далее для обозначения процедуры решения. Для первой задачи учащиеся должны изучить шаги решения строк 1, 2 и 3 в соответствующем исходном примере, а затем сгенерировать параллельные шаги решения для целевой проблемы, которые обозначены строками 2, 3 и 4. При изучении целевой задачи мы ожидаем, что учащиеся восстановят свои предварительные знания о выражении sin30 ° в десятичном числе, а затем заполнят строку 2 целевой задачи. При этом учащиеся, скорее всего, заметят сходство между строкой 1 соответствующего исходного примера (1,2 = х /3) и первый шаг решения целевой задачи (0,5 = х /6). Следовательно, мы утверждаем, что посредством действий по картированию это будет направлять создание шагов решения для строк 3 и 4 целевых проблем, которые аналогичны шагам решения строк 2 и 3 соответствующего исходного примера. Соответственно, с нашей точки зрения, наилучшее согласование между релевантным исходным примером и первым шагом решения целевой проблемы будет иметь место, если оба имеют схожие объекты и отношения (Richland et al.
Для первой задачи учащиеся должны изучить шаги решения строк 1, 2 и 3 в соответствующем исходном примере, а затем сгенерировать параллельные шаги решения для целевой проблемы, которые обозначены строками 2, 3 и 4. При изучении целевой задачи мы ожидаем, что учащиеся восстановят свои предварительные знания о выражении sin30 ° в десятичном числе, а затем заполнят строку 2 целевой задачи. При этом учащиеся, скорее всего, заметят сходство между строкой 1 соответствующего исходного примера (1,2 = х /3) и первый шаг решения целевой задачи (0,5 = х /6). Следовательно, мы утверждаем, что посредством действий по картированию это будет направлять создание шагов решения для строк 3 и 4 целевых проблем, которые аналогичны шагам решения строк 2 и 3 соответствующего исходного примера. Соответственно, с нашей точки зрения, наилучшее согласование между релевантным исходным примером и первым шагом решения целевой проблемы будет иметь место, если оба имеют схожие объекты и отношения (Richland et al. , 2006).
, 2006).
Рис. 2. Процедура решения соответствующего исходного примера и целевой задачи.
Сгенерировав недостающие шаги параллельного решения целевой задачи, учащиеся переходят ко второму заданию. Мы рекомендуем использовать открытые вопросы в качестве дополнительных вспомогательных сигналов для размышлений, консолидации и понимания, например: «Почему может быть полезно сравнить релевантный исходный пример и целевую проблему?» Мы утверждаем, что вопросы на размышление могут помочь учащимся глубоко проработать соответствующий исходный пример и целевую проблему (Rittle-Johnson and Star, 2007). В конечном счете, выполнив обе задачи на рис. 2, мы ожидаем, что учащиеся сделают вывод со ссылкой на схему процедуры совместного решения линейного уравнения с дробью (например, 1,2 = 9).1398 x /3) и первый шаг решения задачи тригонометрии (например, 0,5 = x /6), в результате чего sin30° в целевом значении заменено десятичным числом.
Резюме
Мы предлагаем мысленное представление трех вариантов исходных примеров, что приводит к выбору соответствующего исходного примера для целевой задачи. Наше предложение отличается от предыдущих исследований (Holyoak and Koh, 1987; Ngu and Yeung, 2012), которые предполагают мысленное представление только одного исходного примера. Существующие рекомендации подчеркивают взаимное соответствие между случаями или примерами для облегчения обучения по аналогии (Alfieri et al., 2013; Goldwater and Schalk, 2016). Однако, в отличие от существующих рекомендаций, мы подчеркиваем общую процедуру решения между соответствующим исходным примером и первым шагом решения целевой проблемы (т. е. подмножества целевой проблемы).
Наше предложение отличается от предыдущих исследований (Holyoak and Koh, 1987; Ngu and Yeung, 2012), которые предполагают мысленное представление только одного исходного примера. Существующие рекомендации подчеркивают взаимное соответствие между случаями или примерами для облегчения обучения по аналогии (Alfieri et al., 2013; Goldwater and Schalk, 2016). Однако, в отличие от существующих рекомендаций, мы подчеркиваем общую процедуру решения между соответствующим исходным примером и первым шагом решения целевой проблемы (т. е. подмножества целевой проблемы).
В соответствии с концепцией обучения путем сравнения (Rittle-Johnson et al., 2017) мы размещаем соответствующий исходный пример и целевую проблему рядом. Мы также помечаем процедуру решения соответствующего исходного примера, а также отсутствующую параллельную процедуру решения целевой задачи. Наша цель здесь, в этом анализе, состоит в том, чтобы привлечь внимание студентов к важной особенности шагов решения, которая составляет общую структуру между соответствующей исходной и целевой проблемой. Активное сравнение по аналогии будет результатом, когда учащиеся создадут недостающие шаги параллельного решения для целевых задач. Предоставление наводящего вопроса в сочетании с созданием отсутствующих параллельных шагов решения целевой проблемы, с нашей точки зрения, поможет учащимся вывести схему процедуры совместного решения между соответствующим исходным примером и первым шагом решения. целевой проблемы.
Активное сравнение по аналогии будет результатом, когда учащиеся создадут недостающие шаги параллельного решения для целевых задач. Предоставление наводящего вопроса в сочетании с созданием отсутствующих параллельных шагов решения целевой проблемы, с нашей точки зрения, поможет учащимся вывести схему процедуры совместного решения между соответствующим исходным примером и первым шагом решения. целевой проблемы.
В целом, мы утверждаем, что предложенные нами два основных этапа дают важные сведения, которые могут способствовать обучению по аналогии: (i) мысленное представление трех вариантов исходных примеров и затем выбор из них соответствующего исходного примера, и (ii) выполнение сопоставления деятельности между релевантным исходным примером и целевой проблемой. Мы утверждаем, что наше предложение, в отличие от существующих исследований, является информативным благодаря своей структурированной последовательности, позволяющей учащимся встроить свое понимание в решение задач тригонометрии, которые включают навыки алгебраического преобразования посредством использования как обучения по аналогии, так и обучения путем сравнения. концепции.
концепции.
В исследовании эффекта обращения опыта особое внимание уделялось специфическому взаимодействию между методом обучения и опытом учащегося в соответствующей области (Калюга и др., 2003). Вкратце, с акцентом на эффект обращения опыта, отмечается, что учащимся с разным уровнем знаний потребуются разные типы методов обучения. Соответственно, учащиеся-эксперты могут не обязательно мысленно представлять три варианта исходных примеров и выбирать соответствующий исходный пример и/или мысленно представлять целевую проблему плюс ее первый шаг решения. Обладая глубокими знаниями и пониманием линейных уравнений и тригонометрических соотношений, опытные учащиеся могут понять, что sin20° = х /6 аналогично 3 = х /8. Как только они поймут, что sin20° — десятичное число, у них будет решение для sin20° = x /6. Действительно, обнаружение сходства между sin20° = x /6 и 3 = x /8 приведет к тому, что опытные учащиеся получат выученную процедуру решения для решения 3 = x /8, которую затем можно будет использовать для решите sin20° = x /6.
Теоретическое обоснование, объясняющее процедуру решения задач тригонометрии с прочислителями в качестве числителя, может быть применено к задачам тригонометрии, которые имеют прочислители в качестве знаменателя, учитывая, что оба типа задач тригонометрии связаны с линейными уравнениями с дробью. В следующем разделе мы подробно рассмотрим решение задач тригонометрии, в знаменателе которых есть прочислительные.
Задачи тригонометрии с прочислителем в знаменателе
Как отмечалось ранее, относительное расположение прочислителя (т. е. числителя и знаменателя) определяет сложность задачи тригонометрии. Дифференциальные шаги решения отдают предпочтение задачам тригонометрии, в которых прочислители используются в качестве числителя. В частности, задачи тригонометрии с прочислителями в качестве знаменателя более сложны, чем задачи тригонометрии с прочислителями в качестве числителя. В этом анализе у первого больше операционных линий (2 против 1) и реляционных линий (3 против 2) по сравнению со вторым (см. рис. 2, 4). Обоснование продвижения аналогичного обучения для двух типов задач тригонометрии, которые различаются расположением местоимения (т. е. числителя и знаменателя), также одинаково. Поэтому, как и в случае обучения решению задач тригонометрии с прочислительными в качестве числителя (например, sin30° = x /6), мы утверждаем, что обучение решению cos60° = 4/ x потребует от учащихся выполнения следующих действий: (i) мысленно представить три варианта исходных примеров, а затем выбрать соответствующий исходный пример из этих исходные примеры (рис. 3), (ii) сопоставление соответствующего исходного примера и целевой проблемы (рис. 4).
рис. 2, 4). Обоснование продвижения аналогичного обучения для двух типов задач тригонометрии, которые различаются расположением местоимения (т. е. числителя и знаменателя), также одинаково. Поэтому, как и в случае обучения решению задач тригонометрии с прочислительными в качестве числителя (например, sin30° = x /6), мы утверждаем, что обучение решению cos60° = 4/ x потребует от учащихся выполнения следующих действий: (i) мысленно представить три варианта исходных примеров, а затем выбрать соответствующий исходный пример из этих исходные примеры (рис. 3), (ii) сопоставление соответствующего исходного примера и целевой проблемы (рис. 4).
Рисунок 3. Три варианта исходных примеров.
Рисунок 4. Сопоставление соответствующего исходного примера и целевой проблемы.
Три варианта исходных примеров представляют собой одношаговые линейные уравнения с двумя операционными линиями и тремя реляционными линиями (рис. 3). Уравнения 1, 2 аналогичны, за исключением расположения пронумерации (слева или справа). Для уравнения 2 положение пронумерала находится в правой части уравнения (4 = 32/ x ), что аналогично расположению пронумерала для целевой задачи (Cos60° = 4/ x ) (Курц и Гентнер, 2013). Уравнения 2 и 3 аналогичны, за исключением десятичного числа для последнего. Как отмечалось ранее, наличие специальных признаков (например, прочислительное, расположенное в правой части уравнения, десятичное число и т. д.) способствует сложности одношаговых уравнений. Соответственно, три варианта линейных уравнений усложняются по сравнению с уравнениями. 1–3. Следует отметить, что смысл выполнения заданий на рисунках 3, 4 для обучения задачам тригонометрии с прочислителем в знаменателе аналогичен смыслу выполнения заданий на рисунках 1, 2 для изучения задач тригонометрии с местоимением в качестве числителя. . Таким образом, мы не будем здесь отдельно обсуждать задачи на рисунках 3, 4.
Уравнения 1, 2 аналогичны, за исключением расположения пронумерации (слева или справа). Для уравнения 2 положение пронумерала находится в правой части уравнения (4 = 32/ x ), что аналогично расположению пронумерала для целевой задачи (Cos60° = 4/ x ) (Курц и Гентнер, 2013). Уравнения 2 и 3 аналогичны, за исключением десятичного числа для последнего. Как отмечалось ранее, наличие специальных признаков (например, прочислительное, расположенное в правой части уравнения, десятичное число и т. д.) способствует сложности одношаговых уравнений. Соответственно, три варианта линейных уравнений усложняются по сравнению с уравнениями. 1–3. Следует отметить, что смысл выполнения заданий на рисунках 3, 4 для обучения задачам тригонометрии с прочислителем в знаменателе аналогичен смыслу выполнения заданий на рисунках 1, 2 для изучения задач тригонометрии с местоимением в качестве числителя. . Таким образом, мы не будем здесь отдельно обсуждать задачи на рисунках 3, 4.
Проверка процедуры решения двух типов задач тригонометрии (т. е. прочислитель в качестве числителя и прочислитель в качестве знаменателя) показывает, что есть несколько заметных различий. Как отмечалось ранее, например, дифференциальное число реляционных (3 против 4) и операционных (1 против 2) благоприятствует задачам тригонометрии, в которых в качестве числителя используются прочислительные (Нгу и Фан, 2016). Следовательно, исходя из этого несоответствия, мы утверждаем, что научиться решать Cos60° = 4/ x будет сложнее, чем научиться решать sin30° = 9.1398 x /6 (т. е. см. рис. 2 и рис. 4). Однако, сказав это, мы утверждаем, что предварительные знания (например, знания об алгебраическом преобразовании) помогут учащемуся уменьшить количество реляционных строк. Например, обращаясь к рисунку 4, учащийся может пропустить строку 2 соответствующего исходного примера (т. е. 2,4 × x = 3) и соответствующую строку 3 целевой задачи (т. е. 0,5 × x = 4). . Следует отметить, что опытные учащиеся также могут признать и понять, что cos40° = 5/9.
е. прочислитель в качестве числителя и прочислитель в качестве знаменателя) показывает, что есть несколько заметных различий. Как отмечалось ранее, например, дифференциальное число реляционных (3 против 4) и операционных (1 против 2) благоприятствует задачам тригонометрии, в которых в качестве числителя используются прочислительные (Нгу и Фан, 2016). Следовательно, исходя из этого несоответствия, мы утверждаем, что научиться решать Cos60° = 4/ x будет сложнее, чем научиться решать sin30° = 9.1398 x /6 (т. е. см. рис. 2 и рис. 4). Однако, сказав это, мы утверждаем, что предварительные знания (например, знания об алгебраическом преобразовании) помогут учащемуся уменьшить количество реляционных строк. Например, обращаясь к рисунку 4, учащийся может пропустить строку 2 соответствующего исходного примера (т. е. 2,4 × x = 3) и соответствующую строку 3 целевой задачи (т. е. 0,5 × x = 4). . Следует отметить, что опытные учащиеся также могут признать и понять, что cos40° = 5/9. 1398 х и 3 = 12/ х подобны друг другу. Как только они поймут, что cos60° — это десятичное число (т. е. 0,5), они поймут, что для решения обеих задач можно использовать один и тот же метод.
1398 х и 3 = 12/ х подобны друг другу. Как только они поймут, что cos60° — это десятичное число (т. е. 0,5), они поймут, что для решения обеих задач можно использовать один и тот же метод.
Как мы можем помочь учащимся различать два типа тригонометрических задач: прочислитель как числитель (например, sin30° = x /6) и прочислитель как знаменатель (например, cos60° = 4/ x )? Предыдущие исследования показали, что учащиеся средней школы лучше успевают, когда местоимение является числителем, а не знаменателем (Кендал и Стейси, 19).98; Вебер, 2005). Количество операционных и реляционных линий, как мы утверждали, отражает сложность процедуры решения. Как отмечалось ранее, задачи тригонометрии с прочислительными в качестве числителя имеют меньше операционных (например, 1 против 2) и реляционных (3 против 4) линий, чем задачи тригонометрии с прочислителями в качестве знаменателя.
Различение двух типов тригонометрических задач
Концепция обучения путем сравнения, с нашей точки зрения, может помочь учащимся различать два типа тригонометрических задач. Мы предлагаем поставить два типа задач по тригонометрии рядом и поручить учащимся определить сходства и различия между ними (Rittle-Johnson et al., 2017). Например, со ссылкой на рисунок 5 мы можем попросить учащихся указать основные сходства и/или различия. В результате нашего рассмотрения есть ряд возможностей: (i) расположение прочислительного (т. е. числитель против знаменателя), (ii) sin30° подобен cos50°, оба из которых являются десятичными числами, (iii ) как только мы заменим sin30° или cos50° десятичным числом, оно станет линейным уравнением с дробью (например, рис. 2, 4), (iv) дифференциальным числом реляционных линий (т. е. 2 против 3) и операционных линий (т. е. 1 против 2) отдает предпочтение задаче тригонометрии, в которой в качестве числителя используется прочислитель, и (v) обратный метод используется для решения обоих типов задач тригонометрии. После того, как учащиеся сравнили и определили сходства и различия между двумя типами задач тригонометрии, мы предполагаем, что они заметили бы навыки дифференциального алгебраического преобразования, необходимые для решения этих двух типов задач тригонометрии.
Мы предлагаем поставить два типа задач по тригонометрии рядом и поручить учащимся определить сходства и различия между ними (Rittle-Johnson et al., 2017). Например, со ссылкой на рисунок 5 мы можем попросить учащихся указать основные сходства и/или различия. В результате нашего рассмотрения есть ряд возможностей: (i) расположение прочислительного (т. е. числитель против знаменателя), (ii) sin30° подобен cos50°, оба из которых являются десятичными числами, (iii ) как только мы заменим sin30° или cos50° десятичным числом, оно станет линейным уравнением с дробью (например, рис. 2, 4), (iv) дифференциальным числом реляционных линий (т. е. 2 против 3) и операционных линий (т. е. 1 против 2) отдает предпочтение задаче тригонометрии, в которой в качестве числителя используется прочислитель, и (v) обратный метод используется для решения обоих типов задач тригонометрии. После того, как учащиеся сравнили и определили сходства и различия между двумя типами задач тригонометрии, мы предполагаем, что они заметили бы навыки дифференциального алгебраического преобразования, необходимые для решения этих двух типов задач тригонометрии.
Рис. 5. Сравнение процедуры решения двух типов задач тригонометрии.
Для начинающих учащихся, напротив, мы утверждаем, что базовым шагом для понимания было бы идеальное сравнение линейных уравнений с дробью, чтобы определить их сходство и/или различие (см. рис. 6). Одна примечательная характеристика для идентификации в этом случае связана с расположением пронумерации (т. Е. Как числитель по сравнению со знаменателем), что влияет на навыки алгебраического преобразования, необходимые для решения этих двух типов линейных уравнений. Мы утверждаем, что изучение и освоение этого базового шага может облегчить понимание задач тригонометрии, в которых прочислительные используются как в числителе, так и в знаменателе. Например, сравнение cos60° = 2/ x и cos60° = x /2 рядом указывают на то, что основное различие заключается в расположении пронумерации, то есть 2/ x против x /2. Эта идентификация, в свою очередь, подготовит новичков к решению обоих типов тригонометрических задач — в данном случае sin30° = 8/ x против cos60° = x /2.
Рис. 6. Сравнение уравнения с прочислителем в числителе и уравнением с прочислителем в знаменателе.
Обсуждение
Тригонометрия действительно является трудной темой для многих учащихся средней школы, особенно когда мы смешиваем задачи тригонометрии с расположением местоимения (т. е. числителя и знаменателя) (Kendal and Stacey, 1998). Мы утверждаем, что можно противостоять этой широко распространенной проблеме, рассматривая использование теорий обучения — в данном случае обучения по аналогии и обучения путем сравнения (Kurtz et al., 2001; Rittle-Johnson and Star, 2007; Alfieri et al. ., 2013). Наша концептуализация, подробно описанная в предыдущих разделах, предлагала мысленное представление трех вариантов исходных примеров. Из этих трех вариантов исходных примеров мы выбираем один, соответствующий исходной задаче. Мы выделяем сопоставление соответствующего исходного примера и первого шага решения целевой проблемы, чтобы добиться оптимального согласования между этими двумя проблемами. Наше предложение в своей совокупности продвинуло изучение обучения по аналогии для его рассмотрения на соответствующем исходном примере из трех вариантов исходных примеров. Это педагогическое утверждение отличается от предыдущих исследований (например, Holyoak and Koh, 19).87), в котором делается упор на использование одного исходного примера. Более того, мы подчеркиваем подмножество целевой проблемы, а не всю целевую проблему, с целью реализации задачи однозначного сопоставления между соответствующим исходным примером и первым шагом решения целевой проблемы. Поэтому мы рекомендуем сравнивать исходный пример и подмножество целевой задачи, чтобы облегчить обучение по аналогии.
Наше предложение в своей совокупности продвинуло изучение обучения по аналогии для его рассмотрения на соответствующем исходном примере из трех вариантов исходных примеров. Это педагогическое утверждение отличается от предыдущих исследований (например, Holyoak and Koh, 19).87), в котором делается упор на использование одного исходного примера. Более того, мы подчеркиваем подмножество целевой проблемы, а не всю целевую проблему, с целью реализации задачи однозначного сопоставления между соответствующим исходным примером и первым шагом решения целевой проблемы. Поэтому мы рекомендуем сравнивать исходный пример и подмножество целевой задачи, чтобы облегчить обучение по аналогии.
В то же время, используя значение обучения путем сравнения, мы рассматриваем использование сравнения в контексте задач тригонометрии на предмет их сходства и различия. Наша концептуализация, которую до настоящего времени исследователи не изучали, является новаторской, поскольку делает акцент на одновременном сравнении различных типов задач тригонометрии. Это сравнение двух типов задач по тригонометрии бок о бок, в частности, направлено на преодоление давней трудности изучения задач по тригонометрии, которые различаются из-за относительного положения местоимения (т. е. числитель против знаменателя). Имея это в виду, мы призываем преподавателей рассмотреть возможность использования учебных практик, которые помогают учащимся распознавать и понимать два основных типа задач по тригонометрии.
Это сравнение двух типов задач по тригонометрии бок о бок, в частности, направлено на преодоление давней трудности изучения задач по тригонометрии, которые различаются из-за относительного положения местоимения (т. е. числитель против знаменателя). Имея это в виду, мы призываем преподавателей рассмотреть возможность использования учебных практик, которые помогают учащимся распознавать и понимать два основных типа задач по тригонометрии.
Как концепции обучения по аналогии и обучения по сравнению могут помочь нам в нашей педагогической практике в других областях математики? Рассмотрим в этом случае изучение задач алгебраического выражения , которое представлено на рисунке 7. Фокус понимания в этом случае связан с нашим предыдущим упоминанием сравнения, т. 3 + 5)» и « a (2 + b )». Наш постулат состоит в том, что выравнивание реляционных элементов может помочь учащимся понять логику работы с переменными. Например, как показано, 2 a просто означает, что 2 умножается на a (переменная). Исходя из этого, в средней школе учащийся может сравнить два уравнения рядом и сделать вывод, что 2 равно и , а 5 равно b . В том же духе мы утверждаем, что полезно рассматривать обучение путем сравнения как учебный инструмент, который мог бы облегчить изучение линейных уравнений . В качестве точки сравнения линейных уравнений, которые имеют дробь (например, рисунок 7), например, мы отмечаем, что меньшее количество шагов решения (метод 1) более выгодно, поскольку это приведет к меньшей когнитивной нагрузке (Ngu et al., 2018). ).
Исходя из этого, в средней школе учащийся может сравнить два уравнения рядом и сделать вывод, что 2 равно и , а 5 равно b . В том же духе мы утверждаем, что полезно рассматривать обучение путем сравнения как учебный инструмент, который мог бы облегчить изучение линейных уравнений . В качестве точки сравнения линейных уравнений, которые имеют дробь (например, рисунок 7), например, мы отмечаем, что меньшее количество шагов решения (метод 1) более выгодно, поскольку это приведет к меньшей когнитивной нагрузке (Ngu et al., 2018). ).
Рисунок 7. Примеры обучения математике через обучение по аналогии и обучение по сравнению.
В заключение, как преподаватели, мы признаем важную тему тригонометрии. Более того, исходя из нашего профессионального опыта, мы признаем, что существует широко распространенная проблема, когда в задачах тригонометрии есть прочислительные, которые действуют как числитель и знаменатель. Мы утверждаем, что это различие (т. е. прочислитель в качестве числителя и прочислитель в качестве знаменателя) является относительно уникальным, затрудняя понимание учащимися того, как решать различные типы задач по тригонометрии, требующие навыков алгебраического преобразования. Из наших существующих эмпирических исследований и запросов и выводов других исследователей мы вывели педагогическую концепцию, которая может помочь учащимся понять сложность задач тригонометрии. В этом анализе, принимая во внимание эффективность как обучения по аналогии, так и обучения по сравнению, мы предложили ученикам альтернативную последовательность шагов. Мы рекомендуем преподавателям реализовать и изучить возможности нашего предложения при обучении двум типам задач по тригонометрии, которые различаются относительным расположением местоимения (т. е. числителя и знаменателя).
е. прочислитель в качестве числителя и прочислитель в качестве знаменателя) является относительно уникальным, затрудняя понимание учащимися того, как решать различные типы задач по тригонометрии, требующие навыков алгебраического преобразования. Из наших существующих эмпирических исследований и запросов и выводов других исследователей мы вывели педагогическую концепцию, которая может помочь учащимся понять сложность задач тригонометрии. В этом анализе, принимая во внимание эффективность как обучения по аналогии, так и обучения по сравнению, мы предложили ученикам альтернативную последовательность шагов. Мы рекомендуем преподавателям реализовать и изучить возможности нашего предложения при обучении двум типам задач по тригонометрии, которые различаются относительным расположением местоимения (т. е. числителя и знаменателя).
Вклад авторов
BN и HP отвечали за концептуализацию и написание этой рукописи. Оба автора внесли свой вклад в статью и одобрили представленную версию.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы хотели бы выразить признательность и благодарность двум рецензентам и редактору за их проницательные комментарии.
Ссылки
Альфьери Л., Нокес-Малах Т.Дж. и Шунн К.Д. (2013). Обучение через сравнение случаев: метааналитический обзор. Учеб. Психол. 48, 87–113. doi: 10.1080/00461520.2013.775712
CrossRef Полный текст | Google Scholar
Бехер, Т. (1987). «Дисциплинарное формирование профессий», в The Academic Profession , изд. Б. Р. Кларк (Беркли, Калифорния: University of California Press), 271–303.
Google Scholar
Блэкетт Н. и Талл Д. О. (1991). «Гендер и универсальное изучение тригонометрии с использованием компьютерного программного обеспечения», в материалах Proceedings of the 15th Meeting of the International Group for the International Group for the Psychology of Mathematics Education , ed. Ф. Фурингетти (Италия: PME), 144–151.
Ф. Фурингетти (Италия: PME), 144–151.
Google Scholar
Бут Дж. Л., Ланге К. Э., Кёдингер К. Р. и Ньютон К. Дж. (2013). Использование примеров задач для улучшения обучения учащихся алгебре: различение правильных и неправильных примеров. Учиться. Инстр. 25, 24–34. doi: 10.1016/j.learninstruc.2012.11.002
CrossRef Full Text | Google Scholar
Cummins, DD (1992). Роль рассуждений по аналогии в индукции проблемных категорий. Дж. Экспл. Психол. Учиться. Мем. Познан. 18, 1103–1124. doi: 10.1037/0278-7393.18.5.1103
Полный текст CrossRef | Google Scholar
Дин, М. (2016). Возможности для обучения: обратные отношения в американских и китайских учебниках. Матем. Считать. Учиться. 18, 45–68. doi: 10.1080/10986065.2016.1107819
CrossRef Full Text | Google Scholar
Дуркин, К., и Риттл-Джонсон, Б. (2012). Эффективность использования неправильных примеров для поддержки изучения десятичной величины. Учиться. Инстр. 22, 206–214. doi: 10.1016/j.learninstruc.2011.11.001
22, 206–214. doi: 10.1016/j.learninstruc.2011.11.001
CrossRef Full Text | Google Scholar
Гентнер, Д. (1983). Структурное картирование: теоретическая основа для аналогии. Познан. науч. 7, 155–170. дои: 10.1207/s15516709cog0702_3
CrossRef Полный текст | Google Scholar
Гентнер Д., Левенштейн Дж. и Томпсон Л. (2003). Обучение и передача: общая роль аналогового кодирования. Дж. Образование. Психол. 95, 393–405. doi: 10.1037/0022-0663.95.2.393
Полный текст CrossRef | Google Scholar
Голдуотер, М. Б., и Шалк, Л. (2016). Реляционные категории как мост между когнитивными и образовательными исследованиями. Психология. Бык. 142, 729–757. дои: 10.1037/bul0000043
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
Große, CS, and Renkl, A. (2007). Поиск и исправление ошибок в проработанных примерах: может ли это способствовать результатам обучения? Учиться. Инстр. 17, 612–634. doi: 10.1016/j.learninstruc.2007.09.008
doi: 10.1016/j.learninstruc.2007.09.008
CrossRef Full Text | Google Scholar
Холиок, К. Дж. (1984). «Аналогическое мышление и человеческий интеллект», в Достижения в области психологии человеческого интеллекта , изд. Р. Дж. Штернберг (Хиллсдейл, Нью-Джерси: Эрлбаум), 19 лет.9–230.
Google Scholar
Холиок К.Дж. и Кох К. (1987). Поверхностное и структурное сходство при аналоговом переносе. Пам. Познан. 15, 332–340. doi: 10.3758/bf03197035
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Калюга С., Эйрес П., Чендлер П. и Свеллер Дж. (2003). Эффект обращения опыта. Учеб. Психол. 38, 23–31. doi: 10.1207/s15326985ep3801_4
CrossRef Full Text | Академия Google
Кендал М. и Стейси К. (1998). Обучение тригонометрии. Австрал. Мат. Учить. 54, 34–39.
Google Scholar
Kurtz, KJ, and Gentner, D. (2013). Обнаружение аномальных признаков в сложных стимулах: роль структурированного сравнения. Дж. Экспл. Психол. заявл. 19, 219–232. doi: 10.1037/a0034395
Дж. Экспл. Психол. заявл. 19, 219–232. doi: 10.1037/a0034395
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Kurtz, KJ, Miao, C.-H., and Gentner, D. (2001). Обучение с помощью аналоговой начальной загрузки. Дж. Учиться. науч. 10, 417–446. doi: 10.1207/s15327809jls1004new_2
Полный текст CrossRef | Google Scholar
Матлен Б. Дж., Гентнер Д. и Франконери С. Л. (2020). Пространственное выравнивание облегчает визуальное сравнение. Дж. Экспл. Психол. 46, 443–457. doi: 10.1037/xhp0000726
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Нгу, Б. Х., Чанг, С. Ф., и Юнг, А. С. (2015). Познавательная нагрузка в алгебре: элемент интерактивности при решении уравнений. г. Образовательный. Психол. 35, 271–293. doi: 10.1080/01443410.2013.878019
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Фан, Х. П. (2016). Распаковка сложности линейных уравнений с точки зрения теории когнитивной нагрузки. Учеб. Психол. Ред. 28, 95–118. doi: 10.1007/s10648-015-9298-2
Учеб. Психол. Ред. 28, 95–118. doi: 10.1007/s10648-015-9298-2
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Фан, Х. П. (2017). Станет ли задача для учащихся 8-го класса научиться решать одношаговые уравнения? Междунар. Дж. Матем. Образовательный науч. Технол. 48, 876–894. doi: 10.1080/0020739x.2017.1293856
CrossRef Full Text | Google Scholar
Нгу, Б. Х., Фан, Х. П., Йенг, А. С., и Чанг, С. Ф. (2018). Управление интерактивностью элементов при решении уравнений. Учеб. Психол. Ред. 30, 255–272. doi: 10.1007/s10648-016-9397-8
CrossRef Full Text | Google Scholar
Нгу, Б.Х., и Юнг, А.С. (2012). Содействие аналоговому переносу: многокомпонентный подход к решению задач по алгебре в контексте химии. г. Контемп. Образовательный Психол. 37, 14–32. doi: 10.1016/j.cedpsych.2011.09.001
CrossRef Полный текст | Google Scholar
Новик Л. Р. и Холиок К. Дж. (1991). Решение математических задач по аналогии. Дж. Экспл. Психол. Учиться. Мем. Познан. 17, 398–415.
Дж. Экспл. Психол. Учиться. Мем. Познан. 17, 398–415.
Google Scholar
Ортон Дж. М., Анггоро Ф. К. и Джи Б. Д. (2012). Взаимное сопоставление выравнивания облегчает абстракцию и передачу сложной научной концепции. Учеб. Стад. 38, 473–477. doi: 10.1080/03055698.2011.643104
Полный текст CrossRef | Google Scholar
Рид, С. К. (1987). Модель отображения структуры для текстовых задач. Дж. Экспл. Психол. Учиться. Мем. Познан. 13, 124–139. doi: 10.1037/0278-7393.13.1.124
Полный текст CrossRef | Google Scholar
Рид, С. К. (1989). Ограничения на абстракцию решений. Дж. Образование. Психол. 81, 532–540. doi: 10.1037/0022-0663.81.4.532
Полный текст CrossRef | Академия Google
Рид С.К., Демпстер А. и Эттингер М. (1985). Полезность аналогичных решений для решения задач по алгебре. Дж. Экспл. Психол. Учиться. Мем. Познан. 11, 106–125. doi: 10.1037/0278-7393.11.1.106
Полный текст CrossRef | Google Scholar
Рид С. К., Стебик С., Коми Б. и Кэрролл Д. (2012). Нахождение сходства и различия в решениях текстовых задач. Дж. Образование. Психол. 104, 636–646. doi: 10.1037/a0027181
К., Стебик С., Коми Б. и Кэрролл Д. (2012). Нахождение сходства и различия в решениях текстовых задач. Дж. Образование. Психол. 104, 636–646. doi: 10.1037/a0027181
Полный текст CrossRef | Академия Google
Richland, L.E., Begolli, K.N., Simms, N., Frausel, R.R., and Lyons, EA (2017). Поддержка математических дискуссий: роли сравнения и когнитивной нагрузки. Учеб. Психол. Ред. 29, 41–53. doi: 10.1007/s10648-016-9382-2
Полный текст CrossRef | Google Scholar
Richland, LE, and McDonough, IM (2010). Обучение по аналогии: различение потенциальных аналогов. Контемп. Образовательный Психол. 35, 28–43. doi: 10.1016/j.cedpsych.2009.09.001
CrossRef Полный текст | Google Scholar
Richland, LE, and McDonough, IM (2010). Обучение по аналогии: различение потенциальных аналогов. Контемп. Образовательный Психол. 35, 28–43. doi: 10.1016/j.cedpsych.2009.09.001
CrossRef Полный текст | Google Scholar
Richland, L. E., Morrison, R.G., and Holyoak, KJ (2006). Развитие аналогии у детей: выводы из проблем аналогии сцен. Дж. Экспл. Детская психология. 94, 249. doi: 10.1016/j.jecp.2006.02.002
E., Morrison, R.G., and Holyoak, KJ (2006). Развитие аналогии у детей: выводы из проблем аналогии сцен. Дж. Экспл. Детская психология. 94, 249. doi: 10.1016/j.jecp.2006.02.002
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Richland, L. E., Zur, O., and Holyoak, K. J. (2007). Когнитивная поддержка аналогий на уроках математики. Наука 316, 1128–1129. doi: 10.1126/science.1142103
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Риттл-Джонсон, Б., и Стар, Дж. Р. (2007). Способствует ли сравнение методов решения концептуальным и процедурным знаниям? Экспериментальное исследование по обучению решать уравнения. Дж. Образовательный. Психол. 99, 561–574. doi: 10.1037/0022-0663.99.3.561
Полный текст CrossRef | Google Scholar
Риттл-Джонсон, Б., и Стар, Дж. Р. (2009). По сравнению с чем? Влияние различных сравнений на концептуальные знания и процедурную гибкость при решении уравнений. Дж. Образование. Психол. 101, 529–544. doi: 10.1037/a0014224
Дж. Образование. Психол. 101, 529–544. doi: 10.1037/a0014224
Полный текст CrossRef | Google Scholar
Риттл-Джонсон Б., Стар Дж. Р. и Дуркин К. (2017). «Сила сравнения в обучении математике: экспериментальные данные в классах», в Математическое познание и обучение: приобретение сложных арифметических навыков и математических концепций высшего порядка , редакторы Д. К. Гири, Д. Б. Берч и К. М. Кепке (Уолтем, Массачусетс: Элсевие), 273–295. doi: 10.1016/b978-0-12-805086-6.00012-6
Полный текст CrossRef | Google Scholar
Росс, Б.Х. (1984). Напоминания и их влияние на обучение когнитивным навыкам. Познан. Психол. 16, 371–416. doi: 10.1016/0010-0285(84)
-8
CrossRef Full Text | Академия Google
Росс, Б.Х., и Кеннеди, П.Т. (1990). Обобщение на основе использования более ранних примеров при решении задач. Дж. Экспл. Психол. Учиться. Мем. Познан. 16, 42–55. doi: 10.1037/0278-7393.16.1.42
Полный текст CrossRef | Google Scholar
Стар Дж. Р., Поллак К., Даркин К., Риттл-Джонсон Б., Линч К., Ньютон К. и др. (2015). Учимся на сравнениях в алгебре. Контемп. Образовательный Психол. 40, 41–54. doi: 10.1016/j.cedpsych.2014.05.005
Р., Поллак К., Даркин К., Риттл-Джонсон Б., Линч К., Ньютон К. и др. (2015). Учимся на сравнениях в алгебре. Контемп. Образовательный Психол. 40, 41–54. doi: 10.1016/j.cedpsych.2014.05.005
CrossRef Полный текст | Академия Google
Винсент Дж., Прайс Б., Карузо Н., Ромерил Г. и Тайнан Д. (2012). MathsWorld 9 Австралийская учебная программа. Южная Ярра, Виктория: Macmillan.
Google Scholar
Вебер, К. (2005). Понимание учащимися тригонометрических функций. Матем. Образовательный Рез. J. 17, 91–112. doi: 10.1007/bf03217423
Полный текст CrossRef | Google Scholar
Вебер, К., Нотт, Л., и Эвиттс, Т.А. (2008). Преподавание тригонометрических функций: уроки, извлеченные из исследований. Матем. Учить. 102, 144–150.
Google Scholar
Зиглер Э. и Стерн Э. (2014). Отсроченные преимущества изучения элементарных алгебраических преобразований посредством контрастных сравнений. Учиться. Инстр. 33, 131–146. doi: 10.1016/j.learninstruc.2014.04.006
doi: 10.1016/j.learninstruc.2014.04.006
CrossRef Полный текст | Google Scholar
Решение окружностей, радианов и длин дуг
Ключевые термины
Цели
Окружности и тригонометрия
Обратите внимание, что отношение двух сторон в прямоугольном треугольнике изменяется при изменении острых углов:
Для простоты зафиксируем гипотенузу треугольника заданной длины: назовем ее пока r . Назовем один из острых углов θ (другой острый угол равен 90° – θ .)
При изменении угла θ, противоположные и прилежащие стороны треугольника также изменяются.
В этот момент вы можете заметить, что когда мы «вращаем» гипотенузу длины р, заканчиваем круг. Окружность имеет радиус r, , а ее центр является вершиной, соответствующей углу θ.
Если мы наложим набор осей координат на эту окружность с началом в центре, мы увидим, что смежная сторона прямоугольного треугольника представляет собой расстояние по оси x , а противоположная сторона — расстояние, параллельное оси y . Кроме того, вершина треугольника на окружности должна иметь координаты ( х 1 , у 1 ), где х 1 — длина соседней стороны и у 1 — длина противоположной стороны.
По теореме Пифагора мы знаем следующее соотношение между r , x 1 и 9092 1 , и 9092 1
903.
Если мы «нормализуем» гипотенузу до длины 1 (то есть установим r равно 1), то получившуюся окружность назовем единичной окружностью . В этом случае окружность пересекает оси y = ±1 и x = ±1.
В этом случае окружность пересекает оси y = ±1 и x = ±1.
Итак, что все это дает нам? Почему мы должны заботиться? Во-первых, обратите внимание, что мы объединили наши концепции координатных графиков, окружностей и прямоугольных треугольников вместе — они взаимосвязаны. Таким образом, логически мы ожидаем, что тригонометрия сыграет роль в нашем понимании окружностей, а также прямоугольных треугольников. Но прежде чем мы углубимся в эту взаимосвязь, мы должны сначала определить некоторые свойства угла θ в этом контексте.
Измерения угла
До сих пор мы полагались исключительно на градусы как на единицу измерения угла. Еще одна единица измерения, с которой вы должны быть знакомы, — это радиан. Во-первых, обратите внимание, что длина окружности равна 2 πr, , где r — радиус. Если мы отделим радиус от окружности, то останется просто 2 π: это в каком-то смысле то, как «далеко» окружность проходит вокруг своего центра, независимо от радиуса. Другими словами, 2 π — угол, охватываемый радиусом окружности.
Другими словами, 2 π — угол, охватываемый радиусом окружности.
Как вы, наверное, уже поняли, 2 π также эквивалентно 360°. Единицей измерения угла в этом случае является радиан. Один радиан определяется как угол, образованный таким образом, что часть окружности (или длина дуги ), охватываемая этим углом, равна радиусу окружности.
Другой способ посмотреть на это так: если мы взяли отрезок длины r (радиус) и прилепить его к окружности, угол, образованный радиусами, соединяющими центр окружности с концами дуги, будет иметь меру 1 радиан. Оказывается, один радиан равен примерно 57,3°.
По соглашению угол θ измеряется от оси x- против часовой стрелки. Если используется направление по часовой стрелке, углу просто присваивается отрицательное значение. Так, например, π радиан (180°) и –π радиан (–180°) соответствуют одной и той же точке на окружности.
Для наших целей мы будем иметь дело с углами между –2 π и 2 π, включительно (то есть –2 π stry θ ≤ θ ≤ . π ). Углы больше 2 π определены, но они перекрываются с углами меньшего значения, поэтому мы не будем их подробно рассматривать.
Практическая задача: Преобразуйте каждую из следующих мер угла в радианы. Обязательно используйте точные выражения для ответов.
а. 60° б. 270° с. -90° д. 120°
Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus?
Решение: Во-первых, обратите внимание, что 360° равно 2 π радиан. Мы можем использовать это соотношение для преобразования градусов в радианы. Ниже приведен расчет для части а; остальные части следуют той же схеме. Обратите внимание, что отрицательный знак (часть c) переводится непосредственно из градусов в радианы.
а. б. 3 Пи / 2 радиана c. -Пи/2 радиана d.
Практическая задача: Преобразуйте каждую из следующих мер угла из радианов в градусы.
а. б. в.
Решение: Здесь просто используйте тот же процесс, что и в предыдущей практической задаче, но используйте обратное отношение радианов и градусов. Опять же, ниже показан расчет только для части а; остальные похожи.
а. -22,5° б. 360° с. 36°
Приложение к тригонометрическим функциям
Теперь мы наконец можем посмотреть, какое отношение окружности имеют к тригонометрии. Давайте снова посмотрим на наш единичный круг.
Каждая точка P на единичной окружности, обозначенная координатами ( x 1 , y 1 ), также можно выразить через угол θ . Обратите внимание на следующее, где мы применяем то, что мы узнали о триггера правого треугольника:
Обратите внимание на следующее, где мы применяем то, что мы узнали о триггера правого треугольника:
В других словах, точка PHA-координаты (Cope Cope Cordinates (Cose 99
В других словах. θ, sin θ ), где θ — угол, образованный между x- -Ось и радиус к P. То, что мы также сделали, -это определение двух функций:
SIN θ = Расстояние точки P от x -оси
COS x —
COS . θ = расстояние точки P от оси y Как угол θ изменяется, эти расстояния меняются; однако мы можем изобразить их графически, чтобы увидеть, как они себя ведут. Ниже приведены функции синуса, косинуса и тангенса, построенные для области θ [-2 π , 2 π ]. Обратите внимание, что для вычисления триггерных функций, использующих радианы вместо градусов, вы должны убедиться, что ваш калькулятор находится в режиме радианов, а не в режиме градусов.
Практическая задача: Шина имеет радиус (внешний радиус) 10 дюймов. В самом верху шины наносится небольшая отметка, а затем шина слегка катится вперед, так что отметка поворачивается на угол, равный пи/4 радиан. На каком расстоянии от земли находится отметка в этой точке?
Решение: Эта задача требует применения большей части того, что мы узнали. Сначала нарисуйте «шину» (круг) радиусом 10 дюймов и нарисуйте точку в верхней части шины, чтобы обозначить отметку.
Теперь «повернем» шину на 4 градуса (также на радианов). Мы покажем метку в ее исходном и новом положении. (Для ясности мы опускаем «внутренний круг» шины.)
Мы можем использовать более знакомые факты в этой простой ситуации, чтобы перерисовать основные факты.


 Радiани i градуси
Радiани i градуси


 — 384 с.: ил.- ISBN 5-09-013651-3.
— 384 с.: ил.- ISBN 5-09-013651-3.