Радианная мера угла. Радиан.
- Альфашкола
- Статьи
- Радианная мера угла
Для его измерения рассмотрим единичную окружность, где вершина угла совпадает с его центром. Затем нарисуем дугу, равную радиусу окружности и соединим концы дуги с центром.
Это и есть один радиан, один градус равен \(\frac{π}{180}\) радиан и \(1\) радиан равен \(\frac{180}{π}\) градусов.
Вся окружность равна \(2π\).
Определение радиана:
Краткая история радиана
Слово «радиан» было придумано Томасом Муиром или Джеймсом Томпсоном около 1870 года, математики измеряли углы таким образом в течение длительного времени. Например, Леонард Эйлер (1707-1783) в своих исследованиях в алгебре измерял углы по длине дуги, отрезанной в единичной окружности.
Найдите градусную меру углов, если его радианная мера равна: \(\frac{π}{2};\frac{π}{4};\frac{π}{8};\frac{5π}{6};\)
Решение.
- \(\frac{π}{2}*\frac{180}{π}=\)\(90°\)
- \(\frac{π}{4}*\frac{180}{π}=\)\(45°\)
- \(\frac{π}{8}*\frac{180}{π}=\)\(22,5°\)
- \(\frac{5π}{6}*\frac{180}{π}=\)\(150°\)
Таблица градусов в радианах
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Валерия Сергеевна Архипова
Репетитор по математике
Стаж (лет)
Образование:
МГУ им. А.Кулешова
А.Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-8 классов и по физике 5-7 классов. «Числа управляют миром», – говорили пифагорейцы. Но числа дают возможность человеку управлять миром, и в этом нас убеждает весь ход развития науки и техники наших дней. Цель моих занятий — объяснить, а не заучить, поэтому даже после прохождения курса у ученика остаются знания, ведь понимание — ключ к дальнейшему развитию.
Анастасия Сергеевна Роствинская
Репетитор по математике
Стаж (лет)
Образование:
Нижегородский Государственный Технический университет имени Р. Е. Алексеева
Е. Алексеева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии для 7-9 классов. Подготовка к ОГЭ. Я занимаюсь репетиторством уже 3 года, являюсь именным стипендиатом от крупной компании Теплоэнерго, так же победитель конкурса Профстажировки 2.0 2019 и 2021 года, уже со второго курса написала 2 статьи по химическим технологиям, университет закончила с аттестатом отличия. Мои ученики с достоинством сдали ОГЭ и уже закончили школу. Так же я оказывала помощь студентам младших курсов.
Светлана Михайловна Радова
Репетитор по математике
Стаж (лет)
Образование:
Тираспольский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по биологии 5-11 классы, химии 7-9 классы, подготовка к ОГЭ. Химия — это область чудес! Можно не любить химию, но прожить без нее в современном мире невозможно. Помогу вашему ребенку в освоении химии и биологии. Индивидуально подойду к обучению каждого ученика. Учиться легко, когда рядом хороший помощник!
Химия — это область чудес! Можно не любить химию, но прожить без нее в современном мире невозможно. Помогу вашему ребенку в освоении химии и биологии. Индивидуально подойду к обучению каждого ученика. Учиться легко, когда рядом хороший помощник!
Похожие статьи
- Цилиндр
- Формулы параболы
- Факультет Психологии МГУ: экзамены, ЕГЭ, проходной балл
- РУДН: Ландшафтная Архитектура
- ЕГЭ по математике. Логарифмические неравенства
- Топ-7 фильмов про математиков
- Новогодние блюда, которые подойдут детям и тем, кто на диете
- Как объяснить ребёнку, что нет денег на дорогой подарок?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Радианная мера углов
§ 11. Радианная мера углов
Радианная мера углов
1. Понятие угла
В геометрии
Угол — геометрическая фигура, образованная двумя лучами, которые выходят из одной точки.
В тригонометрии*
Угол — фигура, образованная при повороте луча на плоскости около начальной точки.
2. Измерение углов
Градусная мера углачасть развернутого угла)
Каждому углу ставится в соответствие градусная мера α ∈ [0°; 180°].
Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол. Угол поворота
α ∈ (–×; +×).
Объяснение и обоснование
1. Понятие угла. В курсе геометрии угол определяется как геометрическая фигура, образованная двумя лучами, которые выходят из одной точки. Например, угол AOB, изображенный в первом пункте таблицы 16, — это угол, образованный лучами OA и OB.
Угол можно рассматривать также как результат поворота луча на плоскости около начальной точки. Например, поворачивая луч OA около точки O от начального положения OA до конечного положения OB, также получим угол AOB. Заметим, что достичь конечного положения ОВ можно при повороте луча OA как по часовой стрелке, так и против нее.
Например, поворачивая луч OA около точки O от начального положения OA до конечного положения OB, также получим угол AOB. Заметим, что достичь конечного положения ОВ можно при повороте луча OA как по часовой стрелке, так и против нее.
2. Измерение углов. Данные выше различные определения угла приводят к различному пониманию измерения углов.
В курсе геометрии каждому углу соответствует его градусная мера, которая может находиться только в пределах от 0° до 180°, и поэтому, например, для прямого угла AOB его мера записывается однозначно: ∠ AOB = 90° (1° — это 1/180 часть развернутого угла).
При измерении углов поворота договорились, что направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным.
Поэтому при измерении углов, образованных при повороте луча около начальной точки, мы можем получить как положительные, так и отрицательные значения углов поворота. Например, если угол AOB, в котором лучи ОА и ОВ являются взаимно перпендикулярными, получен при повороте луча OA на угол 90° против часовой стрелки, то значение угла поворота β (см.
Выбрав как значение угла поворота произвольное отрицательное или положительное число (градусов), мы всегда можем повернуть луч OA (по часовой стрелке или против нее) и получить соответствующий угол AOB. Таким образом, величина угла поворота (в градусах) может принимать все действительные значения от.
Для измерения углов принимают определенный угол за единицу измерения и с ее помощью измеряют другие углы.
За единицу измерения можно принять любой угол, например один градус (1°) — 1/180 часть развернутого угла.
В технике за единицу измерения углов принимают полный оборот (заметим, что 1 градус — это 1/360 часть полного оборота).
В мореходстве за единицу измерения углов принимают румб, равный 1/32 час ти полного оборота.
В математике и физике, кроме градусной меры углов, используется также радианная мера углов.
Если рассмотреть некоторую окружность,
то 1 радиан — это центральный угол, соответствующий дуге, длина которой равна радиусу окружности.
Таким образом, если угол AOB равен одному радиану (рис. 59), то это означает, что ∪AB = OA = R.
Установим связь между радианной и градусной мерами углов. Центральному развернутому углу AOC, с градусной мерой 180°, соответствует полуокружность, то есть дуга, длина которой равна πR, а углу в один радиан — дуга длиной R. Итак, радианная мера развернутого угла AOC равна радиан. Таким образом, одному и тому же развернутому углу АОС соответствует градусная мера 180° и радианная мера π радиан. Это соответствие часто записывают так:
Задача 1 Выразите в радианах величины углов, градусная мера которых равна: 30°; 45°; 60°; 90°; 270°; 360°.
Поскольку 30° — это 1/6часть угла 180°, то из соответствия 180° = π (рад)
получаем, что 30°=6/π (рад).
Аналогично можно вычислить и величины других углов.
В общем случае учитываем, что 1°=π/180 радиан, тогда:
Поскольку радианными мерами рассмотренных углов приходится пользоваться достаточно часто, запишем полученные результаты в виде справочной таблицы:
Замечание. Чаще всего при записи радианной меры углов наименование единицы измерения «радиан» (или сокращенно рад) не пишут, но подразумевают его. Например, вместо равенства 90 2 °=π радиан пишут иногда 90 °=π/2 .
Задача 2 Выразите в градусах величины углов, радианнная мера которых равна: π/10 ; 2π/3 ; 3π/4 ; 5.
Поскольку π/10 — это 1/10 часть угла π, то из соответствия π = 180° получаем, что π/10=18° . Аналогично можно вычислить и величины углов 2π /3 и 3π/4 .
В общем случае учитываем, что 1 радиан=180°/π , тогда:
Отметим, что далее в этом разделе будет рассматриваться в основном радианная мера угла и утверждения будут доказаны для радианной меры угла. Однако их можно переформулировать и для градусной меры угла, пользуясь приведенными выше соотношениями.
Однако их можно переформулировать и для градусной меры угла, пользуясь приведенными выше соотношениями.
Условимся далее вместо слов «угол, радианная мера которого равна α радиан» говорить коротко «угол α».
Вопросы для контроля
1. Объясните, как можно определить угол с помощью поворота луча. Как при таком определении измеряются углы?
2. Как вы понимаете такие утверждения: «Величина угла равна 450°», «Величина угла равна (–225°)»? Изобразите эти углы.
3. Как можно определить угол в 1°?
4. Дайте определение угла в 1 радиан.
5. Чему равна градусная мера угла в π радиан?
6. Объясните на примерах, как по радианной мере угла найти его градусную меру и наоборот — по градусной мере угла найти его радианную меру.
Упражнения
1°. Изобразите угол, образованный поворотом луча OA около точки O на: 1) 270°; 2) –270°; 3) 720°;
4) –90°; 5) 225°; 6) –45°;
7) 540°; 8) –180°; 9) 360°; 10) –60°.
2°. Чему равны градусные и радианные меры углов поворота, показанных на рисунке 60?
Чему равны градусные и радианные меры углов поворота, показанных на рисунке 60?
3. Выразите в радианной мере величины углов, градусная мера которых равна:
1 °) 225°; 2°) 36°; 3) 100°; 4) –240°; 5) –22,5°; 6) –150°.
4. Выразите в градусной мере величины углов, радианная мера которых равна:
1) 3π; 2) 3 4 π; 3) −2 5 π;
4) 7 6 π; 5) − π 18 ;
6) 11 6 π;7) −π 8 ; 8) 3.
5. С помощью калькулятора (или таблиц) найдите радианные меры углов, градусная мера которых равна:
1) 27°; 2) 132°; 3) 43°; 4) 114°.
6. С помощью калькулятора (или таблиц) найдите градусные меры углов, радианная мера которых равна:
1) 0,5585; 2) 0,8098; 3) 3,1416; 4) 4,4454.
Урок 29. радианная мера угла — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №29. Радианная мера угла
Перечень вопросов, рассматриваемых в теме:
1) Понятие тригонометрической окружности;
2) Поворот точки вокруг начала координат;
3) Длина дуги окружности и площадь кругового сектора.
Глоссарий по теме
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Теоретический материал для самостоятельного изучения
На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.
На окружности можно выделить дугу. А если рассмотреть круг — часть плоскости, ограниченной окружностью — то можно выделить круговой сектор.
«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)
Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, . А учитывая, что R=1, , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.
Вычислите длину каждой дуги.
Ответ. длина каждой дуги равна части окружности или
длина каждой дуги равна части окружности или
Длина полуокружности равна А так как образовался развернутый угол, то 180.
Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.
рис.3
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад.
;
α рад=(180/π α)° (1)
Длину дуги l окружности радиуса R (рис.4)
можно вычислять по формуле(3)
А площадь S кругового сектора радиуса R и дугой рад (рис.5)
находят по формуле: , где (4)
Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
Введём понятие поворота точки. (рис.2)
- Пусть Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки.
 Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол - Пусть точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на
угол (рис.6)
(рис.6)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найти градусную меру угла, равного рад.
Решение: Используя формулу (1),
находим .
Так как , то рад, тогда (2)
Ответ: .
Пример 2. Найти радианную меру угла, равного 60.
Решение:
Вычисляем по формуле (2): рад
рад
При обозначении мер угла, наименование «рад» опускают.
Ответ: рад, рад.
Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .
Решение: Используя формулу (3),
получим:
Ответ: .
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .
Решение:
По формуле (4) вычисляем
Ответ: 45 м2
Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны Учитывая, что точка М находится в I координатной четверти, её координаты положительны.
На окружности можно найти координаты любой точки.
Ответ:
Радианная мера угла
Прежде, чем приступить к рассмотрению новой темы, давайте
вспомним, что градусом называют величину
центрального угла, которому соответствует часть
окружности.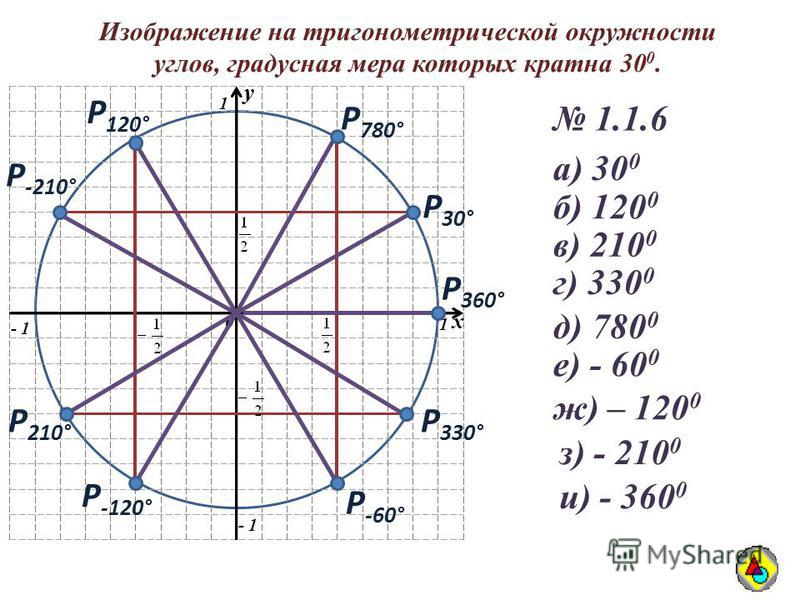 Градусная мера угла – это положительное число, которое
показывает, сколько раз градус и его части укладываются в измеряемом угле.
Градусная мера угла – это положительное число, которое
показывает, сколько раз градус и его части укладываются в измеряемом угле.
А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.
Давайте изобразим окружность с центром в точке и радиусом . Затем проведём вертикальную прямую, которая касается окружности в точке . Эту прямую мы будем считать числовой осью с началом отсчёта в точке . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.
Отметим на прямой несколько точек: и , и , и , и , и .
Теперь
представим нашу прямую в виде нерастяжимой нити, которая закреплена на
окружности в точке .
Будем наматывать нить на окружность. При этом точки на числовой прямой с
координатами ,
,
,
перейдут
соответственно в точки окружности ,
,
,
. При этом длина дуги равна
,
длина дуги равна
,
длина дуги равна
,
длина дуги равна
.
При этом длина дуги равна
,
длина дуги равна
,
длина дуги равна
,
длина дуги равна
.
Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.
Так, точке прямой с координатой ставится в соответствие точка . А значит, угол можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол следует считать равным , а угол равным .
А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.
Единичный угол называют углом в один радиан. Записывают так: рад.
И напомним, что длина дуги равна радиусу нашей окружности.
Сейчас
давайте рассмотрим окружность радиуса .
И отметим на ней дугу ,
равную длине радиуса окружности, и угол .
И такой угол называется углом в один радиан? Верно.
Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.
Интересно, а скольким градусам равен угол в один радиан? Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной , то есть полуокружности, соответствует центральный угол, равный . Следовательно, дуге окружности длиной соответствует угол в раз меньший.
Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что рад . , тогда рад .
Если угол содержит рад, то рад . Эту формулу называют формулой перехода от радианной меры к градусной.
Давайте
с вами найдём градусную меру угла, равного рад.
Для этого воспользуемся формулой перехода от радианной меры к градусной.
Подставим вместо
:
. Сократим на и
на .
И в результате получим .
Сократим на и
на .
И в результате получим .
Можно ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой переход будет чуть сложнее. Так как угол в равен рад, то рад. Тогда рад. Такую формулу называют формулой перехода от градусной меры к радианной.
Найдём радианную меру угла, равного . Воспользуемся формулой перехода от градусной меры к радианной. Подставим вместо : . Сократим и на . И в результате получим .
Обратите внимание, что при обозначении меры угла в радианах слово «радиан» обычно не пишут: . При этом обозначение градуса в записи меры угла пропускать нельзя.
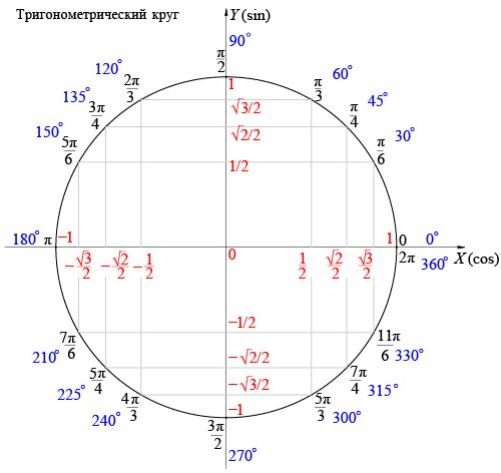
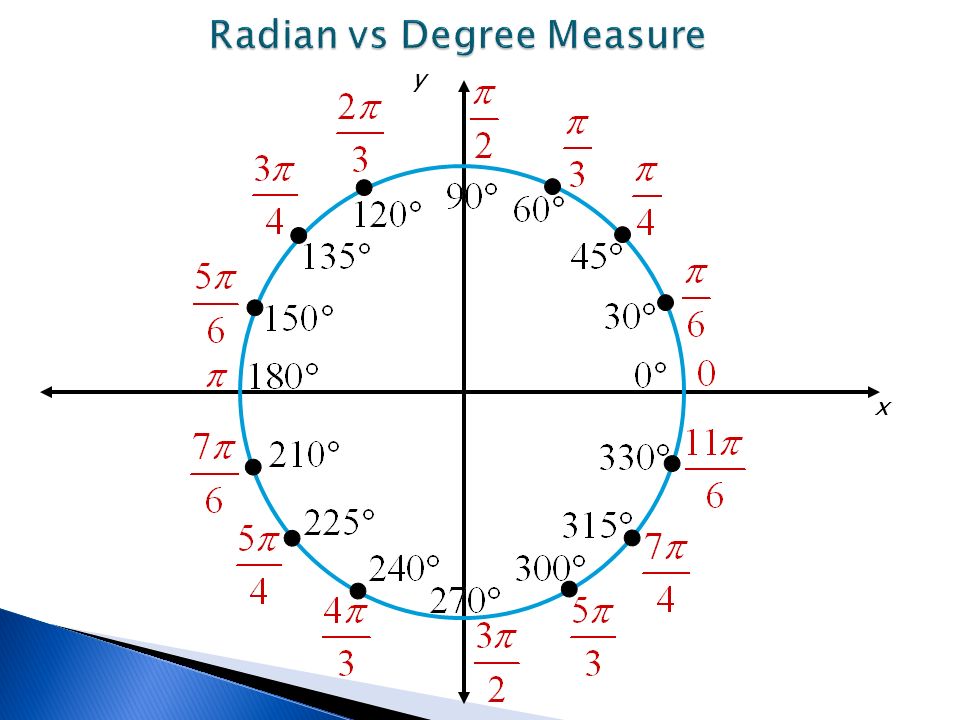
В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.
Отметим,
что радианная мера углов позволяет значительно упростить многие формулы в
математике, физике, механике.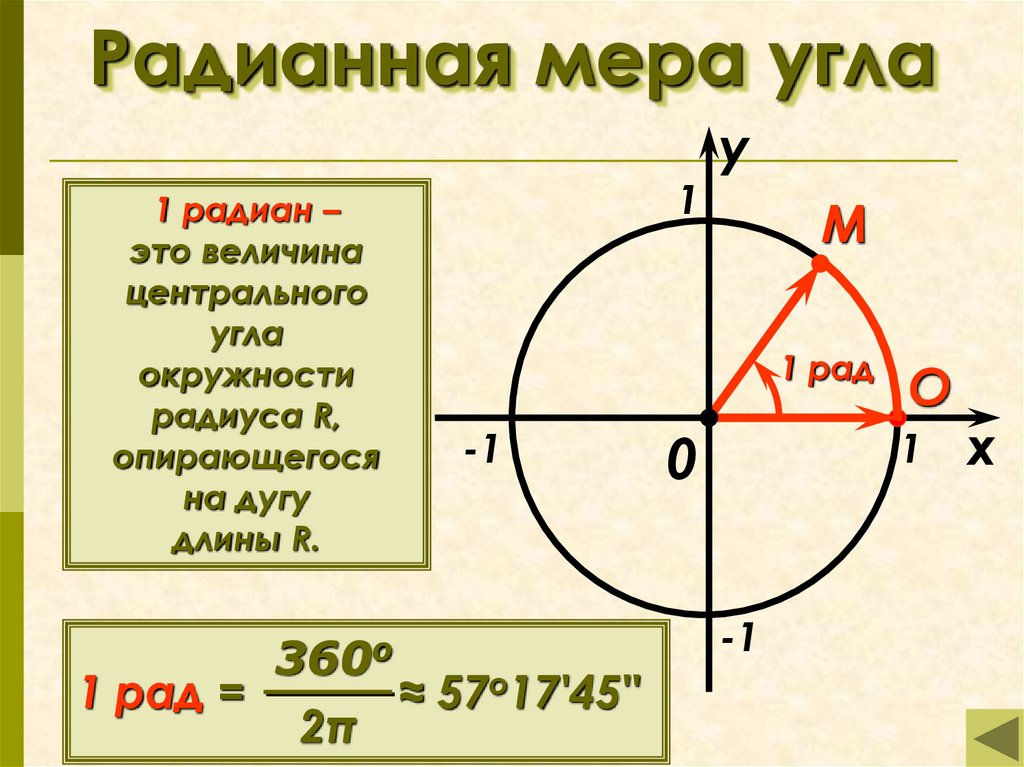 В частности, радианная мера угла удобна для
вычисления длины дуги окружности. Так, выше мы выяснили, что угол в рад
стягивает дугу, длина которой равна радиусу ,
а значит, угол в рад
стягивает дугу длиной: .
Если ,
то эта формула принимает совсем простой вид: ,
то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
В частности, радианная мера угла удобна для
вычисления длины дуги окружности. Так, выше мы выяснили, что угол в рад
стягивает дугу, длина которой равна радиусу ,
а значит, угол в рад
стягивает дугу длиной: .
Если ,
то эта формула принимает совсем простой вид: ,
то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса , образованного углом в рад, равна , где .
Докажем это. Известно, что площадь круга вычисляется по формуле: . Площадь полукруга, то есть кругового сектора в рад: . Тогда площадь сектора в рад в раз меньше, то есть . Следовательно, площадь сектора в рад равна .
Ну а сейчас давайте выполним несколько заданий.
Первое задание.
Найдите градусную меру угла, выраженную в радианах: а) ;
б) ; в) ;
г) ;
д) .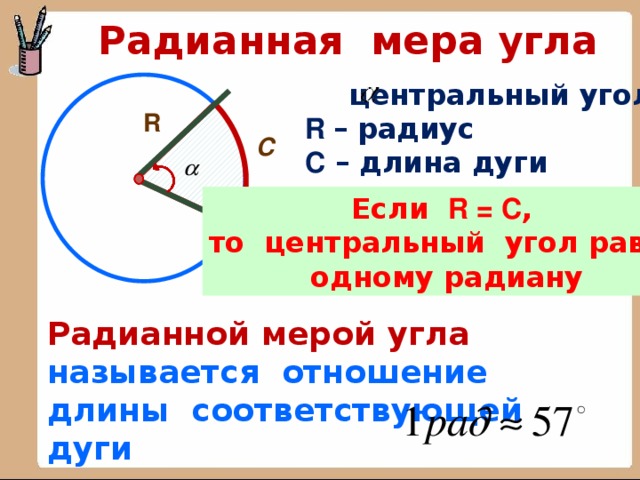
Решение.
Второе задание. Найдите радианную меру угла, выраженного в градусах: а) ; б) ; в) ; г) .
Решение.
Следующее задание. Чему равен радиус окружности, если дуге длиной см соответствует центральный угол в рад?
Решение.
И ещё одно задание. Дуге кругового сектора соответствует угол, равный рад. Чему равна площадь сектора, если радиус круга равен см?
Решение.
Ну а сейчас немного истории.
Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.
В
1960 году XI Генеральной
конференцией по мерам и весам радиан был принят в качестве единицы измерения
плоских углов в Международной системе единиц (СИ).
Радианная и градусная меры угла
ГРАДУСНАЯ МЕРА УГЛА. РАДИАННАЯ МЕРА УГЛА. ПЕРЕВОД ГРАДУСОВ В РАДИАНЫ И ОБРАТНО.
ГРАДУСНАЯ МЕРА УГЛА.
Градусы придумали в Древнем Вавилоне.
Давненько это было… Веков 40 назад…
И придумали просто.
Взяли и разбили окружность на 360 равных частей.
1 градус — это 1/360 часть окружности.
И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360.
Где-то в то же время, в Древнем Египте мучились другим вопросом.
Во сколько раз длина окружности больше длины её диаметра?
И так измеряли, и этак… Всё получалось немного больше трёх. Но как-то лохмато получалось, неровно… Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя. .. В принципе нельзя.
.. В принципе нельзя.
Ну, во сколько раз окружность больше диаметра установили, конечно.
Примерно. В 3,1415926… раз.
Это и есть число «Пи». Вот уж лохматое, так лохматое. После запятой — бесконечное число цифр без всякого порядка… Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.
Для практического применения принято запоминать всего две цифры после запятой.
Раз уж мы поняли, что длина окружности больше диаметра в «Пи» раз, имеет смысл запомнить формулу длины окружности:
Где L — длина окружности,
а d — её диаметр.
Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы.
Высшей математике они не нравятся… Высшая математика — дама серьёзная, по законам природы устроена.
И эта дама заявляет: «Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245.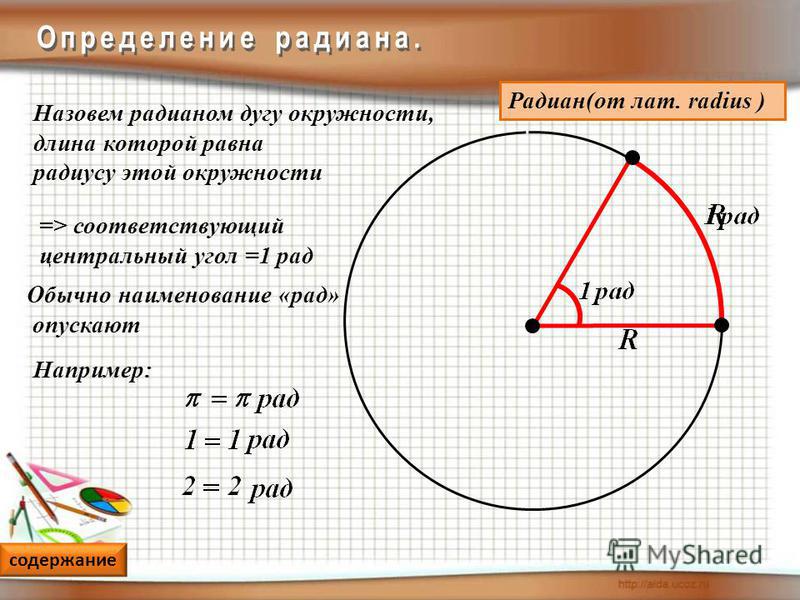 .. И что мне делать? Нет уж…»
.. И что мне делать? Нет уж…»
Пришлось послушаться. Природу не обманешь…
Пришлось ввести меру угла, не зависящую от человеческих придумок.
Знакомьтесь — радиан!
РАДИАННАЯ МЕРА УГЛА.
- Что такое радиан? В основе определения радиана — всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой ( L ) равна длине радиуса ( R ). Смотрим картинки.
- Будем считать, что этот малюсенький угол имеет величину 1 градус:
- Маленький такой угол, почти и нет его…
- Видим примерно один радиан . L = R
- Чувствуете разницу?
- Один радиан много больше одного градуса. А во сколько раз?
- Смотрим следующую картинку. На которой нарисован полукруг. Развёрнутый угол размером, естественно, в 180°.

- А теперь нарежем этот полукруг радианами! И видим, что в 180° укладывается 3 с хвостиком радиана.
- Кто угадает, чему равен этот хвостик!?
- Да! Этот хвостик — 0,1415926…. Здравствуй, число «Пи», мы тебя ещё не забыли!
Действительно, в 180° градусах укладывается 3,1415926… радиан. Как вы сами понимаете, всё время писать 3,1415926… неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
Вот теперь совершенно осмысленно можно записать приближённое равенство:
Или точное равенство:
Определим, сколько градусов в одном радиане. Как? Легко!
Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула — это тоже уравнение!) на 3,14:
- Это соотношение полезно запомнить. В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию.
 Вот тут это знание очень помогает.
Вот тут это знание очень помогает. - Но главное умение этой темы — перевод градусов в радианы и обратно.
- Если угол задан в радианах с числом «Пи», всё очень просто. Мы знаем, что «Пи» радиан = 180°. Вот и подставляем вместо «Пи» радиан — 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле «Пи»/2 радиан ? Вот и пишем:
Или, более экзотическое выражение:
- Обратный перевод чуть сложнее. Но не сильно. Если угол дан в градусах, мы должны сообразить, чему равен один градус в радианах, и умножить это число на количество градусов. Чему равен 1° в радианах?
- Смотрим на формулу и соображаем, что если 180° = «Пи» радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула — это тоже уравнение!) на 180. Представлять «Пи» как 3,14 никакой нужды нет, его всё равно всегда буквой пишут.
 Получаем, что один градус равен:
Получаем, что один градус равен:
Вот и всё. Умножаем число градусов на это значение и получаем угол в радианах. Например:
Отметим, что в тригонометрических функциях значок градусов — пишется. Всегда.
Например, sin35°. Это синус 35 градусов .
А значок радианов ( рад ) — не пишется!
Он подразумевается.
То ли лень математиков обуяла, то ли ещё что… Но решили не писать.
Если внутри синуса — котангенса нет никаких значков, то угол — в радианах ! Например, cos3 — это косинус трёх радианов .
Это и приводит к непоняткам… Человек видит «Пи» и считает, что это 180°. Всегда и везде. Это, кстати, срабатывает. До поры до времени, пока примеры — стандартные. Но «Пи» — это число! Число 3,14, а никакие не градусы! Это «Пи» радиан = 180°!
Ещё раз : «Пи» — это число! 3,14.
Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
Переведите эти углы из градусной меры в радианную:
360°; 30°; 90°; 270°; 45°; 0°; 180°; 60°
Переведите эти углы из радианной меры в градусную:
Радианная мера угла | Презентация к уроку по алгебре (10 класс):
Министерство лесного хозяйства Республики Башкортостан
Государственное бюджетное профессиональное
образовательное учреждение
«Уфимский лесотехнический техникум»
Радианная мера угла
Методическая разработка урока по учебной дисциплине
Математика: алгебра и начала математического анализа; геометрия
Разработали: Аюпова Э.Х., Ахметова Г.Р. | |
Уфа, 2019
Рассмотрена и рекомендована учебной цикловой комиссией № 3 ГБПОУ «Уфимский лесотехнический техникум» Протокол № __ от «___» _________2019 г. Председатель УЦК №3 ___________ Р.М. Латыпова | Соответствует федеральному государственному образовательному стандарту среднего профессионального образования по специальности 35.02.03 Технология деревообработки УТВЕРЖДАЮ Заместитель директора по УР ___________ В.Ф. Валеева |
Урок по теме «Радианная мера угла» по типу – урок изучения новых знаний. Методической целью урока является реализация деятельностного подхода и критического мышления, основанное на анализе ситуации, самостоятельном поиске информации, построению логической цепочки и принятию взвешенного и аргументированного решения при обучении математики. в условиях реализации ФГОС
.
Разработчики: Аюпова Э.Х., Ахметова Г.Р., преподаватели математики ГБПОУ «Уфимский лесотехнический техникум»
Рецензия
на методическую разработку открытого урока
по учебной дисциплине
Математика: алгебра и начала математического анализа; геометрия
на тему: Радианная мера угла
для специальности 35.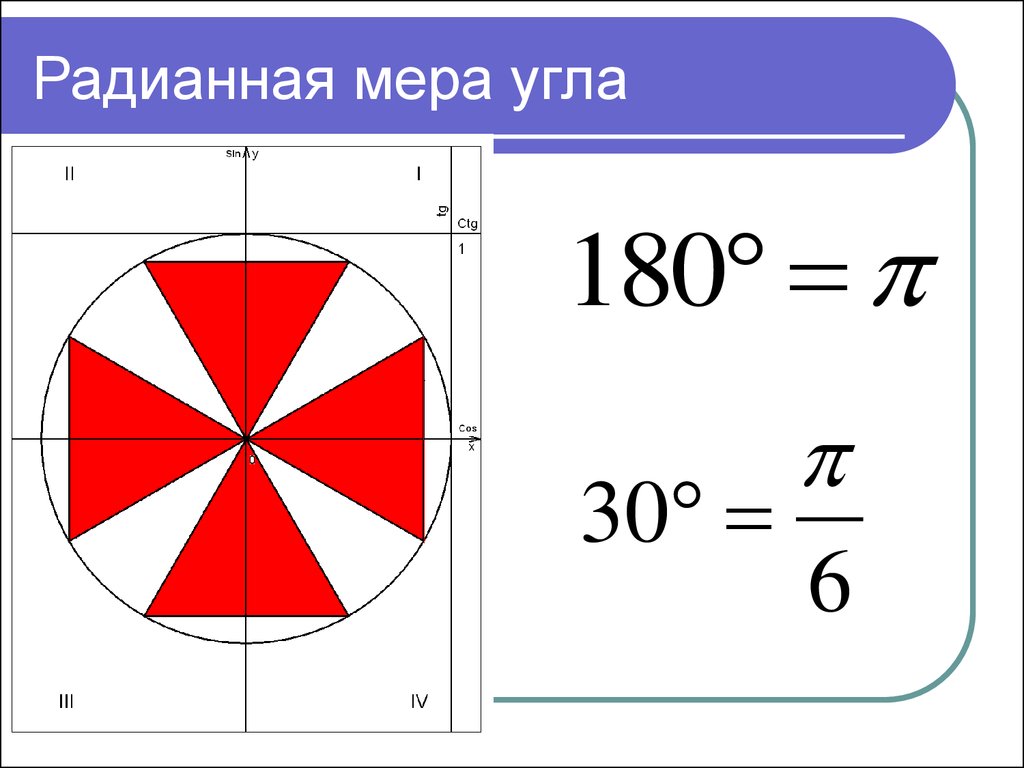 02.03 Технология деревообработки на базе основного общего образования
02.03 Технология деревообработки на базе основного общего образования
преподавателя Аюповой Эльмиры Хафизовны
Методическая разработка теоретического занятия по теме «Радианная мера угла» составлена в соответствии с требованиями ФГОС СПО и предназначена для проведения комбинированного занятия. Разработка включает в себя организационный, информационный и контролирующий блоки, приложения, список использованной литературы.
Цели занятия четко сформулированы, разработано поэтапное содержание занятия, позволяющее достичь эти цели.
В информационном блоке раскрыты все основные понятия изучаемой темы, даны четкие определения, приведены все формулы.
Контролирующий блок содержит вопросы фронтального опроса исходного уровня знаний и проверки уровня успешности по изучаемой теме, тестовые задания, предполагающие выбор ответа из предложенных, задачи, требующие применения изученных формул при решении задач, также представлены задания для работы студентов в группах. Ко всем заданиям приведены эталоны ответов.
Структура методической разработки предполагает использование в ходе занятия задач связь с жизнью по изучаемой теме. Она позволяет не только углубить знания студентов, но и расширяет их кругозор.
Можно проследить межпредметные связи с такими дисциплинами, как физика, астрономия, алгебра, связь изучаемой темы с будущей профессией.
Данная методическая разработка может быть рекомендована преподавателям математики для проведения занятия по изучаемой теме.
Развивать критическое мышление,
Содержание
Цели методической разработки
Приобретаемые знания, умения и навыки
Задачи занятия
Обоснование выбора технологии
Ход занятия
Приложения:
- Карточки с заданиями
- Лист самооценки
- Домашнее задание
Технологическая карта урока
Литература
Цели методической разработки
Курс, группа: | Первый, 11 ТД |
Профильная дисциплина: | Математика: алгебра и начала математического анализа; геометрия |
Специальность: | 35. |
Тема: | Радианная мера угла |
Форма занятия: | Комбинированный урок |
Цель урока: формировать знание определения угла в один радиан; ввести в речевую практику понятие угла в один радиан; научить находить формулы, устанавливающие связь между радианным и градусным измерением углов.
Цель методическая: Создание условий для формирования основ логического, алгоритмического и математического мышления по данной теме.
Приобретаемые умения и навыки
Уметь: — находить различия между градусной мерой угла и радианной; — приводить примеры из области жизни, где используются разные единицы меры углов; — применять формулы перехода из радианной меры углов в градусную и наоборот при решении задач. | Знать: — определение радианной меры угла — формулы перехода радианной меры углов в градусную и градусной меры в радианную. | |
Тип урока: | Урок открытия новых знаний, обретения новых умений и навыков | |
Виды урока: | Проблемная лекция, беседа, дискуссия, презентация, самостоятельная работа учащихся | |
Мотивация учебной деятельности | Изучение программного материала по теме «Радианная мера угла» дает возможность получить представление о широте применения измерения углов в различных областях человеческой деятельности | |
Методы обучения: | По характеру учебной деятельности: проблемный, поисковый, объяснительно-иллюстративный, эвристический; по источнику учебного материала: словесный, наглядный, практический | |
Формы учебной работы: |
| |
Приемы обучения: | Проблемный, частично-поисковый, творческой деятельности | |
Средства обучения: | Дидактические средства: слайд-презентация в программе PowerPoint, раздаточный материал; домашнее задание для студентов. Оборудование: персональный компьютер; проектор, деревянный круг для наглядного изучения радианной меры угла, лист самоконтроля, карточки с заданиями. | |
Внутри дисциплинарные связи: | Градусная мера угла | |
Междисциплинарные связи: | Физика, астрономия | |
Целесообразность использования медиа продукта на занятии: |
|
Цели занятия: формировать знание определения угла в один радиан; ввести в речевую практику понятие угла в один радиан; отработать формулы, устанавливающие связь между радианным и градусным измерением углов при выполнении упражнений.
Задачи:
— образовательные (формирование познавательных УУД): обеспечить усвоение определения угла в один радиан; обеспечить запоминание формул перехода от градусной меры угла к радианной и от радианной к градусной; сформировать умение пользоваться радианным измерением углов на уровне выполнения упражнений по образцу, в измененной и новой ситуации.
— воспитательные (формирование коммуникативных и личностных УУД): умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в пару со сверстником и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
— развивающие (формирование регулятивных УУД): умение обрабатывать информацию и ранжировать ее по указанным основаниям; представлять информацию в табличной форме, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
— методические: создать условия для осознания учащимися ценности математических знаний, как средства познаний окружающего мира; содействовать развитию математической культуры учащихся в процессе решения задач практической направленности; создание условий для усвоения нового материала через продуктивные методы обучения;
— деятельностные: формирование функций мышления (анализ, синтез, сравнение, гипотеза; формирование способности структурировать новый материал.
Обоснование выбора технологии и ее актуальность
Особенность новых Государственных образовательных стандартов образования – их деятельностный характер, который ставит главной задачей развитие личности ученика.
Поставленная задача требует внедрение в современное образовательное учреждение системно-деятельностного подхода к организации учебного процесса, который, в свою очередь, связан с принципиальными изменениями деятельности преподавателя. Также изменяются и технологии обучения.
Встает задача превратить обучение, направленное на накопление знаний, умений, навыков, в процесс развития личности обучающегося. Ещё Сократ говорил о том, что «научиться играть на флейте можно только играя самому». Точно так же деятельностные способности формируются у обучающегося лишь тогда, когда он не пассивно усваивает новое знание, а включён в самостоятельную учебно-познавательную деятельность. Значит, для формирования у учащегося деятельностных способностей необходимо постоянно тренировать его в выполнении различных видов деятельности.
Ещё Сократ говорил о том, что «научиться играть на флейте можно только играя самому». Точно так же деятельностные способности формируются у обучающегося лишь тогда, когда он не пассивно усваивает новое знание, а включён в самостоятельную учебно-познавательную деятельность. Значит, для формирования у учащегося деятельностных способностей необходимо постоянно тренировать его в выполнении различных видов деятельности.
Возникает необходимость формирования у учащихся активной жизненной позиции, устойчивой мотивации к образованию и самообразованию, критичности мышления. Это возможно при использовании технологии критического мышления, так как в ней синтезированы идеи и методы технологий коллективных и групповых способов обучения, а также сотрудничества и развивающего обучения.
Применение технологии критического мышления развивает мыслительные навыки учащихся, необходимые не только в учебе, но и в обычной жизни: умение принимать взвешенные решения, работать с информацией, анализировать различные стороны явлений.
В основе технологии лежит творческое сотрудничество ученика и учителя, а также учеников между собой, развитие у учащихся аналитического подхода к любому материалу. Технология рассчитана не на запоминание материала, а на постановку проблемы и поиск ее решения. Это универсальная, проникающая система приемов, открытая к диалогу с другими педагогическими подходами и технологиями.
Итак, урок с применением технологии критического мышления способствует:
— развитию мышления и способностей учащихся, развитию творческих умений;
— усвоению учащимися знаний и умений, добытых в ходе активного поиска и самостоятельного решения проблемы;
— воспитанию активной творческой личности, умеющей видеть, ставить и разрешать нестандартные проблемы.
План учебного занятия №
Тема: Радианная мера угла
Специальность: 35.02.03 Технология деревообработки
Курс: 1 Группа: 11 ТД
Цели:
- Цели занятия: формировать знание определения угла в один радиан; ввести в речевую практику понятие угла в один радиан; отработать формулы, устанавливающие связь между радианным и градусным измерением углов при выполнении упражнений.

Задачи:
- — образовательные (формирование познавательных УУД): обеспечить усвоение определения угла в один радиан; обеспечить запоминание формул перехода от градусной меры угла к радианной и от радианной к градусной; сформировать умение пользоваться радианным измерением углов на уровне выполнения упражнений по образцу, в измененной и новой ситуации.
- — воспитательные (формирование коммуникативных и личностных УУД): умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в пару со сверстником и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
- — развивающие (формирование регулятивных УУД): умение обрабатывать информацию и ранжировать ее по указанным основаниям; представлять информацию в табличной форме, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Знать:
— Виды углов, градусную единицу измерения углов.
Уметь:
— различать острый, тупой, развернутый, полный углы; находить градусную меру углов.
Место проведения –58
Норма времени – 45мин
Тип занятия – урок получения новых знаний
Формы работы обучающихся: фронтальная, парная, индивидуальная.
Метод обучения — словесный, наглядный, деятельностный.
Организация деятельности обучающихся на уроке:
-самостоятельно выходят на проблему и решают её;
-работают с «бортовой» картой;
-отвечают на вопросы;
-решают самостоятельно задачи;
-оценивают результаты своей деятельности на уроке.
Оборудование:
- Алгебра и начала математического анализа, 10 кл., Колягин Ю.М.
- Компьютер, экран, проектор.
- Карточки с заданиями.
- Деревянный круг с веревкой.
План урока:
- Организационный этап.
- Мотивация учебной деятельности учащихся. Постановка цели и задач урока обучающимися.

- Актуализация знаний.
- Первичное усвоение новых знаний.
- Первичная проверка понимания
- Первичное закрепление.
- Информация о домашнем задании, инструктаж по его выполнению
- Рефлексия (подведение итогов занятия)
Структура и ход урока
1. Организационный этап (3 мин)
Преподаватель приветствует обучающихся. Отмечает отсутствующих в журнале. Проверяет внешнее состояние аудиторного помещения, проверяет подготовленность группы к занятию, организует внимание готовность студентов.
2. Мотивация учебной деятельности (2 мин)
(слайд 2) Дорогие ребята, урок начнем со следующих строк «С малой удачи начинается большой успех». Вспомним прошлый курс и ответим на вопрос:
— Что наз33ывается углом?
3. Актуализация знаний (20 мин)
(слайд 3) — В планиметрии углом называется част плоскости, заключенная между двумя лучами с общей вершиной
— Какие виды углов вы знаете?
(Слайд 4) Учащиеся по всплывающим рисункам определяют виды углов: острый, прямой, тупой и развернутый.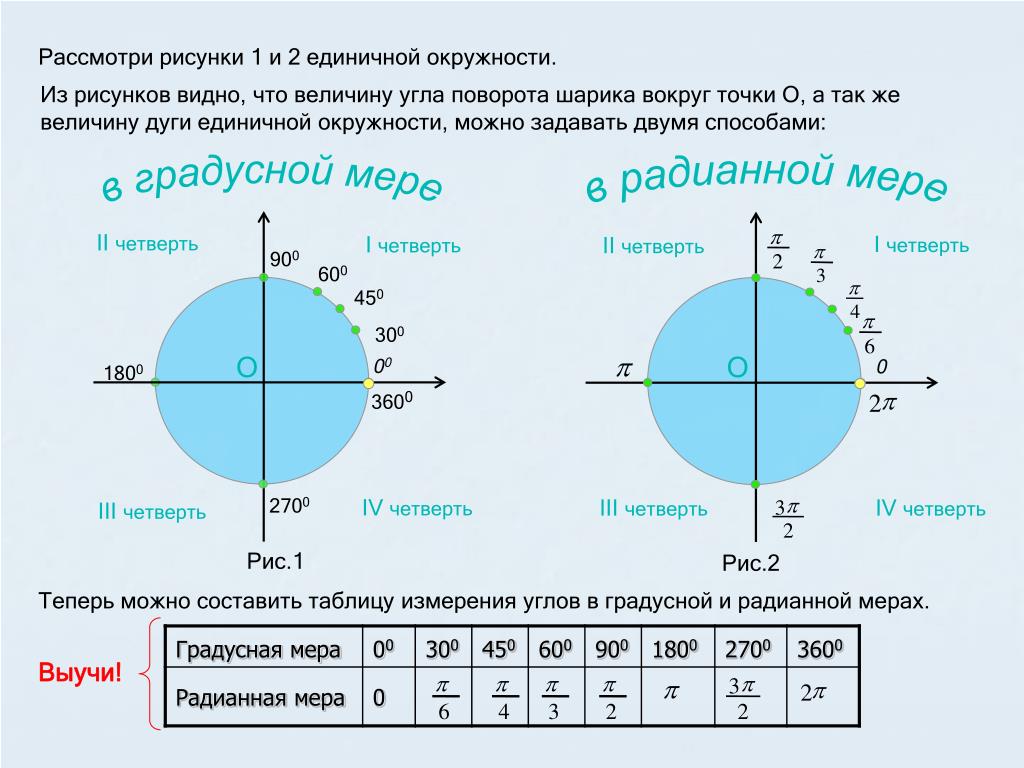
— (Слайд 5) Ребята обратите внимание,
плоскость, содержащая обе стороны угла, делится углом на две области. Каждая из этих областей, объединённая со сторонами угла, называется плоским углом (или просто углом). Один из плоских углов (обычно меньший из двух) иногда условно называют внутренним, а другой — внешним.
— В чем же измеряются углы? (Учащиеся отвечают, что углы измеряются в градусах)
(Слайд 6) Вместе с ребятами обсуждается, что наиболее распространенная мера – это градусная мера углов. Градус — это 1/360 часть полного угла.
(Слайд 7) Если любую окружность разделить на 360 равных частей и точки деления соединить с центром окружности, то круг разделится на 360 центральных углов. Каждый такой угол будет равен 1°.
(Слайд 8) Градусная мера применяется в элементарной геометрии (измерение углов на чертежах транспортиром), в геодезии для измерения углов по карте и на местности (для измерения углов на местности используют весьма точный прибор — универсал/теодолит).
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
За единицу измерения углов можно принять любой угол, но на практике уже более трех тысяч лет используют 1 ° — 1/360 часть полного угла. В мореплавании за единицу измерения углов принимают румб, равный 1/32 части полного угла. В артиллерии за единицу измерения углов принята 1/60 часть полного угла.
(Слайд 9) После повторения важных определений дети на карточках самостоятельно определяют виды углов и их размерность. После проверки по эталону производится оценка своих работ.
(Слайд 10)- Рассмотрим окружность с центром в т. О и различные углы с вершиной в центре. Такие углы по отношению к окружности называются центральными. Равным центральным углам одной и той же окружности соответствуют и равные дуги, и наоборот. Это позволяет перенести градусную меру углов на дуги? Можем ли мы вместо измерения углов в градусах измерять их в дугах?
— Итак ребята, попробуйте сказать, что мы будем изучать сегодня на уроке?
Ребята предполагают, что тема связана с измерением углов дугами.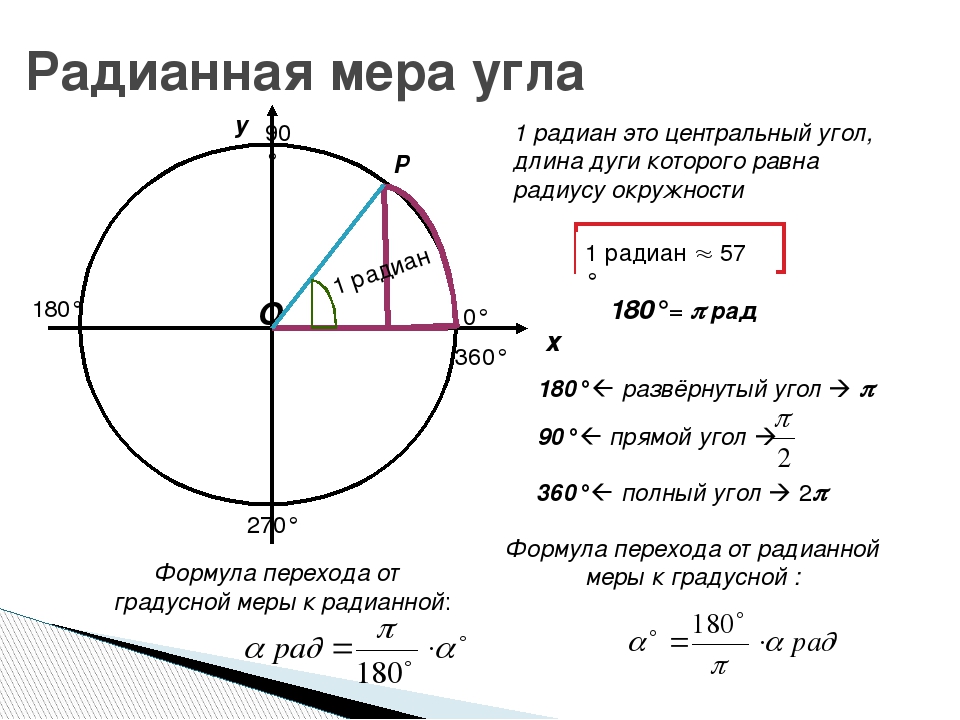 Возникает следующий вопрос, а какую дугу взять за единицу измерения? Может дугой равной радиусу окружности?
Возникает следующий вопрос, а какую дугу взять за единицу измерения? Может дугой равной радиусу окружности?
— Проведем исследование и попробуем измерить сколько раз в окружности укладывается его радиус. Для этого возьмем круг и шнур, измерим шнуром радиус окружности и наложим на край круга. Отметим точку – начало отсчета и измерим сколько раз шнур равный радиусу окружности уложится по краю нашего круга. Результаты показывают- 6,25раз.
Берем меньший круг и повторяем исследование. Опыт показывает, что радиус укладывается в окружности столько же раз – 6,25.
(Слайд 11) Тема урока: Измерение углов радиусом (Радианная мера угла)
Радиа́н (русское обозначение: рад, международное: rad; от лат. radius — луч, радиус)
(Слайд 12) Вместе с ребятами ставим цель урока и задачи для достижения цели урока
Цель нашего урока:
Выяснить, что такое радианная мера угла и как им пользоваться
Для достижения цели ставим следующие задачи:
— Дать определение радианной мере угла.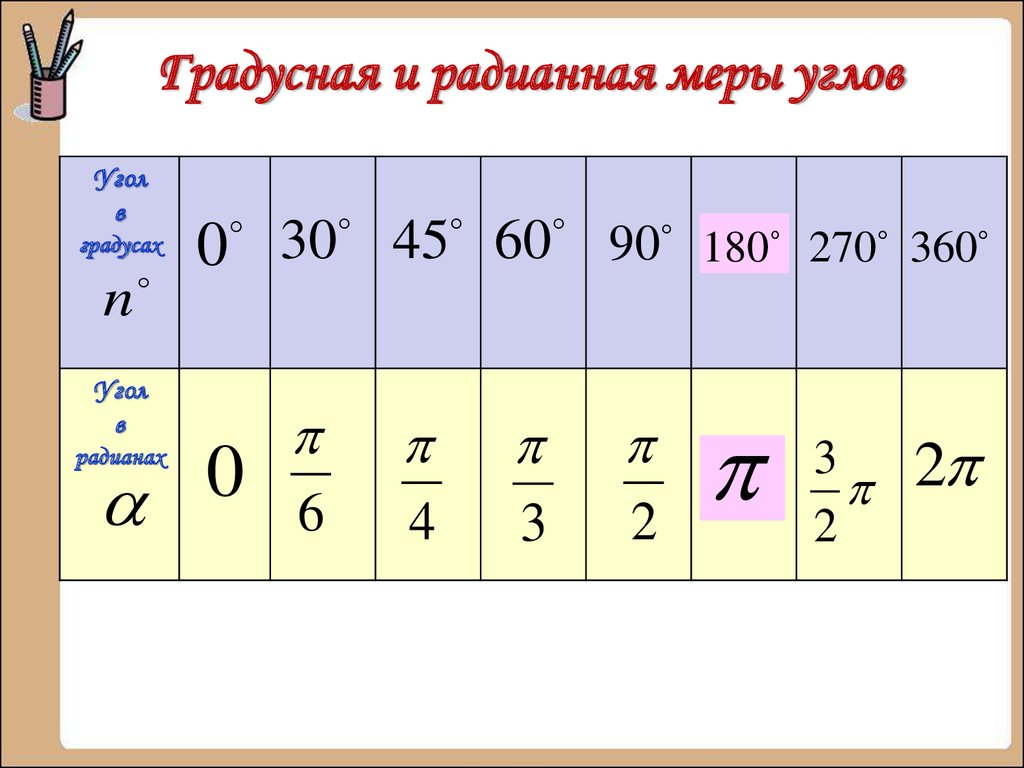
— Выяснить связь между градусной и радианной мерой углов.
— Применить полученные знания при решении задач из жизни.
— Еще в глубокой древности люди пытались измерить длину окружности ее диаметром. Как мы знаем из курса геометрии, длина окружности пропорциональна ее радиусу и выражается формулой L = 2πR. Из формулы видно, что если длину окружности разделить на его диаметр получается число π. Это число иррациональное и было измерено достаточно точно древними учеными. Оно равно приблизительно 3,14. Значит в окружность укладывается ровно три диаметра и еще немного или чуть больше 6 радиусов.
(слайды 13-15) Немного из истории числа π
(Слайд 16) Дуге, равной радиусу окружности соответствует вполне определенный центральный угол, он и будет углом в 1 радиан.
(Слайд 17) Геометрический смысл числа π – это длина окружности с единичным диаметром.
(Слайд 18) — Ребята откройте учебник и выпишите определение угла в 1 радиан в тетради, стр. 272.
После этого все хором повторяем новое определение: Центральный угол опирающийся на дугу, длина которого равна радиусу окружности, называется углом в один радиан.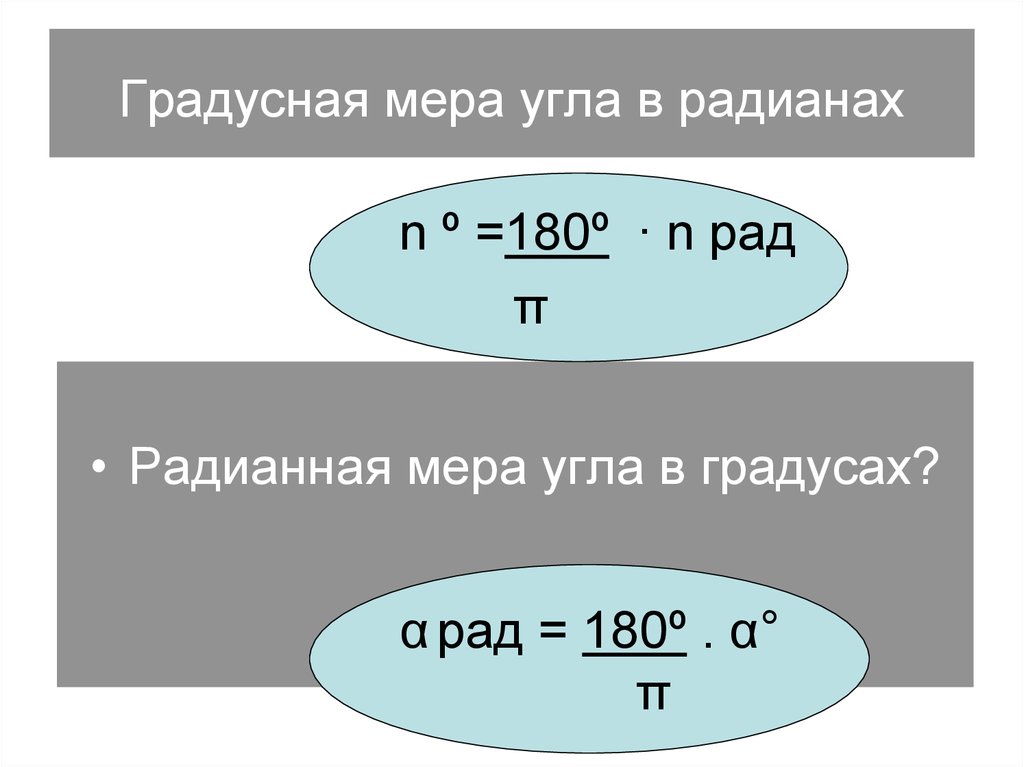
4 Первичное усвоение новых знаний
(Слайд 19) Видеовырезка про радианную меру угла и связь градусной меры с радианной.
(Слайд 20) — Давайте определим, сколько же градусов в одном радиане? Для этого запишем соответствие, которое мы определили. 2π рад соответствует 360°, πрад = 180°. Разделив обе части равенства на π, получим 1 рад = 180°/π = 180° /3,14 ≈ 57,3°
5 Первичная проверка понимания ( мин)
(Слайд 21) Самостоятельная работа. Определить сколько градусов в 2рад, 3 рад и 4рад? Проверка по образцу.
(Слайд 22) – Найдем формулу перехода из радианной меры углов в градусную. Если
1 рад = 180°/π, α рад = α 180°/π
(Слайд 23) – Найдем формулу перехода из градусной меры в радианную. Для этого запишем соответствие, которое мы определили. 2π рад соответствует 360°, πрад = 180°. Разделив обе части равенства на 180, получим 1 ° = π /180°. Соответственно α° = α π /180°рад.
(Слайд 24) Самостоятельная работа. Определить сколько радиан в 30°, 90° и 45°
Проверяем по образцу.
(Слайд 25) №925. Решаем пример из учебника на переход из радианной меры угла в градусную.
(Слайд 26) №926. Решаем пример из учебника на переход из градусной меры угла в радианную.
(Слайд 27) Решаем задачу из учебника, №928
(Слайд 28) Повторяем определение угла в 1 рад.
(Слайд 29) На слайде появляется формула, дети определяют название.
6 Повторное закрепление ( мин)
(Слайд 30) Контрольная работа. Дети делают на отдельных листочках. После выполнения проверяют друг у друга по образцу.
7 Рефлексия
Таблица №1
(заполнить таблицу 1) ЛИСТ САМООЦЕНКИ
Утверждение | Задание 1 Угол. Виды углов | Задание 2 Величина углов | Задание 3 Перевод рад в градусы | Задание 4 Перевод град в радианы | №925 | №926 | №928 | Определение угла в 1 рад | Проверяем себя Формулы перехода | Контрольная работа |
Оцениваю на «5» | ||||||||||
Оцениваю на «4» | ||||||||||
Оцениваю на «3» |
Выводим среднюю оценку
Выставляются положительные оценки за урок. Тем, у кого 3ки предлагается быть на следующих уроках более активными на всех этапах.
Тем, у кого 3ки предлагается быть на следующих уроках более активными на всех этапах.
8 Домашнее задание
(Слайд 31) Записываем домашнее задание
1) §1 Радианная мера угла, стр. 272
2) №933, заполнить таблицу
Знать:
— определение радианной меры угла;
— формулы перехода.
Уметь:
— переводить градусную меру угла в радианную;
— переводить радианную меру угла в градусную.
— Какие есть вопросы?
Обучающиеся задают вопросы. Преподаватель отвечает на них.
Разбираем поэтапно заполнение таблицы в номере 933.
9 Завершение
(Слайд 32) — Занятие окончено! До свидания!
Учащиеся собираются, уходят кабинета, преподаватель приводит рабочее место в порядок.
Приложение 1
Контрольная работа
I вариант
Определить градусную и радианную меру углов равностороннего треугольника.
II вариант
Определить градусную и радианную меру углов равнобедренного прямоугольного треугольника.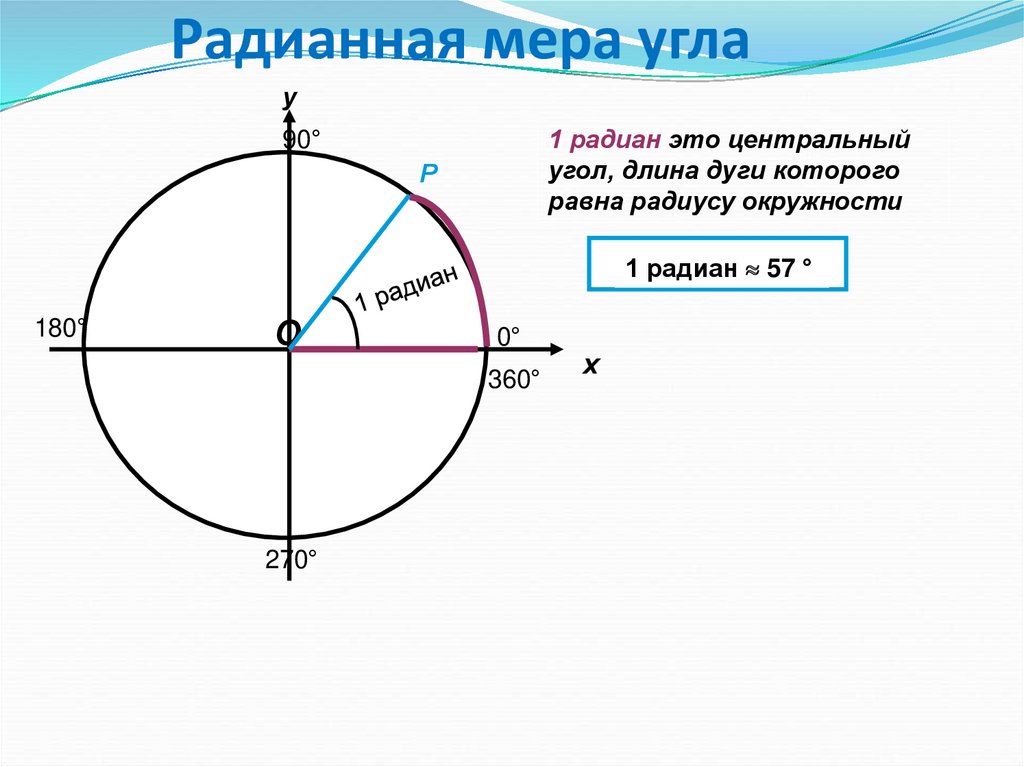
Приложение 2
Лист самооценки
Ф. И. _____________________________________________________________
Утверждение | Задание 1 Угол. Виды углов | Задание 2 Величина углов | Задание 3 Перевод рад в градусы | Задание 4 Перевод град в радианы | №925 | №926 | №928 | Определение угла в 1 рад | Проверяем себя Формулы перехода | Контрольная работа |
Оцениваю на «5» | ||||||||||
Оцениваю на «4» | ||||||||||
Оцениваю на «3» |
Конец урока (ставим «+»)
Знаю все ___________ Знаний стало больше _________
Ничего нового не узнал _______ Могу рассказать другим _______
Лист самооценки
Ф.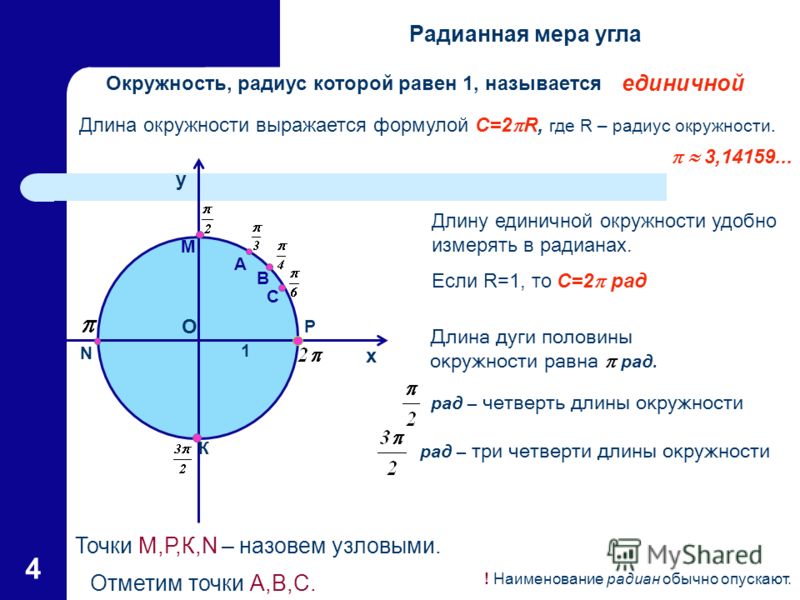 И. _____________________________________________________________
И. _____________________________________________________________
Утверждение | Задание 1 Угол. Виды углов | Задание 2 Величина углов | Задание 3 Перевод рад в градусы | Задание 4 Перевод град в радианы | №925 | №926 | №928 | Определение угла в 1 рад | Проверяем себя Формулы перехода | Контрольная работа |
Оцениваю на «5» | ||||||||||
Оцениваю на «4» | ||||||||||
Оцениваю на «3» |
Конец урока (ставим «+»)
Знаю все ___________ Знаний стало больше _________
Ничего нового не узнал _______ Могу рассказать другим _______
Интернет -урок — Радиан угловой мера
Акции
Приоритет урока: высокий
Pre -Calculus $ \ longrightarrow $
Тригонометрия $ \ longrightarrow $
Углы и угол измерения
Цели
- УЧЕБНО.
 радианы и понять, почему это мера без измерения
радианы и понять, почему это мера без измерения - Преобразование между обычными градусными мерами углов и их эквивалентной мерой в радианах
- Вернитесь к измерению углов в координатной плоскости, но на этот раз в радианах
- Станьте экспертом в измерении углов в радианах вместо градусов — это понадобится вам в будущем!
Описание урока
На протяжении большей части пути по тригонометрии (и особенно в исчислении) мы не можем использовать градусы как способ измерения углов. Этот урок знакомит с очень важным альтернативным, безразмерным способом измерения углов, измеряемых в единицах, которые мы называем радианами.
Практические задачи
Практические задачи и рабочие листы скоро появятся!
Градусов недостаточно
До сих пор мы использовали градусы для измерения величины углов. Градус — это несколько произвольная единица измерения, которая была создана задолго до современной математики, и, как мы знаем, она определяется как $1/360$ окружности. 2$? Градусы в квадрате ничего не значат, в отличие от квадратных футов.
2$? Градусы в квадрате ничего не значат, в отличие от квадратных футов.
Решение — радианы
Чтобы решить эту проблему, математики придумали безразмерный способ измерения углов в координатной плоскости. Вместо использования фиксированных, заранее определенных единиц измерения углы измеряются в виде дроби. Таким образом, любая единица измерения сокращается сама с собой, и как число без единиц измерения, если вы возьмете измерение угла и возведете его в квадрат, извлечете из него корень или сделаете с ним что-нибудь еще, оно останется безразмерным числом. Число основан на центральных углах и соответствующих им длинах дуг сектора. Измерение угла — это количество длин радиуса, которое занимает длина дуги сектора. Давайте определим и поймем это правильно.
Измерение угла в радианах Измерение угла в радианах равно длине дуги сектора окружности центрального угла, измеренной по числу длин радиуса окружности.
Как и градусы, это измерение является универсальным и не зависит от размера круга, который вы используете для сектора, потому что любые два сектора с одинаковым углом имеют одинаковое измерение длины дуги при измерении в числе радиусов длин дуг Если круг увеличивается, увеличивается и длина радиуса. Однако, как выясняется, угол, измеренный целым числом радиан, никогда не будет «хорошим» углом. На самом деле, вы никогда не будете работать с углами, подобными $2$ или $3$ радианам, во время ваших исследований тригонометрии (за исключением редких вопросов, которые обычно являются вопросами с подвохом). Вместо этого, общие углы, с которыми вы будете работать, будут кратны $\pi $ и доли $\pi$. Основная причина заключается в том, что количество длин радиуса, охватывающих всю окружность, не является целым числом — оно равно $\pi$, умноженному на $2$. Другими словами, в длине дуги есть $\pi$ длин радиуса. полукруга: 9{\circ}$ в центральном углу, охватывающем окружность ровно один раз.
Однако, как выясняется, угол, измеренный целым числом радиан, никогда не будет «хорошим» углом. На самом деле, вы никогда не будете работать с углами, подобными $2$ или $3$ радианам, во время ваших исследований тригонометрии (за исключением редких вопросов, которые обычно являются вопросами с подвохом). Вместо этого, общие углы, с которыми вы будете работать, будут кратны $\pi $ и доли $\pi$. Основная причина заключается в том, что количество длин радиуса, охватывающих всю окружность, не является целым числом — оно равно $\pi$, умноженному на $2$. Другими словами, в длине дуги есть $\pi$ длин радиуса. полукруга: 9{\circ}$ в центральном углу, охватывающем окружность ровно один раз.
Вы должны знать
В химии нас учат, как использовать размерный анализ для преобразования величин из одного набора единиц измерения в другой, например, литров газа в число молекул. Хотя нам не нужно возвращаться к этому материалу в явном виде, есть огромная польза от запоминания этой концепции здесь — это помогает вам отслеживать, какое число должно быть первым при преобразовании между градусами и радианами или наоборот. {\ circ} & \ longrightarrow & \ frac {\ pi} {3} \\ \\
9{\circ}$ для этой задачи, вычисления на основе радиана будут использовать $2\pi$.
{\ circ} & \ longrightarrow & \ frac {\ pi} {3} \\ \\
9{\circ}$ для этой задачи, вычисления на основе радиана будут использовать $2\pi$.
Пример 3. Найдите положительный и отрицательный смежные углы для $7\pi / 6$.$\blacktriangleright$ Нам не нужно преобразовывать этот угол в градусы или даже знать, где он находится в плоскости, чтобы выполнить эту задачу. . Давайте просто добавим и вычтем $2\pi$, чтобы получить каждый ответ. Положительный котерминал: $$\frac{7\pi}{6} + 2\pi$$$$= \frac{7\pi}{6} + \frac{12\pi}{6}$$$$= \frac{19\pi}{6}$$Отрицательный котерминал:$$\frac{7\pi}{6} — 2\pi$ $$$= \frac{7\pi}{6} — \frac{12\pi}{6}$$$$= -\frac{5\pi}{6}$$Как видите, ключ состоит в том, чтобы превратить $2\pi$ в любой знаменатель, с которым вы работаете. Обратите внимание, что нам нужно было прибавлять и вычитать $2\pi$ только один раз для каждого ответа, потому что угол был «типичным» положительным углом, который не превышает одного оборота. В противном случае нам пришлось бы прибавлять или вычитать $2\pi$ несколько раз. {\,\circ}$, и его нельзя упростить или изменить. Мы могли бы использовать калькулятор, чтобы примерно получить 229 долларов.{\circ}$$
{\,\circ}$, и его нельзя упростить или изменить. Мы могли бы использовать калькулятор, чтобы примерно получить 229 долларов.{\circ}$$
Пример 12. Найдите положительный и отрицательный смежные углы, равные $8\pi / 3$.
Показать решение
$\blacktriangleright$ Сначала вычтем $2 \pi$:$$\frac{8 \pi}{3} — 2\pi$$$$ \longrightarrow \frac{8 \pi}{3} — \frac{6 \pi}{3} = \frac{2 \pi}{3}$$Здесь мы нашли котерминальный положительный угол путем вычитания, потому что наш первоначальный угол $8 \pi / 3$ уже был больше чем один полный оборот. Мы могли бы добавить $2 \pi$ и получить положительный котерминальный угол, но таким образом мы приблизимся к другой половине нужного нам ответа. Вычтем $2\pi$ еще раз, чтобы получить отрицательный конечный угол.$$\frac{2 \pi}{3} — \frac{6 \pi}{3} = — \, \frac{4\pi }{3}$$Поэтому угол, положительный и котерминальный с $8 \pi / 3$, равен $2 \pi / 3$, а отрицательный и котерминальный угол с $8 \pi / 3$ равен $-4\пи/3$. Есть много других правильных способов ответить на этот вопрос. 9{\circ}$$Помните, что когда вы работаете с числом в радианах, которое не является дробью от $\pi$, вы получите $\pi$ в знаменателе вашего ответа.
Есть много других правильных способов ответить на этот вопрос. 9{\circ}$$Помните, что когда вы работаете с числом в радианах, которое не является дробью от $\pi$, вы получите $\pi$ в знаменателе вашего ответа.
Выводы из урока
- Понимать, что такое радианы и как мы их используем
- Уметь переводить градусы и радианы вперед и назад
- Знать, как быстро определить квадрант любого измеренного угла в радианах
- 90∘
- 30∘
- 55∘
- Радианы и градусы являются единицами измерения углов.
- Один радиан — это угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности.

- Мы можем преобразовать градусы в радианы, используя
- 2𝜋=360радиан∘,
- 𝜋=180радиан∘,
- 𝜋2=90радиан∘.
- В качестве альтернативы, мы можем преобразовать угол в градусах в единицу в радианах, умножив заданный угол на 𝜋180, и мы можем преобразовать угол в радианах в единицу в градусах, умножив заданный угол на 180𝜋.
5 Что такое преимущество измерения угла в радианах?
Я хочу предложить другую точку зрения, которая не противоречит другим ответам, но смотрит на них под другим углом…
Краткий ответ
Определение углов в радианах имеет то преимущество, что оно больше соответствует тому, как мы стремятся определить другие величины.
Длинный ответ
Давайте на мгновение отложим в сторону углы и подумаем, как мы вообще определили типы величин.
Возьмем пример из естественных наук. Мы хотим определить «плотность» вещества, которая отражала бы наше интуитивное восприятие понятия. Плотность означает, сколько вещества содержится в некотором объеме, поэтому мы определяем плотность как отношение числа частиц вещества к его объему:
Мы хотим определить «плотность» вещества, которая отражала бы наше интуитивное восприятие понятия. Плотность означает, сколько вещества содержится в некотором объеме, поэтому мы определяем плотность как отношение числа частиц вещества к его объему:
$\mathrm{плотность=\frac{число\: of\: частиц}{объем}}$ .
Мы могли бы также определить его как
$\mathrm{density=62.112\times\frac{number\: of\: частиц}{volume}}$ ,
, и это все равно было бы нам полезно, но поскольку у нас нет никаких причин добавлять число $62.112$, мы просто этого не делаем. Нам кажется проще просто использовать $1$. То же самое относится и к большинству наших определений количественных типов. (Мы могли бы возразить, что число $62,112$ столь же произвольно, как и число $1$, но, хотя это может быть правдой в некотором философском смысле, факт в том, что мы, люди, думаем, что $1$ проще. Нам больше нравится $1$.) .
Теперь это относится и к математическим определениям. Например, функция $\sin\alpha$ первоначально была определена как отношение двух сторон прямоугольного треугольника с углом $\alpha$: стороны, противоположной этому углу, и гипотенузы.
$\sin\alpha=\mathrm{\frac{противоположный\: длина}{гипотенуза\: длина}}$
Почему $\sin$ был определен в первую очередь? И почему было выбрано именно это определение? Я не знаю точно, но могу предположить, что ответ на предыдущий вопрос заключается в том, что кто-то (несколько тысячелетий назад) интересовался количественной оценкой форм различных прямоугольных треугольников, и $\sin$, как определено выше, действительно является хорошим такое количество. Как насчет последнего вопроса? Почему они не выбрали определение
$\sin\alpha=\mathrm{62.112\times \frac{напротив\: длина}{гипотенуза\: длина}}$ ?
Опять же, потому что это менее просто (а еще, наверное, с такими номерами тогда вообще не работали).
Теперь попробуем определить величину, характеризующую величину угла. У нас есть интуитивное понимание угла, и мы должны попытаться дать ему количественную оценку. Итак, что такое угол? Я думаю об этом как об открытии между двумя линиями:
Как мы можем это измерить? Сразу приходят на ум два варианта. Мы можем взять площадь, «ограниченную» между двумя линиями, или мы можем взять длину линии, соединяющей концы линий. Давайте посмотрим на последний вариант:
Мы можем взять площадь, «ограниченную» между двумя линиями, или мы можем взять длину линии, соединяющей концы линий. Давайте посмотрим на последний вариант:
Это хорошее определение величины угла? Нет, потому что в нашем интуитивном представлении величина угла не должна зависеть от длины сторон, и здесь мы получаем, что чем длиннее одна из линий, тем больше угол. Эту проблему можно решить, используя отношения длин вместо абсолютной длины. Например, отношение пунктирной линии к отношению нижней линии. Но результат все равно зависит от соотношения длин верхней и нижней линий. Итак, давайте решим, что при измерении угла мы также следим за тем, чтобы линии имели некое фиксированное заранее заданное соотношение длин. Это соотношение будет «стандартным».
Какой коэффициент выбрать? он может реально любым числом, например $62.112$… Вы уже поняли — проще использовать $1$.
У этого определения все еще есть проблема, которая делает его менее полезным — оно не является аддитивным. Что величина угла, который можно разделить на два неперекрывающихся угла, не равна сумме величин отдельных углов:
Что величина угла, который можно разделить на два неперекрывающихся угла, не равна сумме величин отдельных углов:
Как мы можем улучшить наше определение, чтобы обойти эту проблему? вместо этого мы можем использовать длину дуги окружности, центр которой является пересечением двух линий. 9\circ$. (Я назову это определение «градусы»). Правда, у этого определения есть некоторые преимущества. Это делает максимально достижимый угол кратным многим целым числам. Но, с другой стороны, мы обычно определяем количество с помощью $1$, когда нам не нужно никакого числа. Вот как мы определили $\sin\alpha$. И поскольку именно так мы обычно определяем величины, определение новой величины в противном случае привело бы к тому, что в наших расчетах появилось бы множество чисел, которые не равны $1$. В качестве примера рассмотрим $\sin\alpha$ и $\alpha$. Их определение очень похоже — отношения двух длин. На самом деле, для очень малых углов прямоугольный треугольник и прямые + дуга почти неразличимы:
Если мы определим значения $\sin\alpha$ и $\alpha$ совместимым образом, мы можем превратить это наблюдение в красивое математическое утверждение, что $\sin\alpha\приблизительно\альфа$. Так давайте сделаем их совместимыми! Один из способов — определить
Так давайте сделаем их совместимыми! Один из способов — определить
$\sin\alpha=\mathrm{57.29577951308\times \frac{opposite\: length}{hypotenuse\: length}}$
и использовать определение «градусов» для углов. Но опять же, мы несовместимы со многими другими определениями, которые мы делаем, такими как другие тригонометрические функции или площади. Площадь треугольника будет иметь формулу $\frac{1}{2\times57,29577951308}ab\sin\alpha$ вместо более удобной формулы $\frac{1}{2}ab\sin\alpha$. Лучшее решение — просто использовать $1$ в определении угла. Это совместимо со всем остальным, что мы определили, и многое упрощает.
Между прочим, я хотел бы добавить, что мне не нравится думать о радианах и градусах как о единицах измерения, а скорее как о различных определениях величины угла. Это не разные методы измерения, это разные определения. Точно так же, определяя плотность как количество частиц, деленное на дважды объем, который они занимают, будет другим определением плотности, а не другой системой единиц. Но я не буду вдаваться в подробности здесь…
Но я не буду вдаваться в подробности здесь…
Преобразование градусов в радианы
Деление окружности на 360 частей является произвольным выбором, хотя и создает привычное измерение градусов. Мы можем выбрать другие способы разделения круга. Чтобы найти другую единицу, подумайте о процессе рисования круга. Представьте, что вы останавливаетесь до того, как круг завершится. Часть, которую вы нарисовали, называется дугой. дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется длины окружности этого круга.
Длина окружности [латекс]C=2\pi r[/латекс]. Если мы разделим обе части этого уравнения на [латекс]r[/латекс], мы получим отношение длины окружности к радиусу, которое всегда равно [латекс]2\пи [/латекс], независимо от длины радиуса. Таким образом, длина окружности любого круга равна [латекс]2\пи \приблизительно в 6,28[/латекс], умноженной на длину радиуса. {\circ}\hfill \end{массив}[/latex]
{\circ}\hfill \end{массив}[/latex]
Обратите внимание, что когда угол описывается без конкретной единицы измерения, это относится к радианам. Например, угол, равный 3, соответствует 3 радианам. На самом деле, мера радиана безразмерна, так как это частное длины (окружности), деленной на длину (радиус), и единицы длины сокращаются.
Рис. 11. Угол t заметает меру в один радиан. Обратите внимание, что длина перехваченной дуги равна длине радиуса окружности.
Отношение длины дуги к радиусу
Длина дуги [латекс]с[/латекс] — это длина кривой вдоль дуги. Точно так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, создаваемая любым заданным углом, также имеет постоянное отношение к радиусу, независимо от длины радиуса.
Это отношение, называемое радианной мерой , одинаково независимо от радиуса круга — оно зависит только от угла. Это свойство позволяет определить меру любого угла как отношение длины дуги [латекс]s[/латекс] к радиусу [латекс]r[/латекс].
[латекс]\begin{array}{l}s=r\theta \\ \theta =\frac{s}{r}\end{array}[/latex]
Если [латекс]s=r[ /latex], затем [latex]\theta =\frac{r}{r}=\text{ 1 радиан}\text{.}[/latex]
Рис. 12. (a) В углу 1 радиан, длина дуги [latex]s[/latex] равна радиусу [latex]r[/latex]. (b) Угол в 2 радиана имеет длину дуги [латекс]s=2r[/латекс]. (c) Полный оборот составляет [латекс]2\пи [/латекс] или около 6,28 радиана.
Чтобы развить эту идею, рассмотрим две окружности, одну с радиусом 2, а другую с радиусом 3. Вспомним, что длина окружности равна [латекс]C=2\pi r[/латекс], где [латекс]r[ /латекс] — это радиус. Тогда меньший круг имеет окружность [латекс]2\pi \left(2\right)=4\pi [/latex], а больший круг имеет окружность [латекс]2\pi \left(3\right)=6\pi [ /латекс]. Теперь мы рисуем угол 45° на двух окружностях, как показано на Рисунке 13. 9.0003
Рис. 13. Угол 45° содержит одну восьмую длины окружности независимо от радиуса.
Обратите внимание, что произойдет, если мы найдем отношение длины дуги к радиусу окружности.
[латекс]\begin{array}{c}\text{Меньший круг:}\frac{\frac{1}{2}\pi }{2}=\frac{1}{4}\pi \\ \text{Большой круг: }\frac{\frac{3}{4}\pi }{3}=\frac{1}{4}\pi \end{array}[/latex]
Так как оба соотношения [latex]\frac{1}{4}\pi [/latex], меры угла обеих окружностей одинаковы, хотя длина дуги и радиус различаются.
A Общее примечание: радианы
Один радиан — это мера центрального угла окружности, при которой длина дуги между начальной и конечной сторонами равна радиусу окружности. Полный оборот (360°) равен [латекс]2\пи [/латекс] радианам. Половина оборота (180°) эквивалентна [латекс]\пи [/латекс] радианам.
радиан мера угла представляет собой отношение длины дуги, образуемой углом, к радиусу окружности. Другими словами, если [латекс]s[/латекс] — это длина дуги окружности, а [латекс]r[/латекс] — радиус окружности, то центральный угол, содержащий эту дугу, измеряет [латекс] \frac{s}{r}[/latex] радианы. В круге радиусом 1 мера радиана соответствует длине дуги. 9\circ [/латекс].
9\circ [/латекс].
Использование радианов
Поскольку радиан мера представляет собой отношение двух длин, это безразмерная мера. Например, на рисунке 12 предположим, что радиус равен 2 дюймам, а расстояние по дуге также равно 2 дюймам. Когда мы вычисляем радианную меру угла, «дюймы» сокращаются, и мы получаем результат без единиц измерения. Следовательно, нет необходимости писать метку «радианы» после радианной меры, и если мы видим угол, который не помечен «градусами» или символом градуса, мы можем считать, что это радианная мера. 9\circ \hfill & =\frac{\pi }{2}\hfill & \text{радианы}\hfill \end{array}[/latex]
Идентификация особых углов, измеренных в радианах
В дополнение к знанию измерений в градусах и радианах четверти оборота, половины оборота и полного оборота есть и другие часто встречающиеся углы в одном обороте окружности, с которыми мы должны быть знакомы. Обычно встречаются углы, кратные 30, 45, 60 и 90 градусам. Эти значения показаны на рис. 14. Запоминание этих углов будет очень полезно при изучении свойств, связанных с углами.
14. Запоминание этих углов будет очень полезно при изучении свойств, связанных с углами.
Рисунок 14. Часто встречающиеся углы, измеренные в градусах
Теперь мы можем перечислить соответствующие значения радианов для обычных мер окружности, соответствующих тем, которые перечислены на рисунке 14, которые показаны на рисунке 15. Убедитесь, что вы можете проверить каждую из этих мер.
Рис. 15. Часто встречающиеся углы, измеряемые в радианах
Пример 2. Нахождение радианной меры
Найдите радианную меру одной трети полного оборота.
Решение
Для любого круга длина дуги такого поворота будет равна одной трети длины окружности. Мы знаем, что
[латекс]1\текст{вращение}=2\pi r[/латекс]
Итак,
[латекс]\begin{array}{l}\\ \begin{array}{l} s=\frac{1}{3}\left(2\pi r\right)\hfill \\ =\frac{2\pi r}{3}\hfill \end{массив}\end{массив}[/ латекс]
Радианы будут делением длины дуги на радиус.
[латекс]\begin{array}{l}\begin{array}{l}\begin{array}{l}\text{радианная мера}=\frac{\frac{2\pi r}{3} }{r}\hfill \\ =\frac{2\pi r}{3r}\hfill \end{массив}\hfill \\ =\frac{2\pi }{3}\hfill \end{массив}\ hfill \\ \text{ }\hfill \\ \text{ }\hfill \end{массив}[/latex] 9{R}}{\pi }[/latex]
Эта пропорция показывает, что мера угла [латекс]\тета [/латекс] в градусах, поделенная на 180, равна величине угла [латекс]\тета [/латекс] в радианах, разделенных на [латекс]\пи . {R} \ конец {массив} [/латекс] 9{\circ}\right)[/latex], мы можем найти, что [латекс]\frac{1}{2}\left(\frac{\pi }{6}\right)[/latex] — это [латекс] \frac{\pi }{12}[/латекс].
{R} \ конец {массив} [/латекс] 9{\circ}\right)[/latex], мы можем найти, что [латекс]\frac{1}{2}\left(\frac{\pi }{6}\right)[/latex] — это [латекс] \frac{\pi }{12}[/латекс].
Попробуйте 4
Преобразование 126° в радианы.
Решение
Посмотрите следующее видео, в котором объясняется, что такое радианы, а также примеры преобразования радиан в градусы.
Измерение углов — радианы, отрицательные углы, углы больше 360
Угол: °πрад =
Преобразование в: Радианы0 – 360 градусов от положительного до отрицательного
Когда две линии пересекаются, они дают четыре разных пространства относительно точки пересечения.
Созданные пространства называются углами .
На рисунке показаны 4 различных угла, образованных на пересечении двух прямых AB и CD.
Углы обычно измеряются в градусах, обозначаемых как °.
Когда объект движется по полному циклу, то есть из точки D через B, C, A и обратно в D, мы говорим, что он прошел 360 градусов (360°).
Следовательно, степень — это $\frac{1}{360}$ цикла.
Мы обсуждали, что когда объект совершает один полный оборот вокруг точки, он покрывает 360°, однако, когда объект совершает более одного цикла, он совершает угол больше 360°. Это обычное явление в повседневной жизни. Шина совершает многочисленные циклы, когда транспортное средство движется отсюда; получается угол больше 360°.
Чтобы узнать количество циклов, совершаемых при вращении объекта, мы подсчитываем, сколько раз можно прибавить к нему 360, чтобы получить число, равное или меньше заданного угла. Точно так же мы находим число, которое можно умножить на 360, чтобы получить число меньше, но ближе к заданному углу. 9{\circ} = \frac{260}{360} = \frac{7}{9}$ циклов
9{\circ} = \frac{260}{360} = \frac{7}{9}$ циклов
Объект делает $2\frac{7}{9}$ циклов
На рисунке ниже показан знак угла, измеренного от общей линии, линии 0 градусов
Когда объект вращается по часовой стрелке, он делает 90 267 отрицательных 90 268 углов вращения, а когда он вращается против часовой стрелки, он делает 90 267 положительных 90 268 углов. До сих пор в наших дискуссиях мы рассматривали только положительные стороны.
В форме диаграммы отрицательный угол может быть таким, как показано ниже.
Это означает, что, учитывая отрицательный угол, мы можем получить соответствующий положительный угол.
Например, нижняя часть вертикальной линии равна 270°. При измерении в отрицательном направлении это будет -90°. Мы просто вычитаем 270 из 360.
Учитывая отрицательный угол, мы добавляем 360, чтобы получить соответствующий положительный угол.
Если угол равен -360°, это означает, что объект совершил более одного цикла по часовой стрелке.
Пример 3
1. Найдите соответствующий положительный угол
а) -35°
б) -60°
в) -180°
г) — 670°
2. Найдите соответствующие отрицательные углы 80°, 167°, 330° и 1300°.
Решение
1. Мы добавляем 360 к углу, чтобы получить соответствующий положительный угол.
а) -35°= 360 + (-35) = 360 — 35 = 325°
б) -60°= 360 + (-60) = 360 — 60 = 300°
в) -180°= 360 + ( -180) = 360 — 180 = 180°
г) -670°= 360 + (-670) = -310
Это один цикл по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Мы вычитаем 360 из угла, чтобы получить соответствующий отрицательный угол.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (один цикл выполнен)
940 — 360 = 580 (сделан второй цикл)
580 — 360 = 220 (сделан третий цикл)
220 — 360 = -140°
Угол -360 — 360 — 360 — 140 = -1220° 9{\circ}$
Радиус = r = OA = OB = AB
Угол BOA равен 1 радиан
Так как длина окружности определяется радиусом $2\pi r$ или $2\pi$, то в одном полном цикле содержится $2\pi$ радиан.
Радианы обычно выражаются в виде $\pi$, чтобы не использовать десятичные дроби в вычислениях. В большинстве книг аббревиатура рад не приводится, но читатель должен знать, что когда речь идет об угле, заданном через $\pi$,
единицами автоматически являются радианы.
9{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицательные углы и углы больше $2\pi$ радиан
Чтобы преобразовать отрицательный угол в положительный, мы добавляем к нему $2\pi$.
Чтобы преобразовать положительный угол в отрицательный, мы вычтем из него $2\pi$.
Пример 5
1. Преобразуйте углы $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в положительные углы в радианах.
Решение
Прибавляем $2\pi$ к углу
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4} \pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2} {7}\пи$
Когда объект поворачивается на угол, превышающий $2\pi$; это сделало бы более одного цикла.
Чтобы определить количество циклов такого угла, находим число при умножении на $2\pi$, результат равен или меньше, но ближе к числу.
Пример 6
1. Найдите количество циклов, совершаемых при повороте объекта на следующие углы
а) $-10\pi$
б) $9\pi$
в) $\frac{7}{2}\pi$
Решение
а) $-10\pi = 5(-2\pi)$; поскольку $-2\pi$ подразумевает один цикл по часовой стрелке, это означает, что
объект сделал 5 циклов по часовой стрелке.
б) $9\pi = 4(2\pi) + \pi$, $\pi =$ полупериод
объект совершил четыре с половиной цикла против часовой стрелки
в) $\frac{7}{2}\pi=3.5\pi=2\pi+1.5\pi$, $1.5\pi$ — трехчетвертный цикл $(\frac{1.5\pi}{2\pi} =\frac{3}{4})$
объект совершил один и три четверти цикла против часовой стрелки
Объяснение урока: Преобразование радианов в градусы
В этом объяснении мы узнаем, как преобразовывать радианы в градусы и наоборот.
Радианы, как и градусы, являются единицей измерения углов. Они используются в качестве альтернативы градусам. Давайте формально определим, что мы подразумеваем под радианом.
Они используются в качестве альтернативы градусам. Давайте формально определим, что мы подразумеваем под радианом.
Начнем с окружности с центром 𝑂 и радиусом 𝑟.
Теперь представьте, что мы берем другую длину радиуса 𝑟, которую мы изгибаем по окружности круга.
Теперь у нас есть сектор круга с радиусом 𝑟 и длиной дуги 𝑟. Угол в центре круга определяется как 1 радиан (рад).
Определение: радианы
Один радиан — это угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности.
Теперь, когда мы определили, что мы подразумеваем под одним радианом, мы продемонстрируем, как преобразовать радианы в градусы.
Напомним, что расстояние вокруг окружности — это ее длина окружности, а ее мера находится путем умножения 𝜋 на диаметр, 𝑑. Мы можем записать эту окружность, 𝐶, как 𝐶=𝜋𝑑.
Эквивалентно, мы также можем описать длину окружности через радиус как 𝐶=2𝜋𝑟.
Глядя на сектор круга выше, с длиной дуги 𝑟, мы считаем, сколько дуг длины 𝑟 можно провести по окружности. Поскольку мы определили длину дуги 𝑟 равной радиусу 𝑟, это означает, что количество дуг, которые могут поместиться на окружности, будет 2𝜋𝑟÷𝑟=2𝜋.
Поскольку мы определили длину дуги 𝑟 равной радиусу 𝑟, это означает, что количество дуг, которые могут поместиться на окружности, будет 2𝜋𝑟÷𝑟=2𝜋.
Если мы нарисуем эту диаграмму, мы можем вспомнить, что числовое приближение для 2𝜋 равно 6,283…. На диаграмме 6 полных дуг и оставшаяся часть 0,283… дуги.
Так как 2𝜋 дуг составляют полную окружность круга, то должно быть 2𝜋 секторов, составляющих сам круг. Поскольку угол каждого сектора равен 1 радиану, мы можем сказать, что сумма этих углов равна 2𝜋 радианам.
Однако мы также знаем, что сумма углов в окружности в градусах равна 360∘, а это означает, что мы можем заметить, что 2𝜋=360.радиан∘
Это дает идеальное преобразование между двумя единицами измерения . Кроме того, мы также можем разделить обе части этого уравнения на 2 или на 4, получив два альтернативных факта преобразования: 𝜋=180 радиан∘ и 𝜋2=90.радиан∘
Аналогичным образом, взяв уравнение 𝜋=180радиан∘, мы можем разделить обе части на 𝜋, чтобы найти значение 1 радиана в градусах:
Знание любого из этих фактов преобразования позволит нам преобразовать любой угол из радианов в градусы или наоборот.
Практическое руководство. Преобразование радианов в градусы
2𝜋=360𝜋=180𝜋2=90радианрадианырадианы∘∘∘
Теперь мы рассмотрим несколько примеров преобразования углов в градусах в углы в радианах.
Пример 1. Преобразование угла из градусов в радианы
Преобразуйте следующие меры угла из градусов в радианы. Дайте свои ответы с точки зрения 𝜋 в их простейшей форме.
Ответ
Чтобы перевести угол в градусах в угол в радианах, мы запоминаем факт преобразования: 180=𝜋.∘радиан
Часть 1
В первой части этого вопроса нам нужно преобразовать угол 90∘ в радианах. Мы замечаем, что 90∘ — это половина 180∘. Следовательно, мы можем разделить обе части преобразования на 2, что дает 180=𝜋,∘радиан90=𝜋2.∘радиан
Таким образом, мы можем дать решение, что 90∘ в радианах равно 𝜋2.радиан
Обратите внимание, что поскольку нам нужно дать ответ в виде 𝜋, мы оставляем наш ответ в этой форме, а не преобразовываем в десятичную дробь.
Часть 2
Чтобы найти угол 30∘ в радианах, возьмем уравнение 180=𝜋∘радиан и разделим обе части на 6, получив 30=𝜋6,∘радиан
В качестве альтернативы мы могли бы также использовать измерение угла, которое мы разработали в первой части вопроса, то есть 90=𝜋2,∘радиан и делим обе части на 3, что дает 30=𝜋2×3=𝜋6.∘радиан
Используя любой метод, мы видим, что 30∘ в радианах равно 𝜋6.radians
Часть 3
Когда нам нужно преобразовать угол в градусы, который не является коэффициентом 180∘, часто проще всего сначала найти меру 1∘ в радианах.
Мы знаем, что 180=𝜋.∘радиан
Таким образом, разделив обе части этого уравнения на 180, мы получим 1=𝜋180.∘радиан
Поскольку нам нужно преобразовать 55∘ в радианы, мы можем умножить обе части этого уравнения на 55. Это дает нам 55=55×𝜋180=55𝜋180.∘радианрадианы
Чтобы упростить дробь, мы разделим числитель и знаменатель на наибольший общий делитель 5, что дает
55=11𝜋36. ∘радиан
∘радиан
Таким образом, 55∘ эквивалентно 11𝜋36 радиан.
В предыдущем вопросе мы видели, как преобразовать угол 55∘ в радианы, сначала разделив его на 180∘, а затем умножив на 𝜋. Тот же метод можно применить для нахождения любого измерения угла.
Как: Преобразование угла из градусов в радианы
Чтобы изменить любой угол в градусах на один в радианах, умножьте заданный угол на 𝜋180: 𝜃=𝜃𝜋180.∘радиан
В следующем вопросе мы рассмотрим, как изменить угол, заданный в радианах, на угол, заданный в градусах.
Пример 2. Преобразование угла из радиан в градусы
Преобразование 𝜋3 радиан в градусы.
Ответ
Чтобы преобразовать угол из радианов в градусы, мы помним, что 𝜋=180.радиан∘
Заметим, что для преобразования 𝜋3 радиан в градусы мы разделим обе части этого уравнения на 3, что даст 𝜋3=1803=60.радиан∘∘
Таким образом, 𝜋3 радиана можно записать в градусах как 60∘.
Когда мы конвертируем углы, которые являются простыми коэффициентами 𝜋 радиан или 180∘, мы можем использовать метод, который мы видели в предыдущих вопросах. Однако существует эффективный способ преобразования угла из радианов в градусы за один шаг.
Однако существует эффективный способ преобразования угла из радианов в градусы за один шаг.
Практическое руководство. Преобразование угла из радианов в градусы
Чтобы преобразовать любой угол в радианах в градусы, мы умножаем данный угол на 180𝜋: 𝜃=180𝜃𝜋.radians∘
Теперь мы увидим, как мы можем применить это в следующем примере.
Пример 3. Преобразование угла из радианов в градусы
Преобразование 0,5 рад в градусы с точностью до секунды.
Ответ
Напомним, что для перевода любого угла в радианах в градусы нужно умножить данный угол на 180𝜋: 𝜃=180𝜃𝜋.радиан∘
В этом вопросе мы можем заменить заданный угол 0,5 радиан на угол 𝜃. Это дает 0,5=180×0,5𝜋=90𝜋=28,6788….радиан∘∘∘
Далее нам нужно преобразовать угол в градусах в десятичной форме в градусы, минуты и секунды. Для этого возьмем всю часть ответа в виде степеней. Итак, 28,6788…∘ дает 28∘.
Для минут мы умножаем оставшуюся десятичную дробь на 60 и используем всю часть ответа как 38 минут. Это дает
0,6788…×60=38,873…=38 минут
Это дает
0,6788…×60=38,873…=38 минут
Для секунд мы умножаем новую оставшуюся десятичную дробь на 60 и округляем результат до ближайшего целого числа. Это дает нам 0,873…×60=52,40…=52.секунд
Следовательно, мы можем дать ответ, что 0,5 рад эквивалентны 2838′52∘.
В следующем примере мы продемонстрируем применение этих формул преобразования на более сложном примере.
Пример 4. Решение задачи с использованием градусов и радианов
Найдите значение двух углов в градусах, учитывая, что их сумма равна 74∘, а их разность составляет 𝜋6 радиан. Дайте ответ с точностью до градуса.
Ответ
Мы начнем этот вопрос с определения двух неизвестных углов как 𝑥 и 𝑦. Нам дано, что их сумма в градусах равна 74∘, а их разница в радианах составляет 𝜋6 радиан. Затем мы можем составить два разных уравнения: 𝑥+𝑦=74,𝑥−𝑦=𝜋6.∘радиан
Мы можем решить эти уравнения для 𝑥 и 𝑦, если углы даны в одних и тех же единицах измерения. Следовательно, мы можем использовать преобразование между радианами и градусами:
𝜋=180. радиан∘
радиан∘
Мы можем изменить либо оба угла в градусы, либо оба в радианы, но так как нас просят дать окончательный ответ в градусах, то наиболее эффективно изменить угол 𝜋6 в радианах на один в градусов.
Сравнивая 𝜋=180радиан∘ и 𝜋6, мы замечаем, что должны делить на 6. Следовательно, 𝜋=180𝜋6=1806=30.radiansradians∘∘∘
В качестве альтернативы мы могли бы использовать правило, согласно которому, чтобы изменить угол в радианах на градусы, мы умножаем заданный угол на 180𝜋. Итак, чтобы изменить 𝜋6 радиан на градусы, мы делаем следующее: 𝜋6=𝜋6×180𝜋=1806=30.радиан∘∘∘
Любой метод демонстрирует, что 𝜋6=30радиан∘, что затем можно подставить во второе уравнение, 𝑥−𝑦=𝜋6, чтобы получить 𝑥−𝑦=30,∘
Теперь мы можем решить пару одновременных уравнений, используя метод замены или исключения:
| 𝑥+𝑦 = 74, ∘ | (1) |
| 𝑥 — = 30.∘ | (2) | 𝑥 — 𝑦 = 30.∘ | (2) | 𝑥 — 𝑦 30. ∘ ∘ | (2) | 𝑥 — 𝑦 30.∘𝑥 — 𝑦 30. ∘ | 𝑥 — 𝑦 30. ∘ | . добавьте уравнения (1) и (2) следующим образом:
𝑥+𝑦=74+𝑥−𝑦=302𝑥+0=104∘∘∘ Чтобы решить это уравнение относительно 𝑥, мы делим обе части на 2, что дает 𝑥=52.∘ Далее, подставляя 𝑥=52∘ в первое уравнение, 𝑥+𝑦=74∘, и перестановка дает 52+𝑦=74𝑦=74−52𝑦=22.∘∘∘∘∘ Следовательно, мы обнаружили, что 𝑥=52∘ и 𝑦=22∘, поэтому мы можем дать значение двух углов в градусах как 52,22∘∘. В следующем вопросе мы можем использовать наши знания о преобразовании радианов в градусы, чтобы помочь решить задачу, связанную с углами в треугольнике. Пример 5. Решение задачи с градусами и радианамиДва угла в треугольнике равны 55∘ и 7𝜋18 радиан. Найдите значение третьего угла, дающего ответ в радианах с точки зрения 𝜋. ОтветМы можем нарисовать треугольник с двумя заданными углами 55∘ и 7𝜋18 радиан. Нам нужно найти третий угол в этом треугольнике как угол в радианах, поэтому мы можем определить этот угол как 𝑥 радиан. Чтобы преобразовать угол 55∘ в радианы, мы умножаем угол на 𝜋180. Это даст 55=55𝜋180=55𝜋180=11𝜋36.∘радиан Тогда три угла треугольника можно записать как 11𝜋36 радиан, 7𝜋18 радиан, а неизвестный угол 𝑥 радиан. Чтобы найти неизвестный угол, вспомним, что сумма углов треугольника равна 180∘. Однако, поскольку мы рассматриваем здесь углы в радианах и поскольку 180=𝜋∘радиан, мы также можем сказать, что в радианах сумма углов в треугольнике равна 𝜋 радианам Используя эту информацию, мы можем составить уравнение в 𝑥: 11𝜋36+7𝜋18+𝑥=𝜋. Мы можем переписать и упростить, давая 11𝜋36+14𝜋36+𝑥=𝜋25𝜋36+𝑥=𝜋. Вычитание 25𝜋36 с обеих сторон дает 𝑥=𝜋−25𝜋36=𝜋1−2536=𝜋3636−2536=11𝜋36. Недостающий угол в треугольнике 11𝜋36 радиан. Подведем итоги. Ключевые точкирадиан. Темы по тригонометрииТемы | Дом
4 радиан сколько градус градус сколько радиан Котерминальные углы Кратность числа π В РАДИАННОЙ СИСТЕМЕ измерения углов мера одного полного круга равна 2π. (В следующем разделе «Длина дуги» мы увидим фактическое определение радианной меры.) Таким образом, половина круга — это π. И, самое главное, каждый прямой угол равен половине .
радианы в градусах Часто встречаются следующие меры в радианах, и студент должен знать их эквиваленты в градусах: (Тема 4 и Тема 5.) — это половина прямого угла, поэтому он равен 45°. Навыки арифметики, урок 27, вопрос 4.
Задача 1 . Преобразуйте каждую из этих радианных мер в градусы. Студент должен знать это. Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Задача 2. Преобразуйте каждую из этих радианных мер в градусы.
градус сколько радиан 360° = 2π. Когда мы пишем 2π, мы имеем в виду 2π радиан , что составляет приблизительно 6,28 радиана. Однако мы обычно опускаем слово радианы. Как мы увидим в следующем разделе «Длина дуги», мерой радиана может быть любое действительное число. Проблема 3. Учащийся должен начать с их знания.
Пример 1. Перевести 120° в радианы. Решение . Мы можем перейти от того, что знаем, к тому, чего не знаем. В наиболее важных случаях мы можем распознать число градусов как , кратное 9.0°, или 45°, или 60°, или 30°; или как часть на 360°.
Или, поскольку 120° составляет треть от 360°, что равно 2π, то
или
Задача 4. Переведите каждое из следующих значений в радианы.
72°, таким образом, составляет пятую часть оборота.
В крайнем случае, пропорционально, так что Пример 3. Изменить 140° на радианы.
при делении числителя и знаменателя сначала на 10, а затем на 2. (Урок 21 и Урок 1 арифметики.) Котерминальные углы Углы являются котерминальными, если они имеют одну и ту же конечную сторону. θ котерминал с -φ. У них одинаковая терминальная сторона. Обратите внимание, что θ + φ = 2π, так что θ = 2π — φ . Пример 4. Назовите в радианах неотрицательный угол, котерминальный .
Ответить . Назовем этот угол θ. Тогда по строке (1),
См. урок 23 алгебры, пример 7. В качестве альтернативы, поскольку числитель равен 2π, это пятая часть оборота в отрицательном направлении. Следовательно, θ будет составлять четыре пятых оборота в положительном направлении.
Задача 5. Назовите в радианах неотрицательный угол, котерминальный каждому из следующих углов и меньший 2π.
Это треть оборота в отрицательном направлении. Следовательно, θ будет составлять две трети оборота в положительном направлении.
Или:
Число, кратное числу π Начиная с 0, давайте пройдем по кругу по полукругу за раз. 0 , π, 2 π, 3 π, 4 π, 5 π и т. д. Дело в том, что нечетных кратных π — π, 3 π, 5 π, 7 π и т. д. — котерминальны π. В то время как даже кратных π — 2 π, 4 π, 6 π и т. д. — сотерминал с 0 . Если мы пойдем в отрицательном направлении, мы можем сделать аналогичное наблюдение. Задача 6. Назовите в радианах неотрицательный угол, котерминальный каждому из следующих углов и меньший 2π. а) -π π б) -2π 0 в) -3π π г) -4π 0 д) -5π π е) 3π π г) 4π 0 з) 5π π и) 6π 0 к) 7π π Следующая тема: Длина дуги Темы | Дом Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн. |

 Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
 Вот тут это знание очень помогает.
Вот тут это знание очень помогает. Получаем, что один градус равен:
Получаем, что один градус равен:
 02.03 – Технология деревообработки
02.03 – Технология деревообработки



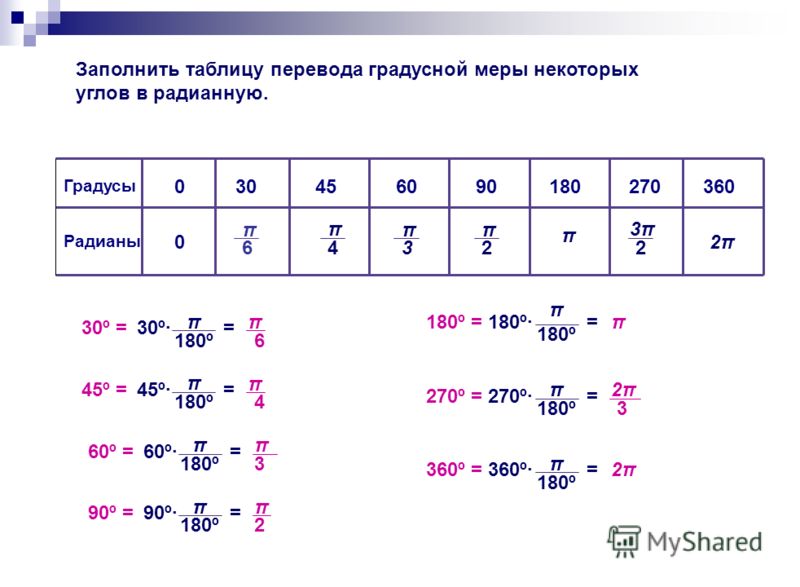

 радианы и понять, почему это мера без измерения
радианы и понять, почему это мера без измерения