Тройной интеграл для чайников: вычисление тройного интеграла

Содержание

как решать, правила вычисления, объяснение. Основные свойства определенного интеграла

Словари. Энциклопедии. История. Литература. Русский язык » Литература » Определенные и неопределенные интегралы сообщение. Интегралы для чайников: как решать, правила вычисления, объяснение. Основные свойства определенного интеграла

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Изучаем понятие « интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились

Ньютон и Лейбниц , но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают.

Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции.

Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

« Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Производная от интеграла равна подынтегральной функции:

Константу можно выносить из-под знака интеграла:

Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

Линейность:

Знак интеграла изменяется, если поменять местами пределы интегрирования:

При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу .

Вычисление определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений.

Прежде чем перейти к основным свойствам определенного интеграла , условимся, что a не превосходит b .

Для функции y = f(x) , определенной при x = a , справедливо равенство .

То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка и любого выбора точек равна нулю, так как , следовательно, пределом интегральных сумм является ноль.

Для интегрируемой на отрезке функции выполняется .

Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b .

для интегрируемых на отрезке функций y = f(x) и y = g(x) .

Доказательство.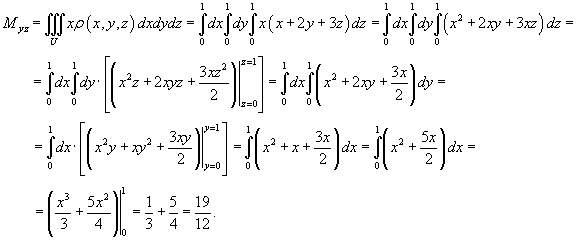

Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек :

где и — интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

Переходя к пределу при получим , что по определению интеграла Римана равносильно утверждению доказываемого свойства.

Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке функции y = f(x) и произвольного числа k справедливо равенство .

Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:

Пусть функция y = f(x) интегрируема на интервале X , причем и , тогда .

Это свойство справедливо как для , так и для или .

Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.

Если функция интегрируема на отрезке , то она интегрируема и на любом внутреннем отрезке .

Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.

Если функция y = f(x) интегрируема на отрезке и для любого значения аргумента , то .

Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).

Следствие.

Для интегрируемых на отрезке функций y = f(x) и y = g(x) справедливы неравенства:

Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.

Пусть функция y = f(x) интегрируема на отрезке , тогда справедливо неравенство .

Доказательство.

Очевидно, что . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо . Это двойное неравенство можно записать как .

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке и для любого значения аргумента , тогда , где и .

Доказательство проводится аналогично.

Следствие.

Если взять g(x) = 1 , то неравенство примет вид .

Первая формула среднего значения.

Пусть функция y = f(x) интегрируема на отрезке , и , тогда существует такое число , что .

Следствие.

Если функция y = f(x) непрерывна на отрезке , то найдется такое число , что .

Первая формула среднего значения в обобщенной форме.

Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке , и , а g(x) > 0 для любого значения аргумента . Тогда существует такое число , что .

Вторая формула среднего значения.

Если на отрезке функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число , что справедливо равенство .

Данные свойства используются для осуществления преобразований интеграла с целью его приведения к одному из элементарных интегралов и дальнейшему вычислению.

1. Производная неопределенного интеграла равна подынтегральной функции:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:

Причем a ≠ 0

5. Интеграл суммы (разности) равен сумме (разности) интегралов:

6. Свойство является комбинацией свойств 4 и 5:

Причем a ≠ 0 ˄ b ≠ 0

7. Свойство инвариантности неопределенного интеграла:

Если , то

8. Свойство:

Если , то

Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной , который более подробно рассмотрен в следующем разделе.

Рассмотрим пример:

Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.

Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.

1. Производная неопределенного интеграла равна подынтегральной функции:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

4. Постоянный множитель можно выносить за знак интеграла:

Причем a ≠ 0

5. Интеграл суммы (разности) равен сумме (разности) интегралов:

6. Свойство является комбинацией свойств 4 и 5:

Причем a ≠ 0 ˄ b ≠ 0

7. Свойство инвариантности неопределенного интеграла:

Если , то

8. Свойство:

Если , то

Рассмотрим пример:

В дифференциальном исчислении решается задача:под анной функции ƒ(х) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F » (x)=ƒ(х) (или дифференциал). Искомую функцию F(x) называют первообразной функции ƒ(х) .

Функция F(x) называетсяпервообразной функции ƒ(х) на интервале (а; b), если для любого х є (а;b) выполняется равенство

F » (x)=ƒ(x) (или dF(x)=ƒ(x)dx).

Например , первообразной функции у=х 2 , х є R, является функция, так как

Очевидно, что первообразными Будут также любые функции

где С — постоянная, поскольку

Tеоpeмa 29. 1. Если функция F(x) является первообразной функции ƒ(х) на (а;b), то множество всех первообразных для ƒ(х) задается формулой F(x)+С, где С — постоянное число.

▲ Функция F(x)+С является первообразной ƒ(х).

Действительно, (F(x)+C) » =F » (x)=ƒ(x).

Пусть Ф(х) — некоторая другая, отличная от F(x), первообразная функции ƒ(х) , т. е. Ф » (x)=ƒ(х). Тогда для любого х є (а;b) имеем

А это означает (см. следствие 25. 1), что

где С — постоянное число. Следовательно, Ф(х)=F(x)+С.▼

Множество всех пepвoобpaзныx функций F(x)+С для ƒ(х) называетсянеопределенным интегралом от функции ƒ(х) и обозначается символом∫ ƒ(х) dx.

Таким образом, по определению

∫ ƒ(x)dx= F(x)+C.

Здесь ƒ(х) называетсяподынтегральнoй функцией , ƒ(x)dx — подынтегральным выражением, х —переменной интегрирования , ∫ —знаком неопределенного интеграла .

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+C (каждому числовому значению С соответствует определенная кривая семейства) (см. рис. 166). График каждой первообразной (кривой) называетсяинтегральной кривой .

Для всякой ли функции существует неопределенный интеграл?

Имеет место теорема, утверждающая, что «всякая непрерывная на (а;b) функция имеет на этом промежутке первообразную», а следoвaтельно, и неопределенный интеграл.

Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) » =ƒ(х).

Дeйcтвительнo, d(∫ ƒ(х) dx)=d(F(x)+С)=dF(x)+d(C)=F » (x) dx =ƒ(х) dx

(∫ ƒ (x) dx) » =(F(x)+C)»=F»(x)+0 =ƒ (x).

Блaгoдapя этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство

∫(3x 2 + 4) dx=х з +4х+С

верно, так как (х 3 +4х+С)»=3x 2 +4.

2. Hеопpедeлeнный интеграл от диффepeнциaла некоторой функции равен сумме этой функции и произвольной постоянной:

∫dF(x)= F(x)+C.

Действительно,

3. Постоянный множитель можно выносить за знак интеграла:

α ≠ 0 — постоянная.

Действительно,

(положили С 1 /а=С.)

4. Неопределенный интеграл от aлгeбpaическoй суммы конечного числа непрерывных функций равен aлгебpaичecкoй сумме интегралов от слагаемых функций:

Пусть F»(x)=ƒ(х) и G»(x)=g(x). Тогда

где С 1 ±С 2 =С.

5. (Инвариантность формулы интегрирования).

Если, где u=φ(х) — произвольная функция, имеющая непрерывную производную.

▲ Пусть х — независимая переменная, ƒ(х) — непрерывная функция и F(x) — ее пepвoобpaзнaя. Тогда

Положим теперь u=ф(х), где ф(х) — непрерывно-дифференцируемая функция. Рассмотрим сложную функцию F(u)=F(φ(x)). В силу инвараинтности формы первого дифференциала функции (см. с. 160) имеем

Отсюда▼

Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

Так, из формулыпутем замены х на u (u=φ(х))получаем

В частности,

Пример 29.1. Найти интеграл

где С=C1+С 2 +С 3 +С 4 .

Пример 29.2. Найти интеграл Решение:

29.3. Таблица основных неопределенных интегралов

Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул диффepeнциaльнoгo исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.

Например , так как

d(sin u)=cos u . du,

Вывод ряда формул таблицы будет дан при рассмотрении основных методов интегрирования.

Интегралы в приводимой ниже таблице называются табличными. Их следует знать наизусть. В интегральном исчислении нет простых и универсальных правил отыскания первообразных от элементарных функций, как в дифференциальном исчислении. Методы нахождения пepвoобpaзных (т. е. интегрирования функции) сводятся к указанию приемов, приводящих данный (искомый) интеграл к табличному. Следовательно, необходимо знать табличные интегралы и уметь их узнавать.

Отметим, что в таблице основных интегралов переменная интегрирования и может обозначать как независимую переменную, так и функцию от независимой переменной (coгласнo свойству инвариантности формулы интeгpиpoвания).

В справедливости приведенных ниже формул можно убедиться, взяв диффepeнциaл правой части, который будет равен подынтегральному выражению в левой части формулы.

Докажем, например, справедливость формулы 2. Функция 1/u определена и непрерывна для всех значений и, отличных от нуля.

Если u > 0, то ln|u|=lnu, тогда Поэтому

Eсли u Значит

Итак, формула 2 верна. Aнaлoгичнo, провepим формулу 15:

Таблица оснoвныx интегралов

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Теорема Ферма для чайников? Не бойтесь, это не больно… | Мир вокруг нас

1. Почему она так знаменита?

Великая теорема Ферма — математическая задача невероятной сложности, и тем не менее ее формулировку может понять каждый с 5-ю классами средней школы, а вот доказательство — даже далеко не всякий математик-профессионал. Ни в физике, ни в химии, ни в биологии, ни в той же математике нет ни одной проблемы, которая формулировалась бы так просто, но оставалась нерешенной так долго.

2. В чем же она состоит? Начнем с пифагоровых штанов

Формулировка действительно проста — на первый взгляд. Как известно нам с детства, «пифагоровы штаны на все стороны равны».

Проблема выглядит столь простой потому, что в основе ее лежало математическое утверждение, которое всем известно:

Теорема Пифагора: в любом прямоугольном треугольнике квадрат, построенный на гипотенузе, равен сумме квадратов, построенных на катетах.

То есть легко подобрать множество чисел, которые прекрасно удовлетворяют равенству х² + y² = z². Начиная с 3, 4, 5 — действительно, младшекласснику понятно, что

9+16=25.

Или 5, 12, 13:

25 + 144 = 169.

Замечательно. Ну и так далее.

А если взять похожее уравнение х³+ y³ = z³? Может, тоже есть такие числа? И так далее.

Так вот, оказывается, что их НЕТ.

Вот тут начинается подвох. Простота — кажущаяся, потому что трудно доказать не наличие чего-то, а наоборот, отсутствие. Когда надо доказать, что решение есть, можно и нужно просто привести это решение.

Доказать отсутствие сложнее: например, некто говорит: такое-то уравнение не имеет решений. Посадить его в лужу? Легко: бац — а вот оно, решение! (приведите решение). И все, оппонент сражен.

А как доказать отсутствие? Сказать: «Я не нашел таких решений»? А может, ты плохо искал? А вдруг они есть, только очень большие, ну очень, такие, что даже у сверхмощного компьютера пока не хватает силенок? Вот это-то и сложно.

В наглядном виде это можно показать так: если взять два квадратика подходящих размеров и разобрать на единичные квадратики, то из этой кучки единичных квадратиков получается третий квадратик:

А проделаем то же с третьим измерением (рис. 3) — не получается. Не хватает кубиков, или остаются лишние:

3. История: более 350 лет поиска решений

Теорема была сформулирована Пьером Ферма в 1637 году на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было здесь поместить:

Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.

Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4, что добавляет сомнений в том, что у него было доказательство общего случая, иначе он непременно упомянул бы о нём в этой статье. Эйлер в 1770 году доказал теорему для случая n = 3, Дирихле и Лежандр в 1825 году — для n = 5, Ламе — для n = 7. Куммер показал, что теорема верна для всех простых n, меньших 100, и так далее.
Доказательство самого Ферма для случая {\displaystyle n=4} n=4 в сорок пятом комментарии к «Арифметике» Диофанта
Фото: общественное достояние

Но все это были частные случаи, а не универсальное доказательство для ВСЕХ ЧИСЕЛ.

Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел.

Считается, что Великая теорема стоит на первом месте по количеству неверных доказательств. Многие начинающие математики считали своим долгом подступиться к Великой теореме, но доказать ее все никак не удавалось.

Сначала не удавалось сто лет. Потом еще сто. Среди математиков стал развиваться массовый синдром: «Как же так? Ферма доказал, а я что, не смогу, что ли?», и некоторые из них на этой почве свихнулись в полном смысле этого слова.

Некоторые пытались прославиться от обратного: доказать, что она не верна. А для этого, как мы говорили, достаточно просто-напросто привести пример: вот три числа, одно в кубе плюс второе в кубе — равно третьему в кубе. И они искали такие тройки чисел. Но безуспешно… И никакие компьютеры, ни с каким быстродействием, никогда не смогли бы ни проверить теорему, ни опровергнуть ее, ведь все переменные этого уравнения (в том числе и показатели степени) могут возрастать до бесконечности.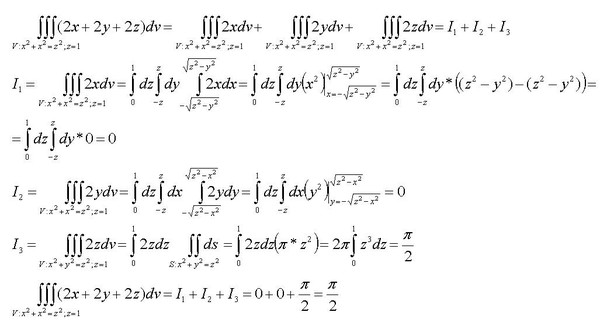

4. Наконец-то!

Наконец 23 июня 1993 года в Кембридже состоялась самая важная лекция по математике в ХХ веке. Лектором был Эндрю Уайлс, англичанин, профессор Принстонского университета. Эндрю Уайлс продемонстрировал ученым полное доказательство Великой теоремы Ферма.

Он шел к этому 30 лет, буквально с десятилетнего возраста. Его доказательство потом еще было уточнено и усовершенствовано в 1995 году, но самое главное — Великая теорема была доказана!

На это человечеству понадобилось 358 лет. Для доказательства была применена «самая высшая» и самая современная математическая наука. Поэтому изложить это доказательство в рамках заметочки никак нельзя, и читателям придется поверить на слово мне, математикам Кембриджа и Принстона и так далее.

Это доказательство закрыло сразу две страницы истории математики: 350-летний поиск доказательств Великой теоремы и бесконечные нашествия ферматистов на все математические кафедры всех университетов и институтов в мире.

5. Кто такие ферматисты?

Как сказано выше, формулировка Великой теоремы очень проста и понятна, поэтому есть стойкая иллюзия, что и доказательство ее также должно быть простым, понятным и вкладываться в знания алгебры в объеме 5−6 классов. Это породило неисчислимые толпы жертв фанатизма, называемых ферматистами, которые пытались ее доказать, думали, что доказали, и атаковали кафедры и отдельных ученых с исписанными тетрадками в клеточку наперевес. Как все фанатики, они нетерпимы к критике, полны намерений снести все преграды и страшно самоуверенны. Обычно их толстые труды сразу выбрасывают или дают студентам кафедры теории чисел для поиска ошибки в качестве упражнения.

Как правило, все доказательства сводятся к нехитрым алгебраическим преобразованиям: там прибавил, тут вычел, возвел все в квадрат, извлек квадратный корень, свернул по формулам сокращенного умножения, применил бином Ньютона — и вот оно, доказал.

Интересно, что бОльшая часть доморощенных ферматистов даже не понимает сути теоремы — они доказывают не то, что уравнение с показателями степени больше 2 не имеет целых решений, а просто пытаются доказать, что х в степени N + y в степени N равно z в степени N, что, как вы уже, я надеюсь, понимаете, лишено всяческого смысла.

И ведь доказывают! Ошибка, как правило, возникает при очередном возведении уравнения в квадрат и последующем извлечении корня. Казалось бы: возвели в квадрат, потом извлекли корень — так на так и получится, но они всегда забывают о том, что х в квадрате и (минус х) в квадрате равны. Это элементарно, Ватсон!

Кафедры отбивались, как могли.

Учёный секретарь одного из московских академических институтов, не избежавшего нашествия ферматистов, однажды был в отпуске в Молдавии и на рынке купил какую-то снедь, которую ему завернули в местную газету.
Вернувшись с рынка, он стал просматривать этот листок и наткнулся на заметку, в которой сообщалось, что местный школьный учитель доказал теорему Ферма, и, как следствие, пелись всякие дифирамбы высокому уровню областной науки.
Учёный секретарь вырезал эту заметку, а по возвращении в Москву вставил её в рамку и повесил на стену своего кабинета. Теперь, когда на него «нападал» очередной ферматист, он широким жестом приглашал того ознакомиться с «текущим положением дел». Жизнь явно стала легче. (Саймон СИНГХ, «ВТФ»).

Я думаю, после всего, что между нами было, читатели уже смогут оценить попавшуюся мне как-то на кафедре в куче таких рукописей, тетрадок и бандеролей телеграмму:

ДОКАЗАЛ ТЕОРЕМУ ФЕРМА ТЧК ИКС СТЕПЕНИ Н ПЛЮС ИГРЕК СТЕПЕНИ Н РАВНО ЗЕТ СТЕПЕНИ Н ТЧК. ДОКАЗАТЕЛЬСТВО ДВТЧ ПЕРЕНОСИМ ИГРЕК СТЕПЕНИ Н ПРАВУЮ ЧАСТЬ ТЧК ПОДРОБНОСТИ ПИСЬМОМ

Теги: теория, математика, теорема Ферма, история математики, математические задачи, фанатизм

15.

4: Тройные интегралы — Математика LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2612

Гилберт Стрэнг и Эдвин «Джед» Герман
OpenStax

Цели обучения

Распознать, когда функция трех переменных является интегрируемой по прямоугольному блоку.
Вычислите тройной интеграл, представив его в виде повторного интеграла.
Распознать, когда функция трех переменных интегрируема в замкнутой и ограниченной области.
Упростите вычисления, изменив порядок интегрирования тройного интеграла.
Вычислить среднее значение функции трех переменных. 93\) как
\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \большой\}. \nonumber \]
Мы следуем той же процедуре, что и ранее. Разделим интервал $[a,b]$ на $l$ подинтервалов $[x_{i-1},x_i]$ одинаковой длины $\Delta x$ с
\[\ Delta x = \dfrac{x_i — x_{i-1}}{l}, \nonumber \]
разделить интервал $[c,d]$ на $m$ подинтервалов $[y_{i -1}, y_i]$ одинаковой длины $\Delta y$ с
\[\Delta y = \dfrac{y_j — y_{j-1}}{m}, \nonumber \] 9*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \], если этот предел существует.
Когда тройной интеграл существует на $B$, функция $f(x,y,z)$ называется интегрируемой на $B$. Кроме того, тройной интеграл существует, если $f(x,y,z)$ непрерывен на $B$. Поэтому в наших примерах мы будем использовать непрерывные функции. Однако преемственности достаточно, но не обязательно; другими словами, $f$ ограничено на $B$ и непрерывно, за исключением, быть может, границы $B$. 2)\, dx \, dy \, dz. \номер\] 92 yz \,dV \nonumber \]
где $B = \big\{(x,y,z)\,|\, — 2 \leq x \leq 1, \, 0 \leq y \leq 3 , \, 1 \leq z \leq 5 \big\} $, как показано на рисунке $\PageIndex{2}$.
Рисунок $\PageIndex{2}$: вычисление тройного интеграла по заданному прямоугольному блоку.
Решение
Порядок не указан, но повторный интеграл можно использовать в любом порядке без изменения уровня сложности. Выберите, скажем, сначала интегрировать $y$, затем $x$, а затем $z$.
93 =18(9-0) =162.\end{align*}\]
Упражнение $\PageIndex{1}$
Вычисление тройного интеграла
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]
где $B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \ dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}$.
Подсказка
Выполните действия, описанные в предыдущем примере.
Ответить
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \] 9{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber \]
Обратите внимание, что область $D$ на любой из плоскостей может относиться к типу I или типу II, как описано выше. Если $D$ в $xy$-плоскости относится к типу I (рис. $\PageIndex{4}$), то
\[E = \big\{(x,y,z) \,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big \}. \nonumber \]
Рисунок $\PageIndex{4}$: Блок $E$, где проекция $D$ на $xy$-плоскость имеет тип I.
Тогда тройной интеграл становится 9{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber \]
Пример $\PageIndex{3A}$: вычисление тройного интеграла по общей ограниченной области
Вычисление тройного интеграла функции $f(x,y,z) = 5x — 3y\ ) над сплошным тетраэдром, ограниченным плоскостями \(x = 0, \, y = 0, \, z = 0$ и $x + y + z = 1$.
Решение
На рисунке $\PageIndex{6}$ показан объемный тетраэдр $E$ и его проекция $D$ на плоскость $xy$.
Рисунок $\PageIndex{6}$: тело $E$ имеет проекцию $D$ на $xy$-плоскость типа I. 9{z=1-x-y}(5x — 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]
Так же, как мы использовали двойной интеграл \[\iint_D 1 \ ,dA \nonumber \] чтобы найти площадь общей ограниченной области $D$ мы можем использовать \[\iiint_E 1\,dV \nonumber \] чтобы найти объем общей сплошной ограниченной области $E$ . Следующий пример иллюстрирует метод.
Пример $\PageIndex{3B}$: нахождение объема путем вычисления тройного интеграла
Найдите объем правильной пирамиды с квадратным основанием в плоскости $xy$ $[-1, 1] \times [-1,1]$ и вершина в точке $(0, 0, 1)$, как показано на следующем рисунке.
Рисунок $\PageIndex{7}$: Нахождение объема пирамиды с квадратным основанием.
Решение
В этой пирамиде значение $z$ изменяется от 0 до 1 и на каждой высоте $z$ поперечное сечение пирамиды при любом значении $z$ равно квадрату
\[[-1 + z, \, 1 — z] \times [-1 + z, \, 1 — z].\nonumber \]
Следовательно, объем пирамиды равен \[\iiint_E 1\ ,dV\nonumber \] где
\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 — z, \, -1 + z \leq x \leq 1 — z \big\}. {x=3} \int_{y=-\sqrt{92}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{кубических единиц}. \конец{выравнивание*}\]
Изменение порядка интегрирования
Как мы уже видели в двойных интегралах по общим ограниченным областям, изменение порядка интегрирования делается довольно часто для упрощения вычислений. При тройном интеграле по прямоугольному ящику порядок интегрирования не меняет уровень сложности вычисления. Однако с тройным интегралом по общей ограниченной области выбор подходящего порядка интегрирования может немного упростить вычисления. Иногда изменение полярных координат также может быть очень полезным. Здесь мы демонстрируем два примера. 9{z=y} f(x,y,z)\,dz\,dy\,dx. \nonumber \]
Порядок интегрирования здесь первый относительно z , затем y , а затем x . Выразите этот интеграл, изменив порядок интегрирования так, чтобы он был сначала по $x$, затем по $z$, а затем по $y$. Убедитесь, что значение интеграла такое же, если мы допустим $f (x, y, z) = xyz$.
Решение
Лучший способ сделать это — нарисовать область $E$ и ее проекции на каждую из трех координатных плоскостей. Итак, пусть 9{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]
Среднее значение функции трех переменных
Напомним, что мы нашли среднее значение функции двух переменных путем вычисления двойного интеграла по области на плоскости и последующего деления на площадь области. Точно так же мы можем найти среднее значение функции от трех переменных, вычислив тройной интеграл по сплошной области и затем разделив его на объем твердого тела.
Среднее значение функции трех переменных
Если $f(x,y,z)$ интегрируема по твердой ограниченной области $E$ с положительным объемом $V \, (E),$, то среднее значение функции равно
\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber \]
Обратите внимание, что объем равен
\[V \, (E) = \iiint_E 1 \,dV. {z=1-xy} (xy + 8z + 20 ) \, dz \, dy \, dx = \dfrac{147}{40}. \номер\] 9{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]
Следовательно, среднее значение равно
\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441} {20} \, \text{°}\text{C} \nonumber \].
Упражнение $\PageIndex{6}$
Найдите среднее значение функции $f(x,y,z) = xyz$ по кубу со стороной 4 единицы в первом октанте с одной вершина в начале координат и ребра параллельны осям координат.
Подсказка
Выполните действия, описанные в предыдущем примере.
Ответить
$f_{ср.} = 8$
Эта страница под названием 15.4: Тройные интегралы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
1. Наверх
- Была ли эта статья полезной?
1. Тип изделия
  Раздел или Страница
  Автор
  ОпенСтакс
  Лицензия
  CC BY-NC-SA
  Версия лицензии
  4,0
  Программа OER или Publisher
  ОпенСтакс
  Показать страницу TOC
  нет
2. Теги
  1. автор @ Эдвин «Джед» Герман
  2. автор@Гилберт Странг
  3. Фубини там
  4. источник@https://openstax. org/details/books/calculus-volume-1
  5. тройной интеграл
Введение в тройные интегралы — Math Insight
Помните, как удвоить интегралы можно записать как повторные интегралы. Тройные интегралы — это, по сути, то же самое, что и двойные интегралы. (Мы просто добавим третье измерение.) Мы превратим тройные интегралы в (тройные) повторные интегралы.
Как и в случае с двойными интегралами, единственная хитрость заключается в определении ограничения на повторные интегралы. (К сожалению, это сложнее рисовать в трех измерениях.)
Перед обсуждением того, как настроить повторные интегралы, мы сначала обратимся к тому, как определить тройные интегралы так же, как мы определяем большинство наших интегралов: с суммой Римана.
Определяется суммами Римана
Пусть $f(x,y,z)$ — плотность трехмерного тела $\dlv$ в точке $(x,y,z)$ внутри тела. Мы хотите определить тройной интеграл от $f$ по $\dlv$ как сумму масса $\dlv$.
Как и в случае двойных интегралов, мы определяем интеграл с помощью сумм Римана. Разбиваем сплошное $\dlv$ на маленькие коробочки, скажем размерами $\Delta х$, $\Delta y$, $\Delta z$. Если бы $\dlv$ оказался кубом, это измельчение может выглядеть примерно так.
Объем каждой маленькой коробки \начать{выравнивать*} \Дельта V = \Дельта х \Дельта у \Дельта z. \конец{выравнивание*}
Представьте себе, что коробки расположены слоями, каждый слой организованы в строки и столбцы. Затем мы можем проиндексировать блоки так, чтобы блок $ijk$ относится к блоку в $i$-й строке, $j$-м столбце и $k$-й слой.
Для каждого блока мы выбираем точку в блоке, представляющую этот блок. Для ящик $ijk$, мы называем эту точку $(x_{ijk}, y_{ijk}, z_{ijk})$. Притворяться что плотность ящика $ijk$ постоянна, т. е. что плотность равна $f(x_{ijk}, y_{ijk}, z_{ijk})$ везде в этом поле. масса ящика $ijk$ равна его плотности, умноженной на объем: \начать{выравнивать*} f(x_{ijk}, y_{ijk}, z_{ijk}) \Delta V. \конец{выравнивание*}
Суммируем эти приблизительные массы, чтобы оценить общую массу твердого тела. $\длв$. Мы получаем сумма Римана \начать{выравнивать*} \sum_{ijk} f(x_{ijk}, y_{ijk}, z_{ijk})\Delta V, \конец{выравнивание*} где сумма по всем маленьким ящикам.
Пусть $\Delta x \to 0$, $\Delta y \to 0$ и $\Delta z \to 0$ (и пусть количество коробочек стремится к бесконечности). Сумма Римана приближается к тройному интегралу по твердому телу $\dlv$, \начать{выравнивать*} \iiint_\dlv f\, dV = \lim_{\Delta x, \Delta y, \Delta z \to 0} \sum_{ijk} f(x_{ijk}, y_{ijk}, z_{ijk}) \Delta V, \конец{выравнивание*} в предположении непрерывности $f$. Тройной интеграл — это реальная масса $\dlv$. 9б f(x,y,z) dx \right ) dy \right) dz. \конец{выравнивание*} Этот порядок интегрирования соответствует определенному способу упорядочения членов в сумме Римана: сначала мы суммируем по строкам $i$, затем суммируем по столбцам $j$ и наконец, суммируем по слоям $k$.
Как и в случае с двойными интегралами, другие порядки интегрирования возможный. q f(x,y,z) dz \right ) dx \right) dy \конец{выравнивание*} 9д f(x,y,z) dz\, dx\, dy. \конец{выравнивание*}
Повторный интеграл прост, когда тело $\dlv$ является прямоугольным твердый (как куб, но где все ребра не обязательно одинаковы) длина). Для более сложных форм нахождение пределов интеграция может быть сложной.
В качестве первого шага просто запомните эти правила, которые аналогичны правилам мы имели для ограничений на двукратные повторные интегралы.
1. Внешние пределы должны быть постоянными. Они не могут зависеть ни от чего переменных. 91 f(x,y,z) dx \, dy \, dz.}}} \конец{выравнивание*} Вы видите, почему? Внешние пределы интеграла зависят как от $x$, так и от $y$ (но $y$ не определен, пока вы не войдете внутрь среднего интеграла, а $x$ не определено, пока вы не войдете внутрь внутреннего интеграла). А также середина интегральные пределы зависят от $x$.
  Сложной частью тройных интегралов является определение пределов интегрирования (или границ).
  No related posts.