Что такое прямоугольник: определение, свойства, признаки, формулы
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
- Определение прямоугольника
- Свойства прямоугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Признаки прямоугольника
- Формулы
Определение прямоугольника
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т. е. являются прямыми).
е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
- длины – более длинная пара сторон. Обычно обозначаются латинской буквой, например, a;
- ширины – более короткая пара сторон. Чаще всего обозначаются как b.
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
- AD = BC = a, AD || BC
- AB = CD = b, AB || CD
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.- a – это высота h1, проведенная к стороне b
- b – это высота h2, проведенная к стороне a
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d2 = a2 + b2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
- AC = BD = d
- AE = EC = BE = ED
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
- Его диагонали равны.
- Все его углы равны.

- Если квадрат диагонали равен сумме квадратов его смежных сторон.
Формулы
1. Площадь прямоугольника (S):
S = a ⋅ b
2. Периметр прямоугольника (P):
P = a + a + b + b = 2a + 2b
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачиФормула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Прямоугольник, свойства, признаки и формулы
Прямоугольник, свойства, признаки и формулы.

Поделиться в:
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение)
Видеоурок “Прямоугольник“
Свойства прямоугольника
Признаки прямоугольника
Формулы прямоугольника
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.
Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
@ https://youtu.be/_EVDcbOydAI
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.
Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника равны.
Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.
Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
Рис. 8. Прямоугольник
8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.
Рис. 9. Прямоугольник
AO = BO = CO = DO = АС / 2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т. е. он является квадратом.
е. он является квадратом.
Рис. 11. Квадрат
AВ = ВC = AD = CD
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):
,
,
,
.
Формула диагонали прямоугольника:
,
d = 2R.
Формулы периметра прямоугольника:
P = 2a + 2b,
P = 2(a + b).
Формулы площади прямоугольника:
S = a · b.
Формула радиуса окружности, описанной вокруг прямоугольника:
.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/_EVDcbOydAI
Коэффициент востребованности 4 838
формул, что такое прямоугольник? Определение, примеры
Прямоугольник — это четырехугольник, в котором все углы равны, а противоположные стороны равны и параллельны. Вокруг нас много прямоугольных объектов. Каждая прямоугольная форма характеризуется двумя размерами: длиной и шириной. Более длинная сторона прямоугольника известна как длина, а более короткая сторона известна как ширина.
| 1. | Что такое прямоугольник? |
| 2. | Свойства прямоугольника |
| 3. | Диагональ прямоугольника |
| 4. | Площадь прямоугольника |
| 5. | Периметр прямоугольника |
| 6. | Часто задаваемые вопросы о прямоугольнике |
Что такое прямоугольник?
Прямоугольник — это замкнутая двумерная фигура с четырьмя сторонами. Противоположные стороны прямоугольника равны и параллельны друг другу, а все углы прямоугольника равны 90°. Посмотрите на прямоугольник, приведенный ниже, чтобы увидеть его форму, стороны и углы.
Свойства прямоугольника
Прямоугольник – это замкнутая фигура, имеющая четыре стороны и угол, образованный смежными сторонами, равен 90°.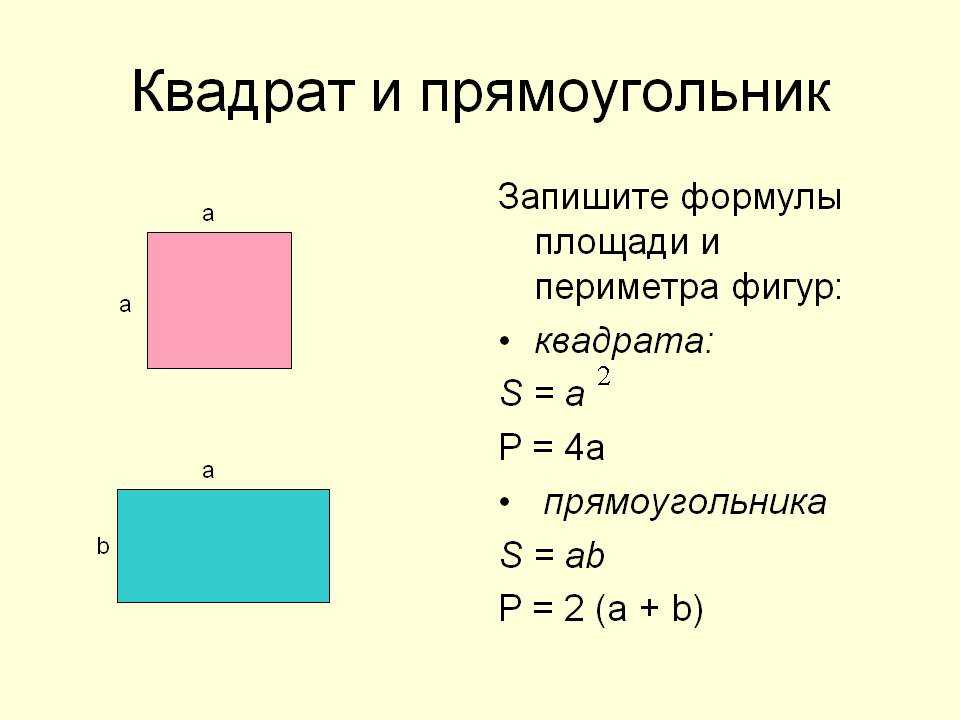 Прямоугольник может иметь широкий спектр свойств. Некоторые из важных свойств прямоугольника приведены ниже.
Прямоугольник может иметь широкий спектр свойств. Некоторые из важных свойств прямоугольника приведены ниже.
- Прямоугольник — это четырехугольник.
- Противоположные стороны прямоугольника равны и параллельны друг другу.
- Внутренний угол прямоугольника при каждой вершине равен 90°.
- Сумма всех внутренних углов равна 360°.
- Диагонали делят друг друга пополам.
- Длины диагоналей равны.
- Длину диагоналей можно получить с помощью теоремы Пифагора. Длина диагонали со сторонами a и b равна, диагональ = √( a 2 + b 2 ).
- Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
- Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.
Диагональ прямоугольника
Диагональ прямоугольника — это отрезок, соединяющий любые две его несмежные вершины. В следующем прямоугольнике AC и BD — диагонали, имеющие одинаковую длину. Диагональ делит прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.
Диагональ делит прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.
Формула диагонали прямоугольника
Формула диагонали прямоугольника выводится с помощью теоремы Пифагора. Следуя приведенному выше рисунку, рассмотрим прямоугольник длины l и ширины w. Пусть длина каждой диагонали равна «d». Применяя теорему Пифагора к треугольнику ABD, d 2 = l 2 + w 2 . Извлекая квадратный корень с обеих сторон, √(d 2 ) = √(l 2 + w 2 ). Таким образом, формула диагонали прямоугольника равна диагонали (d): √(l² + w²) и, таким образом, диагонали прямоугольника можно вычислить, когда длина и ширина прямоугольника известны.
Диагональ прямоугольника (d) = √(l² + w²)
Площадь прямоугольника
Площадь прямоугольника — это количество единичных квадратов, которые могут поместиться в прямоугольник. Другими словами, пространство, занимаемое прямоугольником, является площадью прямоугольника. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, классных досок, холста для рисования и т. Д. Мы можем использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами. Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма. Нарисуем единичные квадраты внутри прямоугольника. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм. Теперь подсчитайте количество единичных квадратов на рисунке ниже. Сколько квадратов вы можете наблюдать? Всего 12 квадратов. Мы уже знаем, что площадь измеряется в квадратных единицах. Поскольку единица измерения этого прямоугольника дана в дюймах, площадь измеряется и записывается в квадратных дюймах. Таким образом, Площадь прямоугольника = 12 квадратных дюймов. Таким образом, площадь прямоугольника можно вычислить, зная его стороны (длину и ширину).
Другими словами, пространство, занимаемое прямоугольником, является площадью прямоугольника. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, классных досок, холста для рисования и т. Д. Мы можем использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами. Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма. Нарисуем единичные квадраты внутри прямоугольника. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм. Теперь подсчитайте количество единичных квадратов на рисунке ниже. Сколько квадратов вы можете наблюдать? Всего 12 квадратов. Мы уже знаем, что площадь измеряется в квадратных единицах. Поскольку единица измерения этого прямоугольника дана в дюймах, площадь измеряется и записывается в квадратных дюймах. Таким образом, Площадь прямоугольника = 12 квадратных дюймов. Таким образом, площадь прямоугольника можно вычислить, зная его стороны (длину и ширину).
Формула площади прямоугольника
Формула площади прямоугольника , длина и ширина которого равны «l» и «w» соответственно, является произведением его длины и ширины, то есть:
Площадь прямоугольника = (д × ш)
Периметр прямоугольника
Периметр прямоугольника — это длина всей границы прямоугольника. Его можно принять как сумму общей меры длины и ширины прямоугольника, и он выражается в линейных единицах, таких как сантиметры, дюймы и так далее. Например, если вам нужно украсить рамку вашего прямоугольного блокнота, вы можете легко рассчитать, сколько ленты вам понадобится, найдя периметр, или если вам нужно поставить забор вокруг вашего сада, периметр сада даст вам точную длину провода, который вам понадобится. Формула, используемая для вычисления периметра прямоугольника, объясняется ниже.
Его можно принять как сумму общей меры длины и ширины прямоугольника, и он выражается в линейных единицах, таких как сантиметры, дюймы и так далее. Например, если вам нужно украсить рамку вашего прямоугольного блокнота, вы можете легко рассчитать, сколько ленты вам понадобится, найдя периметр, или если вам нужно поставить забор вокруг вашего сада, периметр сада даст вам точную длину провода, который вам понадобится. Формула, используемая для вычисления периметра прямоугольника, объясняется ниже.
Формула периметра прямоугольника
Формула для периметра ‘P’ прямоугольника, длина и ширина которого равны ‘l’ и ‘w’ соответственно, равна 2(l + w).
Формула периметра прямоугольника = 2 (длина + ширина)
Типы прямоугольников
Четырехугольник, у которого противоположные стороны равны, а смежные стороны пересекаются под углом 90°, называется прямоугольником. У прямоугольника две равные диагонали. Длина диагоналей рассчитывается с использованием длины и ширины. Есть два типа прямоугольников:
Есть два типа прямоугольников:
- Квадрат
- Золотой прямоугольник
Квадрат
Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Это тип прямоугольника, у которого все четыре стороны равны. Внутренний угол в каждой вершине равен 90º, что соответствует определению прямоугольника. Обратите внимание на приведенный ниже квадрат, который соответствует всем свойствам прямоугольника.
Золотой прямоугольник
Золотой прямоугольник — это прямоугольник, отношение длины к ширине которого аналогично золотому сечению, 1: (1+⎷5)/2. Его стороны определены по золотому сечению, то есть 1:1,618. Например, если ширина составляет около 1 фута, тогда длина будет равна 1,168 фута.
☛ Похожие статьи
- Свойства прямоугольника
- Разница между квадратом и прямоугольником
- Является ли квадрат прямоугольником?
Примеры свойств прямоугольника
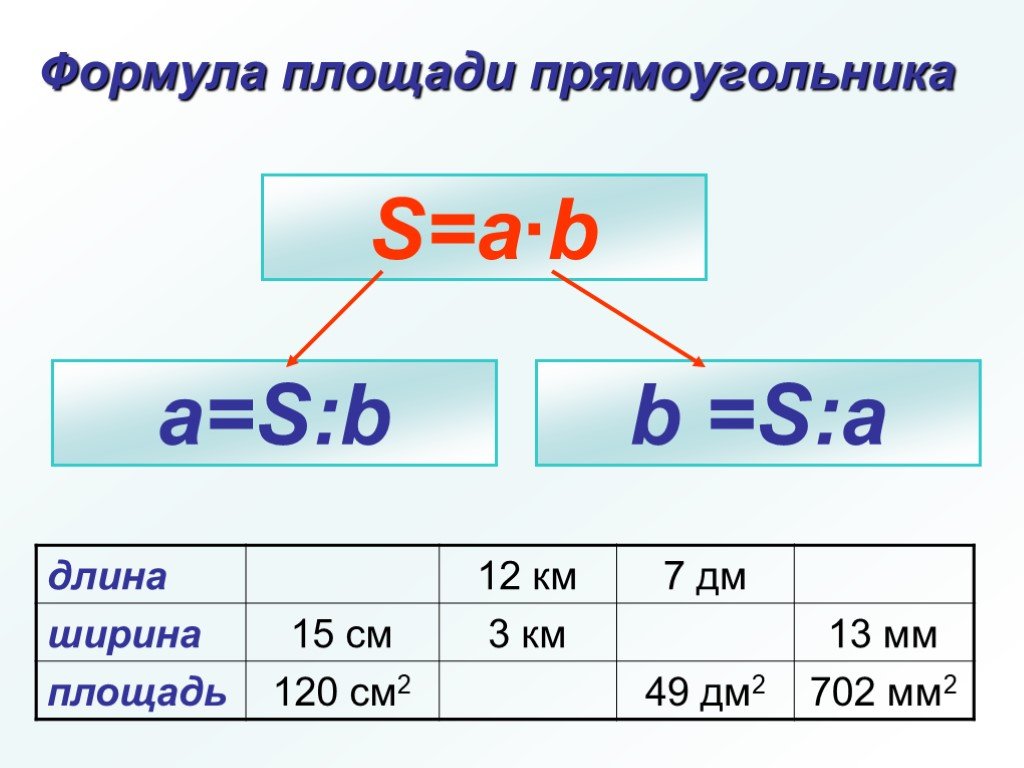
Пример 1: Джордж имеет прямоугольную фоторамку длиной 6 дюймов и шириной 3 дюйма.
 Поможешь Джорджу найти его площадь?
Поможешь Джорджу найти его площадь?Решение:
Мы знаем формулу для вычисления площади прямоугольника. Площадь прямоугольника = (длина × ширина). Таким образом, площадь прямоугольной рамки = 6 × 3 = 18 квадратных дюймов
Следовательно, площадь фоторамки = 18 квадратных дюймов
Пример 2: Эльза хочет построить прямоугольный забор для своего сада. Периметр забора 30 метров. Длина забора 10 футов. Поможешь Эльзе найти ширину забора?
Решение:
Мы знаем, что формула для вычисления периметра прямоугольника: Периметр прямоугольника = 2 (длина + ширина). У нас есть периметр = 30 футов и длина = 10 футов, Итак, давайте найдем ширину, используя формулу периметра. Подставим известные значения в формулу Периметр прямоугольника = 2 (длина + ширина), 30 = 2 (10 + ширина). Решая ее дальше, получаем, 10 + ширина = 15, а ширина = 5 единиц
Следовательно, ширина забора = 5 футов
Пример 3: Укажите верно или неверно:
а.
 ) Противоположные стороны прямоугольника равны и параллельны друг другу.
) Противоположные стороны прямоугольника равны и параллельны друг другу.б.) Длина диагоналей может быть получена с помощью теоремы Пифагора.
в.) Все параллелограммы являются прямоугольниками.
Решение:
а.) Верно, противоположные стороны прямоугольника равны и параллельны друг другу.
б.) Правда, длину диагоналей можно получить по теореме Пифагора.
c.) Неверно, все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по прямоугольнику
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о прямоугольнике
Что такое прямоугольник в геометрии?
Прямоугольник — это двумерная фигура (2D-форма), у которой противоположные стороны параллельны и равны друг другу, а все четыре угла прямые. Меньшая сторона прямоугольника называется его шириной (шириной), а длинная сторона – длиной. Одной из самых распространенных геометрических фигур, с которыми мы сталкиваемся в повседневной жизни, является прямоугольник.
Меньшая сторона прямоугольника называется его шириной (шириной), а длинная сторона – длиной. Одной из самых распространенных геометрических фигур, с которыми мы сталкиваемся в повседневной жизни, является прямоугольник.
☛ Читайте также
- 3D фигуры
- Геометрические фигуры
Как найти длину прямоугольника?
Длину прямоугольника можно вычислить, если известны периметр и ширина. Например, если периметр прямоугольника равен 32 единицам, а его ширина равна 4 единицам, мы можем использовать формулу периметра, чтобы получить длину. Периметр прямоугольника = 2 (l + w). Подставим известные значения в формулу, 32 = 2 (длина + 4). Решив это, мы получим длину + 4 = 16, то есть длину = 12 единиц. Точно так же, если площадь прямоугольника и ширина известны, длину можно рассчитать, используя формулу площади прямоугольника и подставив известные значения.
Как найти ширину прямоугольника?
Ширину прямоугольника можно вычислить, если известны его площадь и длина.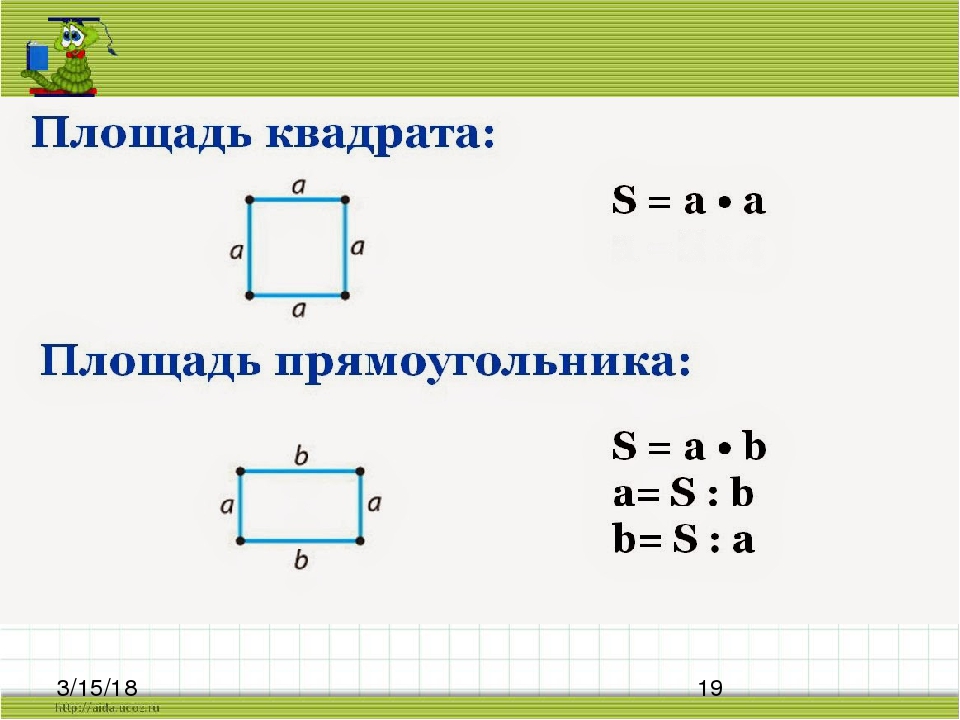 Например, если площадь прямоугольника составляет 48 единиц, а его длина — 12 единиц, мы можем использовать формулу площади, чтобы получить ширину. Площадь прямоугольника = l × w. Подставим известные значения в формулу, 48 = 12 × ширина. Решив это, мы получим ширину = 48/12, то есть ширину = 4 единицы. Точно так же, если периметр прямоугольника и длина известны, ширину можно рассчитать, используя формулу для периметра прямоугольника и подставив известные значения.
Например, если площадь прямоугольника составляет 48 единиц, а его длина — 12 единиц, мы можем использовать формулу площади, чтобы получить ширину. Площадь прямоугольника = l × w. Подставим известные значения в формулу, 48 = 12 × ширина. Решив это, мы получим ширину = 48/12, то есть ширину = 4 единицы. Точно так же, если периметр прямоугольника и длина известны, ширину можно рассчитать, используя формулу для периметра прямоугольника и подставив известные значения.
Как найти диагональ прямоугольника?
Длину диагонали прямоугольника можно вычислить, если известны длина и ширина. Поскольку диагональ прямоугольника образует со своими сторонами прямоугольный треугольник, диагональ становится гипотенузой, и ее значение можно вычислить с помощью теоремы Пифагора. Например, если длина прямоугольника равна 4 единицам, а ширина равна 3 единицам, мы можем найти длину диагонали, используя формулу, диагональ (d) = √ (л² + ш²). Итак, подставим в него значение длины и ширины. Диагональ (d) = √ (l² + w²) = √ (4² + 3²) = √ (16 + 9) = √ 25 = 5 единиц.
Диагональ (d) = √ (l² + w²) = √ (4² + 3²) = √ (16 + 9) = √ 25 = 5 единиц.
Почему прямоугольник не является правильным многоугольником?
Правильный многоугольник — это многоугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. В прямоугольнике только противоположные стороны имеют одинаковую длину, следовательно, прямоугольник не является правильным многоугольником.
☛ Также проверьте:
- Типы полигонов
- Площадь полигонов
Какая формула площади прямоугольника?
Площадь прямоугольника — это площадь, занимаемая им. Площадь прямоугольника есть произведение его длины и ширины. Формула вычисления площади прямоугольника: Площадь = L × B; где (L) — длина, а (B) — ширина прямоугольника.
☛ Ознакомьтесь со списком формул для простых расчетов:
- Формулы периметра
- Объемные формулы
- Формулы площади поверхности
- Формулы измерения
Каковы свойства прямоугольника?
Основные свойства прямоугольника:
- Противоположные стороны параллельны и равны.

- Все углы равны 90°.
- Диагонали равны и делят друг друга пополам.
Площадь прямоугольника равна площади квадрата?
Нет, площадь квадрата не обязательно равна площади прямоугольника, потому что каждый квадрат является прямоугольником, но не все прямоугольники являются квадратами. Формула для вычисления площади прямоугольника: площадь прямоугольника = длина × ширина, а площадь квадрата = (сторона) 2 .
Как найти периметр прямоугольника?
Периметр прямоугольника в два раза больше суммы его длины и ширины и выражается по формуле Периметр = 2 (Длина + Ширина). Он выражается в линейных единицах, таких как см, дюймы и т. д.
Как называется трехмерный прямоугольник?
Трехмерный прямоугольник называется прямоугольной призмой. Прямоугольная призма – это призма, основания которой также являются прямоугольниками. Всего у него 6 граней, из которых 3 пары одинаковых противоположных граней, т. е. в прямоугольной призме все противоположные грани одинаковы.
Как выглядит прямоугольник?
Прямоугольник выглядит как вытянутый квадрат, у которого 2 противоположные стороны равны и параллельны. Несколько распространенных примеров прямоугольников можно увидеть на экране ноутбука, ноутбука, мобильного телефона и так далее.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист площади и периметра
Прямоугольник. Формулы и свойства прямоугольника
Навигация по странице: Определение прямоугольника Основные свойства прямоугольника. Стороны прямоугольника Диагональ прямоугольника Периметр прямоугольника Площадь прямоугольника Описанная окружность прямоугольника (circumcircle) Угол между стороной и диагональю Угол между диагоналями
Определение.
Прямоугольник — это четырехугольник, у которого две противоположные стороны равны и все углы прямые.
Прямоугольники отличаются только отношением длинной стороны к короткой, но четыре угла прямые, то есть 90 градусов.
Стороны прямоугольника — это обе его высоты.
| Рис.1 | Рис.2 |
Основные свойства прямоугольника
Прямоугольник может быть параллелограммом, ромбом или квадратом, у которого все углы прямые.
1. Противоположные стороны прямоугольника имеют одинаковую длину, т.е. равны:
2. Противоположные стороны прямоугольника параллельны:
3. Смежные стороны прямоугольника всегда перпендикулярны:
сумма всех углов прямоугольника равна 360 градусов:
6. Диагонали прямоугольника равны:
Диагонали прямоугольника равны:
7 .Сумма квадратов двух диагоналей равна сумме квадратов сторон:
8. Каждая диагональ делит прямоугольник на две равные фигуры, а именно прямоугольный треугольник.
9. Диагонали прямоугольника пополам делят друг друга:
| AO = BO = CO = DO = | д | ||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника, а также центром описанной окружности (incenter).
11. Диагональ прямоугольника равна диаметру описанной окружности.
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусам:
13. В прямоугольнике с разные размеры сторон никогда не входят в вписанную окружность.
В прямоугольнике с разные размеры сторон никогда не входят в вписанную окружность.
Стороны прямоугольника
Определение.
Длина прямоугольника называется длиной большей пары его сторон. шириной прямоугольника называется длина меньшей пары его сторон.
Формулы сторон прямоугольника A:
1. Формула сторон прямоугольника через диагональ и другую сторону прямоугольника:
2. Формула сторон прямоугольника через площадь и другую сторону прямоугольника:
| а = | А |
| B |
| B = | A |
| A |
3. Формула прямоугольника с точки зрения периметра и другой прямоугольной стороны: сторона: прямоугольник: сторона:
| a = | P — 2b |
| 2 |
| b = | P — 2a |
| 2 |
4. Formula of rectangle sides in terms диагонали и угла α:
Formula of rectangle sides in terms диагонали и угла α:
5. Формула сторон прямоугольника через диагональ и угол β:
| a = d sin | β |
| 2 |
| b = d cos | β |
| 2 |
Диагональ прямоугольника
Определение.
Диагональ прямоугольника — это любой отрезок, соединяющий две противоположные вершины прямоугольника.
Формулы диагонали прямоугольника:
1. Формула диагонали прямоугольника через стороны прямоугольника (по теореме Пифагора):
2. Формула формулы Диагональ прямоугольника через квадрат и сторону прямоугольника:
| d = | √A 2 + a 4 | = | √A 2 + b 4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и сторону прямоугольника:
Формула диагонали прямоугольника через периметр и сторону прямоугольника:
| d = | √P 2 — 4Pa + 8a 2 | = | √P 2 — 4Pb + 8b 2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус вписанной окружности (внеокружности):
5. Формула диагонали прямоугольника через диаметр вписанной окружности (внеокружности):
6. Формула диагонали прямоугольника через синус угла, примыкающего к диагонали и противоположной стороне угла:
| d = | a |
| sin α |
| д = | б |
| cos α |
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадь прямоугольника
Периметр прямоугольника
Определение.
Периметр прямоугольника равен сумме длин всех сторон прямоугольника.
Формулы периметра прямоугольника
1. Формула периметра прямоугольника через стороны прямоугольника:
2. Формула периметра прямоугольника через площадь и сторону прямоугольника:
| P = | 2A + 2A 2 | = | 2A + 2B 2 |
| A | B | A | B | A | B |
4. Формула периметра прямоугольника через радиус описанной окружности (внеокружности) и сторону прямоугольника:
5. Формула описанного периметра прямоугольника через диаметр описанного прямоугольника окружность (внеокружность) и сторона прямоугольника:
Формула описанного периметра прямоугольника через диаметр описанного прямоугольника окружность (внеокружность) и сторона прямоугольника:
Площадь прямоугольника
Определение.
Площадь прямоугольника пространство ограничено сторонами прямоугольника или периметром прямоугольника.
Формулы площади прямоугольника
1. Формула площади прямоугольника через стороны прямоугольника:
2. Формула площади прямоугольника через периметр и сторону прямоугольника:
| А = | Па — 2а 2 | = | PB — 2B 2 |
| 2 | 2 |
3. Формула Площадь прямоугольника с точки зрения диагональной и прямоугольной стороны.
4. Формула площади прямоугольника через синус острого угла между диагоналями и диагональю Прямоугольник:
| А = | d 2 · sin β |
| 2 |
5. Формула площади прямоугольника через радиус описанной окружности (внеокружности) и сторону прямоугольника: a 2 = b√4R 2 — b 2
6. Формула площади прямоугольника через диаметр вписанной окружности (внеокружности) и сторону прямоугольника:
Описанная окружность прямоугольника (circumcircle)
Определение.
Описанная окружность прямоугольника (circumcircle) Окружность, проходящая только через четыре вершины угла и имеющая центр на пересечении диагоналей прямоугольника.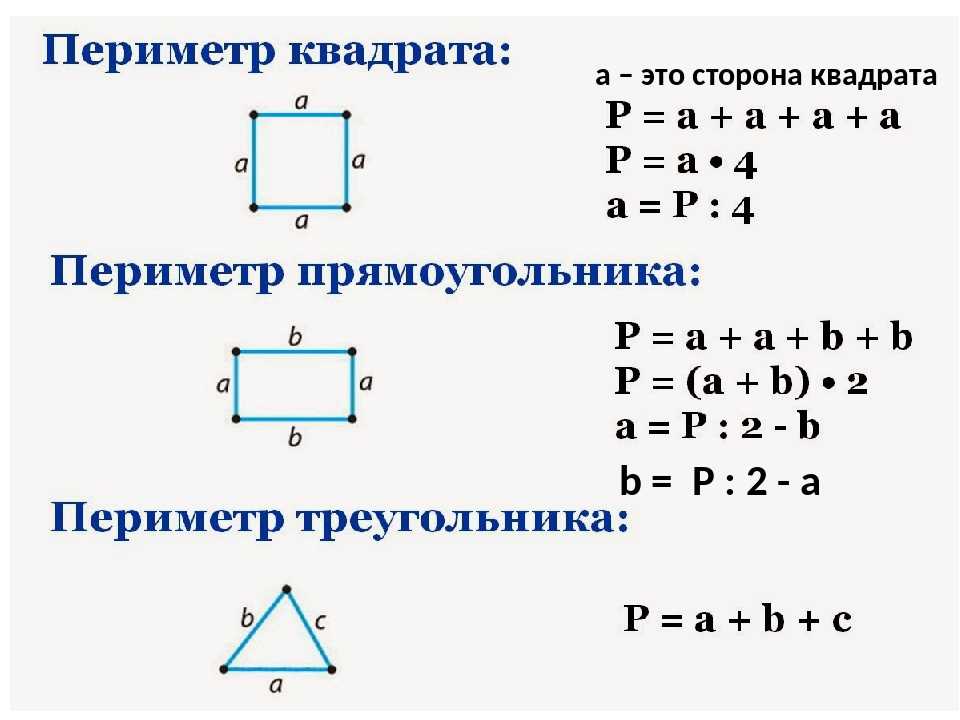
Формулы радиуса прямоугольника:
1. Формула описанного радиуса прямоугольника через стороны прямоугольника:
| R = | √a 2 + b 2 |
| 2 |
| R = | √P 2 — 4Pa + 8a 2 | = | √P 2 — 4Pb + 8b 2 |
| 4 | 4 |
3. Формула описанного радиуса прямоугольника через площадь и сторону прямоугольника:
| R = | √AS 2 + a 4 | = | √S 2 + b 4 |
| 2a | 2b |
4. Formula описанного радиуса прямоугольника через диагональ:
Formula описанного радиуса прямоугольника через диагональ:
| R = | d |
| 2 |
| R = | D c |
| 2 |
| R = | a |
| 2sin α |
| R = | b |
| 2cos α |
| R = | √2A : sin β |
| 2 |
Угол между диагональю и стороной прямоугольника
Угол между диагональю и стороной прямоугольника формулы
1. Формула угла между диагональю и стороной прямоугольника через диагональ и сторону прямоугольника:
| sin α = | a |
| d |
| cos α = | b |
| d |
2. Formula of angle between the diagonal and rectangle сторону через угол между диагоналями:
Formula of angle between the diagonal and rectangle сторону через угол между диагоналями:
| α = | β |
| 2 |
Угол между диагоналями прямоугольника
Угол между диагоналями прямоугольника формулы:
1. Формула угла между диагоналями прямоугольника через угол между диагональю и стороной прямоугольника:
2. Формула угла между диагоналями прямоугольника через площадь и диагональ прямоугольника:
| sin β = | 2А |
| г 2 |
Формулы геометрии
Квадрат. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус.

 Поможешь Джорджу найти его площадь?
Поможешь Джорджу найти его площадь?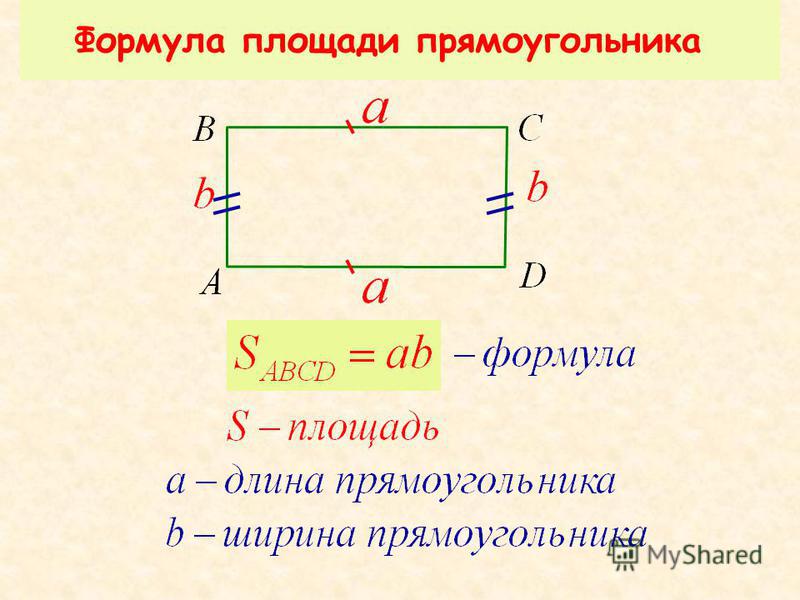 ) Противоположные стороны прямоугольника равны и параллельны друг другу.
) Противоположные стороны прямоугольника равны и параллельны друг другу.