§ Возрастание и убывание функции
Что такое возрастание функции
В начале прочитаем определение возрастания функции.
Запомните!
Функция « y(x) » называется возрастающей на некотором промежутке, если
для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких, что « x2 > x1 »
выполняется неравенство
« y( x2 ) > y( x1 )».
Определение сложно понять без наглядного примера. Поэтому сразу перейдём к разбору задачи на возрастание функции.
По-другому можно сказать, что, если каждому бóльшему значению « x » соответствует бóльшее значение « y », значит, функция « y(x) » возрастает.
x2 > x1 | Обязательное условие возрастания функции |
Давайте разберем определение возрастания функции на конкретном примере.
Разбор примера
Возрастающей или убывающей является функция « y = 9x − 4 » ?
Для начала определим область определения функции « y = 9x − 4 ».
y = 9x − 4
D(y): x ∈ R ,
то есть « x » —
любое действительное число.
Построим график функции
« y = 9x − 4 ».
Так как функция
« y = 9x − 4 »
линейная, ее график — прямая.
Используем правила построения графика линейной функции. Нам достаточно найти две точки, чтобы построить ее график.
Область определения функции
« y = 9x − 4 » — все действительные числа,
поэтому можно подставить любое число вместо « x » и вычислить « y » по
формуле функции
« y = 9x − 4 ». Например, возьмем
« x = 0 ».
x = 0
y(x) = 9x − 4
y(0) = 9 · 0 − 4 = −4
Для второй точки возьмем « x = 1 ».
x = 1
y(x) = 9x − 4
y(1) = 9 · 1 − 4 = 5
Отметим две полученные
точки «(0; −4)» и «(1; 5)» на
координатной плоскости
и проведем через них прямую.
Докажем, что функция « y = 9x − 4 » возрастает на всей своей области определения двумя способами: по ее графику и аналитически (по ее формуле).
Как определить по графику, что
функция возрастаетПо определению возрастания функции мы знаем, что
если « x » увеличивается,
то « y » тоже должен увеличиваться.
На рисунке ниже видно, что график функции « y = 9x − 4 » «идет в гору». Другими словами, при увеличении « x » ↑ растет значение « y » ↑.
В этом можно убедиться, если взять две любые точки на графике. Например, точки, по
которым мы построили график функции. Назовем эти точки:
« (·)A » и « (·)B ».
У первой точки « (·)A »
координаты:
x1 = 0 ; y1 = − 4
У второй точки « (·)B » координаты:
x2 = 1 ; y
На примере точек « (·)A » и « (·)B » видно, что
при увеличении
« x ↑ ( x2 > x1 )»
растет
« y ↑ ( y2 > y1 ) ».
Поэтому график зрительно «идет в гору».
Как по формуле доказать, что функция возрастает
Вернёмся к нашей функции
« y = 9x − 4 ».
По графику мы поняли, что
функция « y = 9x − 4 » возрастает,
так как ее график «идет в гору».
Но как доказать по формуле, что функция
возрастает на всей своей области определения?
Запомните!
Функция возрастает на всей области определения, когда при
« x2 > x1 »
выполняется условие
« y( x2 ) > y( x1 ) ».
Формулировка выше не самая простая для понимания. Давайте разберем ее на практике.
По определению возрастания функции нам нужно доказать, что при
« x 2 > x1 » увеличивается значение функции
« y( x2 ) > y( x1 ) ».
Но как нам найти значения функции
« y( x1 )» и
«y( x2 ) »?
Для нахождения « y( x1 )» и
«y( x2 ) »
достаточно подставить « x1 » и
« x2 » в исходную формулу « y = 9x − 4 ».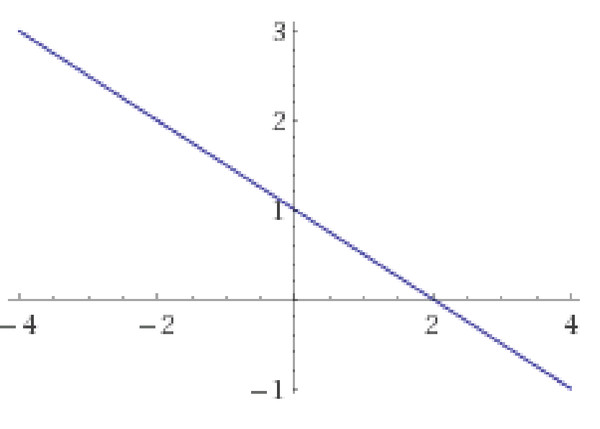
y( x1 ) = 9x1 − 4
y( x2 ) = 9x2 − 4
Теперь запишем обязательное условие возрастания функции.
x2 > x1 | Обязательное условие возрастания функции |
Подставим в неравенство
« y( x2
« y( x1 ) = 9x1 − 4» и
« y( x2 ) = 9x2 − 4 » .
y( x2 ) > y( x1 )
9x2 − 4 > 9x1 − 4
Упростим полученное неравенство.
9x2 − 9x1 > − 4 + 4
9x2 − 9x1 > 0
Вынесем общий множитель в левой части неравенства.
9(x2 − x1) > 0
Разделим левую и правую часть на «9».
9(x2 − x1) > 0 | : 9
| 9(x2 − x1) |
| 9 |
При делении нуля на любое число получается ноль.
x2 − x1 > 0
x2 > x1
Мы доказали, что выполняется исходное условие возрастания функции «x 2 > x1».
Отсюда следует, что функция
« y = 9x − 4 » возрастает на всей области определения.
В завершении вместо ответа следует написать фразу:
«Что и требовалось доказать».
Посмотрим другой пример, где требуется доказать, что функция возрастает.
Разбор примера
Доказать, что функция возрастает на всей области определения: y = 13x − 1
По аналогии с предыдущим примером составим неравенства, которые доказывают, что функция возрастает.
x2 > x1 | Обязательное условие возрастания функции |
Вместо « y( x1 )» и
«y( x2 ) » запишем
формулу функции « y = 13x − 1 » и упростим полученное неравенство.
y( x2 ) > y( x1 )
13x2 − 1 > 13x1 − 1
13x2 − 13x1 > 1 − 1
13(x2 − x1) > 0 |: 13
| 13(x2 − x1) |
| 13 |
>
x2 − x1 > 0
x2 > x1
Что и требовалось доказать.
Что такое убывание функции
Запомните!
Функция « y(x) » называется убывающей на некотором промежутке, если для любых
« x1 » и « x2 »
принадлежащих данному промежутку, таких,
что « x2 > x1 »
выполняется неравенство « y( x2 ) 1 )».
x2 > x1 | Обязательное условие убывания функции |
Как по графику понять, что функция убывает
Разбор примера
Доказать, что функция убывает на всей области определения: y = 1 − 3x
По определению убывания функции мы знаем, что,
если « x »
↑ растет, то
« y » ↓ должен уменьшаться.
Построим график функции
« y = 1 − 3x ». Ее график — прямая, поэтому нам будет достаточно двух точек.
Область определения функции
« y = 1 − 3x » — все действительные числа,
поэтому можно поставить любое число вместо « x » и вычислить « у » по
формуле функции
« y = 1 − 3x ». Например, возьмем
« x = 0 »
и « x = 1 ».
x = 0
y(x) = 1 − 3x
(·) А (0; 1)
x = 1
y(1) = 1 − 3x
y(1) = 1 − 3 · 1 = 1 − 3 = −2
(·) B (1; −2)
Построим график функции
« y = 1 − 3x » по полученным точкам
« (·)A » и « (·)B ».
На графике функции видно, что зрительно график «спускается с горы», то есть функция убывает. Другими словами, при увеличении
« x »
↑ уменьшается
значение
« y » ↓.
Как по формуле доказать, что функция убывает
Вернёмся к нашей функции
« y = 1 − 3x ».
По ее графику мы поняли, что функция убывает, так как график «спускается с горы».
Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?
Запомните!
Чтобы доказать, что функция убывает требуется доказать, что при любых
« x2 > x 1 » выполняется
« y( x2 ) 1 ) ».
Давайте разберем на примере функции
« y = 1 − 3x ». Докажем, что она убывает
на всей своей области определения.
x2 > x1 | Обязательное условие убывания функции |
Подставим « y( x1 )» и «y( x2 ) » в формулу функции « y = 1 − 3x » и упростим полученное неравенство.
y( x2 ) 1 )
1 − 3x21
3x1 − 3x2 3(x1 − x2)
| 3(x1 − x2) |
| 3 |
x1 − x2 −x21
Умножим на « −1 » левую и правую часть неравенства.
−x21 | · (−1)
x2 > x1
Что и требовалось доказать.
Как по графику функции определить
возрастание и убывание
Потренируемся только по графику функции определять промежутки возрастания и убывания функции.
Разбор примера
На рисунке ниже изображён график функции, определенной на множестве действительных чисел. Используя график, найдите промежутки возрастания и промежутки убывания функции.
Отметим с помощью штриховых линий промежутки, где график функции убывает («спускается с горы») и где он возрастает («идет в гору»).
Запишем через знаки неравенств, какие значения принимает « x » на полученных промежутках. Обратите внимание, что во всех случаях при указании промежутков, мы указываем, что их концы входят в промежуток, то есть используем знаки нестрогого неравенства.
Остаётся записать полученные промежутки возрастания и убывания функции в ответ.
Ответ:
- функция убывает при
x ≤ −2; 0 ≤ x ≤ 3,5 - функция возрастает при
−2 ≤ x ≤ 0 ; x ≥ 3,5
Более грамотно будет записать ответ с помощью специальных математических символов.
Ответ:
- функция убывает на промежутках x ∈ (−∞ ; −2] ∪ [0; 3,5]
- функция возрастает на промежутках x ∈ [−2 ; 0] ∪ [3,5 ; +∞]
При каких значениях
« m » функция является убывающей или возрастающей
Ещё один тип заданий, в которых требуется определить,
при каких
« m » ( « а, b » или других буквах) функция убывает или возрастает.
Разбор примера
При каких значениях « m » функция
« y = mx − m − 3 + 2x » является убывающей?
Обратимся снова к определению убывания функции. Вспомним, как записать условия убывания функции с точки зрения формул.
x2 > x1 | Обязательное условие убывания функции |
Запишем эти условия, используя формулу функции « y = mx − m − 3 + 2x », заданную в
задаче.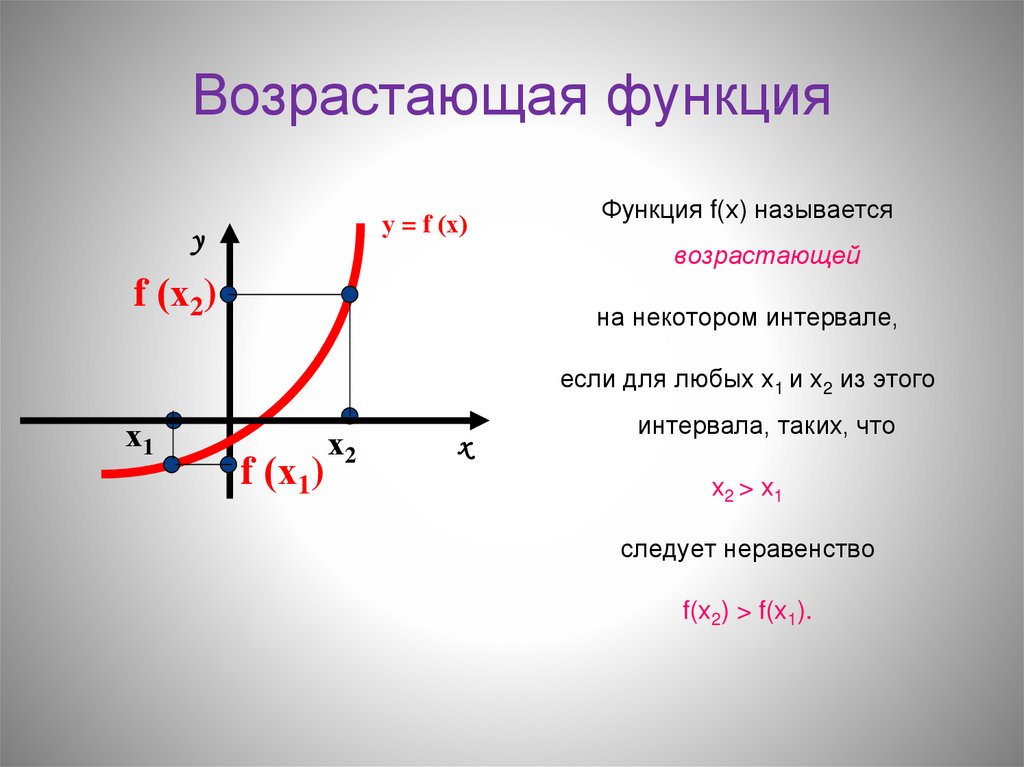
Вместо
« x »
подставим « x1 » и « x2 ».
y( x2 ) 1 )
mx2 − m − 3 + 2x21 − m − 3 + 2x1
Упростим полученное неравенство. Перенесем из правой части все члены неравенства в левую часть с противоположными знаками.
mx2 − m − 3 + 2x2 − mx1 + m + 3 − 2x1
Упростим полученное выражение. Некоторые члены неравенства взаимоуничтожатся.
mx2 − mx1 − m + m − 3 + 3 + 2x2 − 2x1 mx2 − mx1 + 2x2 − 2x1
Вынесем общие множители за скобки.
m( x2 − x1) + 2(x2 − x1)
Теперь
вынесем общий множитель
« ( x2 − x1 ) ».
( x2 − x1) (m + 2)
Вспомним обязательное условие убывания функции.
x2 > x1 | Обязательное условие убывания функции |
Преобразуем исходное условие убывания функции « x2 > x1 ». Перенесем все в левую часть.
x2 > x1
x2 − x1 > 0
По условию убывания функции
« x2 − x1 > 0 »,
значит, чтобы
произведение
«( x2 − x1) (m + 2)
» было меньше нуля, требуется, чтобы множитель «(m + 2)» был меньше нуля. Так как по
правилу знаков:
плюс на минус даёт минус.
| + | · | − | |
| (x2 − x1) | · | (m + 2) |
Решим полученное неравенство.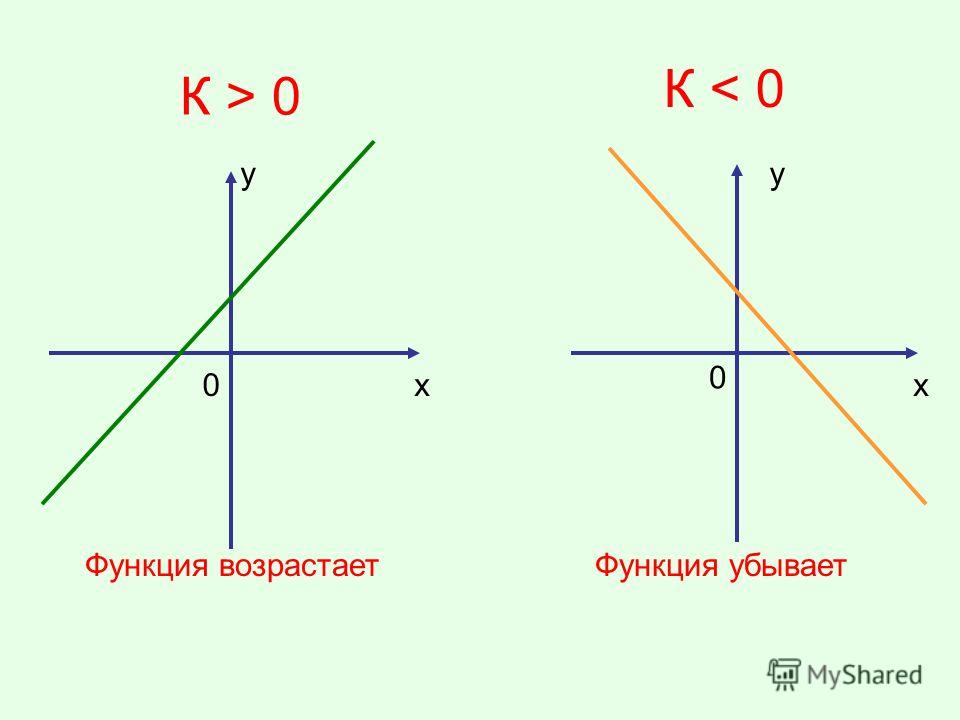
m + 2 m
Ответ: при «m « y = mx − m − 3 + 2x » является убывающей.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Возрастание и убывание функций | Алгебра
Определения
1) Функция y=f(x) называется возрастающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.
То есть для любых двух значений x1,x2 из этого промежутка выполняется условие
Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.
График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).
На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).
Пример 1.
Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x1;x5]:
Функция y=f(x) возрастает на промежутках [x2;x3] и [x4;x5]
Функция y=f(x) убывает на промежутках [x1;x2] и [x3;x4].
Кратко это записывают так:
3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).
4) Если функция возрастает на всей своей области определения, то её называют возрастающей.
Если функция убывает на всей своей области определения, то её называют убывающей.
Например, y=√x, y=x³ — возрастающие функции.
Линейная функция y=kx+b возрастающая при k>0 и убывающая при k<0.
5) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие
то функция y=f(x) называется неубывающей на этом промежутке.
6) Если для любых двух значений x1,x2 из некоторого промежутка выполняется условие
то функция y=f(x) называется невозрастающей на этом промежутке.
7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.
Пример 2.
Пользуясь графиком, найти промежутки, на которых функции y=g(x), определённая на отрезке [x1;x3], является невозрастающей и неубывающей:
Функция y=g(x) является неубывающей на промежутке [x1;x2].
Функция y=g(x) является невозрастающей на промежутке [x2;x3].
Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.
Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?
Для этого при условии x2>x1 на промежутке надо доказать выполнение одного из неравенств: f(x2)>f(x1) либо f(x2)>f(x1), то есть определить f(x2)-f(x1)>0 или f(x2)-f(x1)<0.
Примеры.
1) Доказать, что функция f(x)=x²+4x убывает на промежутке (-∞;-2).
Доказательство:
Функция определена на всей числовой прямой.
Пусть x2>x1.
f(x1)=x1²+4x1, f(x2)=x2²+4x2,
f(x2)-f(x1)=(x2²+4x2)-(x1²+4x1)=x2²+4x2-x1²-4x1=
группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:
=(x2²-x1²)+(4x2-4x1)=(x2-x1)(x2+x1)+4(x2-x1)=
Теперь выносим общий множитель (x2-x1) за скобки:
=(x2-x1)(x2+x1+4).
Так как x2>x1, то x2-x1>0. Следовательно, знак произведения зависит от знака второго множителя.
Для x1, x2 ∈(-∞;-2) x2+x1+4<0.
Значит, (x2-x1)(x2+x1+4)<0 и f(x2)<f(x1). Отсюда следует, что функция функция f(x)=x²+4x убывает на промежутке (-∞;-2).
Что и требовалось доказать.
2) Доказать, что функция
возрастает на промежутке (2;+∞).
Доказательство:
Функция определена при x∈(-∞;2) и (2;+∞).
Пусть x2>x1.
Так как x2>x1, то x2-x1>0.
Для x1, x2 ∈ (2;+∞) (2-x1)(2-x2)>0. Значит,
Отсюда y(x2)-y(x1)>0. Поэтому данная функция возрастает на промежутке (2;+∞).
Что и требовалось доказать.
Исследование функции на монотонность гораздо удобнее проводить с помощью производной (начала математического анализа — производную и её применение — проходят в школьном курсе алгебры в 10-11 классах).
Что это такое, на что указывает, примеры
Что такое нисходящий треугольник?
Нисходящий треугольник — это фигура на диаграмме, используемая в техническом анализе и созданная путем рисования одной линии тренда, соединяющей серию более низких максимумов, и второй горизонтальной линии тренда, соединяющей серию минимумов.
Обычный нисходящий треугольник обычно считается медвежьим графическим паттерном или паттерном продолжения с установленным нисходящим трендом. Однако модель нисходящего треугольника также может быть бычьей с прорывом в противоположном направлении и известна как модель разворота.
Ключевые выводы
- Нисходящий треугольник сигнализирует трейдерам открывать короткую позицию, чтобы ускорить прорыв.
- Нисходящий треугольник можно обнаружить по линиям тренда, проведенным для максимумов и минимумов на графике.
- Нисходящий треугольник является аналогом восходящего треугольника, еще одного графического паттерна, основанного на линиях тренда, используемого техническими аналитиками.
О чем говорит нисходящий треугольник?
Популярный графический паттерн, используемый трейдерами, нисходящие треугольники ясно показывают, что спрос на актив, дериватив или товар ослабевает. Когда цена прорывается ниже нижней поддержки, это указывает на то, что нисходящий импульс, вероятно, продолжится.
Технические трейдеры имеют возможность получить существенную прибыль за короткий период времени. Они часто наблюдают за движением ниже нижней линии тренда поддержки, предполагая, что нисходящий импульс нарастает и прорыв неизбежен. Трейдеры часто открывают короткие позиции, чтобы еще больше снизить цену актива.
Как определить нисходящий треугольник
Нисходящий треугольник является одним из трех треугольных паттернов, используемых в техническом анализе.
Изображение Джули Бэнг © Investopedia 2019
Модель нисходящего треугольника имеет следующие особенности:
- Существующий нисходящий тренд до появления модели нисходящего треугольника.
- Нисходящая верхняя линия тренда может быть проведена путем соединения верхних точек и указывает на то, что продавцы толкают цены вниз.
- Нижняя горизонтальная линия тренда действует как поддержка, когда цены приближаются к этому уровню, пока не произойдет прорыв.
- Нисходящий тренд продолжается после прорыва и проявляется ниже нижней линии тренда.
Как торговать по нисходящему треугольнику
Трейдеры часто открывают короткую позицию после пробоя большого объема от нижней поддержки линии тренда на графике нисходящего треугольника.
Как правило, целевая цена для графического паттерна равна цене входа за вычетом высоты по вертикали между двумя линиями тренда во время пробоя. Сопротивление верхней линии тренда также служит уровнем стоп-лосса для трейдеров, чтобы ограничить их потенциальные убытки.
Трейдеры часто выбирают самый простой способ использования паттерна нисходящего треугольника и покупки на прорыве треугольника, и это одна из нескольких распространенных стратегий получения прибыли с использованием этого паттерна.
Стратегия пробоя паттерна «нисходящий треугольник»
Эта стратегия предвидит прорыв модели нисходящего треугольника и использует комбинацию торговых объемов и утверждения тренда для получения краткосрочной прибыли. Когда акция находится в нисходящем тренде или в фазе консолидации, трейдеры следят за формированием более низких максимумов и более низких минимумов.
Нисходящие треугольники с графиками хейкин-аши
Графики Heikin-Ashi могут применяться к любому рынку и являются торговым инструментом, используемым в сочетании с техническим анализом для помощи в определении тенденций. Перед прорывом свечи Heikin Ashi становятся бычьими. В этой стратегии трейдеры наблюдают за формированием модели нисходящего треугольника и ждут начала бычьего тренда, используя графики Heikin Ashi.
Нисходящий треугольник со скользящими средними
Трейдеры могут комбинировать ценовые методы, такие как скользящее среднее, и графические модели с техническими индикаторами.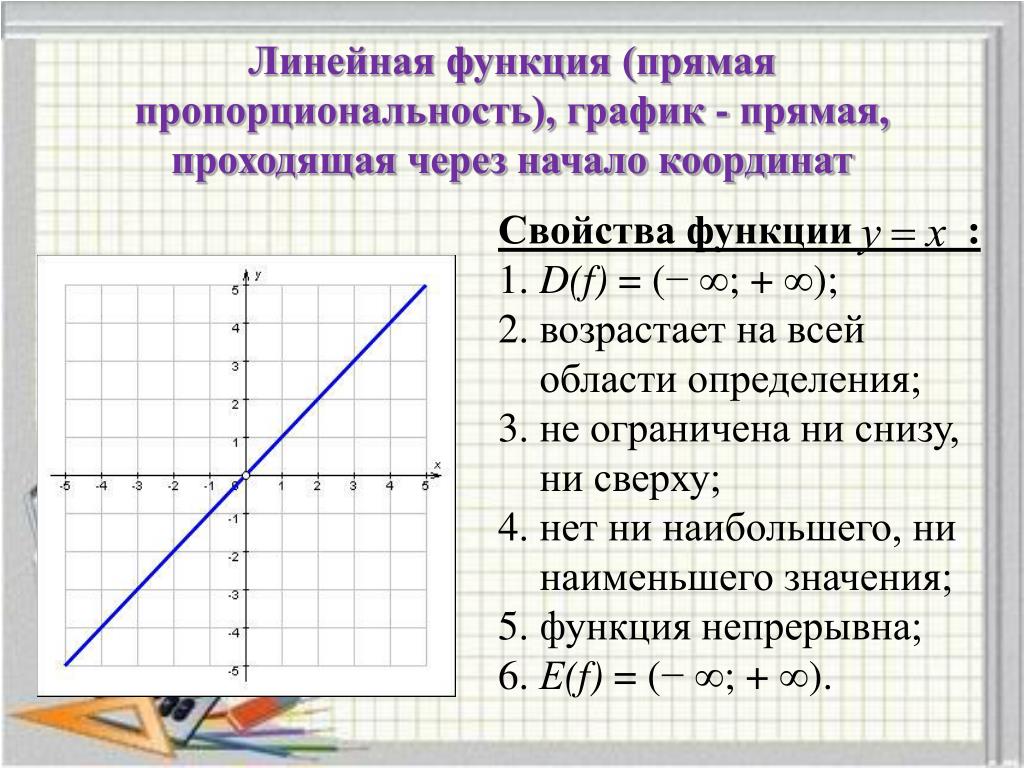
В этой стратегии трейдеры используют модель нисходящего треугольника, чтобы предвидеть потенциальные прорывы, а индикаторы скользящих средних инициируют сигнал для открытия сделки.
Модель разворота «нисходящий треугольник» — вершина
Этот паттерн возникает, когда объем снижается, а новые максимумы цен на акции ограничены. Паттерн указывает на то, что бычья фаза заканчивается. Торговый период начинается, когда перед прорывом раскрывается модель разворота нисходящего треугольника.
Модель разворота «нисходящий треугольник» — дно
Модель разворота нисходящего треугольника на нижнем конце нисходящего тренда — это место, где ценовое действие останавливается, а горизонтальный уровень поддержки отмечает дно. Если ценовое действие прорывается вверх от модели разворота нисходящего треугольника внизу, трейдер может выбрать длинные позиции.
Нисходящие треугольники против восходящих треугольников
И восходящий, и нисходящий треугольники являются фигурами продолжения.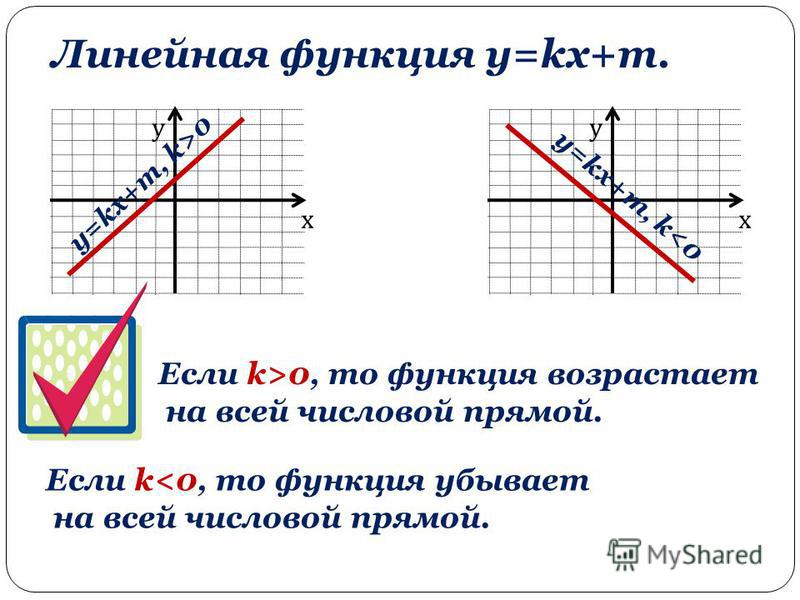
Нисходящий треугольник имеет горизонтальную нижнюю линию тренда и нисходящую верхнюю линию тренда. Восходящий треугольник имеет горизонтальную линию тренда на максимумах и восходящую линию тренда на минимумах.
Треугольники указывают на возможность для продажи и предлагают цель по прибыли, поэтому оба треугольника представляют собой просто разные взгляды на потенциальный прорыв. Восходящие треугольники также могут образовываться при развороте нисходящего тренда, но чаще рассматриваются как бычий паттерн продолжения.
Ограничения нисходящего треугольника
Поскольку ни одна графическая фигура не идеальна, а анализ часто субъективен, использование нисходящих треугольников имеет ограничения. Может произойти ложный пробой или может потребоваться перерисовка линий тренда, если ценовое действие развернется в противоположном направлении. Если пробоя не произойдет, акция может отскочить, чтобы повторно протестировать сопротивление верхней линии тренда, прежде чем совершить еще одно движение вниз, чтобы повторно протестировать уровни поддержки нижней линии тренда.
Чем чаще цена касается уровней поддержки и сопротивления, тем надежнее модель графика.
Что такое прорыв нисходящего треугольника?
Нисходящие треугольники — это медвежья фигура, предвосхищающая прорыв нисходящего тренда. Прорыв происходит, когда цена актива поднимается выше области сопротивления или ниже области поддержки.
В чем разница между пробоем и пробоем в техническом анализе?
Прорыв означает движение цены выше области сопротивления или ниже области поддержки. Прорывы указывают на возможность того, что цена начнет двигаться в направлении прорыва. Пробой — это движение цены ценной бумаги вниз, обычно через определенный уровень поддержки, который предсказывает дальнейшее снижение.
В чем разница между нисходящим треугольником и падающим клином?
Нисходящий клин появляется при нисходящем тренде и указывает на бычий разворот. Нисходящий треугольник появляется после медвежьего тренда с вероятным продолжением пробоя. Нисходящий клин появляется при нисходящем тренде, но указывает на бычий разворот.
Практический результат
Нисходящий треугольник — графическая фигура, используемая в техническом анализе. Паттерн обычно формируется в конце нисходящего тренда, но может также возникать как консолидация в восходящем тренде. Обычный нисходящий треугольник обычно считается медвежьим графическим паттерном с установленным нисходящим трендом. Однако паттерн нисходящего треугольника может быть бычьим, с прорывом в противоположном направлении, известным как паттерн разворота.
по убыванию%20line — английское определение, грамматика, произношение, синонимы и примеры
В другом поезде сиял роскошный салон, из которого произошли Адмирал Уэмисс, Берместер и Невилл, с очень крупным и высокопоставленным генералом.
Дельта-Два подошел, чтобы посмотреть вниз по трапу, где его напарник спустился , и увидел кровь.
Литература В правящей младшей ветви потомков короля Петра имели право на стиль Королевского Высочества, а потомки его младшего брата принца Арсена имели право на стиль Высочества.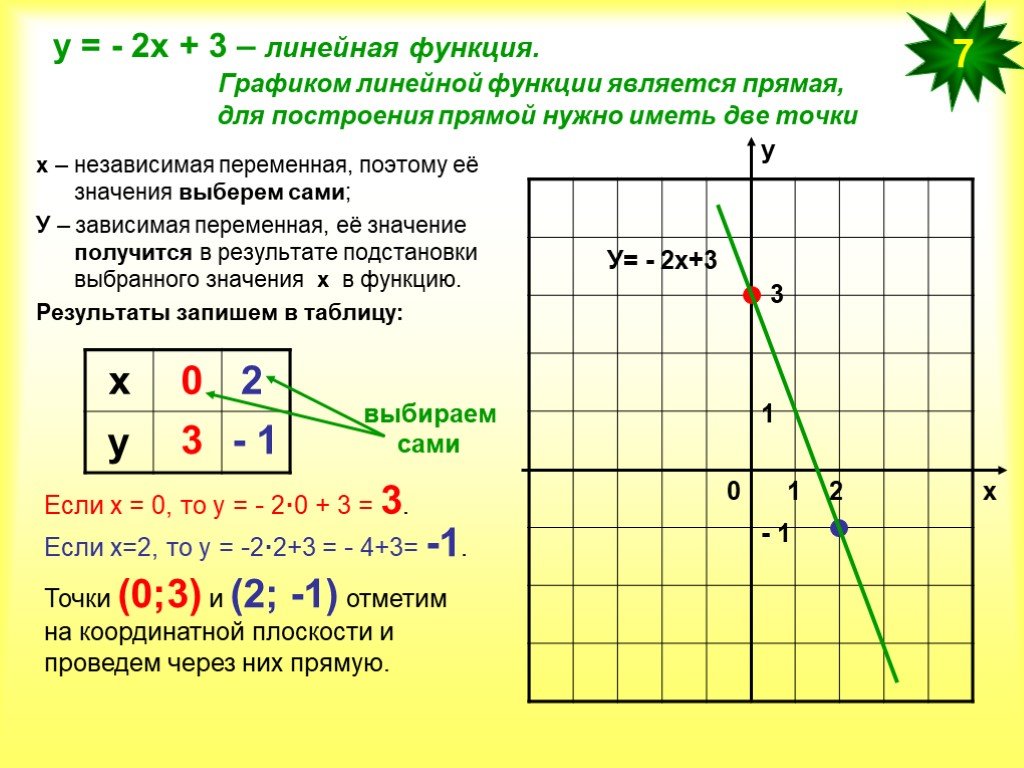
Вооружившись таким образом, он медленно спустился из форта.
WikiMatrixПри указании в типографских размерах (в пунктах, кюсах) высота em-квадрата, невидимого прямоугольника, который обычно немного больше, чем расстояние от самого высокого выносного элемента до самого нижнего выносного элемента , масштабируется так, чтобы равняться указанный размер.
WikiMatrixКонституция также запрещала мужчинам потомкам Дома Савойи въезжать в Италию.
ВикиМатрицаОлда была родственницей Иеремии, оба были потомками Раав по ее браку с Иисусом Навином (Сифре, Числ.
WikiMatrix13 построены на песчаном основании, и когда пойдет дождь , и разольются реки, и подуют ветры, и обрушатся на них, они б упадут , и c врата ада будут готовы принять их.
Она была внучкой бывшего губернатора Северной Каролины У. В. Холдена и прямым потомок Патрика Генри.
Они заставили потомков Ноя оскорбить Иегову, построив город Вавилон как центр ложного поклонения.
jw2019Теперь пришло время нам спуститься
OpenSubtitles2018.v3Меры, принятые для предотвращения размножения или выживания потомков членов группы
MultiUnВ дополнение к подсчету лестничных пролетов и обеспечению набора высоты в тренировка на свежем воздухе Apple Watch Series 5 показывает текущую высоту. Итак, взбираетесь ли вы на холм или спускаясь в каньон, вы знаете, насколько высоко или низко вы находитесь на самом деле.
scb_mt_enth_2020 Через эти страдания Иисус искупил души всех мужчин, женщин и детей, «дабы чрево Его наполнилось милостью по плоти, дабы Он по плоти знал, как помогать Своему народу по их немощи». 18 При этом Христос « нисшел ниже всего» — включая всякую болезнь, немощь и темное отчаяние, переживаемое каждым смертным существом, — для того, чтобы «постичь все, чтобы быть во всем и через все вещи, свет истины».
19
Под эгидой Регионального отделения НПЗУ организовал диалоговые сессии с коренными народами и потомками афро- .
Метелл Сципион, потомок Сципиона, командовал легионами против Юлия Цезаря в Африке до своего поражения в битве при Тапсе в 49 г. до н.э.
WikiMatrixНесомненно, это был он; она спустилась по лестнице, пересекла двор.
ЛитератураФрагменты гранита, найденные Петри в По убыванию Возможно, через эти исчезнувшие двери шел проход.
LASER-wikipedia2Его потомка унаследовали этот титул примерно на два столетия.
WikiMatrixЕсли погода не будет благоприятствовать в течение этих нескольких дней, альпинистам придется спускаться , многие из них возвращаются обратно в базовый лагерь.
WikiMatrixОни спустились на меня.
OpenSubtitles2018.v3 Этот реактивированный человек теперь имеет 88 потомков , которые являются активными членами Церкви.