Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3.  ВЫЧИТАНИЕ ВЫЧИТАНИЕ§ 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2. МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ § 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5.  СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ§ 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ Контрольные вопросы ГЛАВА VI § 1.  ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ§ 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2. ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 3.  КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ § 4. 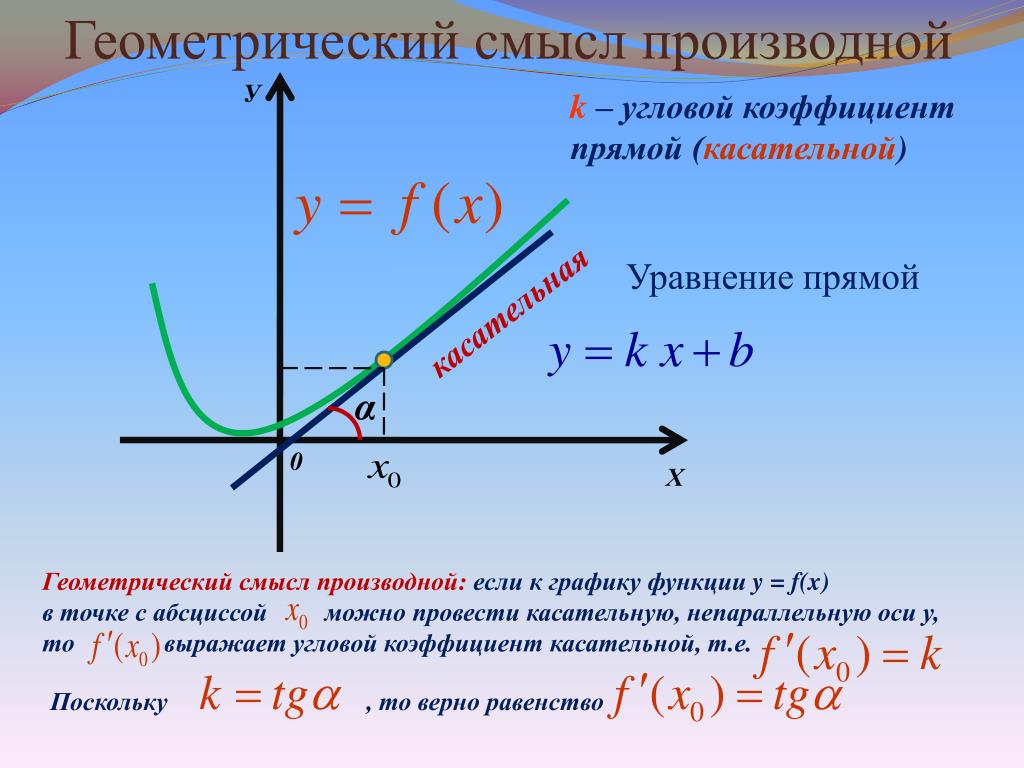 СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросыГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3. СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК § 4.  СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК§ 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2. 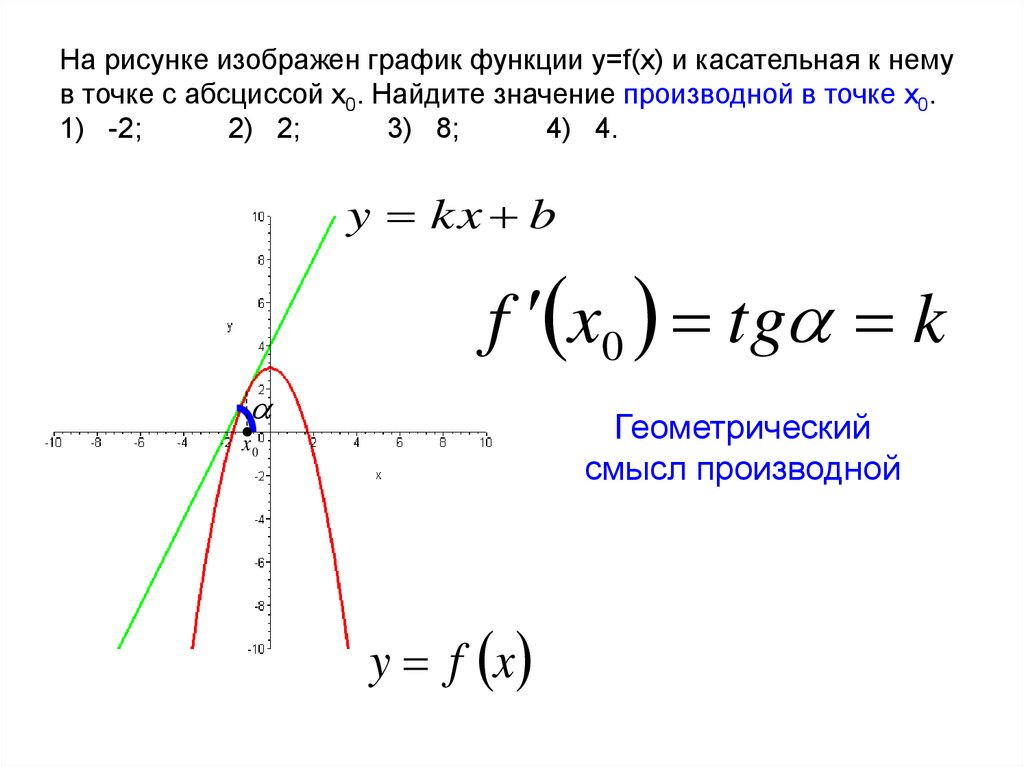 ПРЕДЕЛ ФУНКЦИИ ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Итоговый урок по теме «Уравнение касательной» – Документ 1 – УчМет
Ковалева Елена Ивановна
Учитель 1 категории
МБОУ СОШ№5 г.Рославль, Смоленская область
Учебник Алгебра и начала анализа. 10кл. В 2 ч. (профильный уровень) Мордкович А.Г., Семенов П.В.
ПЛАН-КОНСПЕК УРОКА
Итоговый урок
по теме «Уравнение касательной»
10 класс
Цель урока:
систематизировать и обобщить сведения, полученные учащимися на предыдущем уроке;
расширить представления учащихся о теме;
дополнить и обобщить представления учащихся о применении данной темы в жизни;
познакомить с историей данного вопроса.

9. Задачи:
— обучающие: научиться распознавать сложные функции, знать правила дифференцирования, уметь применять формулу производной сложной функции при решении задач; совершенствовать предметные, в том числе вычислительные, умения и навыки; навыки работы с компьютером.
-развивающие развивать познавательные интересы через применение информационных технологий.
-воспитательные воспитывать адаптивность к современным условиям обучения.
Тип урока урок закрепления изучаемого материала и выработки практических умений и навыков
Формы работы учащихся самостоятельная, индивидуальная, фронтальная работа.
Необходимое техническое
оборудование компьютер, проектор,
экран, презентация для сопровождения
занятия, раздаточный материал для
учащихся.
I. Организационный момент (0.5 мин.).
II. Постановка целей урока. Мотивация учащихся ( 2 мин). (слайд 1)
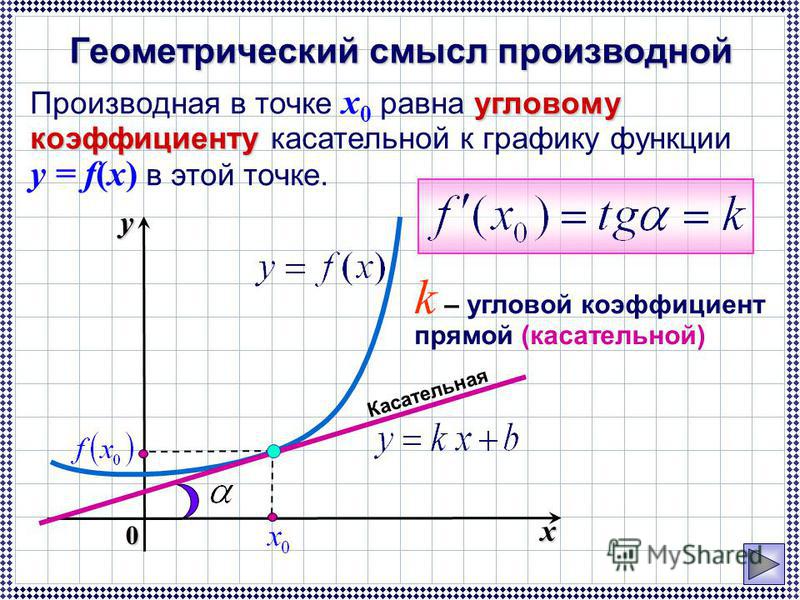
III. Обобщение знаний учащихся по теме «Производная. Уравнение касательной»(15 мин)(слайд 2)
Учитель приветствует учащихся и объявляет цель урока и план, используя презентационное сопровождение. Зачитывается эпиграф к уроку.
Учитель. Сегодня на уроке мы обобщим и закрепим идею геометрического смысла производной, сформируем начальное представление о приложениях производной в математике и истории их развития, «откроем» зависимость между свойствами монотонности функции, экстремумами и значениями производной; эпиграфом к уроку служат слова французского философа-материалиста Дени Дидро (1713 – 1784) – современника Декарта, Лейбница, личного библиотекаря Екатерины Великой.
«Начинать исследования можно
по-разному… Все равно начало почти
всегда оказывается весьма несовершенной,
нередко безуспешной попыткой.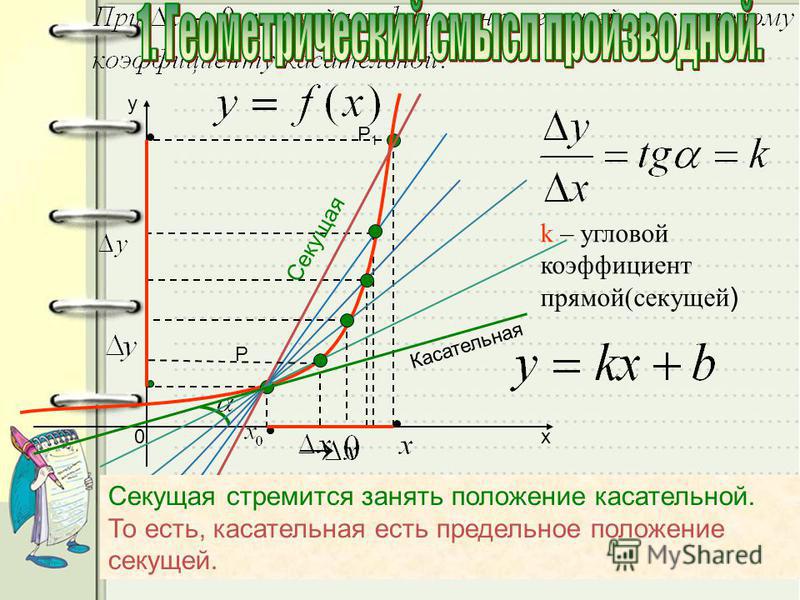 Есть
истины, как страны, наиболее удобный
путь, к которым становится известным
лишь после того, как мы испробуем все
пути. Кому-то приходится, рискуя собой,
сходить с проторенной дороги, чтобы
указать другим правильный путь… На
пути к истине мы почти всегда обречены,
совершать ошибки» (Дени Дидро)
Есть
истины, как страны, наиболее удобный
путь, к которым становится известным
лишь после того, как мы испробуем все
пути. Кому-то приходится, рискуя собой,
сходить с проторенной дороги, чтобы
указать другим правильный путь… На
пути к истине мы почти всегда обречены,
совершать ошибки» (Дени Дидро)
Сегодня мы закрепим материал на тему «Уравнение касательной» решением ключевых или опорных задач, проверим усвоение техники нахождения производной и исследуем связь уравнения касательной с исследованием свойств графика функции , что в дальнейшем нам даст аппарат для построения практически графика любой функции и нахождения ее свойств. Приведет к решению задач на оптимизацию, те нахождения наибольшего и наименьшего значения некоторого конкретного тела, …
Итак, для проверки техники вычисления производной приглашаются учащиеся к компьютерам ( тесты на два варианта)
На местах ребята обсуждают предложенные незавершенные предложения ( слайды 3-4)
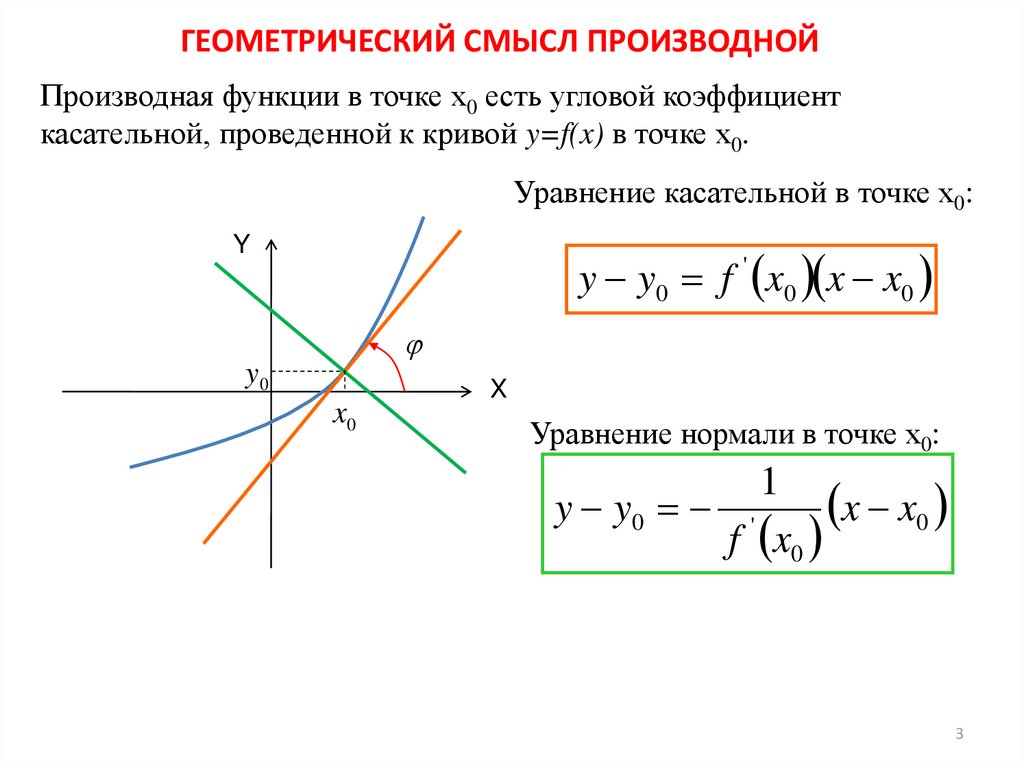
1.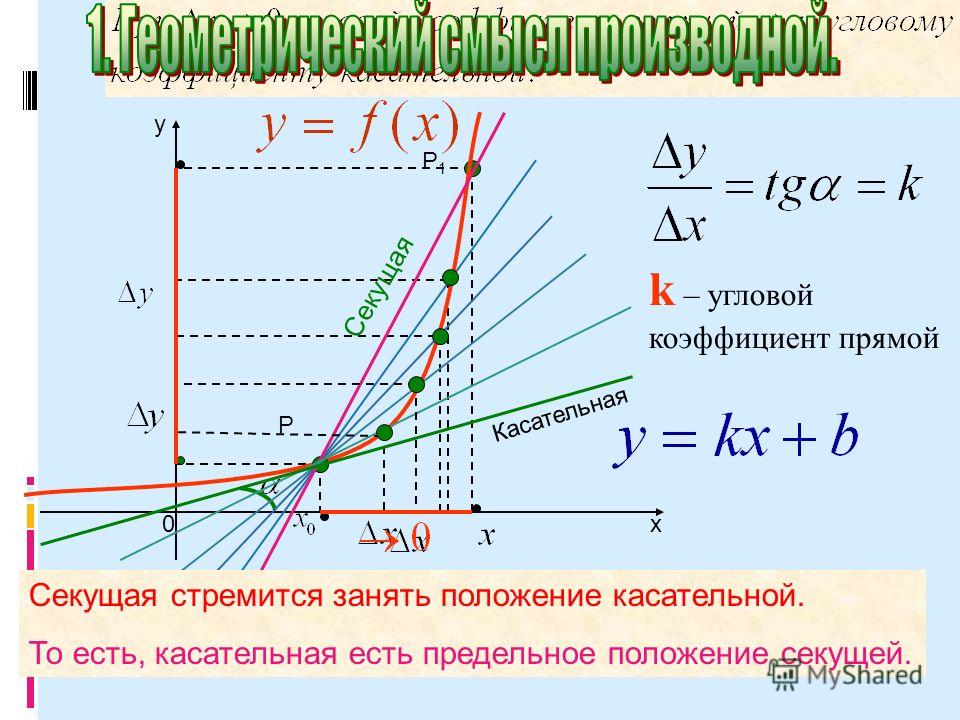 В чем состоит геометрический
смысл производной?
В чем состоит геометрический
смысл производной?
2.В любой ли точке можно построить касательную?
3.Какая функция называется дифференцируемой в точке?
4.Касательная наклонена к под тупым углом к положительному направлению оси Ох ….
5.Кастельная наклонена под острым углом к оси ох…
6.Касательная наклонена под прямым углом к положительному направлению оси Ох…
7.Касательная параллельна оси Ох, следовательно…
8. Что называется секущей для графика функции y=f(x)?
9. Какая прямая называется касательной к графику функции?
10. Какая из отмеченных точек является точкой касания?
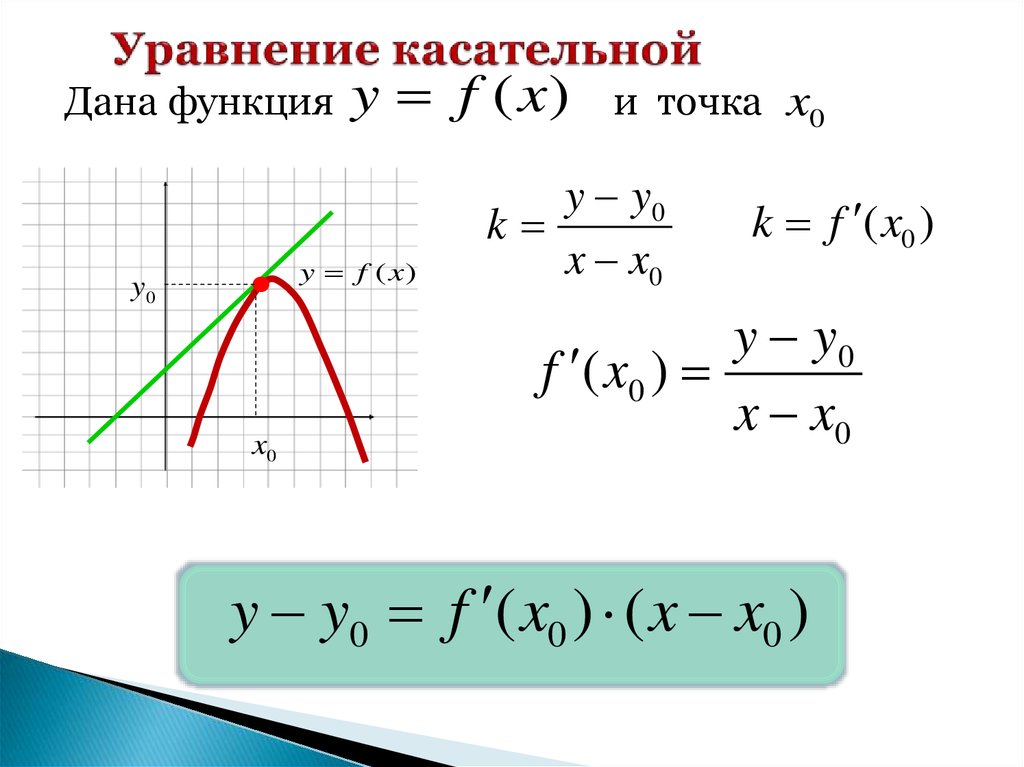
11. Записать уравнение касательной к графику функции в заданной точке в общем виде. 12. Чему равен угол наклона касательной к графику функции в заданной точке? 6. Как найти угловой коэффициент касательной?
13. Известно, что угловой коэффициент
касательной к графику функции в точке
с абсциссой хо, равен 0,6. Чему равно
значение производной в этой точке?
Известно, что угловой коэффициент
касательной к графику функции в точке
с абсциссой хо, равен 0,6. Чему равно
значение производной в этой точке?
14. Касательная к графику функции f(x) в точке с абсциссой хо образует с положительным направлением оси ох угол 45о. Найти f/(xo).
Затем обсуждаем решение ключевых задач. (слайд 5)
Задание из предложенных ключевых задач составить свою задачу.
после обсуждения, решенных у доски задач , учащимся предлагается составить алгоритм решения из ключевых задач.
Учитель. Математический анализ,
ядро которого составляют дифференциальное
и интегральное исчисления, — самая тонкая
область всей математики. Раздел
математики, в котором изучаются
производные и их применения к исследованию
функций, называется дифференциальным
исчислением, а раздел математики, в
котором изучается операция интегрирования
функции, то есть восстановления функции
по её производной, называется интегральным
исчислением.
Немного истории ( небольшое сообщение ученицы) (слайды 6-10)
Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия.
Большой вклад в развитие дифференциального исчисления внесли:
Архимед, который задолго до этого решил задачу на построение касательной к спирали, сумел найти максимум функции f(x) = х2 (а — х),
Пьер Ферма (1601 -1665), математическое определение производной, которого было принято всеми математиками, успешно применявшими в своём методе нахождения экстремумов многочленов задачи о построениях касательных к кривым,
Готфрид Вильгельм Лейбниц
(1646 -1716), который установил геометрический
смысл производной, как тангенс угла
наклона касательной. «Штрихи к портрету»
Готфрида Лейбница : в своей работе
«Новый метод максимумов и минимумов»,
используя геометрическое истолкование,
он кратко разъясняет признаки возрастания
и убывания, максимума
и минимума, выпуклости
и вогнутости (следовательно, и
достаточные условия экстремума
для простейшего случая), а также точки
перегиба. Его знаменитая фраза: «Без
настоящих единиц не может быть и
множества». С ним связаны имена
выдающихся личностей, термины и понятия:
Эпоха Просвещения, Петр I,
Россия, Ньютон, рококо, арифмометр,
кратер на Луне, подводная лодка,
«Философский век». Подумайте над этим
дома.
Его знаменитая фраза: «Без
настоящих единиц не может быть и
множества». С ним связаны имена
выдающихся личностей, термины и понятия:
Эпоха Просвещения, Петр I,
Россия, Ньютон, рококо, арифмометр,
кратер на Луне, подводная лодка,
«Философский век». Подумайте над этим
дома.
V I. Решение задач с практическим содержанием ( слайд 11)
Учитель . Обсуждая успехи своего ученика, учитель математики так отозвался о нем: «Он очень мало знает, но у него положительная производная». Все поняли, что хотел сказать учитель: скорость приращения знаний у ученика положительна, а это есть залог того, что его знания возрастут. Подумайте, как вы могли бы охарактеризовать три кривые роста знаний.
Ответ:I -ого знания не растут т.к.
производная в каждой точке прямой равна
нулю, знания II-го растут быстрее, чем
III-го т.к. угол наклона касательных будет
больше, а следовательно и больше
производная, потому что тангенс функция
возрастающая. (слайд 10-анимированный ,
в музыкальном сопровождении)
(слайд 10-анимированный ,
в музыкальном сопровождении)
У вас на столах график некоторой функции, проведите в указанных точках схематично касательные и охарактеризуйте данную функцию у учетом изученного в 10 и 9-ом классах.
А теперь послушайте музыку, которая сейчас помогала исследованию В чем связь? ( слайд12) Почему именно музыку и график функции мы сегодня связываем?
Не всякую музыку можно слушать легко, для восприятия необходимо произвести усилия, вслушаться , представить действие , проникнуться настроением, поймать мысль композитора.
«Здесь мало увидеть,
Здесь нужно всмотреться,
Здесь мало услышать,
Здесь вслушаться нужно,» Н.Рыленков «Все в тающей дымке»
А может быть и с графиком , его надо не только увидеть, но в него надо всмотреться, почувствовать всю гармонию мелодии графика.
Такую мелодию нам предложит
Семченкова Настя( на гитаре попыталась
проиграть мелодию, повторяющую
предложенный график).
А теперь попробуйте сами. Звучит вальс из балета «Лебединое озеро»
П.И.Чайковского.
Учитель. Ребята, а зачем нужно изучать данную тему.
Выберем ответы из левого столбца:
|
|
Нужна ли производная для будущей профессии?
Российский математик 19века
Панфутий Львович Чебышев говорил, что
«особенную важность имеют те методы
науки, которые позволяют решать задачу,
общую для всей практической деятельности
человека, например, как располагать
своими средствами для достижения
наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
Вам предложены задачи из жизни, необходимо применить для решения свойства касательной.
1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста? (слайд13-анимированный –этапы рассуждений)
2.Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м. Из точки Р, расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е(илиА). Какую
высоту h нужно придать
центральной части теплицы , если
желательно, чтобы струя воды( она имеет
форму параболы с вершиной в точке
Р) не достигла крыши теплицы?
Из точки Р, расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е(илиА). Какую
высоту h нужно придать
центральной части теплицы , если
желательно, чтобы струя воды( она имеет
форму параболы с вершиной в точке
Р) не достигла крыши теплицы?
Во многих приложениях встречается
понятие касания кривых между собой.
Кривые называются касающимися ,если
они имеют в этой точке общую касательную.
3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0
4.Покажите, что кривые у=4х2+2х-8 и у=-х3-х+10 касаются в точке А(3;34). Будут ли они касаться в точке В(2;-4)
5. При каких соотношениях парабола ах2+вх+с-0 касается оси Ох?
6. Найдите те значения х, при которых касательные в соответствующих точках параллельны между собой. При каком значении а кривые будут касаться друг друга?
Вам было предложено дома решить не менее творческую задачу: составления алгоритма решения нестандартной задачи , по теме «Уравнение касательной»
Обсуждаем данные алгоритмы.
Как вы уже заметили, что в данных алгоритмах повторяющиеся блоки, перечислите их: составление уравнения касательной в точке; нахождения точки касания по углу наклона касательной к положительному направлению оси Ох, по известному угловому коэффициенту, который может быть известен по условию параллельности прямых ,описанию условия нахождения точек касания
А теперь перейдем к выполнению
практической работы , при выполнении
которой вы должны применить все на
практике. (Приложение1)
(Приложение1)
V. Постановка дифференцированного домашнего задания
Учитель раздает карточки с вариантами заданий (4 варианта) , которые содержат обязательную и необязательную части домашнего задания, делает соответствующие пояснения о том, что результаты будут необходимы на следующем уроке.
VI. Итог урока.
Учитель предлагает обобщить учащимся свои исследования, демонстрирует на слайдах результаты подведения итогов и дальнейший план изучения темы. На экране непрерывно идут титрами новые математические понятия: необходимое условие, достаточное условие, необходимое и достаточное условие.
Учащиеся высказывают свое мнение, подводят общий итог исследованию
Список используемой литературы
Алгебра и начала анализа. 10 класс. В 2 ч. Ч.1. Учебник (профильный уровень) / А. Г. Мордкович, П.
 В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.
В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.Алгебра и начала анализа: Учеб. Для 10-11 кл. общеобразоват. учреждений
/А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.; Под ред. А.Н.Колмогорова-
10-е изд.- М..: Просвещение,2000. – стр. 160-166Единый государственный экзамен: Математика: Контрол. измерит. материалы
/Л.О.Денищева, Е.М.Бойченко, Ю.А.Глазков и.др.; М-во образования Рос.
Федерации.- М.: Просвещение, 2003.Производная и её применение: Дидакт. матер, по курсу алгебры и начал анализа
для 10-11 кл.ср.шк./Под ред. М.И.Башмакова — СПб, Свет, 1995.Клайн М. Математика. Утрата определённости: Пер. с англ./ Под ред. С предисл. И
примеч. И.М.Яглома.- М.: Мир, 1984.Степанова М.В. Учебно-исследовательская деятельность школьников в профильном обучении: учебно-методическое пособие для учителя/ Под ред.
 А.П.Тряпининой. –
СПб.: КАРО, 2005.
А.П.Тряпининой. –
СПб.: КАРО, 2005.Маркова В. Что такое исследовательская деятельность школьников / Математика (приложение к 1 сентября), №12, 2007.
Интернет – источники
Музыка «Балет «Лебединое озеро» — Вальс A-dur, акт 1» — (Пётр Ильич Чайковский)http://www.rusmusic.su/instrumental.php
Дени Дидро
http://books.atheism.ru/gallery/Diderot/
Екатерина Великая
http://mail.spb.fio.ru/archive/group15/c3wu3/pagehistory1.htm
Лейбниц
http://ru.wikipedia.org/wiki/%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%2C_%D0%93%D0%BE%D1%82%D1%84%D1%80%D0%B8%D0%B4_%D0%92%D0%B8%D0%BB%D1%8C%D0%B3%D0%B5%D0%BB%D1%8C%D0%BC
Ньютон
http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA
Архимед
http://ru. wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4
wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4
Лагранж
http://ru.wikipedia.org/wiki/%D0%9B%D0%B0%D0%B3%D1%80%D0%B0%D0%BD%D0%B6%2C_%D0%96%D0%BE%D0%B7%D0%B5%D1%84_%D0%9B%D1%83%D0%B8
Ферма
http://ru.wikipedia.org/wiki/%D0%A4%D0%B5%D1%80%D0%BC%D0%B0%2C_%D0%9F%D1%8C%D0%B5%D1%80
Ньютон
http://ru.wikipedia.org/wiki/%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD%2C_%D0%98%D1%81%D0%B0%D0%B0%D0%BA
Приложения к плану-конспекту урока
Итоговый урок по теме «Уравнение касательной»
Приложение 1
Геометрическое приложение производной
1.Профиль моста имеет форму параболы с высотой центральной части 10 м и длиной основания 120м. Какой должен быть наклон насыпи на концах моста?
2. Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м.
Из точки Р , расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е (или А ). Какую
высоту h нужно придать
центральной части теплицы, если
желательно, чтобы струя воды ( она имеет
форму параболы с вершиной в точке Р) не
достигла крыши теплицы?
Вертикальный разрез теплицы
имеет форму пятиугольника ABCDE,
в котором FT=8м, AB=DE=1м.
Из точки Р , расположенной на высоте 2м,
подается горизонтально вытекающая
струя воды, которая при максимальном
напоре достигает точки Е (или А ). Какую
высоту h нужно придать
центральной части теплицы, если
желательно, чтобы струя воды ( она имеет
форму параболы с вершиной в точке Р) не
достигла крыши теплицы?
C
Р
В D
А Е
3.Каково необходимое и достаточное условие двух функций у =f(x) и y=g(x) касаются друг друга в точке х0
4.Покажите, что кривые у=4х2+2х-8 и у=-х3-х+10 касаются в точке А (3;34). Будут ли они касаться в точке В (2;-4)
5. При каких соотношениях
парабола ах2+вх+с-0 касается оси О
х?
При каких соотношениях
парабола ах2+вх+с-0 касается оси О
х?
Приложение 2
Вариант 1 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3 Угловой коэффициент касательной, проведенной к графику функции y = , в точке (x0,
y0) равен
.
Найдите x0 ? y0. |
А5. параллельна прямой, заданной уравнением y = -2x ? A) (-4; 0) B) (0; 4) C) (4; 0) D) (0; -4) E) (2; 4) |
А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 1350? |
А5.6.В точке А(5;0) проведена касательная к графику функции .Найти длину отрезка касательной, заключенного между осями координат. |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
Вариант 2 |
А5. |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5.3Угловой
коэффициент касательной, проведенной
к параболе A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 |
А5.4 В какой точке касательная, проведенная к графику функции y = x — 2x + 1, параллельна
прямой y = -4(x + 1)? |
А5. |
А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108 |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5.8. |
Вариант 3 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5. |
А5.4.В каких точках касательная к графику функции образует с осью Ох угол в 450? |
А5.5. При каких значениях x касательная к графику функции y = 2x + 3x — 6x параллельна прямой y = 6x + 1 ? A) -2 и 3 B) 1 и 3 C) -2 и 1 D) 2 и -1 E) -1 и 3 |
А5.6.В
точке А(5;0) проведена касательная к
графику функции .Найти
длину отрезка касательной, заключенного
между осями координат. |
А5.7. Найти площадь треугольника, образованного осями координат и касательной к графику функции у=f(х) в точке с абсциссой х0 |
А5.8. В какой точке нужно провести касательную к графику функции , чтобы она пересекла ось ординат в точке (0;6) ? |
Вариант 4 |
А5.1.Написать уравнение касательной к графику функции в точке с абсциссой х0 |
А5.2.Найти угловой коэффициент касательной к графику функции в точке с заданной абсциссой |
А5. A) y = 4x — 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x — 5 E) y = 4x — 9 |
А5.4. Какая из прямых параллельна касательной
к кривой y = 4 – x
в точке x0 = 2? |
А5.5.В каких точках касательная к графику функции образует с осью Ох угол в 1350? |
А5.6. Найти длину отрезка касательной, заключенного между осями координат к кривой , проведенной в точке с абсциссой х=108 |
А5. в точке с абсциссой х0 |
А5.8.Касательные, проведенные к графику функции в точках с абсциссами х1 и х2 параллельны. Известно, что х1 =. Найдите отношение |
Приложение 3
Математическая сцена — Производные уроки 1
Математическая сцена — Производные уроки 12009 Расмус Эф и Джанн Сак |
Урок 1
Скорость изменения и градиенты.
Теперь посмотрим на строки
которые аккорды
и касательные.
Линия, которая только касается кривая в одной точке называется касательной. Измеряем наклон кривой в эту точку, измерив наклон касательной.
Линия, которая пересекает кривую в двух точках, называется аккордом. Посмотрите на следующую диаграмму.
Сначала рассмотрим, что подразумевается под «скоростью изменения».
и «средняя скорость изменения». Скорость изменения – это скорость изменения за один
определенный момент времени, тогда как средняя скорость изменения – это скорость
изменение, измеренное за заданный интервал.
Рассмотрим скорость автомобиля. Существует разница между скоростью, показанной на
спидометр в любой конкретной точке и среднюю скорость, измеренную за
заданное расстояние.
Пример 1
В следующей таблице показаны отношение между временем и температурой воды в кастрюле, когда она нагревают от 20 С до точки кипения.
Время (мин.) | Температура |
| 0 | 20С |
| 1 | 30С |
| 2 | 40К |
| 3 | 49С |
| 4 | 58С |
| 5 | 66С |
| 6 | 74С |
| 7 | 81С |
| 8 | 88С |
| 9 | 95С |
| 10 | 100К |
С какой скоростью повышение температуры?
Есть много способов
глядя на это уравнение. Например, мы можем измерить среднее повышение температуры в минуту как
вода кипит.
Например, мы можем измерить среднее повышение температуры в минуту как
вода кипит.
Температура повышается на 80°C за 10 минут, поэтому среднее повышение температуры 80/10 = 8 C/мин.
Если же мы посмотрим на таблица значений мы видим, что температура поднимается медленнее по мере того, как вода нагревается. Таким образом, мы можем получить более точную картину происходящего, глядя на среднее повышение температуры в первые две минуты и последние пара минут.
Среднее скорость изменения в первые две минуты (40 20)/(2 0) = 20/2 = 10 Кл/мин.
Средняя скорость изменения за последние две минуты составляет (100 88)/(10 8) = 12/2. = 6 Кл/мин.
Пример 2
Теперь применим эти идеи к функциям.
Посмотрите на функцию f(x) = x 2 и рассмотрим скорость изменения значения функции при увеличении x. Представьте, что значения x измеряются в минутах. Получаем следующую таблицу значения:
х (мин. | f(x) = x 2 |
| 0 | 0 |
| 1 | |
| 2 | 1 |
| 3 | 2 |
| 4 | 4 |
| 5 | 6 |
| 6 | 9 |
| 7 | 12 |
| 8 | 16 |
Средняя скорость изменения функция:
Более весь интервал = (16 0)/8 = 2
Более первые две минуты = (1 0)/2 =
Свыше последние две минуты = (16 9)/(8 6) = 7/2 = 3
Более двух средних минутный интервал, например от 3 до 5 минут = (6 2 )/(5 3) = 2
Ниже приведена формула для средней скорости изменения функции f(x) от x 1 к х 2 :
Средняя скорость изменения знак равно
Если мы используем у вместо f(x) что, конечно же, то же самое значение, мы можем написать формулу для среднего скорость изменения как:
Среднее скорость изменения =
Это точно такая же формула, которую мы используем для
найти градиент (наклон) прямой линии и фактически среднюю скорость
изменение между двумя точками — это просто градиент прямой линии, соединяющей
эти две точки на графике, то есть градиент хорды, соединяющей эти
две точки.
На графике ниже показаны две хорды графика функция е (х) = х 2 . Наклон первой хорды – это среднее скорость изменения для всего интервала от 0 до 8, а наклон второй аккорд — это скорость изменения в течение первых двух минут. Уравнение хорда находится с использованием средней скорости изменения в качестве градиента, а затем выбор фиксированной точки из таблицы значений.
Затем эта информация помещается в уравнение прямой y = k(x x 1 ) + y 1 .
Средняя скорость изменение на интервале х 1 Икс х 2 является |
Пример 3
Найдите среднюю скорость изменение функции f(x) = x 3 на интервале 2 Икс 2.
Сначала находим два точки.
х 1 = 2 и f(2) = (2) 3 = 8
х 2 = 2 и f(2) = 2 3 = 8
Средняя скорость изменения это
Пример 4
Давайте еще раз посмотрим на
функция f(x) =
х 2 и найдите среднюю скорость изменения, когда x близок к значению 4 (x = 4). Сначала мы начнем слева от 4 и будем рассматривать все меньшие и меньшие интервалы.
Воспользуемся таблицей значений из примера 2.
Сначала мы начнем слева от 4 и будем рассматривать все меньшие и меньшие интервалы.
Воспользуемся таблицей значений из примера 2.
Средняя скорость изменения на интервале 1 Икс 4 равно (4 )/(4 1) = 1
В среднем скорость изменения на интервале 2 Икс 4 равно (4 1)/(4 2) = 1
В среднем скорость изменения на интервале 3 Икс 4 равно (4 2)/(4 3) = 1
Аккорды, соответствующие эти расчеты показаны на графике ниже.
Получили «веер» хорды, градиенты становятся все больше и больше по мере приближения к первой точке до 4, чтобы интервал стал меньше.
Теперь давайте сделаем то же самое справа от х = 4.
Средняя скорость изменения на интервале 4 Икс 7 равно (12 4)/(7 4) = 2
Средняя скорость изменения на интервале 4 Икс 6 есть (94)/(6 4) = 2
В среднем скорость изменения на интервале 4 Икс 5 равно (6 4)/(6 5) = 2
Из этих расчетов можно сделать вывод, что
средняя скорость изменения функции вблизи x = 4 находится где-то между 1
и 2.
Пример 5
Мы
может рассчитать
в среднем
скорость изменения на сколь угодно малом интервале. Мы продолжим использовать
функция f(x) = x 2 и выберите крошечный интервал вокруг x
= 4.
Мы делаем это, выбирая точку на расстоянии h от 4 . Это дает нам две точки x = 4 и 4 + h, чтобы мы могли вычислить
средняя скорость изменения на интервале длины h.
Диаграмма ниже
показывает две точки, которые мы выбрали, и хорду, соединяющую их.
Точки (4,
4) и (4+h, f(4+h)).
Нам нужно вычислить f(4+h) = (4 + h) 2 = (16 + 8h + h 2 ) = 4 + 2ч + ч 2 .
Хорда проходит через две точки (4, 4) и (4+ч, 4+2h+h 2 ), поэтому среднее скорость изменения или градиент хорды
Если мы выберем значения h все меньше и меньше мы получим следующие результаты для средней скорости изменения:
ч =
0,04 дает нам 2 + 0,04 = 2,01.
ч = 0,0004 дает нам 2 + 0,0004 = 2,0001.
Чем меньше значение h, тем интервал около 4 становится меньше, мы видим, что средняя скорость изменения становится все ближе и ближе к 2.
и, наконец, когда h доберется до ноль мы получаем
Этот предел дает нам скорость изменения точка (4, 4). Линия, которую мы рисуем, больше не является аккордом, а стала касательной к графику в точке (4, 4). Градиент касательной — это скорость изменения функции в этой точке.
Мы можем найти уравнение этой касательной, используя формула у = к(х х 1 ) + у 1 .
г. = 2(х 4) + 4 = 2х 8 + 4 = 2х 4
г. = 2x 4
Градиент касательной к f(x) в точке (а, б) это Уравнение касательной в той же точке (а, б) равно у = к(х а) +б
|
Пример 6
Найдите уравнение касательной к графику f(x) = x 2 2x + 1 в точке (2, 1).
Сначала находим градиент.
| Квадратные скобки используются, чтобы сделать это
легче отличить ф(2+ч) и f(2).
|
Уравнение касательной поэтому:
г. = 2(х 2) + 1
= 2x 4 + 1
г. = 2x 3
Сейчас мы посмотрим, как мы можем использовать CASIO-калькулятор для проверки нашего результата.
Уравнения для введена функция и тангенс.
Мы получаем следующие графики, которые показывают нам, что линия, которую мы вычислили, касается графика в одной точке и, следовательно, является тангенс.:
Также можно использовать калькулятор, чтобы найти градиент.
Выберите меню RUN, затем нажмите кнопку OPTN на клавиатура (рядом с клавишей SHIFT)
Затем выберите CALC с помощью F4 и d/dx с помощью F2. (d/dx — это обозначение наклона касательной. Это будет объяснено позже).
Далее введите уравнение функции и значение x точки, в которой
уклон должен быть найден (см. ниже)
(d/dx — это обозначение наклона касательной. Это будет объяснено позже).
Далее введите уравнение функции и значение x точки, в которой
уклон должен быть найден (см. ниже)
Результат равен 2, что также подтверждает наши расчеты.
Практикуйте эти методы, а затем пройти тест 1 на дифференциалы.
шт. Запомните свой контрольный список.
Karl’s Calculus Tutor — 4.5 The Soft Touch (нахождение касательных)
© 1997 Карл ХанВы, наверное, уже видели это в своих домашних заданиях: «Найди уравнение линии, которая является касательной к кривой bloppity-blop в такой-то и такой-то пункт.» И если вы еще не сделали, вы скоро будете. Это будет и на экзамене.
Линия, касательная к кривой, имеет два свойства:
- Линия имеет общую точку с рассматриваемой кривой.
 В общей точке производная кривой равна
равно наклону линии.
В общей точке производная кривой равна
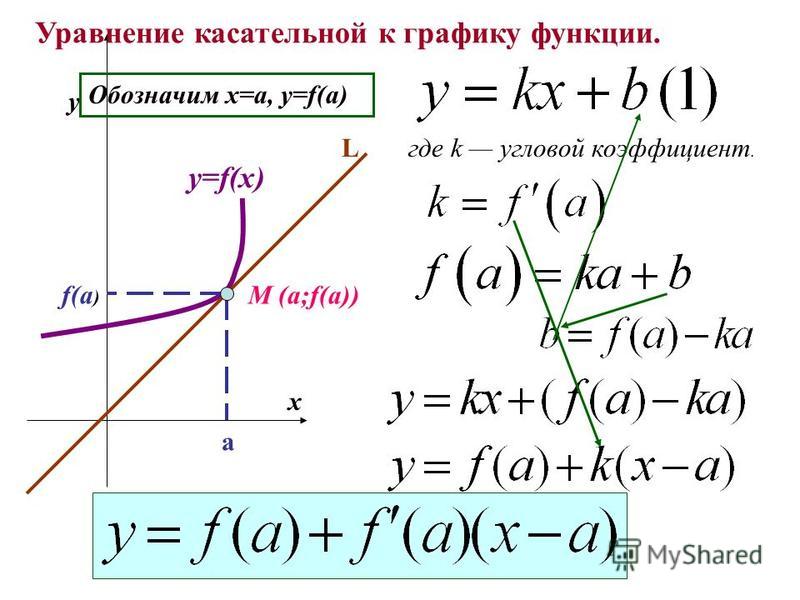
равно наклону линии. Уравнение линии, как вы узнали из алгебры
y = mx + b ур. 4,5-1Итак, все, что вам нужно сделать, это найти m и b.
Возьмем сначала второе свойство. Уклон линии м. Это значение должно совпадать с производной кривой в точке, в которой они дать вам. Итак, чтобы найти m, вам нужно знать производную кривой. И оценивать нужно по той точке, которую дают в проблеме. И это значение равно м.
Затем возьмите первое свойство. Вам нужно найти b, который делает это первое свойство истинным. И теперь ты знаешь, что такое м. равно. Если, например, точка, которую они хотят, чтобы вы касались равно (2, 3), то просто возьмите y = mx + b, подставьте 2 вместо x, 3 для y, что бы вы ни придумали для m, и решить б. Это так просто.
Давайте рассмотрим пример. Пусть кривая
y(x) = x 2 + 1 экв.Обычно считается, что у является функцией от х, поэтому очень часто это будет написано как y = x 2 + 1. Это означает то же самое предмет.4,5-2
Найдем касательную при x = 2. Итак, какая точка в том, что? Мы знаем x-координату точки. Чтобы найти y, просто используйте уравнение кривой (данное в 4.5-2). Это дает нам y = 5, мы хотим, чтобы наша линия была касательной в точке (2, 5).
Шаг 1: Найдите производную кривой. Уравнение кривая дана в 4.5-2. Вы знаете, как взять его производную. Это
y'(x) = 2x экв. 4,5-3
Шаг 2: Оцените производную в заданной точке. Проблема говорит сделать это при x = 2. Производная при этом x равно y'(2) = 4. Это ваше м. Запиши это. м = 4.
Шаг 3: Найдите b. Воспоминание, у = тх + б. Мы знаем, что такое х, что такое у и что такое м. Если вы подключите их все в, вы получаете
5 = 4×2 + b экв.И это тривиальная алгебра, чтобы перейти оттуда к4.5-4а
b = -3 экв. 4.5-4б
Шаг 4: Напишите уравнение. Ты знаешь м и б сейчас. Просто подставьте их в y = mx + b. Ты получать
у = 4x - 3 экв. 4,5-5Вот и все. Были сделаны. Как только вы научитесь брать производную, эти проблемы легкие. Просто выполните четыре шага здесь.
На рис. 4.5-1 показан график этой проблемы. Обратите внимание, как тангенс
линия просто целует кривую в
(2, 5). Угол, под которым они встречаются, фактически равен нулю.
Построение кривой и касательной — это один из способов проверки
работать, чтобы увидеть, если ваш ответ правильный. Другой способ — заменить
x, указанный в задаче (в данном случае 2), в
уравнение для вашей линии и посмотрите, вернетесь ли вы к тому же y
(в данном случае 5)
как вы получите, подставив этот x в уравнение для
изгиб. |
Вот чуть более сложный вариант той же задачи. Найдите две прямые, которые касаются
у = х 2 - 2х + 1и пройти через точку (5, 7). Заметим, что в этом случае точка (5, 7), не лежит на кривой. Итак, вы находите линии, которые проходят через точке вне кривой, но в некоторых других точках, которые пока неизвестно, они касаются кривой. Стратегия заключается в том, чтобы выявить эти точки касания. По ним легко найти строки которые решают проблему.
Шаг 1: Найдите производную кривой. В этом случае мы имеют
у' = 2x - 2Мы делаем это, потому что знаем, что в точке касания производная кривой должен быть равен наклону касательной.
 Итак, мы
нужно знать эту производную.
Итак, мы
нужно знать эту производную.Шаг 2: Напишите как можно больше уравнения прямой как вы можете из того, что вы знаете. Наклон, м, линии до сих пор неизвестен. Но вы знаете, какой смысл он должен пройти. В данном случае это точка (5,7). Итак, используя формула уравнения прямой проходя через данную точку с заданным наклоном, имеем:
у - 7 = м (х - 5)
Шаг 3: Используйте производную, чтобы написать уравнение для наклона. Мы еще не знаем наклона линии, но знаем, что если точка, (x,y) является точкой касания, то наклон линии будет быть равным производной исходной кривой в точке x. Производная мы уже определили, что y’ = 2x — 2. Итак, мы пишем уравнение
м = у' = 2х - 2
Шаг 4: Подставьте выражение наклона в уравнение для линии. У вас есть m = 2x — 2 и у — 7 = т(х — 5). Соедините их вместе, заменив для m во втором уравнении.
у - 7 = (2х - 2)(х - 5) = 2х 2 - 12х + 10 у = 2х 2 - 12х + 17
Шаг 5: Замените уравнение исходной кривой обратно. То есть вы знаете, что у = х 2 — 2х + 1,
где (x, y) — точка касания. Почему? Потому что точка касания
должен лежать на кривой.
Подстановка этого выражения для y в приведенное выше дает:
То есть вы знаете, что у = х 2 — 2х + 1,
где (x, y) — точка касания. Почему? Потому что точка касания
должен лежать на кривой.
Подстановка этого выражения для y в приведенное выше дает:
х 2 - 2х + 1 = 2х 2 - 12х + 17
Шаг 6: Соберите одинаковые термины и решите x. Используя простую алгебру, приведенное выше уравнение становится квадратичный
х 2 - 10х + 16 = 0Вы можете либо использовать квадратичную формулу, либо вы можете факторизовать это в твоей голове, чтобы получить
(х - 2) (х - 8) = 0Таким образом, координата x точки касания равна либо х = 2 или х = 8.
Шаг 7: Подставьте обратно, чтобы получить m.
То есть мы уже видели, что m = 2x — 2 при
любая точка (x, y) касания. Поскольку мы теперь знаем, что
оба x для точек касания, мы можем поместить эти значения
в уравнение для m и получить, что либо
m = 2 или m = 14.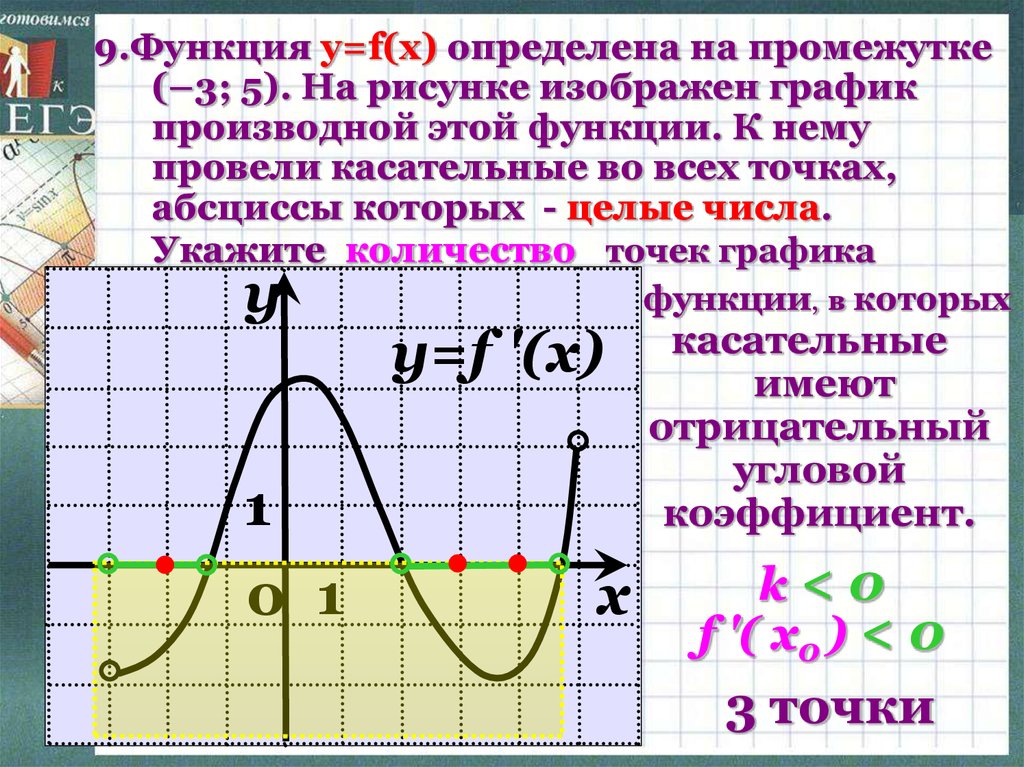 Из уравнения, которое мы имели в
шаг 2,
Из уравнения, которое мы имели в
шаг 2,
у - 7 = 2 (х - 5)и
у - 7 = 14 (х - 5)Когда вы умножаете их и переводите в форму пересечения наклона, уравнения двух прямых, которые касаются y = x 2 — 2x + 1 и проходят через точку (5, 7), являются
у = 2х - 3и
у = 14х - 63и все готово. Кривая и две линии показаны на график справа здесь. Обратите внимание, где две линии пересекаются. Оба точки касания видны на графике, хотя одна из них почти в верхней части графика.
Нажмите здесь, чтобы увидеть альтернативную атаку по этой же проблеме.
Поиск линии
NormalЭто то, что они могут бросить в вас, просто чтобы держать вас в напряжении. Вместо просить уравнение касательной, они спросят вас для уравнение линии, которая нормальная к кривой bloppity-blop в такая-то точка.
Что вы помните из алгебры? Ты
помните, что если две строки нормальный друг к другу (т. е.
они расположены под прямым углом друг к другу), то их наклоны отрицательных обратных величин друг друга? Другими словами, если один
имеет наклон м, то другой должен иметь наклон
-1/м. Можете ли вы расширить это определение, включив в него строку
нормально к кривой? Это всего лишь небольшая вариация правил
мы имели для касательных линий.
е.
они расположены под прямым углом друг к другу), то их наклоны отрицательных обратных величин друг друга? Другими словами, если один
имеет наклон м, то другой должен иметь наклон
-1/м. Можете ли вы расширить это определение, включив в него строку
нормально к кривой? Это всего лишь небольшая вариация правил
мы имели для касательных линий.
- Линия имеет общую точку с рассматриваемой кривой. В общей точке производная кривой является отрицательной
обратным наклону линии.
Давайте возьмем наш пример из предыдущего, где кривая y = x 2 + 1, и нам нужна нормальная линия пройти через (2, 5). Шаг 1 такой же, как до. Это все еще так, у’ = 2х. Однако на шаге 2, после того как мы оценим y'(x) при x = 2 и найдите, что равно 4, вместо того, чтобы присваивать m этому, мы установить m на отрицательное обратное , что равно -1/4.
Остальные шаги такие же. Решите для b с x
и координаты y у вас есть, и m у вас есть только что
определенный.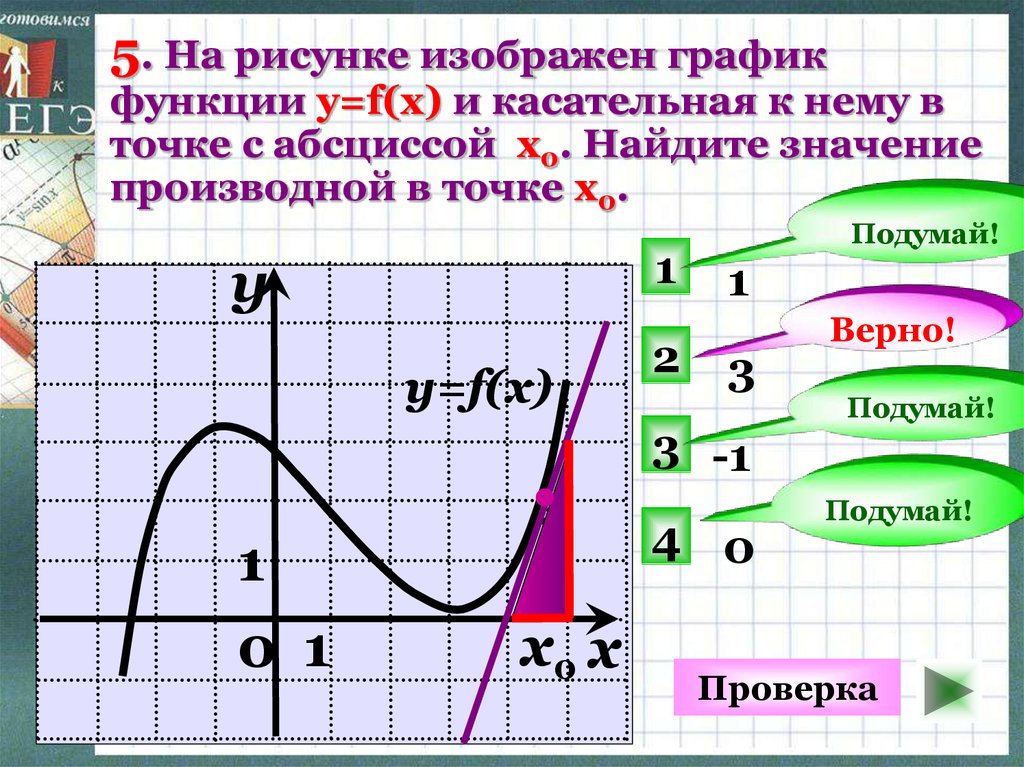 В этом случае имеем:
В этом случае имеем:
5 = (-1/4)×2 + b экв. 4.5-6аи решая для b, мы имеем
б = 5,5 экв. 4.5-6бИтак, ответ здесь
у = (-1/4) х + 5,5 экв. 4,5-7
На рис. 4.5-2 показан график нашей кривой и нормальной линии. к ней в точке x = 2. Обратите внимание, что нормальная линия пересекает нашу кривую в двух местах. В (2, 5) есть пересечение под прямым углом, которое мы ожидали получить. Слева там это еще одно пересечение в точке, которую мы еще не определили. На домашнем задании проблемы или на тесте, вас могут попросить определить это второе пересечение. Но это всего лишь задача по алгебре. Напомним, что найти место пересечения графиков двух функций вам просто
возьмите разность двух функций и найдите x
что делает разницу равной нулю. Наши две функции
у = х 2 + 1 и
у = (-1/4) х + 5,5. |
Вы должны либо иметь для вашей разницы
х 2 + (1/4)х - 4,5 экв. 4.5-7аили негатив этого. Затем описание должно установить это равным ноль и найти х.
x 2 + (1/4)x - 4,5 = 0 экв. 4.5-7бЭто, без сомнения, квадратичный многочлен, и мы имеем квадратичная формула с чем ее решить. Мы получили
_________
-1/4 ± …1/16 + 18
х = экв. 4,5-8
2
Если вы возьмете плюс ±, вы получите
x = 2. И лучше бы одно из решений было x = 2, так как мы уже определили, что это
правая точка пересечения. Если взять минус
±, вы получаете x = -9/4 = -2,25. Подключите это
вернуться к исходному уравнению для кривой, и вы получите
у = 97/16 = 6,0625. Итак, левый перекресток
находится в (-2,25, 6,0625). Вы можете посмотреть на график
чтобы подтвердить это.
Упражнение
Позволять
______
у(х) = Ö1 - х 2 График
это показано на рисунке справа. Вы, наверное, помните из
алгебры, что эта функция имеет график, являющийся полуокружностью. Найди
уравнения как касательной, так и нормальной линии при
х = 0,8. Тогда, не обращаясь к геометрии
полуокружностей, но используя только производные и алгебру, показать, что каждый
линия, нормаль к этой функции, проходит через начало координат независимо от того, в какой точке
на кривой, через которую он проходит.Шаг 1: Найдите производную функции. Вам понадобится за каждый шаг после этого. Обратите внимание, что эта функция является составной. y(x) = f(g(x)), где
_
f(x) = Öx
и
г(х) = 1 — х 2 . Потому что это композит,
вам нужно будет применить
цепное правило, чтобы
найти у'(х). На данный момент я не собираюсь отдавать это
производная — вы должны быть в состоянии сделать это самостоятельно.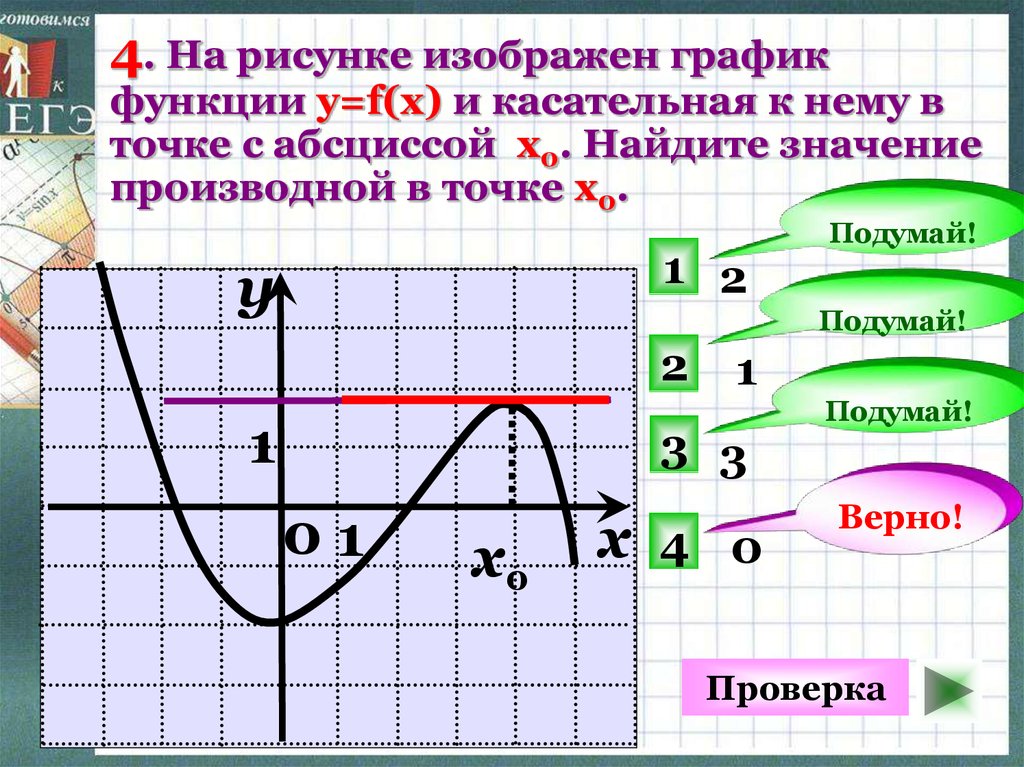 я напомню тебе
что если
я напомню тебе
что если
_
f(x) = Öx
затем
1
f'(х) =
2x
что полезно знать
при нахождении производной от y(x).Шаг 2: Где точка касания? Просто замените x, заданный в задаче, в функцию, чтобы получить значение для у(х). Вам не нужно слишком много думать, потому что я дал это далеко на диаграмме.
Шаг 3: Каков наклон касательной? из обычной линии? Помните, что наклон касательной равен производной функция в точке касания. Так что придерживайтесь значения, данного для x в уравнение, которое у вас есть для y'(x), чтобы найти это значение. Который m для касательной. Это отрицательное взаимное м для обычной линии.
Шаг 4: Найдите b в обоих случаях , то есть
b для касательной линии и b для нормальной линии.
Помните, что теперь вы также знаете букву «м» для них обоих.
как x и соответствующий y.


 В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007.
В. Семенов.
– 4-е изд., доп. – М.: Мнемозина, 2007. А.П.Тряпининой. –
СПб.: КАРО, 2005.
А.П.Тряпининой. –
СПб.: КАРО, 2005.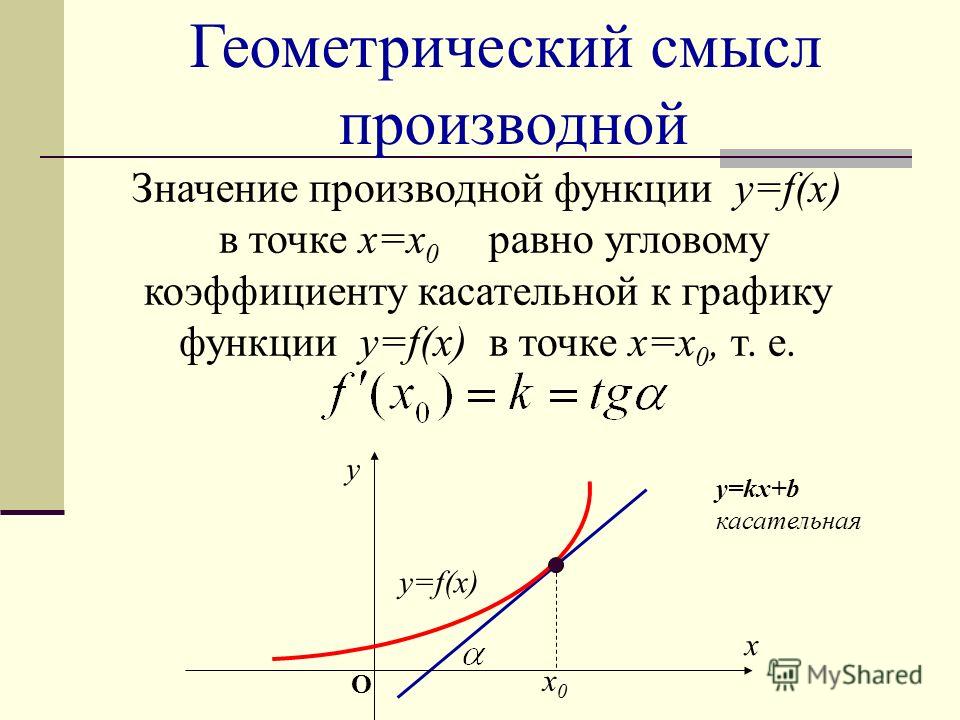 1.Написать
уравнение касательной к графику
функции в точке с абсциссой х0
1.Написать
уравнение касательной к графику
функции в точке с абсциссой х0  5.В каких
точках касательная к графику функции
образует с осью Ох угол в 450?
5.В каких
точках касательная к графику функции
образует с осью Ох угол в 450? 3 Угловой коэффициент касательной,
проведенной к графику функции y =
,в точке (x0, y0) равен
.
Найдите x0, y0.
3 Угловой коэффициент касательной,
проведенной к графику функции y =
,в точке (x0, y0) равен
.
Найдите x0, y0.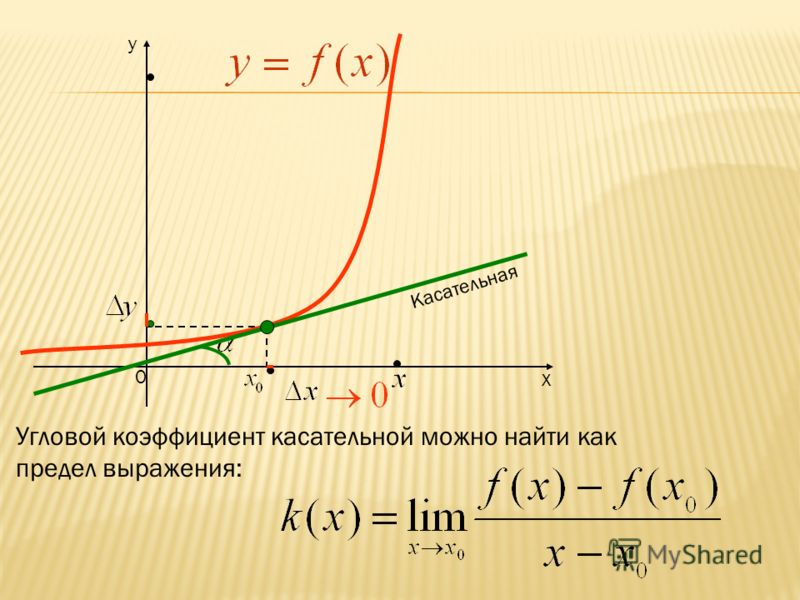
 3. Угловой коэффициент
касательной, проведенной к параболе
3. Угловой коэффициент
касательной, проведенной к параболе  7.Найти
площадь треугольника, образованного
осями координат и касательной к графику
функции у=f(х)
7.Найти
площадь треугольника, образованного
осями координат и касательной к графику
функции у=f(х) )
) 4,5-2
4,5-2
 4.5-4а
4.5-4а
 Действительно, в этой задаче
х 2 + 1 = 4x — 3 = 5, когда
x = 2. Кроме того, вы должны
наклон линии равен y'(x) = 2x = y'(2) = 4
для этой проблемы.
Но этот тест вряд ли может быть провален, так как вы выбрали склон
линии в первую очередь.
Действительно, в этой задаче
х 2 + 1 = 4x — 3 = 5, когда
x = 2. Кроме того, вы должны
наклон линии равен y'(x) = 2x = y'(2) = 4
для этой проблемы.
Но этот тест вряд ли может быть провален, так как вы выбрали склон
линии в первую очередь. Запишите выражение
для разницы между ними, а затем прокрутите вниз.
Запишите выражение
для разницы между ними, а затем прокрутите вниз.