Углы и стороны в треугольниках
85. Построим равнобедренный ∆ABC (чер. 92), у которого AB = BC. Тогда мы знаем, что его углы при основании равны, т. е. ∠A = ∠C. Пронумеруем эти углы, – тогда ∠1 = ∠2. Станем теперь строить новые треугольники ABC’, ABC» и т. д. так, чтобы сторона AB и ∠B оставались неизменными, но сторона BC увеличивалась. Тогда угол A должен увеличиваться (что очевидно), а угол C станет уменьшаться: мы видим, что ∠3 < ∠2, ∠4 < ∠3 и т. д., потому что ∠2 есть внешний угол для ∆ACC’ и, следов., ∠2 > ∠3 или ∠3 < ∠2, также ∠3 есть внешний угол ∆AC’C» и, след., ∠3 > ∠4 или ∠4 < ∠3 и т. д. (уменьшение угла C видно еще из того, что сумма углов треугольника всегда равна 2d: угол B не изменяется, угол A увеличивается, – след., ∠C должен уменьшаться).
Из этих построений мы вправе сделать заключения:
1) Если в треугольнике две стороны равны, то против них лежат равные углы.
2) Если в треугольнике две стороны не равны, то против большей из них лежит и больший угол.
86. Теперь, наоборот, построим: 1) треугольник с двумя равными углами и 2) треугольник с двумя неравными углами и сравним стороны, противолежащие этим углам. Для решения вопросов, здесь возникающих, воспользуемся способом рассуждения, часто употребляемым в математике.
1) Пусть ∆ABC (чер. 93) постоен так, что ∠A = ∠C. Сравнить стороны BC и BA.
Пока, не зная ничего про стороны AB и BC, мы можем сделать об них 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB < BC – иных предположений быть не может. Рассматривая эти предположения, мы можем заметить, что два из них не годятся, так как противоречат предыдущему. В самом деле, 2-е предположение, что AB > BC должно, на основании предыдущего п., повлечь за собою следствие, что ∠C > ∠A, а у нас построено: ∠C = ∠A. Следовательно, это предположение должно быть вычеркнуто. Также из 3-го предположения, что AB < BC следует, что ∠A > ∠C, что также противоречит нашему построению. Следовательно, и это предположение должно быть вычеркнуто.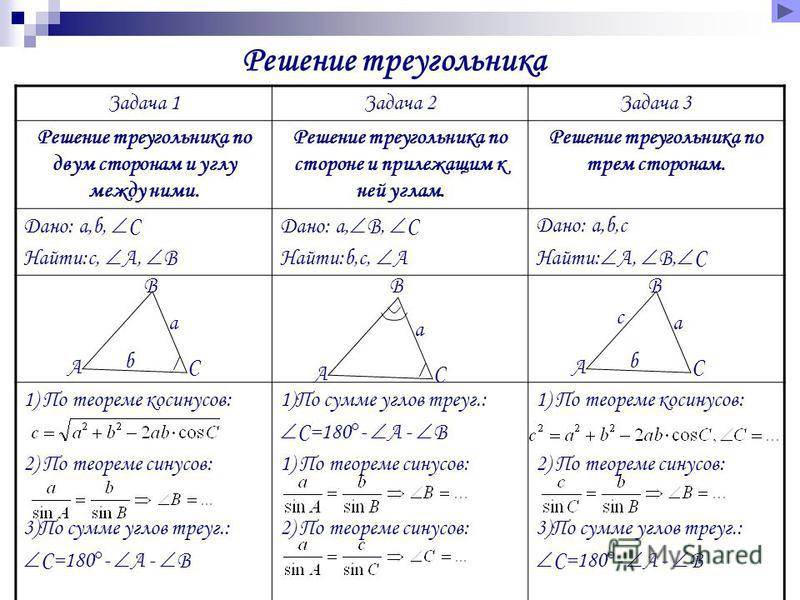
Остается поэтому лишь одно предположение, что AB = BC, которое и должно быть верно, так как иных сделать нельзя. Поэтому имеем:
Если в треугольнике два угла равны, то против них лежат равные стороны.
2) Пусть ∆ABC (чер. 93) постоен так, что ∠A > ∠C. Сравнить стороны BA и BC.
Опять мы можем сделать 3 предположения: 1) AB = BC, 2) AB > BC и 3) AB < BC. Теперь видим, что первое предположение не годится, так как на основании п. 85 из него вытекало бы, что ∠C = ∠A, что противоречит нашему построению; также найдем, что 2-е предположение, что AB > BC не годится, так как из него вытекало бы, что ∠C > ∠A, что противоречит построению. Остается лишь 3-е предположение, что AB < BC, которое и должно быть верно. Поэтому имеем:
Если два угла в треугольнике неравны, то против большего из них лежит большая сторона.
Теперь легко решаются вопросы: 1) какая из сторон прямоугольного треугольника самая большая? 2) Какая из сторон тупоугольного треугольника самая большая?
87.
В двух предыдущих пп. мы имели дело с двумя положениями: 1) против большей стороны лежит больший угол и 2) против большего угла лежит большая сторона. Мы нашли, что эти мысли справедливы для одного треугольника. Возникает вопрос, справедливы ли они для двух треугольников? Несомненно справедливы для двух равных треугольников, так как равные треугольники можно наложением слить в один треугольник. Но, вообще говоря, к двум различным (не равным) треугольникам эти положения не могут быть применимы: мы можем построить два таких треугольника ∆ABC и ∆A’B’C’ (чер. 94), чтобы ∠B был > ∠B’, но AC была бы < A’C’. Чертеж пояснений не требует. Но есть один случай, когда указанные мысли применимы и к двум различным треугольникам).
Этот случай легко уясняется наглядно. Возьмем две палочки AB и BC (чер. 95 bis) и сложим их концами (в точке B). Если вращать палочку BC около точки B по стрелке, то ∠B станет увеличиваться: сторона BC будет менять свое положение (пусть одно из них есть BC’), но все время BC останется равным самому себе; не изменяется также и отрезок AB.
Обратим внимание, что точками A и C определяется еще отрезок AC, на чертеже не изображенный. При вышеуказанном вращении точка C меняет свое место и нам ясно, что этот отрезок AC, не изображенный на чертеже, должен увеличиваться (напр. AC’ > AC), т. е., если 2 стороны треугольника не изменяются, а угол между ними увеличивается, то третья сторона так же увеличивается. В тексте этот случай выяснен без помощи такого наглядного представления.
Построим два таких треугольника, чтобы у них было по две равных стороны, но чтобы углы между ними не были равны. Пусть в ∆ABC и в ∆A’B’C’ (чер. 95) имеем AB = A’B’, BC = B’C’, но ∠B > ∠B’. Сравним стороны AC и A’C’, лежащие против неравных углов. Для этого наложим ∆A’B’C’ на ∆ABC так, чтобы сторона A’B’ совпала с равною ей стороною AB. Тогда сторона B’C’ должна пойти внутри ∠B, потому что ∠B’ < ∠B, но где кончится эта сторона, т. е., где расположится точка C’, неизвестно. Может быть, она расположится как раз на стороне AC, может быть, расположится вне ∆ABC, а может быть внутри этого треугольника.
Разберем эти три случая отдельно.
1) Пусть ∆A’B’C’ расположится так, что займет положение ∆ABD (чер. 96), так что точка C’ попадет в D, на сторону AC; тогда, очевидно, AD < AC или A’C’ < AC (AD есть та же сторона A’C’, только перенесенная в другое место).
2) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 97), т. е. точка C’ расположится в точке D, вне ∆ABC. Тогда, соединив точки C и D, получим ∆BCD, у которого BC = BD, так как, по построению, B’C’ = BC, а BD есть та же сторона B’C’, лишь перенесенная в другое место. Поэтому ∆BCD – равнобедренный, и ∠BCD = ∠BDC. Рассмотрим теперь ∆ACD; про два его угла, а именно про ∠C (или ∠ACD) и про ∠D (или ∠ADC) легко сообразить, пользуясь отмеченными равными углами равнобедренного треугольника, какой из них больше другого. В самом деле, мы видим, что ∠ACD < отмеченного угла BCD при основании равнобедренного треугольника, а ∠ADC > отмеченного угла BDC при основании равнобедренного треугольника. Но ∠BCD = ∠BDC, следовательно, ∠ADC > ∠ACD.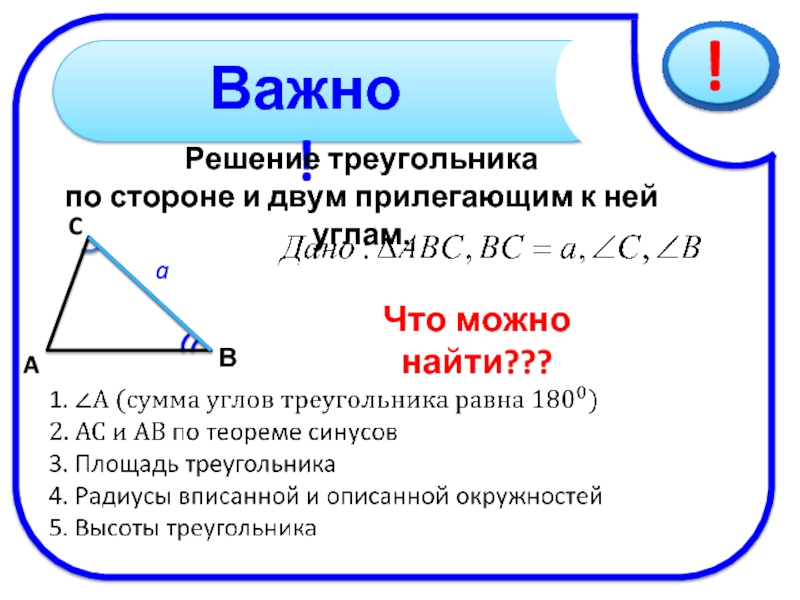
Поэтому на основании п. 86 (применяя его к ∆ACD) имеем AC > AD, но AD есть сторона A’C’, перенесенная в другое место, – следовательно, AC > A’C’.
3) Пусть ∆A’B’C’ при наложении займет положение ∆ABD (чер. 98), т. е. точка C’ расположится внутри ∆ABC. Тогда, соединив точки C и D, получим равнобедренный ∆CBD (BD = BC, ибо BD есть сторона B’C’, перенесенная в другое положение, а B’C’ = BC по построению) и, следовательно, ∠BCD = ∠BDC. Если продолжить стороны BD и BC по направлениям DM и CN, то получим два внешних угла этого равнобедренного треугольника ∠MDC и ∠NCD, но ∠MDC = ∠NCD, следовательно, ∠ADC > ∠ACD, а поэтому, на основании п. 86, имеем AC > AD, или AC > A’C’ (AD есть сторона A’C’, перенаправленная в другое положение).
Итак, во всех трех случаях оказалось, что
AC > A’C’,
т. е., если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, но углы между ними не равны, то против большого угла лежит большая сторона.
88. Разберем обратный вопрос. Пусть построены ∆ABC и ∆A’B’C’ (чер. 95) так, что AB = A’B’, BC = B’C’, но AC > A’C’, т. е. два треугольника имеют по две равных стороны, но третьи стороны их не равны. Сравнить ∠B и ∠B’.
Воспользуемся тем же способом рассуждения, как в п. 86.
Пока мы можем об углах B и B’ сделать три предположения: 1) ∠B = ∠B’, 2) ∠B > ∠B’ и 3) ∠B < ∠B’.
Первое предположение не годится, так как тогда наши треугольники, имея по построению по две равных стороны и равные углы между ними, были бы равны, и, следовательно, AC’ = A’C’, а это противоречит построению. Третье предположение, что ∠B < ∠B’ также не годится, так как тогда к этим треугольникам был бы применим результат, найденный в предыдущем п., на основании которого имели бы AC < A’C’, что также противоречит построению. Остается второе предположение, что ∠B > ∠B’, которое и должно быть верно. Итак:
Если две стороны одного треугольника равны соответственно двум сторонам другого, но третьи стороны этих треугольников не равны, то против большей стороны лежит и больший угол.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Фигура | Рисунок | Формулировка |
| Треугольник | Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. | |
| Большая сторона треугольника | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| | ||
| Углы треугольника | Сумма углов треугольника равна 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство | |
| Больший угол треугольника | Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. | |
| Меньший угол треугольника | Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. | |
| Теорема косинусов | a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство | |
| Теорема синусов | , где R – радиус описанной окружности. Посмотреть доказательство |
| Треугольник | |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. | |
| Большая сторона треугольника | |
| Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | |
| Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | |
| Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | |
| Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c | |
Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| | |
| Углы треугольника | |
Сумма углов треугольника равна 180° Посмотреть доказательство | |
| Внешний угол треугольника | |
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство | |
| Больший угол треугольника | |
Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. | |
| Меньший угол треугольника | |
Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. | |
| Теорема косинусов | |
a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство | |
| Теорема синусов | |
, где R – радиус описанной окружности. Посмотреть доказательство | |
| Треугольник |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки. Определение. Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков – вершинами треугольника. |
| Большая сторона треугольника |
Свойство большей стороны треугольника: Против большей стороны треугольника лежит больший угол |
| Больший угол треугольника |
Свойство большего угла треугольника: Против большего угла треугольника лежит большая сторона |
| Меньшая сторона треугольника |
Свойство меньшей стороны треугольника: Против меньшей стороны треугольника лежит меньший угол |
| Меньший угол треугольника |
Свойство меньшего угла треугольника: Против меньшего угла треугольника лежит меньшая сторона |
| Длины сторон треугольника |
Неравенства трегольника: Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника меньше суммы длин двух других сторон. a < b + c Длины сторон треугольника удовлетворяют неравенству треугольника: длина любой стороны треугольника больше модуля разности длин двух других сторон. a > |b – c| |
| Углы треугольника |
Свойство углов треугольника: Сумма углов треугольника равна 180° Посмотреть доказательство |
| Внешний угол треугольника |
Свойство внешнего угла треугольника: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним. δ = α + β . Посмотреть доказательство |
| Больший угол треугольника |
Свойство большего угла треугольника: Величина большего угла треугольника не может быть меньшей, чем 60°. , где α – больший угол треугольника. |
| Меньший угол треугольника |
Свойство меньшего угла треугольника: Величина меньшего угла треугольника не может быть большей, чем 60°. , где β – меньший угол треугольника. |
| Теорема косинусов |
Теорема косинусов: a2 = b 2 + c 2 – 2bc cos α , Посмотреть доказательство |
| Теорема синусов |
Свойство меньшего угла треугольника: , где R – радиус описанной окружности. Посмотреть доказательство |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Самаров
Правила треугольника — стороны, углы, внешние углы, градусы и другие свойства
Калькулятор треугольника (Этот бесплатный онлайн-инструмент позволяет вычислить все измерения сторон и углов на основе введенных вами данных и нарисовать бесплатно загружаемое изображение вашего треугольника!)
Рабочие листы треугольника 90 $$
Правило 2: Стороны треугольника — Теорема о неравенстве треугольника: Эта теорема утверждает, что сумма длин любых двух сторон треугольника должна быть больше третьей стороны. )
Правило 3: Соотношение между измерением сторон и углов в треугольнике: Наибольший внутренний угол и сторона лежат друг против друга. Это же правило относится и к наименьшему размеру. угол и сторона, а средний угол и сторона.
Правило 4 Удаленные внешние углы. Эта теорема утверждает, что мера внешнего угла $$ \angle A$$ равна сумме измерений удаленных внутренних углов.
еще) Чем отличаются внутренние и внешние углы треугольника?
На этот вопрос отвечает картинка ниже. Вы создаете внешний угол, продолжая любую сторону треугольника.
9{\circ} $$.Чтобы проверить истинность этого правила, попробуйте интерактивный треугольник Math Warehouse, который позволяет вам перетаскивать разные стороны треугольника и исследовать взаимосвязь между углами и стороны. Независимо от того, как вы расположите три стороны треугольника, сумма градусов всех внутренние углы (три угла внутри треугольника) всегда равны 180°.
Это свойство внутренних углов треугольника является просто частным примером общее правило для внутренних углов любого многоугольника.
Внутренние углы треугольника (рабочий лист)
Интерактивная демонстрация внутренних углов
| ∠ А | |
| ∠ Б | |
| ∠ С | |
| Итого | 180 |
|---|
Перетащите точки треугольника, чтобы начать демонстрацию
Практические задачи (правило внутренних углов)
Проблема 1
Чему равен m$$\angle$$LNM в приведенном ниже треугольнике?
$$ \угол $$ LMN = 34°
$$ \угол $$ MLN = 29°
Используйте правило для внутренних углов треугольника:
м$$ \угол $$ LNM +m$$ \угол $$ LMN +m$$ \угол $$ MLN =180°
м$$ \угол $$ LNM +34° + 29° =180°
м$ $ \угол $$ LNM +63° =180°
м$$ \угол $$ LNM = 180° — 63° = 117°
Проблема 2
Внутренние углы треугольника равны $$ \angle $$ HOP, $$ \angle $$ HPO и $$ \angle $$ PHO.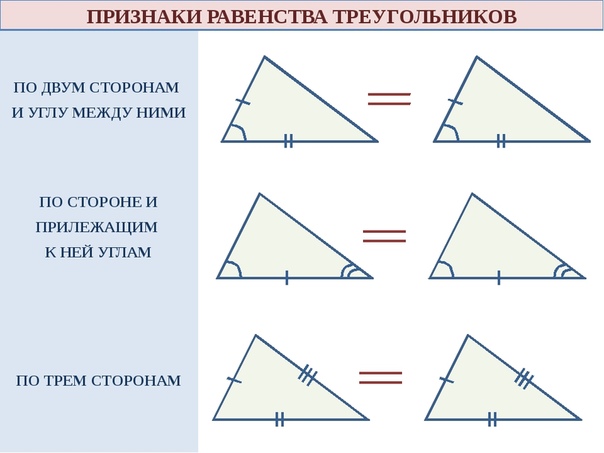
Что такое m$$ \angle $$ PHO?
Использовать внутренние углы правила треугольника:
м$$ \угол $$ PHO = 180° — 26° -64° = 90°
Взаимосвязь — Измерения сторон и углов
В любом треугольнике
- наибольший внутренний угол равен против наибольшей стороны
- наименьший внутренний угол против наименьшая сторона
- внутренний угол среднего размера равен напротив средняя сторона
Чтобы проверить истинность утверждений, вы можете использовать интерактивный треугольник Math Warehouse, который позволяет вам перетаскивать разные стороны треугольника и исследовать отношения между мерами углов и стороны. Независимо от того, как вы расположите три стороны треугольника, вы обнаружите, что утверждения в параграфе выше верны.
(Хорошо, равнобедренный и равносторонний треугольник являются исключениями из-за того, что у них нет ни одного наименьшего
сторона или, в случае равностороннего треугольника, даже наибольшая сторона.
Рабочий лист по взаимосвязи между длинами сторон и измерениями углов треугольника
Калькулятор треугольника (Этот бесплатный онлайн-инструмент позволяет вычислить все измерения сторон и углов на основе введенных вами данных и нарисовать бесплатно загружаемое изображение вашего треугольника!)
Рабочие листы треугольника
Удаленные, внешние и внутренние углы треугольника
Удаленный, внешний вид, внутренний рабочий лист Бесплатный PDF
Что такое удаленный и внутренний углы?
Это все о расширении стороны треугольникаВнешний угол треугольника или любой многоугольник, образованный расширением одной из сторон.
В треугольнике каждый внешний угол имеет два
удаленные внутренние углы. Удаленные внутренние углы — это всего лишь два угла, которые находятся внутри
треугольник и противоположный от внешнего угла.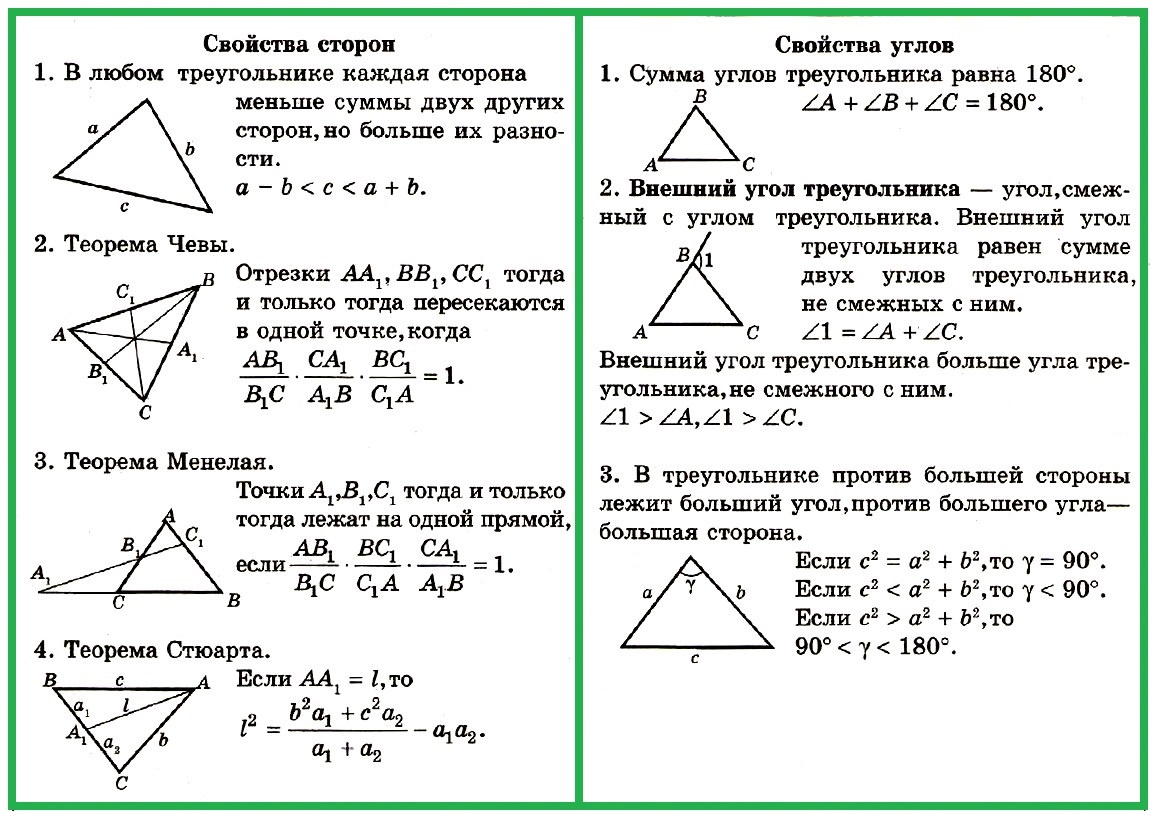
Формула
Как видно из рисунка выше, формула для дальнего и внутреннего углов гласит, что мера внешнего угла $$ \angle A $$ равна сумме удаленных друг от друга внутренних углов.
Перефразируя, угол «вне треугольника» (внешний угол A) равен D + C (сумма удаленных внутренних углов).
Интерактивная демонстрация удаленных и внешних углов
Интерактивная программа ниже позволяет вам перетаскивать точки треугольник вокруг. Обратите внимание, что сумма удаленных внутренние углы (C и D) равны внешнему углу A.
∠ С =
∠ Д =
∠ А =
Выберите удаленные углы C и DC и BB и DПеретащите точки треугольника, чтобы начать демонстрацию
Практические задачи
Проблема 1
Используйте формулы, описанные на этой странице, для расчета значений x (дальнего внутреннего угла) и Y.