«Свойства углов, образованных при пересечении двух параллельных прямых секущей»
Тема урока:
« Свойства углов, образованных при пересечении двух параллельных прямых секущей»
Подготовила: Н.И. Натальченко
г. Лиман
Донецкая область
Тема: « Свойства углов, образованных при пересечении двух параллельных прямых секущей
Зашифрованное название темы.
Каждой букве соответствует ее порядковый номер в алфавите
(19,3,16,11,19,20,3,1 21,4,13,16,3 16,2,18,1,9,16,3,1,15,15,29,23 17,18,10 17,6,18,6,19,6,25,6,15,10,10 5,3,21,23 17,1,18,1,13,13,6,13,30,15,29,23 17,18,33,14,29,23 19,612,21,27,6,11)
Цель:
закрепить и обобщить знания учащихся о свойствах углов образованных при пересечении параллельных прямых и секущей
Задачи:
Обучающие:
повторить понятие, свойство смежных и вертикальных углов, параллельных прямых; отработать навыки нахождения накрест лежащих, односторонних и соответственных углов;
Развивающие:
активизировать познавательную деятельность учащихся; развивать логическое мышление, умения анализировать, сравнивать, обобщать, выделять главное, делать выводы; развивать быстроту реакции, развивать память; развивать умения и навыки применять математические знания к решению практических задач;
Воспитательные:
воспитывать у учащихся интерес к познанию геометрии; воспитывать аккуратность построений геометрических рисунков; культуру речи и культуру общения; воспитывать самостоятельность, волю и настойчивость, уверенность в своих силах, стремление к достижению результата.
Тип урока: урок обобщения и систематизации знаний, умений, навыков.
Оборудование:
Компьютер, мультимедийный проектор, экран, презентация в программе Power Point, индивидуальный раздаточный материал для учащихся (карточки с заданиями) и для работы в парах.
ХОД УРОКА
I. Организационный момент
Эпиграфом нашего сегодняшнего урока хотелось бы взять такое четверостишье:
Да, путь познания не гладок!
Но знаем мы со школьных лет
Загадок больше чем отгадок
И поискам предела нет!
На сегодняшнем уроке, мы с вами должны вспомнить ранее пройденный материал и продолжить решать задания на нахождение углов при параллельных прямых.
II. Проверка домашнего задания
Домашнее задание проверяем устно. Из ответов полученных при решении домашних заданий с помощью алфавита ищем зашифрованное слово.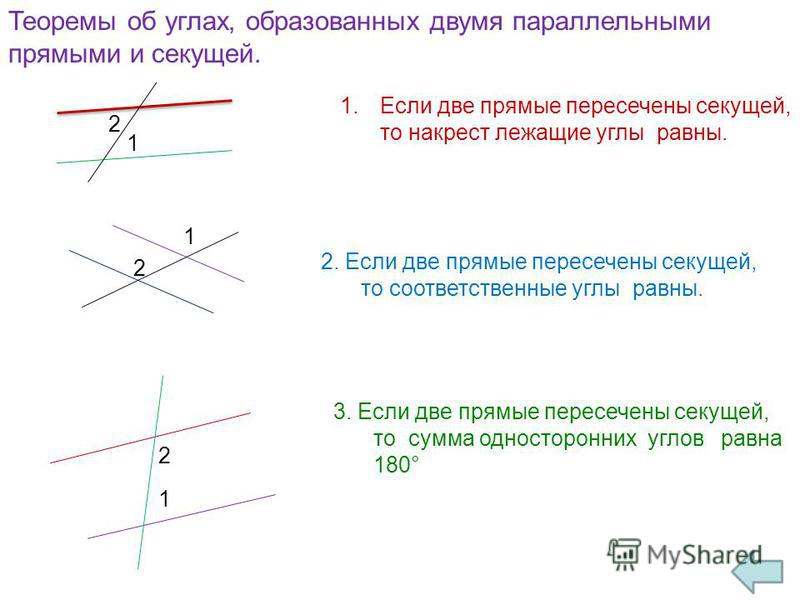
1.Какой угол образует с углом ∟11 внутренние накрестлежащие углы? (14)
2. Какой угол соответственный углу ∟12?(16)
3. Какой угол вертикален углу ∟16? (13)
4. ∟14 =… (16)
5. Угол ∟4 и ∟? — называются внутренние односторонние углы. (5)
6. (∟15 — ∟8)*8 =…(24)
7. ∟2+∟10=…(29)
14,16,13,16,5,24,29 слово – МОЛОДЦЫ
III. Актуализация опорных знаний
ПАЗЛЫ
Глядя на рисунок, заполните таблицу.
Углы | Свойство углов | Название углов |
1,4 | Равны между собой | вертикальные |
4,6 | Их сумма равна 180 ͦ только при параллельных прямых | Внутренние односторонние |
4,5 | Равны только при параллельных прямых | Внутренние накрестлежащие |
5,6 | Их сумма равна 180 ͦ | смежные |
2,6 | Равны только при параллельных прямых | соответственные |
| Один из углов в 2 раза больше другого | Внешние накрестлежащие |
| Их сумма равна 90 ͦ | Внешние односторонние |
Физкульт.
Минутка
Знают угол все, все, все на этой планете.
Кто не знает, показать можем людям этим.
Раз- прямой, (присели)
Два- тупой, (наклон влево, вправо)
Третий – острый, вот такой. (наклон вперед до колен)
А четвертый угол класс!
Мы покажем вам сейчас. ( стали на пальчики подняв руки вверх)
Это угол 60ͦ, все выходит у ребят.
Вот такие вот углы на уроке нам нужны.
Подровнялись, тихо сели.
Все на доску посмотрели.
IV. Закрепление знаний, умений, навыков
Решение задач
1. По данным рисунка найдите угол x
V. Самостоятельная работа.
Карточка №1 (низкий, средний уровни)
Дано:
аІІв, с – секущая
∟2 = 138 ͦ
Найти : ∟6 — ?
Карточка №2 (низкий, средний уровни)
Дано:
аІІв, с – секущая
∟5 = 40 ͦ
Найти : ∟3, ∟4 — ?
Карточка №3 (достаточный уровень)
Дано:
аІІв, с – секущая
∟2>∟1 в 2 раза
Найти : ∟6 — ?
Карточка №4 (достаточный уровень)
Дано:
аІІв, с – секущая
∟4+∟5 =68 ͦ
Найти : ∟5,∟6 — ?
Карточка №5 (достаточный уровень)
Дано:
аІІв, с – секущая
∟3>∟5в 4 раза
Найти : ∟2 , ∟5- ?
VІ.
Домашнее задание Повторить п.4-8 решить задание на листочках.
Начальный уровень
1. Разница двух с восьми углов, образовавшихся при пересечении двух параллельных прямых секущей, равен 54° . Найдите каждый из восьми углов.
Средний уровень
2. Секущая пересекает две данные прямые; при этом образовались внутренние односторонние углы, разность которых равен 108°, а отношение — 4 : 1. Докажите, что данные прямые параллельны.
Достаточный уровень
3. Отрезки AB и CD есть параллельными и ровными. Докажите, что Δ ABC = Δ DCB, если отрезки AD и BC пересекаются
Высокий уровень
4. Через точки A и B, что лежат на сторонах тупого угла AOB, проведены прямые, параллельные сторонам данного угла и пересекающиеся в точке C. Найдите угол AOB, если прямые AC и BC пересекаются под углом 40°.
VІІ. Итог урока
Я предлагаю поиграть в игру «Верю – не верю» и проверить хорошо ли вы усвоили, какими свойствами наделены углы
1.
2. Если мне надо доказать, что прямые параллельны – я вспоминаю свойства углов образованных при пересечении параллельных прямых и секущей.
3. Через точку, которая не належит прямой, можно провести множество параллельних ей прямых.
4.Если в результате пересечения параллельных прямых с секущей образовались два угла по 80º. Могут ли они быть:
соответственными;
внутренними односторонними;
мне нужно доказать, что две прямые параллельны – я вспоминаю признаки параллельности прямых.
5. Если один из соответственных углов острый, то другой тупой.
6. Если один из внутренних односторонних углов острый, то другой тупой.
7. Если сумма внутренних накрестлежащих углов140º, то один из них 70º.
VІІІ. Рефлексия
У вас на партах лежат наборы смайликов. Какой из них подходит вашему настроению тот и бросьте при выходе из класса в почтовый ящик на двери.
Углы при пересечении двух прямых третьей прямой (секущей). Виды углов урок 5. Геометрия 7 класс
12+
6 месяцев назад
Математика от Баканчиковой300 подписчиков
Геометрия 7 класс. Сколько углов получается при пересечении 2-х прямых третьей (секущей)? Как называются эти углы, как их запомнить находить на разных рисунках? Сегодня на 5 уроке про виды углов мы ответим на эти вопросы. А чтобы Вы лучше и быстрее запомнили новый материал, сначала мы поясним Вам, что такое секущая, и как она расположена. Затем напомним Вам об углах, которые получаются при пересечении двух прямых или углов «в паре»: вертикальных и смежных. Подробно мы остановимся на 5 видах углов: внутренние односторонние, внешние односторонние, внутренние накрест лежащие, внешние накрест лежащие и соответственные. Объясним, почему они так называются, и дадим подсказки, как их находить. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:32 Что такое секущая?
02:31 Сколько углов получается при пересечении 2-х прямых третьей?
03:29 Вспомним углы, получающиеся при пересечении 2-х прямых.
04:27 Внутренние односторонние углы.
05:59 Внешние односторонние углы.
06:53 Внутренние накрест лежащие углы.
07:52 Внешние накрест лежащие углы.
08:45 Соответственные углы.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки по геометрии, то рекомендуем Вам посмотреть следующие видео:
Геометрия 7 класс. Основные понятия и фигуры геометрии. Их компоненты. https://rutube.ru/video/321ccc54b501c6dbc235d9b52b266abb/
Геометрия 7 класс. Взаимное расположение прямых на плоскости. Перпендикулярные прямые. Примеры построения перпендикулярных прямых. https://rutube.ru/video/c46955ce83ccef0dee45f4c72fc2583e/
Свойства биссектрисы равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника. Геометрия 7 класс. https://rutube.ru/video/2a2b7dfc5b44830f209dc9cc4e28d2f7/
Геометрия 7 класс.
Треугольники. Признаки равенства треугольников. Урок 3. https://rutube.ru/video/0339e0588490b1b5ca732547aac3ec06/
Геометрия 7 класс. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач на свойства медианы и биссектрисы. Урок 5.
https://rutube.ru/video/3c88c497ce7a312249ea9e2b770fb8b1/
Геометрия 7 класс. Треугольники. Высота треугольника. Определение, свойства, точки пересечения высот. Примеры построения. Урок 6. https://rutube.ru/video/575bead43e6717ec773788d15e7380c1/
Геометрия 7 класс. Вертикальные углы. Определение. Доказательство теоремы о свойстве вертикальных углов. Виды углов урок 3. https://rutube.ru/video/10ca7111475a4f1a6dbe6b67fd71588c/
Геометрия 7 класс. Смежные углы. Определение. Свойства. Примеры задач на свойство смежных углов. Виды углов урок 2. https://rutube.ru/video/f12d3379fb0751e037c1f1bede88805f/
Что такое обратная и прямая теоремы. Примеры обратных и прямых теорем. Геометрия 7 класс. https://rutube.ru/video/f72250e5edd8eeed8948bd0664a23692/
Доказательство теорем методом «от противного».
Параллельность прямых на плоскости. Геометрия 7 класс. https://rutube.ru/video/d4f7b6c064dd143c73b738ebe92373dd/
#Геометрия7класс #углыприпересечениидвухпараллельныхпрямых #углыприпересечениидвухпрямыхтретьей #углыприпересечениидвухпрямыхсекущей #углыприпересечениидвухпараллельныхпрямыхсекущей #углыприпересечениидвухпараллельныхпрямыхтретьей #соответственныеуглыприпересечениидвухпрямых #найдитеуглыобразованныеприпересечениидвухпрямых #углыобразованныеприпересечениидвухпрямыхсекущей #накрестлежащиеодносторонниеисоответственныеуглы #внутренниеодносторонниеуглы #внешниеодносторонниеуглы #внутренниенакрестлежащиеуглы #внешниенакрестлежащиеуглы #соответственныеуглы #секущаянакрестлежащиеуглы #односторонниеуглыприпараллельных #односторонниеуглырисунок #соответственныеуглыприпересечениипрямых #соответственныеуглырисунок #накрестлежащиеуглырисунок #МатематикаОтБаканчиковой
Геометрия 7 класс, углы при пересечении двух параллельных прямых, углы при пересечении двух прямых третьей, углы при пересечении двух прямых секущей, углы при пересечении двух параллельных прямых третьей, соответственные углы при пересечении двух прямых, углы образованные при пересечении двух прямых секущей, накрест лежащие односторонние и соответственные углы, внутренние односторонние углы, внешние односторонние углы, внутренние накрест лежащие углы, внешние накрест лежащие углы, соответственные углы, секущая накрест лежащие углы, односторонние углы при параллельных, односторонние углы рисунок, соответственные углы при пересечении прямых, соответственные углы рисунок, накрест лежащие углы рисунок
Пересекающиеся линии и углы — SAT Mathematics
Все ресурсы SAT по математике
137 Практические тесты Вопрос дня Карточки Learn by Concept
SAT Mathematics Help » Треугольники, линии и углы » Пересекающиеся линии и углы
На приведенном выше рисунке линия a параллельна линии b , а линия d параллельна линии e .
Сколько стоит и , в градусах?
Возможные ответы:
25
10
15
30
Правильный ответ:
15
Пояснение:
Пересекающиеся и параллельные линии встречаются во множестве различных геометрических фигур: параллелограммах, трапециях, квадратах и т. д. Всякий раз, когда вы видите их в вопросе, вы должны правильно использовать основные свойства дополнительных и вертикальных углов. В этой задаче самый быстрый способ найти y — понять, что 5x в левом нижнем углу является дополнительным к 2x + 5 в правом нижнем углу (из-за пересечения двух параллельных прямых). Следовательно, 5x + 2x + 5 = 180 и x = 25. Получив эту информацию, вы можете использовать тот факт, что сумма внутренних углов треугольника равна 180, и увидеть, что x + 5x + 2y = 180. Подставляя вместо x 25, вы видите, что 25+125+2y = 180 и 2y = 30.
Правильный ответ 15.
Сообщить об ошибке
На рисунке выше . Что из следующего должно быть правдой?
I.
II. Две горизонтальные линии параллельны.
III.
Возможные ответы:
Только I и II
Только II и III
I, II и III
Только I и III
Правильный ответ:
Только I и II
Объяснение:
Здесь SAT дает вам пару прямых с секущей, но не говорит вам, что прямые параллельны — он просит вас это доказать. Вам это говорят. Поскольку угол и угол являются вертикальными углами, а углы и являются вертикальными углами, вы знаете, что и . Это означает, что вы можете написать уравнение как:
, или
Если это означает и это. Прямая линия содержит 180 градусов, так что вы это знаете . И так как , вы можете заключить, что также.
Отсюда вы можете реконструировать то же самое уравнение, которое вы решили с первым набором углов. Если и и являются вертикальными углами, а и являются вертикальными углами, вы можете заключить, что . Оттуда вы можете настроить уравнение . Утверждение I верно.
Чтобы горизонтальные линии были параллельны, необходимо знать, что либо альтернативные внешние углы, либо альтернативные внутренние углы равны. Поскольку вы это уже доказали, вы знаете и это. Поскольку у вас есть пара альтернативных внешних углов, две прямые должны быть параллельны. Утверждение II также верно.
Утверждение III, однако, не обязательно верно. Если тогда все углы были бы равны 90. Однако без этого знания вы не можете прийти к каким-либо выводам о взаимосвязи между и . Утверждение III не обязательно верно, поэтому правильным ответом будет только I и II.
Сообщить об ошибке
Две пересекающиеся прямые образуют углы, указанные выше. Если мера угла x в три раза больше угла y, то какова мера угла z?
Возможные ответы:
60
45
120
135
Правильный ответ:
135 9 0005
Объяснение:
Поскольку линии x и y в сумме дают 180 градусов, у вас есть два уравнения для работы:
x + y = 180
x = 3y
Это означает, что вы можете заменить 3y на x в порядке найти у:
3у + у = 180
4у = 180
у = 45
А так как z также в сумме с y дает 180, то z должно быть 180 — 45 = 135 градусов.
Сообщить об ошибке
Если на рисунке выше прямые g и k параллельны, а угол h равен 121 градусу, каково значение p?
Возможные ответы:
59
71
49
61
Правильный ответ:
59
Объяснение:
Если h равно 121, то угол непосредственно под h должен быть равен 59, так как это дополнительный угол, образованный диагональной линией. Поскольку g и k параллельны, этот угол в 59 градусов должен точно соответствовать p, поскольку они являются альтернативными внутренними углами.
Сообщить об ошибке
На приведенном выше рисунке прямые AD и BE пересекаются в точке C. Чему равен угол ACE?
Возможные ответы:
145
115
125
135
Правильный ответ: 90 005
125
Объяснение:
Два правила углов очень важны для этого вопроса:
1) Сумма внутренних углов треугольника всегда равна 180.
Здесь, поскольку у вас есть угол 90 градусов (CED) и угол 35 градусов (EDC) в нижнем треугольнике, тогда можно заключить, что угол ECD должен быть равен 55.
2) Дополнительные углы, смежные углы при пересечении двух прямых, должны в сумме давать 180 градусов. Если вы знаете, что ECD равно 55, то ACE как дополнительный угол должен образовывать остальные 125 градусов, чтобы сумма этих двух углов составила 180. Следовательно, правильный ответ — 125.
Сообщить об ошибке
Что такое a + b + c + d?
Возможные ответы:
110
130
120
150
Правильный ответ: 90 005
150
Объяснение:
В этой задаче важно понимать, что вы имеете дело с двумя пересекающимися треугольниками, которые образуют внешние дополнительные углы вдоль прямой линии внизу. Чтобы убедиться в этом, рассмотрите приведенную ниже диаграмму, для которой добавлены углы x и y:
Угол y является внешним дополнительным углом к треугольнику рядом с ним, поэтому y = a + c.
Почему? Помните, что y является дополнительным к углу рядом с ним (x + 30), а (a + c) является дополнительным к тому же самому углу (сумма внутренних углов треугольника = 180). Следовательно, y и (a + c) идентичны. . Всякий раз, когда у вас есть прямая линия, проведенная из треугольника, вы должны понимать, что внешний дополнительный угол равен сумме двух противоположных углов.
Используя ту же логику, вы можете увидеть, что x = b + d в другом пересекающемся треугольнике. Поскольку проблема заключается в том, чтобы задать a + b + c + d, вы должны признать, что этот вопрос на самом деле такой же, как и вопрос о том, что такое x + y. Почему? Вы можете заменить x на b + d и y на a + c в основе вопроса. Так как x + y = 180 — 30 на прямой внизу, правильный ответ 150.
Обратите внимание, что еще один способ решить эту задачу состоит в том, чтобы увидеть два больших тупоугольных треугольника: один с углами a, c и (x+30), а другой с углами b, d и (y+30). Если вы сделаете это, у вас будет:
a+c+x+30=180, поэтому a+c+x=150
b+d+y+30=180, поэтому b+d+y= 150
И вы знаете, что x+y+30=180, потому что x, 30 и y — это все углы, которые составляют прямую линию в 180 градусов, проходящую через нижнюю часть рисунка.
Итак, х+у=150.
Затем можно суммировать уравнения треугольника:
a+c+x+b+d+y=150+150=300
А затем подставьте x+y = 150, и у вас останется a+b+c+d=150.
Сообщить об ошибке
На изображении выше . Каково значение
Возможные ответы:
70
60
80
50
Правильный ответ:
60
Пояснение:
Эта задача основана на двух важных правилах геометрии:
1) Сумма всех внутренних углов треугольника равна 180. Здесь вы знаете, что в верхнем треугольнике углы равны 30 и 80, а это означает, что угол при точка пересечения линий должна быть равна 70, так как 30+80=110, а сумма последнего угла должна равняться 180.
2) Вертикальные углы — углы, противоположные друг другу при пересечении двух прямых — равны. Поскольку вы определили, что угол в основании треугольника наверху равен 70°, это также означает, что верхний, непомеченный угол нижнего треугольника равен 70°.
Это позволяет добавить 70+50+ в качестве трех углов в нижний треугольник, а так как их сумма должна равняться 180, это означает, что .
Сообщить об ошибке
ПРИМЕЧАНИЕ. Рисунок выполнен не в масштабе.
Какое значение на рисунке выше?
Возможные ответы:
115
135
150
125
Правильный ответ: 90 005
135
Объяснение:
В этой задаче сильно используются два правила:
1) Сумма углов треугольника равна 180.
2) Дополнительные углы — смежные углы, образующиеся при пересечении одной прямой другой — должны в сумме давать 180.
Здесь вы можете сначала использовать угол в 140 градусов, чтобы указать, что его соседний сосед — его дополнительный партнер — должен быть равен 40. Это дает вам два из трех углов в самом верхнем треугольнике: 20 и 40.
Вы можете использовать чтобы определить, что третий угол должен быть равен 120.
Отсюда вы должны увидеть, что угол в 120 градусов является вертикальным углом, а это означает, что его противоположность также будет равна 120. И это дает вам второй угол в нижний правый треугольник. Знание того, что у вас есть углы 15 и 120, означает, что третий угол этого треугольника должен быть равен 45. А поскольку этот угол является дополнительным к углу x, тогда x должен быть равен 135.
Сообщить об ошибке
На рисунке выше линии и параллельны. Какова ценность ?
Возможные ответы:
95
125
105
115
Правильный ответ: 900 05
125
Объяснение:
Эта задача сильно зависит от двух важных правил для прямых и углов:
1) Сумма трех внутренних углов треугольника всегда равна 180.
2) Дополнительные углы — углы рядом друг с другом, образованные двумя пересекающимися линиями — также должны в сумме давать 180. нижний правый угол маленького треугольника вверху, вы можете закрыть этот треугольник. Для углов 40° и 85° это означает, что нижний левый угол должен быть равен 55°.
Отсюда вы можете использовать тот факт, что параллельные линии приведут к конгруэнтным углам. Поскольку прямые и параллельны, угол рядом с будет равен 55 градусам, а это означает, что будет равен 125.
Сообщить об ошибке
На диаграмме выше линии и все пересекаются в точке A. Если и , каково значение ?
Возможные ответы:
20
50
30
40
Правильный ответ:
30
Объяснение:
Эта задача проверяет два важных правила. Во-первых, угловая мера прямой линии равна 180.
Здесь, если вы проследите за линией, вы увидите, что ее угол разбит на три сегмента: и пустой угол между ними. Сумма этих трех углов должна равняться 180, поэтому, если вы уже знаете, что и , тогда неотмеченный угол между ними должен быть равен так что .
Далее, знайте, что когда линии пересекаются, образуя углы в определенной точке, противоположные (вертикальные) углы конгруэнтны. Угол измерения прямо противоположен углу, который вы только что рассчитали в градусах, поэтому должен быть таким же.
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по математике SAT
137 Практические тесты Вопрос дня Карточки Learn by Concept
Угол между двумя линиями — Infinity Learn
Угол, образованный двумя линиями Полезно понимать взаимосвязь между двумя линиями. Это будет угол наклона между двумя линиями. Есть два угла, образованных двумя пересекающимися прямыми: острый угол и тупой угол.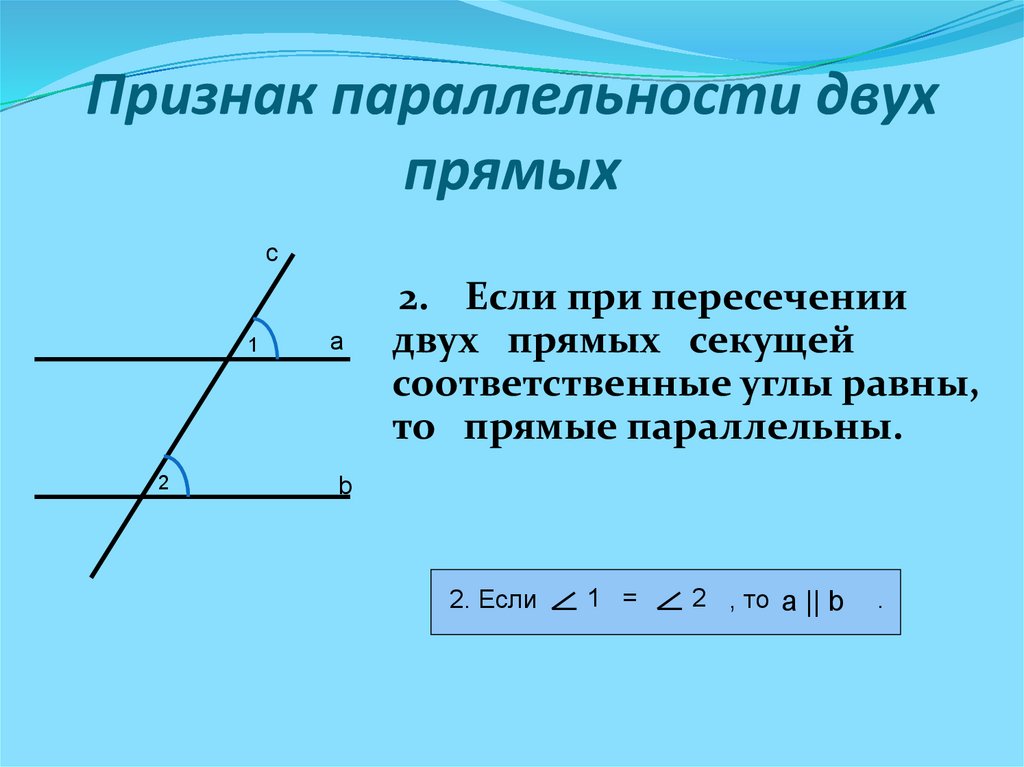
При пересечении двух прямых образуются два набора углов. Пересечение образует два острых и два тупых угла. Абсолютные значения образующихся углов определяются наклонами пересекающихся линий. Мы учитываем острый угол между двумя линиями при вычислении угла между ними. Мы могли бы использовать угол, образованный двумя линиями, для вычисления угла, образованного двумя сторонами замкнутого многоугольника.
Также стоит отметить, что угол, образованный пересечением двух прямых, не может быть рассчитан, если одна из прямых параллельна оси y, потому что наклон линии, параллельной оси y, не определен.
Зарегистрируйтесь, чтобы получить индивидуальный план обучения, который поможет вам улучшить свои результаты!
Класс
—Класс 6Класс 7Класс 8Класс 9Класс 10Класс 11Класс 12
Целевой экзамен
JEENEETCBSE
+91
Проверка OTP-кода (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Формула угла между двумя прямымиЕсли θ — угол, образованный двумя пересекающимися линиями, определяемыми y 1 = m 1 x 1 +c 1 9042 1 и у 2 = м 2 x 2 +c 2, угол будет:
tanθ = ±(m 2 -m 1 ) / (1+m 1 904 21 м 2 )
Угол между двумя прямыми Вывод Линии L 1 и линия L 2 пересекаются в точке на рисунке выше.
Теперь измерение уклона выглядит следующим образом:
tan a 1 = m 1 и tan a 2 = m 2
Тогда, исходя из рисунка, мы можем если θ = a 2 -a 1
Итак, tan θ = tan (a 2 -a 1 ) = (tan a 2 – tan a 1 ) / (1- загар 1 tan a 2 )
При подстановке значений tan a 1 и tan a 2 как m 1 и m 2 соответственно имеем ,
tanθ= (м 2 – m 1 ) / (1+m 1 m 2 )
Следует отметить, что в этом уравнении значение тангенса θ будет положительным, если θ острое, и отрицательным, если θ тупым.
Угол между двумя линиями Координатная геометрияЕсли в аналитической геометрии действительно заданы координаты трех точек A, B и C, то угол между линиями AB и BC можно вычислить следующим образом:
Наклон линии с конечными точками (x 1 , y 1 ) и (x 2 , y 2 ) определяется уравнением:
9000 4 Всякий раз, когда известен наклон каждой линии из уравнения угол между двумя линиями можно рассчитать, вычислив наклон каждой линии, а затем используя его в формуле для определения угла между двумя линиями.