Виды углов | Презентация к уроку по математике (2 класс) по теме:
— Назовите лишнюю фигуру здесь (замкнутые линии). Почему?
— Лишняя фигура здесь? (Треугольник. )
— А здесь? (Круг.)
Молодцы!
2. Повторение об угле.
— Ребята, а вы знаете, что кроме этих геометрических фигур в Геометрии есть и другие.
— Скажите, с какой фигурой мы познакомились на уроке математике вчера? (С углом.)
— Что такое угол ? (Фигура из двух лучей, выходящих из одной точки.)
— Как называются лучи у угла? (Его стороны.)
— А точка, из которой выходят стороны? (Его вершина.)
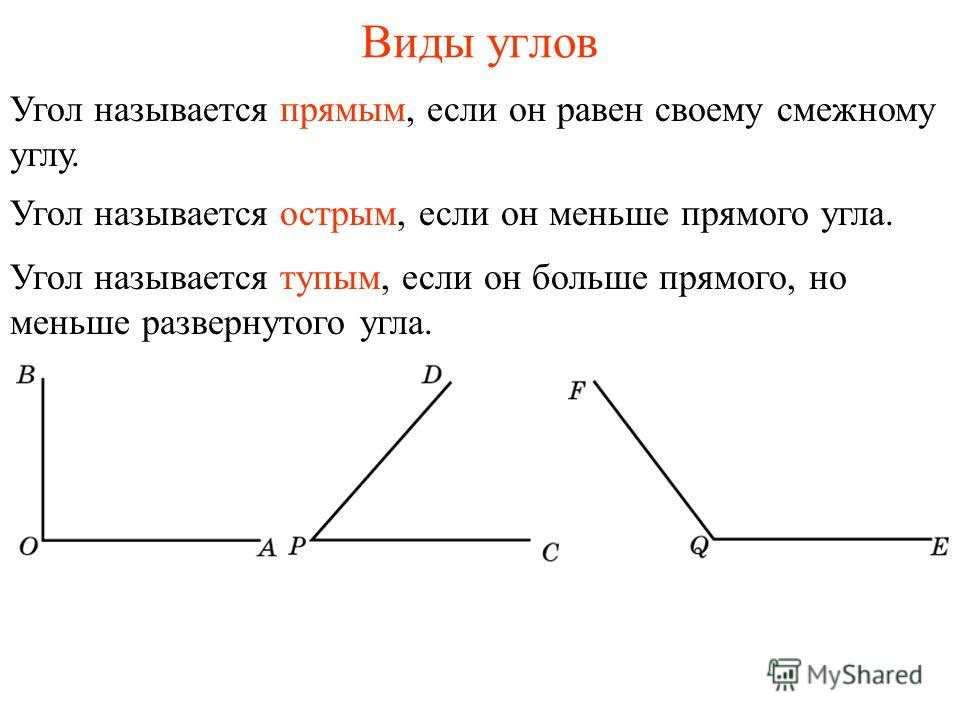
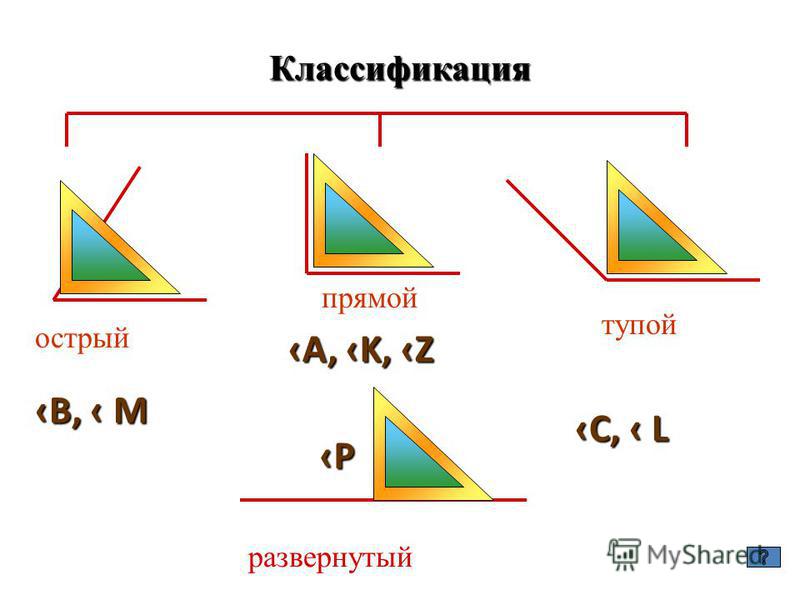
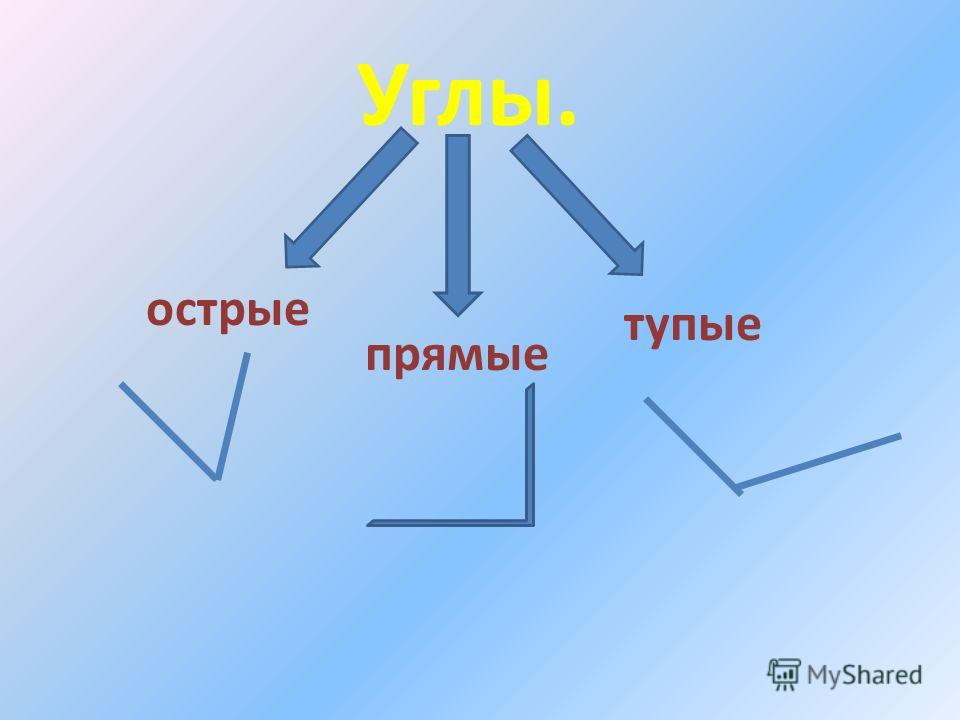
— Какие бывают углы? (Прямые и непрямые.)
III. Новый материал.
Виды углов.
(2 слайд)
— Посмотрите на экран и скажите, какой это угол? (Прямой.)
— Верно.
— Ребята, а где в жизни можно встретить прямой угол?
А) – Что можете сказать про этот угол? (Он меньше прямого. )
)
— Раньше мы его называли непрямым.
— Посмотрите, этот угол наложили на прямой угол. Одна сторона этого угла совпала со стороной прямого угла, а другая оказалась внутри прямого угла, значит такой угол назовём острым.
Б) – А что вы можете сказать про этот угол? (Он больше прямого.)
— Этот угол мы тоже называли непрямым. Учёные ему придумали научное имя.
— Посмотрите, если этот угол наложить на прямой угол так, чтобы одна его сторона совпала со стороной прямого угла, то другая пройдёт вне прямого угла, значит, такой угол будем называть тупым.
3. – Повторим, как называются углы?
Физминутка.
IV. Закрепление. «Узнай углы».
1. — Рассмотрите углы на экране:
1 2 3 4 5 6
(3 сл.)
— Вам надо разделить их на 2 группы.
— Возьмите ручку и листочек.
— Запишите в строчку номера острых углов. ( 1, 2, 5)
— Во вторую строчку, через запятую запишите номера тупых углов. (2, 4, 5)
(2, 4, 5)
— Проверим. (3 сл.) Обменяйтесь тетрадями. Проверьте.
— Верните тетради.
— Поднимите руку, кто правильно выполнил задание?
— Кто допустил одну ошибку? две ошибки?
2. Построение углов.
— Начертим углы в тетрадь.
— Какие инструменты понадобятся?
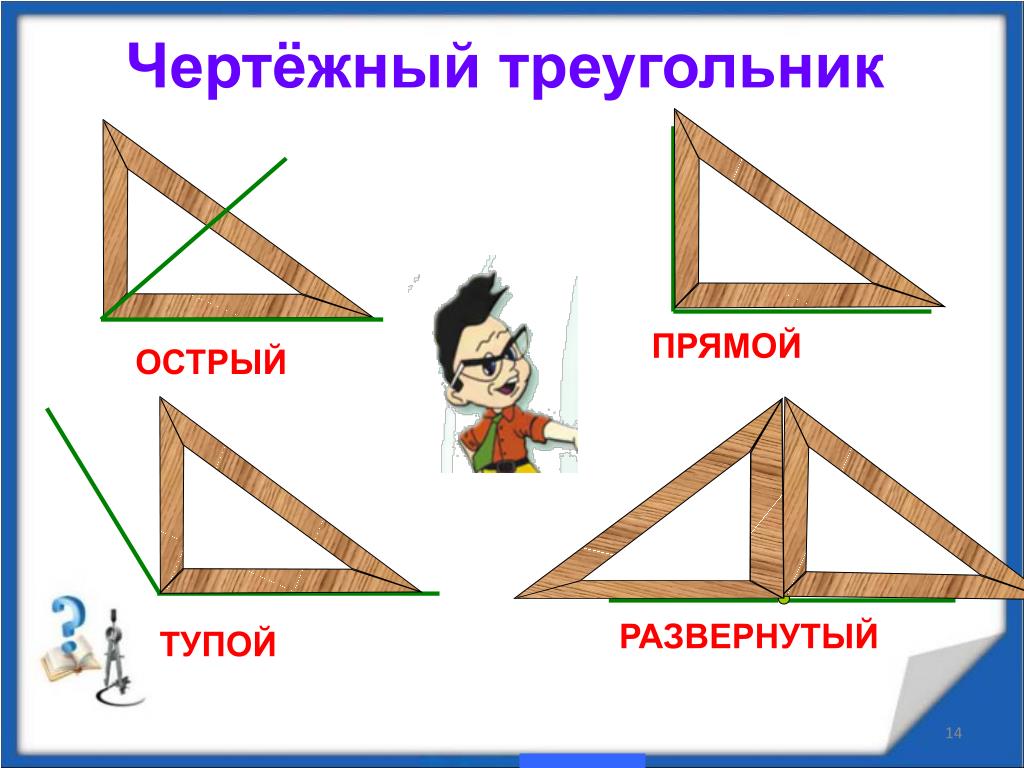
1) Постройте прямой угол.
1. Возьмите угольник. Покажите вершину прямого угла – возьмите пальчиками за неё.
2. Возьмите карандаш.
3. Обведите прямой угол треугольника.
2) Начертим острый угол.
1. Возьмите линейку и карандаш.
2. Поставьте в уголке клетки точку.
3. Проведите луч.
4. А затем из этой точки ещё 1 луч, как у меня.
5. Приложите треугольник прямым углом. Что скажете?
3) Построим тупой угол.
1. Возьмите линейку и карандаш.
2. Поставьте в уголке клетки точку.
3. Проведите луч.
4. А затем из этой точки ещё 1 луч, как у меня.
5. Приложите треугольник прямым углом. Что скажете?
— Обозначим углы тремя буквами.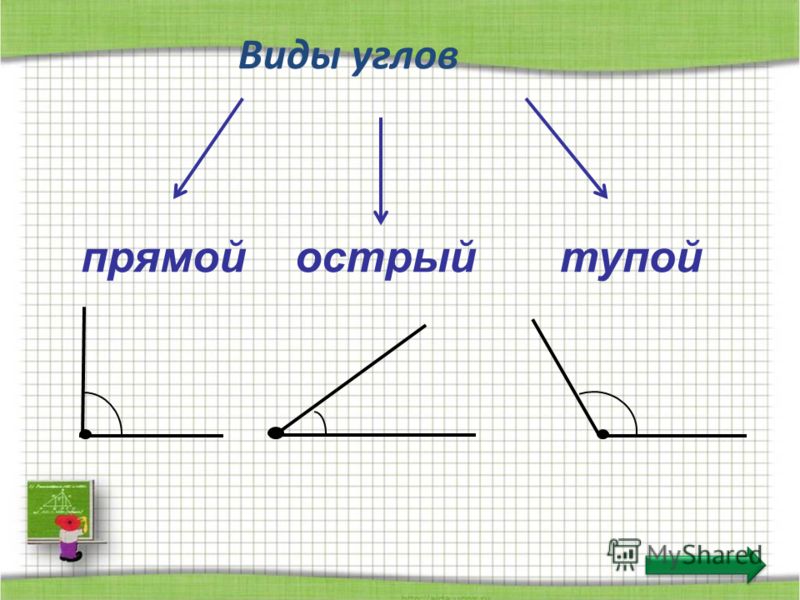
А С К
О В Д М М В
— Прочитайте название прямого угла, острого угла, тупого.
— Мы учились правильно строить углы, записывать и читать их.
Гимнастика для глаз. (4 слайд)
— Сделаем зарядку для глаз.
* — Следите только глазками, головой не крутите. Следите за появлением и движением снежинок на экране.
(5 слайд) 3. – Ребята, при построении снежинки, какие получились углы? (Острые)
— А есть ли тупые, прямые углы?
— Посмотрите на экран.
— Молодцы, и здесь вы увидели разные углы.
4. – Продолжим путешествие. (6 слайд)
— Вот один из сказочных домиков страны «Геометрии». Рассмотри его.
— Из каких геометрических фигур он построен?
— Сосчитайте, сколько прямоугольников. ( 2)
— Какие у них углы? (Прямые, прямо – угольник.)
— Сколько треугольников? (3)
— У них какие углы? (Острые и прямые. )
)
— Продолжим.
IV. Итог.
1. Закончи предложение. (7 слайд)
- Геометрическая фигура, образованная двумя лучами, исходящими из
одной точки – это… (Угол)
- Лучи, выходящие из одной точки – это… (Стороны угла)
- Показанный угол читается как… (МОК или КОМ)
- Угол, который меньше прямого угла – это… (Острый угол)
- Угол, который больше прямого угла – это… (Тупой угол)
2.
— С каким новым геометрическим материалом вы сегодня познакомились?
— Сегодня мы узнали название острого и тупого углов, учитесь их строить, находить.
Дополнительно: (8 слайд)
— Предлагаю вам игру «Весёлый конструктор»
— Соберите предмет из этих фигур. Фигуры можно менять по размеру, а по количеству берите столько, сколько надо.
Нарисуйте на листе цветными карандашами.
— Вот и закончилось наше путешествие по стране «Геометрия»!
Углы в пространстве — Умскул Учебник
На этой странице вы узнаете- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.
На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
| Как мы сталкиваемся с двугранными углами, когда читаем книгу? Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами. |
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
Как и обычные углы, углы между плоскостями бывают трех видов:
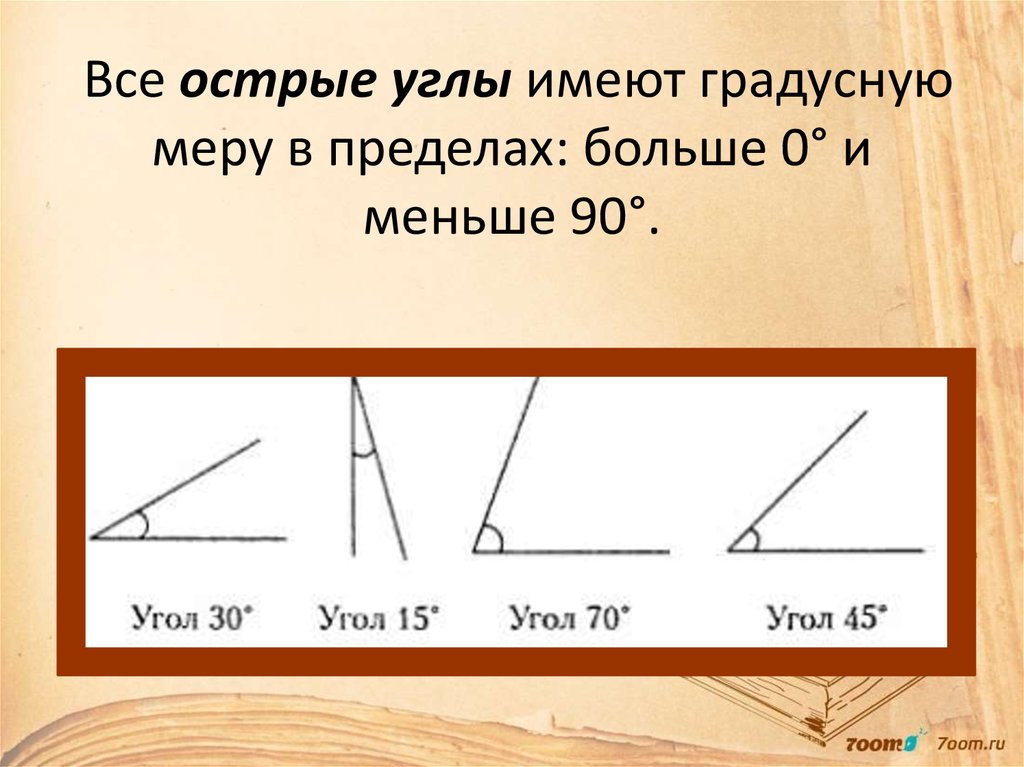
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
| Где в комнате можно найти перпендикулярные плоскости? Достаточно посмотреть на стены и пол, или стены и потолок. |
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
| Алгоритм нахождения угла между плоскостями 1 шаг. Найти линию пересечения плоскостей. 2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости. 3 шаг. Найти острый угол между построенными перпендикулярами. |
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия.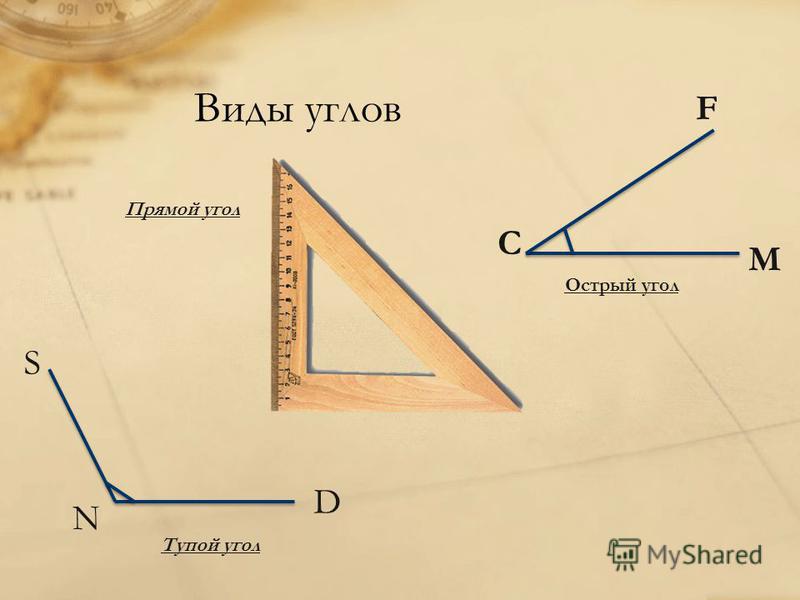 Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость.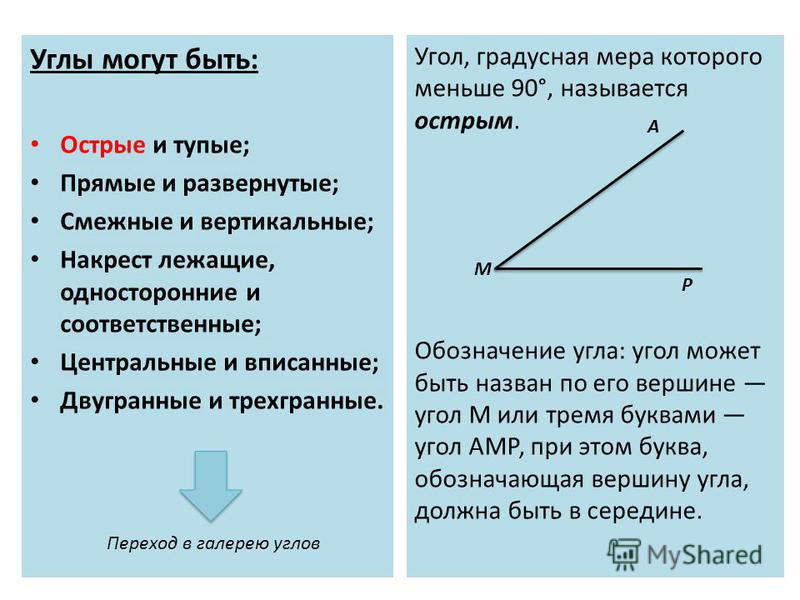 Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
| Алгоритм нахождения угла между прямой и плоскостью Шаг 1. Построить проекцию прямой на плоскость. Шаг 2. Найти угол между прямой и построенной проекцией. |
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.

Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярахРазберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
Для удобства назовем уголок АВС, где С — прямой угол.
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.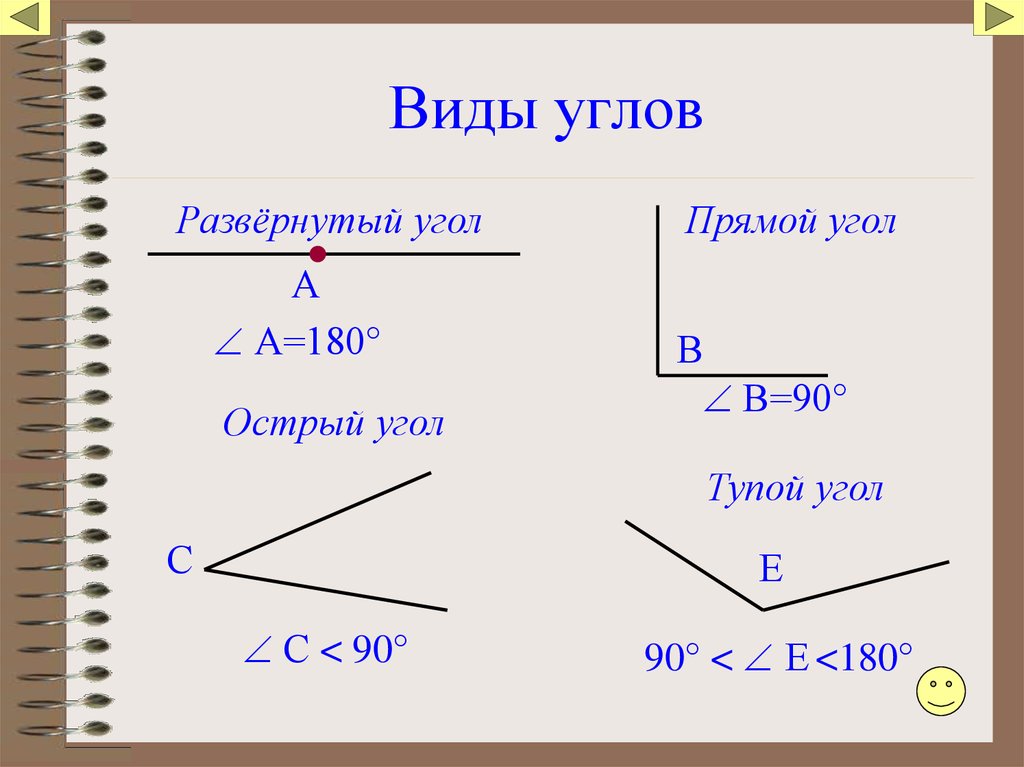
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.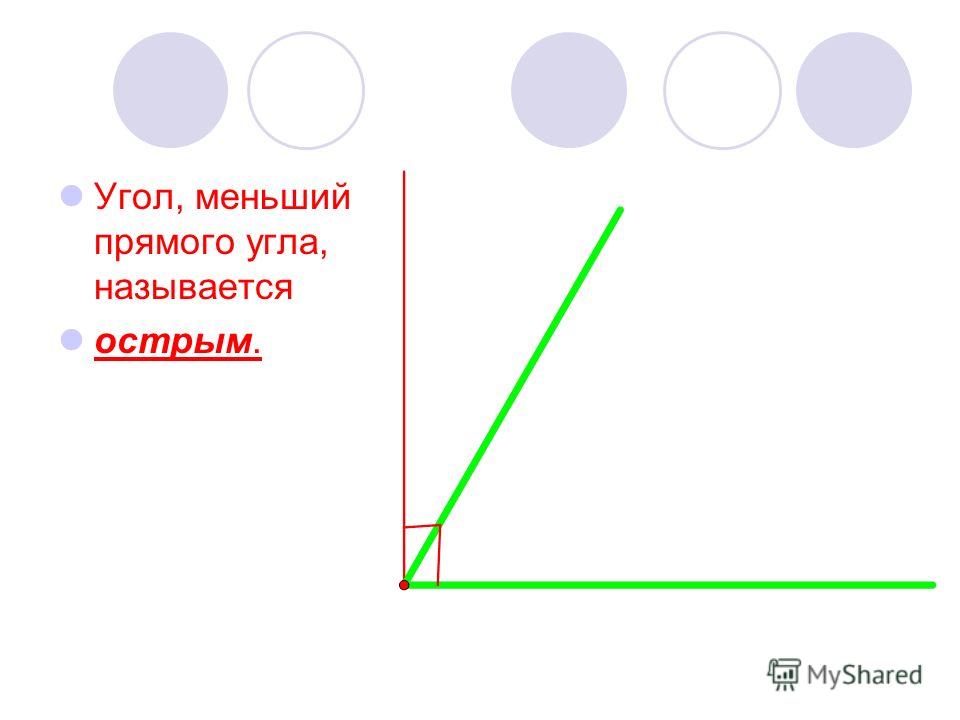
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
| Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах? Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой. Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции. |
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
 Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями. - Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.

- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
«Закругленные углы» против «Острых углов» | Юлиана З.
Сегодня дизайнеры так часто используют закругленные углы, что они стали скорее отраслевым стандартом, чем дизайнерской тенденцией. Они встречаются не только в пользовательском интерфейсе программного обеспечения, но и в дизайне аппаратных продуктов. Так что же такого в закругленных углах, что делает их такими популярными? Действительно, они выглядят привлекательно, но это еще не все.
Любой может оценить эстетическую красоту закругленных углов, но не каждый может объяснить, откуда именно берется эта красота. Ответ на этот вопрос буквально у вас в глазах.
Некоторые эксперты говорят, что прямоугольники со скругленными углами приятнее для глаз, чем прямоугольники с острыми краями, потому что для визуальной обработки требуется меньше когнитивных усилий. Фовеа быстрее всего обрабатывает круги. Обработка краев включает в себя больше «инструментов нейронного изображения» в мозгу [1]. Таким образом, прямоугольники со скругленными углами легче обрабатывать, потому что они выглядят ближе к кругу, чем обычный прямоугольник.
Обработка краев включает в себя больше «инструментов нейронного изображения» в мозгу [1]. Таким образом, прямоугольники со скругленными углами легче обрабатывать, потому что они выглядят ближе к кругу, чем обычный прямоугольник.
Научные исследования углов, проведенные Неврологическим институтом Барроу, показали, что «воспринимаемая значимость угла изменяется линейно в зависимости от угла угла. Острые углы порождали более сильную иллюзорную значимость, чем пологие углы» [2]. Другими словами, чем острее угол, тем ярче он выглядит. И чем ярче выглядит угол, тем труднее на него смотреть.
На какой объект легче смотреть?
Еще одно объяснение того, почему мы присматриваемся к закругленным углам, заключается в том, что они более органичны для того, как мы используем повседневные предметы в физическом мире [3]. Закругленные углы есть везде. А в детстве мы быстро усваиваем, что острые углы причиняют боль, а закругленные углы безопаснее. Вот почему, когда ребенок играет с мячом, большинство родителей не пугаются.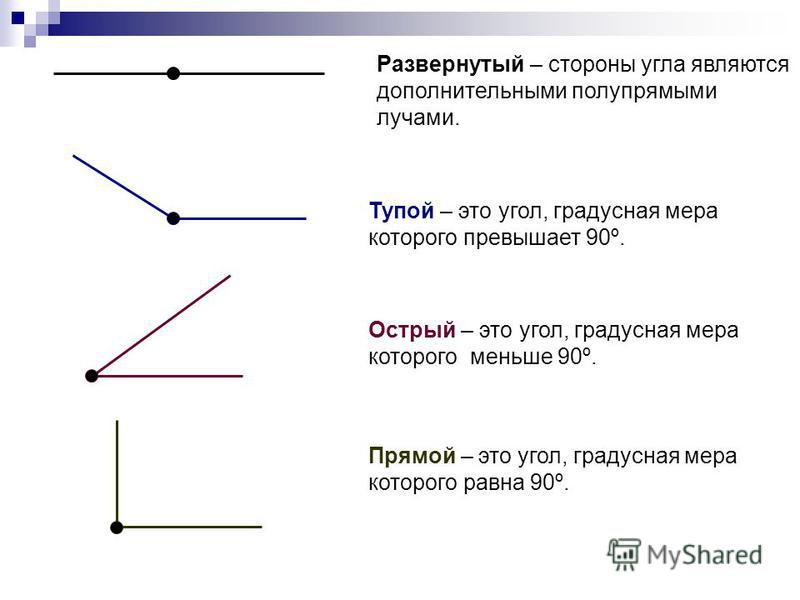
Но если бы ребенок играл с вилкой, родители отобрали бы вилку, опасаясь, что ребенок навредит себе. Это провоцирует то, что нейробиологи называют «реакцией избегания» с острыми краями. Таким образом, мы склонны «избегать острых краев, потому что в природе они могут представлять угрозу» [4].
Какой предмет вы бы доверили своему ребенку?
Закругленные углы более эффективны для карт и диаграмм, поскольку они позволяют нашим глазам легко следовать линиям, «так как это лучше соответствует естественному движению головы и глаз соответственно» [5]. Острые углы отбрасывают взгляд от пути линии, поэтому вы в конечном итоге испытываете резкие паузы, когда линия меняет направление. Но с закругленными углами линия ведет ваш взгляд за каждый угол, чтобы плавно продолжить путь.
Какая диаграмма легче воспринимается вашими глазами?
Закругленные углы также являются эффективными контейнерами для содержимого. Это связано с тем, что закругленные углы направлены внутрь к центру прямоугольника. Это помещает фокус на содержимое внутри прямоугольника. Это также позволяет легко увидеть, какая сторона принадлежит какому прямоугольнику, когда два прямоугольника находятся рядом друг с другом.
Это помещает фокус на содержимое внутри прямоугольника. Это также позволяет легко увидеть, какая сторона принадлежит какому прямоугольнику, когда два прямоугольника находятся рядом друг с другом.
Острые углы направлены наружу, что снижает внимание к содержимому внутри прямоугольника. Они также затрудняют определение того, какая из двух сторон принадлежит какому прямоугольнику, когда два прямоугольника находятся рядом друг с другом. Это потому, что каждая сторона прямоугольника представляет собой в точности прямую линию. Стороны прямоугольника со скругленными углами уникальны, потому что линии изгибаются в сторону прямоугольника, которому он принадлежит.
Закругленные углы — это нечто большее, чем кажется на первый взгляд. Закругленные углы не только легче воспринимаются нашими глазами, но и облегчают обработку информации. Нет никаких сомнений в том, что закругленные углы привлекательны. Но эти дополнительные причины делают их еще более привлекательными для использования.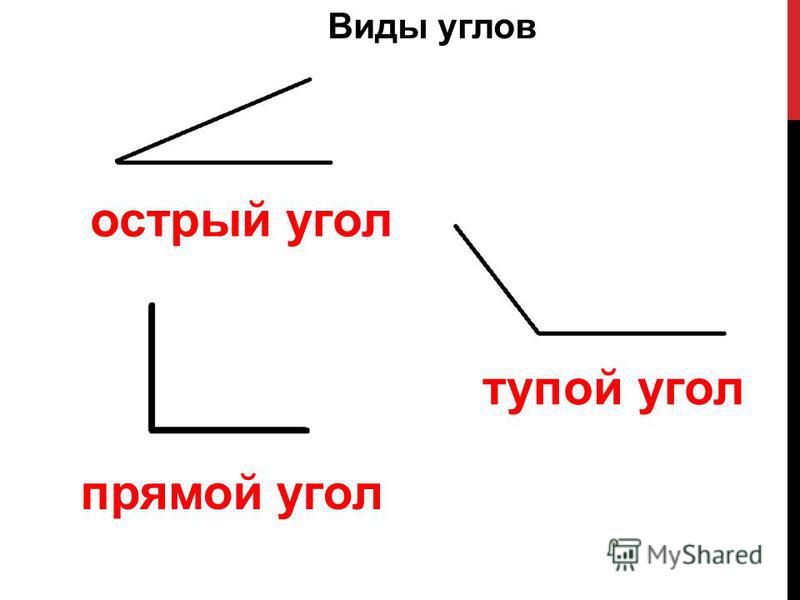 Когда вы говорите с клиентом о закругленных углах, у вас теперь есть что сказать, кроме того, что это выглядит хорошо.
Когда вы говорите с клиентом о закругленных углах, у вас теперь есть что сказать, кроме того, что это выглядит хорошо.
[1] Реализации прямоугольников со скругленными углами
[2] Заметность угла изменяется линейно с углом угла во время контраста с мерцанием
[3] Почему нам нравятся закругленные углы?
[4] Исследование NeuroFocus показывает, что пошло не так с новым логотипом бренда Gap
[5] Руководство по визуализации FMC
глаза/
Закругленные углы над острыми углами | by Andrea Perera
Почему закругленные углы в тренде
Вы заметили, что самые популярные продукты, такие как Facebook, Netflix и Spotify, чаще используют закругленные/закругленные углы в своих пользовательских интерфейсах?
Несмотря на то, что использование острых углов для пользовательского интерфейса и продуктов является отраслевым стандартом, изогнутые углы постепенно становятся тенденцией. Давайте разберемся, почему изогнутые углы более привлекательны, чем острые углы, и когда их использовать в своих проектах.
Некоторые из вас, возможно, уже сталкивались с сообщениями в LinkedIn от UI/UX-дизайнеров, спрашивающих: «Какой UI лучше?».
В контексте этой темы я проанализировал несколько сообщений, в которых предлагается сравнение элементов пользовательского интерфейса с изогнутыми и острыми углами. В большинстве случаев большинство проголосовало за элементы с изогнутыми углами.
Однако самый волнующий вопрос заключается в том, стоит ли за этим какая-то наука?
По мнению экспертов, визуальная обработка прямоугольников с кривыми углами намного проще, чем прямоугольников с острыми краями, поскольку они требуют меньше когнитивных усилий.
Острые углы подчеркивают опасность или отсутствие безопасности. Поэтому наш разум приучен избегать их, насколько это возможно.
Но, с другой стороны, изогнутые углы создают дружелюбную и безопасную атмосферу. Следовательно;
Изогнутые углы выглядят более привлекательно просто потому, что они приятнее для глаз 👀.
Примечание: Все варианты использования, упомянутые в этой статье, публикуются публично через форму Google для сбора мнений конечных пользователей.
Кнопки (отдельные)
После проведения опроса я обнаружил, что 65% предпочитают изогнутые углы для сравнения пользовательского интерфейса кнопок.
Слева: Острый угол | Центр: Изогнутый угол | Справа: Полностью изогнутый уголТаким образом, можно с уверенностью заключить, что изогнутые углы для кнопок имеют большое значение для общих случаев использования.
Диалоговые окна (отдельные)
Когда дело доходит до информационных диалоговых окон, многие предпочитают центральное диалоговое окно с умеренными изогнутыми углами.
Слева: Острый угол | Центр: Изогнутый угол | Справа: полностью изогнутый уголКроме того, конкуренция между острыми и изогнутыми углами была близкой, поэтому полностью изогнутый угол был наименее предпочтительным выбором.
Но значит ли это, что мы должны избегать использования острых углов?
Нет! Существуют варианты использования острых углов. Давайте узнаем, когда людям нравится видеть Острые углы, на основе результатов моего опроса.
Кнопки и диалоговые окна (отдельные)
Как я уже упоминал ранее, острые углы в некоторых случаях привлекают наше внимание. При рассмотрении кнопок и диалоговых окон некоторые варианты использования, найденные по результатам опроса, предназначены для;
- Ящики с важным и внимательным содержанием.
- Кнопки, которые должны быть заметны.
Таким образом, элементы пользовательского интерфейса с острыми углами хорошо вписываются в элементы, требующие внимания пользователя.
Затем я провел тот же опрос, сгруппировав эти кнопки, чтобы понять их действие.
Группировка кнопок
Интересно, что когда мы группируем несколько кнопок, люди начинают менять свои предпочтения.
Большинство участников опроса предпочли кнопку с острыми углами (самая левая на изображении ниже) даже в тех случаях, когда она не требует пристального внимания.
Затем я оценил, будет ли влияние, если мы используем сочетание разных контейнеров для этих групп.
Слева: Острый угол | Центр: Изогнутый угол | Справа: полностью изогнутый угол. Результаты оказались намного интереснее. Большинство предпочло иметь контейнер Sharp Corner для групп кнопок с изогнутыми углами.
Однако многие предпочитают не смешивать разные типы углов. Так что лучше держаться подальше, если нет веской причины. 😊
Кнопка группировки: поэкспериментируйте с компонентами фильтра
Я оценил использование кнопок в качестве элемента фильтра, чтобы понять последствия группировки кнопок при рассмотрении различных типов углов. .
1-я секция: теги для фильтров с острыми угламиОпять же, результаты опроса показывают, что большинство предпочитает фильтры с острыми углами.
Кроме того, важно отметить, что могут быть и другие контекстуальные воздействия при выборе различных типов углов. Например, люди, работающие в медицинской отрасли, могут предпочесть что-то одно, а в творческой работе — другое.
Поэтому не делайте поспешных выводов и принимайте результаты опроса за эмпирическое правило. Вместо этого я настоятельно рекомендую вам провести дополнительные A/B-тесты для аудитории вашего приложения.
Тем не менее, я обобщил результаты опроса для вашего быстрого ознакомления, как показано ниже.
Примечание: Выбор углов может различаться в зависимости от устройства или режима, например, мобильной версии или веб-версии.
Не создавайте веб-монолиты. Используйте Bit для создания и компоновки несвязанных программных компонентов — в ваших любимых средах, таких как React или Node. Создавайте масштабируемые интерфейсы и серверные части с мощным и приятным опытом разработки.

 А еще на углы потолка — в них будет три перпендикулярные плоскости.
А еще на углы потолка — в них будет три перпендикулярные плоскости. 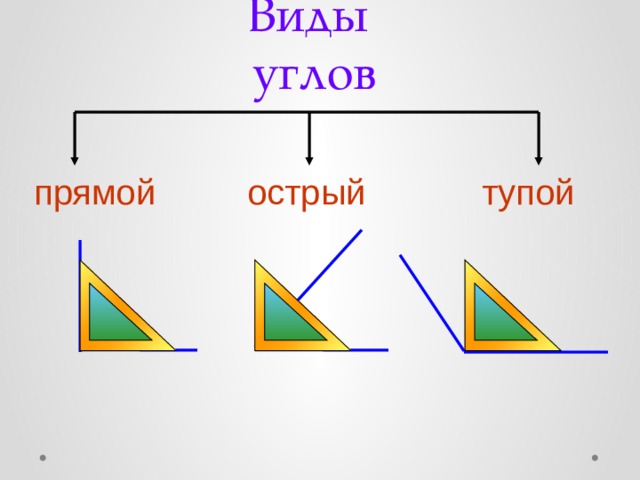
 Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.