| 1 | Найти число возможных исходов | 7 выбор 3 | |
| 2 | Найти число возможных исходов | 8 выбор 3 | |
| 3 | Найти число возможных исходов | 5 выбор 2 | |
| 4 | Найти число возможных исходов | 4 выбор 2 | |
| 5 | Найти число возможных исходов | 8 выбор 4 | |
| 6 | Найти число возможных исходов | 10 выбор 3 | |
| 7 | Найти число возможных исходов | 7 выбор 4 | |
| 8 | Найти число возможных исходов | 6 выбор 3 | |
| 9 | Найти число возможных исходов | 9 выбор 3 | |
| 10 | Найти число возможных исходов | 3 выбор 2 | |
| 11 | Найти число возможных исходов | 6 выбор 4 | |
| 12 | Найти число возможных исходов | 5 выбор 4 | |
| 13 | Найти число возможных исходов | 7 перестановка 3 | |
| 14 | Найти число возможных исходов | 7 выбор 2 | |
| 15 | Найти число возможных исходов | 10 выбор 5 | |
| 16 | Найти число возможных исходов | 10 выбор 6 | |
| 17 | Найти число возможных исходов | 13 выбор 5 | |
| 18 | Найти число возможных исходов | 3 выбор 3 | |
| 19 | Найти число возможных исходов | 4 выбор 1 | |
| 20 | Найти число возможных исходов | 4 выбор 4 | |
| 21 | Найти число возможных исходов | ||
| 22 | Найти число возможных исходов | 6 перестановка 3 | |
| 23 | Найти число возможных исходов | 8 выбор 5 | |
| 24 | Найти число возможных исходов | 9 перестановка 4 | |
| 25 | Найти число возможных исходов | 13 выбор 3 | |
| 26 | Найти число возможных исходов | 12 выбор 2 | |
| 27 | Найти число возможных исходов | 12 выбор 4 | |
| 28 | Найти число возможных исходов | 12 выбор 3 | |
| 29 | Найти число возможных исходов | 9 выбор 5 | |
| 30 | Найти число возможных исходов | 9 выбор 2 | |
| 31 | Найти число возможных исходов | 7 выбор 5 | |
| 32 | Найти число возможных исходов | 6 перестановка 6 | |
| 33 | Найти число возможных исходов | 8 перестановка 5 | |
| 34 | Найти число возможных исходов | 8 перестановка 3 | |
| 35 | Найти число возможных исходов | 7 перестановка 5 | |
| 36 | Найти число возможных исходов | 52 выбор 5 | |
| 37 | Найти число возможных исходов | 5 перестановка 3 | |
| 38 | Найти число возможных исходов | 12 выбор 5 | |
| 39 | Найти число возможных исходов | 3 выбор 1 | |
| 40 | Найти число возможных исходов | 11 выбор 5 | |
| 41 | Найти число возможных исходов | 10 выбор 2 | |
| 42 | Найти число возможных исходов | 15 выбор 3 | |
| 43 | Найти число возможных исходов | 52 выбор 4 | |
| 44 | Найти число возможных исходов | 9 выбор 4 | |
| 45 | Найти число возможных исходов | 9 перестановка 3 | |
| 46 | Найти число возможных исходов | 7 перестановка 4 | |
| 47 | Найти число возможных исходов | 7 перестановка 2 | |
| 48 | Найти число возможных исходов | ||
| 49 | Найти число возможных исходов | 11 выбор 2 | |
| 50 | Найти число возможных исходов | 11 выбор 3 | |
| 51 | Найти число возможных исходов | 10 перестановка 5 | |
| 52 | Найти число возможных исходов | 5 выбор 5 | |
| 53 | Найти число возможных исходов | 6 выбор 1 | |
| 54 | Найти число возможных исходов | 8 перестановка 4 | |
| 55 | Найти число возможных исходов | 8 выбор 6 | |
| 56 | Найти число возможных исходов | 13 выбор 4 | |
| 57 | Вычислить | e | |
| 58 | Найти уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найти число возможных исходов | 13 выбор 2 | |
| 60 | Найти число возможных исходов | 10 перестановка 2 | |
| 61 | Найти число возможных исходов | 10 перестановка 3 | |
| 62 | Найти число возможных исходов | 10 выбор 7 | |
| 63 | Найти число возможных исходов | 20 выбор 4 | |
| 64 | Найти число возможных исходов | 6 перестановка 4 | |
| 65 | Найти число возможных исходов | 5 перестановка 4 | |
| 66 | Найти число возможных исходов | 6 выбор 5 | |
| 67 | Найти число возможных исходов | 52 выбор 3 | |
| 68 | Найти число возможных исходов | 4 выбор 0 | |
| 69 | Найти число возможных исходов | 9 перестановка 7 | |
| 70 | Найти число возможных исходов | 6 выбор 2 | |
| 71 | Найти число возможных исходов | 5 перестановка 5 | |
| 72 | Найти число возможных исходов | 5 перестановка 2 | |
| 73 | Найти число возможных исходов | 6 выбор 6 | |
| 74 | Найти число возможных исходов | 7 выбор 6 | |
| 75 | Найти число возможных исходов | 8 перестановка 6 | |
| 76 | Найти число возможных исходов | 7 перестановка 7 | |
| 77 | Найти число возможных исходов | 9 перестановка 5 | |
| 78 | Найти число возможных исходов | 2 перестановка 2 | |
| 79 | Найти число возможных исходов | 10 выбор 8 | |
| 80 | Найти число возможных исходов | 12 выбор 7 | |
| 81 | Найти число возможных исходов | 15 выбор 5 | |
| 82 | Найти обратный элемент | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Определить область значений | 1/4x-7 | |
| 84 | Найти число возможных исходов | 10 перестановка 7 | |
| 85 | Найти число возможных исходов | 12 выбор 6 | |
| 86 | Найти число возможных исходов | 2 выбор 1 | |
| 87 | Найти число возможных исходов | 30 выбор 3 | |
| 88 | Найти число возможных исходов | 9 выбор 6 | |
| 89 | Найти число возможных исходов | 8 перестановка 2 | |
| 90 | Найти число возможных исходов | 7 выбор 1 | |
| 91 | Найти число возможных исходов | 6 перестановка 2 | |
| 92 | Найти число возможных исходов | 4 перестановка 2 | |
| 93 | Найти число возможных исходов | 4 перестановка 3 | |
| 94 | Найти число возможных исходов | 3 перестановка 3 | |
| 95 | Найти число возможных исходов | 46 выбор 6 | |
| 96 | Найти число возможных исходов | 5 перестановка 1 | |
| 97 | Найти число возможных исходов | 52 выбор 7 | |
| 98 | Найти число возможных исходов | 52 перестановка 5 | |
| 99 | Найти число возможных исходов | 9 выбор 1 | |
| 100 | Найти число возможных исходов | 9 перестановка 6 |
Умножение натуральных чисел / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Умножение натуральных чисел
Умножение — одна из операций математики, предназначена для упрощения сложения одинаковых чисел.
Например: 4 + 4 + 4 = 4 · 3 = 12.
Умножение обозначают точкой «·» или крестиком «х».
Числа, которые умножаются, называют «множителями», результат умножения, называют «произведением»
Пример:
Алгоритм умножения чиселРазберем порядок умножения чисел на примере. Умножим число 25 на 16
1. Сначала записываем множители в столбик.
Второй множитель записывается под первым множителем так, что разряды второго множителя находились под соответствующими разрядами первого множителя, т.е. единицы второго множителя записываются под единицами первого, десятки под десятками и т.д. Снизу под записанными множителями проводится горизонтальная линия, а слева ставится знак умножения.
2. Производим последовательное умножение.
Сначала число, обозначающее разряд единиц класса единиц второго множителя последовательно умножаем на все разряды первого множителя.
Умножим цифру 6 на 5, получаем 30 — 3 десятка 0 единиц. 0 запишем под единицами, 3 «запомним». После этого 6 умножаем на цифру десятков первого множителя на 2, получаем 12. Прибавим к 12 получившиеся в предыдущем действии десятки, т.е. 3, в результате получаем 15. Поскольку разрядов в первом множителе больше нет., запишем число 15 под десятками. Первое неполное произведение 150.
0 запишем под единицами, 3 «запомним». После этого 6 умножаем на цифру десятков первого множителя на 2, получаем 12. Прибавим к 12 получившиеся в предыдущем действии десятки, т.е. 3, в результате получаем 15. Поскольку разрядов в первом множителе больше нет., запишем число 15 под десятками. Первое неполное произведение 150.
3. Найдем второе неполное произведение. Последовательно умножим десятки второго множителя — 1 на все разряды первого слагаемого. Сначала 1 умножим на 5, получаем 5, запишем полученное произведение под десятками. После этого 1 умножаем на 2, получим 2, записываем 2 впереди 5. Второе неполное произведение 25. Поскольку мы умножали десяток второго слагаемого на первое слагаемое, запись второго неполного произведения 25 будет находиться под разрядом десятков. Получается «смещение» числа влево.
4. Последовательно сложим цифры полученных неполных произведений по правилам сложения.
Свойства умножения натуральных чисел.1. Переместительное свойство умножения.
Переместительное свойство умножения.
a · b = b · a
От перемены мест множителей произведение не изменится.
12 · 4 = 4 · 12
12 · 4 = 48
4 · 12 = 48
2. Сочетательное свойство умножения.
a · (b · c) = (a · b) · c
Произведение не зависит от группировки сомножителей.
2 · (3 · 6) = (2 · 3) · 6
2 · (3 · 6) = 36
1) 3 · 6 = 18; 2) 18 · 2 = 36
(2 · 3) · 6 = 36
1) 2 · 3 = 6; 2) 6 · 6 = 36
3. Распределительное свойство умножения относительно сложения.
a · (b + c) = ab + ac
При умножении числа на сумму двух других чисел, можно данное число умножить на каждое из слагаемых, а полученные результаты сложить.
3 · (5 + 4) = 3 · 5 + 3 · 4
3 · (5 + 4) = 27
1) 5 + 4 = 9; 2) 9 · 3 = 27
3 · 5 + 3 · 4 = 27
1) 3 · 5 = 15; 2) 3 · 4 = 12; 3) 12 + 15 = 27
4. Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания
a · (b — c) = ab — ac
При умножении числа на разность двух других чисел, можно данное число умножить на уменьшаемое и на вычитаемое, а полученные результаты вычесть.
6 · (7 — 5) = 6 · 7 — 6 · 5
6 · (7 — 5) = 12
1) 7 — 5 = 2; 2) 2 · 6 = 12
6 · 7 — 6 · 5 = 12
1) 6 · 7 = 42; 2) 6 · 5 = 30; 3) 42 — 30 = 12
5. Свойство умножения единицы на натуральное число
a · 1 = a
При умножении единицы на любое число, получим равное ему число.
1 · 76 = 76
6. Свойство умножения нуля на натуральное число
0 · a = 0
При умножении 0 на любое число, получим 0
0 · 123 = 0
Произведение всех натуральных чисел от 1 до называют факториал, записывают: , читают: «эн факториал». Следовательно, справедливо равенство:
= 123. ..
..
Пример:
3! = 123 = 6;
5! = 12345 =120.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 509, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 524, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 700, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 905, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1046, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1338, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1845, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 483, Мерзляк, Полонский, Якир, Учебник
Номер 736, Мерзляк, Полонский, Якир, Учебник
Номер 1080, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 195, Мерзляк, Полонский, Якир, Учебник
Номер 196, Мерзляк, Полонский, Якир, Учебник
Номер 625, Мерзляк, Полонский, Якир, Учебник
Задание 16, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 49, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 464, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 569, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 667, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1168, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1579, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 11, Мерзляк, Полонский, Якир, Учебник
Номер 12, Мерзляк, Полонский, Якир, Учебник
Номер 17, Мерзляк, Полонский, Якир, Учебник
Номер 201, Мерзляк, Полонский, Якир, Учебник
Номер 227, Мерзляк, Полонский, Якир, Учебник
Номер 228, Мерзляк, Полонский, Якир, Учебник
Номер 247, Мерзляк, Полонский, Якир, Учебник
Номер 432, Мерзляк, Полонский, Якир, Учебник
Номер 564, Мерзляк, Полонский, Якир, Учебник
Номер 1006, Мерзляк, Полонский, Якир, Учебник
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example |
|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 |
| — | знак минус | вычитание | 1 1/2 — 2/3 |
| * | asterisk | multiplication | 2/3 * 3/4 |
| × | times sign | multiplication | 2 /3 × 5/6 |
| : | division sign | division | 1/2 : 3 |
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Умножить на 25 | МатЧатСообщений с тегами «Умножить на 25»Как умножить на 25 в уме Это простой прием, которому может легко научиться каждый. Это всего лишь трюк для Если бы кто-то спросил вас, чему равно 25, умноженное на 36, у вас, вероятно, возникло бы искушение Так как 25 составляет одну четвертую от 100, умножение на 25 — это то же самое, что Вот пример: Задача: 36 x 25 Другой пример: 88 x 25 А теперь попробуйте в уме следующие задачи: а) 25 х 12 Вот ответы: Но, вы говорите, что, если число, с которого вы начинаете, не делится на 4? Итак, возьмем такую задачу: 25 x 17 Другой пример: 25 x 18 Другой пример: 25 x 19 А теперь попробуйте в уме: А вот и Ответы: A) 525 , Умственная арифметика, Умножение, Элементарная математика, Изучение фактов о математике, Математические приемы, Приемы умножения, Черепаший разговорТрюк с умножением №3 — БЫСТРО умножить на 25! Вот третий из моей серии трюков с умножением. ТРЮК №3: ЧТО ПОЗВОЛЯЕТ СДЕЛАТЬ ТРЮК: Быстро умножать числа на 25. пятицентовиков, десятицентовиков и четвертаков». Так как четыре четверти составляют доллар, а доллар стоит 100 центов, концепция четвертей помогает детям понять, что 4 x 25 = 100. Поскольку четыре четверти составляют один доллар, дети могут видеть, что в два раза больше четвертей, 8 , должно составить два доллара (200 центов). И из этого факта дети могут видеть, что 8 x 25 = 200. Следуя этой схеме, дети могут видеть, что двенадцать четвертаков составляют три доллара (300 центов). Итак, 12 х 25 = 300. И так далее. Ладно. Но как все это приводит к трюку с умножением? Хитрость вот в чем. Чтобы умножить число на 25, разделите число на 4, а затем прикрепите два нуля в конце, что равносильно умножению на 100. Еще несколько примеров: 16 x 25. Разделите 16 на 4, чтобы получить . 4 , поэтому ответ равен 4 00. [В денежном выражении 16 четвертей составляют 4 = 4 00 центов] 24 x 25. Разделите 24 на 4, чтобы получить 6, поэтому ответ: 6 00. [В денежном выражении 24 квартала составляют $ 6 = 6 00 центов] 48 x 25. Разделите 48 на 4, чтобы получить 12 , поэтому ответ будет 12 00. 00 центов.] Попробуйте это для практики: 20 x 25 32 x 25 36 x 25 16 x 25 24 x 25 44 x 25 52 x 25 76 x 25 Ответы: 20 x 25 = 500 32 x 25 = 800 36 x 25 = 900 16 x 25 = 400 24 x 25 = 600 44 x 25 = 1100 52 x 25 = 1300 76 x 25 = 1900 Но подождите, вы протестуете… как насчет всех чисел, которые не делятся на 4? Хороший вопрос! Но оказывается, есть обходной путь. Если остаток равен 1, это как иметь 1 дополнительную четверть, дополнительные 25 центов, поэтому вы добавляете 25 к ответу. Пример: 17 x 25. Поскольку 17 ÷ 4 = 4 остаток 1, ответ будет 4 00 + 25 = 425. , так что вы добавляете 50 к ответу. Пример: 26 x 25. Так как 26 ÷ 4 = 6 остаток 2, ответ будет 6 00 + 50 = 650. Если остаток равен 3, это как иметь 3 лишних четверти, дополнительные 75 центов , так что вы добавляете 75 к ответу. Пример: 51 x 25. Так как 51 ÷ 4 = 12 Остаток 3, Ответ — 1200 + 75 = 1275. Теперь попробуйте их для практики: 9 x 25 11 x 25 14 x 25 195 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 x 25 25 x 25 34 x 25 49 x 25 Ответы: 9 x 25 = 225 11 x 25 = 275 14 x 25 = 350 19 x 25 = 475 22 x 25 = 550 25 x 25 = 625 34 x 25 = 850 49 x 25 = 1225 Удачного обучения! — Джош Джош Раппапорт — автор пяти книг по математике, в том числе отмеченного наградой Parents Choice «Руководства по выживанию в алгебре». |

 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 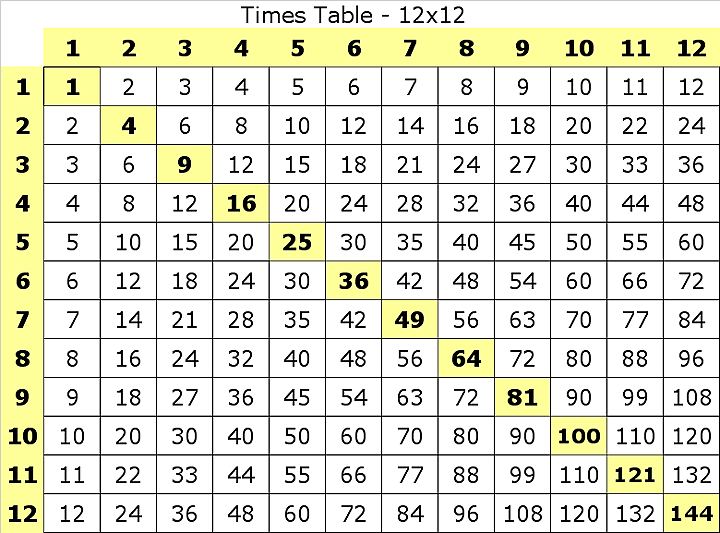 У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце? Какая часть от общей суммы была использована?
Какая часть от общей суммы была использована?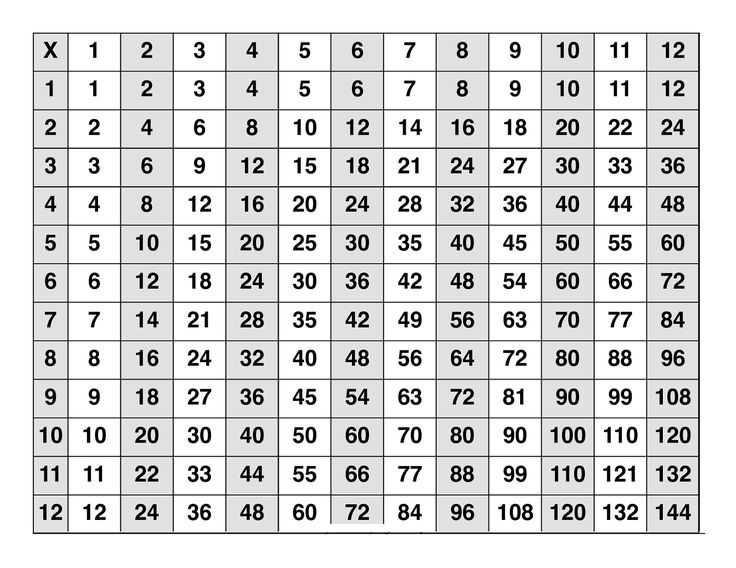

 Первым был трюк с умножением на 5. Второй трюк с умножением на 15, а теперь этот трюк с умножением на 25. Кто-нибудь видел закономерность?
Первым был трюк с умножением на 5. Второй трюк с умножением на 15, а теперь этот трюк с умножением на 25. Кто-нибудь видел закономерность? 
 Вы по-прежнему делите на 4, но теперь обращаете внимание на остаток.
Вы по-прежнему делите на 4, но теперь обращаете внимание на остаток.