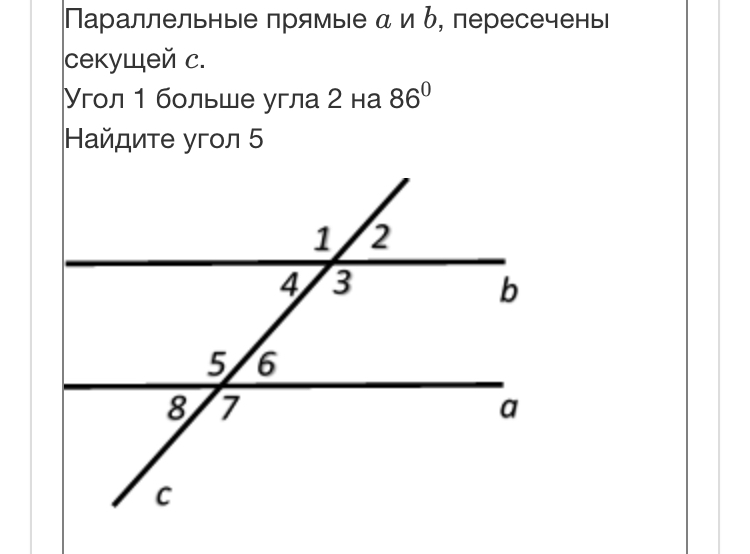
Признаки параллельности прямых. Секущая • Образавр
Содержание
Как мы выяснили на прошлом уроке, прямая, пересекающая данную прямую, пересечет также прямую, параллельную данной. Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам.
Что такое секущаяДаны прямые $a$ и $b$, параллельные друг другу, и прямая $c$, которая пересекает данные прямые в двух точках.
Подобная прямая, пересекающая две прочие прямые, в геометрии называется секущей. Секущая может проводиться как по отношению к параллельным прямым, так и к непараллельным.
Секущая — прямая пересекающая две прямые, лежащие в одной плоскости, в двух разных точках.
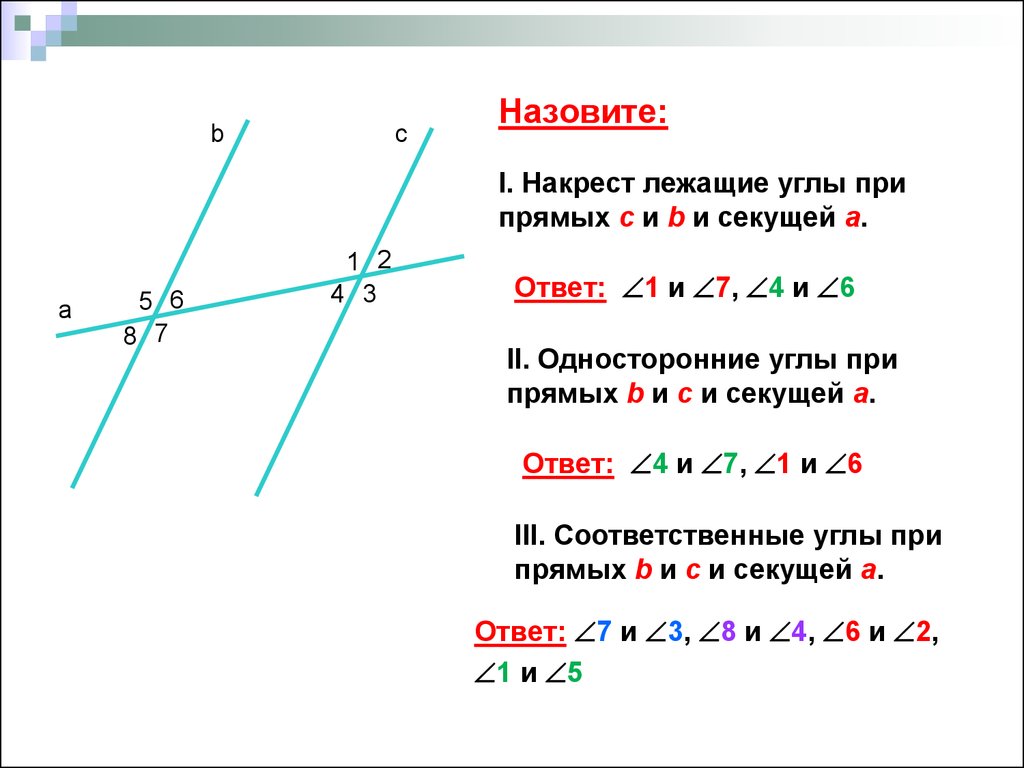
Обращаем внимание на углы при секущей: секущая при пересечении с параллельными прямыми образует восемь углов, которые на чертеже обозначены заглавными латинскими буквами: A, B, C и так далее. Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:
Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:
- односторонние углы — $\angle{A}$ и $\angle{H}$, $\angle{B}$ и $\angle{G}$;
- накрест лежащие углы — $\angle{A}$ и $\angle{G}$, $\angle{B}$ и $\angle{H}$;
- соответственные углы — $\angle{A}$ и $\angle{E}$, $\angle{B}$ и $\angle{F}$, $\angle{D}$ и $\angle{H}$,
$\angle{C}$ и $\angle{G}$;
Внутренние и внешние углы при секущей
Внутренние углы при секущей — это углы, которые находятся в общих для прямых полуплоскостях. Однако секущая также образует и внешние углы — те, что располагаются в не пересекающихся полуплоскостях прямых. Посмотрите на чертежи: для наглядности «зоны» внутренних и внешних углов выделены цветом.
К внутренней «зоне» относятся углы $\angle{A}$, $\angle{B}$, $\angle{H}$ и $\angle{G}$.
К внешней «зоне» относятся углы $\angle{D}$, $\angle{C}$, $\angle{E}$ и $\angle{F}$.
Примечательно, что соответственные углы — это пары, состоящие из одного внутреннего и одного внешнего угла. А при должном внимании вы могли догадаться, что накрест лежащие и односторонние углы были выше нами указаны только для внутренней «зоны». Аналогичные пары вообще-то имеются и во внешней «зоне».
{"questions":[{"content":"Закрепим. Расположите пары углов согласно их названию. Теперь мы будем учитывать как внутреннюю область, так и внешнюю. [[image-2]] [[grouper-1]]","widgets":{"grouper-1":{"type":"grouper","labels":["Внутренние накрест лежащие углы","Внешние накрест лежащие углы","Внутренние односторонние углы","Внешние односторонние углы","Соответственные углы"],"items":[["$\\angle{A}$ и $\\angle{G}$","$\\angle{B}$ и $\\angle{H}$"],["$\\angle{D}$ и $\\angle{F}$","$\\angle{C}$ и $\\angle{E}$"],["$\\angle{A}$ и $\\angle{H}$","$\\angle{B}$ и $\\angle{G}$"],["$\\angle{D}$ и $\\angle{E}$","$\\angle{C}$ и $\\angle{F}$"],["$\\angle{A}$ и $\\angle{E}$","$\\angle{B}$ и $\\angle{F}$","$\\angle{D}$ и $\\angle{H}$","$\\angle{C}$ и $\\angle{G}$"]]},"image-2":{"type":"image","url":"https://obrazavr. ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}
ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}Признаки параллельности прямых: накрест лежащие углыОчевидно, что проведение секущей — это специальный геометрический метод для определения параллельности прямых. По тому, являются ли те или иные пары углов, образованные секущими, равными, можно заключать о параллельности или непараллельности прямых. Одна из таких пар — накрест лежащие углы.
Признак параллельности прямых по накрест лежащим углам. Если при пересечении двух прямых секущей накрест лежащие углы равны, то такие прямые параллельны.
Доказательство. Проведем прямые $a,$ $b$ и секущую $c$, пересекающую прямые в точках $A$ и $B$ соответственно. По условию прямые образуют с секущей пару равных накрест лежащих углов$\angle{1}$ и $\angle{2}$. Воспользуемся методом от противного и предположим, что прямые не параллельны. Тогда они будут пересекаться в некоторой точке $C$. \circ$. Мы пришли к противоречию.
\circ$. Мы пришли к противоречию.
Следовательно прямые параллельны. Теорема доказана.
Внешние
накрест лежащие углы!Заметьте, что при доказательстве мы опирались на равенство внутренних накрест лежащих углов, хотя, если взять признак параллельности прямых, тексте теоремы указана общая формулировка — «накрест лежащие углы», без обозначения их расположения относительно полуплоскостей прямых.
Ответ прост: если доказать признаки параллельности прямых, опираясь на равенство внутренних накрест лежащих углов, внешнее расположение — не более чем условность.
Возьмем для примера $\angle{B}$ и $\angle{H}$. Для $\angle{B}$: внешний $\angle{D}$ — с ним вертикальный; внешний $\angle{C}$ — смежный. Аналогично для $\angle{H}$: $\angle{F}$ и $\angle{E}$ соответственно.
Вертикальные углы равны, поэтому получаем равенство $\angle{D}$ и $\angle{F}.$ У равных углов смежные с ними углы также будут равны, отсюда $\angle{C}=\angle{E}$. Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.
Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.
Признаки параллельности прямых: задача
Отрезки $AB$ и $CD$ пересекаются в общей середине $O$. Докажите, что прямые $AC$ и $BD$ при этом параллельны.
Дано:
$AB, CD$
$AO=OB$
$CO=OD$
Найти:
$AC\parallel{BD}$
Решение
Рассмотрим треугольники $\bigtriangleup{AOC}$ и $\bigtriangleup{BDO}$. Они равны по первому признаку: по условию $AO=OB$ и $CO=OD$, углы $\angle{COA}$ и $\angle{BOD}$ равны как вертикальные. Следовательно $\angle{ACD}=\angle{BDC}$. Данные углы являются внутренними накрест лежащими. Тогда $AC\parallel{BD}$ согласно признаку параллельности по накрест лежащим углам.
Признак параллельности прямых по соответственным углам.
Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Доказательство. Пусть прямые $a$ и $b$ при пересечении секущей $c$ образуют пару равных соответственных углов — $\angle{A}=\angle{B}$. Угол $\angle{D}$ является вертикальным по отношению к $\angle{A}$. Следовательно $\angle{A}=\angle{D}=\angle{B}$. Поскольку $\angle{D}$ и $\angle{B}$ — накрест лежащие углы, прямые $a$ и $b$ являются параллельными. Теорема доказана.
{"questions":[{"content":"[[image-1]] Можно ли говорить о том, что прямые $a$ и $b$ параллельны, если известно, что углы $\\angle{A}$ и $\\angle{B}$ равны? [[choice-5]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/03/test-angles.svg"},"choice-5":{"type":"choice","options":["Да","Нет"],"explanations":["Естественно! 😊Углы $\\angle{A}$ и $\\angle{B}$ являются соответственными. Их равенство определяет параллельность $a$ и $b$, так как если соответственные углы равны, то прямые параллельны. \circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
\circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
«Признак» или «теорема»?
Все доказанные признаки параллельности прямых так или иначе в научном понимании является теоремами. При этом, тем не менее, в формулировках слово «теорема» не фигурировало: мы все время пользовались обозначением «признак».
Причина здесь — амбивалентность, создаваемая словосочетанием «теорема параллельности». Есть аксиома параллельности, а есть, значит, еще и теорема? Тогда аксиома совсем не аксиома, если ей можно противопоставить теорему параллельности. Замена «теорема» на «признак» разрешает данную двойственность.
Есть, конечно, еще одна причина… Но это разговор для целого отдельного урока. Этот урок, к слову, следующий. Загляните.
{"questions":[{"content":"Время подвести итог. Выберите из предложенных вариантов три доказанных нами признака параллельности прямых. \\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
\\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
ОглавлениеВВЕДЕНИЕЧасть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел.  Тригонометрическая форма комплексного числа. Тригонометрическая форма комплексного числа.17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 32. График функции. Способы задания функций.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения).  60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. 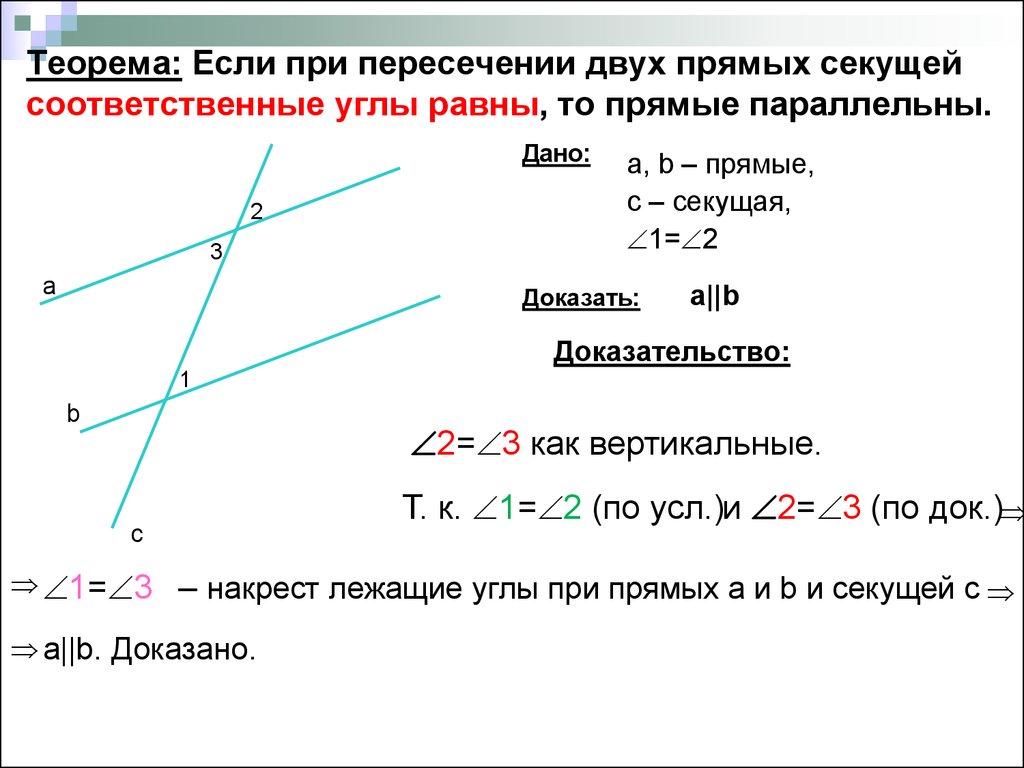 § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. 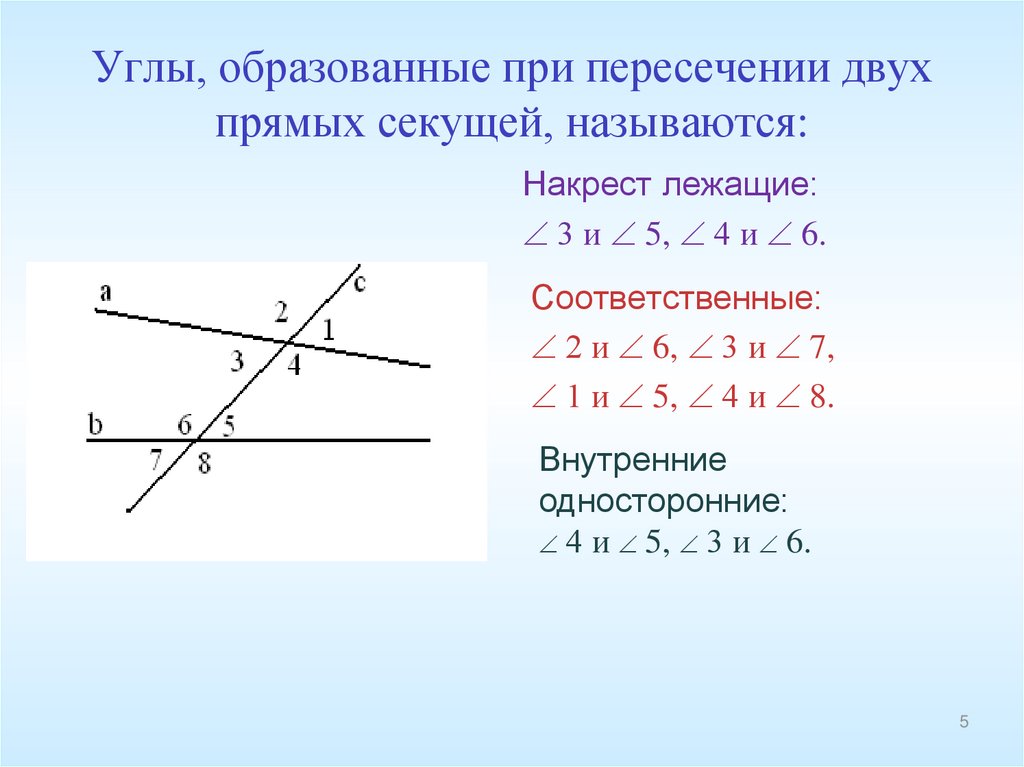 Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
важнейших теорем геометрии - PraxisMathGuru: сайт №1 для сдачи экзамена Praxis Math 5161!
Какие ключевые теоремы геометрии вы должны обязательно знать для экзамена Praxis 5161?Вы должны хорошо знать и, если применимо, доказать следующие теоремы.
Конгруэнтные дополнения / дополнения Теорема: Если 2 угла являются дополнительными или дополнительными к одному и тому же углу (или к конгруэнтным углам), то они конгруэнтны.
Вертикальные углы Теорема: Вертикальные углы равны.
Теоремы о параллельных прямых:
- Альтернативные внутренние углы Теорема: Если две параллельные прямые пересекаются секущей, то обе пары альтернативных внутренних углов равны.
- Альтернативные внешние углы Теорема: Если две параллельные прямые пересечены секущей, то обе пары альтернативных внешних углов равны.
- Последовательные внутренние углы Теорема: Если две параллельные прямые пересечены секущей, то обе пары последовательных внутренних углов являются дополнительными.
- Альтернативные внутренние углы Обратная теорема: Если две прямые пересечены секущей так, что внутренние углы равны, то прямые параллельны.
- Альтернативные внешние углы Обратная теорема: Если две прямые пересечены секущей так, что альтернативные внешние углы равны, то прямые параллельны.
- Смежные внутренние углы Обратная теорема: Если две прямые пересечены секущей так, что последовательные внутренние углы являются дополнительными, то прямые параллельны.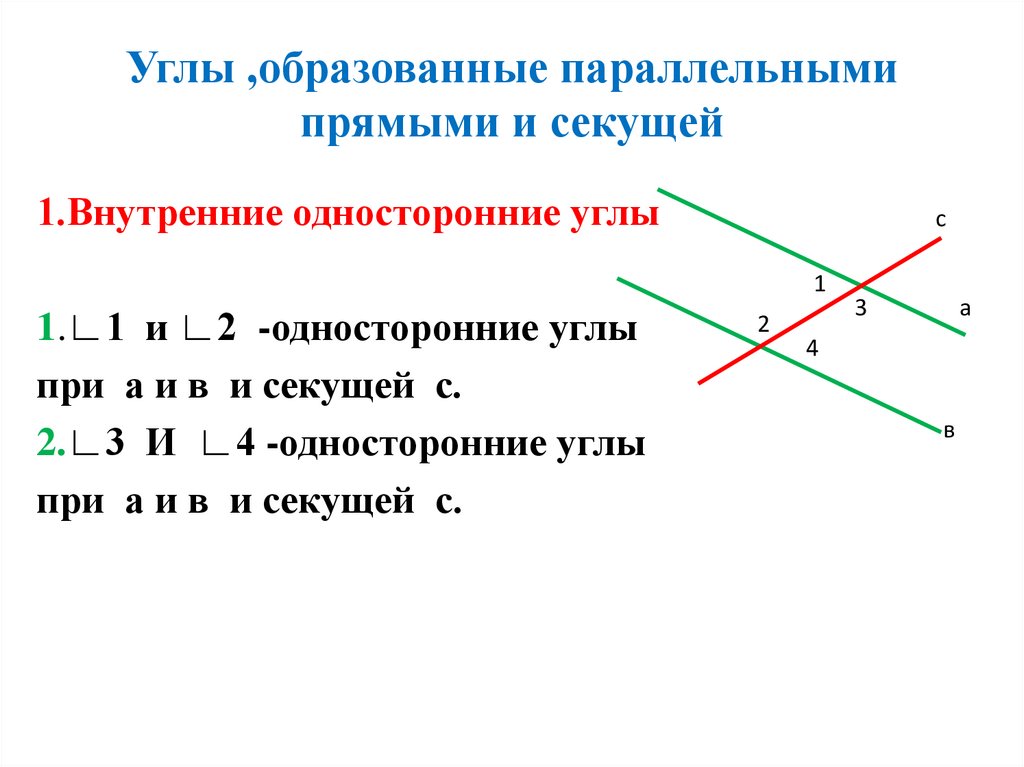
Теорема о треугольнике:
- Теорема о сумме треугольника: Сумма внутренних углов равна 180 градусам.
- Внешний угол Теорема: Мера внешнего угла треугольника равна сумме мер двух его несмежных внутренних углов.
- Теорема о 3-х углах: Если два угла одного треугольника равны двум углам другого треугольника, то 3-й угол также равен.
- Теорема о соответствии угла-угла-стороны (AAS): Если два угла и не заключенная между ними сторона одного треугольника равны двум углам и соответствующей не заключенной между ними стороне второго треугольника, то эти два треугольника равны.
- Углы при основании Теорема: Если две стороны треугольника равны, то равны и противоположные им углы.
- Углы при основании Обратная теорема: Если два угла треугольника равны, то стороны, противоположные им, равны.
- P эрпендикулярная биссектриса Теорема: Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от концов отрезка.
- Теорема о биссектрисе перпендикуляра Обратное: Если точка равноудалена от концов отрезка, то она находится на серединном перпендикуляре к отрезку.
- Биссектриса угла Теорема: Если точка лежит на биссектрисе угла, то она равноудалена от двух сторон угла.
- Обратная биссектриса угла: Если точка находится внутри угла, равноудаленная от его сторон, то она лежит на биссектрисе угла.
- Теорема о середине отрезка: Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и половине третьей стороны.
- Неравенство треугольника: Если одна сторона треугольника длиннее другой стороны, то угол, противоположный самой длинной стороне, больше угла, противоположного меньшей стороне.
Параллелограмм Теоремы:
- Если четырехугольник является параллелограммом, то его противоположные стороны конгруэнтны.
- Если четырехугольник является параллелограммом, то его смежные углы являются дополнительными.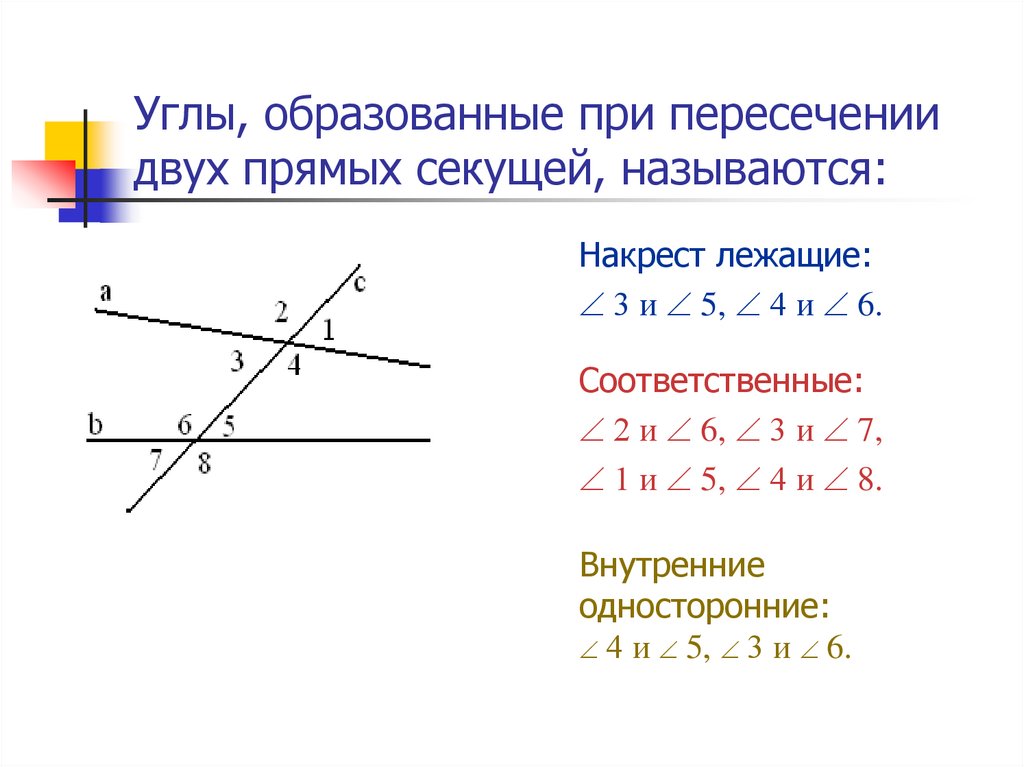
- Если четырехугольник является параллелограммом, то его противоположные углы равны.
- Если четырехугольник является параллелограммом, то его диагонали делят друг друга пополам.
- Если обе пары противоположных сторон четырехугольника равны, то этот четырехугольник является параллелограммом.
- Если обе пары противоположных углов четырехугольника равны, то этот четырехугольник является параллелограммом.
- Если угол четырехугольника является дополнительным к обоим его последовательным углам, то четырехугольник является параллелограммом.
- Если параллелограмм является ромбом, то его диагонали перпендикулярны.
- Если диагонали параллелограмма перпендикулярны, то это ромб.
Теоремы подобия:
- SSS Теорема подобия : Если длины соответствующих сторон двух треугольников пропорциональны, то треугольники подобны.
- SAS Теорема подобия: Если угол одного треугольника равен углу другого треугольника и длины сторон, включающих эти углы, пропорциональны, то треугольники подобны.
- Теорема пропорциональности треугольника: Если прямая, параллельная одной стороне треугольника, пересекает две другие стороны, то она пропорционально делит 2 стороны.
- Теорема о равных произведениях: Если 2 секущие пересекаются вне круга, произведение длин одной секущей и ее внешнего сегмента равно произведению длин другой секущей и ее внешнего сегмента.
- Биссектрисы соответствующих углов двух треугольников имеют то же отношение, что и пара соответствующих сторон.
- Соответствующие медианы двух подобных треугольников имеют то же отношение, что и пара соответствующих сторон.
- Если 2 хорды пересекаются по окружности, произведение длин отрезков одной хорды равно произведению длин отрезков другой.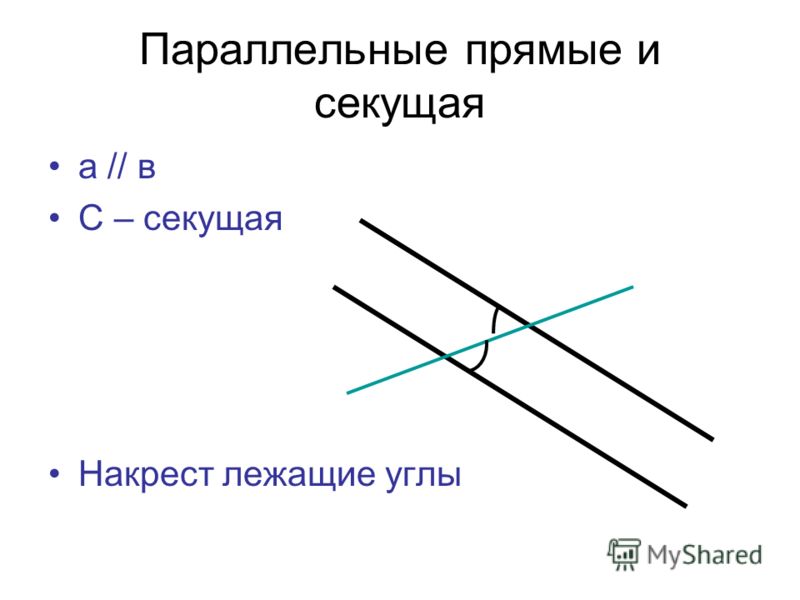
- Если касательная и секущая пересекаются вне окружности, то длина касательной равна среднему геометрическому длины секущей и ее внешнего отрезка.
- Если 2 секущие пересекаются вне круга, то произведение длин одной секущей и ее внешнего сегмента равно длине другой секущей и ее внешнего сегмента.
- Когда высота проведена к гипотенузе прямоугольного треугольника, длина высоты равна среднему геометрическому длин сегментов гипотенузы.
- Когда высота проведена к гипотенузе прямоугольного треугольника, длина каждого катета равна среднему геометрическому смежного отрезка гипотенузы и длины гипотенузы.
Теорема Пифагора
Теоремы окружности:
- Если прямая касается окружности, то прямая перпендикулярна радиусу в точке касания.
- Если два отрезка из одной и той же внешней точки касаются окружности, то они конгруэнтны.
- Если угол вписан в окружность, то его мера равна половине длины дуги, на которую он опирается.
- Если два вписанных угла окружности пересекают одну и ту же дугу, то углы равны.
- Угол в полуокружности является прямым углом (если одна сторона вписанного треугольника равна диаметру окружности, то треугольник прямоугольный).
- Если прямоугольный треугольник вписан в окружность, то гипотенуза является диаметром окружности.
- Хорды, равноудаленные от центра окружности, конгруэнтны.
- В окружности конгруэнтные хорды равноудалены от центра.
- В окружности диаметр, перпендикулярный хорде, делит пополам хорды и ее дуги.
- В окружности диаметр, который делит хорду пополам (не является диаметром), перпендикулярен хорде.
- В окружности серединный перпендикуляр к хорде содержит центр окружности.
- Противолежащие углы четырехугольника, вписанного в окружность, являются дополнительными.
- Угол, образованный касательной и хордой, равен половине длины дуги, на которую он опирается.
- Мера угла, образованного двумя прямыми, пересекающимися внутри окружности, равна половине суммы мер дуг, на которые она опирается.
- Угол, образованный двумя прямыми, пересекающимися вне круга, равен половине разности мер дуг, на которые он опирается.
Теоремы об углах многоугольника:
* Сумма внутренних углов n-стороннего многоугольника равна (n-2)180 градусов.
* Сумма внешних углов n-стороннего многоугольника равна 360 градусов.
Комментарии? Напишите мне по адресу [email protected]
- * Указывает обязательное поле
Имя *
Первый
Последний
Электронная почта *
Комментарий *
Представлять на рассмотрение
Раздел 7.
 6: Касательные и секущие Section_7_6
6: Касательные и секущие Section_7_6 7.6
Касательные и секущие
Начнем с некоторых вопросов о параллельных прямых и круги.
- Теорема 7.14:
Параллельные секущие пересекают конгруэнтные дуги между собой на окружности.
| Дано:
$\overleftrightarrow{AB}\parallel \overleftrightarrow{CD}$ Докажите: $\overparen{AC}\cong\overparen{BD}$ Доказательство: Нарисуйте аккорд $\overline{BC}$. Поскольку $\overleftrightarrow{AB}\parallel \overleftrightarrow{CD}$, у нас есть $\angle 1\cong \angle 2$. С $m\overparen{AC}=2\cdot m\угол 1$ и $m\overparen{BD}=2\cdot m\угол 2$, то имеем $m\overparen{AC}=m\overparen{BD}$, так что $\overparen{AC}\cong\overparen{BD}$. | |
- Теорема 7.15:
Если секущая и касательная к окружности параллельны, то они пересекают
конгруэнтные дуги между ними на окружности.

| Дано:
$\overleftrightarrow{AT}$ касается $\odot P$ в точке $T$.
$\overleftrightarrow{BC}\parallel \overleftrightarrow{AT}$. Доказать: $\overparen{BT}\cong\overparen{CT}$ Доказательство: мы рисовать диаметр $\overline{TQ}$. Этот диаметр перпендикулярен касательная $\overleftrightarrow{AT}$. Так как касательная и секущая $\overleftrightarrow{BC}$ параллельны, диаметр перпендикулярен также для аккорда $\overline{BC}$. Но такой диаметр перпендикуляр хорде делит хорду и ее дуги пополам. Поэтому $m\overparen{BQ}=m\overparen{CQ}$. Две дуги $\overparen{TBQ}$ и $\overparen{TCQ}$ — полуокружности. Использование добавления дуги Постулат, тогда мы знаем, что $\overparen{BT}\cong\overparen{CT}$. | |
- Теорема 7.16:
Параллельные касательные к окружности пересекают конгруэнтные дуги между собой.
Дано:
$\overleftrightarrow{AT}$ и $\overleftrightarrow{BQ}$ касаются
$\odot P$ в $T$ и $Q$ соответственно.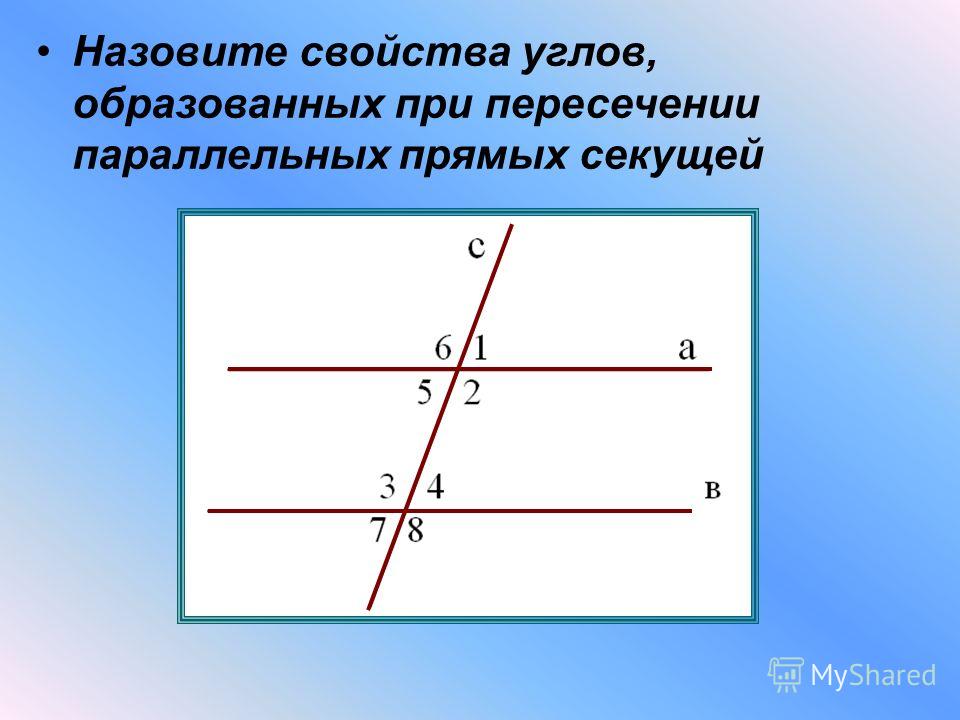 $\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$. $\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$.Доказать: $\overparen{TXQ}\cong\overparen{TYQ}$ | |
Доказательство: это все
слишком заманчиво предположить (из-за картинки), что
$\overleftrightarrow{PT}$ и $\overleftrightarrow{PQ}$ одинаковы
линия. Они есть, но это требует некоторого объяснения.
$\overleftrightarrow{PT}\perp \overleftrightarrow{AT}$ в $T$.
Любая линия, перпендикулярная $\overleftrightarrow{AT}$, будет
также перпендикулярно $\overleftrightarrow{BQ}$, так как
$\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$.
Поэтому $\overleftrightarrow{PT}\perp\overleftrightarrow{BQ}$.
Мы знаем также, что
$\overleftrightarrow{PQ}\perp\overleftrightarrow{BQ}$, так как это
радиус, проведенный к точке касания. Здесь только один
перпендикуляр к $\overleftrightarrow{BQ}$, проведенный через точку $P$, поэтому
$\overleftrightarrow{PT}$ и $\overleftrightarrow{PQ}$ должны быть
та же линия. Тогда $\overparen{TXQ} и $\overparen{TYQ} оба
полуокружности, значит, они равны.
Все это приводит к теореме о мере угла, образованного касательной и хордой.
- Теорема 7.17:
Теорема о касательной хорде
Мера угла, образованного касательным отрезком а хорда, проведенная к точке касания, равна половине меры перехваченная дуга.
| Дано:
$\overline{AT}$ касается окружности в точке $T$. Доказать: $m\angle ATB=\dfrac{1}{2}m\overparen{TB}$ Анализ: Есть три случая: $\angle ATB$ прямой, $\angle ATB$ острый и $\угол ATB$ тупой. Мы разберемся с первыми двумя и оставим третий для упражнений. | |
Случай 1. Если $\angle ATB$ — прямой угол, тогда $\overline{TB}$ — диаметр и дуга $\overparen{TB}$ — полуокружность. Мера угла 90, в то время как мера дуги равна 180. Мера угла действительно, половина меры пересекаемой дуги.
Вариант 2:
Если $\угол ATB$ острый, то проведем хорду $\overline{BC}$, параллельную
касательная $\overleftrightarrow{AT}$. $м\угол 1=м\угол 2$;
$м\угол
2=\frac{1}{2}m\overparen{TC}$; $m\overparen{TC}=m\overparen{TB}$ (поскольку
$\overline{BC}\parallel\overleftrightarrow{AT}$), поэтому
$\frac{1}{2}m\overparen{TC}=\frac{1}{2}m\overparen{TB}$. Затем
$м\угол
ATB=\frac{1}{2}m\overparen{TB}$. $м\угол 1=м\угол 2$;
$м\угол
2=\frac{1}{2}m\overparen{TC}$; $m\overparen{TC}=m\overparen{TB}$ (поскольку
$\overline{BC}\parallel\overleftrightarrow{AT}$), поэтому
$\frac{1}{2}m\overparen{TC}=\frac{1}{2}m\overparen{TB}$. Затем
$м\угол
ATB=\frac{1}{2}m\overparen{TB}$. | |
Мы рассмотрели углы, образованные линиями, которые пересекаются внутри круга и по (специальным) линиям, которые пересекаются на круг. Теперь рассмотрим прямые, которые пересекаются вне круга.
- Теорема 7.18:
Мера угла, образованного двумя секущими, секущей и тангенсом,
или две касательные, пересекающиеся в точке вне круга, составляют половину
разница перехваченных дуг.
Опять же, есть три случая для рассмотрения. Докажем первое один, а два других оставьте для упражнений.
Данный: $\overline{ABC}$ и $\overline{ADE}$ — секущие окружности.
Докажите: $m\угол A=\frac{1}{2}\left(m\overparen{CE}-m\overparen{BD}\right)$
Доказательство:
Теорема о внешнем угле, $m\угол 2=m\угол 1+m\угол A$.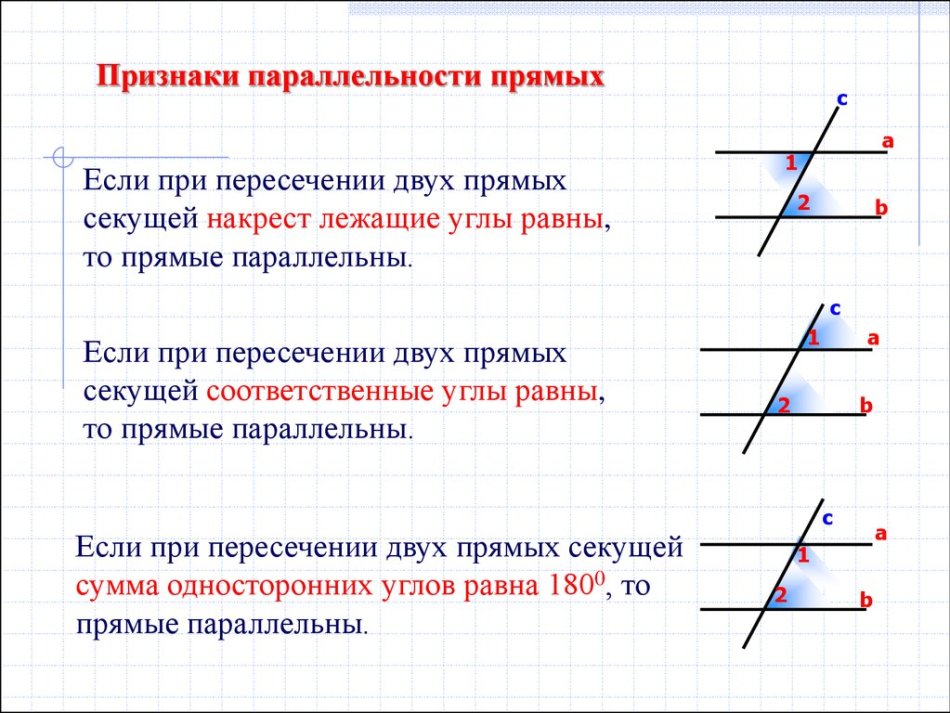

 ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}
ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}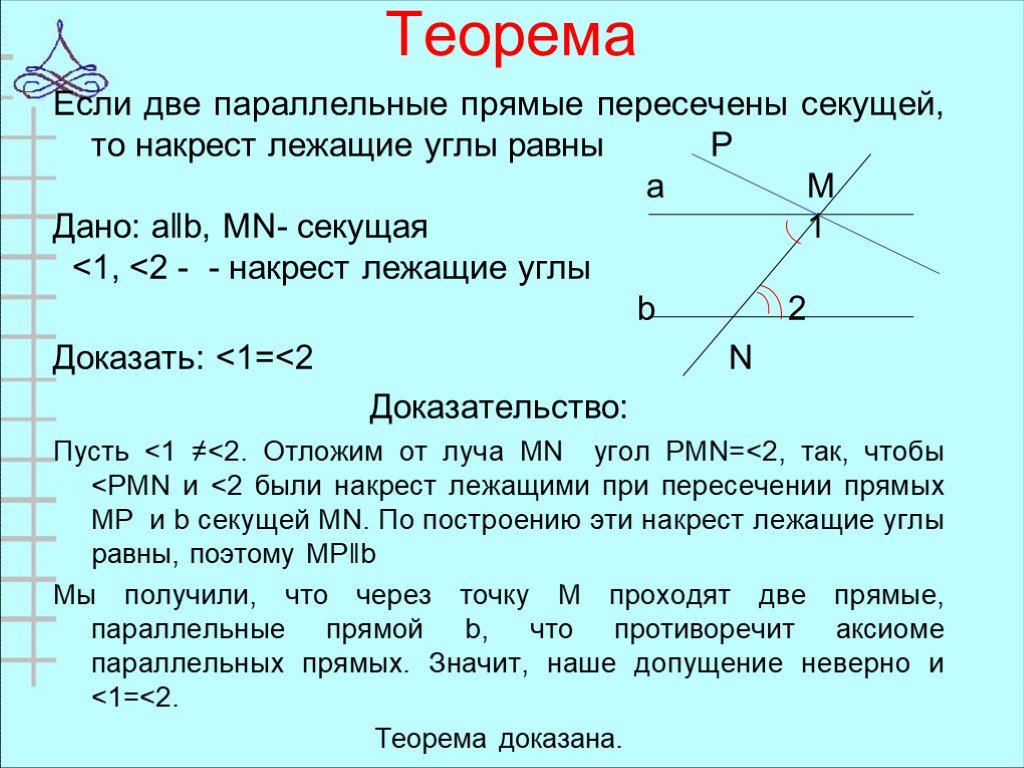 Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.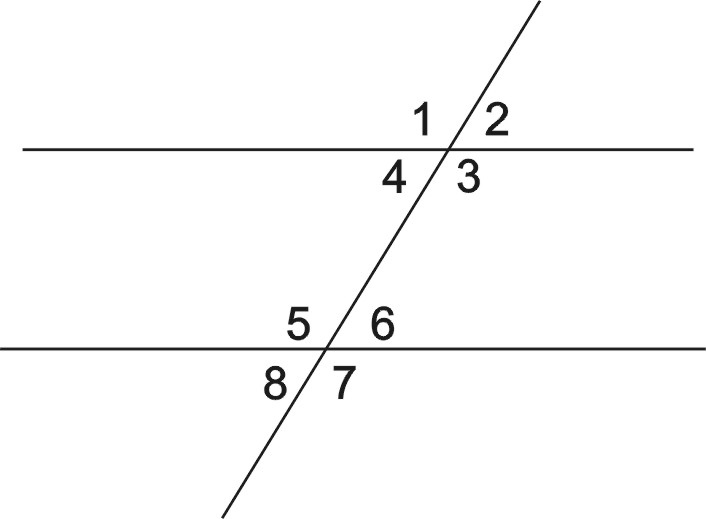 \circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
\circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$. \\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
\\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}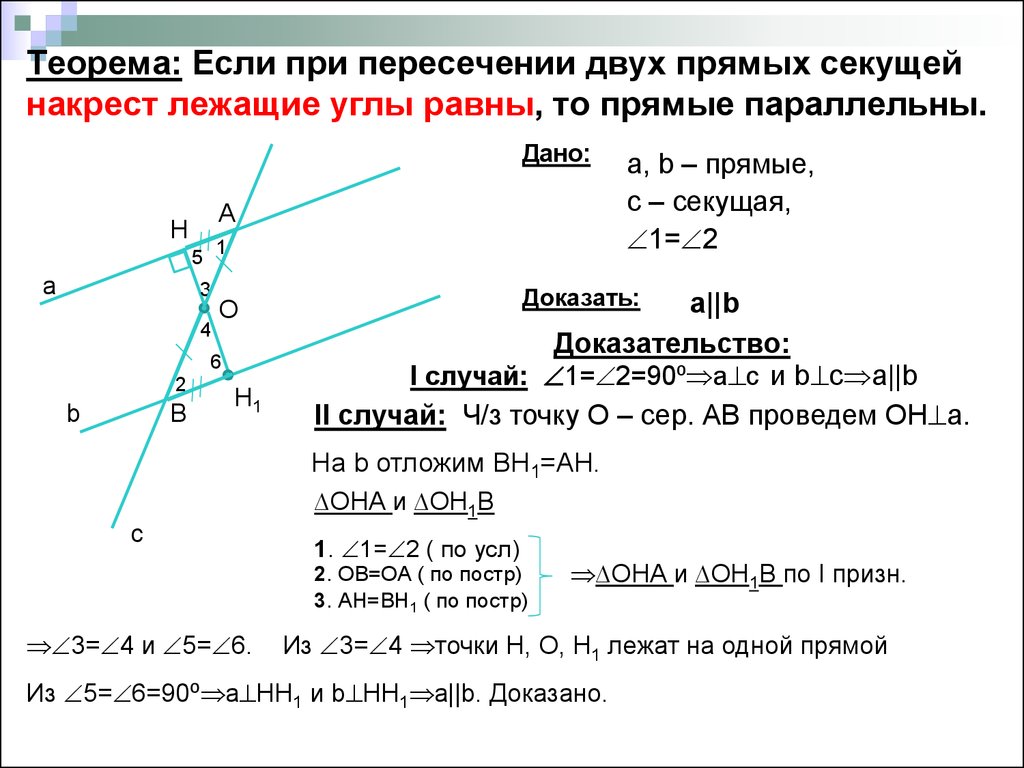 )
)