Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис. 1). Найдем .
1). Найдем .
Решение:
Из теоремы косинусов имеем:
Откуда
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).
Решение. Из формул (1) и (2) находим:
Используя онлайн калькулятор для arcsin и arccos находим углы A и B:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Решение:
Найдем сторону c используя теорему косинусов:
Далее, из формулы
найдем cosA:
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: и (Рис. 2). Найти сторону c и углы A и B.
2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
Вычисления выше легко производить инженерным онлайн калькулятором.
Из формулы (3) найдем cosA:
Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Решение:
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Откуда
Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Ответ:
По двум сторонам и углу между ними. Параметры треугольника
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.
 25: Сравнение углов и сторон в треугольниках
25: Сравнение углов и сторон в треугольниках- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4822
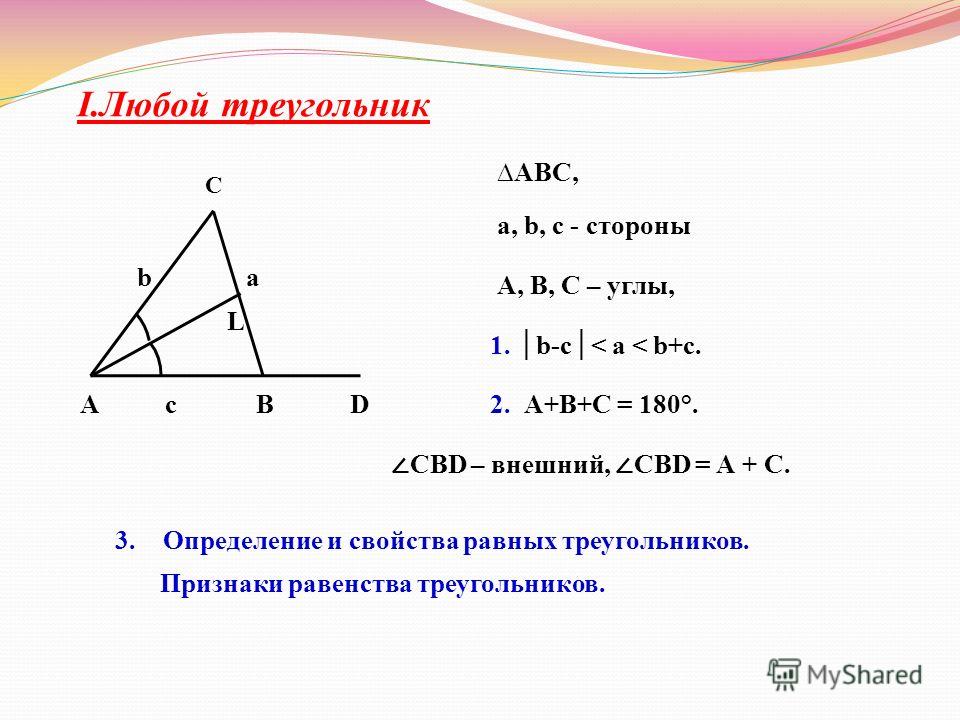
Теоремы о неравенстве и порядок углов и сторон треугольников.
Теоремы SAS и SSS о неравенстве
Посмотрите на треугольник ниже. Даны стороны треугольника. Сможете ли вы определить, какой из углов больше? Наибольший угол будет напротив 18, потому что это самая длинная сторона. Точно так же наименьший угол будет лежать напротив 7, самой короткой стороны.
Рисунок \(\PageIndex{1}\) Эта идея на самом деле является теоремой: если одна сторона треугольника длиннее другой стороны, то угол, противоположный более длинной стороне, будет больше, чем угол, противолежащий более короткой стороне.
Верно и обратное: если один угол в треугольнике больше другого угла в этом треугольнике, то сторона, противоположная большему углу, будет длиннее стороны, противоположной меньшему углу.
Мы можем расширить эту идею до двух теорем, которые помогут нам сравнить стороны и углы в двух треугольниках. Если у нас есть два конгруэнтных треугольника \(\Delta ABC\) и \(\Delta DEF\), отмеченные ниже:
Рисунок \ (\PageIndex{2}\)Следовательно, если \(AB=DE\), \(BC=EF\) и \(m\угол B=m\угол E\), то \(AC=DF\ ).
Теперь составим \(m\угол B>m\угол E\). Получится ли это \(AC>DF\)? Да. Эта идея называется теоремой SAS о неравенстве .
Рисунок \(\PageIndex{3}\) Теорема SAS о неравенстве: Если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но угол между ними имеет большую меру, чем угол между ними другого треугольника, то третья сторона первого треугольника длиннее третьей стороны второго треугольника.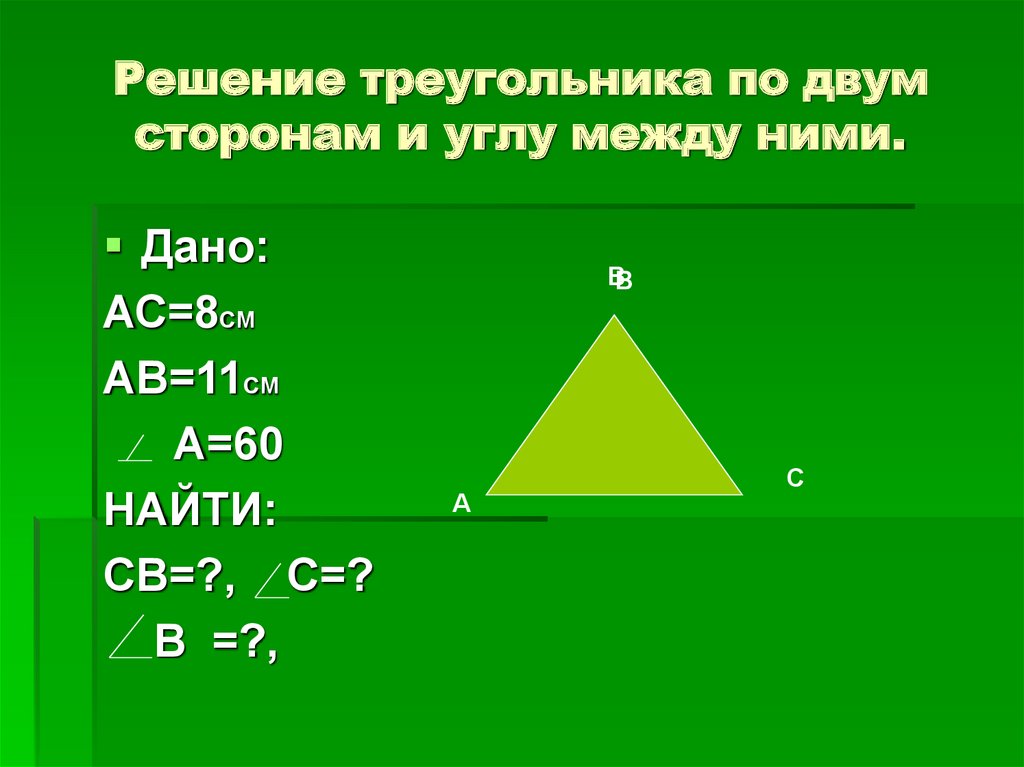
Если \(\overline{AB}\cong \overline{DE}\), \(\overline{BC}\cong \overline{EF}\) и \(m \угол B>m\угол E\), затем \(\overline{AC}>\overline{DF}\).
Если мы знаем третьи стороны в отличие от углов, противоположная идея также верна и называется Теорема о неравенстве SSS .
SSS Теорема о неравенстве: Если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но третья сторона первого треугольника длиннее третьей стороны второго треугольника, то внутренний угол первого треугольника две конгруэнтные стороны больше, чем угол между двумя конгруэнтными сторонами второго треугольника.
Рисунок \(\PageIndex{5}\)Если \(\overline{AB}\cong \overline{DE}\), \(\overline{BC}\cong \overline{EF}\) и \(\ overline{AC}>\overline{DF}\), затем\( m\угол B>m\угол E\).
Что, если бы вам сказали, что стороны треугольника равны 3, 4 и 5? Как определить, какой из углов треугольника больше? Самый маленький?
youtube.com/embed/P9RmhYBwcDk?vq=hd1080″ frameborder=»0″ allowfullscreen=»true»>Пример \(\PageIndex{1}\)
Если \(\overline{XM}\) является медианой \(\Delta XYZ\) и \(XY>XZ\), что мы можем сказать о \(m\угол 1\) и \(m\угол 2\)?
Рисунок \(\PageIndex{6}\)Решение
M является серединой \(\overline{YZ}\), поэтому \(YM=MZ\). \(MX=MX\) по рефлексивному свойству, и мы знаем \(XY>XZ\).
Мы можем использовать обратную теорему о неравенстве SSS, чтобы сказать \(m\угол 1>m\угол 2\).
Пример \(\PageIndex{2}\)
Ниже показан равнобедренный треугольник \(\Delta ABC\). Перечислите все, что вы можете о сторонах и углах треугольника и почему.
Рисунок \(\PageIndex{7}\)Решение
M является серединой \(\overline{YZ}\), поэтому \(YM=MZ\). \(MX=MX\) по рефлексивному свойству, и мы знаем \(XY>XZ\).
\(AB=BC\), потому что он дан.
\(m\угол A=m\угол C\), потому что если стороны равны, то их противоположные углы должны быть равны. .
.
\(AD Пример \(\PageIndex{3}\) Перечислите стороны по порядку, от самой короткой до самой длинной. 9{\circ}\) — наименьший угол, поэтому \(AB\) — самая короткая сторона. По порядку ответ: \(AB\), \(BC\), \(AC\). Пример \(\PageIndex{4}\) Перечислите углы по порядку, от большего к меньшему. Решение Как и в случае со сторонами, наибольший угол находится напротив самой длинной стороны. Самая длинная сторона равна \(BC\), поэтому наибольший угол равен \(\угол A\). Далее будет \(\угол B\), а затем \(\угол C\). Пример \(\PageIndex{5}\) 9{\circ}\). Опять же, по теореме, представленной в этом разделе, порядок сторон от наименьшей к наибольшей таков: \(BD\), \(CD\) и \(BC\). По теореме о неравенстве SAS мы знаем, что \(BC>DE\), поэтому порядок всех сторон будет следующим: \(BD\), \(CE\), \(CD\), \(DE \), \(ДО Н. В вопросах 1-3 перечислите стороны в порядке от самой короткой до самой длинной. Чтобы просмотреть ответы на вопросы, откройте этот PDF-файл и найдите раздел 5.6. Э\).
Э\). Обзор
Обзор (Ответы)
Ресурсы
Словарь
Срок Определение Теорема SAS о неравенстве Теорема SAS о неравенстве утверждает, что если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но прилежащий угол одного треугольника имеет большую меру, чем прилежащий угол другого треугольника, то третья сторона первого треугольника равна длиннее третьей стороны второго треугольника. 
Теорема SSS о неравенстве Теорема о неравенстве SSS утверждает, что если две стороны треугольника конгруэнтны двум сторонам другого треугольника, но третья сторона первого треугольника длиннее третьей стороны второго треугольника, то угол между двумя сторонами первого треугольника конгруэнтных сторон больше, чем угол между двумя конгруэнтными сторонами второго треугольника. Теорема о сумме треугольников Теорема о сумме треугольников утверждает, что три внутренних угла любого треугольника в сумме составляют 180 градусов.
Дополнительные ресурсы
Интерактивный элемент
Видео: сравнение углов и сторон треугольников. Принципы — основы
Задания: сравнение углов и сторон треугольников.0023 Практика: сравнение углов и сторон треугольников
Реальный мир: теорема о сумме треугольников
Эта страница под названием 4. 25: Сравнение углов и сторон в треугольниках распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
25: Сравнение углов и сторон в треугольниках распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.
Заказ сторон и углов треугольника
В треугольнике стороны, противоположные углам, расположены в том же порядке, что и углы, и наоборот. Если мы упорядочим три угла треугольника от меньшего к большему, стороны, противоположные углам, будут в том же порядке.
Таким образом, сторона, противоположная наибольшему углу, будет самой длинной стороной. Тот же образец можно применить к углам, когда даны стороны. Угол, противоположный наименьшей стороне, будет наименьшим углом.
В треугольнике выше наименьшая сторона АС (= 6 см) лежит против наименьшего угла 24°, следующая длинная сторона ВС (= 13 см) лежит напротив следующего большего угла 24° и самая длинная сторона АВ (= 15 см) лежит против угла 97°.
Порядок сторон от самой короткой до самой длинной:
AC, BC, AB (или) 6 см, 13 см, 15 см
Порядок углов от меньшего к большему:
∠B, ∠A, ∠C (или) 24°, 59°, 97°
Пример 1 :
В приведенном ниже ΔGEF расположите стороны от самой короткой до самой длинной.
Отвечать :
Укажите углы от меньшего к большему:
55°, 62°, 63°
Сторона, противоположная наименьшему углу, является самой короткой стороной, а сторона, противоположная наибольшему углу, является самой длинной стороной.
сторона, противоположная 55° —-> GE
сторона, противоположная 62° —-> GF
сторона, противоположная 63° —-> EF
Порядок сторон от самой короткой к самой длинной :
ГЭ, ГФ, ЭФ
Пример 2:
В ΔABC ниже расположите стороны от самой длинной до самой короткой.
Отвечать :
В ΔABC выше,
m∠A + m∠B + m∠C = 180°
Замените m∠B = 102° и m∠C = 46°.
м∠A + 102° + 46° = 180°
м∠A + 148° = 180°
Вычтите 148° с каждой стороны. — —> AB
сторона, противоположная 32° —-> BC
Порядок сторон от самой длинной к самой короткой:
AC, AB, BC
Пример 3:
В ΔEFD ниже расположите стороны от самой короткой до самой длинной.
Отвечать :
m∠E = 48°, а оставшиеся два угла m∠F и m∠D равны, то есть 66°.
сторона, противоположная m∠E —-> FD
сторона, противоположная m∠F —-> ED
сторона, противоположная m∠D —-> EF
В ΔEFD выше, самая короткая сторона FD, а оставшиеся две стороны ED и EF равны по длине.
Пример 4:
В приведенном ниже ΔJKL расположите углы от наименьшего к наибольшему.
Ответ:
Упорядочите стороны от самой короткой к самой длинной:
14 ярдов, 16 ярдов, 18 ярдов
Угол, противоположный самой короткой стороне, является наименьшим углом, а сторона, противоположная самой длинной стороне, является наибольшим углом.
угол против стороны длиной 14 ярдов —-> ∠J
угол против стороны длиной 16 ярдов —-> ∠K
угол против стороны длиной 18 ярдов —-> ∠ L
Порядок углов от меньшего к большему:
∠J, ∠K, ∠L
Пример 5:
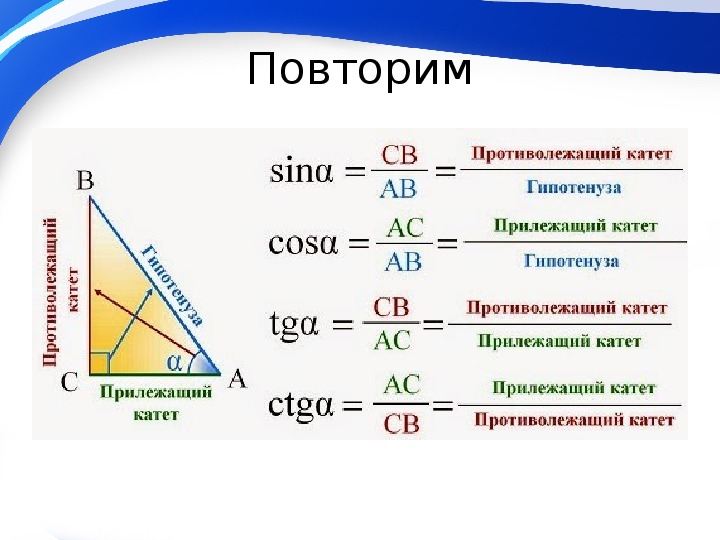
В ΔKLM ниже KL = 18 см, LM = 20 см и KM = 13 см.

 Первые полторы тысяч разложений.
Первые полторы тысяч разложений.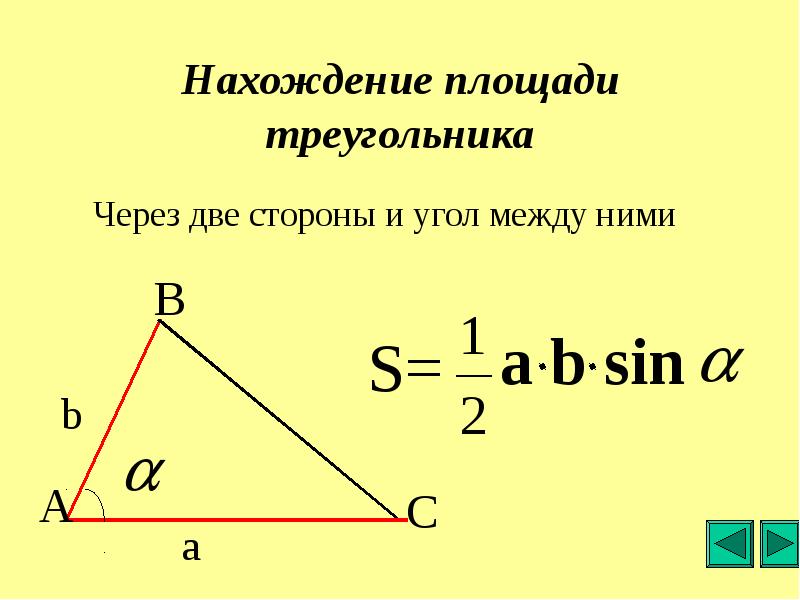 Не все могут отыскать этот калькулятор, поэтому с помощью частных решений , мы предоставляем возможность узнавать параметры треугольника по двум сторонам и углу между ними.
Не все могут отыскать этот калькулятор, поэтому с помощью частных решений , мы предоставляем возможность узнавать параметры треугольника по двум сторонам и углу между ними. В противном случае, непонимание условия задачи влечет за собой неспособность её решить.
В противном случае, непонимание условия задачи влечет за собой неспособность её решить.  9827959392127
9827959392127 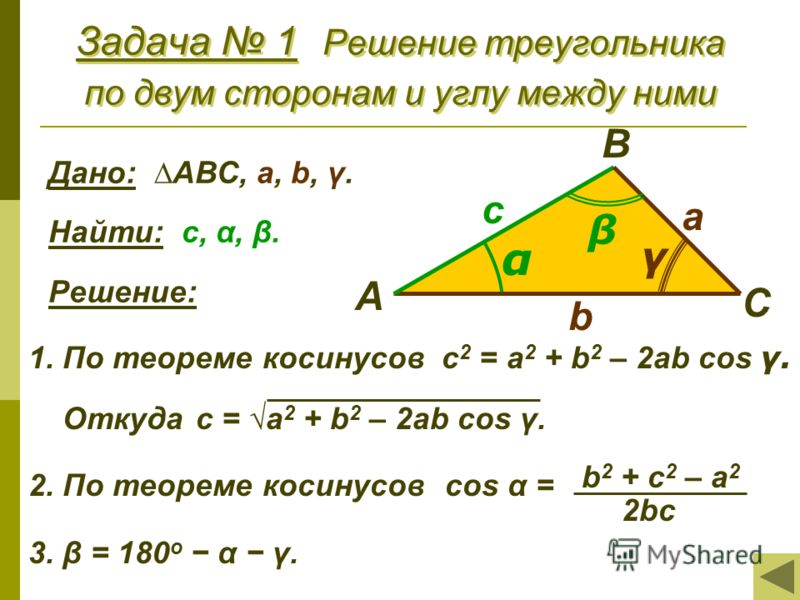
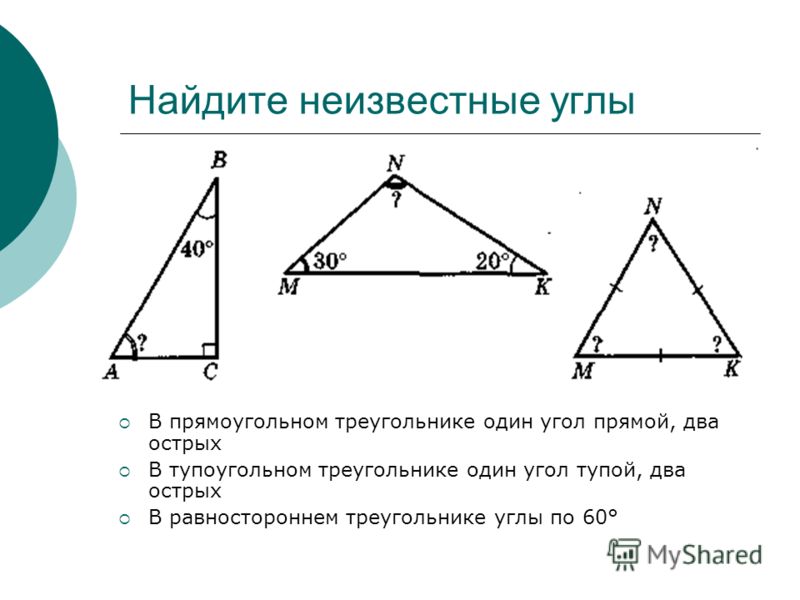 Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн ck12.org/c/geometry
ck12.org/c/geometry