а=6
r=а=6 (см)
с=2пr=2*3,14*6=37,68 кв см
Ответ разместил: Гость
100град-(90+60)=30град
т.к.cab=30грал,то : ab/2=bc
bc=26,4-ab
ab/2=26,4-ab
ab*2=26,4-ab
ab=(26,4-ab)/2
2ab/2=(26,4-ab)/2
(2ab-26,4+ab)/2=0
3ab-26,4=0
ab=8,8см.
Другие вопросы по: Геометрия
Диагонали ромба образуют с его стороной углы, один из которых в два раза меньше другого. вычислите длину меньшей диагонали ромба, если его периметр равен 16 см….
Опубликовано: 01.03.2019 07:50
Ответов: 2
Диктант из 10 слов с безударными гласными и парными согласнымив корне. включите в него 2-3 слова которые одинаково звучат но по разному пишутся….
Опубликовано: 01.03.2019 11:00
Ответов: 1
На расстоянии 2 м девочка делает 6 шагов. сколько таких же шагов она сделает, пройдя 10 м? 100 м?…
сколько таких же шагов она сделает, пройдя 10 м? 100 м?…
Опубликовано: 04.03.2019 11:50
Ответов: 3
Расстояние от точки до m до каждой из вершин правильного треугольника abc равно 4 см. найдите расстояние от точки до m до плоскости abc, если ab=6 см (полное решение)…
Опубликовано: 07.03.2019 15:20
Ответов: 3
Высота сд проведенная к основанию ав равнобедренного треугольника авс равна 5 см , а само основание 24 см . наидите радиусы вписанной в треугольник и описанной около треугольника о…
Опубликовано: 07.03.2019 16:00
Ответов: 1
Выберите верные утверждения: а) развитые страны на современном этапе переходят на индустриальный путь развития б) отрасль специализации германии – газовая промышленность в) на раз…
Опубликовано: 07. 03.2019 18:50
03.2019 18:50
Ответов: 1
Знаешь правильный ответ?
Начертим треугольник def так, чтобы угол e ,был прямым. назовите: a)стороны, лежащие против углов d,…
Популярные вопросы
.(Реши с уравнения .в школе 671 ученик, причем девочек в 1,2 раза больше, чем мальчиков. сколько девочек и мальчиков учатся в школе?)….
Опубликовано: 28.02.2019 08:30
Ответов: 2
Вмагазине всего 330 кг яблок и груш, 410 кг яблок и апельсинов, и 320 кг груш и апельсинов. сколько кг фруктов каждого вида в магазине….
Опубликовано: 28.02.2019 22:50
Ответов: 1
Решить уравнения (29-х0+(3х-16)= след.115-(7х—8х)= след.23х-(2х-+8)= след 29-(3х—7х)+(169—8)=…
Опубликовано: 01.03.2019 07:00
Ответов: 3
Вариант №1 1. какое ускорение будет сообщать камню массой 3 кг сила 9 н? 2. каким импульсом обладает тело массой 200 г движущееся со скоростью 18 км/ч? 3. под действием силы тело…
какое ускорение будет сообщать камню массой 3 кг сила 9 н? 2. каким импульсом обладает тело массой 200 г движущееся со скоростью 18 км/ч? 3. под действием силы тело…
Опубликовано: 01.03.2019 20:00
Ответов: 2
Два токаря изготовили за смену 90 деталей. производительность первого токаря на 2 дет./ч больше, чем второго. сколько деталей изготовил каждый токарь за смену, если смена длится 8…
Опубликовано: 02.03.2019 03:20
Ответов: 1
Решите уравнение-52 * x+8 * x=12300….
Опубликовано: 02.03.2019 06:00
Ответов: 3
Сочинение на тему летняя ночь со словам тишь, глушь, ночь, полночь, сыч, камыш, рожь, дрожь….
Опубликовано: 02.03.2019 11:20
Ответов: 3
Какова длина стороны квадрата если его площадь100см в квадрате. ..
..
Опубликовано: 02.03.2019 12:40
Ответов: 3
Укажите верный промежуток-решение неравенства: |2x — 3| < 5…
Опубликовано: 03.03.2019 06:50
Ответов: 1
Токарь за час обрабатывает16 заготовок а его ученик 12 над выполнением сначала работал токарь3часа затем токарь и ученик вместе работали еще в течении3 часов сколько всего заготов…
Опубликовано: 03.03.2019 18:30
Ответов: 3
Больше вопросов по предмету: Геометрия Случайные вопросы
Доказать что треугольник это треугольник
Треугольник
В любом треугольнике три угла и три стороны.
Сумма углов любого треугольника равна .
Против большего угла треугольника лежит большая сторона.
Виды треугольников
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).

- равнобедренным, если две его стороны равны.
- равносторонним, если все три стороны равны,
- разносторонним, если все его стороны разные.
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
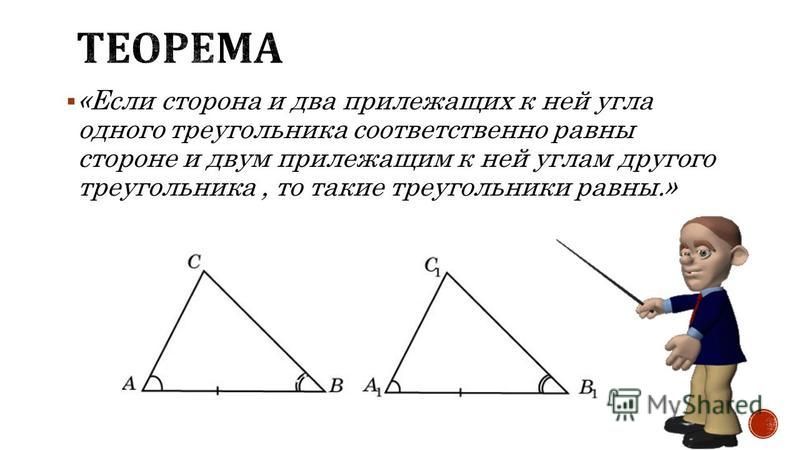
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
Треугольники называются подобными, если их стороны пропорциональны.
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.
Примеры решения задач
| Задание | Доказать, что в равнобокой трапеции диагонали равны. |
| Доказательство | В равнобокой трапеции рассмотрим треугольники и (рис. 1). Так как – общая сторона, то треугольники и равны по первому признаку, а значит, равны все их элементы, т.е. . |
Что и требовалось доказать.
| Задание | В треугольнике стороны см см см. На стороне отмечена точка так, чтобы см. Найти отрезок . |
| Решение | Рассмотрим треугольники и . Запишем отношение сторон и : |
Так как выполняется равенство отношений, то соответствующие стороны треугольников пропорциональны, а также – общий угол. Следовательно, треугольники и – подобны (по второму признаку подобия). Найдем сторону :
Следовательно, треугольники и – подобны (по второму признаку подобия). Найдем сторону :
откуда см.
Признаки равенства треугольников
Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.
Давайте рассмотрим три признака равенства треугольников.
Теорема 1. Равенство треугольников по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
При наложении △A1B1C1 на △ABC вершина A1 совмещается с вершиной A, и сторона A1B1 накладывается на сторону AB, AC — на сторону A1C1.
Сторона A1B1 совмещается со стороной AB, вершина B совпадает с вершиной B1, сторона A1С1 совмещается со стороной AС, вершина C совпадает с вершиной C1.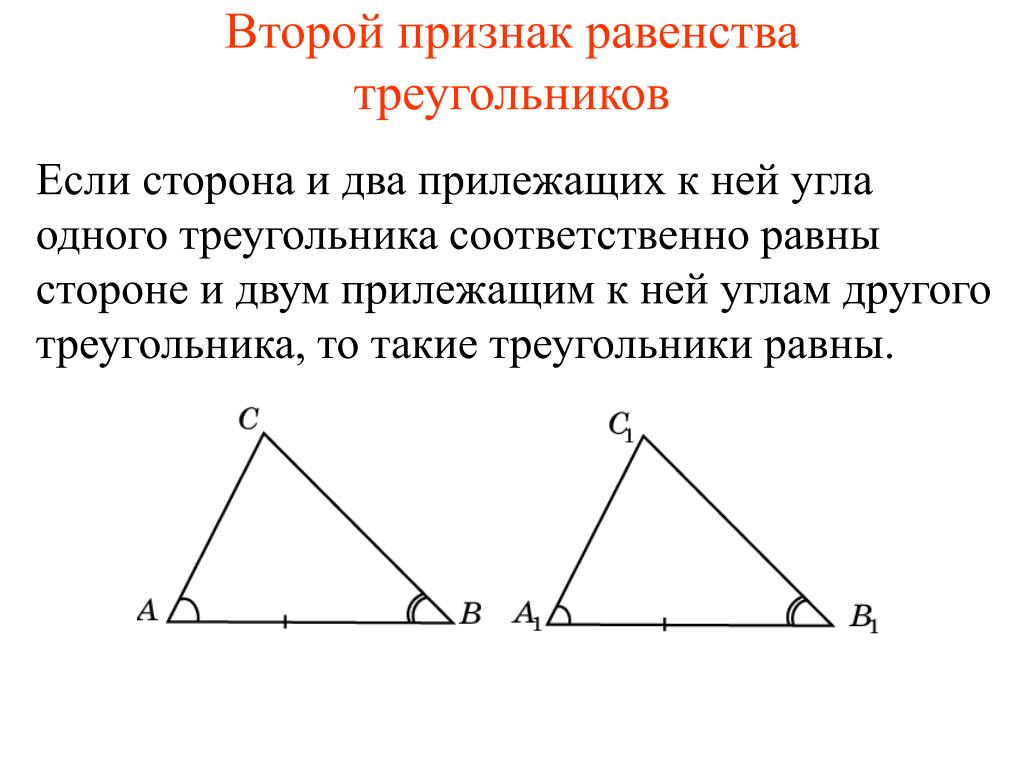
Значит, происходит совмещение вершин В и В1, С и С1.
Второй признак равенства треугольников
Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.
Тогда АС совмещается с A1C1, вершина C совпадает с C1, поскольку мы знаем, что АС = A1C1.
AB накладывается на A1B1, поскольку мы знаем, что ∠A = ∠A1.
CB накладывается на C1B1, поскольку мы знаем, что ∠C = ∠C1.
Вершина B совпадает с вершиной B1.
Третий признак равенства треугольников
Теорема 3. Равенство треугольников по трем сторонам.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство 3 признака равенства треугольников:
Приложим △ABC к △A1B1C1 таким образом, чтобы вершина A совпала с вершиной A1, вершина B — с вершиной B1, вершина C и вершина C1 лежат по разные стороны от прямой А1В1.
Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.
Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.
- Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
- Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.

- Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
- Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
- Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.
Доказать что треугольник это треугольник
Треугольники
Треугольники: равные, равнобедренные. Первый, второй и третий признаки равенства треугольников.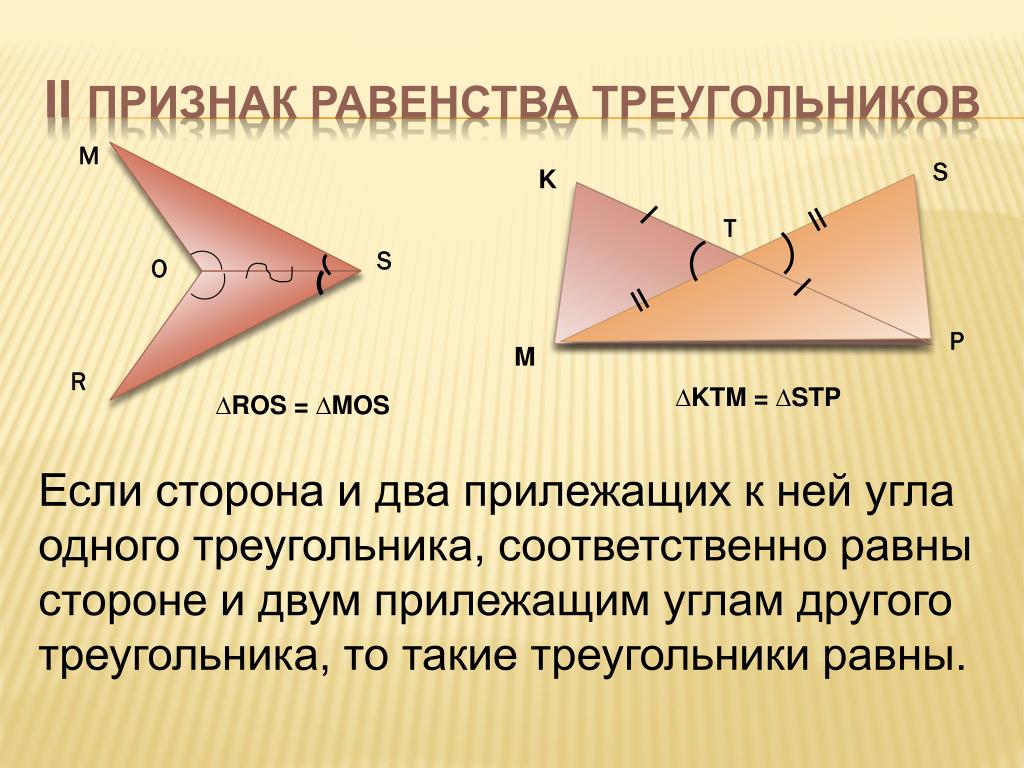 Перпендикуляр, высота, медиана, биссектриса, основание, вершина, боковая сторона. Свойства и признаки равнобедренного треугольника. Серединный перпендикуляр, геометрическое место точек, первая замечательная точка. Подробные доказательства теорем.
Перпендикуляр, высота, медиана, биссектриса, основание, вершина, боковая сторона. Свойства и признаки равнобедренного треугольника. Серединный перпендикуляр, геометрическое место точек, первая замечательная точка. Подробные доказательства теорем.
Треугольник — одна из самых замечательных и самых важных фигур в геометрии. Все знают, как он выглядит. Но что же такое треугольник? Допустим, что треугольник — это замкнутая ломаная из трех звеньев. Можно представить себе треугольник, сделанный из проволоки. Но известно, что у него есть площадь. Поэтому треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Представьте себе треугольник, сделанный из фанеры или вырезанный из картона.
Очень важным моментом при решении геометрических задач является нахождение равных треугольников. Очевидно, что если у двух треугольников все стороны и углы окажутся соответственно равными, то и треугольники будут равны. На практике равные треугольники определяют, прикладывая их друг к другу. Если треугольники совпадут при наложении, значит, они равны. Этот способ и позволяет дать определение равных треугольников.
На практике равные треугольники определяют, прикладывая их друг к другу. Если треугольники совпадут при наложении, значит, они равны. Этот способ и позволяет дать определение равных треугольников.
Но вот, допустим, у каждого из двух треугольников есть две стороны, которые равны 5 см и 6 см, и какой-то из углов равен 50°. Можно ли утверждать, что треугольники равны? Оказывается, нет. На рисунке вы видите два треугольника с указанными размерами. Они не равны.
При каких же минимальных условиях треугольники будут равны? Существуют по крайней мере три признака равенства треугольников, когда по равенству некоторых сторон и углов можно абсолютно точно сказать, что они равны. Например, если бы угол 50° был образован сторонами длиной 5 см и 6 см, то треугольники были бы равны между собой.
Опорный конспект «Треугольники»Треугольник — это трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает. Сумма длин всех трех сторон треугольника называется периметром. Треугольники называются равными, если совпадают при наложении. Если равные треугольники наложить так, что они совпадут, то окажется, что в равных треугольниках против равных сторон лежат равные углы, а против равных углов лежат равные стороны.
Треугольники называются равными, если совпадают при наложении. Если равные треугольники наложить так, что они совпадут, то окажется, что в равных треугольниках против равных сторон лежат равные углы, а против равных углов лежат равные стороны.
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Действительно, если наложить треугольники друг на друга равными углами, то совпадут и равные стороны. Значит, совпадут и оставшиеся две вершины.
Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если наложить треугольники друг на друга равными сторонами, то совпадут углы, прилежащие к этим сторонам. Значит, совпадут и третьи вершины.
Перпендикуляром, опущенным из данной точки на данную прямую, называется отрезок прямой, перпендикулярной данной, проходящей через данную точку, с концами в данной точке и в точке пересечения с данной прямой.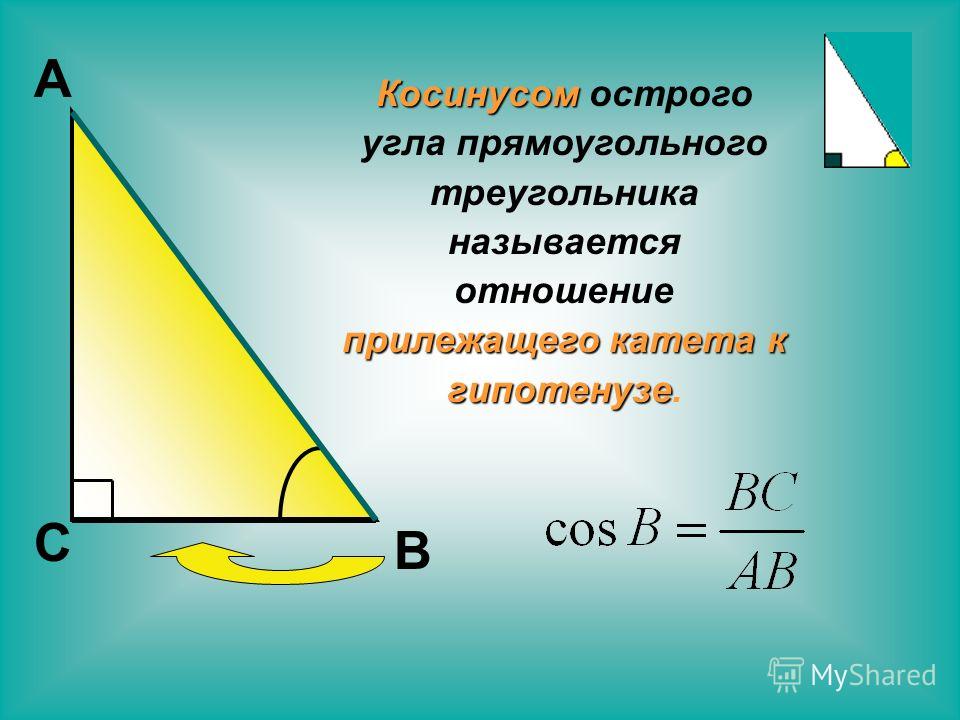 Точка пересечения называется основанием перпендикуляра.
Точка пересечения называется основанием перпендикуляра.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, заключенный между вершиной и точкой пересечения биссектрисы угла и стороны треугольника.
Треугольник, у которого две стороны равны, называется равнобедренным. Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина напротив этой стороны — вершиной равнобедренного треугольника. Причем названия «основание», «боковые стороны» и «вершина» равнобедренного треугольника сохраняются, как бы треугольник ни был расположен.
Свойства равнобедренного треугольника. 1. В равнобедренном треугольнике углы при основании равны. 2. Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является высотой и медианой.
2. Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является высотой и медианой.
Признак равнобедренного треугольника (по двум углам). Если в треугольнике два угла равны, то он равнобедренный.
Есть еще три признака равнобедренного треугольника. Треугольник является равнобедренным, если:
- высота треугольника является и медианой;
- высота треугольника является и биссектрисой;
- медиана треугольника является и биссектрисой (доказывается продлением медианы на ее длину).
Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.
Свойство точек серединного перпендикуляра. Любая точка серединного перпендикуляра равноудалена от концов отрезка.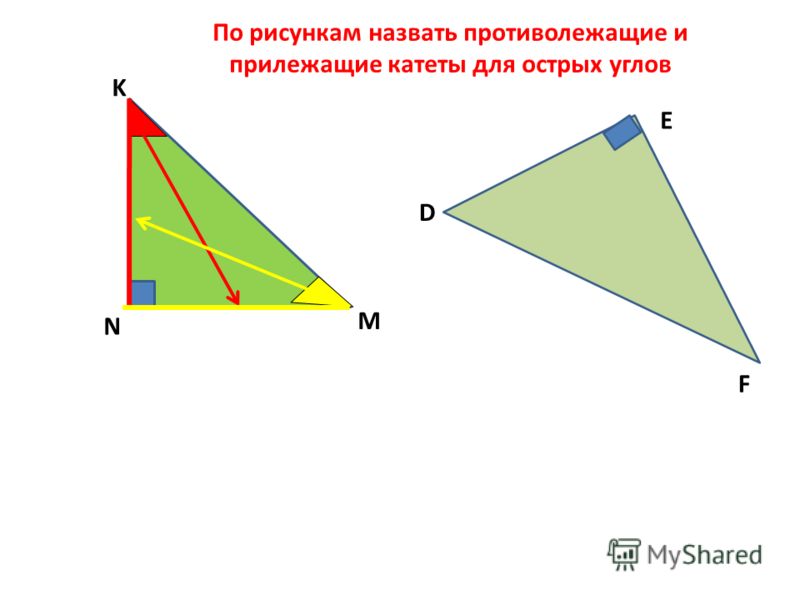 Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Геометрическое место точек (ГМТ) — это множество всех точек плоскости, обладающих общим свойством. Например, все точки серединного перпендикуляра равноудалены от концов отрезка, и все точки плоскости, равноудаленные от концов отрезка, лежат на серединном перпендикуляре.
Первая замечательная точка. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке — центре описанной окружности.
Презентация по геометрии на тему Треугольники (7 класс) доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по геометрии на тему Треугольники (7 класс), предмет презентации: Геометрия. Этот материал в формате pptx (PowerPoint) содержит 21 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 21 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
*
Пожванова Г.А.
Глава II
Треугольники
*
Пожванова Г.А.
УРОК 1
*
Пожванова Г.А.
Содержание:
Найди треугольники
Определение треугольника.
Периметр треугольника
Задача
Тест
Практическое задание
Тест
Задача
Домашнее задание
Для учителя
Н
*
Пожванова Г. А.
А.
1
2
3
4
5
6
7
8
9
10
11
Найдите треугольники
Оглавление
*
Пожванова Г.А.
А
В
С
Треугольник АВС, обозначается Δ АВС,
точки А, В, С – вершины; отрезки АВ, АС, ВС – стороны,
Сумма длин сторон треугольника называется периметром
P = AB + BC + AC
Оглавление
*
Пожванова Г.А.
задание 87.
87.Начертите треугольник и обозначьте его вершины
буквами М, N и Р.
а) Назовите все углы и стороны треугольника;
б) с помощью масштабной линейки измерьте стороны
и найдите периметр треугольника.
Забыл, что такое периметр? Нажми здесь.
Оглавление
*
Пожванова Г. А.
А.
88.Начертите треугольник DEF так,
чтобы угол Е был прямым. Назовите:
а) стороны, лежащие против углов D, E, F;
.
Оглавление
*
Пожванова Г.А.
88.Начертите треугольник DEF так,
чтобы угол Е был прямым. Назовите:
б) углы, лежащие против сторон DE, EF, FD;
DE
EF
FD
Оглавление
*
Пожванова Г.А.
88.Начертите треугольник DEF так,
чтобы угол Е был прямым. Назовите:
в) углы, прилежащие к сторонам DE, EF, FD.
DE
EF
FD
Оглавление
Начертите треугольник АВС и проведите отрезок, соединяющий вершину А с серединой противоположной стороны.
*
Пожванова Г.А.
Практическое задание
Оглавление*
Пожванова Г.А.
Начертите треугольник МNР. На стороне МР отметьте произвольную точку К, и соедините ее с вершиной, противолежащей стороне МР.
Оглавление
*
Пожванова Г.А.
Какие углы: а) треугольника ОЕК, прилежащие к стороне ЕК; б) треугольника МNР, прилежащие к стороне МN.
Е
О
К
M
N
P
M
N
P
M
N
P
M
N
P
M
N
P
M
N
P
M
N
P
Оглавление
*
Пожванова Г.
Назовите угол: а) треугольника ОЕК, заключенный между сторонами ОЕ и ОК; б) треугольника МNР, заключенный между сторонами NР и РМ.
Е
О
К
P
M
N
Оглавление
*
Пожванова Г.А.
Между какими сторонами: а) треугольника ОЕК заключен
Е
О
К
N
M
P
ОЕ и ЕК
ОЕ и ОК
ОК и ЕК
MN и PN
PN и PM
NP и MP
Оглавление
*
Пожванова Г.А.
Упражнение 91
Периметр треугольника равен 48 см, а одна из сторон равна 18 см. Найдите две другие стороны, если их разность равна 4,6 см.
Дано:ΔАВС, РАВС =48 см,
АС= 18 см, ВС – АВ=4,6см.
Решение.
А
В
С
Оглавление
Проверим?
Забыл, что такое периметр? Нажми здесь.
*
Пожванова Г.А.
Домашнее задание:
Вопросы для повторения к главеII : в. 1;
№ 89, 90, 156
Оглавление
*
Пожванова Г.А.
*
Пожванова Г.А.
*
Пожванова Г.А.
Сумма длин сторон треугольника называется периметром
P = AB + BC + AC
A
B
C
*
Пожванова Г.А.
Решение. Обозначим длину стороны АВ в сантиметрах буквой х см, тогда ВС =( х + 4,6) см;
х + 18 + х + 4,6 = 48
2х = 25,4
х=12,7 см.
АВ = 12,7 см,
ВС = (12,7 + 4,6) см = 17,3 см.
Ответ: 12,7 см и 17,3 см
*
Пожванова Г. А.
А.
Назначение первого урока — ввести понятия треугольника и его элементов.
В результате изучения учащиеся должны уметь объяснить, какая фигура называется треугольником, и назвать его элементы; знать, что такое периметр треугольника.
Во второй главе изучаются признаки равенства треугольников. Они являются основным рабочим аппаратом всего курса геометрии. Доказательства большей части теорем курса строятся по схеме: поиск равных треугольников, доказательство их равенства — следствия, вытекающие из равенства треугольников. Признаки равенства треугольников открывают широкие возможности для решения задач и, таким образом, позволяют накапливать опыт доказательных рассуждений. Доказательства первого и второго признаков состоят в том, что один треугольник совмещается с другим путем наложения, а это означает, что треугольники равны по определению равенства фигур. Этот прием нагляден, понятен учащимся, вполне соответствует их представлениям о равенстве фигур.
На начальном этапе изучения признаков равенства треугольников полезно больше внимания уделять решению задач по готовым чертежам, применяя таблицы и ТСО. В дальнейшем при решении задач данной главы нужно нацеливать учащихся на самостоятельное выполнение рисунка по условию задачи, что во многих случаях помогает быстрее найти и применить подходящий признак равенства треугольников.
В дальнейшем при решении задач данной главы нужно нацеливать учащихся на самостоятельное выполнение рисунка по условию задачи, что во многих случаях помогает быстрее найти и применить подходящий признак равенства треугольников.
Второй важный момент данной главы — введение нового класса задач на построение с помощью циркуля и линейки.
Оглавление
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Смежные углы — определение, свойства, примеры
LearnPracticeDownload
Смежные углы — это углы, которые имеют общую сторону (сторону) и общую вершину, однако они не пересекаются.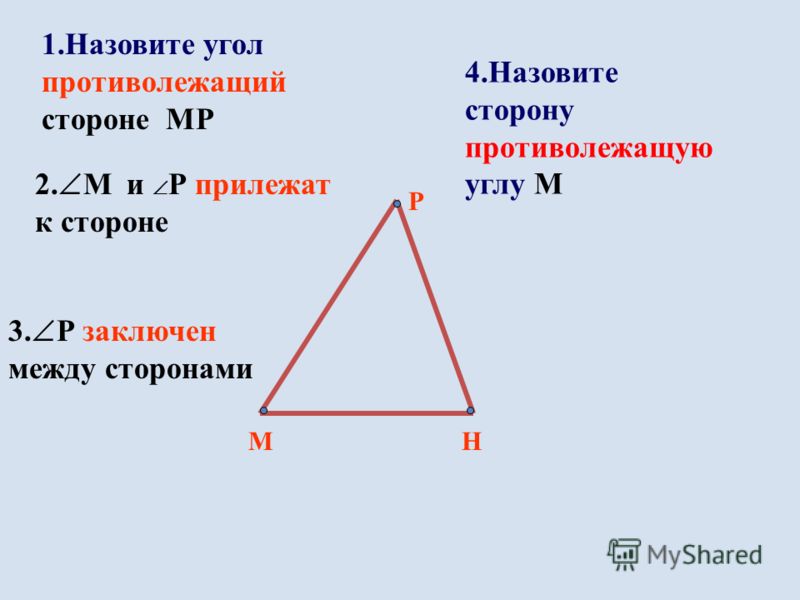 Угол образуется, когда два луча встречаются в общей конечной точке, а смежные углы — это те углы, которые всегда располагаются рядом друг с другом. Давайте узнаем больше о смежных углах на этой странице.
Угол образуется, когда два луча встречаются в общей конечной точке, а смежные углы — это те углы, которые всегда располагаются рядом друг с другом. Давайте узнаем больше о смежных углах на этой странице.
| 1. | Что такое смежные углы? |
| 2. | Свойства смежных углов |
| 3. | Примеры смежных углов |
| 4. | Часто задаваемые вопросы о смежных углах |
Что такое смежные углы?
Два угла называются смежными углами , если они имеют общую вершину, общую сторону и не пересекаются. Обратите внимание на следующий рисунок, чтобы понять, как выглядят смежные углы. Углы 1 и 2 смежные, так как имеют общую сторону BD и общую вершину B.
Смежные углы Определение
Смежные углы — это углы, которые всегда расположены рядом друг с другом таким образом, что они имеют общую вершину и общую сторону, но не перекрывают друг друга.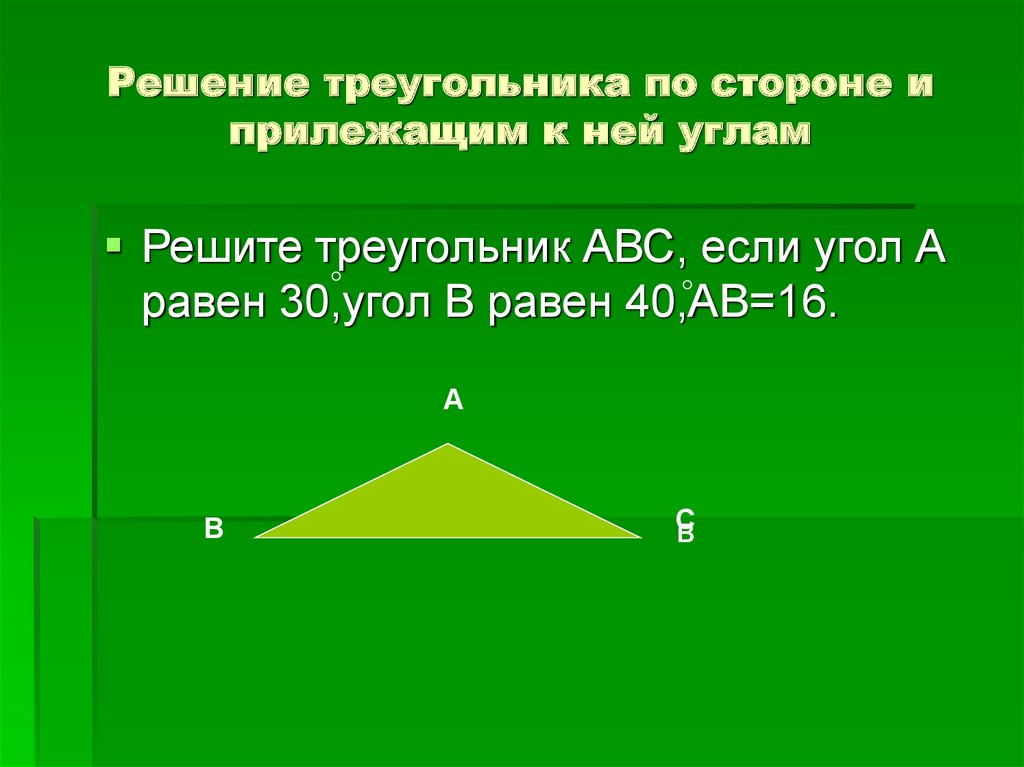
Примеры смежных углов
Мы можем видеть множество реальных примеров смежных углов.
- Самый распространенный пример смежных углов в реальной жизни можно увидеть в двух кусках пиццы, которые расположены рядом друг с другом.
- Другой распространенный пример можно увидеть в часах, которые показывают часовую, минутную и секундную стрелки, которые образуют смежные углы, когда все 3 находятся далеко друг от друга.
- Мы можем найти 3 смежных угла в руле автомобиля.
Свойства смежных углов
Приведенные ниже свойства смежных углов помогают нам легко их идентифицировать.
- Смежные углы всегда имеют общее плечо.
- У них общая вершина.
- Они не пересекаются.
- У них есть необычная рука по обеим сторонам общей руки.
- Два смежных угла могут быть дополнительными или дополнительными на основании суммы мер отдельных углов.

Как определить смежные углы?
Смежные углы легко идентифицировать с помощью двух основных свойств — смежные углы всегда имеют общую сторону и общую вершину. Если любые два угла удовлетворяют только одному из этих свойств, они не будут считаться смежными углами. Необходимо, чтобы углы выполняли оба свойства. Например, если любые два угла имеют общую вершину, но между ними есть угол, это означает, что они не имеют общей стороны. Следовательно, они не могут быть смежными углами. Обратите внимание на следующий рисунок, чтобы определить смежные углы.
Важные примечания
Вот список нескольких важных примечаний, относящихся к соседним углам.
- Если два угла смежные, то их сумма равна углу, образованному двумя не общими плечами и одним общим плечом.
- Если луч стоит на прямой, то сумма образующихся смежных углов равна 180°.
- Если сумма двух смежных углов равна 180°, то они называются линейной парой углов.
 Все линейные пары являются дополнительными, поскольку сумма дополнительных углов составляет 180°. Однако не обязательно, чтобы все дополнительные углы были линейными парами. Чтобы образовать линейную пару, линии должны пересекаться друг с другом и образовывать смежные углы.
Все линейные пары являются дополнительными, поскольку сумма дополнительных углов составляет 180°. Однако не обязательно, чтобы все дополнительные углы были линейными парами. Чтобы образовать линейную пару, линии должны пересекаться друг с другом и образовывать смежные углы. - Если сумма двух смежных углов равна 180°, то необщие стороны образуют прямую.
☛Статьи по теме
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о смежных углах и связанных с ними темах.
- Пары уголков
- Дополнительные уголки
- Измерение углов
- Прямой угол
- Типы уголков
Примеры смежных углов
Пример 1: Перечислите 5 пар смежных углов на следующем рисунке.
Решение: Ниже приведены пять пар смежных углов.
∠AOE, ∠EOC
∠EOC, ∠COB
∠COB, ∠BOD
∠BOD, ∠AOD
∠AOD, ∠03E
∠COB, ∠BOD
Пример 2: Смежны ли углы, отмеченные цифрами 1 и 2 на следующих рисунках? Обоснуйте свои ответы.

Решение: Ясно, что ∠1, ∠2 имеют общую вершину O и общий луч OB. Следовательно, ∠1, ∠2 — смежные углы.
Пример 3: Укажите истинное или ложное значение относительно свойств смежных углов.
а) Смежные углы всегда являются дополнительными.
б.) Смежные углы всегда имеют общую вершину и общее плечо.
Решение:
а.) Ложь, смежные углы не всегда могут быть дополнительными. Если любые два смежных угла образуют вместе прямую, то они образуют дополнительные смежные углы.
б.) Правда, смежные углы всегда имеют общую вершину и общее плечо.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по смежным углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о смежных углах
Что такое смежные углы в геометрии?
Два угла называются смежными углами , если они имеют следующие характеристики:
- Они имеют общую вершину.

- У них общая сторона или луч.
- Они не пересекаются.
Могут ли 2 смежных угла быть дополнительными?
Да, смежные углы могут быть дополнительными, если их сумма составляет 180°. Смежные углы можно определить как два угла, которые имеют общую вершину и общую сторону. Любые два смежных угла могут быть дополнительными углами или дополнительными углами в зависимости от суммы измерения углов.
Могут ли вертикальные углы быть смежными?
Нет, вертикальные углы никогда не могут быть смежными. Смежные углы — это два угла рядом друг с другом, в то время как вертикальные углы противоположны друг другу.
Приведите примеры смежных углов в повседневной жизни.
Смежные углы часто встречаются в нашей повседневной жизни. Например, в руле автомобиля, трех стрелках часов, двух кусочках пиццы, которые лежат рядом друг с другом в коробке из-под пиццы, и так далее.
Могут ли 2 смежных угла перекрываться?
Нет, смежные углы никогда не могут находиться один над другим, или, другими словами, углы не могут перекрываться. Углы, расположенные рядом друг с другом в одной вершине и имеющие общую сторону, являются смежными углами.
Углы, расположенные рядом друг с другом в одной вершине и имеющие общую сторону, являются смежными углами.
Что дают в сумме смежные углы?
Сумма двух смежных углов может быть либо дополняющей, либо дополняющей в зависимости от их величин. Если два смежных угла положить рядом друг с другом на прямой линии, они дадут в сумме 180°, потому что это будут смежные дополнительные углы. Если смежные углы не образуют линейных пар, то их сумма не будет равна 180°.
В чем разница между смежными углами и парой линейных углов?
Смежные углы могут образовывать или не образовывать вместе прямую линию. Им просто нужно выполнить то свойство, что они имеют общую вершину и общую сторону. Однако линейная пара углов всегда образует прямую линию, и, следовательно, их сумма всегда равна 180°.
Как определить смежные углы?
Смежные углы легко идентифицировать с помощью двух основных свойств:
- Смежные углы всегда имеют общую сторону.
- Смежные углы всегда имеют общую вершину.

Если любые два угла удовлетворяют только одному из этих свойств, они не будут считаться соседними углами. Необходимо, чтобы углы выполняли оба свойства.
В чем разница между смежными углами и вертикальными углами?
Смежные углы всегда имеют общую вершину и общую сторону и не пересекаются друг с другом. Вертикальные углы – это углы, которые образуются при пересечении двух прямых.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по углам
Рабочие листы по математике и
наглядный учебный план
Что такое смежный?, значение, смежные углы, решенные примеры, часто задаваемые вопросы формы, сегменты линий, углы, стороны и т. д. Как и в обычном использовании, слово «примыкающий» в геометрии относится к соседним (бок о бок) элементам друг к другу по форме. Обычно применяется к линиям, дугам или углам. В тригонометрии прилежащей стороной прямоугольного треугольника называется сторона, следующая за углом.
1. | Значение соседнего |
| 2. | Смежные углы |
| 3. | Что такое смежный угол, а что нет? |
| 4. | Решенные примеры |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о соседнем |
Значение смежного
Значение соседнего означает рядом или рядом с. Примером смежности являются два соседних дома. Мы обычно считаем людей на нашей улице своими соседями. Кто тогда наш ближайший сосед? Человек, который живет в доме или квартире рядом с нами. Соседний может относиться к двум вещам, соприкасающимся друг с другом или разделяющим одну и ту же стену или границу. А как насчет двух линий, которые пересекаются в вершине многоугольника? Можно ли считать их смежными сторонами? В треугольниках и других многоугольниках две стороны, которые встречаются в вершине многоугольника, являются смежными.
Смежные углы
В математике соседними могут быть разные вещи, но смежные в основном применяются к отрезкам прямых и углам. Любые два угла, имеющие общий луч или сторону, общую вершину и внутренние части которых не пересекаются, называются смежными углами. Например, посмотрите на изображение ниже: внутренности ∠ABD и ∠CBD не перекрываются и, следовательно, являются смежными углами.
Что такое смежный угол, а что нет?
Ниже перечислены несколько важных моментов о том, что можно считать смежным углом, а что нельзя считать смежным углом, даже если у него одна и та же вершина и сторона.
- Смежные углы имеют общую вершину и сторону, как показано на рисунке ниже
- Углы не считаются смежными, если они имеют только общую вершину, а не сторону
- Углы не считаются смежными углами, если они имеют общую сторону, а не вершину
- Углы не считаются смежными, когда углы a и b перекрываются, как показано на рисунке ниже
Статьи по теме на сайте Adjacent
Ознакомьтесь с этими интересными статьями на сайте Adjacent. Нажмите, чтобы узнать больше!
Нажмите, чтобы узнать больше!
- Симметрия
- Уголки
- Дополнительные углы
- Вертикальные углы
- Равные углы
- Дополнительные уголки
Пример 1: Посмотрите на стрелки часов. Образуют ли они пару смежных углов?
Решение:
В данных часах часовая стрелка образует угол с секундной стрелкой, а секундная стрелка образует другой угол с минутной стрелкой. Обе эти пары углов лежат рядом друг с другом и образуют пару смежных углов. Следовательно, стрелки часов образуют пары смежных углов.
Пример 2 : Смежны ли углы, отмеченные цифрами 1 и 2 на следующих рисунках? Обоснуйте свои ответы.
Решение
На данном рисунке
Ясно, что ∠1 и ∠2 имеют общую вершину O и общее плечо OB. У них есть необщие плечи OA и OC по обе стороны от общего плеча OB.
 Итак, ∠1 и ∠2 – смежные углы.
Итак, ∠1 и ∠2 – смежные углы.Да, ∠1 и ∠2 — смежные углы.
Пример 3. Перечислите 5 пар смежных углов на следующем рисунке.
Решение:
Ниже приведены пять пар смежных углов.
Старший № Пары смежных углов 1. ∠AOE, ∠EOC 2. ∠EOC, ∠COB 3. ∠АОС, ∠СОВ 4. ∠COB, ∠BOD 5. ∠ОБ, ∠БПК
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы на соседнем сайте
Что такое определение смежности?
Смежный означает, что две вещи находятся рядом или рядом друг с другом. В классе каждая скамья, на которой сидят 2 ученика, считается смежной. Когда состояния имеют общую границу, мы можем называть их соседними состояниями, поскольку они имеют общую границу и находятся рядом друг с другом. В математике смежный используется для обозначения двух сторон или углов, которые лежат рядом друг с другом, и мы называем их смежными сторонами и смежными углами.
В классе каждая скамья, на которой сидят 2 ученика, считается смежной. Когда состояния имеют общую границу, мы можем называть их соседними состояниями, поскольку они имеют общую границу и находятся рядом друг с другом. В математике смежный используется для обозначения двух сторон или углов, которые лежат рядом друг с другом, и мы называем их смежными сторонами и смежными углами.
Что такое определение смежных углов?
Углы считаются смежными, если два угла имеют общую сторону и вершину и не пересекаются. Смежные углы не обязательно должны быть равными или дополнительными. Между двумя углами не должно быть зазоров или перекрытий, чтобы они считались соседними углами.
Что такое смежные стороны?
Смежные стороны — это стороны многоугольника, имеющие общую вершину. Например, в треугольнике PQR соседними сторонами являются PQ и QR, поскольку между обеими сторонами лежит общая вершина (то есть Q).
Смежные углы равны?
Смежные углы не всегда должны быть равны.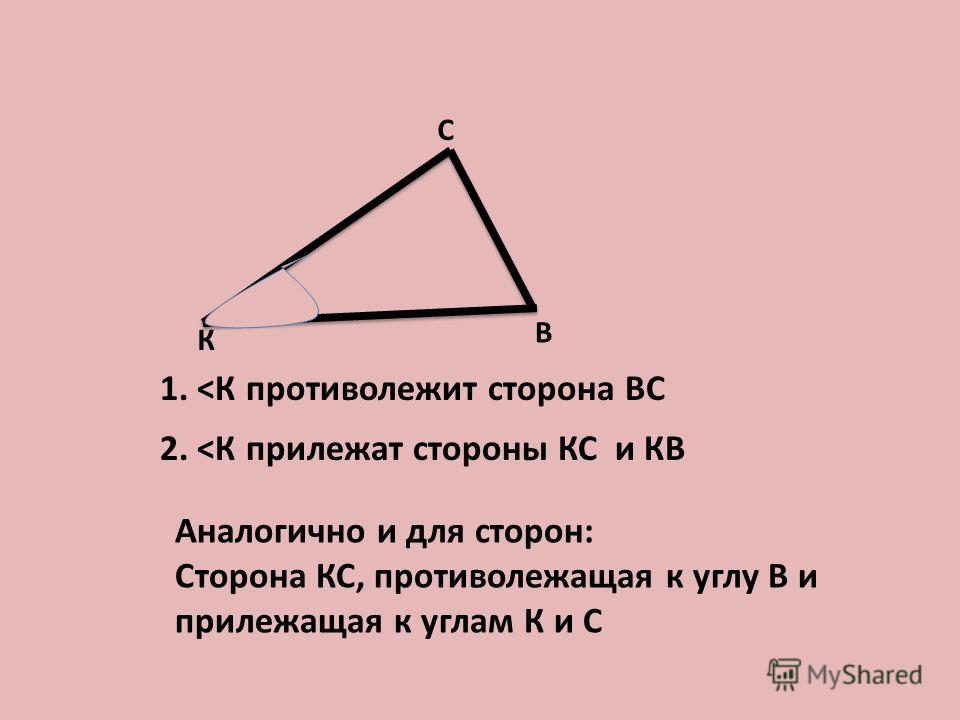 Два различных угла также могут считаться смежными, если они удовлетворяют всем условиям, относящимся к смежным углам. В случае квадрата или прямоугольника смежные углы равны, так как все углы равны 90º.
Два различных угла также могут считаться смежными, если они удовлетворяют всем условиям, относящимся к смежным углам. В случае квадрата или прямоугольника смежные углы равны, так как все углы равны 90º.
Вертикальные углы не являются смежными?
Нет, вертикальные углы всегда несмежные. При пересечении двух прямых образуются вертикальные углы, не являющиеся смежными углами. Эти углы имеют общую вершину, но никогда не имеют общей стороны.
Соседний означает Бок о бок?
Да, смежные означает рядом расположенные, т. е. когда углы расположены рядом друг с другом, имеют одну и ту же вершину и одну и ту же сторону. Прилегающая сторона треугольника — это сторона, ближайшая к углу, а противоположная сторона — это сторона, расположенная напротив угла.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по углам
Рабочие листы по математике и
наглядный учебный план
Углы треугольника – объяснение и примеры
Мы знаем, что каждая фигура во Вселенной основана на углах. Квадрат состоит из четырех линий, соединенных так, что каждая линия образует угол 9°.0 градусов с другой линией. Таким образом, квадрат имеет четыре угла по 90 градусов на четырех сторонах.
Квадрат состоит из четырех линий, соединенных так, что каждая линия образует угол 9°.0 градусов с другой линией. Таким образом, квадрат имеет четыре угла по 90 градусов на четырех сторонах.
Аналогично, прямая, вытянутая в обе стороны на 180 градусов. Если он поворачивается в любой точке, он становится двумя линиями, разделенными определенным углом. Точно так же треугольник — это, по сути, три линии, соединенные под определенными значениями углов.
Эти меры углов определяют тип треугольника. Поэтому углы необходимы при изучении любой геометрической формы.
В этой статье вы узнаете углы треугольника и как найти неизвестные углы треугольника когда вы знаете только некоторые из углов. Чтобы узнать важные концепции треугольников, вы можете обратиться к предыдущим статьям.
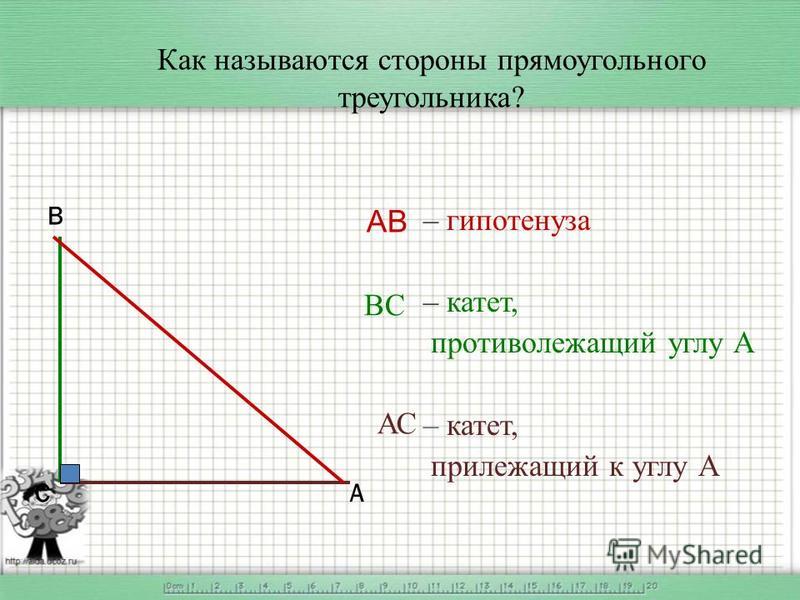
Какие углы треугольника?
Угол треугольника — это пространство, образованное между двумя длинами сторон треугольника. Треугольник содержит внутренние и внешние углы.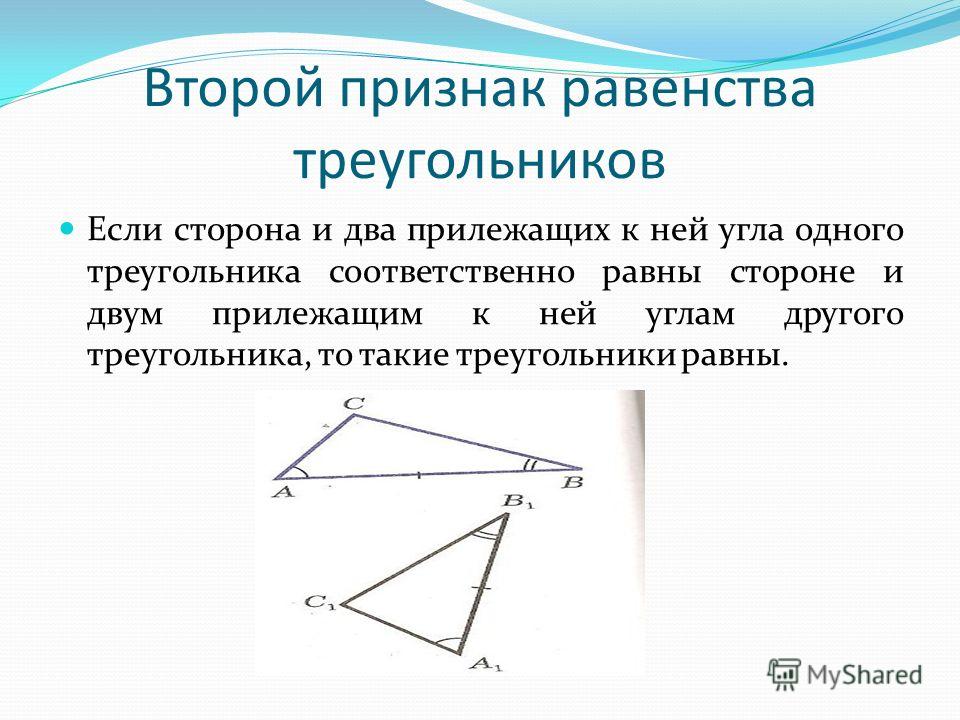 Внутренние углы — это три угла, лежащие внутри треугольника. Внешние углы образуются при продолжении сторон треугольника до бесконечности.
Внутренние углы — это три угла, лежащие внутри треугольника. Внешние углы образуются при продолжении сторон треугольника до бесконечности.
Таким образом, внешние углы образуются вне треугольника между одной стороной треугольника и вытянутой стороной. Каждый внешний угол примыкает к внутреннему углу. Смежные углы – это углы, имеющие общую вершину и сторону.
На рисунке ниже показан угол треугольника . Внутренние углы равны a, b и c, а внешние углы равны d, e и f.
Как найти углы треугольника?
Чтобы найти углы треугольника, вам нужно вспомнить следующие три свойства треугольников:
- Теорема о сумме углов треугольника: утверждает, что сумма всех трех внутренних углов треугольника равна 180 градусам. .
a + b + c = 180º
- Теорема о внешнем угле треугольника: утверждает, что внешний угол равен сумме двух противоположных и несмежных внутренних углов.

е = б + а
e = c + b
d = b + c
- Прямые углы. Мера углов на прямой равна 180º
c + f = 180º
a + d = 180º
e + b = 180º
Давайте решим несколько примеров задач.
Пример 1
Вычислите величину недостающего угла x в треугольнике ниже.
Решение
По сумме углов треугольника, теорема, имеем,
x + 84º + 43º = 180º
Упрощение.
x + 127º = 180º
Вычтите 127º с обеих сторон.
x + 127º – 127º = 180º – 127º
x = 53 º
Следовательно, величина недостающего угла равна 53º.
Пример 2
Найдите размер внутренних углов треугольника, которые образуют последовательные положительные целые числа.
Решение
Так как треугольник имеет три внутренних угла, то пусть последовательные углы равны:
⇒ 1 ST угол = x
⇒ 2 ND угол = x + 1
⇒ 3 RD угол = x + 2
Но мы знаем, что сумма трех углов равна 180 градусов, следовательно,
⇒ x + x + 1 + x + 2 = 180°
⇒ 3x + 3 = 180°
⇒ 3x = 177°
x = 59°
Теперь подставим значение x в исходных трех уравнениях.
⇒ 1 ST угол = x = 59°
⇒ 2 ND угол = x + 1 = 59° + 1 = 60°
⇒ 3 RD угол = x + 2 = 59°+ 2 = 61°
Итак, последовательные внутренние углы треугольника равны; 59°, 60° и 61°.
Пример 3
Найдите внутренние углы треугольника, углы которого равны; 2у°, (3у + 15)° и (2у + 25)°.
Решение
В треугольнике um внутренних углов = 180°
2y° + (3y + 15) ° + (2y + 25) ° = 180°
Упростить.
2у + 3у + 2у + 15° + 25° = 180°
7y + 40° = 180°
Вычтите 40° с обеих сторон.
7y + 40 ° — 40 ° = 180 ° — 40 °
7y = 140 °
Разделение обеих сторон на 7.
y = 140/7
y = 20 °
,
2y ° = 2(20) ° = 40°
(3y + 15) ° = (3 x 20 + 15) ° = 75°
(2y + 25) ° = (2 x 20 + 25) ° = 65°
Итак, три внутренних угла треугольника равны 40°, 75° и 65°.
Пример 4
Найдите значение недостающих углов на диаграмме ниже.
Решение
По теореме о внешнем угле треугольника имеем;
(2x + 10) ° = 63° + 87°
Упростить
2x + 10° = 150°
Вычесть 10° с обеих сторон.
2x + 10° – 10 = 150° – 10
2x = 140°
Разделите обе стороны на 2, чтобы получить;
x = 70°
Теперь путем замены;
(2x + 10) ° = 2(70°) + 10 ° = 140 ° + 10 ° = 150 °
Следовательно, внешний угол равен 150°
Но прямые углы в сумме составляют 180°. Итак, у нас есть;
у + 150° = 180°
Вычесть 150° с обеих сторон.
y + 150° – 150° = 180° – 150°
y = 30°
Следовательно, недостающие углы 30° и 150°.
Пример 5
Внутренние углы треугольника относятся как 4:11:15. Найдите углы.
Раствор
Пусть x будет отношением трех углов. Итак, углы
4x, 11x и 15x.
В треугольнике сумма трех углов = 180°
4x + 11x + 15x = 180°
Упростить.
30x = 180°
Разделите 30 на обе стороны.
x = 180°/30
x = 6°
Подставьте значение x.
4x = 4(6) ° = 24°
11x = 11(6) ° = 66°
15x = 15(6) ° = 90°
Значит, углы треугольника 24°, 66 ° и 90°.
Пример 6
Найдите величину углов x и y на диаграмме ниже.
Решение
Внешний угол = сумма двух несмежных внутренних углов.
60° + 76° = x
x = 136°
Аналогично, сумма внутренних углов = 180°. Следовательно,
60° + 76° + y = 180°
136° + y = 180°
Вычесть 136° с обеих сторон.
136° – 136° + y = 180° – 136
y = 44°
Следовательно, величина угла x и y равна 136° и 44° соответственно.
Пример 7
Три угла некоторого треугольника таковы, что первый угол на 20 % меньше второго угла, а третий на 20 % больше второго угла. Найдите величину трех углов.



 Все линейные пары являются дополнительными, поскольку сумма дополнительных углов составляет 180°. Однако не обязательно, чтобы все дополнительные углы были линейными парами. Чтобы образовать линейную пару, линии должны пересекаться друг с другом и образовывать смежные углы.
Все линейные пары являются дополнительными, поскольку сумма дополнительных углов составляет 180°. Однако не обязательно, чтобы все дополнительные углы были линейными парами. Чтобы образовать линейную пару, линии должны пересекаться друг с другом и образовывать смежные углы.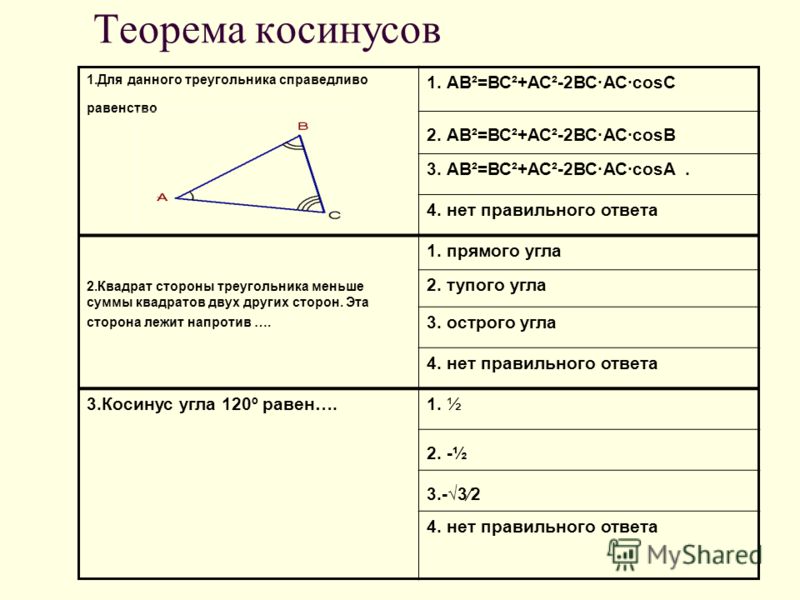
 Итак, ∠1 и ∠2 – смежные углы.
Итак, ∠1 и ∠2 – смежные углы.