Что такое модуль числа математика 6 класс?
Что такое модуль числа математика 6 класс?
Расстояние от данной точки до начала отсчёта, до точки О(0), называют модулем числа. Расстояние от точки M(-4) до нуля (см. рисунок) и от точки N(4) до нуля равно 4 единичным отрезкам. Число 4 является модулем числа -4 и числа 4.
Что такое модуль и как его найти?
Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой «A» — расстояние от точки «A» до начала отсчёта (то есть до нуля, длина отрезка «OA») будет называться модулем числа «a».
Что такое модуль числа для чего он нужен?
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат. Так, модулем числа 5 будет 5. … Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Чему равен модуль числа 5?
Обозначают как: |a|. Геометрически, модуль числа а — это расстояние (в единичных отрезках) от начала координат до точки А(а). Модулем числа 5 будет 5, т.
Что можно сказать о модулях противоположных чисел?
Если «отбросить» знаки у двух противоположных чисел, то они будут равны. Модуль — все то же «отбрасование» знаков => Модули двух противоположных чисел р вны.
Чему равен модуль 7?
Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, —7, то его модуль будет равен |7| — числу, противоположному исходному. Для нуля модуль всегда будет равен нулю.
Чему равен модуль разности двух чисел?
Определение. Модуль разности двух чисел a и b равен расстоянию между точками координатной прямой с координатами a и b. То есть, если даны точки на координатной прямой A(a) и B(b), то расстояние от точки A до точки B равно модулю разности чисел a и b.
Чему равен модуль 4?
Точка «A», соответствующая числу «−4», находится на расстоянии 4 единичных отрезков от точки 0 (начала отсчёта), то есть длина отрезка «OA» равна 4 единицам. Число 4 (длина отрезка «OA») называют модулем числа «−4». Читают символы выше следующим образом: «модуль числа минус четыре равен четырём».
Как можно раскрыть модуль?
Базовые сведения о модуле Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.
Чему равен модуль комплексного числа?
Длина радиус-вектора, который изображает заданное комплексное число z = a + b i , называется модулем данного комплексного числа. Модуль заданного комплексного числа вычисляется по следующей формуле: r = | z | = | a + b i | = a 2 + b 2 .
Что обозначают модуль числа?
Модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки a . Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного — противоположному числу.
Каким числом выражается модуль отрицательного числа приведите примеры?
Модуль отрицательного числа равен числу, ему противоположному, например: |−5| = 5; |−2,8| = 2,8. Модуль нуля равен нулю.
В каком классе изучается модуль?
С понятием модуля обучающиеся знакомятся в 6 классе. Модуль числа используется при формулировке правил действий над числами.
Как сравнить два модуля?
Правило сравнения отрицательных чисел:
- Если модуль одного из отрицательных чисел больше, то такое число является меньшим;
- если модуль одного из отрицательных чисел меньше, то такое число является большим;
- если модули чисел равны, то отрицательные числа равны.

Что значит сравнить два числа?
Сравнить два числа — это значит определить, равны они или нет, если нет, то определить, какое из них больше, а какое — меньше.
Какое из двух отрицательных чисел больше?
Правило сравнения отрицательных чисел меньше то число, модуль которого больше, больше то число, модуль которого меньше, отрицательные числа равны, если их модули равны.
Как сравнить два числа по модулю?
Говорят, что два целых числа a и b сравнимы по модулю натурального числа n, если при делении на n они дают одинаковые остатки. Другими словами, a и b сравнимы по модулю n, если их разность a – b делится на n.
Что такое вычет по модулю?
Любое число класса называется вычетом по модулю m. Вычет получаемый при , равный самому остатку r, называется наименьшим неотрицательным вычетом. Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.
Как правильно сравнивать числа?
Итак, для того, чтобы сравнить два числа, нужно определить, какое число больше, какое число меньше. И чтобы узнать, на сколько одно число больше другого, необходимо из большего числа вычесть меньшее.
Онлайн урок: Модуль числа по предмету Математика 6 класс
Обратите внимание на картинку.
Для того чтобы узнать тему нашего урока, попробуйте отгадать ребус.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
На этом уроке разберемся, что называют модулем числа, раскроем его геометрический смысл, рассмотрим основные свойства модуля, научимся находить модуль числа и применять эти знания при решении задач.
В переводе с латинского «модуль» (modulus) означает мера, размер.
Считается, что данный термин впервые ввел в пользование английский философ и математик Роджер Котс, друг и ученик Исаака Ньютона.
Многие ученые использовали в своих научных трудах понятие модуль, однако символьное обозначение он приобрел только в конце XIX века.
В 1841 году выдающийся немецкий ученый Карл Теодор Вильгельм Вейерштрасс ввел символьное обозначение модуля числа, которое используют и применяют по сегодняшний день.
В некоторых случаях вместо «модуль числа» говорят: «абсолютная величина», но надо понимать, что это тождественно равные понятия.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
В математике модуль имеет несколько значений. Разберем, что в математике называют модулем числа (абсолютной величиной).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Рассмотрим понятие модуль с геометрической точки зрения.
Вам уже известно, что на координатной прямой мы отмечаем действительные числа, а каждому действительному числу на этой прямой соответствует определенная точка и наоборот, каждой точке на координатной прямой соответствует действительное число.
Точка задается некоторым расстоянием от начала координат.
Длина отрезка от начала координат до точки вмещает в себя определенное количество единичных отрезков координатной прямой.
Длина такого отрезка всегда неотрицательная величина.
Рассмотрим пример:
Два мяча катнули по одной прямой. Первый мяч откатился вправо от исходной точки на 4 м, второй мяч влево от исходной точки на 6 м.
Изобразим координатную прямую и отметим на ней координаты точек остановки этих двух мячей.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Точка О— это исходная точка мячей- точка начала отсчета.
Единичный отрезок координатной прямой равен
Вправо откладываем координату первого мяча А (+4)
Влево откладываем координату второго мяча В (-6)
Расстояние от точки А до начала отсчета 4 единичных отрезка.
Длина ОА = 4 единичных отрезка.
Расстояние от точки В до начала отсчета 6 единичных отрезков.
Длина ОВ = 6 единичных отрезков.
Расстояние ОА и ОВ называют абсолютной величиной, модулем числа, они всегда положительны.
Таким образом, модулем числа называют расстояние на координатной прямой от начала отсчета до заданной точки (выраженной в единичных отрезках).
Обозначается модуль двумя вертикальными чертами слева и справа от числа | |.
Запись |A| читается как «Модуль А» или «Модуль числа А».
Пример 1
|7|— модуль числа 7
Изобразим координатную прямую, отметим на ней точку с координатой 7
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Зная определение модуля числа, мы можем утверждать, что 
Значит, модуль числа 7 равен самому числу 7
|7| = 7
Пример 2
|-5| — модуль числа (-5)
Изобразим координатную прямую, отметим на ней точку с координатой (-5).
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Зная определение модуля числа, мы можем утверждать, что от точки с координатой (-5) до точки начала отсчета О помещается 5 единичных отрезков.
5 единичных отрезков — это и есть расстояние от точки с координатой (-5) до точки начала отсчета (модуль числа).
Значит, модуль числа (-5) равен 5
|-5| = 5
Пример 3
|-1|— модуль числа (-1)
В расстояние от точки с координатой (-1) до точки начала отсчета помещается только один единичный отрезок этой прямой, поэтому модуль (-
|-1| = 1
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Рассмотрим некоторые свойства модуля числа.
1. Модуль нуля равен нулю
Так как от нуля до начала отсчета нет никакого расстояния (0 единичных отрезков), модуль нуля и есть нуль.
|0| = 0
2. Модуль числа всегда число неотрицательное (т.е. положительное или нуль)
Модуль положителен, так как по определению модуль — это расстояние, а расстояние всегда является положительным числом.
Приведем пример:
Мяч катнули вдоль прямой на расстояние, равное 3 м вправо, мяч ударился о стену и покатился вдоль прямой в обратном направлении на 3 м и остановился.
Изобразим на координатной прямой координаты точек в момент каждой остановки мяча.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Точка О на координатной прямой- это точка откуда катнули мяч- точка начала отсчета.
Единичный отрезок координатной прямой равен 1 деление- 1метр.
Точка А с координатой А (+3) — момент удара мяча о стенку.
Точка В с координатой В (0) — совпадает с точкой отсчета.
Можно ли утверждать, что мяч не преодолевал никакого расстояния, оставаясь в исходной точке в состоянии покоя, ведь в конечном счете мяч оказался в точке 0 м (от точки ноль до начала отсчета О не помещается ни одного единичного отрезка)? Конечно же, нет!
Путь мяча был бы равен нулю, если бы его вообще никуда не пинали, и он оставался в состоянии покоя в точке О.
Но мы должны понимать, что путь (расстояние), которое преодолел мяч, состоит из 3 единичных отрезков в правую сторону и 3 единичных отрезков в левую сторону; сложив все единичные отрезки, получим:
3 единичных отрезка + 3 единичных отрезка = 6 единичных отрезков
6 единичных отрезков = 6 м
Для определения пути мы складывали только числовое значение без учета направления. Это числовое значение и есть модуль числа.
Таким образом, можно сказать, что любое число состоит из знака и абсолютного значения (модуля).
Поэтому, чтобы найти модуль числа, нужно записать это число без учета знака.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
3. Модули противоположных чисел равны
Рассмотрим на примере данное утверждение:
Пусть модуль х равен 4, получим равенство |x| = 4
Отметим на координатной прямой точки, которые удовлетворяют этому равенству:
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Точка О — начало отсчета координатной прямой х.
Модул ь- это расстояние от начала отсчета до точки в единичных отрезках, равное в данном случае четырем.
Откладываем 4 единичных отрезка вправо, получаем точку с координатой 4
Но такое же количество единичных отрезков можно отложить влево, тогда получим точку с координатой (-4)
Получим на координатной прямой две точки, которые удовлетворяют условию |x| = 4
В данном примере значение х может быть равным:
х = 4
х = —4
Числа 4 и —4 отличаются только знаками, поэтому смело можем сказать, что это противоположные числа.
На координатной прямой противоположные числа, хоть и по разные стороны от точки начала отсчета, но находятся на равных расстояниях от этой точки, т.е. по модулю равны.
4. Модуль произведения двух чисел равен произведению модулей этих чисел
В буквенном выражении это можно записать так:
\(\mathbf{|a \cdot b| = |a| \cdot |b|}\)
Пример: \(\mathbf{|5 \cdot 6| = |5| \cdot |6| = 5 \cdot 6 = 30}\)
5. 2 = 4}\)
2 = 4}\)
6. Модуль частного двух чисел равен частному их модулей
\(\mathbf{\Bigl| \frac{x}{y}\Bigr| = \frac{|x|}{|y|} , y \neq 0}\)(так как на нуль делить нельзя).
Пример:
\(\mathbf{\Bigl| \frac{8}{2}\Bigr| = \frac{|8|}{|2|}= \frac{8}{2} = 4 }\)
\(\mathbf{\Bigl| -\frac{8}{2}\Bigr| = \frac{|-8|}{|2|}= \frac{8}{2} = 4 }\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Рассмотрим несколько примеров таких задач.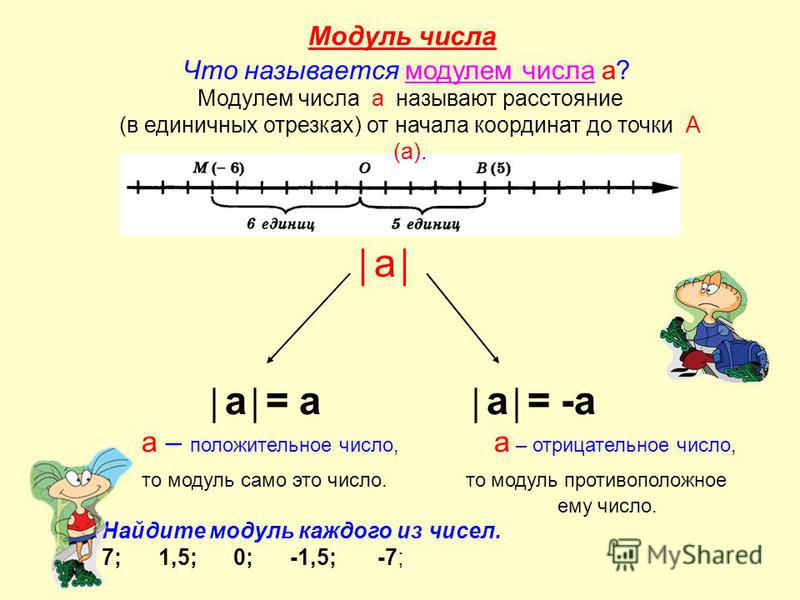
Задача 1
Запишите все числа, имеющие модуль 142.
Решение:
Представим координатную прямую с началом отсчета в точке О
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Нам известно, что модуль числа — это расстояние (количество единичных отрезков) от нуля до какой-либо точки.
142 единичных отрезка мы можем отложить на координатной прямой вправо и получим точку с координатой 142.
Также 142 единичных отрезка мы можем отложить влево от нуля, в этом случае получаем точку с координатой 142.
На координатной прямой находятся два числа, которые имеют модуль 142, а расстояние до этих точек содержат по 142 единичных отрезка.
|142| = 142
|-142| = 142
Ответ: числа 142 и —142 имеют модуль 142
Задача 2
Расположите числа —15; —1; 4; 7 в порядке возрастания модулей.
Решение:
Надо понимать, что в порядке возрастания будем располагать не сами числа —15; —1; 4; 7, а их модули.
Для этого найдем модули каждого из них:
|-15| = 15
|-1| = 1
|4| = 4
|7| = 7
Модули чисел получились: 15, 1, 4, 7
Расположим эти числа в порядке возрастания (от самого маленького к самому большому):
1, 4, 7, 15.
Получаем такую последовательность равенств,
|-1| = 1
|4| = 4
|7| = 7
|-15| = 15
Следовательно, числа в порядке возрастания их модулей должны располагаться так: -1, 4, 7, -15
Ответ: —1, 4, 7, —15
Задача 3
На координатной прямой отметили две точки -73 и 68. Модуль какого числа больше?
Решение:
Представим, что на координатной прямой на определенном расстоянии от точки О (налала отсчета) отмечены две точки.
Слева от точки начала отсчета расположена точка с координатой -73
Справа от точки начала отсчета расположена точка с координатой 68
Нам известно, что модуль — это расстояние от заданной точки до точки начала отсчета, выраженное в единичных отрезках.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Расстояние от точки О до точки с координатой -73 содержит больше единичных отрезков, чем расстояние от точки О до точки с координатой 68 (т.е. координата точки -73 находится дальше от начала координат, чем точка с координатой 68).
Значит, модуль числа -73 больше модуля числа 68
|-73| = 73
|68| = 68
73 > 68, а это значит:
|-73| > |68|
Ответ: |-73| > |68|
Задача 4
На координатной прямой точка А отмечена левее точки начала отсчета на 2 единицы и точка В — правее от точки начала отсчета на 6 единиц.
Чему равны координаты этих точек?
Чему равен модуль каждой координаты?
Решение:
Построим координатную прямую, за начала отсчета примем точку О
Единичный отрезок равен 1 деление- 1 единица.
На координатной прямой отметим точки А и В
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Точка А имеет координату A (-2), так как она отодвинута влево от точки О на расстояние в два единичных отрезка.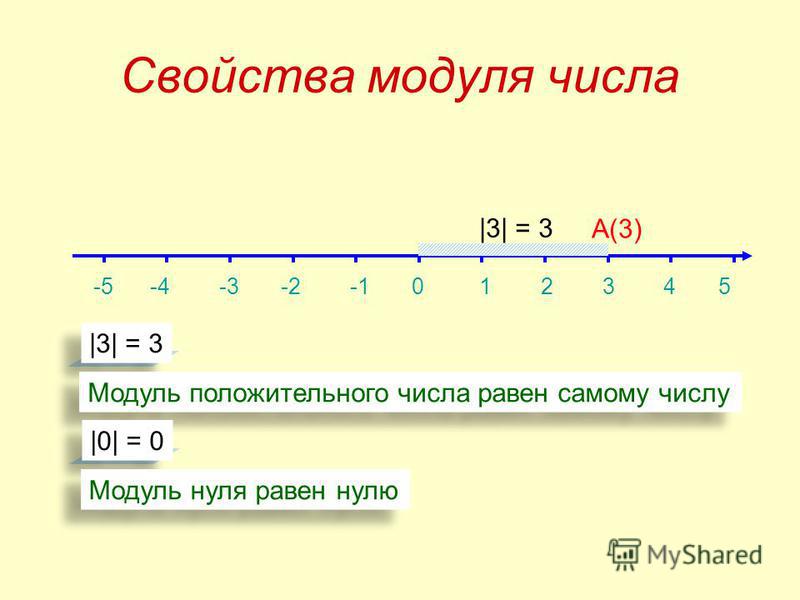
Точка В имеет координату В (6), так как она отодвинута вправо от точки О на расстояние в шесть единичных отрезков.
Получили точки с координатами A (-2) и В (6)
Модуль-это расстояние в единичных отрезках от заданной точки до начала отсчета.
Таким образом:
Модуль —2 равен 2
|-2| = 2
Модуль 6 равен 6
|6| = 6
Ответ: Модули координат точек A (-2) и В (6) равны 2 и 6 соответственно.
Наверное, вы уже заметили, что значение координат может быть положительным и отрицательным, а модули только положительными.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Чему равен модуль 7. Что такое модуль числа в математике
Модуль — математическое понятие, которое проходят в шестом классе. Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.
Как найти модуль числа?
Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника. Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.
Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.
- Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
- Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
- Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.
- То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z. Результат будет одним и тем же.
Модуль числа — это расстояние от этого числа до нуля на координатной прямой.
Модуль обозначается с помощью символа: | |.
- Запись |6| читается как «модуль числа 6», или «модуль шести».

- Запись |8| читается как «модуль 8-ми».
Модуль положительного числа равен самому числу. Например, |2| = 2. Модуль отрицательного числа равен противоположному числу |-3| = 3. Модуль нуля равен нулю, то есть |0| = 0. Модули противоположных чисел равны, то есть |-a| = |a|.
Для лучшего понимания темы: «модуль числа» предлагаем воспользоваться методом ассоциаций.
Представим, что модуль числа — это баня , а знак «минус» — грязь .
Оказываясь под знаком модуля (то есть в «бане») отрицательное число «моется» , и выходит без знака «минус» — чистым .
В бане могут «мыться» (то есть стоять под знаком модуля) и отрицательные , и положительные числа , и число ноль . Однако будучи «чистым» положительные числа , и ноль свой знак при выходе из «бани» (то есть из под знака модуля) не меняют !
История модуля числа или 6 интересных фактов о модуле числа
1. Слово «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера».
2. Ввел в обращение этот термин ученик Исаака Ньютона — английский математик и философ Роджер Котс (1682 – 1716).
3. Великий немецкий физик, изобретатель, математик и философ Готфрид Лейбниц в своих работах и трудах использовал функцию модуля, которую он обозначил mod x .
4. Обозначение модуля было введено в 1841 году немецким математиком
Карлом Вейерштрассом (1815 — 1897).
5. При написании модуль обозначается с помощью символа: | |.
6. Еще одной версии термин «модуль» был введен в 1806 году французским
математиком по имени Жан Робер Аргáн (1768 — 1822). Но это не совсем так.
В начале девятнадцатого века математики Жан Робер Аргáн (1768 — 1822)
и Огюстен Луи Коши (1789 — 1857) ввели понятие «модуль комплексного числа»,
который изучается в курсе высшей математики.
Решение задач на тему «Модуль числа»
Задача №1. Расположи выражения: -|12|, 0, 54, |-(-2)|, -17 в порядке возрастания.
— | 12 | = — 12
| — (— 2) | = 2
17 -17
Ответ: -17
Задача№2. Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
Нужно расположить выражения: -|-14|, -|30|, |-16|, -21, | -(-9) |
в порядке убывания.
Для начала раскроем скобки и модули:
— | — 14| = — 14
— |30| = -30
|-16| = 16
| -(-9) | = 9
16 > 9 > -14 > — 21 > — 30 что будет равносильно:
|-16| > | -(-9) | > — | — 14| > — 21 > — |30|.
Ответ: |-16| > | -(-9) | > — | — 14| > — 21 > — |30|
Цели урока
Познакомить школьников с таким математическим понятием, как модуль числа;
Научить школьников навыкам нахождения модулей чисел;
Закрепить изученный материал с помощью выполнения различных заданий;
Задачи
Закрепить знания детей о модуле числа;
С помощью решения тестовых заданий проверить, как усвоили ученики изученный материал;
Продолжать прививать интерес к урокам математики;
Воспитывать у школьников логическое мышление, любознательность и усидчивость.
План урока
1. Общие понятия и определение модуля числа.
2. Геометрический смысл модуля.
3. Модуль числа его свойства.
4. Решение уравнений и неравенств, которые содержат модуль числа.
5. Историческая справка о термине «модуль числа».
6. Задание на закрепление знаний пройденной темы.
7. Домашнее задание.
Общие понятия о модуле числа
Модулем числа принято называть само число, если оно не имеет отрицательного значения, или это же число отрицательное, но с противоположным знаком.
То есть, модулем неотрицательного действительного числа a является само это число:
А, модулем отрицательного действительного числа х будет противоположное число:
В записи это будет выглядеть так:
Для более доступного понимания приведем пример. Так, например, модулем числа 3 будет 3, и также модулем числа -3, является 3.
Из этого следует, что под модулем числа подразумевается абсолютная величина, то есть, ее абсолютное значение, но без учета его знака. Если говорить еще более просто, то необходимо от числа отбросить знак.
Обозначаться и выглядеть модуль числа может так: |3|, |х|, |а| и т.д.
Так, например, модуль числа 3 обозначается |3|.
Также, следует помнить, что модуль числа никогда не бывает отрицательным: |a|≥ 0.
|5| = 5, |-6| = 6, |-12,45| = 12,45 и т.д.
Геометрический смысл модуля
Модулем числа называют расстояние, которое измеряется в единичных отрезках от начала координат до точки. В этом определении раскрывается модуль с геометрической точки зрения.
Возьмем координатную прямую и обозначим на ней две точки. Пускай этим точкам будут соответствовать такие числа, как −4 и 2.
Теперь давайте обратим внимание на данный рисунок. Мы видим, что обозначенная на координатной прямой точка А соответствует числу -4 и если вы внимательно посмотрите, то увидите, что эта точка находится от точки отсчета 0 на расстоянии 4 единичных отрезков. Отсюда следует, что длина отрезка OA равняется четырем единицам. В этом случае, длина отрезка ОА, то есть число 4 будет модулем числа -4.
Обозначается и записывается в данном случае модуль числа таким образом: |−4| = 4.
Теперь возьмем, и на координатной прямой обозначим точку В.
Эта точка В будет соответствовать числу +2, и находится она, как мы видим, от начала отсчета на расстоянии двух единичных отрезков. Из этого следует, что длина отрезка OB равняется двум единицам. В этом случае число 2 будет модулем числа +2.
В записи это будет выглядеть так: |+2| = 2 или |2| = 2.
А теперь подведем итог. Если мы с вами возьмем какое-то неизвестное число а и обозначим его на координатной прямой точкой А, то в этом случае расстояние от точки A до начала отсчёта, то есть длинна отрезка ОА, как раз и является модулем числа «a».
В записи это будет выглядеть так: |a| = OA.
Модуль числа его свойства
А теперь давайте попробуем выделить свойства модуля, рассмотреть всевозможные случаи и записать их с помощью буквенных выражений:
Во-первых, модулем числа является число неотрицательное, а значит модуль положительного числа, равен самому числу: |a| = a, если a > 0;
Во-вторых, модули, которые состоят из противоположных чисел, равны: |а| = |–а|. То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны.
То есть это свойство говорит нам о том, что противоположные числа всегда имеют равные модули, та как на координатной прямой, хотя они и имеют противоположные числа, но они находятся на одинаковом расстоянии от точки отсчета. Из этого следует, что и модули этих противоположных чисел равны.
В-третьих, модуль нуля равняется нулю в том случае, если это число является нулем: |0| = 0, если a = 0. Здесь можно с уверенностью сказать, что модулем нуля является ноль по определению, так как ему соответствует начало отсчета координатной прямой.
Четвертым свойством модуля является то, что модуль произведения двух чисел равен произведению модулей этих чисел. Теперь подробнее рассмотрим, что это значит. Если следовать определению, то мы с вами знаем, что модуль произведения чисел a и b будет равен a b, или −(a b), если, а в ≥ 0, или же – (а в), если, а в больше 0. В записи это будет выглядеть так: |а b| = |а| |b|.
Пятым свойством является то, что модуль частного от деления чисел равен отношению модулей этих чисел: |а: b| = |а| : |b|.
И следующие свойства модуля числа:
Решение уравнений и неравенств, которые содержат модуль числа
Приступив к решению задач, которые имеют модуль числа, следует помнить, что чтобы решить такое задание, необходимо раскрыть знак модуля, используя знания свойств, которым эта задача соответствует.
Задание 1
Так, к примеру, если под знаком модуля стоит выражение, которое зависит от переменной, то раскрывать модуль следует в соответствии с определением:
Конечно же, при решении задач бывают случаи, когда модуль раскрывается однозначно. Если, например, взять
, здесь мы видим, что такое выражение под знаком модуля неотрицательно при любых значениях х и у.
Или, же для примера берем
, мы видим, что это выражение под модулем не положительно при любых значениях z.
Задание 2
Перед вами изображена координатная прямая. На этой прямой необходимо отметить числа, модуль которых будет равен 2.
Решение
В первую очередь, мы должны начертить координатную прямую. Вам уже известно, что для этого, вначале на прямой необходимо выбрать начало отсчета, направление и единичный отрезок. Далее, нам нужно от начала отсчета поставить точки, которые равны расстоянию двух единичных отрезков.
Как видим, таких точек на координатной прямой две, одна из которых соответствует числу -2, а другая числу 2.
Историческая справка о модуле числа
Термин «модуль» произошел от латинского названия modulus, что в переводе обозначает слово «мера». Ввел в обращение этот термин английский математик Роджер Котес. А вот знак модуля был введен благодаря немецкому математику Карлу Вейерштрассу. При написании модуль обозначается с помощью такого символа: | |.
Вопросы на закрепление знаний материала
На сегодняшнем уроке мы с вами познакомились с таким понятием, как модуль числа, а теперь давайте проверим, как вы усвоили эту тему, ответив на поставленные вопросы:
1. Как называется число, которое противоположно положительному числу?
Как называется число, которое противоположно положительному числу?
2. Какое название носит число, которое противоположно отрицательному числу?
3. Назовите число, которое является противоположным нулю. Существует ли такое число?
4. Назовите то число, которое не может являться модулем числа.
5. Дайте определение модулю числа.
Домашнее задание
1. Перед вами изображены числа, которые вам нужно расположить в порядке убывания модулей. Если вы правильно выполните задание, то узнаете фамилию человека, который впервые ввел в математику термин «модуль».
2. Начертите координатную прямую и найдите расстояние от М(-5) и К (8) до начала отсчета.
Предмети > Математика > Математика 6 класс
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.
Графически абсолютное значение а обозначается как |a| .
Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.
Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.
Геометрическое значение
Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.
Графически это можно выразить следующим образом: |a| = OA.
Свойства абсолютной величины
Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:
Особенности решения уравнений с модулем
Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.
К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.
|А + 5| = А + 5 , если, А больше или равняется нулю.
5-А , если, А значение меньше нуля.
В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.
Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.
Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.
Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.
Модуль числа a — это расстояние от начала координат до точки А (a ).
Чтобы понять это определение, подставим вместо переменной a любое число, например 3 и попробуем снова прочитать его:
Модуль числа 3 — это расстояние от начала координат до точки А (3 ).
Становится ясно, что модуль это ни что иное, как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3 )
Расстояние от начала координат до точки А(3 ) равно 3 (трём единицам или трём шагам).
Модуль числа обозначает двумя вертикальными линиями, например:
Модуль числа 3 обозначается так: |3|
Модуль числа 4 обозначается так: |4|
Модуль числа 5 обозначается так: |5|
Мы искали модуль числа 3 и выяснили, что он равен 3.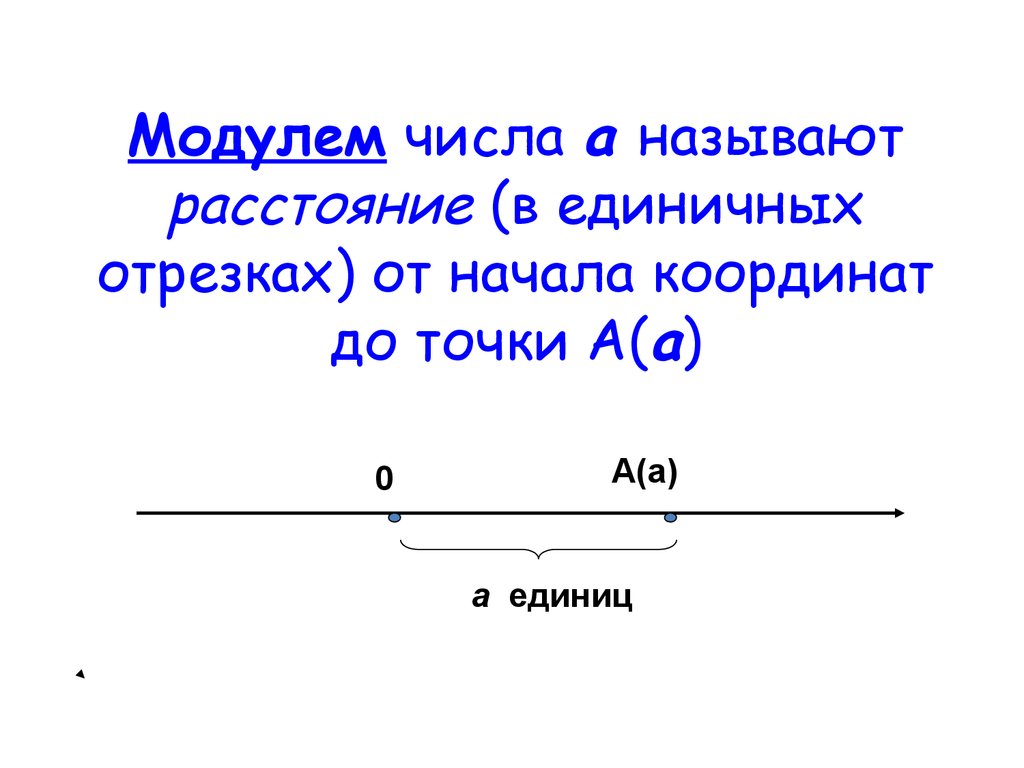 Так и записываем:
Так и записываем:
Читается как: «Модуль числа три равен три»
Теперь попробуем найти модуль числа -3. Опять же возвращаемся к определению и подставляем в него число -3. Только вместо точки A используем новую точку B . Точку A мы уже использовали в первом примере.
Модулем числа —3 называют расстояние от начала координат до точки B (—3 ).
Расстояние от одного пункта до другого не может быть отрицательным. Поэтому и модуль любого отрицательного числа, будучи являясь расстоянием тоже не будет отрицательным. Модуль числа -3 будет число 3. Расстояние от начала координат до точки B(-3) равно также трём единицам:
Читается как: «Модуль числа минус три равен три»
Модуль числа 0 равен 0, та как точка с координатой 0 совпадает с началом координат, т.е. расстояние от начала координат до точки O(0) равно нулю:
«Модуль нуля равен нулю»
Делаем выводы:
- Модуль числа не может быть отрицательным;
- Для положительного числа и нуля модуль равен самому числу, а для отрицательного – противоположному числу;
- Противоположные числа имеют равные модули.

Противоположные числа
Числа, отличающиеся только знаками называют противоположными . Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числа −2 знак минуса, а у 2 знак плюса, но мы его не видим, потому что плюс, как мы говорили ранее, по традиции не пишут.
Еще примеры противоположных чисел:
Противоположные числа имеют равные модули. Например, найдём модули для −2 и 2
На рисунке видно, что расстояние от начала координат до точек A(−2) и B(2) одинаково равно двум шагам.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Определение и значение — Merriam-Webster
мод·у·лус ˈmä-jə-ləs
1
а
: множитель, на который умножается логарифм числа по одному основанию для получения логарифма числа по новому основанию
б
: Абсолютное значение 2
с(1)
: число (например, положительное целое число) или другая математическая единица (например, многочлен) в сравнении, которое делит разность двух конгруэнтных членов без остатка
сравнение в смысле остатка b
(2)
: количество различных чисел, используемых в системе модульной арифметики
2
: константа или коэффициент, обычно численно выражающий степень, в которой тело или вещество обладает определенным свойством (например, эластичностью)
Примеры предложений
Недавние примеры в Интернете
Он обернут более жестким материалом с высоким модулем . Карбон 0042 переплетен со стекловолокном, что добавляет прочности.
Стефани Пирсон, Outside Online , 30 августа 2022 г.
Модульная операция — это получение остатка при делении числа на по модулю . Популярная механика , 21 фев. 2021
В этом сценарии единственным спасением для респондентов будет использование слабого RSA 9.0041 модуль .
Дэн Гудин, Ars Technica , 7 июня 2018 г.
Карбон 0042 переплетен со стекловолокном, что добавляет прочности.
Стефани Пирсон, Outside Online , 30 августа 2022 г.
Модульная операция — это получение остатка при делении числа на по модулю . Популярная механика , 21 фев. 2021
В этом сценарии единственным спасением для респондентов будет использование слабого RSA 9.0041 модуль .
Дэн Гудин, Ars Technica , 7 июня 2018 г.
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «модуль».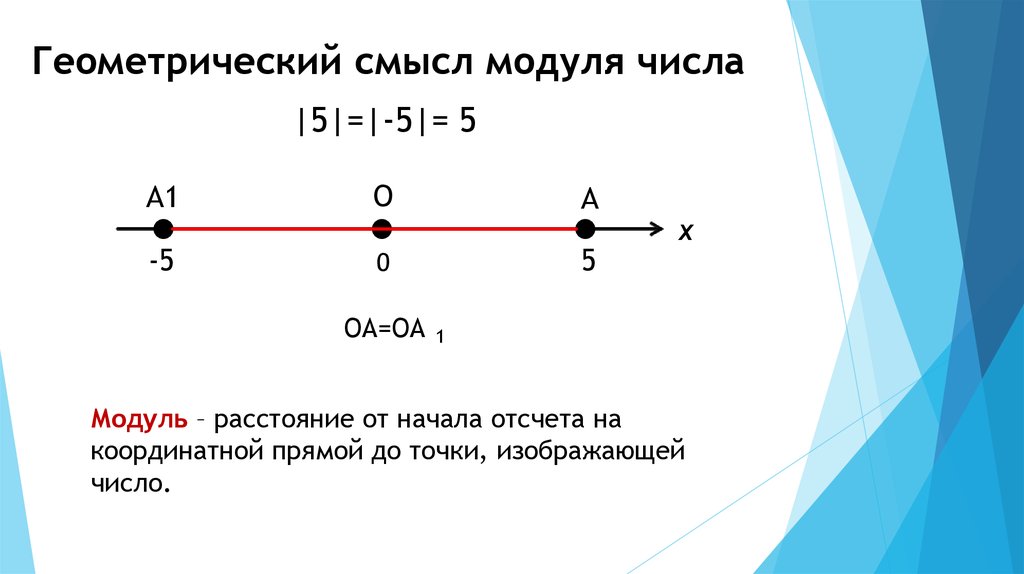 Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
Новая латынь, от латинского, малая мера
Первое известное использование
1753, в значении, определенном в смысле 1a
Путешественник во времени
Первое известное использование модуля было в 1753 г.
Посмотреть другие слова того же года
Словарные статьи Около
модульпо модулю
модуль
модуль логарифма
Посмотреть другие записи поблизости
Процитировать эту запись «Модуль».
 Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/modulus. По состоянию на 13 октября 2022 г.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/modulus. По состоянию на 13 октября 2022 г.Копировать цитирование
Определение для детей
Модуль
мод·у·лус ˈmäj-ə-ləs
: фиксированное целое число, на которое делятся все числа в системе модульной арифметики
с использованием модуля 5, произведение 3 умножить на 4 равно 2, потому что 12 разделить на 5 дает остаток 2
Медицинское определение
модуль
мод·у·лус ˈmäj-ə-ləs
: константа или коэффициент, обычно численно выражающий степень, в которой вещество или тело обладает свойством (например, эластичностью)
Последнее обновление: 13 сентября 2022 г.
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений поиск — без рекламы!
Merriam-Webster без сокращений
Развлечение с модульной арифметикой – BetterExplained
Недавно один читатель предложил мне написать о модульной арифметике (также известной как «вычисление остатка»). Я не особо задумывался об этом, но понял, что модуль чрезвычайно мощный: он должен быть в нашем умственном наборе инструментов рядом со сложением и умножением.
Вместо того, чтобы бить вас формулами по лицу, давайте рассмотрим идею, которую мы ненавязчиво вынашивали годами. Есть хорошая статья о модульной арифметике, которая вдохновила меня на этот пост.
Нечетное, четное и трехчетное
Вскоре после открытия целых чисел (1, 2, 3, 4, 5…) мы поняли, что они делятся на две группы:
- Четное: делится на 2 (0, 2, 4, 6). ..)
- Нечетное: не делится на 2 (1, 3, 5, 7…)
Почему это различие важно? Это начало абстракции — мы замечаем свойства числа (например, быть четным или нечетным), а не только само число («37»).
Это огромно — это позволяет нам исследовать математику на более глубоком уровне и находить отношения между типами чисел, а не конкретными. Например, мы можем создать такие правила:
- Четный x Четный = Четный
- Нечетное x Нечетное = Нечетное
- Чет x Нечет = Чет
Эти правила являются общими — они работают на уровне свойства. (Интуитивно у меня есть химическая аналогия, что «четность» — это молекула, которую имеют некоторые числа, и ее нельзя удалить путем умножения.)
Но четность/нечетность — очень специфическое свойство: деление на 2. А как насчет числа 3? Как насчет этого:
- «Три» означает, что число делится на 3 (0, 3, 6, 9…)
- «Тродд» означает, что вы , а не делится на 3 (1, 2, 4, 5, 7, 8…)
Странно, но работает. Вы заметите несколько вещей: есть два типа throdd. Такое число, как «4», на 1 меньше, чем тричетырнадцать (остаток 1), а число 5 — на два (остаток 2).
Быть «три-семь» — это еще одно свойство числа. Возможно, это не так полезно сразу, как чет/нечет, но оно есть: мы можем создавать правила, такие как «три семь х тривен = тривен» и так далее.
Но это сводит с ума. Мы не можем все время составлять новые слова.
Ввод по модулю
Операция по модулю (сокращенно «мод» или «%» во многих языках программирования) — это остаток при делении. Например, «5 mod 3 = 2», что означает, что 2 – это остаток при делении 5 на 3.
Преобразуя повседневные термины в математические выражения, «четное число» – это число, в котором «0 mod 2», т. е. имеет остаток 0 при делении на 2. Нечетное число равно «1 mod 2» (имеет остаток 1).
Почему это круто? Итак, наши «четные/нечетные» правила становятся такими:
- Четный x Четный = 0 x 0 = 0 [четный]
- Нечетное x Нечетное = 1 x 1 = 1 [нечетное]
- Четный x Нечетный = 0 x 1 = 0 [четный]
Круто, да? Довольно легко разобраться — мы преобразовали «свойства» в настоящие уравнения и нашли несколько новых фактов.
Сколько будет четное x четное x нечетное x нечетное? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете видеть, что если есть четное умножение где-нибудь на , весь результат будет равен нулю… Я имею в виду даже :).
Математика часов
Коварная особенность модульной математики заключается в том, что мы уже использовали ее для учета времени — иногда называемую «арифметикой часов».
Например: сейчас 7:00 (утра/вечера не имеет значения). Где будет часовая стрелка через 7 часов?
Хрм. 7 + 7 = 14, но мы не можем показать «14:00» на часах. Значит, должно быть 2. Мы рассуждаем интуитивно и в математических терминах:
- (7 + 7) по модулю 12 = (14) по модулю 12 = 2 по модулю 12 [2 — это остаток от деления 14 на 12]
Уравнение «14 mod 12 = 2 mod 12» означает, что «14 часов» и «2 часа» выглядят одинаково на 12-часовых часах. Они конгруэнтны , обозначены тройным знаком равенства: 14 ≡ 2 по модулю 12.
Другой пример: сейчас 8:00. Где будет большая рука через 25 часов?
Вместо того, чтобы прибавлять 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час». Таким образом, часы переведутся на 1 час вперед, в 9:00.
- (8 + 25) по модулю 12 ≡ (8) по модулю 12 + (25) по модулю 12 ≡ (8) по модулю 12 + (1) по модулю 12 ≡ 9мод 12
Вы интуитивно преобразовали 25 в 1 и добавили это к 8.
Забавное свойство: математика просто работает
Используя часы в качестве аналогии, мы можем выяснить, «просто работают» ли правила модульной арифметики (они работают).
Сложение/Вычитание
Допустим, два раза на наших часах выглядят одинаково («2:00» и «14:00»). Если мы добавим к ним одинаковые «x» часов, что произойдет?
Ну меняют на столько же на часах! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба будут показывать 7:00.
Почему? Ну, нас никогда не волновали лишние «12:00», которые таскал с собой 14-й. Мы можем просто добавить 5 к остатку 2, который есть у обоих, и они продвинутся одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.
Мы можем просто добавить 5 к остатку 2, который есть у обоих, и они продвинутся одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.
Умножение
Труднее понять, остается ли умножение неизменным. Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?
Посмотрим — что получится, если умножить на 3?
Ну, 2 часа * 3 ≡ 6 часов. Но что такое «14:00» * 3?
Помните, 14 = 12 + 2. Итак, мы можем сказать
- 14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12
Первую часть (12 * 3) можно игнорировать! «12-часовое переполнение», которое носит с собой 14, просто повторяется несколько раз. Но кого это волнует? Мы все равно игнорируем переполнение.
При умножении важен только остаток, который равен 2 часам 14:00 и 2:00. Интуитивно я вижу, что умножение не меняет отношения с модульной математикой (вы можете умножить обе части модульного отношения и получить тот же результат). Смотрите ссылку выше для более строгих доказательств — это мои интуитивные карандашные линии.
Смотрите ссылку выше для более строгих доказательств — это мои интуитивные карандашные линии.
Использование модульной арифметики
Теперь самое интересное — чем полезна модульная арифметика?
Простые расчеты времени
Мы делаем это интуитивно, но неплохо дать этому название. Ваш рейс прибывает в 15:00. Задержка на 14 часов. В какое время он приземлится?
Ну, 14 ≡ 2 mod 12. Поэтому я думаю об этом как о «2 часах и переключении утра/вечера», поэтому я знаю, что это будет «3 + 2 = 5 утра».
Это немного сложнее, чем простой оператор по модулю, но принцип тот же.
Размещение элементов в случайных группах
Предположим, у вас есть люди, которые купили билеты в кино с номером подтверждения. Вы хотите разделить их на 2 группы.
Чем ты занимаешься? «Шансы здесь, четы там». Вам не нужно знать, сколько билетов было выдано (первая половина, вторая половина), каждый может определить свою группу мгновенно (без обращения в центральный орган), и схема работает по мере того, как все больше людей покупают билеты.
Нужно 3 группы? Разделите на 3 и возьмите остаток (он же мод 3). У вас будут группы «0», «1» и «2».
В программировании по модулю вы можете разместить элементы в хеш-таблице: если в вашей таблице N записей, преобразуйте ключ элемента в число, выполните mod N и поместите элемент в это ведро (возможно, сохраняя связанный список там). По мере увеличения размера вашей хэш-таблицы вы можете пересчитать модуль для ключей.
Выбор случайного предмета
В реальной жизни я использую модуль. Действительно. У нас есть 4 человека, играющих в игру, и нужно выбрать кого-то, кто пойдет первым. Сыграй в мини-игру мод N! Назовите людям номера 0, 1, 2 и 3.
Теперь все кричат: «Раз, два, три, стрелять!» и высовывает случайное количество пальцев. Сложите их и разделите на 4 — тот, кто точно наберет остаток, ходит первым. (Например: если сумма пальцев равна 11, тот, у кого было «3», ходит первым, так как 11 по модулю 4 = 3).
Это быстро и работает.
Запуск задач в цикле
Предположим, задачи должны выполняться по определенному расписанию:
- Задача A выполняется 3 раза в час
- Задача B выполняется 6 раз в час
- Задача C выполняется 1 раз в час
Как вы храните эту информацию и составляете расписание? В одну сторону:
- Таймер, работающий каждую минуту (отслеживайте минуты как «n»)
- 3x/час означает один раз каждые 60/3 = 20 минут. Таким образом, задача A запускается всякий раз, когда «n % 20 == 0» 90 140
- Задача B запускается всякий раз, когда «n % 10 == 0»
- Задача C запускается всякий раз, когда «n % 60 == 0»
О, вам нужна задача C1, которая выполняется 1 раз в час, но не в то же время, что и задача C? Конечно, запустите его, когда «n mod 60 == 1» (по-прежнему один раз в час, но не так, как C1).
Мысленно я вижу цикл, который хочу «побить» с различными интервалами, поэтому вставляю мод. Удобно то, что хиты могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).
В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).
Точно так же при программировании вы можете распечатать каждый сотый элемент журнала, выполнив: if (n % 100 == 0){ print… }.
Это очень гибкий и простой способ запуска элементов по расписанию. На самом деле, это способ ответить на проверку вменяемости FizzBuzz. Если в вашем batbelt нет операции по модулю, вопрос становится намного сложнее.
Нахождение свойств чисел
Предположим, я сказал вам следующее:
- a = (47 * 2 * 3)
Что вы можете сделать быстро? Что ж, «а» должно быть четным, так как оно равно чему-то, что включает умножение на 2.
Если бы я также сказал вам:
- а = (39 * 7)
Ты бы отказался. Не потому, что вы «знаете», что два продукта разные, а потому, что один явно четный, а другой нечетный. Есть проблема: а не может быть одним и тем же числом в обоих, начиная с 9. Свойства 0041 не соответствуют .
Свойства 0041 не соответствуют .
Такие вещи, как «четный», «три» и «mod n», являются более общими свойствами, чем отдельные числа, и мы можем проверить их согласованность. Таким образом, мы можем использовать модуль, чтобы выяснить, согласуются ли числа, не зная, что они собой представляют!
Если я скажу вам это:
- 3a + 5b = 8
- 3а + б = 2
Можно ли решить эти уравнения с целыми числами? Давайте посмотрим:
- 3a + 5b = 8… давайте «mod 3 it»: 0 + 2b ≡ 2 mod 3 или b ≡ 1 mod 3
- 3a + b = 2… давайте «mod 3 it»: 0 + b ≡ 2 mod 3), или b ≡ 2 mod 3
Противоречие, молодцы! Б не может быть одновременно «1 по модулю 3» и «2 по модулю 3» — это так же абсурдно, как быть четным и нечетным одновременно!
Но есть одна загвоздка: числа вроде «1,5» не четные и не нечетные — они не целые! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .
Потому что на самом деле мы можем решить это уравнение:
- (3а + 5б) – (3а +б) = 8 – 2
- 4б = 6
- б = 1,5
- 3а + 1,5 = 2, поэтому 3а = 0,5 и а = 1/6
Не соблазняйтесь силой модуля! Знайте его пределы: это относится к целым числам.
Криптография
Игра с числами имеет очень важное применение в криптографии. Это слишком много, чтобы охватить здесь, но модуль используется в обмене ключами Диффи-Хеллмана — используется при настройке SSL-соединений для шифрования веб-трафика.
Простой английский
Компьютерщики любят использовать технические слова в обычном контексте. Вы можете услышать «X такое же, как Y по модулю Z», что примерно означает «Игнорируя Z, X и Y одинаковы».
Например:
- b и B идентичны, капитализация по модулю
- iTouch и iPad идентичны по модулю размера 😉
Вперед и вверх
Странно думать о «полезности» оператора по модулю — это все равно, что кто-то спрашивает, почему экспоненты полезны. В повседневной жизни не очень, но это инструмент для понимания закономерностей в мире и создания своих.
В повседневной жизни не очень, но это инструмент для понимания закономерностей в мире и создания своих.
В общем, я вижу несколько общих вариантов использования:
- Редуктор диапазона: возьмите ввод, мод N, и у вас есть число от 0 до N-1.
- Назначение группы: возьмите ввод, мод N, и вы пометите его как группу от 0 до N-1. Эта группа может быть согласована любым количеством сторон — например, разные серверы, которые знают N = 20, могут договориться о том, к какой группе принадлежит ID=57.
- Вывод свойств: обрабатывать числа в соответствии со свойствами (четные, тричетные и т. д.) и разрабатывать принципы, полученные на уровне свойств
Я уверен, что есть еще десятки применений, которые я пропустил — не стесняйтесь комментировать ниже. Удачной математики!
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Краткий обзор: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (как избежать проблемы со столбами забора)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция по золотому сечению
- Различные интерпретации числа ноль
Z мод №
Мы видели в
теорема 3. 1.3 о том, что когда мы выполняем арифметические действия по модулю некоторого числа $n$,
ответ не зависит от того, с какими числами мы вычисляем, а только от того, что они
одинаковы по модулю $n$. Например, чтобы вычислить $16\cdot 30\pmod {11}$,
мы можем точно так же вычислить $5\cdot 8\pmod {11}$, так как $16\эквив 5$ и
30$\экв 8$. Это говорит о том, что мы можем пойти дальше, придумав некоторые
вселенная, в которой на самом деле нет разницы между $16$ и $5$
(при условии, что мы хотим работать по модулю $11$).
1.3 о том, что когда мы выполняем арифметические действия по модулю некоторого числа $n$,
ответ не зависит от того, с какими числами мы вычисляем, а только от того, что они
одинаковы по модулю $n$. Например, чтобы вычислить $16\cdot 30\pmod {11}$,
мы можем точно так же вычислить $5\cdot 8\pmod {11}$, так как $16\эквив 5$ и
30$\экв 8$. Это говорит о том, что мы можем пойти дальше, придумав некоторые
вселенная, в которой на самом деле нет разницы между $16$ и $5$
(при условии, что мы хотим работать по модулю $11$).
В этом разделе, если не указано иное, предполагается, что все эквивалентности по модулю $n$ для некоторого фиксированного, но неопределенного $n$.
Определение 3.2.1. Для каждого целого числа $a$ пусть $[a]$ обладает тем свойством, что $[a] = [a’]$ тогда и только тогда, когда $a\equiv a’$. $\квадрат$
Обратите внимание, что это очень своеобразное определение: мы не даем намека на
что $[a]$ есть — мы указываем только один аспект его поведения. Это, оказывается, не имеет большого значения, но мы в конце концов увидим, что
$[a]$ «действительно» есть.
Это, оказывается, не имеет большого значения, но мы в конце концов увидим, что
$[a]$ «действительно» есть.
Напомним, что если $r$ равно остаток от деления $n$ на $a$, тогда $a\equiv r$, или, по нашему новый язык, $[a]=[r]$. Это означает, что каждый $[a]$ равен некоторому $[r]$ за $0\le r
Определение 3.2.2. Пусть $\Z_n=\{[0], [1], [2],…, [n-1]\}$. $\квадрат$
То есть по предыдущему замечанию $\Z_n$ состоит из всех возможных $[а]$. Это новая вселенная, в которой мы можем исследовать «арифметику».
Пример 3.2.3 $\Z_4=\{[0], [1], [2], [3]\}$. Мы могли бы написать $\Z_4=\{[-80], [25], [102], [-13]\}$ вместо этого, но только для того, чтобы подчеркнуть, а не на практике. $\квадрат$
Пример 3.2.4. В $\Z_5$ $[1]=[6]=[-4]$, $[3] = [8] = [-2]$. $\квадрат$
Теперь мы готовы проверить, действительно ли мы можем выполнять арифметические действия в этом новом
вселенная $\Z_n$. Начнем с самых простых операций,
а именно сложение, вычитание и умножение.
Определение 3.2.5 Если $[a]$, $[b]\in \Z_n$, пусть $[a]+[b]=[a+b]$, $[a]-[b]=[a-b]$ и $[a]\cdot[b]=[ab]$. $\квадрат$
Большинство математиков согласятся, что эти определения естественны и даже неизбежны. Вы можете попытаться подумать о других способах что эти простые операции могут быть определены на $\Z_n$.
Пример 3.2.6 Вот таблицы сложения и умножения для $\Z_4$.
|
|
$\квадрат$
К сожалению, хотя мы охарактеризовали определения
сложение, вычитание и умножение как «естественные», ситуация
не так прост, как может показаться на первый взгляд. определение $[a]+[b]=[a+b]$ зависит от манипулирования конкретными
целые числа $a$ и $b$, но мы знаем, что существуют и другие целые числа $c$
и $d$ с $[a]=[c]$ и $[b]=[d]$. Что, если мы вычислим $[c+d]$? Мы
лучше получить тот же результат, что и $[a+b]$ или определение
добавление не имеет смысла: $[a]+[b]$ будет отличаться от
$[c]+[d]$, но они должны быть одинаковыми. К счастью,
на помощь приходит теорема 3.1.3, и
две величины $[a+b]$ и $[c+d]$ совпадают. Вот почему: поскольку
$[a]=[c]$ и $[b]=[d]$, $a$ и $c$ конгруэнтны по модулю $n$, как и
$b$ и $d$. Следовательно, их суммы $a+b$ и $c+d$ конгруэнтны, что
означает, что $[a+b]=[c+d]$. Вычитание и умножение можно
обосновывается таким же образом. Мы показали, что определения
сложение, вычитание и умножение являются
«четко определенный».
определение $[a]+[b]=[a+b]$ зависит от манипулирования конкретными
целые числа $a$ и $b$, но мы знаем, что существуют и другие целые числа $c$
и $d$ с $[a]=[c]$ и $[b]=[d]$. Что, если мы вычислим $[c+d]$? Мы
лучше получить тот же результат, что и $[a+b]$ или определение
добавление не имеет смысла: $[a]+[b]$ будет отличаться от
$[c]+[d]$, но они должны быть одинаковыми. К счастью,
на помощь приходит теорема 3.1.3, и
две величины $[a+b]$ и $[c+d]$ совпадают. Вот почему: поскольку
$[a]=[c]$ и $[b]=[d]$, $a$ и $c$ конгруэнтны по модулю $n$, как и
$b$ и $d$. Следовательно, их суммы $a+b$ и $c+d$ конгруэнтны, что
означает, что $[a+b]=[c+d]$. Вычитание и умножение можно
обосновывается таким же образом. Мы показали, что определения
сложение, вычитание и умножение являются
«четко определенный».
Многие известные алгебраические свойства целые числа переносятся в $\Z_n$; вот некоторые из наиболее знакомых.
Теорема 3.2.7 В $\Z_n$,
а) $[a]+[b]=[b]+[a]$,
б) $[a]+([b] + [c])=([a] +[b])+[c]$,
в) $[a]\cdot[b]=[b]\cdot[a]$,
г) $[a]\cdot([b]\cdot [c])=([a]\cdot [b])\cdot[c]$,
e) $[a]\cdot([b]+[c])=[a]\cdot[b]+[a]\cdot[c]$.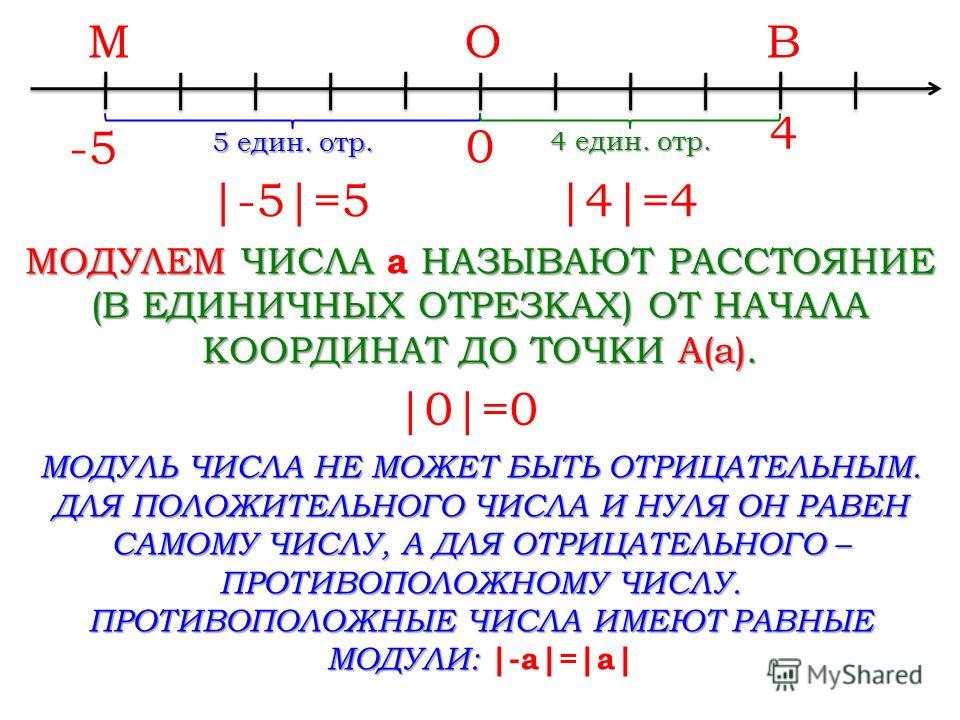
е) $[0]+[а] = [а]$,
ж) $[0]\cdot[a]= [0]$,
h) $[1]\cdot[a]= [a]$.
Доказательство. Докажем две части, а остальные оставим в качестве упражнений.
Часть (а) следует из того, что $[a]+[b]= [a+b]=[b+a]= [b]+[a]$; другими словами, мы просто сводим его к соответствующему утверждению для регулярного добавление. Аналогично (f) следует, поскольку $[0] + [а] = [0+а]=[а]$.$\qed$
Части (a) и (c) являются коммутативными законами, (b) и (d) являются ассоциативные законы и (e) говорит, что умножение опережает сложение. Части (f), (g) и (h) показывают, что $[0]$ и $[1]$ действуют в $\Z_n$ почти так же, как $0$ и $1$ действуют в $\Z$. Хотя многие свойства целых чисел являются общими для $\Z_n$, существуют исключения; вот один.
Пример 3.2.8 В $\Z$, если $ab=0$, то либо $a$, либо $b$ должны быть равны 0, но в $\Z_n$ это не обязательно. Например, в $\Z_{12}$, $[3]\cdot[4]= [12]=[0]$, но $[3]\ne [0]$ и $[4] \ne [0]$. $\квадрат$
Мы еще не знаем, что такое $[a]$, но это точно не целое число,
поэтому $\Z_n$ не является подмножеством $\Z$. Запомните это хорошо; Это
иногда возникает соблазн перепутать $\Z_n=\{[0], [1], [2],…, [n-1]\}$
с $\{0, 1, 2,…, n-1\}\подмножество \Z$. Скобки делают все
разница в мире: в $\Z_5$, $[2]=[7]$, но конечно
$2\не=7$.
Запомните это хорошо; Это
иногда возникает соблазн перепутать $\Z_n=\{[0], [1], [2],…, [n-1]\}$
с $\{0, 1, 2,…, n-1\}\подмножество \Z$. Скобки делают все
разница в мире: в $\Z_5$, $[2]=[7]$, но конечно
$2\не=7$.
Пример 3.2.1 Построить таблицы сложения и умножения для
а) $\Z_2$
б) $\Z_6$.
Пример 3.2.2 Докажите остальные части Теорема 3.2.7.
Пример 3.2.3 Если $[a]$ и $[b]$ лежат в $\Z_n$, докажите, что существует единственный $[x]\in \Z_n$ такой, что $[a]+[x]= [b]$.
Пример 3.2.4 Используйте таблицу из упражнения 1(b), чтобы проверить следующие утверждения:
а) Существует единственный $[x]\in \Z_6$ такой, что $[5]\cdot[x]= [2]$
б) Не существует $[x]\in \Z_6$ такого, что $[3]\cdot [x]= [4]$.
c) Существует $[x]\in \Z_6$ такое, что $[4]\cdot[x]=[2]$, но это не уникальный.
Пример 3.2.5 Найдите все элементы $[x]$ массива $\Z_{15}$ такие, что
$[x]=[p]$ для некоторых
простое число $p$ ($p$ не должно быть меньше 15).



