Программное раскрытие скобок в уравнение : Программирование
| smithlv |
| ||
16/05/13 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
Как бы вы раскрывали?
| smithlv |
| ||
16/05/13 |
| ||
| |||
В моем случае прекрасно подходит обратная польская запись. Алгоритм, который осуществляет предвычисление констант в выражении приведен в статье «обратная польская запись» в википедии. Получается просто и понятно.| Sphinx Pinastri |
| ||
20/10/12 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
08.2013, 11:23 
| smithlv |
| ||
16/05/13 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
Как репетитор по математике оформляет объединение систем — Колпаков Александр Николаевич
Системы уравнений и неравенств входили в состав выпускных и вступительных экзаменов по математике во все времена.
Даже если в экзаменационном варианте нет прямого задания на решение системы, то существует достаточно высокая вероятность ее появления процессе решения других задач. Репетитор по математике обязан это учитывать. Привести к системам могут задачи на модули, на логарифмы, на графики и даже на синусы с косинусы. Несмотря на то, что подготовка к ЕГЭ по математике нередко сводится к натаскиванию на решение однотипных номеров части «В», не стоит полностью отказываться от тренировки навыков поиска пересечения (объединения) ответов разных объектов. Хотя бы на элементарном уровне. Какими приемами репетитор по математике обеспечивает оптимальную работу ученика с системами? Какая техника оформления систем была бы самой удобной и продуктивной?
К сожалению, школьные учителя и даже некоторые профессиональные репетиторы требуют от детей (уже в 8 классе) оформление систем по принципу «все в одном», упаковывая содержащиеся в них неравенства в единый объект согласно строгим правилам проведения равносильных преобразований.
Широко применяются квадратные и фигурные скобки, причем часто в весьма сложном сочетании. Мой опыт репетиторской работы свидетельствует о том, что дети с огромнейшим трудом воспринимают, казалось бы, несложные для математиков логические конструкции с конъюнкциями и дизъюнкциями. Примерно 60-70% всех школьников с трудом припоминают (или не знают вообще) чем отличается квадратная скобка от линейной. А среди тех, кто приходит к репетитору по математике, этот процент повышается в среднем до 90-95%.
Но, тем не менее, для обозначения объединения, некоторые школьные преподаватели все равно используют квадратные скобки. Видимо по привычке. При таком раскладе репетитор по математике оказывается в крайне сложном положении, ибо уровень ученика часто не позволяет осознать сложные логические сочетания. Я не сторонник любой ценой следовать школьным стандартам и часто полностью отказываюсь от постановки квадратных скобок. Без них проще. Особенно когда на носу подготовка к ЕГЭ. Если все же репетитор математики вынужден принимать школьные правила, он мог бы это сделать следующим образом:
Когда репетитор по математике вводит квадратную скобку?
К пониманию разницы между скобками лучше всего подводить ученика постепенно, начиная с 8 класса, когда изучается тема «неравенства».
В решении самих неравенств восьмиклассники используют понятие «пересечение ответов» . Почему бы репетитору по математике не показать что такое «объединение ответов»? Задачи на объединение присутствуют в учебнике Макарычева, но они ограничиваются операцияями с уже сформированными промежутками. Это не совсем то, что нужно. Вот пример, на котором репетитор по математике мог бы объяснить назначение квадратной скобки:
Как видите, используется самое простое сочетание. Скобку лучше всего ввести после того, как ученик поймет суть задания. А она заключается в том, чтобы подобрать числа, обеспечивающие выполнение хотя бы одного неравенства (я употребляю общий термин: «условие»). Фразу «хотя бы одного» репетитор по математике сразу же меняет на фразу «или одно или другое». Процент учеников, правильно нашедших репетитору ответ, оказывается не таким и уж низким. Половина детей схватывают суть задания сразу же. Другим нужно показывать, как проверяется наугад взятое число (главное не объяснять только словами).
Данный номер рассматривается репетитором сразу после примера на совокупность, то есть на поиск числа, обеспечивающего выполнение каждого условия:
К сожалению, родители редко приглашают репетитора по математике в 8 классе и подготовкой к ЕГЭ занимаются только с 10 или с 11 класса. В этом случае репетитору приходится объяснять оформление объединения по формальному признаку фигурной скобки: если для проверки произвольно взятого числа достаточно проверить верность одного из нескольких условий (неравенств, уравнений или их систем), то проверяемые объекты можно заключить в квадратную скобку. Корректируя общую формулировку, репетитор по математике вставляет в нее союз «или». Например, для того, чтобы число x было корнем уравнения необходимо чтобы или первый множитель равнялся нулю, или второй. Преподаватель отдельно акцентирует внимание ученика на участии «или» и в случае его уместного употребления разрешает заключить объекты в квадратную скобку.
Если репетитор математики примет строгое оформление, он усложнит ученику одновременно и понимание и практическую работу. Школьные учителя берут за образец оформление систем в задачниках, в которых решения излагаются кратко. Из-за пропусков некоторых его частей удается компактно расписать все равносильные переходы, сохраняя целостность объекта. Репетитору по математике данная методика не подходит категорически. Почему? Ученики начинают вырывать по отдельности неравенства из огромной системы через весьма приличные промежутки времени. Переключение внимания на частные операции сбивает школьников с главного направления. Они забывают что именно им надо пересекать, а что объединять. Путаница возникает страшная. Хорошо, если репетитор по математике рядом и сможет подсказать. А что делать на ЕГЭ? Вряд ли стоит рисковать. Техника действий должна быть максимально прозрачной и удобной в практическом смысле.
Принимая квадратную скобку, репетитор по математике усложняет еще и сортировку решенного.
Приходится оформлять отдельные неравенства в колонку (одно под другим) и запоминать какое именно решено, а какое еще нет. Если сами решения длинные, то ученику может не хватить страницы и придется ее переворачивать. Рассеивание внимания при этом гарантировано.
Может ли репетитор по математике обойтись без квадратной скобки
?
Да, вполне. Для этого применяются стрелочный эквивалент. Например:
Чаще всего в объединение попадают две системы (если больше — лучше использовать иные методы изначально). В нашем случае одна из систем решается в левой части тетрадного листа, а другая в правой. Репетитор по математике разделяет квадратную скобку на две совокупности отдельных систем. На мой взгляд, это самая удобная форма для практической работы ученика. Почему? Те ответы, которые нужно пересечь, распределены по колонкам, при этом операции в левой и в правой колонке проводятся локально и не перемешиваются. Слева — свое пересечение, справа — свое. Очень удобно. Под каждой системой – решение.
Системы не нужно вырывать из «квадратной скобки», не нужно переписывать. Финальные ответы, которые репетитор по математике и ученик получают слева и справа «сваливаются в общий ответ» без какой-либо коррекции и пересечения.
Исключение составляют случаи, когда промежутки имеют общую часть. Однако практика показывает, что даже если репетитор по математике забудет напомнить о «склеивании частей», то большинство учеников догадаются до него сами.
Преимущество стрелок для запоминания:
Когда ученик разделяет тетрадный лист на две части, то находясь на любом этапе решения по левой колонке, он помнит о том, что предстоит еще заполнить и правую часть. Это очень важно. Если вы репетитр, то наверняка знаете, что школьники часто забывают разобрать какой-нибуь случай или решить какое-нибдуь неравенство из системы.
Сложность работы с объединением и пересечением носит часто чисто технический характер и связана с проблемой механики решений, то есть запоминанием и сортировкой обрабатываемой информации.
При подготовке к ЕГЭ по математике важно получить навык автоматического выполнения операций. Поэтому репетитору по математике крайне необходимо использовать в работе простые и удобные методы, каким является прием стрелочного разделения. Если потребуется объединить три или более системы, репетитор по математике может взять лист формата А4, развернуть его в длину и аккуратно решить задание распределяя системы по нескольким колонкам. Такой подход к оформлению позволит ученику четко разделить и запомнить логическую структуру объекта.
Репетитор по математике, Колпаков А.Н. Москва.
Решение уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.
Урок — закрепление ЗУН учащихся по теме «Решение уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.» Архив содержит конспект урока, электронную презентацию, карточки, оценочные листы.
Оборудование: компьютер, презентация, карточки для индивидуальной работы, карточки с тестовыми заданиями, оценочные листы.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ
Просмотр содержимого документа
«К уроку»
Просмотр содержимого документа
«Решение уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок»
Решение уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.
Цель урока:
Образовательная:— закрепить умения и навыки решения линейных уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок;
контроль уровня усвоения знаний и умений по теме;
Развивающая: — способствовать развитию познавательного интереса учащихся; умению анализировать, сравнивать, сопоставлять.
— способствовать развитию внимания, памяти, а также развитию интереса к предмету через игровую форму работы, повышению активности учащихся;
— способствовать формированию потребности приобретения знаний; развитию математической речи учащихся.
Воспитательная: — способствовать формированию таких качеств личности, как организованность, аккуратность, воспитание чувства ответственности за качество и результат выполняемой работы, а также чувства взаимопомощи.
Тип урока: закрепление ЗУН
Методы: наглядный, словесный, практический, частично-поисковый, групповой, индивидуальный, фронтальный.
Оборудование: компьютер, презентация, карточки с квадратами, карточки для индивидуальной работы, карточки с тестовыми заданиями, оценочные листы.
Ход урока:
Организационный момент
Добрый день! Добрый час!
Как я рада видеть вас
Прозвенел уже звонок.
Начинается урок!
Подготовительный этап:
Устный счет.
4 | 2 | -7 | 1 | -3 | 5 | -5 | 7 | -2 |
3х = -9 (Н) х + 5 = 7 (Р) -2х = -10 (Е)
7 – х = 3 (У) х + 9 = 2 (А) 15х = -30 (Е)
6х + 1 = 7 (В) 7х – 49 = 0 (И) 5х + 25 = 0 (Н)
Итак, тема нашего урока «Решение уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.
»
Цель урока: закрепить умения и навыки решения линейных уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.
Перед вами лежат листы «Лестница успеха». Я предлагаю вам найти себя на этой лестнице и закрасить человечка синим цветом. В конце урока мы вернемся к этим листам.
У каждой группы на столах лежат оценочные листы, в которых на каждом этапе урока каждому участнику группы нужно будет выставить оценку. В конце урока мы подведем итог.
Актуализация знаний.
— Какое уравнение называется линейным?
— Как называются уравнения, имеющие одинаковые корни?
— Какие свойства используются для решения линейного уравнения?
Работа в группах.
Вам предложены части алгоритма решения линейных уравнений. Расположите их в правильном порядке.
Алгоритм решения уравнения
1. Если в уравнении есть дроби, то привести их к общему знаменателю.
2. Раскрыть скобки.
3. Перенести слагаемые, содержащие переменную, в одну часть уравнения, а числа без переменной – в другую часть.
4. Привести подобные слагаемые.
5. Разделить обе части уравнения на коэффициент.
6. Определить корень уравнения.
«Найди ошибку»
— Внимательно рассмотрите три решения одного уравнения.
3(х + 1) = 2(х + 5) | 3(х + 1) = 2(х + 5) | 3(х + 1) = 2(х + 5) |
3х + 1 = 2х + 10 | 3х + 3 = х + 10 | 3х + 3 = 2х + 10 |
3х – 2х = 10 – 1 | 3х – х = 10 – 3 | 3х – 2х = 10 — 3 |
х = 9 | 2х = 7 | х = 7 |
| х = 3 |
|
— Какой способ является верным? Почему?
— Какие ошибки были допущены в других решениях?
Одновременно по карточкам работают 4 учащихся (работа с детьми с повышенной и пониженной мотивацией)
1 карточка (для слабых)
6х + 10 = 4х + 12
2 карточка (для сильных)
– = — 2
Физминутка.
Закрепление.
Работа в группах. У доски 3 человека решают те же задания. Затем самопроверка.
№ 1050 (1, 2, 4), с. 237
+
х = — 9
У = -8
Самостоятельная работа, с последующей взаимопроверкой.
«Установи соответствие»
5х = 2х + 6 А) х = — 2
7х – 4 = х — 16 Б) х = 0
3у – (5 – у) = 11 В) х = 3
4. 3(2х – 2) = 4х – 6 Г) х = 4
5. -8х = -24 Д) х = -3
Е) х = 3
Ж) х = 2
Ответы.
1 – Е
2 – А
3 – Г
4 – Б
5 – В
Домашнее задание : с. 229, № 1007
Итог.
Ответь: да, нет.
1. Корни уравнения изменяются, если обе части уравнения умножить на число (-10) ( )
2. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак ( )
3.
Если перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки слагаемых ( )
4. На ноль делить можно ( )
В оценочных листах подведите итог сегодняшнего урока.
Рефлексия.
Давайте вернемся к «Лестнице успеха». Красным цветом закрасьте человечка на той ступеньке, на которой вы чувствуете себя после нашего урока.
Вывешиваются листы с лестницей успеха.
Просмотр содержимого документа
«Установи соответствие»
Просмотр содержимого документа
«алгоритм»
Просмотр содержимого презентации
«Презентация к уроку»
Добрый день! Добрый час!
Как я рада видеть вас
Прозвенел уже звонок.
Начинается урок!
4
2
-7
1
-3
5
-5
7
-2
н
р
е
3х = -9 х + 5 = 7 -2х = -10
7 – х = 3 х + 9 = 2 15х = -30
6х + 1 = 7 7х — 49 = 0 5х + 25 = 0
у
а
е
и
в
н
Тема: «Решение уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.»
Цель урока: закрепить умения и навыки решения линейных уравнений с помощью переноса слагаемых из одной части уравнения в другую и использования правил раскрытия скобок.
Ответьте на вопросы
1.
Какое уравнение называется линейным?
( уравнение вида ах=в, где х – переменная, а,в – некоторые числа называется линейным уравнением с одной переменной)
2. Как называются уравнения, имеющие одинаковые корни?
(равносильными)
3. Какие свойства используются для решения линейного уравнения?
Алгоритм решения уравнения
1. Если в уравнении есть дроби, то привести их к общему знаменателю.
2. Раскрыть скобки.
3. Перенести слагаемые, содержащие переменную, в одну часть уравнения, а числа без переменной – в другую часть.
4. Привести подобные слагаемые.
5. Разделить обе части уравнения на коэффициент.
6. Определить корень уравнения.
Найди ошибку!
3(х + 1) = 2(х + 5)
3(х + 1) = 2(х + 5)
3х + 1 = 2х + 10
3х + 1 = 2х + 10
3(х + 1) = 2(х + 5)
3(х + 1) = 2(х + 5)
3(х + 1) = 2(х + 5)
3(х + 1) = 2(х + 5)
3х + 3 = х + 10
3х – 2х = 10 – 1
3х + 3 = х + 10
3х – 2х = 10 – 1
х = 9
х = 9
3х + 3 = 2х + 10
3х + 3 = 2х + 10
3х – х = 10 – 3
3х – х = 10 – 3
2х = 7
3х – 2х = 10 — 3
3х – 2х = 10 — 3
2х = 7
х = 3
х = 7
х = 7
Физминутка.
Работа в группах
1 группа — № 1050 (1)
2 группа — № 1050 (2)
3 группа — № 1050 (4)
«Установи соответствие»
1. 5х = 2х + 6 А) х = — 2
2. 7х – 4 = х — 16 Б) х = 0
3. 3у – (5 – у) = 11 В) х = 3
4. 3(2х – 2) = 4х – 6 Г) х = 4
5. -8х = -24 Д) х = -3
Е) х = 3
Ж) х = 2
Ответы. Шкала оценок
1 – Е «5» – 5 ответов
2 – А «4» – 4 ответа
3 – Г «3» – 3 ответа
4 – Б «2» – 1,2 ответа
5 – В
Домашнее задание :
с. 229, № 1007
Ответь: да, нет.
1. Корни уравнения изменяются, если обе части уравнения умножить на число (-10) ( )
2.
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак ( )
3. Если перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки слагаемых ( )
4. На ноль делить можно ( )
Лестница успеха.
Что такое скобки? Определение, правила, примеры
Что такое круглые скобки?
Скобки или «круглые скобки» — это знакомые ( ) символы, которые используются парами для группировки элементов или указания порядка операций в уравнении.
В математике вам часто придется использовать скобки при создании или решении уравнений. Они помогают группировать числа и определять порядок операций. В таких случаях используются три типа скобок:
- Круглые скобки или ( )
- Квадратные или квадратные скобки или [ ]
- Фигурные скобки или угловые скобки или { }
Скобки всегда идут парами, и если есть открывающая скобка, должна быть и закрывающая скобка.
Открывающие скобки: (, [ и {. Соответствующие им закрывающие скобки: ), ] и }.
В этой статье мы изучим правила использования скобок в математике.
Как использовать скобки в математике?В математике вы можете использовать скобки для разделения чисел. Например, вы можете использовать их для упоминания отрицательных чисел при написании уравнения сложения.
Вот пример, чтобы лучше понять это:
3 + (-5) = -2
Второй способ использования скобок в математике — умножение чисел. Если в уравнении нет арифметической операции, наличие скобок означает, что вы должны применить умножение.
Разберем это на примере:
6 (4 + 2)
можно записать как 6 х (4 + 2)
Следовательно, ответ 6 х 6 = 36.
Третий и последний скобки в математике используются для группировки чисел и определения порядка операций.
Порядок операцийСкобки изменяют порядок операций.
Вот порядок, которому вы можете следовать, когда в уравнении присутствует несколько символов:
Если вы столкнетесь со скобками в уравнении, вы сначала посмотрите на термины, присутствующие в них.
Давайте лучше разберемся на примере.
Возьмем задачу: 9 – 10 ÷ 5 – 3 x 2 + 7
Давайте решим ее, используя изученный вами порядок действий.
= 9 – 10 ÷ 5 – 3 x 2 + 7
= 9 – 2 – 3 x 2 + 7 (сначала вы делите)
= 9 – 2 – 6 + 7 (затем умножаете)
= 7 – 6 + 7 (Затем вычесть)
= 1 + 7 (Затем вычесть)
= 8 (И, наконец, сложить)
Теперь давайте рассмотрим ту же задачу со скобками:
9 – 10 ÷ (5 – 3) x 2 + 7
Сначала нужно вычислить числа в скобках.
= 9 – 10 ÷ 2 x 2 + 7 (Решите выражение в скобках)
= 9 – 5 x 2 + 7 (Разделить)
= 9 – 10 + 7 (Умножить)
= –1 + 7 (Сложить)
= 6
Вы заметили? Ответ на то же уравнение изменился, потому что в уравнении присутствовали круглые скобки!
Помните: если внутри других скобок есть скобки, сначала нужно решить внутреннее выражение.
Давайте разберем это на примере:
Упростим выражение (2 + (3 x 4))
Здесь мы сначала решим внутреннюю скобку.
Таким образом, выражение примет вид (2 + 12) = 14
Решенные примеры
Пример 1: Упростим выражение: (2 + 4 x 6) – 4 + (2 x 3)
Решение . Начните с решения выражений в скобках.
= (2 + 24) – 4 + 6 (умножить в скобках)
= 26 – 4 + 6 (решить члены в скобках)
= 22 + 6 (сложить)
= 28
Пример 2: Упростите выражение: ( 2 x (7 – 5)) – ((6 ÷ 3) + 4)
Начните с решения самых внутренних скобок
= (2 x 2) – (2 + 4)
= 4 – 6
= –2
Пример 3: Упростите выражение: 2 (3 + 5) + 8 (4 – 1)
Сначала решите выражения в скобках.
Здесь скобки также обозначают знак умножения.
= 2 x 8 + 8 x 3
= 16 + 24
= 40
Практические задачи45
50
24
40
Правильный ответ: 50
Мы знаем, что уравнение в скобках решается первым.
Итак, 19 — 4 + 35 = 50
7
2
17
10
Правильный ответ: 7
Мы знаем, что уравнение в скобках решается первым.
Итак, (4 x 4) – (4 + 5)
16 — 9 = 7
10
50
20
40
Правильный ответ: 40
Мы знаем, что скобки также обозначают умножение.
Итак, 4 x 5 + 4 x 5
20 + 20 = 40
Часто задаваемые вопросы
Что такое скобки в математике?
Скобки используются для группировки чисел или переменных в математике. Они могут изменить решение выражения и, следовательно, ответ.
Круглые скобки — это то же самое, что фигурные скобки?
Нет. Скобки, обозначенные ( ), отличаются от фигурных скобок { }. Они имеют различные применения в математике. Они используются во вложенных выражениях. Вы узнаете о них больше позже.
Есть ли другое название скобок?
Да. Иногда скобки также называют круглыми скобками.
A2.2 Перестановка формул: скобки и дроби
2 февраля 2021 г., 17:06 — AJ (e67821)
Open image
Преобразование формул, также называемое транспонированием формул, является необходимым навыком для большинства курсов. Этот модуль дает необходимые навыки работы с формулами.
Введение
Формулы используются во многих областях экономики, науки и техники. Например, формула простых процентов:11 Обратите внимание, что когда мы пишем \(nr\), мы имеем в виду \(n\times r\). Большую часть времени мы игнорируем знак умножения «\(\times\)», так как его можно спутать с \(x\). Также, когда мы пишем \(A=P(1+nr)\), \(P\) вне скобок умножает все, что в скобках. То есть мы имеем в виду \(A=P\times\left(1+nr\right)\). По той же причине мы не пишем знак умножения. \[
А=Р(1+номер)
\] Здесь \(A\) – это сумма, которую вы имеете по истечении \(n\) периодов времени (обычно месяцев или лет), \(P\) – сумма, которую вы инвестируете, а \(r\) – процентная ставка.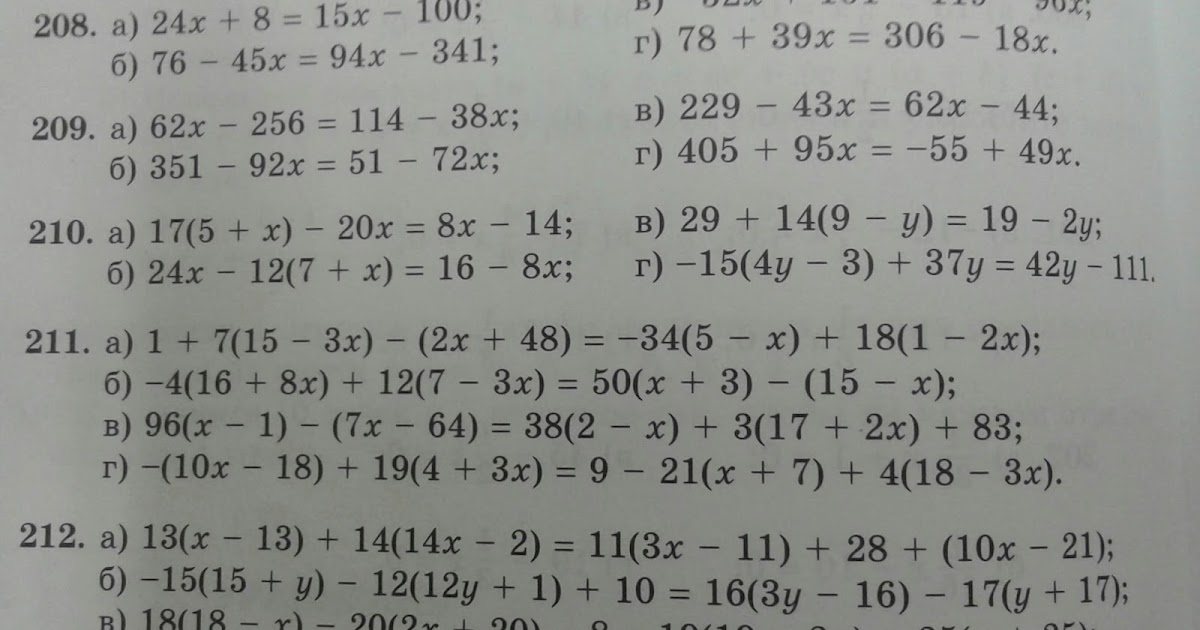
за период времени. \(A\) называется формулой, потому что формула в виде \(A\) равна … .
Что, если мы хотим, чтобы \(P\) был субъектом? В качестве первого шага мы могли бы избавиться от члена \(\left(1+nr\right)\), который умножает \(P\). Противоположностью умножения является деление. Чтобы избавиться от \(\left(1+nr\right)\), мы разделим обе части формулы на \(\left(1+nr\right)\).22 При перестановке формул главное правило: все, что вы делаете с одной стороной, вы должны делать и с другой.
Получаем:
\[ \frac{A}{(1+nr)}=\frac{P(1+nr)}{(1+nr)} \] Теперь условия \((1+nr)\) можно отменить, чтобы получить: \[ \frac{A}{(1+nr)}=P \] или же \[ P=\frac{A}{(1+nr)} \]
При перестановке формул начальная точка зависит от самой формулы. Проиллюстрируем это на примерах ниже.
Примеры:
Предположим, у вас есть 1000 долларов для инвестирования, и вы хотите знать, сколько времени потребуется, чтобы получить 2000 долларов с процентной ставкой 5% в год и простыми процентами.
Формула простых процентов: \[ А=Р(1+рн) \] и мы знаем A=2000$, \(P=\1000$\) и \(r=5%=5/100=0,05\). Мы хотим найти \(n\).
Решение:
Первым делом нужно избавиться от \(P\), умножающего скобку \((1+rn)\). Мы делаем это, разделив обе части на \(P\), чтобы получить \[ \frac{A}{P}=\frac{P(1+rn)}{P}. \] Теперь мы отменяем \(P\), чтобы получить 33. На самом деле есть 1, умножающая скобку, которую мы никогда не показываем. Поскольку умножение на 1 ничего не меняет, мы можем удалить скобки, как показано ниже. \[\начать{выравнивать*} \frac{A}{P} & =\left(1+rn\right)\\ &=1+рн. \end{align*}\] Далее мы хотим получить \(rn\) сам по себе. Мы делаем это, вычитая 1 с обеих сторон, чтобы получить: \[\begin{align*} \frac{A}{P}-1 & =1+rn-1\\ & = рн. \end{align*}\] Последний шаг — получить \(n\) сам по себе. Мы делаем это, разделив обе части на \(r\)44. Помните, что деление на \(r\) равносильно умножению на \(1/r\).
\[ \frac{1}{r}\left(\frac{A}{P}-1\right)=\frac{nr}{r}. \] Отмена \(r\) справа дает: \[\begin{align*} \frac{1}{r}\left(\frac{A}{P}-1\right) & =n\\ n & =\frac{1}{r}\left(\frac{A}{P}-1\right). \end{align*}\] Теперь мы можем вычислить \(n\), подставив значения для \(A\), \(P\) и \(r\): \[\begin{align*}
n & =\frac{1}{r}\left(\frac{A}{P}-1\right)\\
& =\frac{1}{0,05}\left(\frac{2000}{1000}-1\right)\\
& = 20.
\end{align*}\] Таким образом, потребуется 20 лет, чтобы удвоить первоначальные инвестиции в 1000 долларов!Преобразуйте формулу \(P=2(L-W)\), чтобы сделать ‘\(L\)’ подлежащим.
Решение: \[\begin{align*} P & = 2 \ влево (Д-Ш \ вправо) \\ \frac{P}{2} & =\frac{2\left(L-W\right)}{2}\quad\left(\textrm{разделить обе части на 2}\right)\\ \frac{P}{2} & =L-W\quad\left(\textrm{отмените 2 и удалите скобки}\right)\\ \frac{P}{2}+W & =L-W+W\quad\left(\textrm{добавить $W$ с обеих сторон}\right)\\ & =L\\ L & =\frac{P}{2}+W\quad\textrm{переставьте $L$ слева}. \end{align*}\] Обратите внимание, что вам не нужно давать пояснения к каждой строке вашего решения. Мы включаем примечания, чтобы показать вам, что мы делаем.Преобразуйте формулу \(P=2(L-W)\), чтобы сделать \(W\) субъектом.
Решение: \[\begin{align*} P & = 2 \ влево (Д-Ш \ вправо) \\ \frac{P}{2} & =\frac{2\left(L-W\right)}{2}\quad\left(\textrm{разделить обе части на 2}\right)\\ \frac{P}{2} & =L-W\quad\left(\textrm{отмените 2 и удалите скобки}\right)\\ \frac{P}{2}-L & =L-W-L\quad\left(\textrm{вычесть $L$ с обеих сторон}\right)\\ & =-W\\ -W & =\frac{P}{2}-L\quad\textrm{$\left(\textrm{переставьте $-W$ слева}\right)$ }\\ W & =-\frac{P}{2}+L\quad\textrm{$\left(\textrm{умножьте обе стороны на $-1$, чтобы получить +$W$ слева}\right)$ }\\ & =L-\frac{P}{2}\quad\textrm{$\left(\textrm{переставить члены (необязательно)}\right)$ .} \end{выравнивание*}\]Переформулируйте формулу \(L=\left(Mt-g\right)/b\), чтобы в качестве подлежащего сделать «M».55 В этом случае дробная черта справа действует как скобка. То есть \(b\) внизу делится на члены \(Mt\) и \(-g\).
Решение: \[\begin{align*} L & =\frac{Mt-g}{b}\\ Lb & =Mt-g\quad\textrm{$\left(\textrm{умножение обеих частей на $b$ и сокращение $b$ справа}\right)$ }\\ Lb+g & =Mt-g+g\quad\left(\textrm{добавление $g$ с обеих сторон}\right)\\ & =Мт\\ \frac{Lb+g}{t} & =M\quad\textrm{$\left(\textrm{деление обеих сторон на $t$ }\right)$ }\\ M & =\frac{Lb+g}{t}\quad\textrm{$\left(\textrm{переписать, чтобы поместить M слева}\right)$ . }
\end{выравнивание*}\] 9{2} & =\frac{2\left(E-mgh\right)}{m}\\
v & =\pm\sqrt{\frac{2\left(E-mgh\right)}{m}}\quad\textrm{$\left(\textrm{извлечение квадратного корня из обеих сторон}\right)$ }\\
& =\sqrt{\frac{2\left(E-mgh\right)}{m}}\quad\textrm{$\left(\textrm{принимая положительный корень в качестве ответа.}\right)$ }
\конец{выравнивание*}\]Если \(2/k=(j+1)/3,\), найти \(k\).
Решение. Обратите внимание, что дробная черта действует как скобка. Когда мы умножаем обе части на \(k\), член \(j+1\) помещается в скобку \[\begin{align*} \frac{2}{k} & =\frac{j+1}{3}\\ 2 & =\frac{k\left(j+1\right)}{3}\quad\textrm{$\left(\textrm{умножая обе части на $k$ }\right)$ }\\ 6 & =k\left(j+1\right)\quad\left(\textrm{умножение обеих сторон на $3$ }\right)\\ \frac{6}{j+1} & =k\quad\left(\textrm{деление обеих сторон на $j+1$ }\right)\\ k & =\frac{6}{j+1}. \end{align*}\] Первые два шага можно выполнить одним действием следующим образом: \[\begin{align*} 6 & =k\влево(j+1\вправо). \end{align*}\] Это называется перекрестным умножением. 9{2}+2as\), найти \(u.\)\(m=\sqrt{\frac{x+y}{z}}\), найти \(y.\)
\end{align*}\] Теперь мы можем вычислить \(n\), подставив значения для \(A\), \(P\) и \(r\): \[\begin{align*}
n & =\frac{1}{r}\left(\frac{A}{P}-1\right)\\
& =\frac{1}{0,05}\left(\frac{2000}{1000}-1\right)\\
& = 20.
\end{align*}\] Таким образом, потребуется 20 лет, чтобы удвоить первоначальные инвестиции в 1000 долларов!
}
\end{выравнивание*}\] 9{2} & =\frac{2\left(E-mgh\right)}{m}\\
v & =\pm\sqrt{\frac{2\left(E-mgh\right)}{m}}\quad\textrm{$\left(\textrm{извлечение квадратного корня из обеих сторон}\right)$ }\\
& =\sqrt{\frac{2\left(E-mgh\right)}{m}}\quad\textrm{$\left(\textrm{принимая положительный корень в качестве ответа.}\right)$ }
\конец{выравнивание*}\]
9{2}+2as\), найти \(u.\)Ответы
\(A=\frac{S}{C}-B\)
\(A=\frac{3v}{h}\)
\(a=\frac{2A}{h}-b\)
\(B=\frac{AP-C}{2}\)
\(C=B-\frac{3A}{2P}\)
\(r=\pm\sqrt{\frac{2I}{m}}\)
\(b=\frac{k-H}{kt}\) 9{2}г-х\)
Загрузите эту страницу, A2.2 Преобразование формул: скобки и дроби (PDF 212 КБ)
Ключевые слова:
Математика
Алгебра
Дроби
Скобки Формула | Breeding Better Dogs
Примечание редактора: Статьи могут быть воспроизведены только для личного использования. Чтобы воспроизвести для общественного или коммерческого использования, используйте эти рекомендации.
Родительская категория:
- Товары для разведения
К началу 1950-х годов Ллойд С.
Брэкетт стал легендой своего времени. Отчасти из-за качества собак, которых он произвел, и отчасти из-за его откровенности при решении проблем, связанных с разведением собак. Он мог многое сказать о выборе производителей, о том, как исправить проблемы и как внести улучшения. Брэкетт считался одним из отцов немецкой овчарки в США. На момент своей смерти он был старейшим из ныне живущих постоянных любителей породы (с 1912). Его питомник назывался Long Worth, и во всем собачьем мире его помнят за его теории о методах разведения. Брэкетт был начитан и быстро учился. Своими работами он пролил свет на путаницу и недоразумения, связанные с линией и инбридингом. Одним из его величайших достижений было то, что за двенадцать лет он произвел более 90 чемпионов.
Все его методы и идеи не были новыми. Например, он совместил изучение родословных с полученными ими результатами. После многих лет наблюдения за тем, какие комбинации дают лучшее потомство, он усовершенствовал свои идеи о том, как выбирать партнеров для размножения.
Из этого опыта вышла формула, которая позже сделает его знаменитым. Формула не была новой, но его идеи о том, как ее использовать, привлекли внимание. Заводчики домашних животных использовали его в течение многих лет. Он основывался на принципах линии и инбридинга. Но именно Брэкетт и его подход к запланированному разведению сделали его широко известным. Брэкетт верил в анализ родословной, оценку помета, использование линий и инбридинга, а также простую в использовании систему записи. Именно эти идеи отличали его от других, которые занимались лишь искусством разведения. Хотя Брэкетт наиболее известен своим упором на использование линейного разведения, он не боялся инбридинга, если того требовала ситуация. Брэкетт считал, что нет смысла заниматься разведением до тех пор, пока не будет собрана необходимая информация об отце и матери. Он уделял большое внимание здоровью, темпераменту и породным характеристикам. Его запланированные вязки были основаны на результатах, полученных у его щенков.
Другими словами, он учился на своих ошибках.
Брэкетт понимал ценность использования качественных собак, которые были связаны друг с другом. Этот подход позволил ему сконцентрировать гены, необходимые для получения желаемых признаков. Его методы уменьшения ошибок и улучшения качества были сосредоточены на тщательном выборе партнеров для разведения. Они играли центральную роль в поддержании и улучшении специфических признаков, в то же время снижая заболеваемость и другие нежелательные проблемы. Брэкетт прославился разведением качественных собак с последовательным типом. Его стратегия основывалась на серии скрещиваний с использованием родственников. Часто его цитировали: «Никогда не делайте ауткроссинг, когда кажется, что все идет хорошо, делайте это только в качестве эксперимента или когда какую-то ошибку или ошибки нельзя устранить». Он тщательно изучал каждого племенного кобеля и их потомство, исключая тех, кто не соответствовал требованиям, и тех, у кого были недостатки. Тщательный осмотр его родословных показывает, что многие из его производителей сами были инбредными или лайнбредными, и большинство из них, как правило, каким-то образом были связаны с суками в его программе разведения.
Успех Брэкетта помог сделать линейное разведение популярным. Он продемонстрировал, как добиться улучшений, сохранив общий пул генов за счет использования родственных собак. Он считал, что ауткроссинг был наименее желательным методом, потому что он вводил новые гены в его родословные, что, в свою очередь, приводило к различиям и генетическим вариациям среди потомков.
Документально подтверждено, что два полных брата обычно не обладают одинаковым генетическим потенциалом, даже если оба происходят от одних и тех же родителей. Один брат или сестра может унаследовать один набор генов от своего отца, а другой может получить другой набор от дяди через мать. Хотя каждый щенок всегда получает половину своих генов от отца и половину от матери, это не означает, что каждый из них получит одинаковый набор генов. Это объясняет, почему однопометники не всегда выглядят одинаково или обладают одинаковой способностью производить качественные продукты. Брэкетт вел подробные записи о различиях между братьями и сестрами.
Он был хорошо начитан по этому вопросу и иногда упоминал в своих статьях работы Аристотеля и Менделя. На практике все они разделяли схожие убеждения.
Брэкетт обычно быстро комментировал то, что он наблюдал, и то, как можно было бы улучшить ситуацию. В заявлении, взятом из одной из его статей, он сказал: «Всякий раз, когда два или три любителя собак собираются вместе, почти наверняка заговорит о лайнбридинге. Этот термин может использоваться без реального понимания того, что он означает. Кажется, что даже в умах опытных собаководов существует большая путаница в отношении фактического значения терминов и того, как их различать». Он упомянул об этой дилемме в нескольких статьях в различных сценариях. Однажды он поднял несколько вопросов, когда услышал, как два заводчика обсуждают линейное разведение. Он сослался на заводчика, который порекомендовал его, с заявлением, с чем связан? Он знал, что ответ на вопрос будет мерой того, что заводчик на самом деле знает об этом термине. Это был его способ оценить мудрость других.
Он знал, что линейное разведение может означать многое. Например, собаку можно скрещивать по родословной со стороны отца или со стороны матери. Те, кто использует этот термин, обычно понимают, что это означает только то, что собаки связаны друг с другом.
Брэкетт был обеспокоен будущим разведения лучших собак и отсутствием программ обучения заводчиков. Он считал, что «большинство собаководов не формулируют план разведения и редко, если вообще когда-либо, при спаривании думают, как или с чем они будут скрещивать какое-либо из полученного потомства».
Формула Брэкетта предпочитала концентрированные гены в родословной. Он сделал это, сделав акцент на сире сира. Обратите внимание, что на рисунке 1 одна и та же собака указана в родословной со стороны отца и матери. Брэкетту нравилось использовать одну важную собаку, чтобы она появлялась дважды в родословной трех поколений. Основная формула, которую он предпочитал, может быть сформулирована следующим образом: «Пусть отец отца станет великим отцом на стороне матери».
Другими словами, «пусть отец отца станет дедушкой матери».
Рисунок 1. Родословная племенного кобеля брекетта
Отец, обведенный кружком, указан с обеих сторон родословной. Поскольку это одна и та же собака, это должна быть выдающаяся собака, свободная от болезней, потому что его гены сохраняются с обеих сторон родословной и передаются новому племенному кобелю.
Брэкетт знал, что Мендель мог постоянно предсказывать черты своего потомства, особенно когда он знал, какие характеристики были переданы в родословных родителей. Они оба знали, что при разведении двух особей с известным происхождением больше уверенности в том, что они могут произвести, чем при отсутствии информации о них. Мендель продемонстрировал эти принципы в 1860-х годах. Брэкетт использовал эти идеи, потому что знал, что непредвиденное с большей вероятностью может произойти, когда есть пробелы в информации о предках и их однопометниках. В то время как наследственность имеет тенденцию производить сходство, наука генетика учит нас искать под поверхностным сходством фенотипов важные ключи к разгадке генотипов.
Таким образом, когда о человеке говорят, что он доминирует по какому-либо признаку, это следует понимать в том смысле, что у большого процента его потомства наблюдался определенный признак. Это не означает, что все их потомки будут иметь эту черту. Рисунок 2 иллюстрирует подход Брэкетта к разведению гипотетической суки по кличке «А». Родословная таблицы окрасов собак Stick, описанная в книге Баттальи «Разведение лучших собак», используется для иллюстрации подхода Брэкетта. Родословная собаки-палки иллюстрирует, как сильные, слабые стороны и тенденции в родословной могут быть записаны, а затем легко закодированы. Обратите внимание, что каждая фигурка нарисована с семью структурными частями. В соответствии со стандартом породы каждая из семи структурных частей имеет цветовую кодировку, чтобы показать их качество или его отсутствие. Цветовые коды качества:
| Цвет | Ранг | Качество |
|---|---|---|
| Синий | 1-е место | Идеально на основе стандарта |
| Черный | 2-е место | Далеко от идеала на основе стандарта |
| Красный | 3 место | Неисправность на основе стандарта |
| Серый | 4 место | Неисправность по стандарту |
На рис.
2 показано, как Брэкетт собирал информацию об «А». Заметки, которые были собраны об «А», указывают на наличие предупреждающих сигналов о нескольких чертах. Круги вокруг признака или предка используются, чтобы показать, какой информации не хватает.
В примечаниях заводчика может быть написано: «Ее родители были хорошего качества, один из ее четырех братьев был диспластическим, другой — монорицидным. У двух других отсутствовали премоляры, одна сестра была белой. Все шестеро ее однопометников были среднего качества».
Следует помнить, что ценность суки также определяется тем, что она произвела. Заметки заводчика о ее щенках могут гласить: «Ее первая вязка была качественной собакой с открытой родословной. Все четыре ее щенка были плохого качества, один имел дисквалифицирующий окрас; у двух других челюсть была перекусом, у одного была диспластическая. Ее второе разведение было линейным разведением с другой качественной собакой. Эта собака была родственницей ее отца. Двое из восьми щенков умерли от болезни сердца, у одного была диагностирована клиническая дисплазия тазобедренного сустава, а у двух других отсутствовали премоляры».
Краткие заметки о суке «А» полезны, потому что они представляют обзор качеств сук.
Рисунок 2. Родословная Stickdog
Примечание 1. Первое разведение, N=4, с производителем с открытой родословной. Произведено щенков: 1 с белой шерстью, 2 с перекусом челюстей, 1 с дисплазией и 4 некачественных
Примечание 2. Второе разведение, N=5, разведение линии А. Щенки: 2 из 8 умерли от проблем с сердцем, у 2 отсутствовали премоляры, 1 был диспластическим, все среднего качества. , одна сестра была белой. Все среднее по качеству
Примечание 4. Отец и мать «А» — оба были хорошего качества, но ее мать дала только среднее потомство при скрещивании с тремя производителями разного качества. Мало что известно о ее сире.
Брэкетт и Мендель вели бы аналогичные записи о партнерах по размножению «А» и ее потомстве. После двух вязок, которые привели к неподходящему экстерьеру, проблемам со здоровьем и дисквалифицирующему окрасу (белый), ни Брэкетт, ни Мендель не стали бы вязать ее в третий раз, даже если бы был доступен производительный производитель.
Опыт подсказывает, что ее не следует разводить. Однако, если целью было произвести случайного щенка определенного качества, это все равно рискованная сука, потому что ее родословная может произвести нездоровых и посредственных щенков, многие из которых, вероятно, будут носителями. Брэкетта беспокоили эти суки, потому что он знал, что большинство покупателей хотят знать, что их щенок генетически здоров и что он не станет агрессивным или настолько нервным, что испугается чего-нибудь необычного. Одна из лучших причин не использовать «А» заключается в том, что большинство ее щенков, вероятно, станут чьими-то домашними компаньонами и потребуют дорогостоящего ветеринарного ухода на всю жизнь.
Вариации формулы
Заводчики быстро поняли, что в предпочитаемую Брэкеттом формулу могут быть внесены изменения, основанные на сильных и слабых сторонах суки. Хотя они были не такими продуктивными, как предпочтительная формула, они работали над концентрацией необходимых генов. Варианты формулы можно сформулировать следующим образом: пусть отец отца будет дедушкой матери со стороны отца, а не со стороны матери.
В другом варианте отец может быть результатом полного или сводного спаривания брата и сестры и, таким образом, инбредным. В каждом случае выбор пары для дефектной суки, такой как «А», чья широко открытая родословная не предлагает никакой силы, не будет хорошим использованием этих формул.
Выбор партнеров для разведения всегда должен быть направлен на исправление недостатков в родословных и внесение улучшений. Поступать иначе — пустая трата времени.
Ссылки:
Батталья, К.Л. — Разведение лучших собак, Публикации BEI, Атланта, Джорджия, 1986
Белл, Джерольд С. «Выбор с мудростью», AKC Gazette, август 2000 г., Vol. 117, № 8, с-51.
Белл, Джерольд, С. «Разработка программ здорового разведения», Соответствие здоровью собак, Фонд здоровья собак AKC, 15–17, 19 октября.99. Сент-Луис МО.
Брэкетт, Ллойд, К. «Планируемое разведение», журнал Dog World Magazine, Чикаго, Иллинойс, 1961. Сент-Луис, Миссури.
Об авторе
Кармен Л. Батталья имеет докторскую степень.