Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
| 0° | 30° | 45° | 60° | 90° | sin | 0 | 1 | cos | 1 | 0 | tg | 0 | 1 | √3 | – | ctg | – | √3 | 1 | 0 |
|---|
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2πr. Следовательно 360° в радианах равно 2π, а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π.
Например, для угла 90° будет · π = πЧтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
 |
Онлайн тренажер
|
Простые тригонометрические тождества
Используя вышеописанные формулы:
тангенс угла выражается через отношение синуса к косинусу:
Соответственно котангенс выражается аналогично:
Также можно заметить, что произведение тангенса на котангес равно единице:
tg(a) · ctg(a) = · =- sin(a) · cos(a)
- cos(a) · sin(a)
Иными словами, тангенс угла обратно пропорционален котангенсу угла и наоборот:
tg(a) · ctg(a) = 1 ; tg(a) = ; сtg(a) =Используя теорему Пифагора в треугольнике, что сумма квадратов катетов равно квадрату гипотенузы
r2 = s2 + c2 = (sin(a) · r)2 + (cos(a) · r)2;
r2 · (sin(a)2 + cos(a)2
Сократим обе части на r2, получим:
sin2a + cos2a = 1
Разделив обе части на квадрат синуса или квадрат косинуса, получим еще два основных тригонометрических тождества:
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
- Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.
- Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .
- И синус, и косинус принимают значения от до .
- Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.
- Знаки синуса, косинуса, тангенса и котангенса.
- Синус — функция нечётная, косинус — чётная.
- Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .
Вот что мы видим на этом рисунке:
Ты нашел то, что искал? Поделись с друзьями!
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Например:
;
;
;
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
,
.
Простым следствием теоремы Пифагора является основное тригонометрическое тождество
:Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
,
.
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
,
,
где — целое число. То же самое можно записать в радианах:
,
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
,
.
В результате получим следующую таблицу.
| Главная > Учебные материалы > Математика: Тригонометрия | ||||
|
1.Тригонометрия. 2.Тригонометрические функции.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1. Тригонометрия – раздел математики, изучающий зависимости между углами и сторонами в треугольниках и тригонометрические функции. Основная задача тригонометрии — вычисление неизвестных величин треугольника, если известны значения других его величин. В тригонометрии также решают задачу о вычислении углов треугольника, если известны его стороны, задачу о вычислении сторон треугольника и т.д. |
||||
Для измерения углов между сторонами треугольника используется такая единица измерения, как градус. Вся окружность с центром в точке О составляет 360°. Помимо градусной меры углов, также используется радианная мера. 1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″. Радианная и градусная меры связаны зависимостью 180°=π радиан. Угол в n° равен πn/ 180 радиан. Для того, чтобы рассчитать длину дуги угла α, используется следующая формула: l= αr Площадь S сектора круга радиуса r, дуга которого содержит α радиан, рассчитывается так: S = αr² / 2 |
Площадь сектора круга. |
|||
2. Тригонометрические функции. Тригонометрические функции — математические функции от величины угла. Они используются при изучении геометрии, а также при исследовании переодических процессов в разных областях науки. Тригонометрические функции определяют отношения сторон прямоугольного треугольника в единичной окружности. Пусть на плоскости задана прямоугольная система координат с началом в точке O и с осями OX и OY . Возьмем в этой системе координат окружность с центром в точке O и радиусом, равным единице. Пусть отрезок OМ поворачивается на произвольный угол α вокруг центра O. Так как треугольник ОМВ прямоугольный, то тригонометрические функции угла α определяется из соотношений в прямоугольном треугольнике. Тогда: |
||||
| Синусом угла α называется отношение противолежащего катета к гипотенузе или отношение координаты y точки М к длине отрезка OМ=R, где R — радиус окружности. Синус угла α обозначают sinα. Так как длина отрезка OМ=1, следовательно sinα = y. Косинусом угла α называется отношение прилежащего катета к гипотенузе или отношение координаты х точки М к длине отрезка OМ. Косинус угла α обозначают cosα. Так как ОМ=1, то cosα = х. Тангенсом угла α называется отношение противолежащего катета к прилежащему или координаты y точки М к x. Тангенс угла α обозначают tgα. Так как y = sin α и x = cos α, то tgα= sin α / cos α. Котангенсом угла α называется отношение прилежащего катета к противолежащему или отношение координаты х точки М к y. Котангенс угла α обозначают ctgα. Так как y = sin α и x = cos α, то ctgα= cosα / sinα. Из последних двух соотношений следует: ctg α= 1 / tg α |
sin, cos, tg, ctg на тригонометрическом круге. |
|||
y = sin x
|
График функции sin. |
|||
y = cos x
|
График функции cos. |
|||
y = tg x
|
График функции tg. |
|||
y = ctg x
|
График функции сtg. |
|||
Значения синуса и косинуса для некоторых углов. |
||||
| Значения тангенса и котангенса для углов 30, 45 и 60 находятся аналогично. | ||||
Пример 1 |
||||
| Пример 2 | ||||
| 1 2 3 4 5 6 7 8 9 | ||||
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.
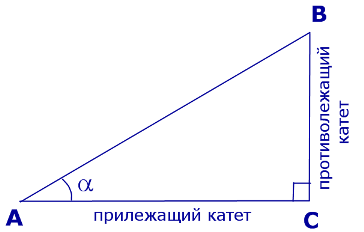

Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
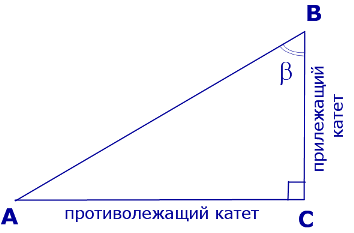
Рис.2
Синусом угла называют дробь:
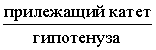
Косинусом угла называют дробь:
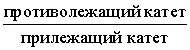
Тангенсом угла называют дробь:
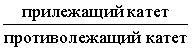
Котангенсом угла называют дробь:
Синус, косинус, тангенс и котангенс, и их комбинации называют тригонометрическими функциями. В данном разделе справочника тригонометрические функции вводятся для острых углов. В следующем разделе даётся определение тригонометрических функций для произвольных углов.
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения
sin α , cos α , tg α , ctg α
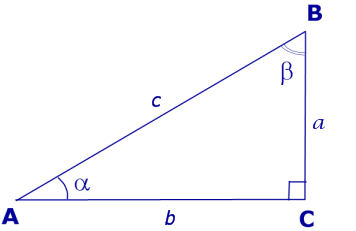
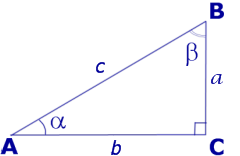
Рис.3
В соответствии с рисунком 3 справедливы формулы:
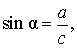

Следовательно,
Кроме того, справедливы формулы:
sin α = cos β, cos α = sin β, tg α = ctg β, ctg α = tg β,
которые можно переписать в виде:
sin α = cos (90° – α), cos α = sin (90° – α),
tg α = ctg (90° – α), ctg α = tg (90° – α).
Пример. Найти тригонометрические функции углов 30°, 45°, 60°.
Решение. Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
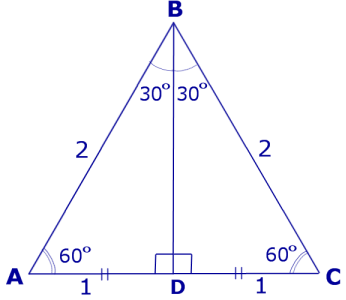
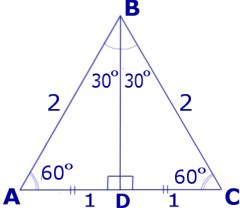
Рис.4
Тогда
Поэтому
Кроме того
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).

Тогда
Поэтому
Определение тригонометрических функций произвольного угла приводится в разделе справочника «Тригонометрические функции произвольного угла».

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
|
Тригонометрические функции
|
Величины углов (аргументы функций): α, x |
Радиус круга: r |
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0
9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
12. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
13. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞<tanx<∞
14. График функции котангенс
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞<cotx<∞
15. График функции секанс
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞)
16. График функции косеканс
y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞)
Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в астрономии:
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крес
Урок 2: Функции тригонометрические — 100urokov.ru
План урока:
Синус и косинус угла на единичной окружности
График синуса и косинуса
Тангенс угла
График тангенса
Котангенс угла
Синус и косинус угла на единичной окружности
Впервые мы познакомились с синусом, косинусом и другими тригонометрическими функциями ещё в 8 класс на уроках геометрии, при изучении прямоугольного треугольника. Пусть есть некоторый треуг-ник АВС, у которого∠ С – прямой, а ∠ВАС принимается за α. Тогда sinα – это отношение ВС к АВ, а cosα– это отношение АС к АВ. В свою очередь tgα– это отношение ВС к АС:

С помощью тригонометрических функций удобно было находить стороны прямоугольного треугол-ка. Например, пусть известно, что гипотенуза АВ равна 5, а sinα = 0,8. Тогда из формулы sinα = ВС/АВ легко получить, что
ВС = АВ•sinα = 5•0,8 = 4
Если известно, что cosα = 0,6, то мы сможем найти и второй катет:
cosα = АС/АВ
АС = АВ•cosα = 5•0,6 = 3
Отдельно заметим, что тангенс угла может быть рассчитан не как отношение двух катетов, а как отношение синуса к косинусу:
tgα = ВС/ АС = (АВ•sinα)/(АВ•cosα) = (sinα)/(cosα)
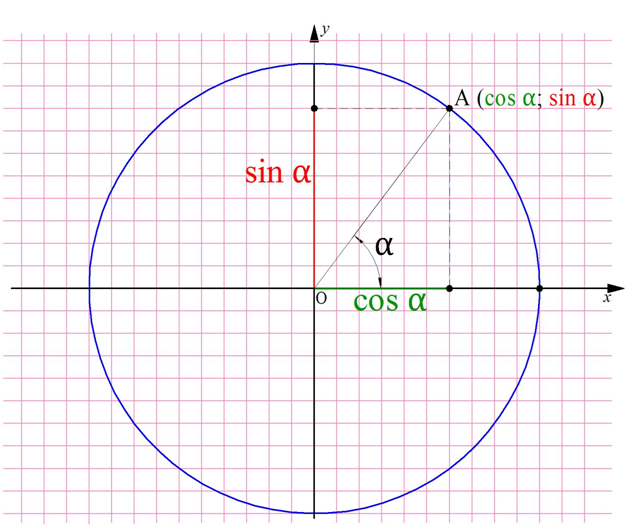
Отметим на единичной окружности произвольную точку А, которой соответствует некоторый угол α. У этой точки есть свои координаты хА и уА:

Попытаемся определить, чему равны координаты точки А. Для этого обозначим буквой B точку, в которой перпендикуляр, опущенный из А, пересекает горизонтальную ось Ох, и рассмотрим треугольник ОАВ:

Ясно, что ОАВ – это прямоугольный треугольник, ведь∠ АОВ = 90°. Значит, отрезок АВ можно рассчитать по формуле
АВ = sinα•ОА
Но ОА – это радиус единичной окружности. Это значит, что ОА = 1. Тогда
АВ = sinα•ОА = sinα•1 = sinα
С другой стороны, видно, что величина отрезка АВ равна координате уА. Получается, что уА = АВ = sinα, или
уА = sinα
Отрезок ОВ также можно найти из прямоугольного треугольника АОВ, используя косинус:
ОВ = cosα•ОА
Учитывая, что ОА = 1, а длина ОВ равна координате хА, мы получим следующее:
хА = ОВ = cosα•ОА = cosα•1 = cosα
то есть координата хА равна cos α:
хА = cosα
Итак, мы выяснили, что координаты точки, лежащей на единичной окружности, равны синусу и косинусу угла, соответствующего этой точке.
Таким образом, нам удалось дать новое определение синусу и косинусу угла:


Заметим, что в прямоугольном треугольнике углы, помимо самого прямого угла, могут быть только острыми. Поэтому предыдущее определение синуса и косинуса, данное в 8 классе в курсе геометрии, было пригодно лишь для углов из диапазона 0 <α < 90°. На единичной окружности можно отложить любой угол, то есть теперь мы можем вычислять тригонометрические ф-ции для произвольных значений α. При этом синус и косинус могут оказаться отрицательными величинами. Например, для угла α = 2π/3 косинус окажется отрицательным, ведь координата хА соответствующей ему точки окажется левее нуля на горизонтальной оси Ох:

Заметим, что знак синуса и косинуса определяется той четвертью, в которой будет располагаться точка на окружности. Углам в диапазоне 0 <α<π/2 соответствует Iчетверть, здесь все тригонометрические ф-ции принимают положительные значения. Ко II четверти относятся углы из промежутка π/2 <α<π. Здесь косинус становится меньше нуля, а синус остается положительным. В III четверти будут располагаться точки, соответствующие углам из интервала π <α< 3π/2, у них отрицательны и синус, и косинус. Наконец, к IV четверти относят углы из диапазона 3π/2 <α< 2π. Здесь отрицателен синус, а косинус больше нуля.



Как же определять значение синуса угла и его косинуса? Из геометрии нам уже известны их значения для трех углов: 30°, 45° и 60°:

Далее определим тригонометрические ф-ции угла, равного нулю. Если такой угол отложить на единичной окружности, то ему будет соответствовать точкаА с координатами (1; 0). Поэтому
sin 0° = уА = 0
cos 0° = xА = 1
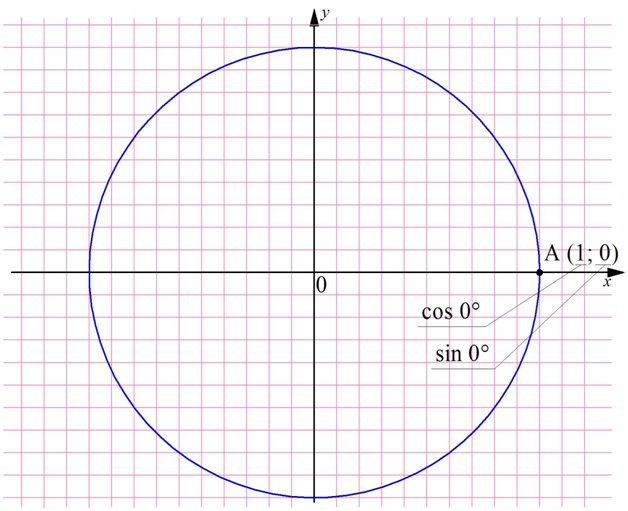
Аналогичным образом можно найти значение этих ф-ций и для угла 90°. Прямому углу на единичной окружности соответствует точка В с координатами (0; 1). Поэтому
sin90° = уВ = 1
cos90° = xВ = 0

Для определения тригонометрических ф-ций у углов, больших 90°, удобно использовать симметрию. Например, пусть необходимо вычислить синус для угла 120°. Отложим на окружности две точки, В и А. Первая будет соответствовать 120°, а вторая 60°:

Видно, что эти точки находятся на одном горизонтальном уровне, то есть их ординаты (координаты у) одинаковы. При этом абсциссы у них противоположны, ведь точки симметричны относительно оси Оу. Отсюда можно сделать вывод, что
уВ = уА
хВ = – хА
Но координаты А – это синус и косинус 60°, а координаты В являются тригонометрическими ф-циями угла 120°. То есть можно записать
sin 120° = sin 60°
cos 120° = – cos 60°
Так как для угла 60° значения синуса и косинуса нам уже известны, то можно записать:

В будущем мы изучим более простые способы вычисления синуса и косинуса углов, больших 90°, когда построения нам уже не потребуются. Однако сразу заметим, что в первую очередь необходимо запомнить значения синуса и косинуса для пяти углов: 0°, 30°, 45°, 60°, 90°. Приведем таблицу значений тригонометрических функций:

Некоторые люди испытывают проблемы с запоминанием этой таблицы. Однако ее можно представить в более простом виде. Заменим числа 0, 1 и 1/2 следующими выражениями с корнями:
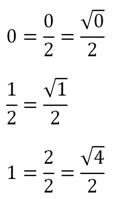
С учетом этого таблицу тригонометрических функций можно переписать так:

Теперь в каждой ячейке стоит дробь, у которой знаменатель равен двум. В числителе же стоит корень. Обратите внимание, что у синуса под корнем последовательно стоят числа 0, 1, 2, 3, и 4. У косинуса эти же числа идут в обратном порядке – от четверки до нуля. В таком виде таблицу запомнить проще.
Для вычисления тригонометрических ф-ций углов, не попадающих в диапазон 0 ⩽ α < 2π их надо привести к этому самому диапазону. Напомним, что для этого можно просто добавить к углу несколько полных оборотов, или отнять их.
Задание. Вычислите cos 7π/3.
Решение. Угол 7π/3 равен углу π/3:
7π/3 = 6π/3 + π/3 = 2π + π/3 = π/3
Значит, и косинус у угла 7π/3 будет равен косинусу угла π/3:
cos 7π/3 = cosπ/3 = 1/2
Ответ: 1/2.
График синуса и косинуса
Заметим, что координаты точек, лежащей на единичной окружности, варьируются в пределах от – 1 до 1. Это означает, что значение синуса и косинуса также может находиться только в интервале между этими числами. Получается, что область значения этих ф-ций – это промежуток [– 1; 1].
Вычислить синус и косинус можно для абсолютно любого угла поворота, поэтому область определения этих тригонометрических ф-ций – вся числовая прямая, то есть промежуток (– ∞; + ∞).
Изучение графиков тригонометрических функций начнем с синуса. В тригонометрии при построении графика синуса принято по оси Ох откладывать значение угла в радианах, а не в градусах. Из-за этого в школьной тетради тяжело точно отметить точки, через которые проходит этот график. Например, возьмем угол, равный 90°. Его величина в радианах π/2, а sinπ/2 = 1. Получается, график должен пройти через точку (π/2; 1). Однако число π/2 – иррациональное, равное примерно 1,5708…, и точно отложить отрезок длиной π/2 невозможно.
Поэтому в учебных целях график строят приближенно (естественно, что на практике точный график можно построить с помощью компьютера с любой требуемой точностью). Считают, что величина π/2 примерно равна 1,5, то есть дроби 3/2. Если выбрать масштаб, при котором единице равны 2 клеточки, то π/2 – это 3 клеточки. Тогда π/6 – это одна клеточка, а π/3 – две.
Мы знаем, что
sin 0 = 0
sin π/6 = 1/2
sin π/2 = 1
Значит, график синуса должен проходить через точки (0; 0), (π/6; 1/2) и (π/2; 1). Отметим их на координатной плоскости:

С помощью некоторых соображений симметрии можно вычислить ещё несколько точек в диапазоне от 0 до 2π. Не будем перечислять их координаты, а просто отметим их на рисунке:

Теперь соединим их плавной кривой:

Мы получили график синуса на промежутке от 0 до 2π. Но ведь мы можем вычислить синус для любого другого угла! При этом мы используем тот факт, что углам, отличающимся на 2π (на один полный оборот), на единичной окружности соответствует одинаковая точка. То есть этим двум углам будут соответствовать точки на графике с одинаковой ординатой (координатой у), но абсциссами, отличающимися на 2π. Другими словами, точку графика можно перенести на 2π (то есть 12 клеточек) влево или вправо:

Перенести можно не одну точку, а сразу всё множество точек, лежащих между 0 и 2π:

Получили ещё два участка графика, на промежутках [– 2π; 0] и [2π; 4π]. Эти участки также можно переместить влево и вправо. Продолжая этот процесс бесконечно, мы получим весь график у = sinx:

В результате мы получили кривую, которую называют синусоидой.
Теперь построим график косинуса. Мы знаем что
cos 0 = 1
cos π/3 = 1/2
cos π/2 = 1
Получается, что график должен проходить через точки (0;1), (π/3; 1/2) и (π/2; 0). Отметим их на плоскости:

Можно вычислить, используя симметрию на единичной окружности, ещё несколько точек, которые должны лежать на графике. Не приводя этих вычислений, просто отметим эти точки на плоскости:

Соединяем эти точки плавной линией:

Как и в случае с синусом, участок графика косинуса можно перенести на 2π (12 клеточек влево и вправо). В результате таких действий получим окончательный вид ф-ции у = cosх:

Можно заметить несколько особенностей полученных графиков. Во-первых, все точки обоих графиков лежат в «полосе» между прямыми у = 1 и у = – 1. Это следствие того, что и у синуса, и у косинуса область значений – это промежуток [– 1; 1]:

Во-вторых, график косинуса очень похож на синусоиду. Он имеет такую же форму, но просто смещен на π/2 (3 клеточки) влево. Это не случайно, в будущих уроках мы узнаем причину этого явления. Но, так как график косинуса – это просто смещенная синусоида, то термин «косинусоида» для его обозначения почти не используется – он просто избыточен.

В-третьих, графики обладают периодичностью. Они «повторяются» с периодом 2π. Дело в том, что углам, отличающимся друг от друга на 2π (то есть ровно на один полный поворот в 360°), на единичной окружности соответствует одна и та же точка. То есть справедливы формулы:
sin (x+ 2π) = sinx
cos (x+ 2π) = sinx


В-четвертых, можно заметить, что график косинуса симметричен относительно оси Ох, а график синуса симметричен относительно начала координат. Это значит, что синус является нечетной функцией, а косинус – четной функцией. Напомним, что ф-ция f(x) является нечетной, если справедливо условие
f(x) = – f(– x)
Если f(x) – четная ф-ция, то должно выполняться условие:
f(x) = f(– x)
Действительно, если отложить на единичной окружности углы α и (– α), то можно заметить, что их косинусы будут равны друг другу, и синусы окажутся противоположными:


Поэтому верны формулы:
sin (– α) = – sinα
cos (– α) = cosα


Эффективно подготовиться к ЕГЭ по математике помогут тщательно продуманные онлайн-курсы
Перейти
Тангенс угла
Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:


Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):
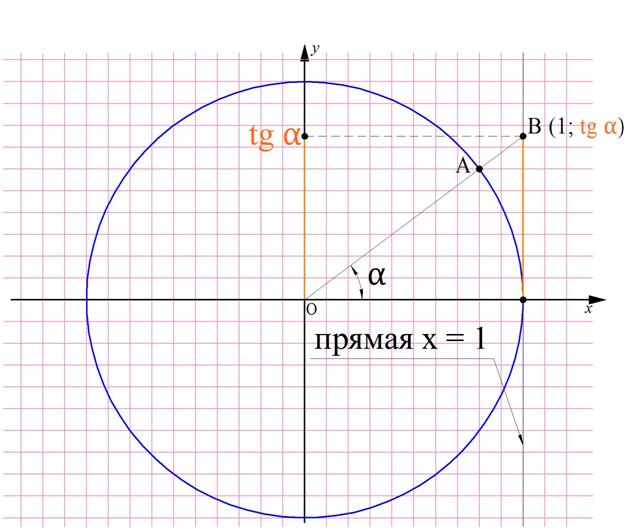
Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:

С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:
Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:

Это значит, что справедлива формула:
tg(α + π) = tg α

С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:

Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):

Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.

Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:

Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:

Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.
Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.

В частности, тангенс не определен при х = – π/2.

Мы сделали подборку лучших онлайн-курсов по школьным предметам
Перейти
График тангенса
Так как тангенс обладает периодом, равным π, достаточно построить его график на каком-нибудь промежутке длиной π. Далее его можно будет просто перенести на π единиц влево и вправо. Удобно выбрать промежуток от – π/2 до π/2. Дело в том, что на нем она определена во всех точках, кроме его концов.
Через точки х = – π/2 и х = π/2 проведем штриховые линии – они означают, что график НЕ должен пересекать их. Ясно, что график проходит через точку (0; 0), ведь tg 0 = 0. Тангенс представляет собой дробьsinx/cosx. При увеличении х от 0 до π/2 знаменатель возрастает, а числитель убывает, стремясь к нулю. Поэтому вся дробь неограниченно растет, и график тангенса возрастает до бесконечности:

Так как мы строим график нечетной ф-ции, то мы можем полученную ветвь отобразить симметрично относительно начала координат:

Полученный график называют тангенсоидой. Осталось воспользоваться тем, что мы рассматриваем периодическую ф-цию с периодом π, и перенести тангенсоиду влево и вправо:

Котангенс угла
Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:

Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:

Почти во всех задачах с помощью формулы
можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.
Значения этой ф-ции рассчитываются так:
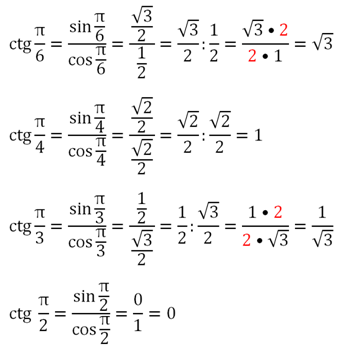
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.
График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:

Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.
Для сравнения покажем на одной плоскости графики тангенса и котангенса:

Котангенс, как и тангенс – нечетная ф-ция, то есть
ctg (– x) = – ctgx
Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.
Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.

Только усвоенная информация становится знанием. В этом вам помогут онлайн-курсы
Перейти
90000 Trigonometry 90001 90002 90003 90004 Trigonometry 90005 (from Greek trigonon «triangle» + metron «measure») 90006 90007 90002 Want to learn Trigonometry? Here is a quick summary. 90009 Follow the links for more, or go to Trigonometry Index 90007 90011 90012 90013 90014 90013 90004 Trigonometry 90005 … is all about 90004 triangles. 90005 90014 90021 90022 90002 Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more! 90007 90025 Right-Angled Triangle 90026 90002 The triangle of most interest is the right-angled triangle.The right angle is shown by the little box in the corner: 90007 90002 90007 90002 Another angle is often labeled θ, and the three sides are then called: 90007 90033 90034 90004 Adjacent 90005: adjacent (next to) the angle θ 90037 90034 90004 Opposite 90005: opposite the angle θ 90037 90034 and the longest side is the 90004 Hypotenuse 90005 90037 90046 90002 90007 90049 Why a Right-Angled Triangle? 90050 90002 Why is this triangle so important? 90007 90002 Imagine we can measure along and up but want to know the direct distance and angle: 90007 90002 90007 90002 Trigonometry can find that missing angle and distance.90007 90002 Or maybe we have a distance and angle and need to «plot the dot» along and up: 90007 90002 90007 90002 Questions like these are common in engineering, computer animation and more. 90007 90002 And trigonometry gives the answers! 90007 90025 Sine, Cosine and Tangent 90026 90002 The main functions in trigonometry are 90004 90005 Sine, Cosine and Tangent 90007 90002 They are simply one side of a right-angled triangle divided by another. 90007 90002 For any angle «90004 90003 θ 90006 90005»: 90007 90002 90007 90002 90003 (Sine, Cosine and Tangent are often abbreviated to sin, cos and tan.) 90006 90007 90002 90007 90049 Example: What is the sine of 35 °? 90050 90002 90007 90002 Using this triangle (lengths are only to one decimal place): 90007 90002 sin (35 °) = 90096 Opposite 90097 90098 Hypotenuse 90099 = 90096 2.8 90097 90098 4.9 90099 = 90004 0.57 … 90005 90007 90002 The triangle could be larger, smaller or turned around, but 90004 that angle will always have that ratio 90005. 90007 90002 Calculators have sin, cos and tan to help us, so let’s see how to use them: 90007 90002 90007 90049 Example: How Tall is The Tree? 90050 90002 We can not reach the top of the tree, so we walk away and measure an angle (using a protractor) and distance (using a laser): 90007 90033 90034 We know the 90004 Hypotenuse 90005 90037 90034 And we want to know the 90004 Opposite 90005 90037 90046 90002 90004 Sine 90005 is the ratio of 90004 Opposite / Hypotenuse 90005: 90007 90002 sin (45 °) = 90096 Opposite 90097 90098 Hypotenuse 90099 90007 90002 90007 90002 Get a calculator, type in «45», then the «sin» key: 90007 90002 sin (45 °) = 90004 0.7071 … 90005 90007 90002 90007 90002 What does the 90004 0.7071 … 90005 mean? It is the ratio of the side lengths, so the Opposite is 90003 about 0.7071 90006 times as long as the Hypotenuse. 90007 90002 90007 90002 We can now put 90004 0.7071 … 90005 in place of sin (45 °): 90007 90002 90004 0.7071 … 90005 = 90096 Opposite 90097 90098 Hypotenuse 90099 90007 90002 And we also know the hypotenuse is 90004 20 90005: 90007 90002 0.7071 … = 90096 Opposite 90097 90098 90004 20 90005 90099 90007 90002 To solve, first multiply both sides by 20: 90007 90002 20 × 0.7071 … = Opposite 90007 90002 Finally: 90007 90002 Opposite = 90004 14.14m 90005 (to 2 decimals) 90007 When you gain more experience you can do it quickly like this: 90002 90007 90049 Example: How Tall is The Tree? 90050 90002 Start with: sin (45 °) = 90096 Opposite 90097 90098 Hypotenuse 90099 90007 90002 We know: 0.7071 … = 90096 Opposite 90097 90098 20 90 099 90007 90002 Swap sides: 90096 Opposite 90097 90098 20 90 099 = 0.7071 … 90007 90002 Multiply both sides by 90004 20 90005: Opposite = 0.7071 … × 20 90007 90002 Calculate: Opposite = 90004 14.14 90005 (to 2 decimals) 90007 90002 The tree is 14.14m tall 90007 90025 Try Sin Cos and Tan 90026 90002 Play with this for a while (move the mouse around) and get familiar with values of sine, cosine and tangent for different angles, such as 0 °, 30 °, 45 °, 60 ° and 90 °. 90007 90002 Also try 120 °, 135 °, 180 °, 240 °, 270 ° etc, and notice that positions can be 90004 positive or negative 90005 by the rules of Cartesian coordinates, so the sine, cosine and tangent change between positive and negative also .90007 90002 So 90004 trigonometry is also about circles 90005! 90007 90002 90007 90025 Unit Circle 90026 90002 What you just played with is the Unit Circle. 90007 90002 It is a circle with a radius of 1 with its center at 0. 90007 90002 Because the radius is 1, we can directly measure sine, cosine and tangent. 90007 90002 Here we see the sine function being made by the unit circle: 90007 90002 90003 Note: you can see the nice graphs made by sine, cosine and tangent.90006 90007 90025 Degrees and Radians 90026 90002 Angles can be in Degrees or Radians. Here are some examples: 90007 90011 90012 90259 Angle 90260 90259 Degrees 90260 90259 Radians 90260 90021 90266 90013 Right Angle 90014 90013 90 ° 90014 90013 π / 2 90014 90021 90266 90013 __ Straight Angle 90014 90013 180 ° 90014 90013 π 90014 90021 90266 90013 Full Rotation 90014 90013 360 ° 90014 90013 2π 90014 90021 90022 90025 Repeating Pattern 90026 90002 Because the angle is 90004 rotating around and around the circle 90005 the Sine, Cosine and Tangent functions 90004 repeat once every full rotation 90005 (see Amplitude, Period, Phase Shift and Frequency).90007 90002 90007 90002 When we want to calculate the function for an angle larger than a full rotation of 360 ° (2π radians) we subtract as many full rotations as needed to bring it back below 360 ° (2π radians): 90007 90049 Example: what is the cosine of 370 °? 90050 90002 370 ° is greater than 360 ° so let us subtract 360 ° 90007 90002 370 ° — 360 ° = 10 ° 90007 90002 cos (370 °) = cos (10 °) = 90004 0.985 90005 (to 3 decimal places) 90007 90002 And when the angle is less than zero, just add full rotations.90007 90049 Example: what is the sine of -3 radians? 90050 90002 -3 is less than 0 so let us add 2π radians 90007 90002 -3 + 2π = -3 + 6.283 … = 3.283 … radians 90007 90002 sin (-3) = sin (3.283 …) = 90004 -0.141 90005 (to 3 decimal places) 90007 90025 Solving Triangles 90026 90002 Trigonometry is also useful for general triangles, not just right-angled ones. 90007 90002 It helps us in Solving Triangles. «Solving» means finding missing sides and angles. 90007 90002 We can also find missing side lengths.The general rule is: 90007 90002 90004 When we know any 3 of the sides or angles we can find the other 3 90005 90009 (except for the three angles case) 90007 90002 See Solving Triangles for more details. 90007 90025 Other Functions (Cotangent, Secant, Cosecant) 90026 90002 Similar to Sine, Cosine and Tangent, there are three other 90004 trigonometric functions 90005 which are made by dividing one side by another: 90007 90002 90007 90348 90012 90013 90002 Cosecant Function: 90007 90014 90013 90004 csc (90003 θ 90006) = Hypotenuse / Opposite 90005 90014 90021 90012 90013 90002 Secant Function: 90007 90014 90013 90004 sec (90003 θ 90006) = Hypotenuse / Adjacent 90005 90014 90021 90012 90013 90002 Cotangent Function: 90007 90014 90013 90004 cot (90003 θ 90006) = Adjacent / Opposite 90005 90014 90021 90022 90002 90007 90025 Trigonometric and Triangle Identities 90026 90002 And as you get better at Trigonometry you can learn these: 90007 90002 90007 90002 Enjoy becoming a triangle (and circle) expert! 90007 90002 90007 .90000 Trigonometry: Angles: Measuring Angles | SparkNotes 90001 90002 There are three units of measure for angles: revolutions, degrees, and radians. In trigonometry, radians are used most often, but it is important to be able to convert between any of the three units. 90003 90004 Revolutions 90005 90002 A revolution is the measure of an angle formed when the initial side rotates all the way around its vertex until it reaches its initial position. Thus, the terminal side is in the same exact position as the initial side.In trigonometry, angles can have a measure of many revolutions — there is no limit to the magnitude of a given angle. A revolution can be abbreviated «rev». 90003 90004 Degrees 90005 90002 A more common way to measure angles is in degrees. There are 360 degrees in one revolution. Degrees can be subdivided, too. One degree is equal to 60 minutes, and one minute is equal to 60 seconds. Therefore, an angle whose measure is one second has a measure of 90011 degrees. When perpendicularity is discussed, it is most often defined as a situation in which a 90 degree angle exists.Often degrees are used to describe certain triangles, like 30-60-90 and 45-45-90 triangles. As previously mentioned, however, in most cases that concern trigonometry, radians are the most useful and manageable unit of measure. Degrees are symbolized with a small superscript circle after the number (measure). 360 degrees is symbolized 360 90012 o 90013. 90003 90004 Radian 90005 90002 A radian is not a unit of measure that is arbitrarily defined, like a degree. Its definition is geometrical.One radian (1 rad) is the measure of the central angle (an angle whose vertex is the center of a circle) that intercepts an arc whose length is equal to the radius of the circle. The measure of such an angle is always the same, regardless of the radius of the circle. It is a naturally occurring unit of measure, just like 90018 Π 90019 is the natural ratio of the circumference of a circle and the diameter. If an angle of one radian intercepts an arc of length 90018 r 90019, then a central angle of 2 90018 Π 90019 radians would intercept an arc of length 2 90018 Πr 90019, which is the circumference of the circle.Such a central angle has a measure of one revolution. Therefore, 1 rev = 360 90012 o 90013 = 2 90018 Π 90019 rad. Also, 1 rad = (90030) 90012 o 90013 = 90033 rev. 90003 90004 Conversion between Revolutions, Degrees, and Radians 90005 90002 Below is a chart with angle measures of common angles in revolutions, degrees, and radians. Any angle can be converted from one set of units to another using the definition of the units, but it will save time to memorize a few simple conversions.It is particularly important to be able to convert between degrees and radians. 90003 90039 Figure%: Some common angles measured in all three units of measurement .90000 Angle definition and properties (Trigonometry) 90001 Angle definition and properties (Trigonometry) — Math Open Reference Definition: An angle which has its vertex at the origin, and one side lying on the positive x-axis. It can have a measure which positive or negative and can be greater than 360 °. 90002 Try this: Adjust the angle below by dragging point A and see how the angle ABC behaves. 90003 90002 In trigonometry, an angle is drawn in what is called the «standard position».The vertex of the angle is on the origin, and one side of the angle is fixed and drawn along the positive x-axis (At the 3 o’clock position as shown as BC above). 90003 90006 Names of the parts 90007 90002 90009 The side that is fixed along the positive x axis (BC) is called the initial side. To make the angle, imagine of a copy of this side being rotated about the origin to create the second side, called the terminal side. 90003 90002 The amount we rotate it is called the measure of the angle and is measured in degrees or radians.This measure can be written in a short form: 90003 90002 mABC = 54 ° 90003 which is spoken as 90015 «the measure of angle ABC is 54 degrees» 90016. 90002 If it is not ambiguous, we may use just a single letter to denote an angle. In the figure above, we could refer to the angle as ABC or just angle B. 90003 90002 In trigonometry, you will often see Greek letters used to name angles. For example the letter θ (theta), but on this site we always use ordinary letters like A, B, C.90003 90006 The measure can be positive or negative 90007 By convention, angles that go counterclockwise from the initial side are positive and those that go clockwise are negative. In the figure above, click on ‘reset’. The angle shown goes counterclockwise and so is positive. Drag A down across the x-axis and see that angles going clockwise from the initial side are negative. See Trig functions of large and negative angles 90006 The measure can exceed 360 ° 90007 90002 In the figure above click ‘reset’ and drag the point A around counterclockwise.Once you have made a full circle (360 °) keep going and you will see that the angle is greater than 360 °. In fact you can go around as many times as you like. The same thing happens when you go clockwise. The negative angle just keeps on increasing. See Trig functions of large and negative angles 90003 90006 Coterminal angles 90007 90002 If you have one angle of say 30 °, another of 390 °, the two terminal sides will be in the same place (390 = 360 + 30). These two angles would then be called coterminal angles.They would be in the same place on the plane but have different measures (30 ° and 390 °). For more on this see Coterminal angles. 90003 90006 Degrees and radians 90007 90002 The measure of an angles can be expressed in degrees or radians, but in trigonometry radians are the most common. See Radians and Degrees. Recall than there are 2π radians in a full circle of 360 °, so 1 radian is approximately 57 °. In the figure above, click on «radians» to change units. 90003 90002 See also the definition of an angle in plane geometry.90003 90006 Other trigonometry topics 90007 90039 Angles 90040 90039 Trigonometric functions 90040 90039 Solving trigonometry problems 90040 90039 Calculus 90040 90002 (C) 2011 Copyright Math Open Reference. 90048 All rights reserved 90003 .90000 trigonometry | Definition, Formulas, Ratios, & Identities 90001 90002 The word 90003 trigonometry 90004 comes from the Greek words 90003 trigonon 90004 ( «triangle») and 90003 metron 90004 ( «to measure»). Until about the 16th century, trigonometry was chiefly concerned with computing the numerical values of the missing parts of a triangle (or any shape that can be dissected into triangles) when the values of other parts were given. For example, if the lengths of two sides of a triangle and the measure of the enclosed angle are known, the third side and the two remaining angles can be calculated.Such calculations distinguish trigonometry from geometry, which mainly investigates qualitative relations. Of course, this distinction is not always absolute: the Pythagorean theorem, for example, is a statement about the lengths of the three sides in a right triangle and is thus quantitative in nature. Still, in its original form, trigonometry was by and large an offspring of geometry; it was not until the 16th century that the two became separate branches of mathematics. 90009 90010 Ancient Egypt and the Mediterranean world 90011 90002 Several ancient civilizations-in particular, the Egyptian, Babylonian, Hindu, and Chinese-possessed a considerable knowledge of practical geometry, including some concepts that were a prelude to trigonometry.The Rhind papyrus, an Egyptian collection of 84 problems in arithmetic, algebra, and geometry dating from about 1 800 bce, contains five problems dealing with the 90003 seked 90004. A close analysis of the text, with its accompanying figures, reveals that this word means the slope of an incline-essential knowledge for huge construction projects such as the pyramids. For example, problem 56 asks: «If a pyramid is 250 cubits high and the side of its base is 360 cubits long, what is its 90003 seked 90004?» The solution is given as 5 90017 1 90018/90019 25 90020 palms per cubit, and, since one cubit equals 7 palms, this fraction is equivalent to the pure ratio 90017 18 90018/90019 25 90020.This is actually the «run-to-rise» ratio of the pyramid in question-in effect, the cotangent of the angle between the base and face. It shows that the Egyptians had at least some knowledge of the numerical relations in a triangle, a kind of «proto-trigonometry.» 90009 90026 Egyptian 90003 seked 90004 90029 The Egyptians defined the 90003 seked 90004 as the ratio of the run to the rise, which is the reciprocal of the modern definition of the slope. 90032 Encyclopædia Britannica, Inc. 90033 Get exclusive access to content from our тисяча сімсот шістьдесят вісім First Edition with your subscription.Subscribe today 90002 Trigonometry in the modern sense began with the Greeks. Hipparchus (90003 c. 90004 190-120 bce) was the first to construct a table of values for a trigonometric function. He considered every triangle-planar or spherical-as being inscribed in a circle, so that each side becomes a chord (that is, a straight line that connects two points on a curve or surface, as shown by the inscribed triangle 90003 A 90004 90003 B 90004 90003 C 90004 in the figure). To compute the various parts of the triangle, one has to find the length of each chord as a function of the central angle that subtends it-or, equivalently, the length of a chord as a function of the corresponding arc width.This became the chief task of trigonometry for the next several centuries. As an astronomer, Hipparchus was mainly interested in spherical triangles, such as the imaginary triangle formed by three stars on the celestial sphere, but he was also familiar with the basic formulas of plane trigonometry. In Hipparchus’s time these formulas were expressed in purely geometric terms as relations between the various chords and the angles (or arcs) that subtend them; the modern symbols for the trigonometric functions were not introduced until the 17th century.90009 90026 triangle inscribed in a circle 90029 This figure illustrates the relationship between a central angle θ (an angle formed by two radii in a circle) and its chord 90003 A 90004 90003 B 90004 (equal to one side of an inscribed triangle). 90032 Encyclopædia Britannica, Inc. 90033 90026 Study how Ptolemy tried to use deferents and epicycles to explain retrograde motion 90029 Ptolemy’s theory of the solar system. 90032 Encyclopædia Britannica, Inc. 90033 See all videos for this article 90002 The first major ancient work on trigonometry to reach Europe intact after the Dark Ages was the 90003 Almagest 90004 by Ptolemy (90003 c.90004 100-170 ce). He lived in Alexandria, the intellectual centre of the Hellenistic world, but little else is known about him. Although Ptolemy wrote works on mathematics, geography, and optics, he is chiefly known for the 90003 Almagest 90004, a 13-book compendium on astronomy that became the basis for humankind’s world picture until the heliocentric system of Nicolaus Copernicus began to supplant Ptolemy’s geocentric system in the mid-16th century. In order to develop this world picture-the essence of which was a stationary Earth around which the Sun, Moon, and the five known planets move in circular orbits-Ptolemy had to use some elementary trigonometry.Chapters 10 and 11 of the first book of the 90003 Almagest 90004 deal with the construction of a table of chords, in which the length of a chord in a circle is given as a function of the central angle that subtends it, for angles ranging from 0 ° to 180 ° at intervals of one-half degree. This is essentially a table of sines, which can be seen by denoting the radius 90003 r 90004, the arc 90003 A 90004, and the length of the subtended chord 90003 c 90004, to obtain 90003 c 90004 = 2 90003 r 90004 sin 90017 90003 A 90004 90018/90019 2 90020.Because Ptolemy used the Babylonian sexagesimal numerals and numeral systems (base 60), he did his computations with a standard circle of radius 90003 r 90004 = 60 units, so that 90003 c 90004 = 120 sin 90017 90003 A 90004 90018/90019 2 90020. Thus, apart from the proportionality factor 120, his was a table of values of sin 90017 90003 A 90004 90018/90019 2 90020 and therefore (by doubling the arc) of sin 90003 A 90004. With the help of his table Ptolemy improved on existing geodetic measures of the world and refined Hipparchus’s model of the motions of the heavenly bodies.90009 90026 constructing a table of chords 90029 By labeling the central angle 90003 A 90004, the radii 90003 r 90004, and the chord 90003 c 90004 in the figure, it can be shown that 90003 c 90004 = 2 90003 r 90004 sin (90003 A 90004/2). Hence, a table of values for chords in a circle of fixed radius is also a table of values for the sine of angles (by doubling the arc). 90032 Encyclopædia Britannica, Inc. 90033.

