Онлайн калькуляторы для расчета статистических показателей
Выбор статистического метода
В данном сервисе реализован алгоритм выбора оптимальной методики статистического анализа, который позволит исследователю на основании информации о количестве сравниваемых совокупностей, типе распределения, шкале измерения переменных, отпределить наиболее подходящий статистический метод, статистический критерий.
перейти к сервису
Расчет относительных величин
Калькулятор позволит найти значение любой относительной величины по заданным параметрам: числителю, знаменателю, десятичному коэффициенту. Учитывается вид относительной величины для правильного обозначения вводимых данных и формирования грамотного ответа. Для каждого результата также выводится средняя ошибка m.
перейти к вычислениям
Оценка значимости различий средних величин по t-критерию Стьюдента
Данный статистический метод служит для сравнения двух средних величин (M), рассчитанных для несвязанных между собой вариационных рядов. Для вычислений также понадобятся значения средних ошибок средних арифметических (m). Примеры сравниваемых величин: среднее артериальное давление в основной и контрольной группе, средняя длительность лечения пациентов, принимавших препарат или плацебо.
перейти к вычислениям
Оценка значимости изменений средних величин при помощи парного t-критерия Стьюдента
Парный t-критерий Стьюдента используется для сравнения связанных совокупностей — результатов, полученных для одних и тех же исследуемых (например, артериальное давление до и после приема препарата, средний вес пациентов до и после применения диеты).
перейти к вычислениям
Анализ динамического ряда
Этот калькулятор позволит вам быстро рассчитать все основные показатели динамического ряда, состоящего из любого количества данных. Вводимые данные: количество лет, значение первого года, уровни ряда. Результат: показатели динамического ряда, значения, полученные при его выравнивании, а также графическое изображение динамического ряда.
перейти к вычислениям
Расчет демографических показателей
7)€: aперейти к вычислениям
Прямой метод стандартизации
Здесь вы сможете быстро решить любую задачу по стандартизации, с использованием прямого метода. Вводите данные о сравниваемых совокупностях, выбирайте один из четырех способов расчета стандарта, задавайте значение коэффициента, используемого для расчета относительных величин. Результаты применения метода стандартизации выводятся в виде таблицы.
перейти к вычислениям
Расчет относительного риска
Относительный риск — позволяет проводить количественную оценку вероятности исхода, связанной с наличием фактора риска. Находит широкое применение в современных научных исследованиях, выборки в которых сформированы когортным методом. Наш онлайн-калькулятор позволит выполнить расчет относительного риска (RR) с 95% доверительным интервалом (CI), а также дополнительных показателей, таких как разность рисков, число пациентов, трующих лечения, специфичность, чувствительность.
перейти к вычислениям
Расчет отношения шансов
Метод отношения шансов (OR), как и относительный риск, используется для количественной оценки взаимосвязи фактора риска и исхода, но применяется в исследованиях, организованных по принципу «случай-контроль».
перейти к вычислениям
Анализ четырехпольной таблицы
В данном калькуляторе представлены все основные статистические методы, используемые для анализа четырехпольной таблицы (фактор риска есть-нет, исход есть-нет). Выполняется проверка важнейших статистических гипотез, рассчитываются хи-квадрат, точный критерий Фишера и другие показатели.
перейти к вычислениям
Расчет показателей вариационного ряда
Онлайн-калькулятор в автоматизированном режиме поможет рассчитать все основные показатели вариационного ряда: средние величины (средняя арифметическая, мода, медиана), стандартное отклонение, среднюю ошибку средней арифметической. Поддерживается ввод как простых, так и взвешенных рядов.
перейти к вычислениям
Расчет критерия Манна-Уитни
При помощи данного сервиса вы сможете рассчитать значение U-критерия Манна-Уитни — непараметрического критерия, используемого для сравнения двух выборок, независимо от характера их распределения.
перейти к вычислениям
Корреляционно-регрессионный анализ
Онлайн-калькулятор для проведения корреляционного анализа используется для выявления и изучения связи между количественными признаками при помощи расчета коэффициента корреляции Пирсона. Также выводится уравнение парной линейной регрессии, используемое при описании статистической модели.
перейти к вычислениям
Расчет коэффициента корреляции Спирмена
Данный калькулятор используется для расчета рангового критерия корреляции Спирмена, являющегося методом непараметрического анализа зависимости одного количественного признака от другого. Оценка значимости корреляционной связи между переменными выполняется как по коэффициенту Спирмена, так и по t-критерию Стьюдента.
перейти к вычислениям
Анализ произвольных сопряженных таблиц при помощи критерия χ2 (хи-квадрат)
Критерий хи-квадрат является непараметрическим аналогом дисперсионного анализа для сравнения нескольких групп по качественному признаку. Онлайн калькулятор по расчету критерия хи-квадрат позволяет оценить связь между двумя качественными признаками по частоте их значений. Число сравниваемых групп может быть от 2 до 9.
перейти к вычислениям
medstatistic.ru
Расчет доверительных интервалов
Доверительный интервал — термин, используемый в математической статистике при интервальной оценке статистических параметров, что предпочтительнее при небольшом объёме выборки.
Доверительный интервал для математического ожидания
Найдем доверительный интервал для математического ожидания при условии, что дисперсия генеральной величины неизвестна, а доверительная вероятность равна 1 – α.
Для расчета доверительного интервала применим формулу:
x – среднее значение величины
–квантиль распределения Стьюдента с степенью свободы
–несмещенное выборочное стандартное отклонение
–объем выборки
Определим квантиль распределения Стьюдента, для этого воспользуемся стандартной таблицей:
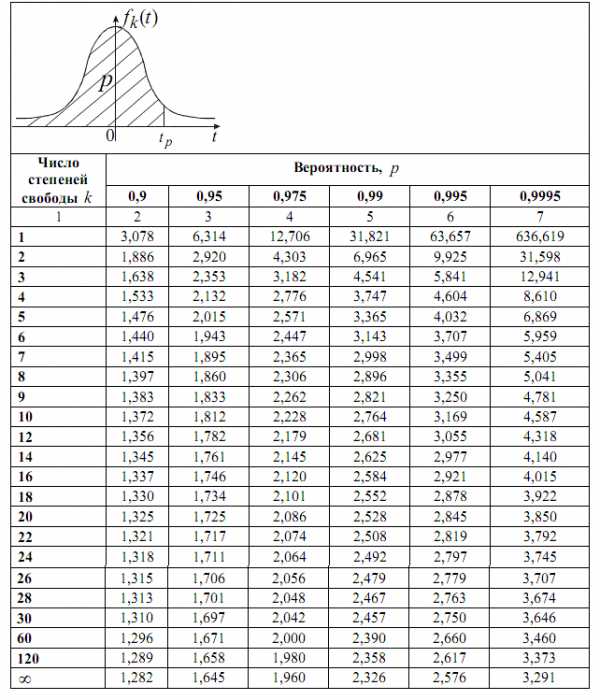
возьмем равным 0,05.
Выберем значение = 2,571
Найдем S:
10.15
2.94
Подставим все известные значения в формулу из пункта 1):
Для M[X]:
Для M[Y]:
Доверительный интервал для дисперсии
Найдем доверительный интервал для дисперсии при условии, что среднее значение величины неизвестно, а доверительная вероятность равна 1 – α.
Для расчета доверительного интервала применим формулу:
–дисперсия
–несмещенное выборочная дисперсия
–квантиль распределения со степенями свободы.
Определим квантиль распределения , для этого воспользуемся специальной таблицей:
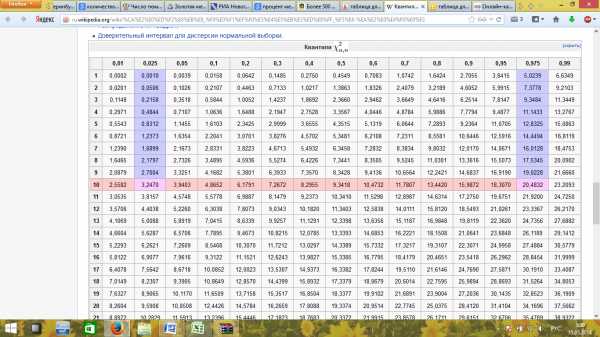
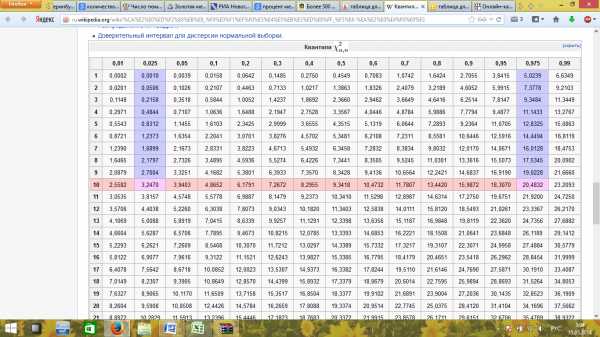
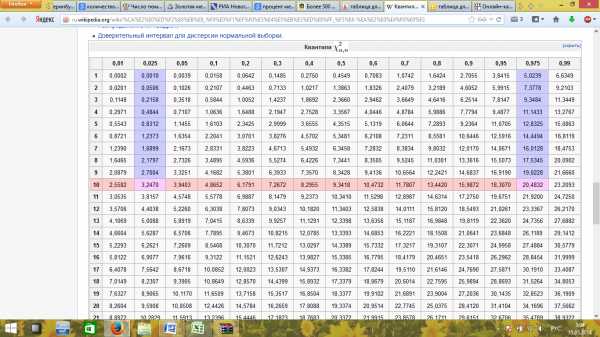
12,8325
0,8312
Подставим найденные значения в формулу из пункта 1):
Для Х:
Для У:
Доверительный интервал для корреляции
Найдем доверительный интервал для корреляции при условии, что выборка получена из генеральной совокупности, r – выборочный коэффициент корреляции.
Для расчета доверительного интервала применим формулу:
Рассчитаем :
возьмем из таблицы квантилей нормального распределения:
Подставим все в формулы:
Найдем с помощью таблицы гиперболических тангенсов:
Проверка гипотез
Таким образом было установлено, что между заработной платой сотрудников ДПС и количеством оштрафованных существует связь. Искомая корреляция равна -0.7132. Это высокая степень взаимосвязи – значения коэффициента корреляции находится в пределах от 0,7 до 0,99. Нам удалось выявить зависимость, и результаты в данном случае оказались вполне ожидаемы. Чем выше средняя заработная плата по субъекту РФ, тем меньше оштрафованных. Почему получились такие результаты, нам остается только гадать. Да и не было нашей целью объяснять почему именно так. Мы должны были, ради личного интереса, посмотреть есть ли связь.
Регрессия
Любая нелинейная регрессия, в которой уравнение регрессии для изменений в одной переменной (у) как функции t изменений в другой (х) является квадратичным, кубическим или уравнение более высокого порядка. Хотя математически всегда возможно получить уравнение регрессии, которое будет соответствовать каждой «загогулине» кривой, большинство этих пертурбаций возникает в результате ошибок в составлении выборки или измерении, и такое «совершенное» соответствие ничего не дает. Не всегда легко определить, соответствует ли криволинейная регрессия набору данных, хотя существуют статистические тесты для определения того, значительно ли увеличивает каждая более высокая степень уравнения степ совпадения этого набора данных.
Теперь, будем считать, что выборочная криволинейная регрессия определяется уравнением:
Коэффициенты называются выборочными коэффициентами регрессии.
Из ранее изученных пунктов, нам известны следующие параметры:
х = 20,35
у = 9,47
= 85,79
= 7,21
= -0.71
Теперь мы можем подставить все значения в уравнение:
studfiles.net
Распределение t-критерия Стьюдента для проверки гипотезы о средней и расчета доверительного интервала в MS Excel
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2 (знаю-знаю, что так не бывает, но не нужно меня перебивать!). Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
будет иметь стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннеса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Т.к. Гиннесс строго-настрого запретил выдавать секреты пивоварения, Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
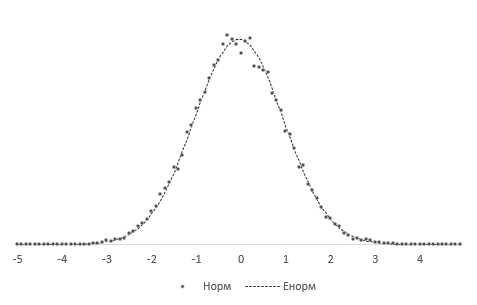
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
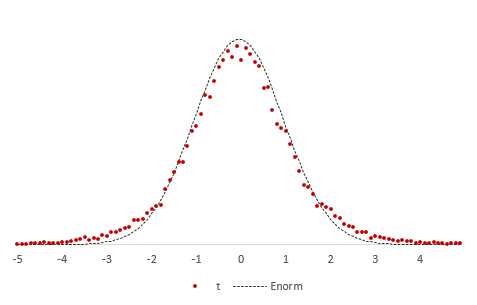
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
На этом законе основывается множество других результатов в статистике нормальных моделей.
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Все равно ей никто не пользуется, т.к. вероятности приведены в специальных таблицах распределения Стьюдента (иногда называют таблицами коэффициентов Стьюдента), либо забиты в формулы ПЭВМ.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
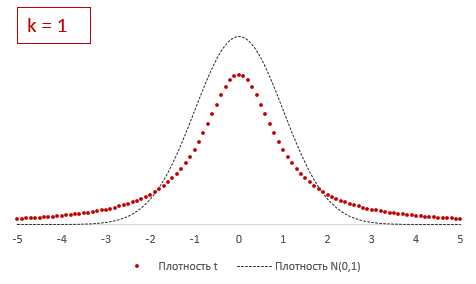
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двухсторонним. Обычно пользуются двухсторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность, т.к. при фиксированном уровне значимости критическое значение немного приближается к нулю.
Условия применения t-критерия Стьюдента
{module 111}
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
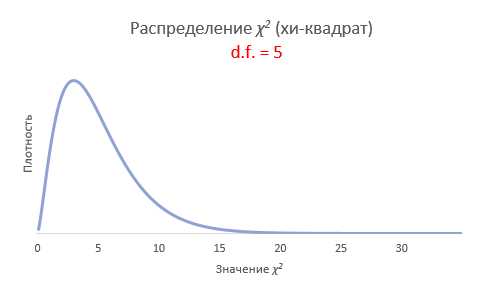
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
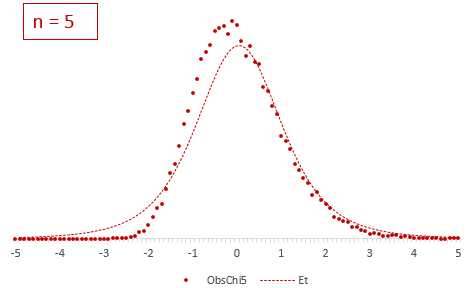
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
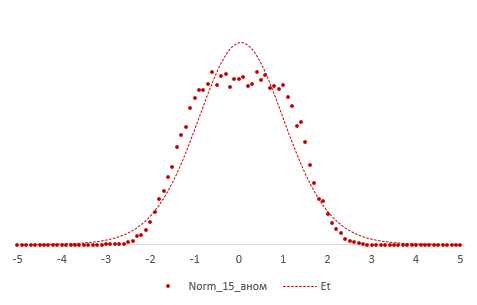
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия, т.е. фактический уровень значимости (p-level).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-level.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-level.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
H1: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двухсторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей t-распределения Стьюдента (есть в любом учебнике по статистике).
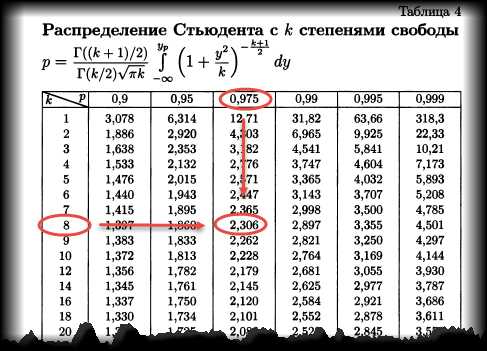
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двухсторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-level попробовать найти, но он будет приближенным. А, как правило, именно p-level используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
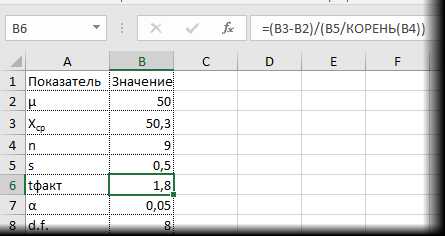
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двухсторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
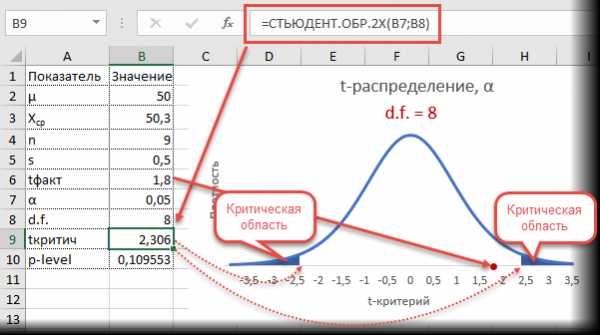
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-level, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
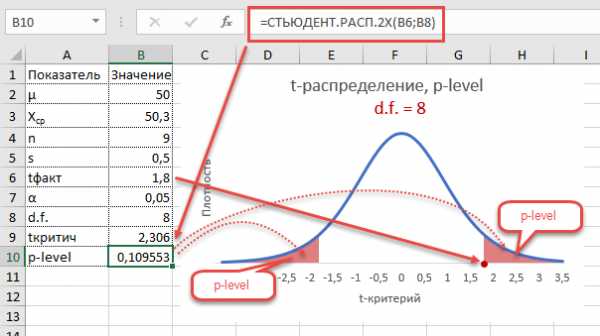
P-level равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-level оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
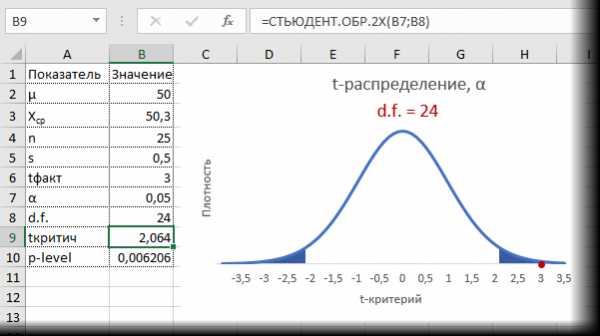
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-level (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала с помощью t-распределения Стьюдента
{module 111}
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
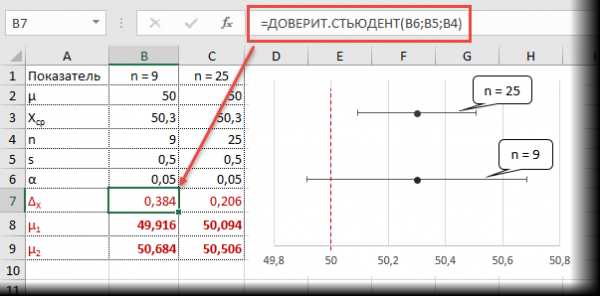
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-level, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю посмотреть видеоролик о том, как проводить расчеты, связанные с t-критерием Стьюдента в Excel.
Меня иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
statanaliz.info
Онлайн калькулятор: Оценка погрешности прямых измерений
Измеряя линейные размеры предметов измерительными инструментами : линейкой, штангенциркулем, микрометром, проводя измерения времени секундомером или силы электрического тока или величины напряжения соответствующими электроизмерительными приборами Вы проводите прямые измерения.
Погрешность измерений
Любое измерение проводится с определенной точностью, при этом измеренное значение всегда отличается от истинного, так как инструменты измерения, методики и органы чувств человека несовершенны. Поэтому важную роль играет оценка погрешности измерений, результат измерений с учетом погрешности записывается в виде: X ± ΔX, где ΔX — абсолютная погрешность измерений.
Случайные и систематические погрешности
Погрешности подразделяются на случайные и систематические.
Систематические погрешности остаются постоянными или закономерно меняются в процессе измерения. Например неточность прибора, неправильная его регулировка ведет к систематической погрешности. Если причина систематической погрешности известна, то чаще всего такую погрешность можно исключить.
Случайные погрешности вызваны различными случайными факторами, влияющими на точность измерений. Например, при измерении секундомером отрезков времени, случайные погрешности связаны с различным (случайным) временем реакции экспериментатора на события запускающие и останавливающие секундомер. Чтобы уменьшить влияние случайной погрешности необходимо проводить многократное измерение физической величины.
Калькулятор ниже вычисляет случайную погрешность выборки прямых измерений для заданного доверительного интервала. Немного теории можно найти сразу за калькулятором.
Измерения
Размер страницы: 5102050100chevron_leftchevron_rightТочность вычисленияЗнаков после запятой: 3
Среднее значение
Абсолютная погрешность
Относительная погрешность в %
Коэффициент Стьюдента
Сохранить share extension
В большинстве случаев результат измерения подчиняется нормальному закону распределения, поэтому истинное значение измерения будет равно пределу:
В случае ограниченного количества измерений, наиболее близким к истинному будет среднее арифметическое:
Согласно элементарной теории ошибок Гаусса случайную погрешность отдельного измерения характеризует так называемое среднеквадратическое отклонение:
, квадрат этой величины называется дисперсией. При увеличении этой величины возрастает разброс результатов измерений, т. е. увеличивается погрешность.
Для оценки погрешности всей серии измерений, вместо отдельного измерения надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение от истинного значения искомой величины .
По закону сложения ошибок среднее арифметическое имеет меньшую ошибку, чем результат каждого отдельного измерения. Cредняя квадратичная погрешность среднего арифметического равна:
Стандартная случайная погрешность Δх равна:
, где — коэффициент Стьюдента для заданной доверительной вероятности и числа степеней свободы k = n-1.
Коэффициент Стьюдента можно получить по таблице или воспользоваться нашим калькулятором для вычисления квантилей распределения Стьюдента: Квантильная функция распределения Стьюдента. Следует иметь в виду, что квантильная функция выдает значения одностороннего критерия Стьюдента. Значение двустороннего квантиля для заданной доверительно вероятности соответствует значению одностороннего квантиля для вероятности:
planetcalc.ru
Найти доверительный интервал
Продолжаем разбирать индивидуальное задание по теории вероятностей. Приведенная схема вычислений поможет найти доверительный интервал. Формулы для интервала доверия несложные, в этом Вы скоро убедитесь. Приведенные задачи задавали экономистам ЛНУ им. И.Франка. ВУЗы других городов Украины имеют подобную программу обучения, поэтому для себя часть полезного материала найдет каждый студент.
Индивидуальное задание 1
Вариант 11
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
а) если γ=0,92, генеральная среднее квадратичное отклонение σ=4,0, выборочное среднее =15,0, а объем выборки n=16;
б) если γ=0,99, подправленное среднее квадратичное отклонение s=4,0, выборочное среднее =20,0, а объем выборки n=16.
Решение: а) Из уравнения с помощью функции Лапласа методом интерполяции находим t
Границы интервала доверия ищем по формулам:
После вычислений получим интервал доверия с надежностью 0,92.
2, б) Поскольку n=16<30 и среднее квадратичное отклонение неизвестно, то для нахождения границ интервала доверия используем формулу
где ищем с помощью таблиц (распределение Стьюдента):
Таким образом доверительный интервал равный с надежностью =0,99.
Задача 3. Найти интервал доверия для оценки с надежностью γ=0,99 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 35, а подправленное среднее квадратичное отклонение s=13,3.
Решение: Задача сводится к отысканию интервала доверия который покрывает с заданной надежностью 0,99.
По таблице находим q
Искомый доверительный интервал лежит в пределах или
.
Вариант 1
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
- а) если =0,9, генеральная среднее квадратичное отклонение s=3,0, выборочное среднее =7,0, а объем выборки n=9;
- б) если =0,95, подправленное среднее квадратичное отклонение s=3,0, выборочное среднее =15,0, а объем выборки n=9.
Решение: а) Из уравнения на функцию Лапласа с помощью таблиц методом интерполяции находим t
Интерполяцию используем для уточнения t (когда в таблице значений функции Лапласа Ф(t) находится между двумя соседними).
Границы интервала доверия ищем по формулам:
Окончательно получаем такой интервал доверия с надежностью =0,9 2.
б) Поскольку n=9<30 и среднее квадратичное отклонение неизвестно, то для нахождения границ интервала доверия используем формулы
,
где значение t ищем с помощью таблиц распределения Стьюдента:
Формулы как видите не сложные и найти интервал доверия может как студент, так и школьник.
Мы нашли интервал доверия с надежностью =0,95.
Задача 3. Найти интервал доверия для оценки с надежностью =0,95 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 17, а подправленное среднее квадратичное отклонение σ=11,2.
Решение: Формулы для интервала доверия достаточно просты.
По таблице находим значение функции q
Далее по формулам вычисляем интервал доверия
После вычислений он будет лежать в пределах
Вариант-12
Задача 2. Найти доверительный интервал для оценки с надежностью неизвестного математического ожидания и нормально распределенного признака Х генеральной совокупности:
а) если =0,94, генеральная среднее квадратичное отклонение =5,0, выборочное среднее =18,0, а объем выборки n=25;
б) если =0,999, подправленное среднее квадратичное отклонениеs=5,0, выборочное среднее =26,0, а объем выборки n=25.
Решение: а) Из уравнения на функцию Лапласа с помощью таблиц распределения методом интерполяции находим t
Крайние точки доверительного интервала ищем по формуле:
Итак, интервал принимает множество значений с надежностью 0,94.
2, б) Поскольку n=25<30 и среднее квадратичное отклонение неизвестно, то для нахождения границ интервала доверия используем формулы
где значение t — ищем с помощью таблиц распределения Стьюдента:
Далее находим границы интервала доверия.
Таким образом нашли доверительный интервал с надежностью 0,999.
Задача 3. Найти доверительный интервал для оценки с надежностью =0,999 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 45, а подправленное среднее квадратичное отклонение s=15,1.
Решение: Найдем интервал доверия по формуле
По таблице находим значение функции q
После этого выполняем вычисления границ интервала доверия
Как видите формулы для вычисления доверительного интервала не сложные, поэтому с легкостью применяйте их на контрольных и тестах по теории вероятностей.
Готовые решения по теории вероятностей
yukhym.com
Доверительный интервал для математического ожидания
Доверительный интервал для математического ожидания — это такой вычисленный по данным интервал, который с известной вероятностью содержит математическое ожидание генеральной совокупности. Естественной оценкой для математического ожидания является среднее арифметическое её наблюденных значений. Поэтому далее в течение урока мы будем пользоваться терминами «среднее», «среднее значение». В задачах рассчёта доверительного интервала чаще всего требуется ответ типа «Доверительный интервал [95%; 90%; 99%] среднего числа [величина в конкретной задаче] находится от [меньшее значение] до [большее значение]». С помощью доверительного интервала можно оценивать не только средние значения, но и удельный вес того или иного признака генеральной совокупности. Средние значения, дисперсия, стандартное отклонение и погрешность, через которые мы будем приходить к новым определениям и формулам, разобраны на уроке Характеристики выборки и генеральной совокупности.
Если среднее значение генеральной совокупности оценивается числом (точкой), то за оценку неизвестной средней величины генеральной совокупности принимается конкретное среднее, которое рассчитано по выборке наблюдений. В таком случае значение среднего выборки — случайной величины — не совпадает со средним значением генеральной совокупности. Поэтому, указывая среднее значение выборки, одновременно нужно указывать и ошибку выборки. В качестве меры ошибки выборки используется стандартная ошибка , которая выражена в тех же единицах измерения, что и среднее. Поэтому часто используется следующая запись: .
Если оценку среднего требуется связать с определённой вероятностью, то интересующий параметр генеральной совокупности нужно оценивать не одним числом, а интервалом. Доверительным интервалом называют интервал, в котором с определённой вероятностью P находится значение оцениваемого показателя генеральной совокупности. Доверительный интервал, в котором с вероятностью P = 1 — α находится случайная величина , рассчитывается следующим образом:
,
где — критическое значение стандартного нормального распределения для уровня значимости α = 1 — P, которое можно найти в приложении к практически любой книге по статистике.
Формулу доверительного интервала можно использовать для оценки среднего генеральной совокупности, если
- известно стандартное отклонение генеральной совокупности;
- или стандартное отклонение генеральной совокупности не известно, но объём выборки — больше 30.
Среднее значение выборки является несмещённой оценкой среднего генеральной совокупности . В свою очередь, дисперсия выборки не является несмещённой оценкой дисперсии генеральной совокупности . Для получения несмещённой оценки дисперсии генеральной совокупности в формуле дисперсии выборки объём выборки n следует заменить на n-1.
Пример 1. Собрана информация из 100 случайно выбранных кафе в некотором городе о том, что среднее число работников в них составляет 10,5 со стандартным отклонением 4,6. Определить доверительный интервал 95% числа работников кафе.
Решение:
,
где — критическое значение стандартного нормального распределения для уровня значимости α = 0,05.
Таким образом, доверительный интервал 95% среднего числа работников кафе составил от 9,6 до 11,4.
Пример 2. Для случайной выборки из генеральной совокупности из 64 наблюдений вычислены следующие суммарные величины:
сумма значений в наблюдениях ,
сумма квадратов отклонения значений от среднего .
Вычислить доверительный интервал 95 % для математического ожидания.
Решение:
вычислим стандартное отклонение:
,
вычислим среднее значение:
.
Подставляем значения в выражение для доверительного интервала:
.
где — критическое значение стандартного нормального распределения для уровня значимости α = 0,05.
Получаем:
.
Таким образом, доверительный интервал 95% для математического ожидания данной выборки составил от 7,484 до 11,266.
Пример 3. Для случайной выборки из генеральной совокупности из 100 наблюдений вычислено среднее значение 15,2 и стандартное отклонение 3,2. Вычислить доверительный интервал 95 % для математического ожидания, затем доверительный интервал 99 %. Если мощность выборки и её вариация остаются неизменными, а увеличивается доверительный коэффициент, то доверительный интервал сузится или расширится?
Решение:
Подставляем данные значения в выражение для доверительного интервала:
.
где — критическое значение стандартного нормального распределения для уровня значимости α = 0,05.
Получаем:
.
Таким образом, доверительный интервал 95% для среднего данной выборки составил от 14,57 до 15,82.
Вновь подставляем данные значения в выражение для доверительного интервала:
.
где — критическое значение стандартного нормального распределения для уровня значимости α = 0,01.
Получаем:
.
Таким образом, доверительный интервал 99% для среднего данной выборки составил от 14,37 до 16,02.
Как видим, при увеличении доверительного коэффициента увеличивается также критическое значение стандартного нормального распределения, а, следовательно, начальная и конечная точки интервала расположены дальше от среднего, и, таким образом, доверительный интервал для математического ожидания увеличивается.
Удельный вес некоторого признака выборки можно интерпретировать как точечную оценку удельного веса p этого же признака в генеральной совокупности. Если же эту величину нужно связать с вероятностью, то следует рассчитать доверительный интервал удельного веса p признака в генеральной совокупности с вероятностью P = 1 — α:
.
Пример 4. В некотором городе два кандидата A и B претендуют на пост мэра. Случайным образом были опрошены 200 жителей города, из которых 46% ответили, что будут голосовать за кандидата A, 26% — за кандидата B и 28% не знают, за кого будут голосовать. Определить доверительный интервал 95% для удельного веса жителей города, поддерживающих кандидата A.
Решение:
Таким образом, доверительный интервал 95% удельного веса горожан, поддерживающих кандидата A, составил от 0,391 до 0,529.
Пример 5. Чтобы проверить отношение покупателей к новому квасу, проведён опрос случайной выборки в 50 человек. Результаты обобщены в следующей таблице (0 — не понравился, 1 — понравился, 2 — нет ответа):
| 1 | 0 | 0 | 1 | 2 |
| 0 | 1 | 0 | 2 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 2 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 2 | 2 | 0 | 0 | 1 |
| 1 | 0 | 2 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 |
Найти доверительный интервал 95 % удельного веса покупателей, которым новый квас не понравился.
Решение.
Найдём удельный вес указанных покупателей в выборке: 29/50 = 0,58. Таким образом, , . Мощность выборки известна (n = 50). Критическое значение стандартного нормального распределения для уровня значимости α = 0,05 равно 1,96. Подставляем имеющиеся показатели в выражение интервала для удельного веса:
Таким образом, доверительный интервал 95% удельного веса покупателей, которым новый квас не понравился, составил от 0,45 до 0,71.
Всё по теме «Математическая статистика»
function-x.ru
Как найти доверительный интервал с заданной надежностью — 11 Декабря 2012 — Примеры решений задач
Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.
Для оценки математического ожидания случайной величины , распределенной по нормальному закону, при известном среднем квадратическом отклонении служит доверительный интервал
где — точность оценки, — объем выборки, — выборочное среднее, — аргумент функции Лапласа, при котором
Пример 166. Найти доверительный интервал для оценки с надежностью 0,9 неизвестного математического ожидания нормально распределенного признака генеральной совокупности, если среднее квадратическое отклонение , выборочная средняя и объем выборки .
Решение. Требуется найти доверительный интервал
Все величины, кроме , известны. Найдем из соотношения .
По таблице приложения находим и получаем доверительный интервал .
Если среднее квадратическое отклонение неизвестно, то для оценки служит доверительный интервал
где находится в приложении 4 по заданным и , а вместо часто бывает возможно подставить любую из оценок
— исправленное среднеквадратическое, статистическое среднеквадратическое отклонения соответственно. При увеличении обе оценки и будут различаться сколь угодно мало и будут сходиться по вероятностям к одной и той же величине .
Пример 167. Из генеральной совокупности извлечена выборка объема
= 50:
| -1 | 0 | 1 | 2 | 3 | |
| 10 | 5 | 15 | 15 | 5 |
Оценить с надежностью математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней.
Решение. Выборочную среднюю и исправленное среднее квадратическое отклонение найдем соответственно по формулам
Пользуясь таблицей приложения 4, по и находим .
Найдем искомый доверительный интервал:
подставляя , , , , получим .
Пример 168. Результаты исследования длительности оборота (в днях) оборотных средств торговых фирм города Ярославля представлены в группированном виде:
| — | 24 — 32 | 32 — 40 | 40 — 48 | 48 — 56 | 56 — 64 | 64 — 72 | 72 — 80 |
| 2 | 4 | 10 | 15 | 11 | 5 | 3 |
Построить доверительный интервал с надежностью для средней длительности оборотных средств торговых фирм города.
Решение. Найдем выборочную среднюю длительности оборотных средств.
Для упрощения вычисления исправленного среднеквадратического отклонения выберем приближенное значение . Тогда
В приложении 4 по и находим , а следовательно, и доверительный интервал
или .
Рассматривая независимых испытаний, можно оценить вероятность по относительной частоте.
Пример 169. Сколько раз надо подбросить монету, чтобы с вероятностью можно было ожидать, что относительная частота появления «герба» отклонится от вероятности этого события по абсолютной величине не более чем на ?
Решение. По условию , , .
Тогда
Из таблицы значений функции Лапласа находим, что , откуда .
Точечные оценки неизвестных параметров распределения можно находить по методу наибольшего правдоподобия, предложенному Р. Фишером.
Пример 170. Найти методом наибольшего правдоподобия оценку параметра биномиального распределения
если в независимых испытаниях событие появилось раз и в независимых испытаниях событие появилось раз.
Решение. Составим функцию правдоподобия:
Найдем логарифмическую функцию правдоподобия:
Вычислим первую производную по :
Запишем уравнение правдоподобия, для чего приравняем первую производную нулю:
Решив полученное уравнение относительно , найдем критическую точку:
в которой производная отрицательна. Следовательно, — точка максимума и, значит, ее надо принять в качестве наибольшего правдоподобия неизвестной вероятности биномиального распределения.
Вопросы для самоконтроля
- Какая оценка называется точечной?
- Какие точечные оценки генеральных числовых характеристик вы знаете?
- Чем определяется интервальная оценка?
- Надежность оценки и другое ее название.
- На чем основано нахождение доверительного интервала для оценки математического ожидания?
- Каким образом оценивают истинное значение измеряемой величины?
- Точечная и интервальная оценка вероятности биномиального распределения.
- В чем суть метода наибольшего правдоподобия?
Задачи
I 331. Игральная кость подбрасывается 300 раз. Какова вероятность того, что относительная частота появления шести очков на верхней грани кости отклонится от вероятности появления события в одном испытании по абсолютной величине не более чем на 0,05?
332. Сколько раз надо подбросить монету, чтобы с вероятностью 0,95 можно было ожидать, что относительная частота появления «герба» отклонится от вероятности этого события по абсолютной величине не более чем на 0,1?
333. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением . Найдите доверительные интервалы для оценки неизвестного математического ожидания по выборочным средним , если объем выборки и задана надежность оценки .
334. Исследовалось время безотказной работы 50 лазерных принтеров. Из априорных наблюдений известно, что среднее квадратическое отклонение времени безотказной работы ч. По результатам исследований получено среднее время безотказной работы ч. Постройте 90%-й доверительный интервал для среднего времени безотказной работы.
335. Количественный признак генеральной совокупности распределен нормально. По выборке объема найдено «исправленное» среднее квадратическое отклонение . Найдите доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью .
336. Произведено 16 измерений одним прибором некоторой физической величины, причем исправленное среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0,7. Найдите интервал ошибок прибора с надежностью 0,99. Предполагается, что ошибки измерений распределены нормально.
II 337. Время (в минутах) обслуживания клиентов в железнодорожной кассе представлено выборкой: 2,0; 1,5; 1,0; 1,0; 1,25; 3,5; 3,0; 3,0; 3.75; 3,7; 4,0; 6,0; 7,0; 1,5; 8,0; 3,5; 5,0; 3,5; 14,0; 12,0; 15,1; 18,0; 18,5; 17,0. Определите процент клиентов, время обслуживания которых более 12 минут и менее 5 минут.
338. Из генеральной совокупности извлечена выборка объема :
| -0,4 | -0,2 | -0,1 | 0 | 0,2 | 0,5 | 0,7 | 1 | 1,2 | 1,6 | |
| 1 | 3 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 2 |
Оцените с надежностью 0,9 математическое ожидание нормально распределенного признака генеральной совокупности с помощью доверительного интервала.
III 339. Результаты исследования длительности оборота оборотных средств торговых фирм города (в днях) представлены в группированном виде:
| 24-33 | 33-42 | 42-51 | 51-60 | 60-69 | 69-78 | 78-87 | |
| 1 | 4 | 9 | 18 | 10 | 6 | 2 |
Постройте доверительный интервал с надежностью 0,95 для средней длительности оборотных средств торговых фирм города при условии, что среднее квадратическое отклонение неизвестно (известно и равно 10 дням).
340. Найти методом наибольшего правдоподобия оценку параметра распределения Пуассона
www.reshim.su
