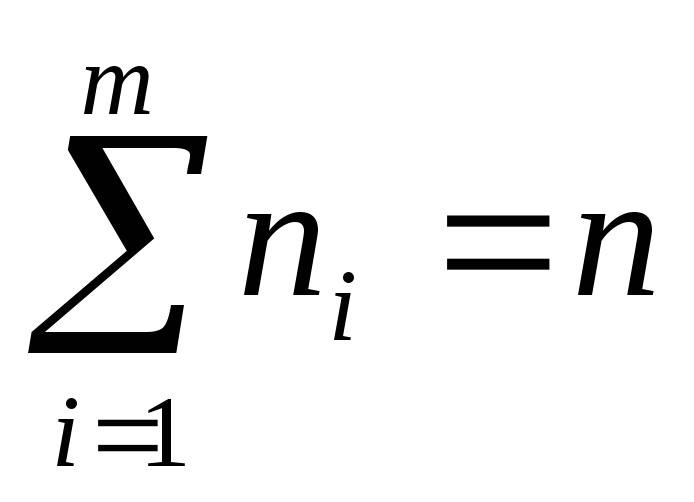Однако в большинстве статистических тестов, используемых для проверки гипотез, (например, t-тест, регрессионный анализ, дисперсионный анализ) рядом с p-value всегда соседствует такой показатель как число степеней свободы, он же degrees of freedom или просто сокращенно df, о нем мы сегодня и поговорим.
Степени свободы, о чем речь?
По моему мнению, понятие степеней свободы в статистике примечательно тем, что оно одновременно является и одним из самым важных в прикладной статистике (нам необходимо знать df для расчета p-value в озвученных тестах), но вместе с тем и одним из самых сложных для понимания определений для студентов-нематематиков, изучающих статистику.
Проведем необходимые расчеты и получим, что значение t-критерия равняется 3, отлично, осталось рассчитать p-value и задача решена. Однако, ознакомившись с особенностями t-распределения мы выясним, что его форма различается в зависимости от числа степеней свобод, рассчитываемых по формуле n-1, где n — это число наблюдений в выборке:
Сама по себе формула для расчета df выглядит весьма дружелюбной, подставили число наблюдений, вычли единичку и ответ готов: осталось рассчитать значение p-value, которое в нашем случае равняется 0.004.
Но почему n минус один?
Когда я впервые в жизни на лекции по статистике столкнулся с этой процедурой, у меня как и у многих студентов возник законный вопрос: а почему мы вычитаем единицу? Почему мы не вычитаем двойку, например? И почему мы вообще должны что-то вычитать из числа наблюдений в нашей выборке?
В учебнике я прочитал следующее объяснение, которое еще не раз в дальнейшем встречал в качестве ответа на данный вопрос:
“Допустим мы знаем, чему равняется выборочное среднее, тогда нам необходимо знать только n-1 элементов выборки, чтобы безошибочно определить чему равняется оставшейся n элемент”. Звучит разумно, однако такое объяснение скорее описывает некоторый математический прием, чем объясняет зачем нам понадобилось его применять при расчете t-критерия. Следующее распространенное объяснение звучит следующим образом: число степеней свободы — это разность числа наблюдений и числа оцененных параметров. При использовании одновыборочного t-критерия мы оценили один параметр — среднее значение в генеральной совокупности, используя n элементов выборки, значит df = n-1.
Однако ни первое, ни второе объяснение так и не помогает понять, зачем же именно нам потребовалось вычитать число оцененных параметров из числа наблюдений?
Причем тут распределение Хи-квадрат Пирсона?
Давайте двинемся чуть дальше в поисках ответа. Сначала обратимся к определению t-распределения, очевидно, что все ответы скрыты именно в нем. Итак случайная величина:
имеет t-распределение с df = ν, при условии, что Z – случайная величина со стандартным нормальным распределением N(0; 1), V – случайная величина с распределением Хи-квадрат, с ν числом степеней свобод, случайные величины Z и V независимы. Это уже серьезный шаг вперед, оказывается, за число степеней свободы ответственна случайная величина с распределением Хи-квадрат в знаменателе нашей формулы.
Давайте тогда изучим определение распределения Хи-квадрат. Распределение Хи-квадрат с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Кажется, мы уже совсем у цели, по крайней мере, теперь мы точно знаем, что такое число степеней свободы у распределения Хи-квадрат — это просто число независимых случайных величин с нормальным стандартным распределением, которые мы суммируем. Но все еще остается неясным, на каком этапе и зачем нам потребовалось вычитать единицу из этого значения?
Давайте рассмотрим небольшой пример, который наглядно иллюстрирует данную необходимость. Допустим, мы очень любим принимать важные жизненные решения, основываясь на результате подбрасывания монетки. Однако, последнее время, мы заподозрили нашу монетку в том, что у нее слишком часто выпадает орел. Чтобы попытаться отклонить гипотезу о том, что наша монетка на самом деле является честной, мы зафиксировали результаты 100 бросков и получили следующий результат: 60 раз выпал орел и только 40 раз выпала решка. Достаточно ли у нас оснований отклонить гипотезу о том, что монетка честная? В этом нам и поможет распределение Хи-квадрат Пирсона. Ведь если бы монетка была по настоящему честной, то ожидаемые, теоретические частоты выпадания орла и решки были бы одинаковыми, то есть 50 и 50. Легко рассчитать насколько сильно наблюдаемые частоты отклоняются от ожидаемых. Для этого рассчитаем расстояние Хи-квадрат Пирсона по, я думаю, знакомой большинству читателей формуле:
Где O — наблюдаемые, E — ожидаемые частоты.
Дело в том, что если верна нулевая гипотеза, то при многократном повторении нашего эксперимента распределение разности наблюдаемых и ожидаемых частот, деленная на корень из наблюдаемой частоты, может быть описано при помощи нормального стандартного распределения, а сумма квадратов k таких случайных нормальных величин это и будет по определению случайная величина, имеющая распределение Хи-квадрат.
Давайте проиллюстрируем этот тезис графически, допустим у нас есть две случайные, независимые величины, имеющих стандартное нормальное распределение. Тогда их совместное распределение будет выглядеть следующим образом:
При этом квадрат расстояния от нуля до каждой точки это и будет случайная величина, имеющая распределение Хи-квадрат с двумя степенями свободы. Вспомнив теорему Пифагора, легко убедиться, что данное расстояние и есть сумма квадратов значений обеих величин.
Пришло время вычесть единичку!
Ну а теперь кульминация нашего повествования. Возвращаемся к нашей формуле расчета расстояния Хи-квадрат для проверки честности монетки, подставим имеющиеся данные в формулу и получим, что расстояние Хи-квадрат Пирсона равняется 4. Однако для определения p-value нам необходимо знать число степеней свободы, ведь форма распределения Хи-квадрат зависит от этого параметра, соответственно и критическое значение также будет различаться в зависимости от этого параметра.
Теперь самое интересное. Предположим, что мы решили многократно повторять 100 бросков, и каждый раз мы записывали наблюдаемые частоты орлов и решек, рассчитывали требуемые показатели (разность наблюдаемых и ожидаемых частот, деленная на корень из ожидаемой частоты) и как и в предыдущем примере наносили их на график.
Легко заметить, что теперь все точки выстраиваются в одну линию. Все дело в том, что в случае с монеткой наши слагаемые не являются независимыми, зная общее число бросков и число решек, мы всегда можем точно определить выпавшее число орлов и наоборот, поэтому мы не можем сказать, что два наших слагаемых — это две независимые случайные величины. Также вы можете убедиться, что все точки действительно всегда будут лежать на одной прямой: если у нас выпало 30 орлов, значит решек было 70, если орлов 70, то решек 30 и т.д. Таким образом, несмотря на то, что в нашей формуле было два слагаемых, для расчета p-value мы будем использовать распределение Хи-квадрат с одной степенью свободы! Вот мы наконец-то добрались до момента, когда нам потребовалось вычесть единицу. Если бы мы проверяли гипотезу о том, что наша игральная кость с шестью гранями является честной, то мы бы использовали распределение Хи-квадрат с 5 степенями свободы. Ведь зная общее число бросков и наблюдаемые частоты выпадения любых пяти граней, мы всегда можем точно определить, чему равняется число выпадений шестой грани.
Все становится на свои места
Теперь, вооружившись этими знаниями, вернемся к t-тесту:
в знаменателе у нас находится стандартная ошибка, которая представляет собой выборочное стандартное отклонение, делённое на корень из объёма выборки. В расчет стандартного отклонения входит сумма квадратов отклонений наблюдаемых значений от их среднего значения — то есть сумма нескольких случайных положительных величин. А мы уже знаем, что сумма квадратов n случайных величин может быть описана при помощи распределения хи-квадрат. Однако, несмотря на то, что у нас n слагаемых, у данного распределения будет n-1 степень свободы, так как зная выборочное среднее и n-1 элементов выборки, мы всегда можем точно задать последний элемент (отсюда и берется это объяснение про среднее и n-1 элементов необходимых для однозначного определения n элемента)! Получается, в знаменателе t-статистики у нас спрятано распределение хи-квадрат c n-1 степенями свободы, которое используется для описания распределения выборочного стандартного отклонения! Таким образом, степени свободы в t-распределении на самом деле берутся из распределения хи-квадрат, которое спрятано в формуле t-статистики. Кстати, важно отметить, что все приведенные выше рассуждения справедливы, если исследуемый признак имеет нормальное распределение в генеральной совокупности (или размер выборки достаточно велик), и если бы у нас действительно стояла цель проверить гипотезу о среднем значении роста в популяции, возможно, было бы разумнее использовать непараметрический критерий.
Схожая логика расчета числа степеней свободы сохраняется и при работе с другими тестами, например, в регрессионном или дисперсионном анализе, все дело в случайных величинах с распределением Хи-квадрат, которые присутствуют в формулах для расчета соответствующих критериев.
Таким образом, чтобы правильно интерпретировать результаты статистических исследований и разбираться, откуда возникают все показатели, которые мы получаем при использовании даже такого простого критерия как одновыборочный t-тест, любому исследователю необходимо хорошо понимать, какие математические идеи лежат в основании статистических методов.
Онлайн курсы по статистике: объясняем сложные темы простым языком
Основываясь на опыте преподавания статистики в Институте биоинформатики , у нас возникла идея создать серию онлайн курсов, посвященных анализу данных, в которых в доступной для каждого форме будут объясняться наиболее важные темы, понимание которых необходимо для уверенного использования методов статистики при решении различного рода задача. В 2015 году мы запустили курс Основы статистики, на который к сегодняшнему дню записалось около 17 тысяч человек, три тысячи слушателей уже получили сертификат о его успешном завершении, а сам курс был награждён премией EdCrunch Awards и признан лучшим техническим курсом. В этом году на платформе stepik.org стартовало продолжение курса Основы статистики. Часть два, в котором мы продолжаем знакомство с основными методами статистики и разбираем наиболее сложные теоретические вопросы. Кстати, одной из главных тем курса является роль распределения Хи-квадрат Пирсона при проверке статистических гипотез. Так что если у вас все еще остались вопросы о том, зачем мы вычитаем единицу из общего числа наблюдений, ждем вас на курсе!
В основе статистических оценок нормально распределенных случайных величин по выборочным параметрам лежит распределение Стьюдента, связывающее три важнейших характеристики выборочной совокупности — ширину доверительного интервала, соответствующую ему доверительную вероятность и объем выборки п (или число степеней свободы выборки / = [c.833]
Распределение Стьюдента. Пусть 2 нормально распределенная случайная величина с нулевым математическим ожиданием и единичной дисперсией, а V — независимая от Г случайная величина, которая распределена по закону «хи-квадрат» с К степенями свободы. Тогда величина [c.14]
Таким образом, распределение Стьюдента зависит только от числа степеней свободы /, с которым была определена выборочная дисперсия (рис. 18). На рис. 18 приведены графики плотности t-распределения для /=1, f = 5 и нормальная кривая. Кривые рас-пре/.еления по своей форме напоминают нормальную кривую, но [c.41]Распределение величины I по = п—степеням свободы носит название распределения Стьюдента. Сравним его с распределением Лапласа. Если мера отклонения среднего результата измерений от математического ожидания в единицах генерального стандартного отклонения среднего о(л ), то коэффициент Стьюдента — аналогичная мера в единицах выборочного стандартного отклонения среднего результата и- = (Х — ц)/а (Г) = АХ- л/п/а-, 1- = (Х — ц)/5 (X) = АХ- / 3 . [c.833]
Попытка подставить выборочное д в изложенное выше решение задачи приводит к уменьшению по сравнению с истинными доверительных интервалов. Это объясняется тем, что величина (х — МУб распределена уже не нормально, а по распределению Стьюдента с N—1 степенью свободы. Плотность распределения Стьюдента имеет вид [c.175]
Распределением Стьюдента (или распределением) с п степенями свободы называется распределение, которым обладает с. в. [c.292]
Если число измерений мало п 20 для практических целей), то распределение Гаусса дает слишком оптимистичные оценки в этом случае применяют распределение Стьюдента. В этом распределении учитывается число степеней свободы V = га — 1. При V -> оо нормальное распределение и распределение Стьюдента совпадают. Кривая плотности распределения Стьюдента более размазана , чем кривая распределения Гаусса. [c.38]
Можно доказать, что при исходных нормальных совокупностях величина 1-) имеет расиределение Стьюдента с / = /п—2 степенями свободы. При проверке гипотезы нормальности по большому числу малых выборок из каждой выборки случайным образом отбирается по одному значению. Здесь возможно некоторое упрощение — можно отобрать только первые измерения, только вторые и т. д. Такой отбор также можно рассматривать как случайный. Если число элементов в выборках велико, например т>10, то мой- ет быть сделано несколько самостоятельных проверок гипотезы, например, по первым и последним элементам каждой выборки. Затем, если т==4, для каждого отобранного значения по формуле (П. 131) вычисляется т, если тфА, по формуле (П. 134) т). После перехода к величинам т и т) для проверки гипотезы равномерного распределение т илп распределения Стьюдента т] (и, следовательно, нормальности исходного распределения) может быть применен любой из ра смотренных ранее критериев согласия. [c.68]
&e
Предположим нам необходимы вычислить отличается ли от нормального интеллект детей обучающихся по специальной программе. Для этого используем статистический критерий t-Стьюдента.
У нас есть данные IQ 30 учащихся. Они указаны в таблице ниже:
| № | IQ |
| 1 | 100 |
| 2 | 111 |
| 3 | 112 |
| 4 | 105 |
| 5 | 105 |
| 6 | 104 |
| 7 | 94 |
| 8 | 89 |
| 9 | 113 |
| 10 | 125 |
| 11 | 96 |
| 12 | 100 |
| 13 | 98 |
| 14 | 124 |
| 15 | 121 |
| 16 | 116 |
| 17 | 95 |
| 18 | 92 |
| 19 | 118 |
| 20 | 96 |
| 21 | 94 |
| 22 | 117 |
| 23 | 130 |
| 24 | 90 |
| 25 | 114 |
| 26 | 119 |
| 27 | 120 |
| 28 | 100 |
| 29 | 96 |
| 30 | 102 |
Шаг 2. Проверим соответствует ли распределение нормальному.
Шаг 3. Вычислим среднее арифметическое и стандартное отклонение , также определим нормативное значение с которым будем производить сравнение (для IQ такое значение равно 100)
Шаг 4. Вычислим эмпирическое значение t-критерия Стьюдента используя формулу:
Шаг 5. Вычислим число степеней свободы t-критерия Стьюдента для одной выборки:
Шаг 6. Определим по таблице критических значений t-критерия Стьюдента уровень значимости.
Шаг 6.1 В таблице критических значений находим значений df = 29.
Шаг 6.2. В соответствующей df=29 строке находим значение равное . В нашем случае оно расположено ближе, чем 3,659 (p=0,001), но дальше, чем 2,756 (p=0,01). Это говорит нам, что уровень значимости <0,01.
Шаг 7. Если уровень значимости ниже 0,05 то средние значения в исследуемой выборке отличаются от нормальных.
Рассчитайте критерий Т-Стьюдента за 5 минут
Онлайн сервис расчета статистики
Распределение Стьюдента и малые выборки
Если среднее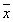 
рассчитывается по данным малой выборки, то отклонение 
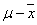имеет распределение Стьюдента, называемое также t-распределением. Распределение Стьюдента близко к нормальному
распределению, но отличается от него: концентрация отклонений в центральной части распределения меньше.
Если случайная величина X1 распределена по нормальному закону, а случайная величина X2 распределена по закону Хи-квадрат с v степенями свободы, тогда случайная величина, получаемая как
,
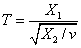имеет распределение Стьюдента (t-распределение) с v степенями свободы.
Преимущество распределения Стьюдента заключается в его независимости от параметров генеральной совокупности: оно зависит только от объёма выборки n. В случае малых выборок (с объёмом менее 30 наблюдений) для определения доверительного интервала среднего значения нельзя использовать критические значения стандартизированного нормального распределения, так как это приводит к грубым оценкам.
Нередко проведение каждого наблюдения настолько сложно, трудоёмко и связано с высокой стоимостью, что невозможно многократное повторение эксперимента. Чтобы оценить среднее значение малой выборки, нужно учитывать, что дисперсия малой выборки рассчитывается по формуле несмещённой оценки дисперсии:
.
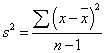Функцию плотности распределения Стьюдента в рассчётах непосредственно не используют, обычно используют таблицы интегральных функций, которые есть в приложениях почти ко всем книгам по статистике, или же её значение выдаёт программа, в которой выполняются рассчёты, например, STATISTICA. В таблицах значения интегральной функции даны для тех же пределов интегрирования, что и у функции нормального распределения. Функция нормального распределения рассчитана для определённого значения аргумента z, а интегральная функция распределения Стьюдента — для аргумента t и числа степеней свободы v = n — 1. Если число степеней свободы стремится к бесконечности, то распределение Стьюдента стремится к нормальному распределению.
Числом степеней свободы в статистике называют число взаимно независимых элементов информации, используемых для вычисления стандартной ошибки. Число степеней свободы равно числу элементов выборки, из которого вычтено число условий, связывающих данные.
Если объём выборки мал и стандартное отклонение генеральной совокупности неизвестно, то доверительный интервал оценки среднего рассчитывается следующим образом:
,
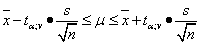где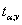 
—
критическое значение распределения Стьюдента для уровня значимости α = 1 — P
и числа степеней свободы v
s — стандартное отклонение выборки.
Распределение Стьюдента названо в честь Уильяма Госсета, который впервые использовал свойства этого распределения и публиковал свои работы под псевдонимом Стьюдент.
Пример. Производитель кваса решил выяснить, каков доверительный интервал 95% незаполненного уровня в бутылках с квасом (в миллимитрах от пробки). Рассчитать этот доверительный интервал.
Решение.
Случайно выбраны 20 бутылок с квасом, по которым собраны значения незаполненного уровня.
С помощью функций MS Excel рассчитаны сумма этих значений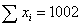 
и сумма отклонений 
.
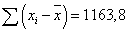Тогда среднее 
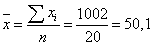, а
стандартное отклонение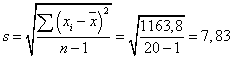 
.
Так как для проверки выбраны только 20 бутылок, то для определения доверительного интервала среднего следует использовать распределение Стьюдента:
,
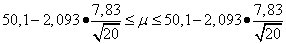
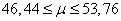где 2,093 — критическое значение распределения Стьюдента для уровня значимости 0,05 и числа степеней свободы 19 (найдено по статистической таблице, которые есть в приложениях почти во всех книгах по статистике).
Таким образом, доверительный уровень 95% незаполненного уровня бутылок с квасом составил от 46,44 до 53,76 миллиметров.
Всё по теме «Математическая статистика»
Критерий согласия Пирсона χ2 (Хи-квадрат)
До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть знамений критерий Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение критерия будет относительно не большим (т.к. большинство отклонений находится около нуля). Но если критерий оказывается большим, то это свидетельствует в пользу существенных различий между частотами.
«Большим» критерий Пирсона становится тогда, когда появление такого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение критерия при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем их больше, тем большее значение должно быть у критерия, ведь каждое слагаемое внесет свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистического критерия может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. А формальное определение критерия хи-квадрат следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Проверка гипотезы по критерию хи квадрат Пирсона
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по критерию хи-квадрат. Далее либо сам критерий сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т.е. вероятность получить такое или еще больше значение критерия при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда критерий окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение критерия хи-квадрат.
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный критерий оказался меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение критерия при заданной вероятности слева (как в статистических таблицах)
ХИ2.ОБР.ПХ – критическое значение критерия при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит хи-квадрат тест. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Сам критерий хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
7. Распределение Стьюдента с степенями свободы
(t-распределение)
В нормальном
распределении средняя арифметическая
зависит от дисперсии слагаемых величин.
Однако на практике дисперсия исследуемой
величины, как правило, неизвестна. В
этой связи возникла задача определения
закона распределения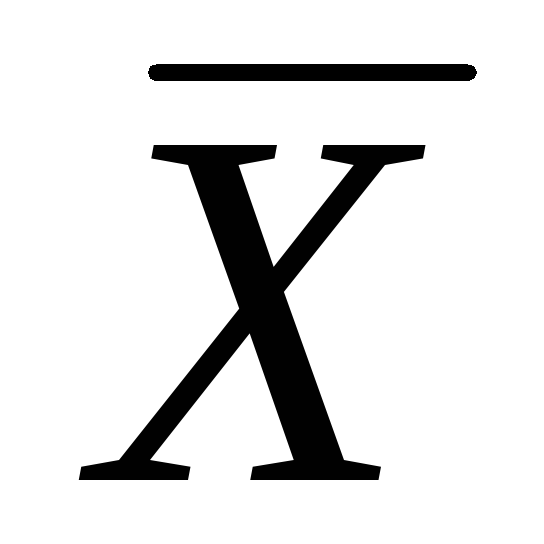 
,
не зависящего от
,
которую решил английский статистик В.
Госсет, публиковавшийся под псевдонимом
Стьюдент. Дадим следующее определение:
Если случайная
величина Z
имеет нормальное нормированное
распределение N(0,1),
а величина U2 имеет распределение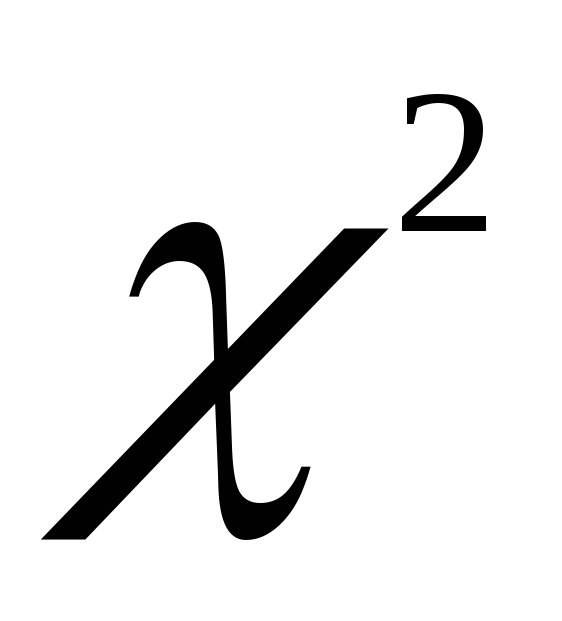 
с
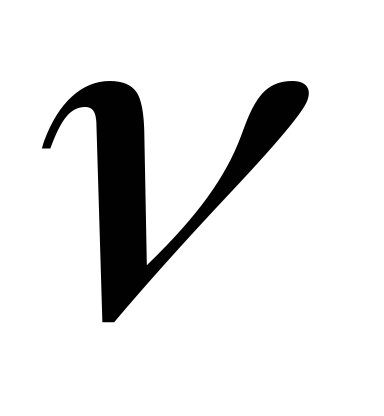степенями
свободы, причемZ
и U
взаимно независимы, то случайная величина
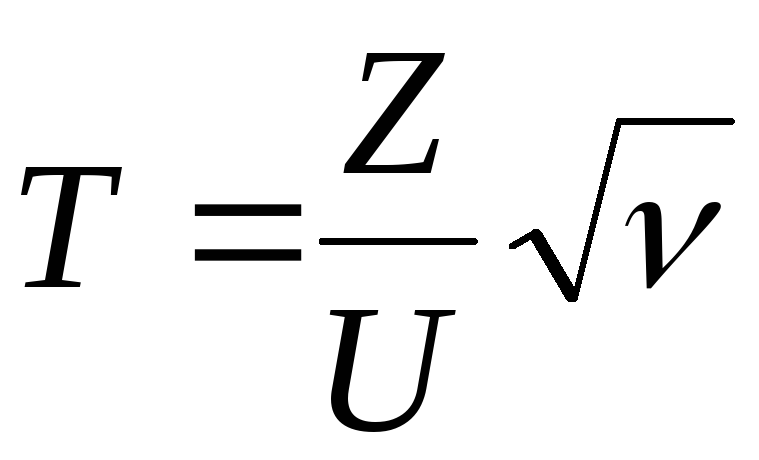
имеет t-распределение
с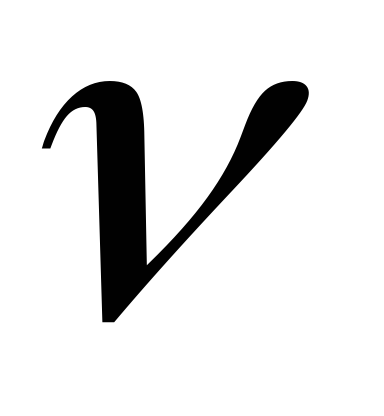 
степенями свободы. Плотность распределения
описывается формулой
.
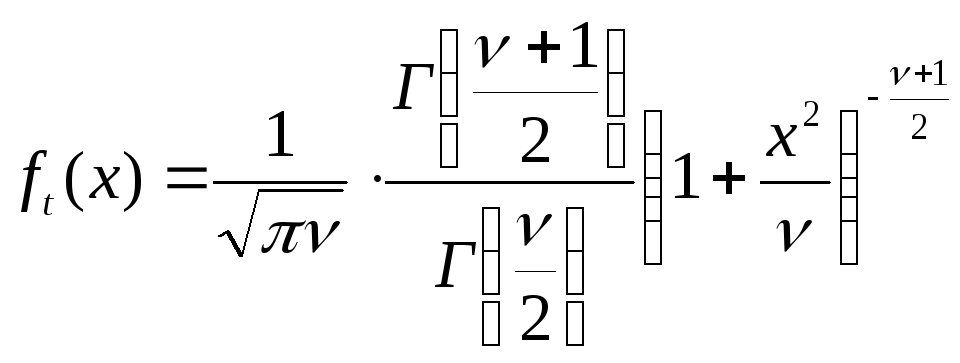Функция плотности
является унимодальной и симметричной
относительно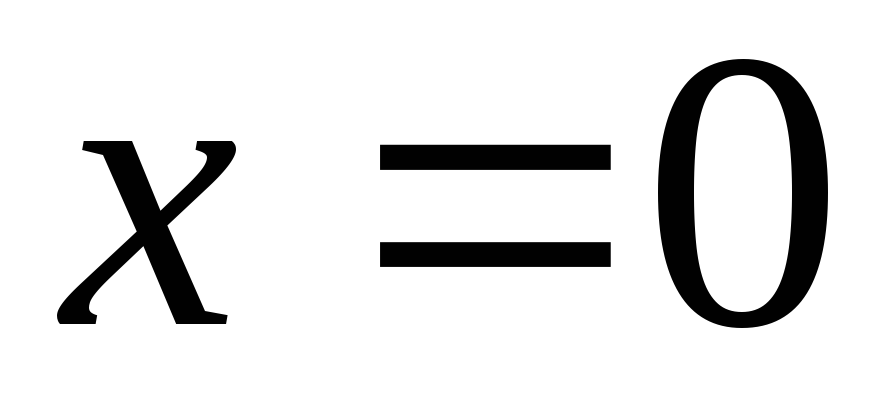 
.
Основные числовые характеристики:
среднее, мода,
медиана: 
;
дисперсия: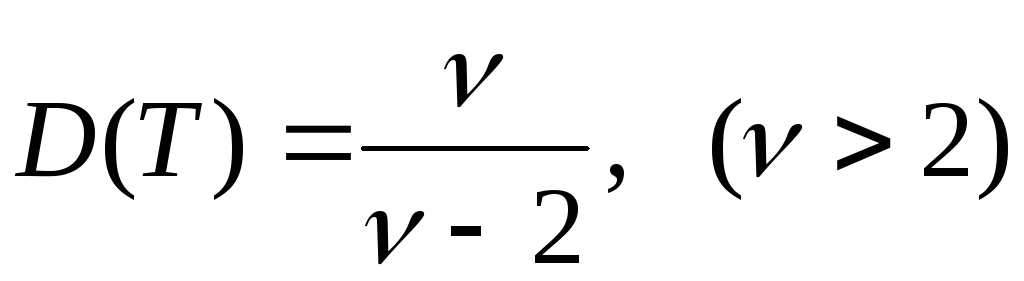 
;
асимметрия: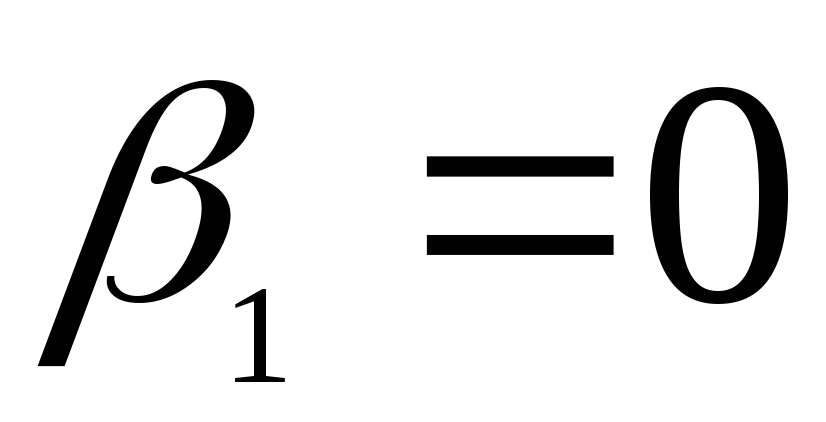 
;
эксцесс: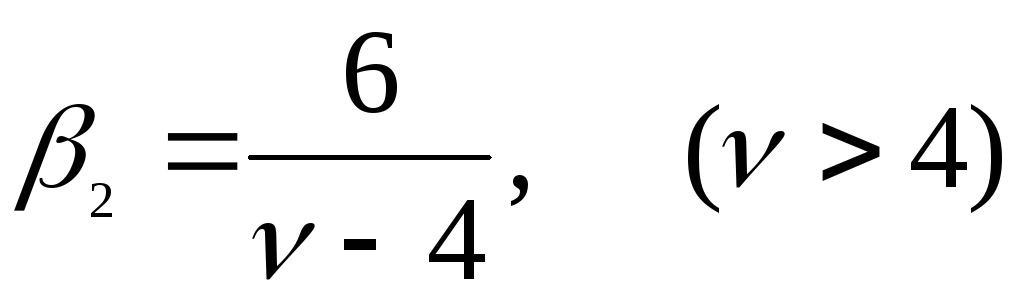 
.
Ниже на рисунке
приведены сравнительные графики функции
плотности t-распределения
при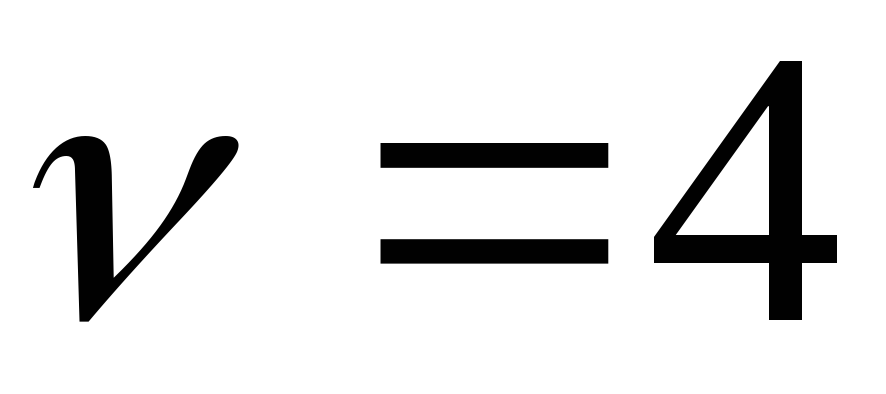 
и стандартного нормального распределенияN(0,1).
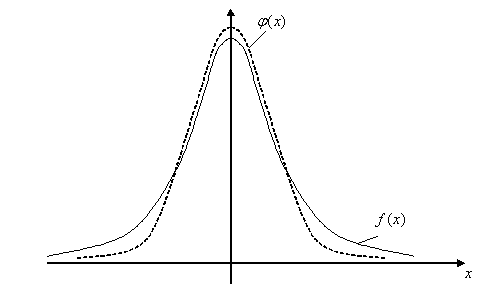
Рис. 9.2.График t-распределения
при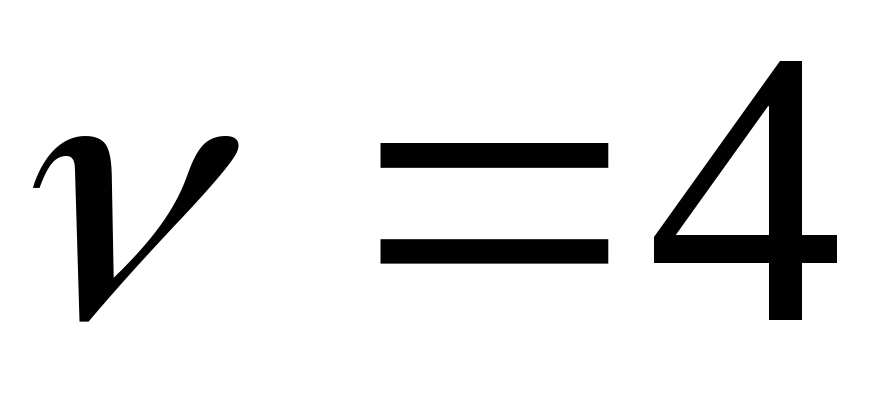 
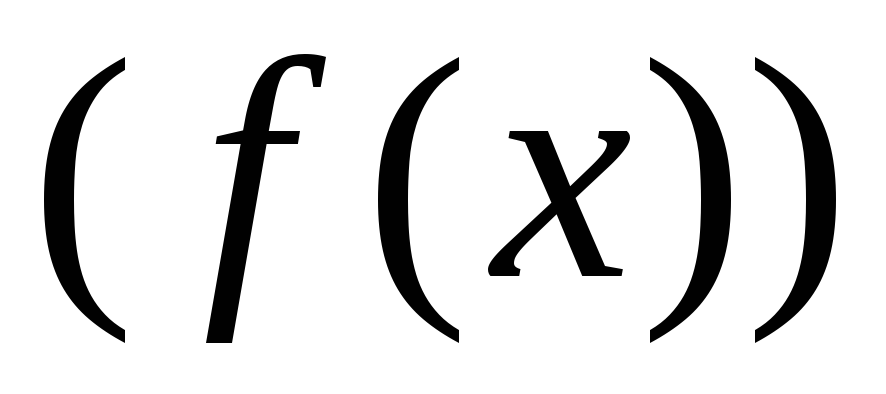и нормального
нормированного распределения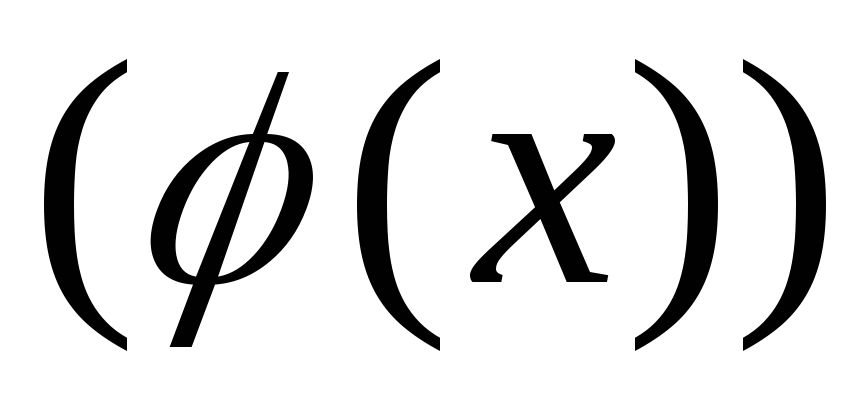 
Если из генеральной
совокупности Х с нормальным законом распределения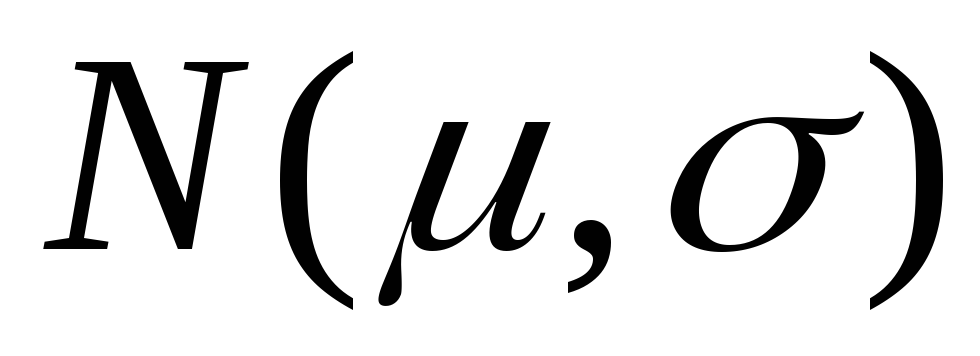 
взята случайная выборка объёмаn,
то статистика
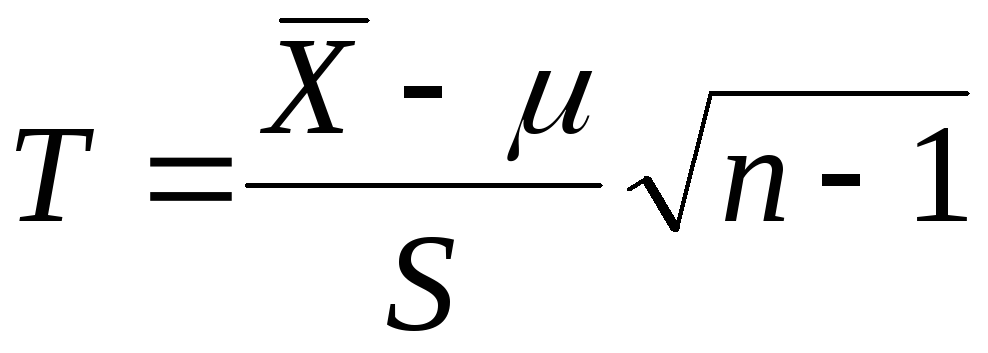
имеет распределение
Стьюдента с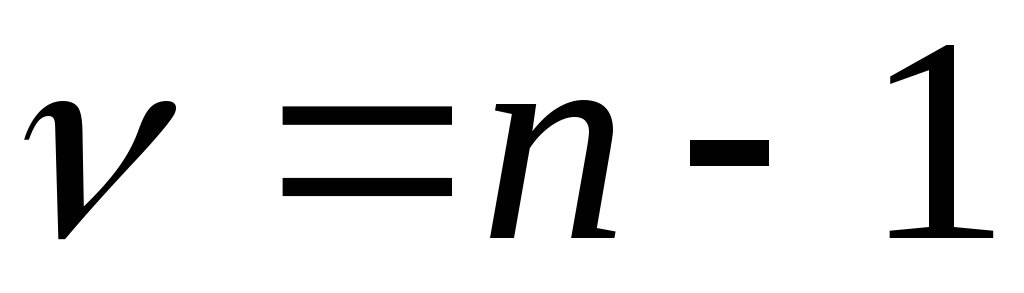 
степенями свободы. ЗдесьS-выборочное
среднее квадратическое отклонение.
Распределение
Стьюдента используется при интервальной
оценке математического ожидания при
неизвестном значении среднего
квадратического отклонения 
.
8. Распределение Фишера-Снедекора (f-распределение).
Пусть имеются две
независимые случайные величины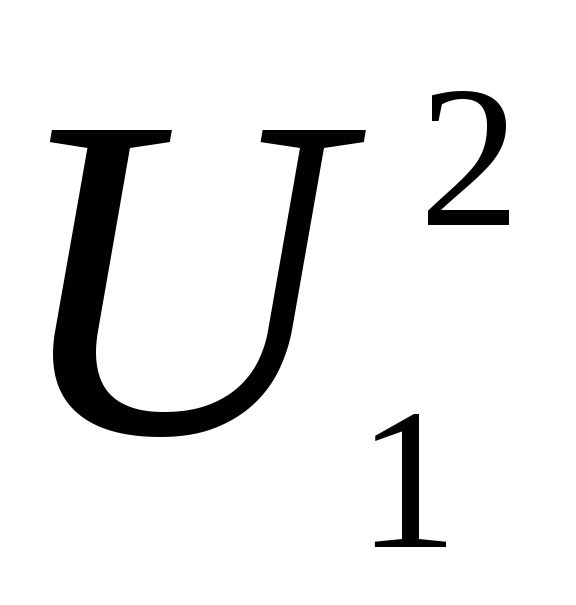 
и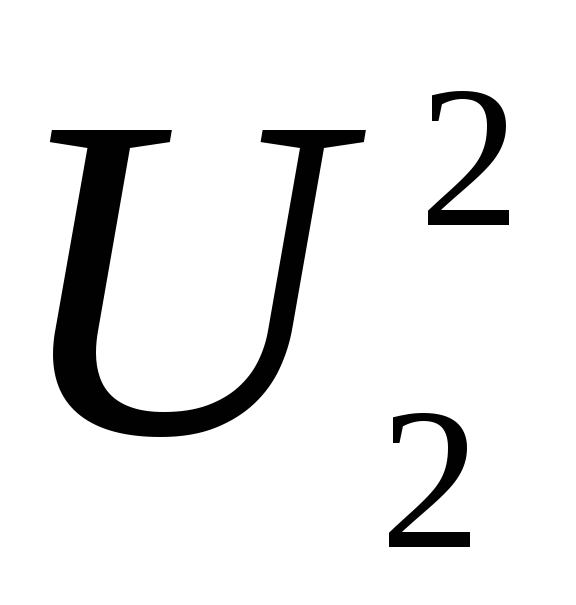
имеющие
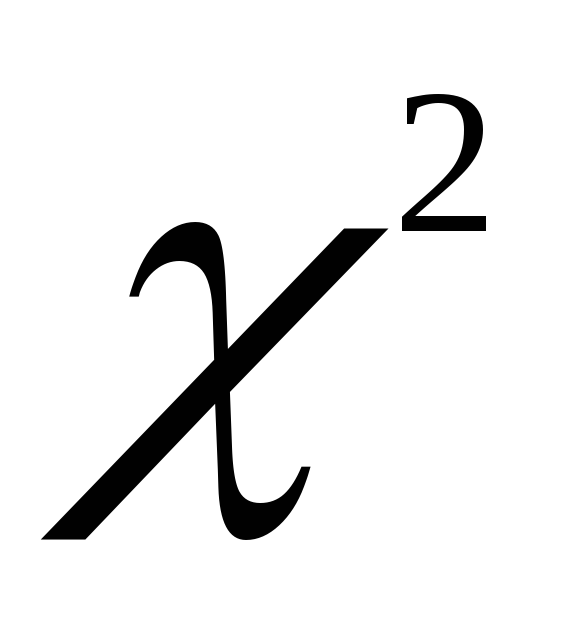-распределение
соответственно со степенями свободы
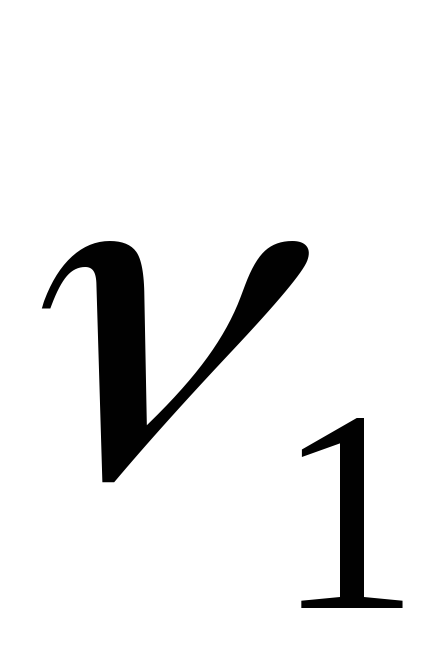и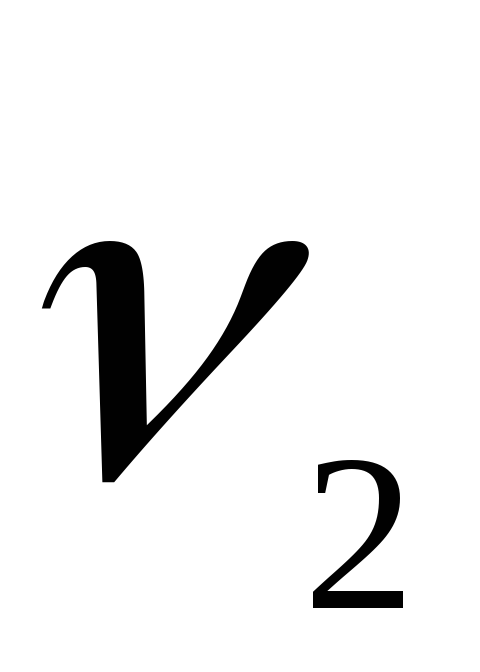
.
Тогда величина
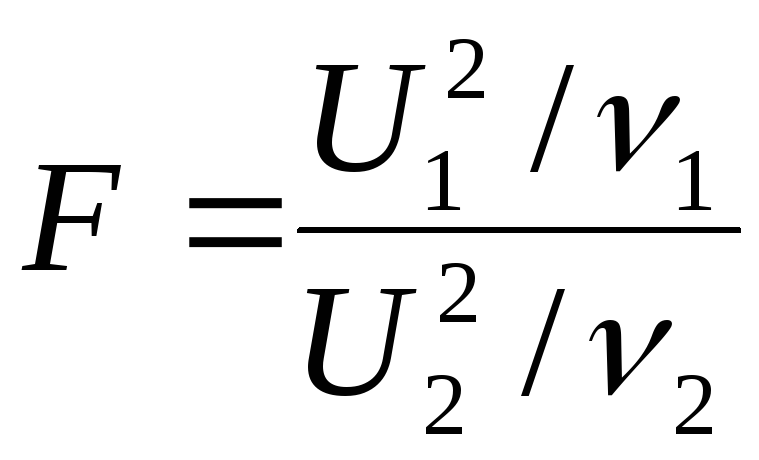
имеет F-распределение
с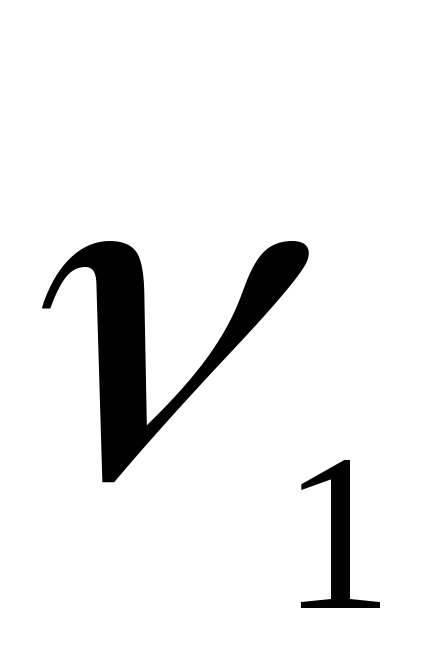 
истепенями свободы, причем
,
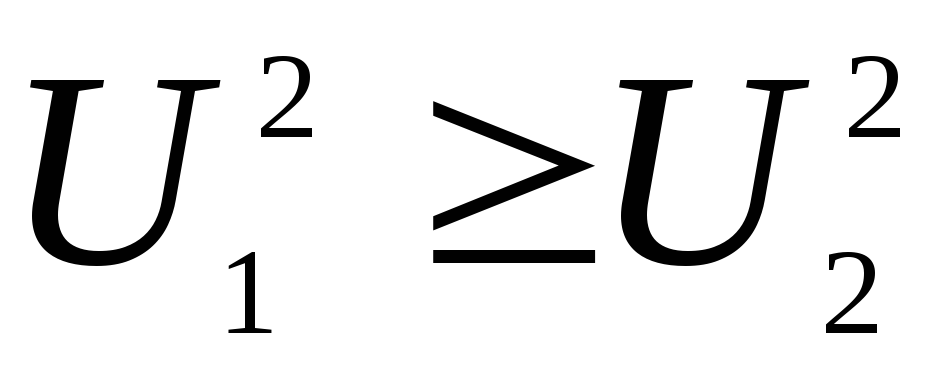так что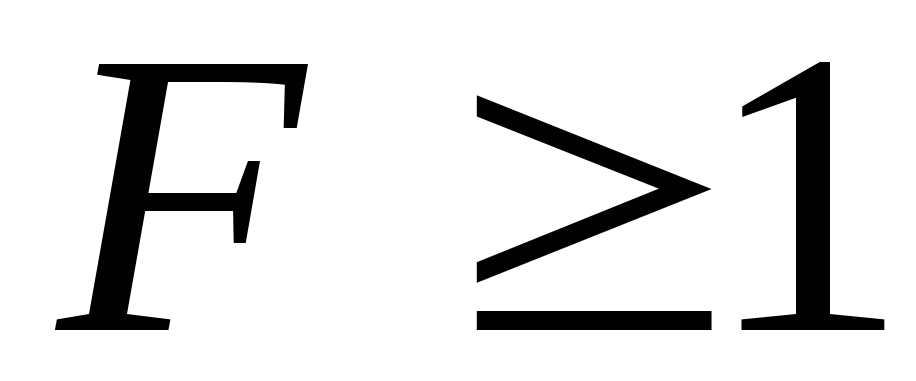
.
Это распределение впервые было построено английским статистиком Р. Фишером. Американский статистик Дж. Снедекор составил таблицы для данного распределения, поэтому его часто называют распределением Фишера-Снедекора.
Используется в дисперсионном анализе при проверке статистических гипотез.
Раздел II математическая статистика Лекция 1. Генеральная совокупность. Выборка. Способы образования выборки. Статистическая оценка параметров распределения.
В математической статистике множество возможных значений случайной величины Х называют генеральной совокупностью случайной величины Х или просто генеральной совокупностью Х.
Исходным материалом для изучения свойств генеральной совокупности являются экспериментальные (статистические) данные, под которыми понимают значения случайной величины, полученные в результате независимых повторных наблюдений (имеется ввиду, что эксперимент может, хотя бы теоретически, быть повторен сколько угодно раз в одних и тех же условиях).
Совокупность
независимых случайных величин Х1,
… , Хn , имеющих
на множествах исходов 1, … , n-го
экспериментов (наблюдений) то же
распределение, что и случайная величина
Х, называется случайной
выборкой.
При этом число n называют объемом выборки. Любое возможное
значение (х1
, … , хn)
случайной выборки — эмпирическим рядом,
а числа хi его вариантами. При этом некоторые
варианты могут повторяться. Число
повторений вариант называют эмпирической
частотой и обозначают ni (или mi).
Таблица, в которой варианты записаны
по одному разу и в порядке возрастания,
а также указаны их частоты или частости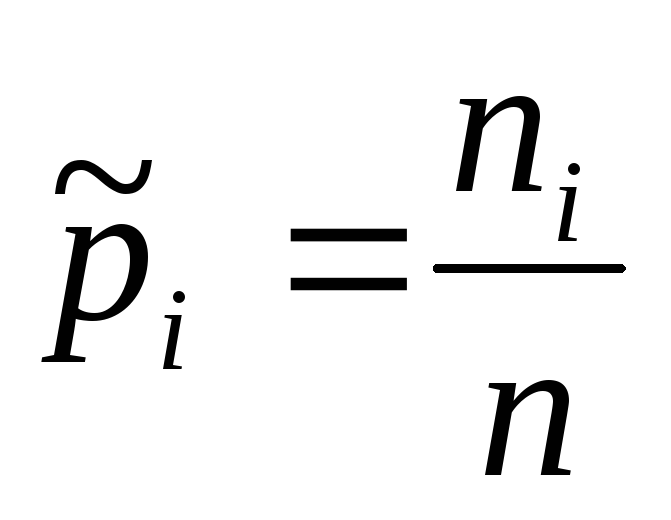 
,
называемыевесами, называется
вариационным дискретным рядом.
Пример 1. В течении суток измеряют напряжение Х тока в электросети в вольтах. В результате опыта получена выборка объема n = 30:
107 108 110 109 110 111 109 110 111 107
108 109 110 108 107 110 109 111 111 110
109 112 113 110 106 110 109 110 108 112
Построим вариационный ряд этой выборки.
Наименьшее значение в выборке х1 = 106, наибольшее – х8 = 113. Подсчитываем частоту каждого хi, i = 1,…, 8 и строим таблицу 1.1.
хi
106
107
108
109
110
111
112
113
ni
1
3
4
6
9
4
2
1
При большом объеме
выборки ( свыше 50 ) исходные данные
рассматривают на интервале J = ( х1, хn).
Этот интервал разбивают на m промежутков равной длины 
.
При этом считают, что каждый промежуток
содержит свой левый конец, но лишь
последний содержит и правый. При таком
соглашении каждая точка отрезкаJ содержится в одном и только в одном
интервале Jk.
Далее, для каждого промежутка Jk, k = 1,…, m подсчитывается число элементов выборки
попавших в него, а результаты представляют
в виде таблицы 1.2., которую называют интервальным
рядом.
Таблица 1.2.
J1
J2
. . .
Jm
n1
n2
. . .
nm
В зависимости от того, является ли генеральная случайная величина Х дискретной или непрерывной, результаты выборки записывают в виде вариационного или интервального рядов. Для интервального ряда вводят понятие эмпирической плотности распределения, как функции, определяемой формулой:
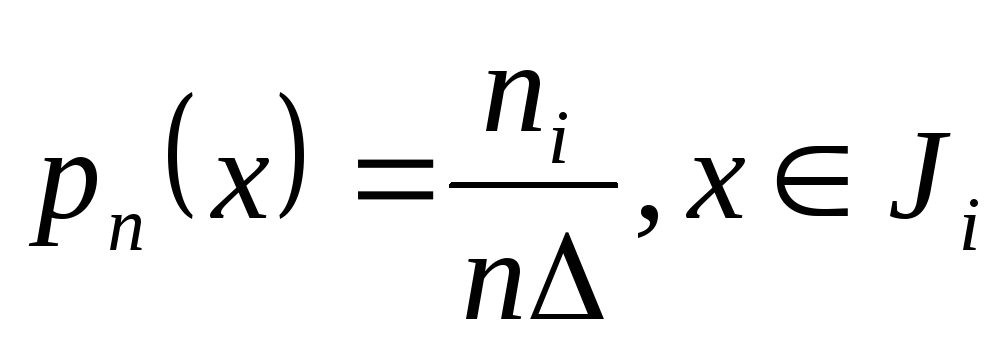и равна 0, если 
.
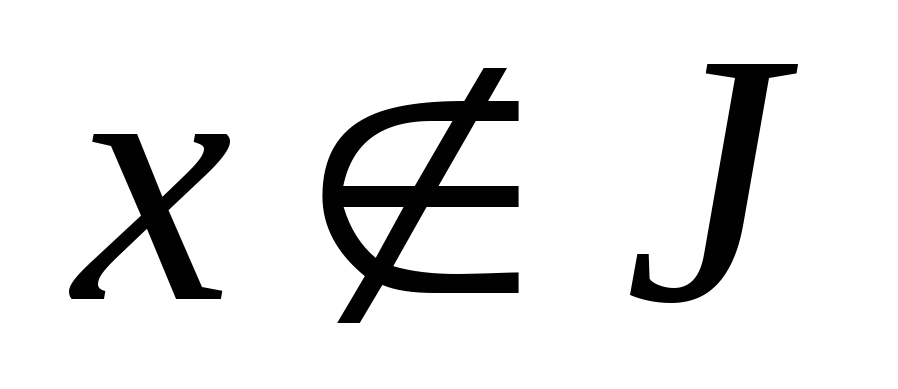График функции плотности называют гистограммой.
Стью́дента распределение
С f степенями свободы, распределение отношения Т = X/Y независимых случайных величин Х и Y, где Х подчиняется нормальному распределению (См. Нормальное распределение) с математическим ожиданием EX = 0 и дисперсией DX = 1, а fY2 имеет «Хи-квадрат» распределение (См. Хи-квадрат распределение) с f степенями свободы. Функция распределения Стьюдента выражается интегралом
.
Если X1,…, Xn — независимые случайные величины, одинаково нормально распределённые, причём EXi = a и DXi= σ2 (i = 1,…, n), то при любых действительных значениях а и σ > 0 отношение 
подчиняется С. р. с f = п-1 степенями свободы (здесь 
и 
). Это свойство было впервые (1908) использовано для решения важной задачи классической теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы а = a0 (a0 = заданное число, дисперсия σ2 предполагается неизвестной). Гипотезу а =a0 считают не противоречащей результатам наблюдений X1,…, Xn, если справедливо неравенство 
, в противном случае гипотеза а = а0 отвергается (так называемый критерий Стьюдента). Критическое значение t = tn-1(α) представляет собой решение уравнения Sn-1(t) = 1 – 
,α — заданный Значимости уровень (0 < α < ½). Если проверяемая гипотеза а = а0 верна, то критерий Стьюдента, соответствующий критическому значению tn–1(α), может её ошибочно отвергнуть с вероятностью а.
С. р. используется для решения множества др. задач математической статистики (см. Малые выборки, Ошибок теория, Наименьших квадратов метод).
Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.
Источник: Большая советская энциклопедия на Gufo.me
Значения в других словарях
- Стьюдента Распределение — С f степенями свободы, t-распределение, — распределение вероятностей случайной величины где U — случайная величина; подчиняющаяся стандартному нормальному N(0, 1) закону, — случайная величина, не зависящая от Uи подчиняющаяся «хиквадрат Математическая энциклопедия
90000 r — Plot Student’s t distribution with degrees of freedom 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 r — Understanding degrees of freedom in lavaan 90001 Stack Overflow 90002 90003 Products 90004 90003 Customers 90004 90003 Use cases 90004 90009 90010 90003 Stack Overflow Public questions and answers 90004 90003 Teams Private questions and answers for your team 90004 90003 Enterprise Private self-hosted questions and answers for your enterprise 90004 90003 Jobs Programming and related technical career opportunities 90004 90003 Talent Hire technical talent 90004 90003 Advertising Reach developers worldwide 90004 90009 .90000 When to use «depend» vs. «Depending» — Espresso English 90001 90002 90003 90004 Advanced English Grammar Course 90005 90006 We use 90004 depend 90005 and 90004 depending 90005 when one thing is strongly affected by another thing. 90011 For example, if there is a lot of rain, the flowers in your garden will grow. If there is no rain, the flowers will not grow. This means the growth of the flowers 90004 depends 90005 on the rain — one thing (the flowers ‘growth) is affected by another thing (the rain).90014 90011 However, a lot of students are confused about when to use 90004 depend 90005 vs. 90004 depending. 90005 The answer involves the grammar of each sentence. 90014 90011 Use 90004 depend / depends 90005 when it is the 90004 main verb 90005 in the sentence: 90014 90027 90028 «Will you go to the beach this weekend?» 90006 «I’m not sure. It 90004 depends 90005 on the weather. » 90006 90033 (subject = it; main verb = depends) 90034 90035 90028 The results of the survey 90004 depend 90005 on the types of questions asked.90006 90033 (subject = the results of the survey; main verb = depend) 90034 90035 90043 90011 When 90004 depend 90005 is the 90004 main verb, 90005 it is considered a «state verb» (not an action verb) and is never used in continuous form. NEVER say «It’s depending on …» 90014 90011 Use 90004 depending 90005 when the word begins a 90004 dependent clause. 90005 This means that the sentence already has a separate subject and main verb, and the dependent clause only adds some extra information: 90014 90027 90028 We’re thinking about going to the beach, 90004 depending 90005 on the weather.90006 90033 (subject = we; main verb = are thinking) 90034 90035 90028 90004 Depending 90005 on the types of questions asked, the survey produces different results. 90006 90033 (subject = the survey; main verb = produces) 90034 90035 90043 90011 Important note: we always say 90004 depend / depending ON, 90005 never «of» or «in.» 90014 90011 There’s another way to use 90004 depend / depending, 90005 meaning when one person is 90004 relying 90005 on another — they trust the other person and / or need the other person to do something.With this definition, we can use 90004 depend 90005 for relying on someone 90033 in general, 90034 and 90004 depending 90005 for relying on someone 90033 right now in a specific situation: 90034 90014 90027 90028 I do not have a car, so I 90004 depend 90005 on my colleagues to give me rides to work every day. 90006 90033 (in general) 90034 90035 90028 I’m 90004 depending 90005 on you to get this project done by Friday. 90006 90033 (right now in a specific situation) 90034 90035 90043 .90000 TINV function — Office Support 90001 90002 Returns the two-tailed inverse of the Student’s t-distribution. 90003 90004 90005 Important: 90006 This function has been replaced with one or more new functions that may provide improved accuracy and whose names better reflect their usage. Although this function is still available for backward compatibility, you should consider using the new functions from now on, because this function may not be available in future versions of Excel.90003 90002 For more information about the new functions, see T.INV.2T function or T.INV function. 90003 90010 Syntax 90011 90002 TINV (probability, deg_freedom) 90003 90002 The TINV function syntax has the following arguments: 90003 90016 90017 90004 90005 Probability 90006 Required. The probability associated with the two-tailed Student’s t-distribution. 90003 90022 90017 90004 90005 Deg_freedom 90006 Required.The number of degrees of freedom with which to characterize the distribution. 90003 90022 90029 90010 Remarks 90011 90016 90017 90004 If either argument is nonnumeric, TINV returns the #VALUE! error value. 90003 90022 90017 90004 If probability <= 0 or if probability> 1, TINV returns the #NUM! error value. 90003 90022 90017 90004 If deg_freedom is not an integer, it is truncated.90003 90022 90017 90004 If deg_freedom <1, TINV returns the #NUM! error value. 90003 90022 90017 90004 TINV returns that value t, such that P (| X |> t) = probability where X is a random variable that follows the t-distribution and P (| X |> t) = P (X <-t or X> t). 90003 90022 90017 90004 A one-tailed t-value can be returned by replacing probability with 2 * probability.For a probability of 0.05 and degrees of freedom of 10, the two-tailed value is calculated with TINV (0.05,10), which returns 2.28139. The one-tailed value for the same probability and degrees of freedom can be calculated with TINV (2 * 0.05,10), which returns 1.812462. 90003 90004 90005 Note: 90006 In some tables, probability is described as (1-p). 90003 90004 Given a value for probability, TINV seeks that value x such that TDIST (x, deg_freedom, 2) = probability.Thus, precision of TINV depends on precision of TDIST. TINV uses an iterative search technique. If the search has not converged after 100 iterations, the function returns the # N / A error value. 90003 90022 90029 90010 Example 90011 90002 Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.90003 90068 90069 90070 90071 90004 90005 Data 90006 90003 90076 90071 90004 90005 Description 90006 90003 90076 90083 90084 90085 90086 90070 90088 90004 0.05464 90003 90091 90088 90004 Probability associated with the Student’s two-tailed t-distribution 90003 90091 90084 90070 90088 90004 60 90003 90091 90088 90004 Degrees of freedom 90003 90091 90083 90084 90070 90088 90004 90005 Formula 90006 90003 90091 90088 90004 90005 Description 90006 90003 90091 90088 90004 90005 Result 90006 90003 90091 90084 90070 90088 90004 = TINV (A2, A3) 90003 90091 90088 90004 The t-value of the Student’s t-distribution based on the arguments in A2 and A3.90003 90091 90088 90004 1.96 90003 90091 90084 90142 90143 .