Презентация тему сумма углов треугольника. накрест лежащие углы
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Тема урока: «Сумма углов треугольника». «Величие человека – в его способности мыслить». Б.Паскаль
Цель урока: Выяснить: — Чему равна сумма углов любого треугольника.
Виды углов 1 2 3 4
Рассмотрим рисунок а b с 1 2 3 4 d 5
Лабораторная работа. Указание к работе 1. Постройте в тетради произвольный треугольник АВС. 2. Измерьте градусные меры углов треугольника. 3.Запишите в тетрадь: А =…, В =…, С=… 4. Найдите сумму углов треугольника А + В + С=… 5.Сравните полученные результаты.
Практическая работа. Возьмите бумажный треугольник, лежащий у каждого на парте. Аккуратно оторвите у него два угла. Приложите эти углы к третьему таким образом, чтобы они выходили из одной вершины.
Сумма углов треугольника равна Теорема
Рассмотрим произвольный треугольник АВС В А С Дано: ∆АВС Док-ть: А + В + С= 180 0
и докажем, что А В С
и докажем, что А В С
и докажем, что А В С
и докажем, что А В С
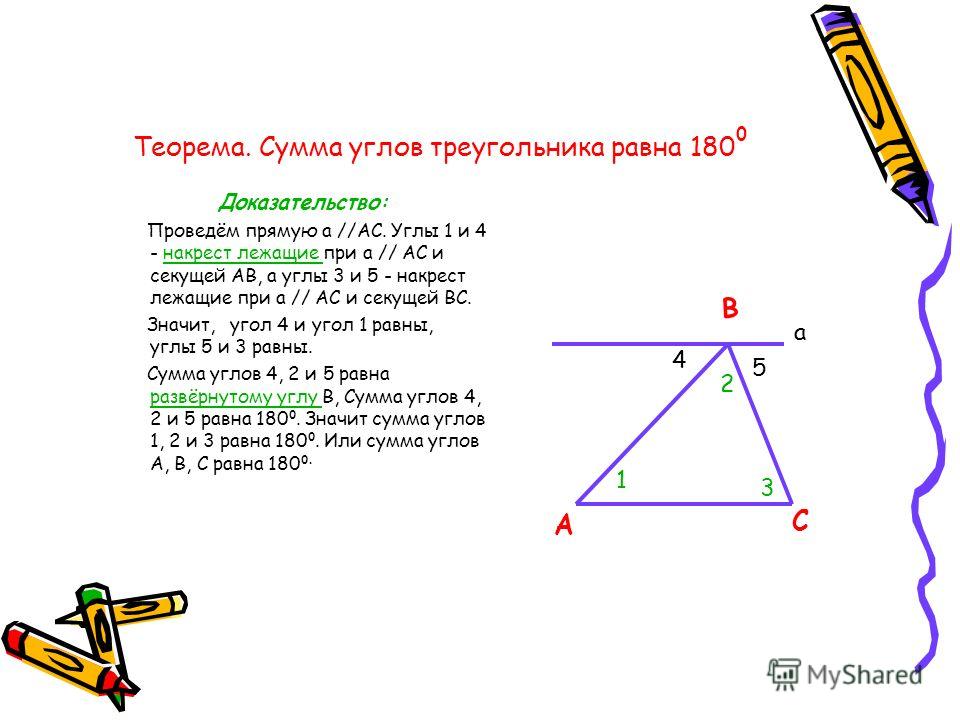
Проведем через вершину В прямую, параллельную стороне АС А С В С
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых и АС и секущей АВ. А С В 1 4 С
А С В 1 4 С
А углы 3 и 5 являются накрест лежащими углами при пересечении параллельных прямых и АС и секущей ВС. А С В С 5 3
Поэтому 4 = 1, 5 = 3 А С 3 В 5 4 1 С
Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т.е. А С 2 С В 4 5
Отсюда, учитывая, что получаем или А 2 С 5 1 3 В 4 4 = 1 ,
Отсюда, учитывая, что получаем или А 2 С В 1 3 5 4 5 = 3 4 = 1 ,
Теорема доказана
Примерный план доказательства
Историческая справка Доказательство данного факта, изложенное в современных учебниках, содержалось ещё в комментарии к «Началам» Евклида древнегреческого учёного Прокла (V в.н.э.) Прокл утверждает, что согласно Евдему Родосскому, это доказательство было открыто ещё пифагорейцами (V в.до н.э.).
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.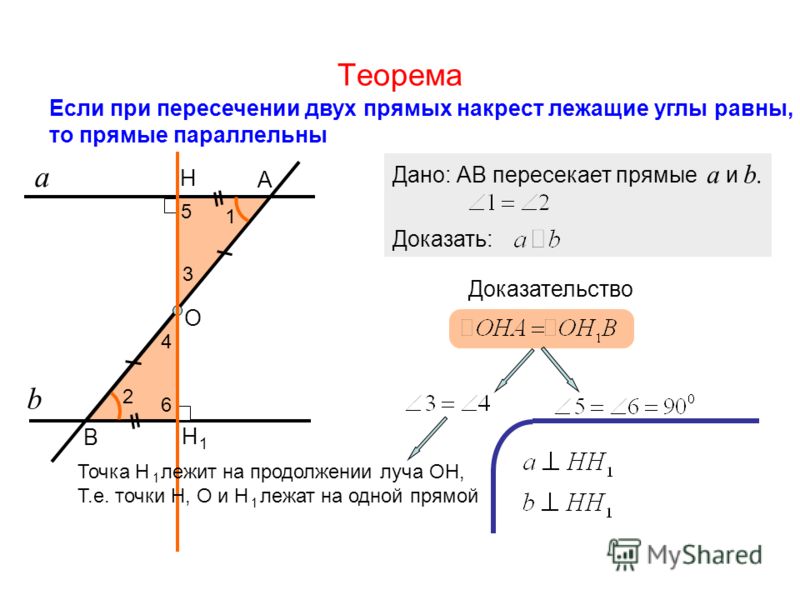
В А С Е 2 1 3 4 5 Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.
Внешний угол треугольника Определение: Внешним углом треугольника называется угол, смежный с одним из углов треугольника. 4 – внешний угол Свойство. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. 4 = 1 + 2 1 2 3 4
Итак, действительно: 1 2 3 4
Устная работа: Найдите углы треугольников 80 º 70 º ? В А С А=30 º
45 º ? L К M L =45 º
80 º ? ? N P R N =50 º R =50 º
В 130 º ? ? А С В=40 º С=50 º
Существует ли треугольник с углами: а) 30˚, 60˚, 90˚ б) 46˚, 160˚, 4˚ в) 75˚, 80˚, 25˚ г) 100˚, 20˚, 55˚
Работа с учебником. Стр.71 №223 а) № 228 а)
Практическое применение знаний. Свойство углов прямоугольного равнобедренного треугольника знал еще один из первых творцов геометрической науки древнегреческий ученый Фалес. Используя его, он измерял высоту египетской пирамиды по длине ее тени. По легенде, Фалес выбрал день и время, когда длина его собственной тени равнялась его росту, поскольку в этот момент высота пирамиды также должна равняться длине тени, которую она отбрасывает. Конечно, длину тени можно было вычислить от средней точки квадратной основы пирамиды, но ширину основы Фалес мог измерять непосредственно. Таким образом, можно измерять высоту любого дерева.
Конечно, длину тени можно было вычислить от средней точки квадратной основы пирамиды, но ширину основы Фалес мог измерять непосредственно. Таким образом, можно измерять высоту любого дерева.
Итог урока. Сегодня на уроке мы доказали исследовательским путем теорему о сумме углов треугольника, научились применять приобретенные знания в практической деятельности. Мы еще раз убедились, что геометрия это наука, которая возникла из потребностей человека. Ведь, как писал Галилей: “Природа разговаривает языком математики: буквы этого языка — окружности, треугольники и прочие математические фигуры».
Домашнее задание П.30, №223(б), №228(в). Другой способ доказательства теоремы о сумме углов треугольника.
Спасибо за внимание!
Класс 7
Тема урока: «Сумма углов треугольника».
Время : сдвоенный урок (пара).
Цели урока:
Образовательная: ознакомить с различными способами доказательства теоремы о сумме углов треугольника, ввести понятие внешнего угла треугольника, рассмотреть его свойство, научится применять теорему для нахождения углов треугольника в процессе решения задач.
Воспитательная: продолжить формирование навыков эстетического оформления записей в тетради и выполнения чертежей,продолжить формировать позитивное отношение к новому учебному предмету,приучать к умению общаться и выслушивать других, воспитание сознательной дисциплины.
Развивающая: выработать навык использования признаков параллельности прямых и свойства углов при параллельных прямых для решения задач и доказательств теорем;выработать умение нахождения углов треугольников при двух заданных углах, при заданных пропорциональностях углов; выработать навык использования теоремы о сумме углов треугольника и её следствие для решении задач;выработать навык нахождения углов треугольников при двух заданных углах, при заданных пропорциональностях углов, при заданных различных элементах треугольников (равные стороны, углы), умение находить углы треугольника если задан угол при биссектрисе, и находить углы при биссектрисе и основании треугольника, если заданы углы треугольника; развивать
сознательное восприятие учебного материала, зрительную память и грамотную математическую речь.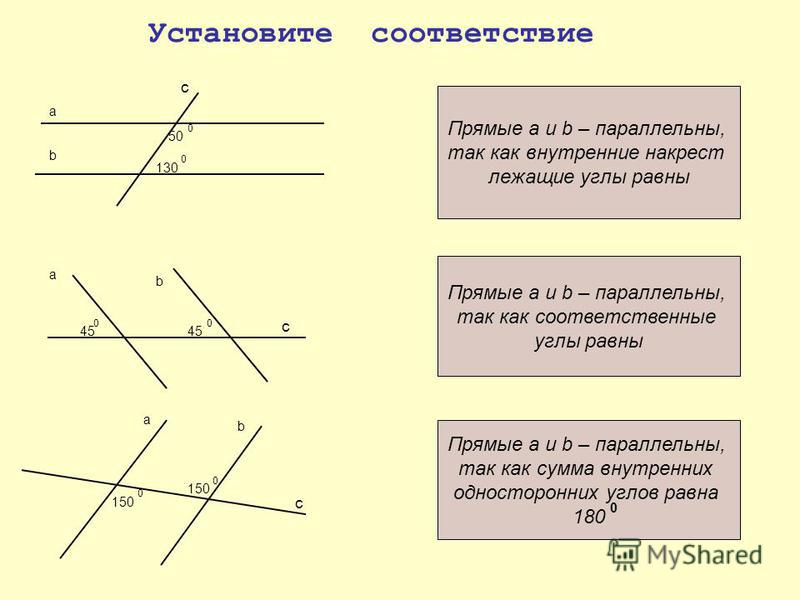
Оборудование: учебник Погорелова А.В., Геометрия 7-9 классы, (стр. 46, 52–53), интерактивная доска, презентация, раздаточный материал (целые бумажные треугольники и разрезанные картонные), большой бумажный треугольник для демонстрации на доске учителем нахождения суммы углов треугольника, карточки для самостоятельной работы
Тип урока: урок изучения нового материала и закрепления его (комбинированный урок).
Ход урока:
Этап
урока
Деятельность учителя
Деятельность учащихся
Орг.
момент
Домашнее задание
Изучение нового материала
(Практическая работа)
Изучение нового материала
Физминутка и развлекат. момент
Закрепле-ние изученного материала
Подведение итогов
Откройте дневники и запишите домашнее задание: выучить конспект 22, (п.33) Номера для домашней работы 19 (2), 22 (2), 24. (слайд 2)
Начнем урок с вами со стихотворения:
Знает даже и дошкольник,
Что такое треугольник,
А уж вам-то как не знать.
Но совсем другое дело –
Быстро, точно и умело
В нём есть стороны – их три,
И углов во всех по три,
И вершин, конечно, три.
Если длины всех сторон
Мы сложением найдём,
То к периметру придём.
Ну, а сумма всех углов
В треугольнике любом
Связана одним числом.
И мы с вами сегодня на уроке узнаем, с каким же числом связана сумма углов в любом треугольнике.
Откройте конспекты, запишите: конспект № 22. Сумма углов треугольника (слайд 3).
Начертите в тетрадях произвольный треугольник (слайд 4). Не очень маленький, примерно на треть странички. Что значит произвольный?
Верно. Чертим треугольник. Берем в руки транспортир.
И начинам по очереди измерять углы начерченного треугольника (слайд 5). Будем вместе с вами измерять углы.
Берем транспортир, прикладываем его к первому измеряемому углу так, чтобы открытая точка на транспортире совпала с вершиной угла, а сторона треугольника и внутренняя прямая часть транспортира совпадали, образуя одну прямую.
Меряем угол, причем от 0, а не от 180. – заметьте у нас 2 шкалы, внутри и снаружи дуги транспортира. Записываем: угол, например, В равен … градусов. У меня получилось 80 0 . Какие углы получились у вас?
И так же работам с остальными углами.
Нашли все углы?
Теперь, посмотрим, какая у нас тема?
Значит, что будем делать с нашими углами треугольника?
Верно. Складываем ваши полученные углы, поднимаем руки и называем, сколько получилось.
Молодцы! Теперь возьмите, пожалуйста, треугольники из бумаги на ваших рабочих столах (слайд 6). И я возьму треугольник (прикреплен на доске магнитом). Посмотрите на него и подумайте, как перегибанием углов этого треугольника найдите сумму его углов.
Не все, наверное, сразу догадались – нам нужно сложить все углы. Как это сделать?
Верно! Показываю еще раз на большом треугольнике на доске.
Скажите, а чему равна сумма всех углов, глядя на наш согнутый треугольник?
Уже два раза меряли треугольники и все равно 180 получается?
(Если нет, даю дополнительный треугольник).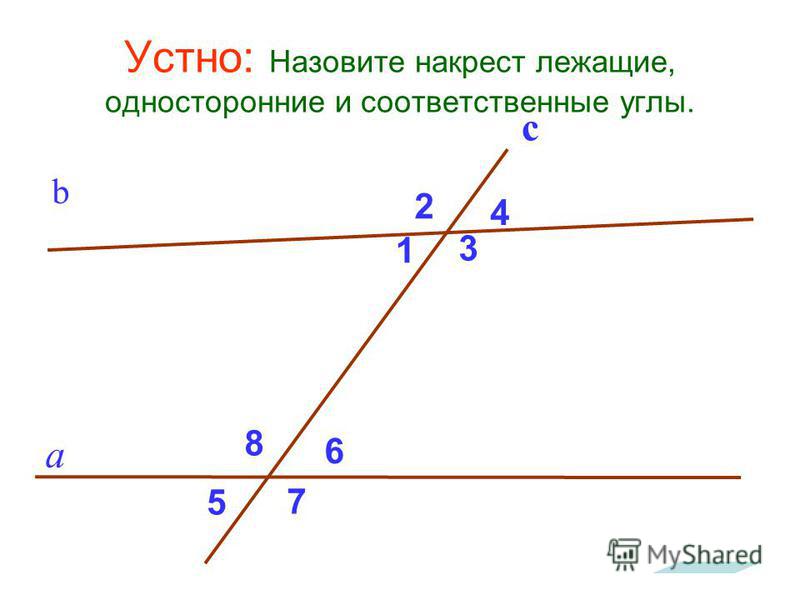 Проверьте, складывается ли треугольник из этих частей?
Проверьте, складывается ли треугольник из этих частей?
Точно у всех получился?
Хорошо. Теперь нам снова нужно показать, что сумма углов в треугольнике чему равна?
(слайд 8)
Отлично! Что будем делать с углами?
Что получилось у нас?
Молодцы, ребята. Теперь запишите в конспектах. Теорема «О сумме углов треугольника». Как вы думаете, о чем она нам говорит?
Верно! Записываем (слайд 9).
Историческая справка (слайд 10).
Теперь мы с вами докажем эту теорему. Это доказательство вам нужно записать, разобрать если что-то будет не понятно. Если сложно, приходите на доп.занятия – сегодня 6-7 уроками.
Записываем: доказательство (слайд 11)
Что нам дано и что нужно доказать?
Записываем дано и чертим небольшой произвольный треугольник в тетради.
Давайте докажем эту теорему , используя известные нам с вами свойства углов при параллельных прямых и секущей. Для этого построим через вершину В прямую а параллельную основанию – стороне АС.
И обозначим полученные углы: те, что даны в треугольнике, и еще два угла.
Записываем:
Построим a || AC, B Î a.
Сколько при параллельных прямых получилось секущих? Назовите их.
Давайте сначала рассмотрим одну секущую.
Что можно сказать об углах при наших парал.прямых и секущей АВ.
Записываем это.
Теперь рассмотри другую секущую ВС. Что здесь можно сказать об углах при парал.прямых a || AC и секущей ВС?
Верно. Записываем.
Теперь давайте посмотрим на развернутый угол В. Чему равен этот угол.
Верно. А чему еще он равен? Сумме каких углов?
Верно, это очень хорошо видно на рисунке.
Теперь глядя на записанную сумму и на ранее доказанные равенства углов что можно сказать об угле В?
Т.е. что получили?
Доказали теорему?
Физминутка (слайд 12).
На слайде буквы записаны разными цветами, что способствует расслаблению мышц глаза.
№ 20 (слайд 14) – решаем устно. Тетради с конспектами не закрываем.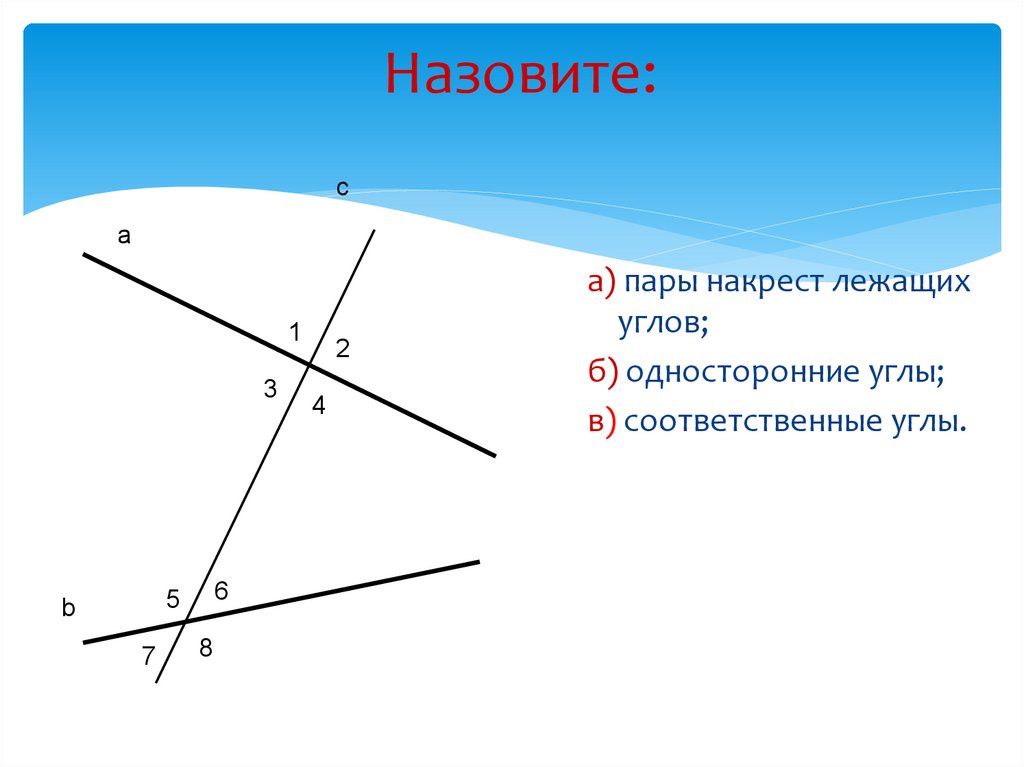
Могут ли быть два угла треугольника прямыми?
А два угла тупыми?
Один прямым, а другой тупым?
Какой вывод можно сделать тогда? Какие углы могут быть в треугольнике?
Т.е. острых углов в любом треугольнике должно быть как минимум …. ?
Запишите это у себя в конспектах – это следствие из теоремы о сумме углов треугольника (слайд 15)
Следствие из теоремы:
У любого треугольника хотя бы два угла острые.
Устная работа с задачами (слайды 16-18)
Ребята. Выходим к доске решаем номера, указанные на слайде (слайд 19): № 18, № 19 (1), № 22 (1,3),№ 21, №25.
На доске начерчен треугольник – по нему решаем задачу 18, 19.
21 устно.
22 – на доске рисунок с р/б треугольником, по нему решаем задачу.
№ 25 у доски с тем же чертежом.
(20 слайд)
(21 слайд)
Ребята, вспомним, что мы сегодня узнали.
Чему равна сумма углов любого треугольника?
Скажите, сколько острых углов должно быть как минимум в любом треугольнике?
А могут быть 2 тупых?
Молодцы!
встретимся на следующем уроке после звонка.
Открывают дневники и записывают домашнее задание.
Открывают конспекты, пишут.
Любой.
Например, 30 0 , 120 0 , 50 0 , 90 0 ….
Да.
Сумма углов треугольника.
Сложим. И найдем, чему равна сумма.
Считают, говорят ответы. Должно у всех быть 180.
Рассматривают треугольники, пробуют складывать, приходят к решению.
Просто согнуть треугольник так чтобы все углы вместе сложились.
Развернутому углу – 180 градусов.
Да.
Да.
Да, складывается.
Точно.
180.
Складывать их, вместе, чтобы показать их сумму.
Снова развернутый угол-180.
Что сумма всех углов треугольника равна 180.
Записывают теорему.
Слушают, задают вопросы.
Дан, треугольник, произвольный. А доказать нужно, что сумма его углов равна 180 0 .
Записывают дано и чертят рисунок:
Дано:
ABC
Доказать:
ÐА+ÐВ+ÐС=180°
Строят за учителем (учитель листает анимацию на слайде).
Две? АВ и ВС.
Ð 4= Ð 1 , как накрест лежащие углы при парал.прямых a || AC и секущей АВ.
Ð 5= Ð 2, как накрест лежащие углы при парал.прямых a || AC и секущей ВС.
180, т.к. он развернутый.
Ð4 + Ð3+ Ð5 = 180°, т.к. ÐВ – развернутый (ÐВ = 180°)
Т.к. Ð4=Ð1 и Ð5=Ð2, ТО
Ð4 + Ð3+ Ð5 = Ð1 + Ð3+ Ð2 = 180.
Что сумма углов треугольника равна 180.
Доказали.
Повторяют упражнения (физминутка) за учителем.
Нет.
Нет.
Нет.
Два острых и один тупой, один прямой и два острых, все три острые.
Два!
Записывают под диктовку или со слайда.
Отгадывают ребусы.
Теорему о сумме углов в треугольнике. И следствие из нее.
180 градусов.
Как минимум два острых угла.
Нет.
Продолжение темы
Закрепление изученного материала
Сам. работа
работа
Подве-дение итогов
Итак, сколько всего углов в треугольнике?
Тогда раз два угла всегда острые, то третий может быть … каким?
Тогда вид треугольника мы с вами будем определять по третьему углу.
Посмотрите на слайд (слайд 22). Назовите угол и определите вид треугольника.
Если два угла треугольника острые, а третий тоже острый, то треугольник …
Если два угла треугольника острые, а третий тоже прямой, то треугольник …
Если два угла треугольника острые, а третий тоже тупой, то треугольник …
Молодцы!
Исторический момент (слайд 23)
Теперь решаем устные задачи.
(слайд 24)
Определите вид треугольника, если:
один из его углов равен 40 0 , а другой – 100 0 ,
один из его углов равен 60 0 , а другой – 70 0 ,
один из его углов равен 40 0 , а другой – 50 0 .
(Слайд 25-26)
Теперь решаем задачи у доски и в тетрадях (слайд 27)
Теперь пишем самостоятельную работу по вариантам, три задания.
Ребята, скажите, что мы сегодня узнали и вспомнили?
Молодцы!
Оценки за урок получают …
любым.
Остроугольный.
Прямоугольный.
Тупоугольный.
Тупоугольный, т.к. есть тупой угол.
Остроугольный, т.к. все углы острые.
Прямоугольный, т.к. 180 – 40 -50 = 90.
По теореме о сумме углов D:
ÐВ = 180
0
– (ÐС + ÐВ) =
= 180
0
– (90
0
+ 50
0
) = Ð40 0
Т.к. D АВС равнобедренный, то ÐА = ÐВ, по свойству р/б D.
По теореме о сумме углов D:
ÐА = (180
0
– ÐС) : 2 =
= (180
0
– 90
0
) : 2 = Ð45 0
Решают задачи с помощью учителя.
Пишут самостоятельную работу в карточках.
— сумма углов любого треугольника равна 180.
Виды треугольников — остроугольные, тупоугольные, прямоугольные.
Узнали что самыми древними инструментами в геометрии были линейка и циркуль.
Задание 2 .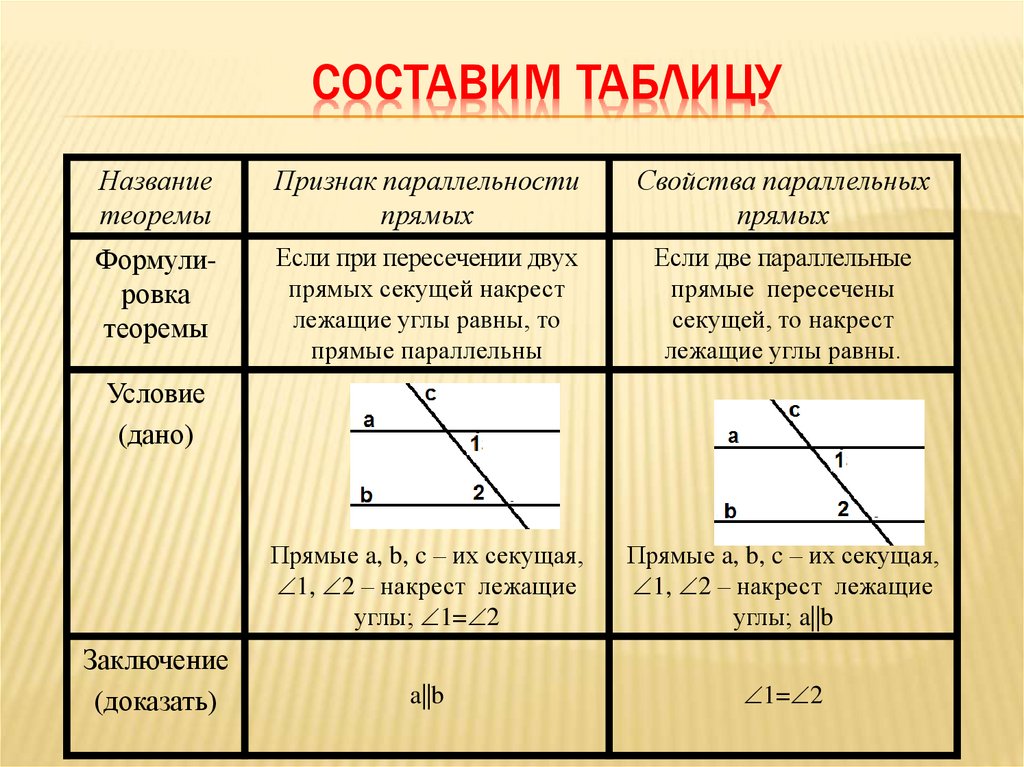
Дано:
Найти:
Ð1 и Ð 2 Решение:
Задание 3.
Дано:
Найти:
Ð1 и Ð 2 Решение:
Цели урока: 1. Закрепить и проверить знания учащихся по теме: «Свойство углов образованных при пересечении двух параллельных прямых третьей и признаки параллельности прямых». 2. Открыть и доказать свойство углов треугольника. 3. Применить свойство при решении простейших задач. 4. Использовать исторический материал для развития познавательной активности учащихся. 5. Прививать навык аккуратности при построении чертежей.
П л а н у р о к а: 1. Самостоятельная работа. 2. Практическая работа. (Подготовка к изучения нового материала). 3. Доказательство теоремы о сумме углов треугольника. (несколько способов). 4. Решение задач.(При решении используется теорема). Л и т е р а т у р а: Газеты «Математика». «Путешествие в историю математики, или как люди учились считать». Авт. Александр Свечников «Педагогика» -пресс. «Физика и астрономия» — учебник физики 7 класс авт. Пинский. Советский энциклопедический словарь М.1989 г. «История математики в школе» IV-VI классы М. «Просвещение» 1981г. авт. Г.И. Глейзер.
«Физика и астрономия» — учебник физики 7 класс авт. Пинский. Советский энциклопедический словарь М.1989 г. «История математики в школе» IV-VI классы М. «Просвещение» 1981г. авт. Г.И. Глейзер.
5) Найдите углы АВС, Найти
Историческая справка. 1.Определение параллельных прямых — Евклид (III век до н.э.), в трудах «Начала» «Параллельные суть прямые, которые находясь в одной плоскости и будучи продолжены в обе стороны неограниченно ни с той, ни с другой стороны между собой не встречаются». 2.Посидоний (I век до н.э.) «Две прямые, лежащие в одной плоскости, равноотстоящие друг от друга» 3.Древнегреческий учёный Папп (вторая половина III века до н.э.) ввёл символ параллельности прямых =. Впоследствии английский экономист Рикардо () этот символ использовал как знак равенства. Только в 18 веке стали использовать символ ||.
Открытие свойств углов треугольника. Древние греки на основе наблюдений и из практического опыта делали выводы, высказывали свои предположения – гипотезы (Hypotesis – основание, предположение) а затем на встречах учёных – симпозиумах (symposium- буквально пиршество, совещание по какому-либо научному вопросу) эти гипотезы пытались обосновать и доказать. В то время сложилось утверждение: «В споре рождается истина»
В то время сложилось утверждение: «В споре рождается истина»
Гипотеза о сумме углов треугольника. Практическая работа. Используя транспортир определите, чему равна сумма углов треугольника. (Используйте модели всех видов треугольников). Определите, какой угол получится, если его составить из углов треугольника. Чему равна его градусная мера? (Используйте модели всех видов треугольников).
Цели: 1. Ввести понятия остроугольного, прямоугольного и тупоугольного треугольников. 2. С помощью эксперимента подвести детей к формулировке теоремы о сумме углов треугольника, доказать ее и научить применять полученные знания в решении задач. 3. Развитие познавательной деятельности, мышления, внимания. 4. Воспитание трудолюбия
ЗАДАЧИ: 1. Закрепить знания по темам: треугольник, параллельные прямые, виды углов; 2. Закрепить навыки использования транспортира; 3. Развивать умение пользоваться учебником; 4. Развивать математическую речь учащихся; 5. Формировать умение анализировать материал и делать выводы; 6.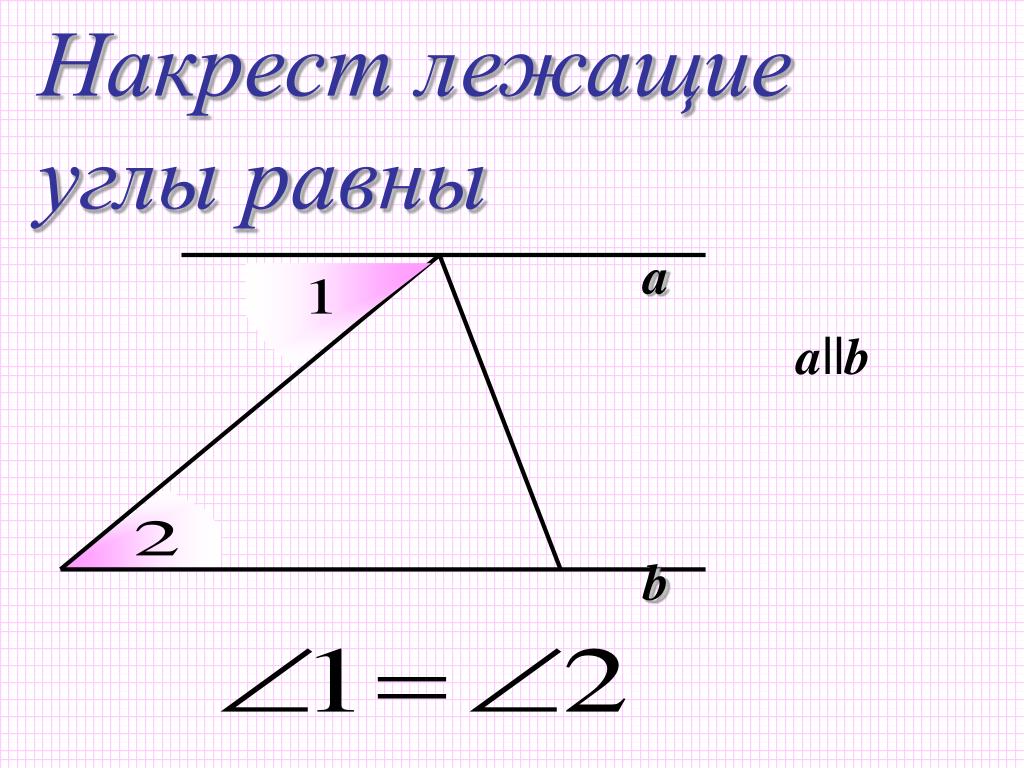 Воспитывать: интерес к предмету, умение доводить дело до конца, уверенность в своих способностях в учебе.
Воспитывать: интерес к предмету, умение доводить дело до конца, уверенность в своих способностях в учебе.
План урока: 1. Организационный момент. 2. Повторение. 3. Устная работа. 4. Постановка проблемы, определение путей ее решения. 5. Выдвижение гипотезы. 6. Подтверждения гипотезы. 7. Доказательство теоремы. 8. Решение заданий на закрепление изученной теоремы. 9. Подведение итогов урока (рефлексия), задание на дом.
Ход урока: 1.Оргмомент Сегодня наш класс превратится в «научно-исследовательский институт», а вы станете «его сотрудниками». И мы не только познакомимся с работой «научно-исследовательского института», но и сами будем делать открытия! И так: «научно – исследовательский институт» имеет подразделения: 1. Лаборатория экспериментов. 2.Лаборатория научных доказательств. 3.Лаборатория испытаний.
2.Повторение На предыдущих уроках мы с вами изучали признаки параллельности прямых и свойства углов при параллельных прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие. Дайте определение параллельных прямых (Две прямые на плоскости называется параллельными, если они не пересекаются)
Дайте определение параллельных прямых (Две прямые на плоскости называется параллельными, если они не пересекаются)
Сформулируйте признаки параллельности прямых (Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны; Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны; Если при пересечении двух прямых секущей сумма односторонних углов равна 180°,то прямые параллельны;)
Сформулируйте свойство углов при параллельных прямых (Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны; Если две параллельные прямые пересечены секущей, то соответственные углы равны; Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°)
1) Сформулируйте определение треугольника. (ТРЕУГОЛЬНИК – это фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.) 2) Назовите элементы треугольника. (Вершины, стороны, углы.) 3) Какие треугольники различают? (По сторонам: разносторонние, равносторонние, равнобедренные; карточки – треугольники) 4) Треугольники различают и по углам.
(Вершины, стороны, углы.) 3) Какие треугольники различают? (По сторонам: разносторонние, равносторонние, равнобедренные; карточки – треугольники) 4) Треугольники различают и по углам.
Давайте с вами составим рассказ по теме: УГОЛ. Для этого используем план, записанный на экране. Угол – это фигура, … (Угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи называют сторонами угла, а точку – вершиной.). 2. Если …, то угол называют … (Если величина угла 90°, то угол называют прямым. Если – 180°, то развернутым. Если больше0°, но меньше 90°, то называют острым. Если больше 90°, но меньше 180°, то называют тупым.)
Т. о. углы бывают тупые, острые, прямые и развернутые. Внутренний угол треугольника – это … Внутренний угол треугольника – угол, образованный его сторонами, вершина треугольника является вершиной его угла. Значит, в треугольнике углы могут быть различными: тупыми, острыми и прямыми.
Лаборатория экспериментов Начертите угол: (3 ученика работают у доски, а остальные- на месте) 1 – ряд – тупой; 2 – ряд – прямой; 3 – ряд острый. Дополните рисунок до треугольника. Что для этого нужно сделать? (Взять по точке на сторонах угла и соединить их отрезками.) Полученные треугольники можно назвать: тупоугольными, прямоугольными и остроугольными. ((карточки – треугольники) Обратите внимание, что у остроугольного треугольника все углы острые.
Дополните рисунок до треугольника. Что для этого нужно сделать? (Взять по точке на сторонах угла и соединить их отрезками.) Полученные треугольники можно назвать: тупоугольными, прямоугольными и остроугольными. ((карточки – треугольники) Обратите внимание, что у остроугольного треугольника все углы острые.
Бывают ли треугольники с прямым и тупым углом? С двумя тупыми углами? С двумя прямыми углами? Как это обосновать? Сделать рисунок: Лучи ВА и СД, КТ и ОН. КЕ и PL не пересекаются, значит, треугольник не получится. Сумма односторонних углов в I случае больше, чем 180°, во II случае также больше, чем 180°, а в III случае равна 180°. В III случае прямые параллельны, а в первых двух случаях прямые расходятся. Делают вывод, что треугольник не может иметь два тупых или два прямых угла. А также в треугольнике не может быть одновременно один тупой и один прямой углы.
Мы выполнили некоторую практическую работу, сделали обоснование того факта, что треугольник не всегда существует. Его существование зависит от величин углов. Как можно узнать, чему равна сумма углов треугольника? Практически измерением, теоретически рассуждением.
Его существование зависит от величин углов. Как можно узнать, чему равна сумма углов треугольника? Практически измерением, теоретически рассуждением.
Лаборатория испытаний (практическое применение) 1. Чему равен третий угол в треугольнике, если один из углов 40°, второй 60°? (80°) 2. Чему равен угол равностороннего треугольника? (60°) 3. Чему равна сумма острых углов прямоугольного треугольника? (90°) 4. Чему равен острый угол прямоугольного равнобедренного треугольника? (45°)
Углы внутренние
Многоуго́льник — это геометрическая фигура, определяется как замкнутая ломаная. Существуют три различных варианта определения:
- Плоские замкнутые ломаные,
- Плоские замкнутые ломаные без самопересечений,
- Части плоскости, ограниченные ломаными.
Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Wikimedia Foundation . 2010 .
Смотреть что такое «Внутренний угол» в других словарях:
Внутренний угол а — 3. 6 Внутренний угол а Угол между верхней поверхностью клыка и передней поверхностью спинки Источник: ГОСТ 30013 93: Машины напольного транспорта. Плиты грузовые, вилы. Технические условия … Словарь-справочник терминов нормативно-технической документации
6 Внутренний угол а Угол между верхней поверхностью клыка и передней поверхностью спинки Источник: ГОСТ 30013 93: Машины напольного транспорта. Плиты грузовые, вилы. Технические условия … Словарь-справочник терминов нормативно-технической документации
внутренний угол (синхронной машины) — угол выбега ротора — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы угол выбега ротора EN torque… … Справочник технического переводчика
УГОЛ — муж. перелом, излом, колено, локоть, выступ или залом (впадина) об одной грани. Угол линейный, всякие две встречные черты и промежуток их, угол плоскостной или в плоскостях, встреча двух плоскостей или стен, угол толстый, теловой, встреча в одной … Толковый словарь Даля
угол потока в абсолютном движении — Внутренний угол в треугольнике скоростей между векторами абсолютной скорости воздуха (газа) и окружной скорости лопаток. Примечание Для турбины в сечении на выходе из рабочего колеса за угол потока в абсолютном движении принимается дополнительный … Справочник технического переводчика
Примечание Для турбины в сечении на выходе из рабочего колеса за угол потока в абсолютном движении принимается дополнительный … Справочник технического переводчика
угол потока в относительном движении — Внутренний угол в треугольнике скоростей между векторами относительной скорости воздуха (газа) и окружной скорости лопатки. Примечание Для турбины ГТД в сечении на входе в рабочее колесо за угол потока в относительном движении принимается… … Справочник технического переводчика
Угол (Angle) — 1. В анатомии например, угол глаза (angle of the eye) внешний или внутренний угол глаза, угол рта (angle of the mouth) места соединения верхней и нижней губы. 2. Степень расходимости двух пересекающихся линий или плоскостей, пространство между… … Медицинские термины
УГОЛ — (angle) 1. В анатомии например, угол глаза (angle of the eye) внешний или внутренний угол глаза, угол рта (angle of the mouth) места соединения верхней и нижней губы. 2. Степень расходимости двух пересекающихся линий или плоскостей, пространство… … Толковый словарь по медицине
2. Степень расходимости двух пересекающихся линий или плоскостей, пространство… … Толковый словарь по медицине
угол наклона линии зуба конического зубчатого колеса — (β) угол наклона линии зуба Ндп. угол спирали Острый угол между пересекающимися в данной точке линией зуба и образующей однотипного соосного конуса, которому принадлежит эта линия зуба. Примечания 1. Различают внешний (βe), средний… … Справочник технического переводчика
угол наклона средней линии зуба (впадины) — (βn) Острый угол между пересекающимися в данной точке средней линией зуба и образующей однотипного соосного конуса, которому принадлежит эта средняя линия зуба (впадины). Примечания 1. Различают внешний (βne), средний (βnm),… … Справочник технического переводчика
Источник: dikc.academic.ru
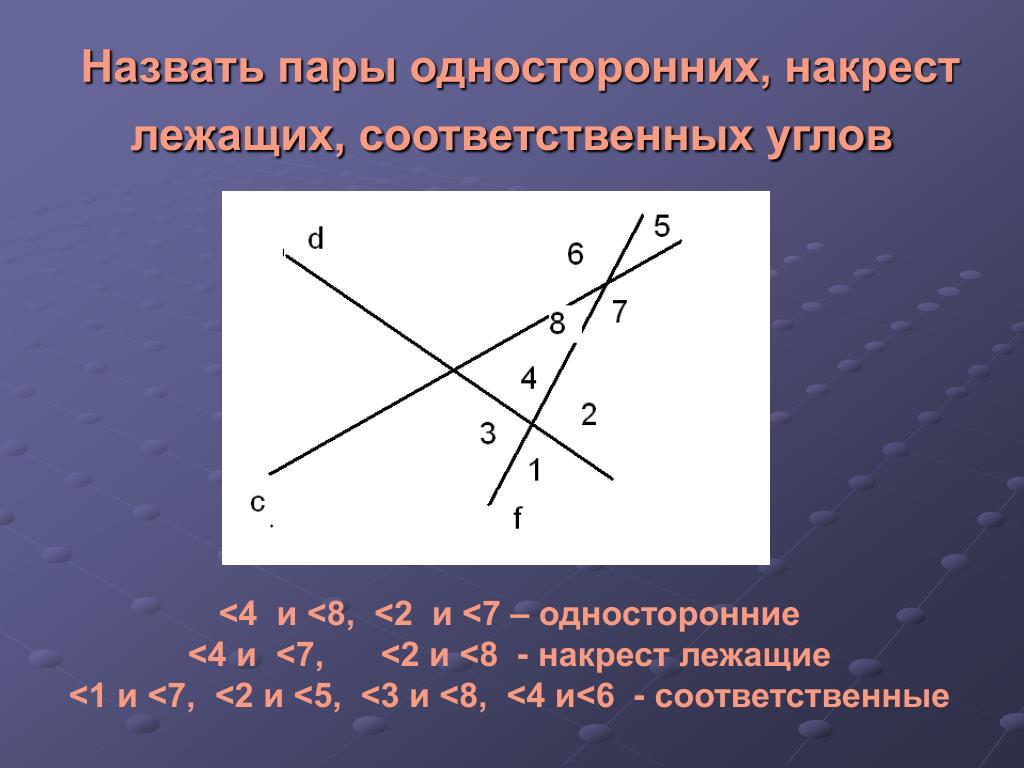
Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7,
внутренние накрест лежащие углы: 3 и 5, 4 и 6,
внешние накрест лежащие углы: 1 и 7, 2 и 8,
внутренние односторонние углы: 3 и 6, 4 и 5,
внешние односторонние углы: 1 и 8, 2 и 7.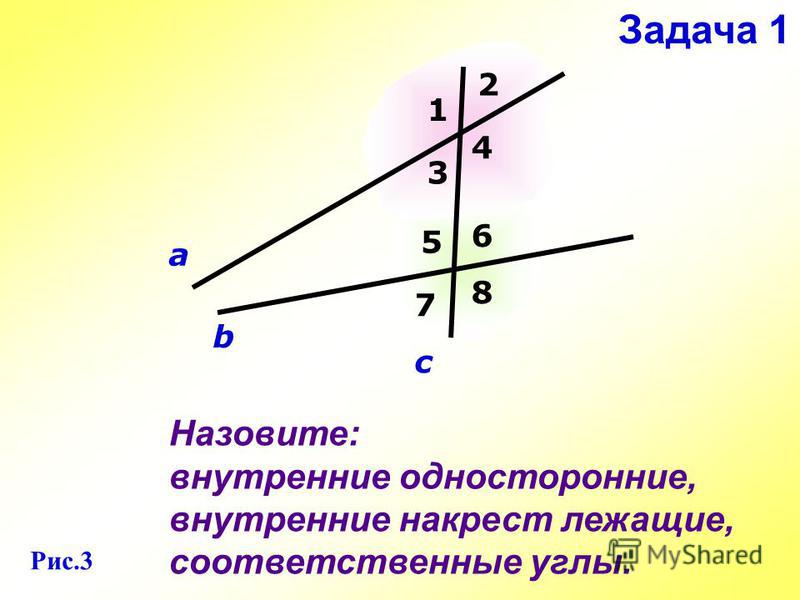
Описанные углы видны на рисунке:
Теорема.
Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:
1. внутренние накрест лежащие углы одинаковы,
2. внешние накрест лежащие углы одинаковы,
3. соответственные углы одинаковы,
4. сумма внутренних односторонних углов будет 2d = 180 0 ,
5. сумма внешних односторонних углов будет 2d = 180 0 ,
Данную теорему иллюстрирует рисунок:
Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.
1. ∠ 4 = ∠ 6 и ∠ 3 = ∠ 5,
2. ∠ 2 = ∠ 8 и ∠ 1 = ∠ 7,
3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8,
4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d,
5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.
1. Из середины E того отрезка прямой MN, который размещается между параллельными прямыми, прочертим на СD перпендикуляр EK и продолжим его до пересечения с AB в точке L. Так как перпендикуляр к одной из параллельных есть также и перпендикуляр к другой параллельной, то образовавшиеся при этом треугольники (заштрихованные на чертеже) — оба прямоугольные. Они одинаковы, потому что в них по равной гипотенузе и по одинаковому острому углу при точке E. Из равенства треугольников получаем, что внутренние накрест лежащие углы 4 и 6 одинаковы. Два прочих внутренних накрест лежащих угла 3 и 5 одинаковы, как дополнения до 2d к одинаковым углам 4 и 6 (как смежные с 4 и 6).
Так как перпендикуляр к одной из параллельных есть также и перпендикуляр к другой параллельной, то образовавшиеся при этом треугольники (заштрихованные на чертеже) — оба прямоугольные. Они одинаковы, потому что в них по равной гипотенузе и по одинаковому острому углу при точке E. Из равенства треугольников получаем, что внутренние накрест лежащие углы 4 и 6 одинаковы. Два прочих внутренних накрест лежащих угла 3 и 5 одинаковы, как дополнения до 2d к одинаковым углам 4 и 6 (как смежные с 4 и 6).
2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.
Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.
Следовательно, ∠ 2 =∠ 8.
3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.
5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.
Из выше доказанного обоснования получаем обратные теоремы.
Когда при пересечении двух прямых произвольной третьей прямой получим, что:
1. Внутренние накрест лежащие углы одинаковы,
или 2. Внешние накрест лежащие углы одинаковые,
или 3. Соответственные углы одинаковые,
или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ,
или 5. Сумма внешних односторонних равна 2d = 180 0 ,
Источник: www. calc.ru
calc.ru
Основное свойство откладывания углов.
Угол — это геометрическая фигура, состоящая из двух различныхлучей, выходящих из однойточки.
Лучи называются сторонами угла, а их общее начало — вершиной угла.
Развернутый угол — этоугол, стороны которого лежат на одной прямой.Градусная мера развёрнутого угла равна 180º.Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами. Угол разделяет плоскость на две части, каждая из которых также называется углом, то может возникнуть неоднозначность в том, какой именно из углов рассматривается. Чтобы наглядно показать, о каком именно угле идёт речь, на чертеже обычно делается какое-нибудь специальное обозначение.
Тот из углов, который рассматривается, на чертеже обычно отмечают дугой, проведённой от одной стороны угла до другой:
От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.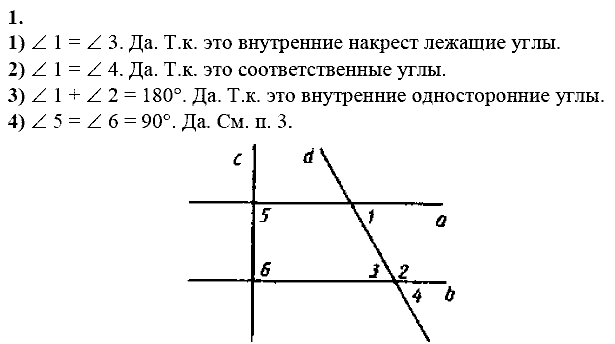
Теорема о существовании и единственности перпендикуляра к прямой.
Теорема.
Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Доказательство
Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a. Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.
Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.
3. Задача по теме «Сумма углов треугольника «.
Углы треугольника DKC относятся как 2:4:3.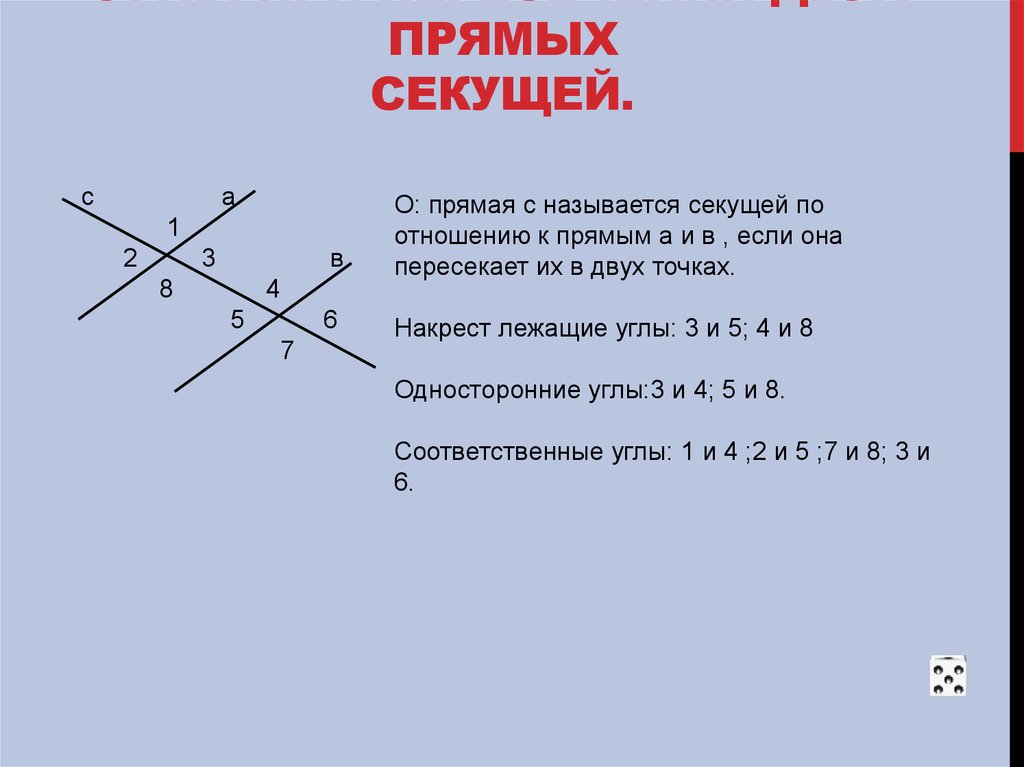 Найдите углы треугольника DKC.
Найдите углы треугольника DKC.
Дата добавления: 2018-05-12 , просмотров: 411 , ЗАКАЗАТЬ РАБОТУ
Источник: studopedia.net
Кривые углы – распространенное явление, которое встречается не только в старых квартирах, но и новостройках. Если небольшие неровности стен можно замаскировать с помощью обоев или декоративных элементов, то дефекты углов после отделки обоями или плиткой будут еще более заметны. Выравнивание внешних и внутренних углов может стать частью процесса чистовой отделки стен финишной штукатуркой и шпаклевкой, а может выполняться отдельно, если состояние поверхности стен не требует серьезного вмешательства. Выясним, как выровнять углы стен разными методами.
Внутренние углы
Выбор одного из трех способов выравнивания в данном случае зависит от того, производится ли оно вместе с оштукатуриванием стен или самостоятельно.
Выравнивание по маякам
Этот метод используется только в процессе работы со всей поверхностью стен.
Необходимые материалы
- маяки – металлические или деревянные рейки,
- шурупы или дюбеля,
- правило,
- отвес,
- гипсовая штукатурка,
- шпатели – прямой и угловой.

Последовательность работ
- Закрепите маяки на поверхности стен с помощью элементов крепежа на расстоянии, равном длине правила. Отступ от угла – 5–7 см.
- С помощью отвеса определите отклонения от вертикали, сделайте отметки на полу и потолке, по мере надобности подложите клинья в нужных местах.
- Наносить штукатурку начинайте с одной стороны. Заполните пространство между маяками, распределите раствор правилом. После высыхания слоя переходите на вторую стену.
Важно! Следите за тем, чтобы на стыке не собиралось большое количество смеси. Для устранения излишков после высыхания состава воспользуйтесь шпателем.
- Для формирования ровного стыка используйте угловой шпатель, смоченный водой.
- После высыхания штукатурки уберите маяки и заделайте пустоты тем же составом.
Использование контрашульца
Наилучшим решением при выравнивании углов будет использование контрашульца – перфорированного уголка из алюминия.
Необходимые материалы
- контрашульц,
- ножницы для резки металла,
- длинное правило,
- наждачная бумага,
- шпаклевочная смесь.
Последовательность работ
- Отмерьте необходимый отрезок алюминиевого уголка и аккуратно отрежьте специальными ножницами, стараясь не погнуть податливый металл.
- Нанесите небольшое количество гипсовой штукатурки на стык стен и приложите контрашульц, слегка вдавив его правилом. Излишки раствора удалите шпателем, двигаясь по направлению от стыка разлаживающими движениями.
- После высыхания шпаклевки пройдитесь по поверхности шкуркой. При наличии небольших неровностей нанесите еще один тонкий слой шпаклевки.
Метод с применением серпянки
Как выровнять угол стены в том случае, если не планируется проведение масштабных работ по оштукатуриванию и шпаклеванию всей поверхности стен? В этой ситуации выручит широкая лента-серпянка.
Необходимые материалы
- армирующая лента-серпянка,
- деревянный прямоугольный брусок длиной 50-60 см,
- гипсовая шпаклевка.

Последовательность работ
- Небольшое количество раствора нанесите на стык стен и на прилегающую к углу поверхность. Ширина полосы нанесенной шпаклевки составит 10 см с каждой стороны.
- Приложите армирующую ленту к верхней части угла и аккуратно раскручивайте рулон, чтобы серпянка не сдвинулась в сторону.
- Прижимая брусок к стыку, придайте углу правильную форму. Если в процессе лента сминается, выровняйте ее шпателем, излишки шпаклевки убирайте, двигаясь по направлению от стыка.
Важно! Движения шпателя должны быть осторожными, не нарушающими положения ленты. В то же время дожидаться подсыхания смеси нельзя, поскольку это лишит вас возможности скорректировать положение серпянки.
Выравнивание внешних углов
Для внешних углов существует два способа выравнивания: с контрашульцем и без него.
Метод выравнивания без контрашульца
Для выравнивания внешнего стыка стен этим способом вам понадобятся:
- гипсовая штукатурка,
- шпатели,
- правило,
- идеально ровная доска или планка, обернутая скотчем,
- мелкозернистая наждачная бумага.

Последовательность работ
- Сбейте крупные выступы, заполните штукатуркой большие щели.
- На поверхности стены в месте прилегания к стыку расположите планку. Сделайте это таким образом, чтобы она выступала из-за угла на расстояние, равное толщине требуемого штукатурного слоя. Закрепите ее на полу и потолке, при правильно подобранной длине ее можно вставить как распорку.
- Нанесите смесь, распределите правилом движениями к стыку с небольшим наклоном вниз. При необходимости повторите процедуру после подсыхания слоя.
- Через два–три дня уберите планку и приложите ее к выступу с другой, уже оштукатуренной, стороны и повторите вышеперечисленные действия.
- После высыхания обработайте поверхность шкуркой.
Формирование внешнего угла с помощью контрашульца
Использование профиля не только упростит процесс выравнивания, но и надежно защитит внешний угол от повреждений.
Необходимые материалы
- контрашульц,
- гипсовая смесь,
- правило,
- шпатель,
- уровень,
- наждачка с мелким зерном.

Последовательность работ
- На прилегающие к стыку стен поверхности нанесите подготовленный раствор.
- Отрезанный в соответствии с нужной длиной контрашульц закрепите на стыке, используя правило для предотвращения деформирования алюминиевого уголка.
- Уберите шпателем излишки смеси, проверьте уровнем правильность крепления уголка, при необходимости скорректируйте его положение.
- После высыхания отшлифуйте поверхность с помощью мелкозернистой наждачной бумаги.
- Окончательное выравнивание производится вместе с нанесением шпаклевки на остальную поверхность стен.
Выравнивание углов штукатуркой или шпаклевкой – более привычный для многих способ, но при этом достаточно «грязный» и трудоемкий. Прибегать к этому методу стоит в том случае, если кривизна минимальна. В случае существенных искривлений стен и углов более целесообразным будет использование гипсокартонных листов.
Источник: mr-build.ru
Читайте также Тротуарная плитка пеньки Поделитесь статьей в соц. сетях:
сетях:
накрест лежащие углы равны
Цели урока: 1. Закрепить и проверить знания учащихся по теме: «Свойство углов образованных при пересечении двух параллельных прямых третьей и признаки параллельности прямых». 2. Открыть и доказать свойство углов треугольника. 3. Применить свойство при решении простейших задач. 4. Использовать исторический материал для развития познавательной активности учащихся. 5. Прививать навык аккуратности при построении чертежей.
П л а н у р о к а: 1. Самостоятельная работа. 2. Практическая работа. (Подготовка к изучения нового материала). 3. Доказательство теоремы о сумме углов треугольника. (несколько способов). 4. Решение задач.(При решении используется теорема). Л и т е р а т у р а: Газеты «Математика». «Путешествие в историю математики, или как люди учились считать». Авт. Александр Свечников «Педагогика» -пресс. «Физика и астрономия» — учебник физики 7 класс авт. Пинский. Советский энциклопедический словарь М.1989 г. «История математики в школе» IV-VI классы М. «Просвещение» 1981г. авт. Г.И. Глейзер.
«Просвещение» 1981г. авт. Г.И. Глейзер.
5) Найдите углы АВС, Найти
Историческая справка. 1.Определение параллельных прямых — Евклид (III век до н.э.), в трудах «Начала» «Параллельные суть прямые, которые находясь в одной плоскости и будучи продолжены в обе стороны неограниченно ни с той, ни с другой стороны между собой не встречаются». 2.Посидоний (I век до н.э.) «Две прямые, лежащие в одной плоскости, равноотстоящие друг от друга» 3.Древнегреческий учёный Папп (вторая половина III века до н.э.) ввёл символ параллельности прямых =. Впоследствии английский экономист Рикардо () этот символ использовал как знак равенства. Только в 18 веке стали использовать символ ||.
Открытие свойств углов треугольника. Древние греки на основе наблюдений и из практического опыта делали выводы, высказывали свои предположения – гипотезы (Hypotesis – основание, предположение) а затем на встречах учёных – симпозиумах (symposium- буквально пиршество, совещание по какому-либо научному вопросу) эти гипотезы пытались обосновать и доказать. В то время сложилось утверждение: «В споре рождается истина»
В то время сложилось утверждение: «В споре рождается истина»
Гипотеза о сумме углов треугольника. Практическая работа. Используя транспортир определите, чему равна сумма углов треугольника. (Используйте модели всех видов треугольников). Определите, какой угол получится, если его составить из углов треугольника. Чему равна его градусная мера? (Используйте модели всех видов треугольников).
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Тема урока: «Сумма углов треугольника». «Величие человека – в его способности мыслить». Б.Паскаль
Цель урока: Выяснить: — Чему равна сумма углов любого треугольника.
Виды углов 1 2 3 4
Рассмотрим рисунок а b с 1 2 3 4 d 5
Лабораторная работа. Указание к работе 1. Постройте в тетради произвольный треугольник АВС. 2. Измерьте градусные меры углов треугольника. 3.Запишите в тетрадь: А =…, В =…, С=… 4. Найдите сумму углов треугольника А + В + С=… 5.Сравните полученные результаты.
Найдите сумму углов треугольника А + В + С=… 5.Сравните полученные результаты.
Практическая работа. Возьмите бумажный треугольник, лежащий у каждого на парте. Аккуратно оторвите у него два угла. Приложите эти углы к третьему таким образом, чтобы они выходили из одной вершины.
Сумма углов треугольника равна Теорема
Рассмотрим произвольный треугольник АВС В А С Дано: ∆АВС Док-ть: А + В + С= 180 0
и докажем, что А В С
и докажем, что А В С
и докажем, что А В С
и докажем, что А В С
Проведем через вершину В прямую, параллельную стороне АС А С В С
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых и АС и секущей АВ. А С В 1 4 С
А углы 3 и 5 являются накрест лежащими углами при пересечении параллельных прямых и АС и секущей ВС. А С В С 5 3
Поэтому 4 = 1, 5 = 3 А С 3 В 5 4 1 С
Очевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т.е. А С 2 С В 4 5
Отсюда, учитывая, что получаем или А 2 С 5 1 3 В 4 4 = 1 ,
Отсюда, учитывая, что получаем или А 2 С В 1 3 5 4 5 = 3 4 = 1 ,
Теорема доказана
Примерный план доказательства
Историческая справка Доказательство данного факта, изложенное в современных учебниках, содержалось ещё в комментарии к «Началам» Евклида древнегреческого учёного Прокла (V в.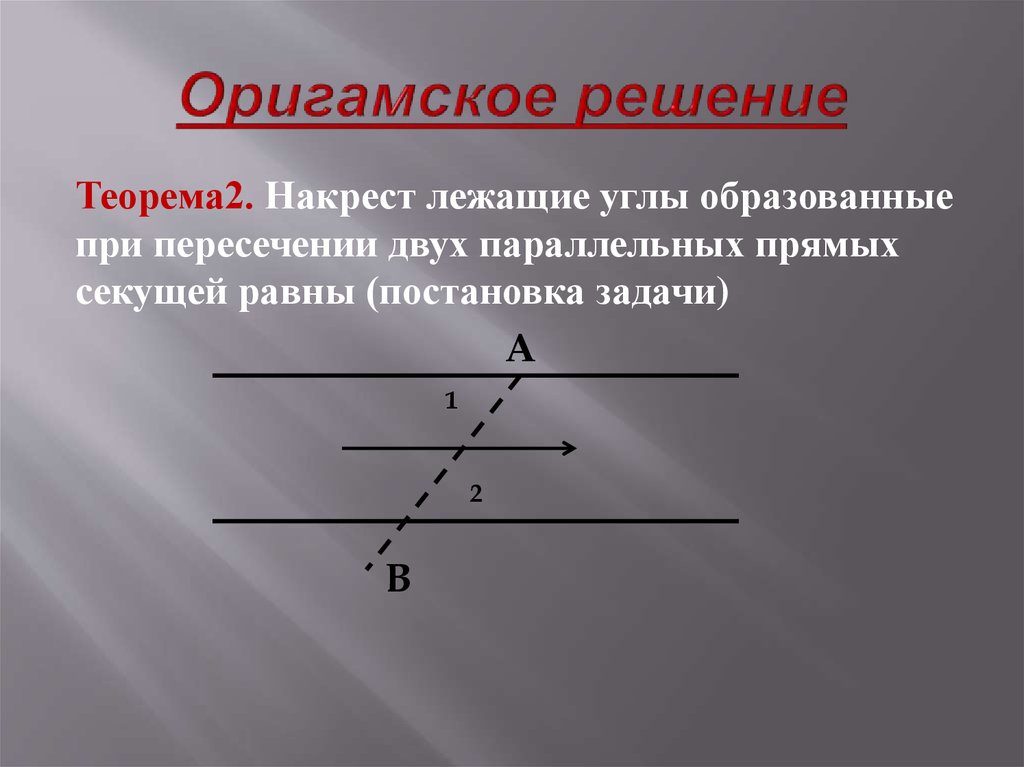 н.э.) Прокл утверждает, что согласно Евдему Родосскому, это доказательство было открыто ещё пифагорейцами (V в.до н.э.).
н.э.) Прокл утверждает, что согласно Евдему Родосскому, это доказательство было открыто ещё пифагорейцами (V в.до н.э.).
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
В А С Е 2 1 3 4 5 Попробуйте доказать дома эту теорему, используя чертеж учеников Пифагора.
Внешний угол треугольника Определение: Внешним углом треугольника называется угол, смежный с одним из углов треугольника. 4 – внешний угол Свойство. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. 4 = 1 + 2 1 2 3 4
Итак, действительно: 1 2 3 4
Устная работа: Найдите углы треугольников 80 º 70 º ? В А С А=30 º
45 º ? L К M L =45 º
80 º ? ? N P R N =50 º R =50 º
В 130 º ? ? А С В=40 º С=50 º
Существует ли треугольник с углами: а) 30˚, 60˚, 90˚ б) 46˚, 160˚, 4˚ в) 75˚, 80˚, 25˚ г) 100˚, 20˚, 55˚
Работа с учебником. Стр.71 №223 а) № 228 а)
Стр.71 №223 а) № 228 а)
Практическое применение знаний. Свойство углов прямоугольного равнобедренного треугольника знал еще один из первых творцов геометрической науки древнегреческий ученый Фалес. Используя его, он измерял высоту египетской пирамиды по длине ее тени. По легенде, Фалес выбрал день и время, когда длина его собственной тени равнялась его росту, поскольку в этот момент высота пирамиды также должна равняться длине тени, которую она отбрасывает. Конечно, длину тени можно было вычислить от средней точки квадратной основы пирамиды, но ширину основы Фалес мог измерять непосредственно. Таким образом, можно измерять высоту любого дерева.
Итог урока. Сегодня на уроке мы доказали исследовательским путем теорему о сумме углов треугольника, научились применять приобретенные знания в практической деятельности. Мы еще раз убедились, что геометрия это наука, которая возникла из потребностей человека. Ведь, как писал Галилей: “Природа разговаривает языком математики: буквы этого языка — окружности, треугольники и прочие математические фигуры».
Домашнее задание П.30, №223(б), №228(в). Другой способ доказательства теоремы о сумме углов треугольника.
Спасибо за внимание!
Класс 7
Тема урока: «Сумма углов треугольника».
Время : сдвоенный урок (пара).
Цели урока:
Образовательная: ознакомить с различными способами доказательства теоремы о сумме углов треугольника, ввести понятие внешнего угла треугольника, рассмотреть его свойство, научится применять теорему для нахождения углов треугольника в процессе решения задач.
Воспитательная: продолжить формирование навыков эстетического оформления записей в тетради и выполнения чертежей,продолжить формировать позитивное отношение к новому учебному предмету,приучать к умению общаться и выслушивать других, воспитание сознательной дисциплины.
Развивающая: выработать навык использования признаков параллельности прямых и свойства углов при параллельных прямых для решения задач и доказательств теорем;выработать умение нахождения углов треугольников при двух заданных углах, при заданных пропорциональностях углов; выработать навык использования теоремы о сумме углов треугольника и её следствие для решении задач;выработать навык нахождения углов треугольников при двух заданных углах, при заданных пропорциональностях углов, при заданных различных элементах треугольников (равные стороны, углы), умение находить углы треугольника если задан угол при биссектрисе, и находить углы при биссектрисе и основании треугольника, если заданы углы треугольника; развивать
сознательное восприятие учебного материала, зрительную память и грамотную математическую речь.
Оборудование: учебник Погорелова А.В., Геометрия 7-9 классы, (стр. 46, 52–53), интерактивная доска, презентация, раздаточный материал (целые бумажные треугольники и разрезанные картонные), большой бумажный треугольник для демонстрации на доске учителем нахождения суммы углов треугольника, карточки для самостоятельной работы
Тип урока: урок изучения нового материала и закрепления его (комбинированный урок).
Ход урока:
Этап
урока
Деятельность учителя
Деятельность учащихся
Орг.
момент
Домашнее задание
Изучение нового материала
(Практическая работа)
Изучение нового материала
Физминутка и развлекат. момент
Закрепле-ние изученного материала
Подведение итогов
Откройте дневники и запишите домашнее задание: выучить конспект 22, (п.33) Номера для домашней работы 19 (2), 22 (2), 24. (слайд 2)
Начнем урок с вами со стихотворения:
Знает даже и дошкольник,
Что такое треугольник,
А уж вам-то как не знать.
Но совсем другое дело –
Быстро, точно и умело
В нём есть стороны – их три,
И углов во всех по три,
И вершин, конечно, три.
Если длины всех сторон
Мы сложением найдём,
То к периметру придём.
Ну, а сумма всех углов
В треугольнике любом
Связана одним числом.
И мы с вами сегодня на уроке узнаем, с каким же числом связана сумма углов в любом треугольнике.
Откройте конспекты, запишите: конспект № 22. Сумма углов треугольника (слайд 3).
Начертите в тетрадях произвольный треугольник (слайд 4). Не очень маленький, примерно на треть странички. Что значит произвольный?
Верно. Чертим треугольник. Берем в руки транспортир.
И начинам по очереди измерять углы начерченного треугольника (слайд 5). Будем вместе с вами измерять углы.
Берем транспортир, прикладываем его к первому измеряемому углу так, чтобы открытая точка на транспортире совпала с вершиной угла, а сторона треугольника и внутренняя прямая часть транспортира совпадали, образуя одну прямую.
Меряем угол, причем от 0, а не от 180. – заметьте у нас 2 шкалы, внутри и снаружи дуги транспортира. Записываем: угол, например, В равен … градусов. У меня получилось 80 0 . Какие углы получились у вас?
И так же работам с остальными углами.
Нашли все углы?
Теперь, посмотрим, какая у нас тема?
Значит, что будем делать с нашими углами треугольника?
Верно. Складываем ваши полученные углы, поднимаем руки и называем, сколько получилось.
Молодцы! Теперь возьмите, пожалуйста, треугольники из бумаги на ваших рабочих столах (слайд 6). И я возьму треугольник (прикреплен на доске магнитом). Посмотрите на него и подумайте, как перегибанием углов этого треугольника найдите сумму его углов.
Не все, наверное, сразу догадались – нам нужно сложить все углы. Как это сделать?
Верно! Показываю еще раз на большом треугольнике на доске.
Скажите, а чему равна сумма всех углов, глядя на наш согнутый треугольник?
Уже два раза меряли треугольники и все равно 180 получается?
(Если нет, даю дополнительный треугольник).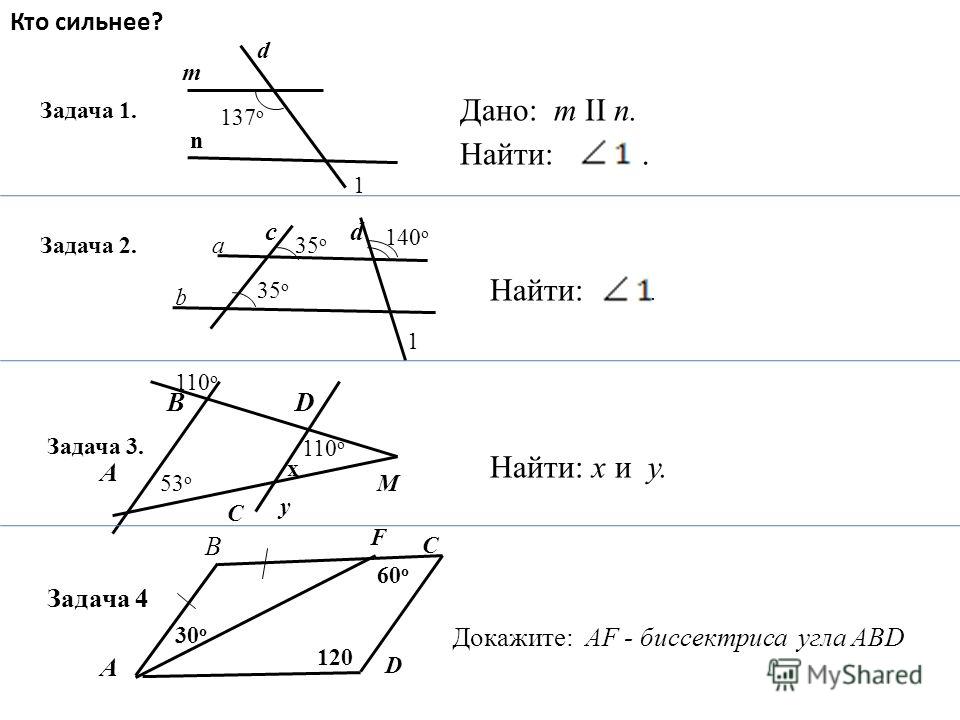 Проверьте, складывается ли треугольник из этих частей?
Проверьте, складывается ли треугольник из этих частей?
Точно у всех получился?
Хорошо. Теперь нам снова нужно показать, что сумма углов в треугольнике чему равна?
(слайд 8)
Отлично! Что будем делать с углами?
Что получилось у нас?
Молодцы, ребята. Теперь запишите в конспектах. Теорема «О сумме углов треугольника». Как вы думаете, о чем она нам говорит?
Верно! Записываем (слайд 9).
Историческая справка (слайд 10).
Теперь мы с вами докажем эту теорему. Это доказательство вам нужно записать, разобрать если что-то будет не понятно. Если сложно, приходите на доп.занятия – сегодня 6-7 уроками.
Записываем: доказательство (слайд 11)
Что нам дано и что нужно доказать?
Записываем дано и чертим небольшой произвольный треугольник в тетради.
Давайте докажем эту теорему , используя известные нам с вами свойства углов при параллельных прямых и секущей. Для этого построим через вершину В прямую а параллельную основанию – стороне АС.
И обозначим полученные углы: те, что даны в треугольнике, и еще два угла.
Записываем:
Построим a || AC, B Î a.
Сколько при параллельных прямых получилось секущих? Назовите их.
Давайте сначала рассмотрим одну секущую.
Что можно сказать об углах при наших парал.прямых и секущей АВ.
Записываем это.
Теперь рассмотри другую секущую ВС. Что здесь можно сказать об углах при парал.прямых a || AC и секущей ВС?
Верно. Записываем.
Теперь давайте посмотрим на развернутый угол В. Чему равен этот угол.
Верно. А чему еще он равен? Сумме каких углов?
Верно, это очень хорошо видно на рисунке.
Теперь глядя на записанную сумму и на ранее доказанные равенства углов что можно сказать об угле В?
Т.е. что получили?
Доказали теорему?
Физминутка (слайд 12).
На слайде буквы записаны разными цветами, что способствует расслаблению мышц глаза.
№ 20 (слайд 14) – решаем устно. Тетради с конспектами не закрываем.
Могут ли быть два угла треугольника прямыми?
А два угла тупыми?
Один прямым, а другой тупым?
Какой вывод можно сделать тогда? Какие углы могут быть в треугольнике?
Т.е. острых углов в любом треугольнике должно быть как минимум …. ?
Запишите это у себя в конспектах – это следствие из теоремы о сумме углов треугольника (слайд 15)
Следствие из теоремы:
У любого треугольника хотя бы два угла острые.
Устная работа с задачами (слайды 16-18)
Ребята. Выходим к доске решаем номера, указанные на слайде (слайд 19): № 18, № 19 (1), № 22 (1,3),№ 21, №25.
На доске начерчен треугольник – по нему решаем задачу 18, 19.
21 устно.
22 – на доске рисунок с р/б треугольником, по нему решаем задачу.
№ 25 у доски с тем же чертежом.
(20 слайд)
(21 слайд)
Ребята, вспомним, что мы сегодня узнали.
Чему равна сумма углов любого треугольника?
Скажите, сколько острых углов должно быть как минимум в любом треугольнике?
А могут быть 2 тупых?
Молодцы!
встретимся на следующем уроке после звонка.
Открывают дневники и записывают домашнее задание.
Открывают конспекты, пишут.
Любой.
Например, 30 0 , 120 0 , 50 0 , 90 0 ….
Да.
Сумма углов треугольника.
Сложим. И найдем, чему равна сумма.
Считают, говорят ответы. Должно у всех быть 180.
Рассматривают треугольники, пробуют складывать, приходят к решению.
Просто согнуть треугольник так чтобы все углы вместе сложились.
Развернутому углу – 180 градусов.
Да.
Да.
Да, складывается.
Точно.
180.
Складывать их, вместе, чтобы показать их сумму.
Снова развернутый угол-180.
Что сумма всех углов треугольника равна 180.
Записывают теорему.
Слушают, задают вопросы.
Дан, треугольник, произвольный. А доказать нужно, что сумма его углов равна 180 0 .
Записывают дано и чертят рисунок:
Дано:
ABC
Доказать:
ÐА+ÐВ+ÐС=180°
Строят за учителем (учитель листает анимацию на слайде).
Две? АВ и ВС.
Ð 4= Ð 1 , как накрест лежащие углы при парал.прямых a || AC и секущей АВ.
Ð 5= Ð 2, как накрест лежащие углы при парал.прямых a || AC и секущей ВС.
180, т.к. он развернутый.
Ð4 + Ð3+ Ð5 = 180°, т.к. ÐВ – развернутый (ÐВ = 180°)
Т.к. Ð4=Ð1 и Ð5=Ð2, ТО
Ð4 + Ð3+ Ð5 = Ð1 + Ð3+ Ð2 = 180.
Что сумма углов треугольника равна 180.
Доказали.
Повторяют упражнения (физминутка) за учителем.
Нет.
Нет.
Нет.
Два острых и один тупой, один прямой и два острых, все три острые.
Два!
Записывают под диктовку или со слайда.
Отгадывают ребусы.
Теорему о сумме углов в треугольнике. И следствие из нее.
180 градусов.
Как минимум два острых угла.
Нет.
Продолжение темы
Закрепление изученного материала
Сам. работа
работа
Подве-дение итогов
Итак, сколько всего углов в треугольнике?
Тогда раз два угла всегда острые, то третий может быть … каким?
Тогда вид треугольника мы с вами будем определять по третьему углу.
Посмотрите на слайд (слайд 22). Назовите угол и определите вид треугольника.
Если два угла треугольника острые, а третий тоже острый, то треугольник …
Если два угла треугольника острые, а третий тоже прямой, то треугольник …
Если два угла треугольника острые, а третий тоже тупой, то треугольник …
Молодцы!
Исторический момент (слайд 23)
Теперь решаем устные задачи.
(слайд 24)
Определите вид треугольника, если:
один из его углов равен 40 0 , а другой – 100 0 ,
один из его углов равен 60 0 , а другой – 70 0 ,
один из его углов равен 40 0 , а другой – 50 0 .
(Слайд 25-26)
Теперь решаем задачи у доски и в тетрадях (слайд 27)
Теперь пишем самостоятельную работу по вариантам, три задания.
Ребята, скажите, что мы сегодня узнали и вспомнили?
Молодцы!
Оценки за урок получают …
любым.
Остроугольный.
Прямоугольный.
Тупоугольный.
Тупоугольный, т.к. есть тупой угол.
Остроугольный, т.к. все углы острые.
Прямоугольный, т.к. 180 – 40 -50 = 90.
По теореме о сумме углов D:
ÐВ = 180
0
– (ÐС + ÐВ) =
= 180
0
– (90
0
+ 50
0
) = Ð40 0
Т.к. D АВС равнобедренный, то ÐА = ÐВ, по свойству р/б D.
По теореме о сумме углов D:
ÐА = (180
0
– ÐС) : 2 =
= (180
0
– 90
0
) : 2 = Ð45 0
Решают задачи с помощью учителя.
Пишут самостоятельную работу в карточках.
— сумма углов любого треугольника равна 180.
Виды треугольников — остроугольные, тупоугольные, прямоугольные.
Узнали что самыми древними инструментами в геометрии были линейка и циркуль.
Задание 2 .
Дано:
Найти:
Ð1 и Ð 2 Решение:
Задание 3.
Дано:
Найти:
Ð1 и Ð 2 Решение:
1.Параллельность прямых.
|
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||||||||||||||||||||||||
1. Параллельность прямых Параллельность прямых
|
|||||||||||||||||||||||||||||
Теорема: если две прямые параллельны третьей прямой, то они параллельны. Доказательство. Пусть даны две прямые а и b. Допустим, что они не параллельны между собой. (Рис.1) Тогда они пересекаются в некоторой точке С. Следовательно, через точку С проходят две прямые, параллельные прямой с. А это невозможно согласно аксиоме: через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Следовательно, прямые а и b не пересекаются. Они параллельны. |
Рис.1 Теорема. Параллельность прямых. |
||||||||||||||||||||||||||||
2. Признаки параллельности прямых Признаки параллельности прямых |
|||||||||||||||||||||||||||||
Теорема. Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 градусов, то прямые параллельны. Доказательство. Пусть даны две прямые a и b, которые образуют с секущей АВ внутренние накрест лежащие углы (Рис. 2 а). Допустим, что прямые a и b не параллельны. Тогда они пересекаются в одной точке С. Секущая АВ разбивает плоскость на две полуплоскости. И, следовательно, точка С лежит в одной из них и образует треугольник АВС. Сторона АС принадлежит прямой а. Сторона ВС принадлежит прямой b. (Рис. 2 б) Отложим равный треугольник ABC1 в другой полуплоскости с вершиной С1 так, чтобы угол А треугольника АВС совпал с углом В треугольника АВС1. |
Рис.2 Теорема. Признаки параллельности прямых. |
||||||||||||||||||||||||||||
3.Свойство углов при пересечении параллельных прямых |
|||||||||||||||||||||||||||||
Теорема. Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны и сумма внутренних односторонних углов равна 180 градусов. Доказательство. Пусть a и b параллельные прямые. Прямая с пересекает их в точках А и В. (Рис. 3) Проведем через точку А прямую а1 так, чтобы внутренние накрест лежащие углы, образованные между прямыми а1 и b и секущей с, были равны. Тогда по признаку параллельности прямых они параллельны. А так как согласно аксиоме о единственной параллельной прямой, проходящей через точку не лежащей на данной прямой, такая прямая может быть только одна, то прямые а и а1 совпадают. А следовательно внутренние накрест лежащие углы, образованные между прямыми а,b и секущей с, равны. |
Рис.3 Теорема. Свойство углов при пересечении параллельных прямых. |
||||||||||||||||||||||||||||
4. Сумма углов треугольника Сумма углов треугольника |
|||||||||||||||||||||||||||||
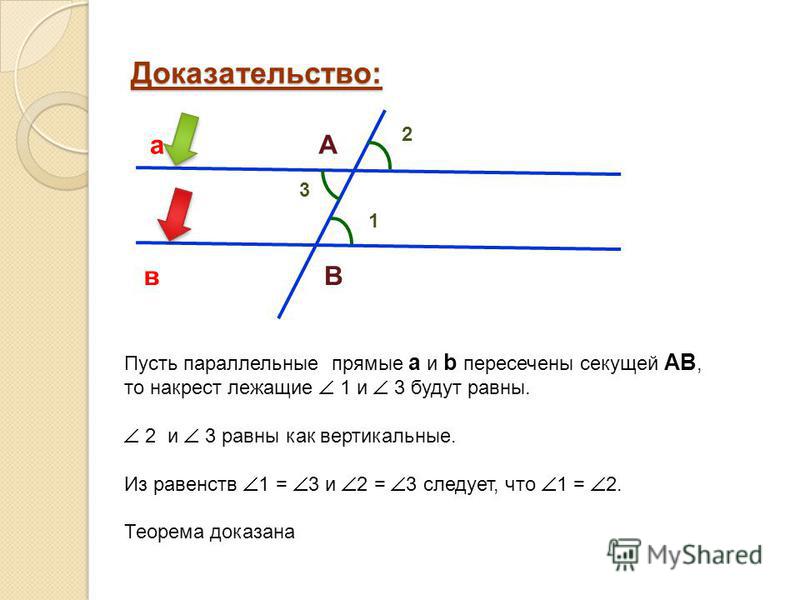
Теорема. Сумма углов треугольника равна 180 градусов. Доказательство. Пусть АВС данный треугольник. Проведем через вершину В прямую BD, параллельную стороне АС (Рис. 4). Тогда углы α и α’, γ и γ’ равны как внутренние накрест лежащие. А так как прямая BD представляет собой развернутый угол с вершиной угла в точке В, который равен 180°, т.е. α’ + β + γ’ = 180°, то сумма углов треугольника равна также 180°. Таким образом, мы пришли к выводу, что сумма углов треугольника, т.е. α + β + γ = 180°. |
Рис.4 Теорема. Сумма углов треугольника. |
||||||||||||||||||||||||||||
5. Единственность перпендикуляра к прямой Единственность перпендикуляра к прямой |
|||||||||||||||||||||||||||||
Теорема. Из любой точки, не лежащей на данной прямой, можно опустить только один перпендикуляр на данную прямую. Доказательство. Пусть дана прямая а и не лежащая на ней точка А. Отметим на прямой а произвольную точку, например D. И проведем через нее перпендикуляр.(Рис. 5) Теперь проведем через точку А прямую, параллельную нашей перпендикулярной прямой. Она также будет перпендикулярна прямой а. Так как прямая а, перпендикулярна одной из параллельных прямых, перпендикулярна и второй прямой. Отрезок АВ и есть перпендикуляр. Если допустить, что существует другой перпендикуляр, допустим в точке С. |
Рис.5 Теорема. Единственность перпендикуляра к прямой. |
||||||||||||||||||||||||||||
6. Высота, биссектриса и медиана треугольника |
|||||||||||||||||||||||||||||
Высотой треугольника, проведенной из данной вершины, называется перпендикуляр, опущенный из данной вершины на противолежащую сторону. Биссектрисой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину угла и противолежащую сторону, и делящий данный угол пополам. Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину и противолежащую сторону, и делящий ее пополам. (Рис.6) |
|||||||||||||||||||||||||||||
|
Рис.6 Высота, биссектриса и медиана треугольника. |
|||||||||||||||||||||||||||||
7. Свойство медианы равнобедренного треугольника |
|||||||||||||||||||||||||||||
|
Теорема. Доказательство: Пусть АВС — данный равнобедренный треугольник с основанием АС. Боковые стороны АВ и ВС равны, ВD — медиана. Необходимо доказать, что BD является биссектрисой и высотой. Рассмотрим треугольники ABD и BDC. Они равны по третьему признаку равенства треугольников. АВ = ВС по условию, AD = DC, так как BD медиана, а сторона BD у них общая. Следовательно, углы при вершине D равны, а так как они являются смежными, то ∠ADB = ∠CDB = 90°. Из равенства треугольников ABD и BDC следует равенство углов при вершине В, т.е. ∠AВD = ∠CВD = α. Отсюда можно сделать вывод, что медиана BD является биссектрисой и высотой. |
Рис. |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
8. Пример 1 |
|||||||||||||||||||||||||||||
Даны прямая а и точка С, не лежащая на этой прямой. Необходимо доказать, что через точку С можно провести прямую, параллельную прямой а. |
|||||||||||||||||||||||||||||
Доказательство: Проведем прямую b, параллельную прямой а. Тогда, согласно аксиоме 9, (через точку, не лежащую на данной прямой, можно провести только одну прямую) проведем прямую с через точку С, параллельную прямой b. Таким образом, получается, что прямая с параллельна прямой b, и прямая a также параллельна прямой b по построению. Следовательно, по теореме о двух прямых, параллельных третьей прямой, имеем, что две прямые a и c параллельны прямой b и, следовательно, они (прямые а и с) параллельны. Т.е. через точку С можно провести прямую, параллельную прямой а. |
Рис.8 Задача. Даны прямая а и точка С . |
||||||||||||||||||||||||||||
Пример 2 |
|||||||||||||||||||||||||||||
Даны две параллельные прямые а и b, и секущая с. Докажите, что биссектрисы внутренних накрест лежащих углов, образованных этими прямыми, параллельны (Рис.9) |
|||||||||||||||||||||||||||||
Доказательство:
Так как прямые а и b параллельны, то углы α и β, образованные этими параллельными прямыми и секущей с, равны как внутренние накрест лежащие, т.е. ∠α = ∠β. Согласно определению, биссектриса — это луч, исходящий из вершины угла между его сторонами, который делит этот угол пополам. Таким образом, так как углы α и β равны, то и углы α/2 и β/2 также равны. А если углы α/2 и β/2 равны, то они являются внутренними накрест лежащими углами, между секущей с и прямыми, на которых лежат лучи d1 и d2, и согласно теореме: признак параллельности прямых, лучи d1 и d2 лежат на параллельных прямых. |
Рис.9 Задача. Даны две параллельные прямые а и b и секущая с… |
||||||||||||||||||||||||||||
Пример 3 |
|||||||||||||||||||||||||||||
Один из углов равнобедренного треугольника АВС равен 100° (Рис. |
|||||||||||||||||||||||||||||
Решение: Так как сумма углов треугольника составляет 180°, а два угла у равнобедренного треугольника равны, то они не могут равняться 100°. Следовательно, углы при вершинах А и С равны, а угол при вершине В = 100°. Отсюда следует, что можно составить соотношение: 2α + β = 180° 2α + 100° = 180° 2α = 80° α = 40° Ответ: углы равнобедренного треугольника составляют: 100°, 40°, 40°. |
Рис.10 Задача. Найти углы треугольника. |
||||||||||||||||||||||||||||
Пример 4 |
|||||||||||||||||||||||||||||
Сумма внешних углов треугольника АВС при вершиах А и В равна 240° (Рис. |
|||||||||||||||||||||||||||||
Решение: Так как сумма углов α + β + α1 + β1 = 360°, а α1 + β1 = 240° по условию задачи, то α + β = 120° А так как сумма углов треугольника составляет 180°, то α + β + γ = 180°, т.е. 120° + γ = 180° И следовательно, γ = 60° Ответ: угол при вершине С = 60°. |
Рис.11 Задача. Найти угол треугольника. |
||||||||||||||||||||||||||||
Пример 5 |
|||||||||||||||||||||||||||||
В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. |
|||||||||||||||||||||||||||||
Доказательство: Так как по условию задачи треугольник АВС равнобедренный, то углы при вершинах А и С равны: α = (180°-36°)/2 α = 72°, а так как AD биссектриса, то ∠BAD = ∠DAC, т.е. α / 2 = 36° Следовательно, треугольник ADB равнобедренный. Углы при вершинах А и В равны 36°. Теперь рассмотрим треугольник ADC. Угол λ равен: λ = 180° — (α / 2 + α) λ = 180° — (36° + 72°) λ = 72° Таким образом, треугольник ADC равнобедренный. Углы при вершинах С и D равны 72°. |
Рис. |
||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||||||||||||||||||||||||
Содержание |
|||||||||||||||||||||||||||||
| Страница 1 | Страница 7 | ||||||||||||||||||||||||||||
1. Основные фигуры планиметрии. Основные фигуры планиметрии.
2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников. |
1.Движение и его свойства.
2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства. |
||||||||||||||||||||||||||||
| Страница 2 | Страница 8 | ||||||||||||||||||||||||||||
|
1.Параллельность прямых.
2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.  Единственность перпендикуляра к прямой. Единственность перпендикуляра к прямой.
6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника. |
1.Вектор и его абсолютная величина.
2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов. |
||||||||||||||||||||||||||||
| Страница 3 | Страница 9 | ||||||||||||||||||||||||||||
|
1.Окружность.
2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек. |
1. Преобразование подобия и его свойства. Преобразование подобия и его свойства.
2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников. |
||||||||||||||||||||||||||||
| Страница 4 | Страница 10 | ||||||||||||||||||||||||||||
|
1.Параллелограмм.
2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. |
1.Углы, вписанные в окружность.
2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике. |
||||||||||||||||||||||||||||
| Страница 5 | Страница 11 | ||||||||||||||||||||||||||||
|
1.Теорема Пифагора.
2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества. |
1.Многоугольники. Правильные многоугольники.
2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.  Длина окружности. Длина окружности.
|
||||||||||||||||||||||||||||
| Страница 6 | Страница 12 | ||||||||||||||||||||||||||||
|
1.Декартова система координат.
2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения. |
1.Площадь прямоугольника.
2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции. |
||||||||||||||||||||||||||||
Сумма углов треугольника
Сумма
треугольника равна 180 градусов.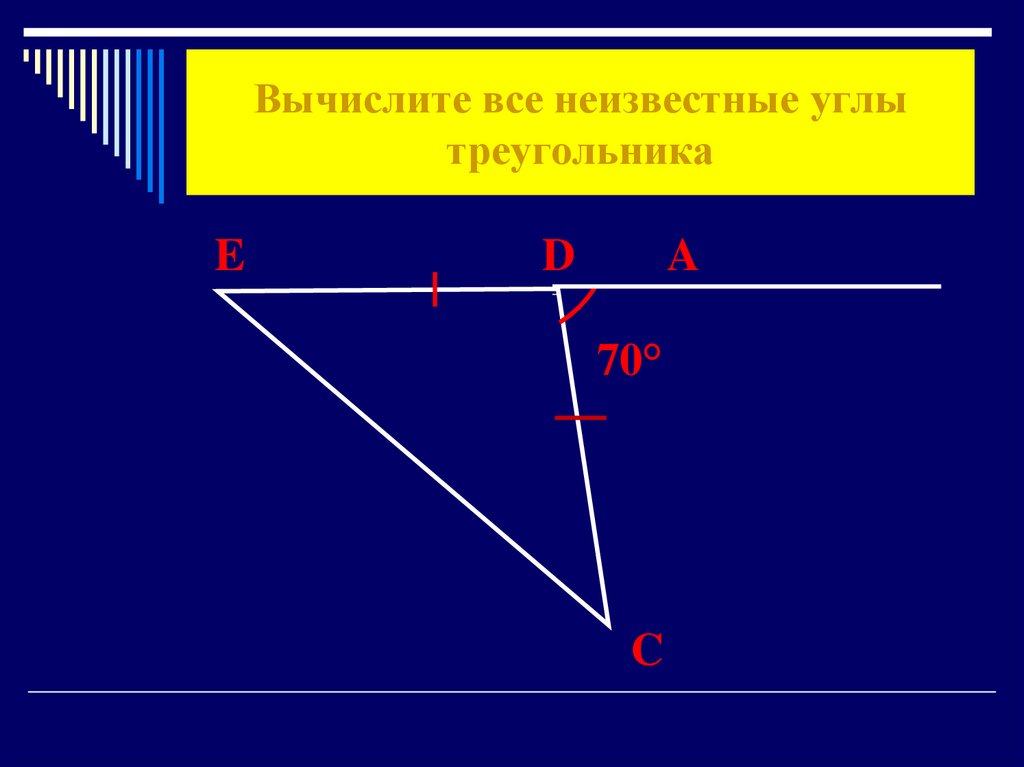
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85º. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85°, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение 2х + 3х = 85 и найдем х = 17. Тогда 3х = 51.
Ответ: 51.
2. Один из углов равнобедренного треугольника равен 98º. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98°?
Нет,
конечно! Ведь сумма углов треугольника
равна 180°.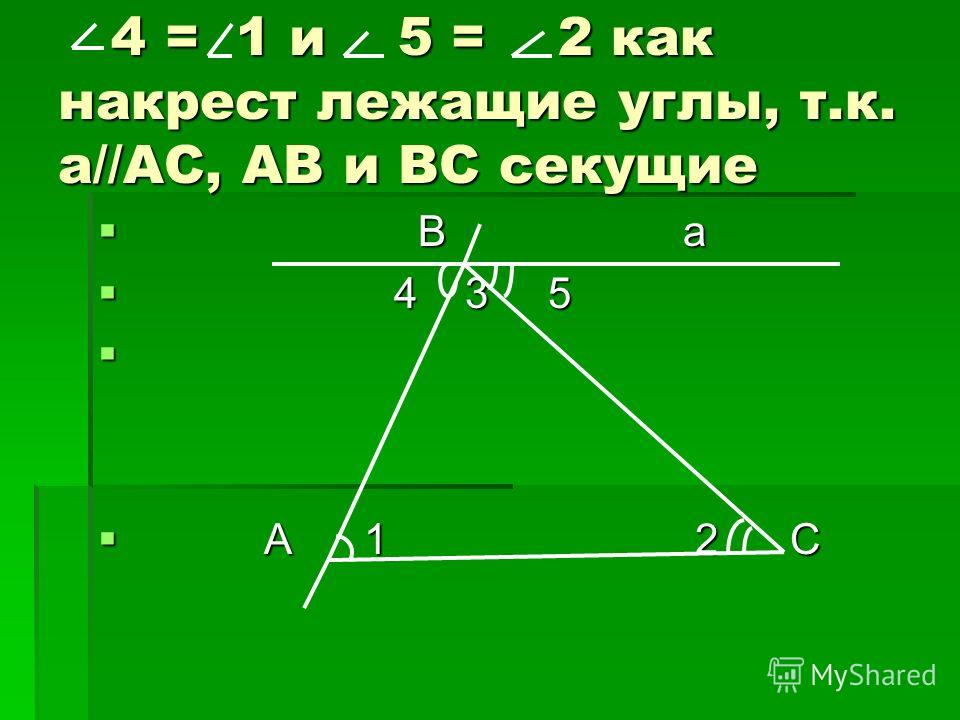 Значит, один из углов треугольника
равен 98°,
а два других равны .
Значит, один из углов треугольника
равен 98°,
а два других равны .
Ответ: 41.
3. На рисунке угол 1 равен 46º, угол 2 равен 30º, угол 3 равен 44º. Найдите угол 4. Ответ дайте в градусах.
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол 5. Он равен 180° — ∠1 — ∠3 = 90° Тогда ∠6 = 90° ∠7 = 180° — ∠2 — ∠6 = 60°, Угол 4, смежный с углом 7 равен 120°.
Ответ: 120.
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
4. Углы треугольника относятся как 2:3:4. Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны 2х, 3х и 4х. Запишем, чему равна сумма углов этого треугольника. 2х + 3х + 4х = 180° 9х = 180° х = 20° Тогда 2х = 40°.
Ответ:
40.
Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол 1 равен углу А (они накрест лежащие). Угол 2 равен углу С (тоже накрест лежащие). Развернутый угол равен 180º. Значит, и сумма углов треугольника тоже равна 180º.
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Пусть прямая с пересекает параллельные прямые а и b. При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.
Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть ∠1 = ∠3, ∠2 = ∠4.
Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.
Углы
1 и 2 — смежные,
это мы уже знаем. Сумма смежных углов
равна 180º.
Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) — накрест лежащие. Накрест лежащие углы равны. ∠3 = ∠5, ∠1 = ∠7, ∠2 = ∠8, ∠4 = ∠6.
Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна 180°, то есть ∠1 + ∠6 = 180°, ∠4 + ∠7 = 180°.
Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.
Соответственные углы равны, то есть ∠2 = ∠6, ∠3 = ∠7.
Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.
Накрест лежащие углы равны, то есть ∠3 = ∠5, ∠1 = ∠7, ∠2 = ∠8, ∠4 = ∠6.
Чтобы
применять все эти факты в решении
задач ЕГЭ, надо научиться видеть
их на чертеже. Например, глядя
на параллелограмм или трапецию, можно
увидеть пару параллельных прямых
и секущую, а также односторонние
углы.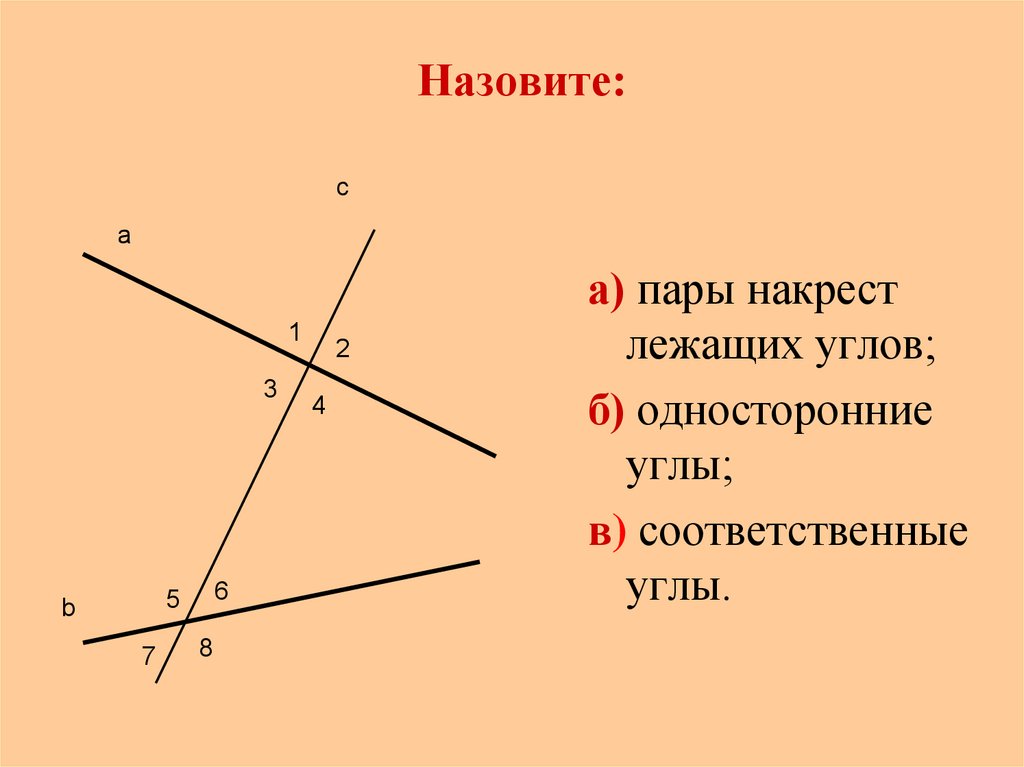 Проведя диагональ параллелограмма,
видим накрест лежащие углы. Это —
один из шагов, из которых и состоит
решение.
Проведя диагональ параллелограмма,
видим накрест лежащие углы. Это —
один из шагов, из которых и состоит
решение.
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.
Пусть ВМ — биссектриса тупого угла В. По условию, отрезки МD и АВ равны 3х и 4х соответственно.
Рассмотрим углы СВМ и ВМА. Поскольку АD и ВС параллельны, ВМ — секущая, углы СВМ и ВМА являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник АВМ — равнобедренный, следовательно, АВ = АМ = 4х.
Периметр параллелограмма — это сумма всех его сторон, то есть 7х + 7х + 4х + 4х = 88. Отсюда х = 4, 7х = 28.
Ответ: 28.
2.
Диагональ
параллелограмма образует с двумя
его сторонами углы 26º
и 34º. Найдите больший угол параллелограмма.
Ответ дайте в градусах.
Найдите больший угол параллелограмма.
Ответ дайте в градусах.
Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: 120º.
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50º? Ответ дайте в градусах.
Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.
Давайте посмотрим на чертеж. По условию, α — β = 50°, то есть α = β + 50°.
Углы α и β — односторонние при параллельных прямых и секущей, следовательно, α + β = 180°.
Итак, 2β + 50° = 180° β = 65°, тогда α = 115°.
Ответ: 115.
EGE-Study » Методические материалы » Геометрия: с нуля до C4 » Высоты, медианы, биссектрисы треугольника
Накрест лежащие углы.
 Накрест лежащие углы равны. Накрест лежащие углы при параллельных.
Накрест лежащие углы равны. Накрест лежащие углы при параллельных.- Альфашкола
- Статьи
- Накрест лежащие углы
Когда секущая пересекает пару параллельных линий, образуются накрест лежащие углы. Накрест лежащие углы равны друг другу.
Один из способов найти накрест лежащие углы — нарисовать зигзагообразную линию на рисунке, \(d\) и \(e\) , \(c\) и \(f\) являются накрест лежащими углами.
Пример 1: На приведенной ниже рисунке определите значения углов \(b, c, d, e, f, g , h\).
Решение:
- \(b + 60° =180° ⇒ b = 180° – 60° = 120°\)
- \(b\) и \(c\) — вертикальные углы. Поэтому \(c = b = 120°\)
- \(d\) и \(60°\) вертикальные углы.
 Поэтому \(d = 60°\)
Поэтому \(d = 60°\) - \(e = d = 60°\)
- \(f+ 60° =180° ⇒ f = 180° – 60° = 120°\)
- \(g\) и \(f-\)вертикальные углы. \(g = f = 120°\)
- \(h\) и \(e-\)вертикальные углы. Поэтому \(h = e = 60°\)
Ответ: \(b = 120°, c = 120°, d = 60°, e = 60°, f = 120°, g = 120° , h = 60°\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Игорь Вячеславович Корюков
Репетитор по математике
Стаж (лет)
Образование:
Бердянский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по информатике для 5-10 классов, по физике для 7-10 классов. Преподаватель высшей категории, учитель-методист. Объясняю доступно и ясно, учитывая индивидуальные способности и характер ученика. По физике и информатике имею свои собственные образовательные сайты.
Преподаватель высшей категории, учитель-методист. Объясняю доступно и ясно, учитывая индивидуальные способности и характер ученика. По физике и информатике имею свои собственные образовательные сайты.
Ольга Яновна Савинова
Репетитор по математике
Стаж (лет)
Образование:
Гродненский государственный университет имени Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку 5-8 классы, и английский язык 3-4 классы. Отлично владею предметом. Умею находить подход к детям, прекрасно с ними лажу благодаря знанию и пониманию основ детской психологии. Умею легко и доступно объяснить даже самые сложные темы, проводя лёгкие и понятные каждому ассоциации.
Отлично владею предметом. Умею находить подход к детям, прекрасно с ними лажу благодаря знанию и пониманию основ детской психологии. Умею легко и доступно объяснить даже самые сложные темы, проводя лёгкие и понятные каждому ассоциации.
Сергей Александрович Москвин
Репетитор по математике
Стаж (лет)
Образование:
Костромской государственный университет им. Н.А. Некрасова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку 2-9 классов, готовлю к ОГЭ. Репетитор по французскому языку 5-11 классы. Магистр филологических наук. Объясняю понятным языком, чтобы ребёнок усвоил правило. Мой ученик набрал за ОГЭ 100 баллов. Если Вашему ребёнку требуется улучшить русский язык, или подготовиться к экзамену, готов Вам помочь.
Репетитор по французскому языку 5-11 классы. Магистр филологических наук. Объясняю понятным языком, чтобы ребёнок усвоил правило. Мой ученик набрал за ОГЭ 100 баллов. Если Вашему ребёнку требуется улучшить русский язык, или подготовиться к экзамену, готов Вам помочь.
Похожие статьи
- Свойства параллелограмма. Параллелограмм и его свойства.
- Модуль числа (Часть 2)
- Чтение графика функций: парабола
- Стадии подготовки к экзамену по математике
- НИУ ВШЭ (Программная инженерия): проходной балл, отзывы
- Смешанные уравнения
- Один дома: чем заняться без родителей и как избежать проблем
- Учимся оказывать первую помощь себе и друзьям
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Почему треугольник имеет 180 градусов?
Вы знаете, что сумма углов треугольника всегда равна 180 0 ? Почему это? В конце концов, 180 0 это угол, который простирается от одной стороны прямой линии до другой, поэтому довольно странно, что это количество градусов в углах треугольника.
Какое отношение имеет треугольник к одной прямой? Как оказалось, довольно много. И треугольники также имеют много общего с прямоугольниками, пятиугольниками, шестиугольниками и целым семейством многогранных фигур, известных как многоугольники.
Через несколько недель мы увидим, что именно я имею в виду. Но сегодня мы начнем с выяснения, почему именно сумма углов треугольника всегда равна 180 0 . Или вы так думали… потому что мы также увидим, что иногда это не так.
Во-первых, обзор: типы треугольников
Краткое напоминание: существует три различных типа основных треугольников. Они равносторонние, равнобедренные и разносторонние.
- Равносторонний треугольник имеет три стороны одинаковой длины
- У равнобедренного треугольника две стороны одинаковой длины и одна сторона разной длины
- Разносторонний треугольник имеет три стороны разной длины
Длина стороны треугольника напрямую влияет на его углы.
СВЯЗАННЫЕ: Что такое треугольник Паскаля?
Внутренние и внешние углы
Прежде чем мы слишком углубимся в нашу историю о треугольниках и общем количестве градусов в их трех углах, мы должны поговорить об одном небольшом геометрическом словаре. И в этом разница между внутренним и внешним углом.
Проще всего описать разницу между этими двумя вещами на примере. Поскольку сегодняшняя тема — треугольник, давайте поговорим о внутренних и внешних углах треугольника. Короче говоря, внутренних углов – это все углы в пределах границ треугольника. Другими словами, это те углы, о которых мы говорили все это время.
внешних углов треугольника — это все углы между одной стороной треугольника и линией, полученной продолжением соседней стороны вне границ треугольника. Если вы подумаете об этом, вы увидите, что если вы прибавите любой внутренний угол треугольника к соседнему с ним внешнему углу, вы всегда получите 180 0 — прямую линию.
Почему треугольники имеют 180 градусов?
Что подводит нас к главному вопросу на сегодня: почему сумма внутренних углов треугольника всегда равна 180 0 ? Как оказалось, это можно понять, подумав о внутренних и внешних углах треугольника. Чтобы понять, что я имею в виду, включите свое воображение или лист бумаги, потому что пришло время для небольшого математического проекта по рисованию декоративно-прикладного искусства.
Начните с рисования прямоугольного треугольника с одним горизонтальным катетом, одним вертикальным катетом и гипотенузой, идущей из верхнего левого угла в нижний правый. Теперь сделайте копию этого треугольника, поверните его на 180 0 и прижмите его гипотенузой к гипотенузе с оригиналом (так же, как мы делали, когда выясняли, как найти площадь треугольника). Наконец, сделайте еще одну копию исходного треугольника и сдвиньте ее вправо так, чтобы она располагалась рядом с только что сформированным прямоугольником. Со мной до сих пор? Если это так, ваша картинка должна выглядеть так:
К чему эта картинка? Взгляните на внутренний угол в правом нижнем углу исходного треугольника (тот, что помечен буквой «А»). Теперь взгляните на два угла, которые составляют внешний угол для этого угла треугольника (обозначены буквами «В» и «С»). Как мы знаем, если сложить внутренний и внешний углы одного угла треугольника, мы всегда получим 180 0 . И наш маленький рисунок показывает, что рассматриваемый внешний угол равен сумме двух других углов треугольника. Другими словами, два других угла треугольника (те, которые в сумме образуют внешний угол) должны соединиться с углом в правом нижнем углу, чтобы получить угол 180 9 .0003 0 угол.
Теперь взгляните на два угла, которые составляют внешний угол для этого угла треугольника (обозначены буквами «В» и «С»). Как мы знаем, если сложить внутренний и внешний углы одного угла треугольника, мы всегда получим 180 0 . И наш маленький рисунок показывает, что рассматриваемый внешний угол равен сумме двух других углов треугольника. Другими словами, два других угла треугольника (те, которые в сумме образуют внешний угол) должны соединиться с углом в правом нижнем углу, чтобы получить угол 180 9 .0003 0 угол.
СВЯЗАННЫЕ: Мир тригонометрии
Для простоты мы сделали наш рисунок, используя прямоугольный треугольник. Но оказывается, что вы можете сделать точно такой же рисунок, используя любой треугольник, который вам нравится, и вы всегда будете приходить к одному и тому же выводу. Попробуйте сделать несколько рисунков, начиная с разных треугольников по вашему выбору, чтобы увидеть это своими глазами. В качестве примера, вот еще один, который я сделал:
Неизбежный вывод из этой игры состоит в том, что сумма внутренних углов треугольника всегда должна составлять 180 0 . Наш милый и изящный маленький рисунок доказывает, что так и должно быть.
Наш милый и изящный маленький рисунок доказывает, что так и должно быть.
Или нет?
Могут ли треугольники иметь более 180 градусов?
Может быть, у нашего рисунка есть какие-то ограничения, которые не позволяют нам увидеть какую-то другую, более экзотическую возможность? Вам есть над чем подумать или попробовать. Возьмите ненадутый воздушный шар, положите его на плоскую поверхность и нарисуйте на нем как можно более совершенный треугольник. Если у вас есть под рукой транспортир, было бы здорово измерить и сложить внутренние углы треугольника и убедиться, что они довольно близки к 180 9 .0003 0 .
Теперь надуйте шарик и посмотрите на свой треугольник. Что случилось с этим? Если у вас есть этот транспортир, попробуйте еще раз просуммировать его внутренние углы. Что случилось с этой суммой? Вы все еще получаете 180 0 ? Что все это означает, когда дело доходит до вопроса о том, всегда ли сумма внутренних углов треугольника равна 180 0 , как мы, кажется, нашли?
К счастью, у меня есть ответ. Перейдите к статье на следующей неделе, где мы начали исследовать странный и удивительный мир, известный как неевклидова геометрия.
Перейдите к статье на следующей неделе, где мы начали исследовать странный и удивительный мир, известный как неевклидова геометрия.
Биссектрисы треугольника
Горячая математикаБиссектриса
биссектриса стороной треугольника называется прямая, перпендикулярная стороне и проходящая через ее середину.
Три перпендикулярные биссектрисы сторон треугольника пересекаются в одной точке, называемой центр окружности . Точка, в которой пересекаются три или более линий, называется точкой параллелизма. Итак, центр описанной окружности — это точка пересечения серединных перпендикуляров треугольника.
Здесь, О является центром окружности Δ Икс Д Z .
Центр описанной окружности равноудален от вершин треугольника. (См. теорему о центре окружности .) То есть
Икс
О
знак равно
Д
О
знак равно
Z
О
. Окружность, проведенная с центром описанной окружности в качестве центра и радиусом, равным этому расстоянию, проходит через все три вершины и называется описанный круг . Это наименьшая окружность, в которую можно вписать треугольник.
Окружность, проведенная с центром описанной окружности в качестве центра и радиусом, равным этому расстоянию, проходит через все три вершины и называется описанный круг . Это наименьшая окружность, в которую можно вписать треугольник.
Центр описанной окружности лежит внутри треугольника для остроугольных треугольников, на гипотенузе для прямоугольных треугольников и лежит вне треугольника для тупоугольных треугольников. Центр описанной окружности совпадает с серединой гипотенузы, если это равнобедренный прямоугольный треугольник.
Пример 1:
Дома Натхи, Хирена и Джо представляют собой три неколлинеарные точки на координатной плоскости. Если они хотят встретиться в общем месте, так что каждый должен будет пройти одинаковое расстояние от своего дома, как вы определите место встречи?
Поскольку точки, представляющие дома, не лежат на одной прямой, три точки образуют треугольник.
Теперь, если вы рассматриваете центр описанной окружности треугольника, он будет равноудален от вершин. То есть, если в качестве точки встречи выбрать центр описанной окружности треугольника, образованного тремя домами, то каждый из них должен будет пройти одинаковое расстояние от своего дома.
Пример 2:
Найдите значение Икс .
Здесь, О точка пересечения трех серединных перпендикуляров сторон Δ К л М .
Так, О является центром описанной окружности треугольника.
Центр описанной окружности равноудален от вершин. Затем, О М знак равно О К .
То есть,
6
Икс
+
1
знак равно
19.
Решить для Икс .
6 Икс + 1 − 1 знак равно 19 − 1 6 Икс знак равно 18 6 Икс 6 знак равно 18 6 Икс знак равно 3
Биссектриса угла
биссектриса угла угла треугольника – это прямая, которая делит угол на два равных угла.
Три биссектрисы углов треугольника сходятся в одной точке, называемой центр .
Здесь,
я
находится в центре
Δ
п
Вопрос
р
.
Центр вписанной равноудален от сторон треугольника. То есть, п я знак равно Вопрос я знак равно р я . Окружность, нарисованная с центром вписанной окружности и радиусом, равным этому расстоянию, касается всех трех сторон и называется обвести или вписанную окружность треугольника. Этот круг является самым большим кругом, который поместится внутри треугольника.
В равностороннем треугольнике центр вписанной окружности и центр описанной окружности совпадают.
Пример 3:
У Мисти есть треугольный участок заднего двора, где она хочет построить бассейн. Как ей найти самый большой круглый бассейн, который можно там построить?
Максимально возможный круглый бассейн будет иметь тот же размер, что и самый большой круг, который можно вписать в треугольный задний двор. Самая большая окружность, которую можно вписать в треугольник, — это вписанная окружность. Это можно определить, найдя точку совпадения биссектрис каждого угла заднего двора, а затем сделав круг с этой точкой в качестве центра и кратчайшим расстоянием от этой точки до границы в качестве радиуса.
Это можно определить, найдя точку совпадения биссектрис каждого угла заднего двора, а затем сделав круг с этой точкой в качестве центра и кратчайшим расстоянием от этой точки до границы в качестве радиуса.
Пример 4:
Найдите длину Дж О .
Здесь, О является точкой пересечения трех биссектрис угла Δ л М Н и, следовательно, является инцентром. Центр вписанной равноудален от сторон треугольника. То есть, Дж О знак равно ЧАС О знак равно я О .
У нас есть размеры двух сторон прямоугольного треугольника. Δ ЧАС О л , значит можно найти длину третьей стороны.
Здесь,
О
является точкой пересечения трех биссектрис угла
Δ
л
М
Н
и, следовательно, является инцентром. Центр вписанной равноудален от сторон треугольника. То есть,
Дж
О
знак равно
ЧАС
О
знак равно
я
О
.
Центр вписанной равноудален от сторон треугольника. То есть,
Дж
О
знак равно
ЧАС
О
знак равно
я
О
.
У нас есть размеры двух сторон прямоугольного треугольника. Δ ЧАС О л , значит можно найти длину третьей стороны.
Используя теорему Пифагора, найдите длину ЧАС О .
ЧАС О знак равно ( л О ) 2 − ( ЧАС л ) 2 знак равно 13 2 − 12 2 знак равно 169− 144 знак равно 25 знак равно 5
С
Дж
О
знак равно
ЧАС
О
, длина
Дж
О
также равно
5
единицы.
Что такое конгруэнтный угол? (Примеры вопросов)
Конгруэнтные углы часто используются в архитектуре, строительстве, дизайне и искусстве. Равные углы имеют одинаковую угловую меру. Например, правильный пятиугольник имеет пять сторон и пять углов, каждый из которых равен 108 градусам. Независимо от размера или масштаба правильного многоугольника, углы всегда будут конгруэнтны.
Примеры вопросов на конгруэнтность углов
Существует множество правил, позволяющих определить, конгруэнтны углы или нет. Например, если два треугольника подобны, их соответствующие углы будут равны. Это означает, что углы, находящиеся в одном и том же совпадающем положении, будут иметь одинаковый угол.
Еще один распространенный тест на конгруэнтность углов требует набора параллельных прямых и поперечной линии, пересекающей набор параллельных прямых. Например, прямые a и b параллельны, а прямая l является секущей, пересекающей параллельные прямые. Когда возникает такая ситуация, образуется несколько конгруэнтных углов. В этом сценарии образуются четыре основных типа конгруэнтных углов: альтернативные внутренние углы, альтернативные внешние углы, соответствующие углы и вертикальные углы.
Когда возникает такая ситуация, образуется несколько конгруэнтных углов. В этом сценарии образуются четыре основных типа конгруэнтных углов: альтернативные внутренние углы, альтернативные внешние углы, соответствующие углы и вертикальные углы.
Альтернативные внутренние углы расположены между двумя параллельными линиями, но на разных сторонах поперечной. В этом конкретном примере конгруэнтными альтернативными внутренними углами будут ∠2 и ∠6, а также ∠7 и ∠3.
Аналогично, Альтернативные внешние углы расположены снаружи параллельных линий и на противоположных сторонах поперечных. ∠5 и ∠1 конгруэнтны, а также ∠4 и ∠8.
Соответствующие углы расположены на одной стороне поперечной и в аналогичном месте. Например, ∠4 и ∠6 — соответствующие углы, поэтому они равны. Другие пары соответствующих углов включают ∠3 и ∠5, ∠1 и ∠7, а также ∠2 и ∠8.
Вертикальные углы образованы углами, противоположными друг другу. Например, ∠1 и ∠3, ∠7 и ∠5, ∠4 и ∠2, ∠6 и ∠8 — все пары равных углов. Вертикальные углы или противоположные углы обычно используются в качестве доказательства конгруэнтности.
Например, ∠1 и ∠3, ∠7 и ∠5, ∠4 и ∠2, ∠6 и ∠8 — все пары равных углов. Вертикальные углы или противоположные углы обычно используются в качестве доказательства конгруэнтности.
Другая категория конгруэнтных углов связана с конгруэнтностью треугольника. Правила конгруэнтности треугольников используются, чтобы доказать, конгруэнтны два треугольника или нет. Эти правила учитывают длины сторон и углы треугольников, чтобы определить конгруэнтность. Четыре критерия используются для определения конгруэнтности треугольников, и они имеют удобные названия.
Например:
S-S-S относится к двум треугольникам, все стороны которых имеют одинаковую длину. Если это так, то все соответствующие меры углов также будут конгруэнтны.
S-A-S относится к двум треугольникам, у которых две конгруэнтные стороны, с одним конгруэнтным углом между ними. Если это так, то все соответствующие углы будут равны.
Аналогично, A-S-A говорит нам, что два треугольника имеют два конгруэнтных угла и одну конгруэнтную длину стороны между ними. Опять же, если это так, то все соответствующие углы будут равны.
Опять же, если это так, то все соответствующие углы будут равны.
Наконец, A-A-S относится к двум треугольникам, которые имеют два соответствующих конгруэнтных угла с соответствующей конгруэнтной длиной стороны. Это говорит нам о том, что все соответствующие углы будут равны.
Конгруэнтные углы обычно используются при изучении геометрии и во многих реальных профессиях. Строители, инженеры, строители и художники регулярно используют конгруэнтные углы. Определение конгруэнтности углов является важным навыком, который помогает заложить основу для изучения геометрии.
Примеры вопросов о конгруэнтных углах Вот несколько примеров вопросов о конгруэнтных углах.
Вопрос №1:
Углы 1 и 2 — соответствующие углы. Если угол 2 равен 67°, то чему равен угол 1?
164 °
24 °
344 °
67 °
Покажите ответ
Ответ:
Когда две параллельные линии вырезаны трансверсовыми, то же и в соответствующих углах будут конгруэнтными. Углы 1 и 2 равны, поэтому оба имеют угловую меру 67°.
Углы 1 и 2 равны, поэтому оба имеют угловую меру 67°.
Скрыть Ответ
Вопрос №2:
Линия r – это секущая, пересекающая две параллельные прямые s и t . Перечислите все углы, равные углу 6.
∠8, ∠3 и ∠2
∠8, ∠4 и ∠2
∠2
∠5 79 ∠2 и 0 0 Показать ответ
Ответ:
∠8 конгруэнтно ∠6, потому что они вертикальные или противоположные углы.
∠2 конгруэнтно ∠6, потому что они являются соответствующими углами (на одной стороне поперечной и в соответствующих углах).
∠4 конгруэнтно ∠6, потому что они представляют собой альтернативные внутренние углы (альтернативные стороны поперечной и между двумя параллельными прямыми).
Скрыть ответ
Вопрос №3:
Если следующие неправильные четырехугольники равны, то угол C должен быть равен какому другому углу?
∠Е
∠Ф
∠G
∠H
Показать ответ
Ответ:
Соответствующие углы конгруэнтны для конгруэнтных многоугольников. Секрет конгруэнтен с секрет
Секрет конгруэнтен с секрет
♂ является конгруэнтен с тром
секрет. строит пешеходную дорожку, пересекающую пару железнодорожных путей. Пешеходная дорожка представлена поперечной буквой t на изображении ниже. Железнодорожные пути представлены параллельными линиями l и m. Если город хочет, чтобы пешеходная дорожка пересекала рельсы под углом 135° (угол 1), каковы будут значения углов 2, 3 и 4?
∠2 = 45° ∠3 = 135° ∠4 = 45°
∠2 = 45° ∠3 = 45° ∠4 = 135°
∠2 = 145° ∠3 = 44° 45°
∠2 = 180° ∠3 = 45° ∠4 = 45°
Показать ответ
Ответ:
∠1 и ∠4 равны, потому что они вертикальные углы. Если ∠1 равно 135°, то ∠2 должно быть равно 45°, потому что их сумма должна быть 180°, чтобы образовать прямую линию. Теперь, когда мы знаем, что ∠2 равно 45°, мы также знаем, что ∠3 равно 45°, потому что это вертикальные углы.
Скрыть ответ
Вопрос № 5:
У Келси есть прямоугольный сад, который она хочет разделить на две равные части по диагонали. Одна секция будет для моркови, а другая для капусты. Она разделяет сад на две треугольные части, как на изображении ниже. Если мера ∠DCA равна 40°, какова мера ∠CAB?
Одна секция будет для моркови, а другая для капусты. Она разделяет сад на две треугольные части, как на изображении ниже. Если мера ∠DCA равна 40°, какова мера ∠CAB?
20°
30°
40°
50°
Показать ответ
Ответ:
Если прямая AC образует поперечную через параллельные прямые DC и AB, то углы DCA и CAB будут равны. Угол DCA и угол CAB образуют чередующиеся внутренние углы, поэтому угол CAB будет равен 40°.
Скрыть ответ
Вернуться к примерам вопросов по математике
Линии и углы — определения, свойства, типы, практические вопросы
Древние математики ввели понятие линий для представления прямых объектов, ширина и глубина которых пренебрежимо малы. Линии, рассматриваемые Евклидом как ширина за вычетом длины, составляют основу евклидовой геометрии.
Когда два луча (часть прямой линии) пересекаются в одной плоскости, они образуют угол. Точка пересечения называется вершиной.
Точка пересечения называется вершиной.
В этой статье мы рассмотрим основные свойства, определения и типы линий и углов, связанных с геометрией. Мы также рассмотрим несколько примеров, чтобы вы лучше поняли свойства линий и углов. Прежде чем мы двинемся дальше, взгляните на план подготовки к GMAT из пяти шагов, чтобы набрать 700+ баллов на GMAT:
Ниже приводится краткое описание тем, которые мы рассмотрим в этой статье. Он имеет бесконечную длину.
Определение сегмента линии
Сегмент линии — это сегмент линии, или, другими словами, мы можем сказать, что сегмент линии — это линия с двумя концами.
Например, , На диаграмме показана линия L, и один сегмент этой линии — AB.
На плоскости может быть много линий или отрезков.
Эти линии можно разделить на несколько типов в зависимости от относительного расположения одной строки по отношению к другой.
Типы линий
Пересекающиеся линии
Две линии являются пересекающимися, если они пересекаются в одной точке.
Например, L 1 и L 2 являются пересекающимися линиями на приведенной ниже диаграмме
Параллельные линии
Пара прямых параллельна, если они никогда не пересекаются.
Например, L 1 , L 2 и L 3 являются параллельными линиями на приведенной ниже диаграмме.
Поперечная линия
Поперечная линия пересекает две или более линий в различных точках.
Например, линия L 3 является поперечной линией на приведенной ниже диаграмме.
Далее мы рассмотрим углы и их свойства.
Набрав Q50-51 на GMAT, вы получите 700+ баллов GMAT. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:
Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:
Угол – что это такое?
Угол образуется при пересечении двух прямых. Обозначим угол символом ∠.
Угол состоит из двух катетов и одной общей вершины, в которой сходятся две линии.
Например, ∠AOD образуется при пересечении прямых AB и CD.
Кроме того, ∠AOD образуется между ветвями AO и OD, поэтому мы включаем A, O и D в название угла.
Знаете ли вы, что положение точек катетов не имеет значения, если общей вершиной является средняя буква в названии угла
Измерение угла
Угол измеряется в градусах.
Угол может измеряться от нуля (0) градусов до 360 градусов. В зависимости от измерения угла они делятся на четыре типа:
- Острый угол
- Прямой угол
- Тупой угол
- Рефлекторный угол
Острый угол
Когда измерение угла находится между 0 градусов и 90 градусов.
Прямой угол
Когда измерение угла равно 90 градусов.
- Если между двумя прямыми имеется прямой угол, то говорят, что эти две прямые перпендикулярны друг другу .
Тупой угол
Когда измерение угла составляет от 90 до 180 градусов.
Угол прямой составляет 180 градусов.
Угол отражения
При измерении угла между 180 и 360 градусами.
Мы обсудили основные типы углов.
Теперь обсудим углы, образованные при пересечении двух прямых.
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки.
Мы являемся наиболее проверенной компанией GMAT Prep на GmatClub с более чем 2200+ обзорами, по состоянию на 4 октября 2021 года.
Углы, образованные между двумя пересекающими линиями
Вертично противоположные
9 22222222222222. пересекаются друг с другом, то образуются 4 угла.
- И углы , которые противоположны друг другу в точке пересечения , известны как вертикально противоположные углы .
- Вертикально противоположные углы всегда равны.
Теперь обсудим углы, образованные при пересечении двух прямых третьей прямой, т. е. поперечной линией.
Углы, образованные поперечной линией
Когда поперечная линия пересекает две прямые, образуются восемь углов, как показано на рисунке.
Из этой диаграммы получаются несколько специальных пар углов.
Например: если вы заметили, что (∠1, ∠3), (∠2, ∠4), (∠5, ∠7) и (∠6, ∠8) являются вертикально противоположными углами.
Аналогично получаем несколько других видов углов. Давайте обсудим их.
Другие типы углов
Внутренние и внешние углы
Внутренние углы — это те, которые присутствуют внутри области между двумя линиями.
- И внешние углы те, что , а не присутствует в этом регионе.
Например:
- ∠2, ∠3, ∠5 и ∠8 — внутренние углы.
- А, ∠1, ∠4, ∠6 и ∠7 — внешние углы.
Соответствующие углы
Два угла называются соответствующими, если они лежат по одну сторону от поперечной линии так, что:
- Один угол является внутренним, а
- Другой угол является внешним Например:
(∠4, ∠8), (∠3, ∠7), (∠1, ∠5) и (∠2, ∠6) — 4 пары соответствующих углов
Чередующиеся внутренние углы
Два внутренних угла , лежащие на противоположной стороне поперечной линии, называются параллельными внутренними углами.
Например:
- (∠2, ∠8) и (∠3, ∠5) — альтернативные внутренние углы.

Альтернативные внешние углы
Два внешних угла, лежащих на противоположной стороне поперечной линии, называются альтернативными внешними углами.
Например:
- (∠1, ∠7) и (∠4, ∠6) — альтернативные внешние углы.
Примечание: Если поперечная линия пересекает две параллельные прямые, то соответствующие углы, альтернативные внутренние углы и альтернативные внешние углы равны.
Итак, мы рассмотрели все типы углов.
Давайте теперь узнаем о некоторых свойствах углов.
Свойства углов
Сумма углов на одной стороне прямой
Сумма всех углов по одну сторону прямой всегда равна 180 градусам.
Например, сумма ∠1, ∠2 и ∠3 составляет 180 градусов.
Сумма углов вокруг точки
Сумма всех углов вокруг точки всегда равна 360 градусам.
Например, сумма углов (∠1, ∠2 и ∠3) вокруг точки O составляет 360 градусов.
Если вам понравилась эта статья, вот еще несколько статей, которые могут вам понравиться:
- Свойства четырехугольника
- Свойства окружности
- Свойства треугольников
- GMAT Геометрические формулы и понятия треугольников
Применение свойств линий и углов в вопросах
Линии и углы – вопрос 1
параллельна прямой EF.
 Если ∠AHD и ∠JIE равны 118° и 30° соответственно, то какова мера угла GIB?
Если ∠AHD и ∠JIE равны 118° и 30° соответственно, то какова мера угла GIB?- 30
- 32
- 34
- 40
- 62
Решение
Шаг 1: Дана
- линия CD параллельна линии EF.
- ↑AHD = 118 °
- ↑джи = 30 °
Шаг 2: Найти
- Измерения угла ▲
Шаг 3: подход и работают
9002 мера угла GIB.- Итак, по заданной информации мы знаем, что прямая CD параллельна прямой EF, а прямая AB им перпендикулярна.
- Следовательно, ∠DHI = ∠FIB, так как оба угла являются соответствующими.
- Мы можем найти ▲ DDHI или omfib AS
- ↑AHD + ↑DHI = 180 °
- 118 ° + ϩfib = 180 °
- ↑FIB = 62 °
- Теперь, ♂FIB = 62 °
- Мы можем найти ▲ DDHI или omfib AS
- . ∠GIB
- Судя по диаграмме, ∠FIG = ∠JIE, так как это вертикально противоположные углы между EF и JG.
- ∠FIB = ∠FIG + ∠GIB
- 62° = ∠JIE + ∠GIB
- 62° = 30° + ∠GIB
- ∠GIB = 32° 9002 5
025
- Следовательно, ∠DHI = ∠FIB, так как оба угла являются соответствующими.
Следовательно, правильный ответ – вариант B.

Линии и углы – Вопрос 2
На приведенной выше диаграмме угол DFE и угол BFC представлены X и Y соответственно. Если ∠AFC = 100° и ∠BFE = 45°, то каково значение Y-X?
- 20
- 25
- 30
- 35
- 40
Solution
Step 1: Given
- ∠DFE = X
- ∠BFC = Y
- ∠AFC = 100°
- ∠BFE = 45°
Шаг 2: найти
- значение Y-X
.
Мера угла Y:
- Нам дано ∠AFC = 100° и
- ∠AFC + ∠BFC = 180°, так как сумма углов на одной стороне прямой равна 9019° 180° 100° + ∠BFC = 180°
- ∠BFC = Y = 80°
- ∠AFC + ∠BFC = 180°, так как сумма углов на одной стороне прямой равна 9019° 180° 100° + ∠BFC = 180°
Мера угла X:
- Нам дано ∠BFE = 45° и,
- ∠DFE + ∠BFE = угол 1°s на той же стороне, что и угол 1°s + ∠BFC прямая 180°.
- X + 45° +80°= 180°
- X = 55°
Следовательно, Y – X = 80° – 55° = 25°.

Таким образом, правильный ответ — вариант B.
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. Мы являемся самой популярной компанией по подготовке к GMAT на gmatclub с более чем 2200 отзывами по состоянию на 4 октября 2021 года.
Внутренние углы. Определение, значение, теорема, примеры прямые, пересекаемые секущей, также называются внутренними углами.
1. Что такое внутренние углы? 2. Типы внутренних углов 3. Внутренние углы треугольника 4. Сумма внутренних углов Формула 5. Нахождение неизвестного внутреннего угла 6. Внутренние углы многоугольников 7. 
Часто задаваемые вопросы о внутренних углах Что такое внутренние углы?
В геометрии внутренние углы образуются двумя способами. Один находится внутри многоугольника, а другой — когда параллельные прямые пересекаются секущей. Углы подразделяются на различные типы в зависимости от их размеров. Существуют и другие типы углов, известные как парные углы, поскольку они появляются парами, чтобы проявлять определенное свойство. Внутренние углы являются одним из таких видов.
Внутренние углы можно определить двумя способами:
- Углы внутри многоугольника: Углы, лежащие внутри фигуры, обычно многоугольника, называются внутренними углами. На приведенном ниже рисунке (а) углы ∠a, ∠b и ∠c являются внутренними углами.
- Внутренние углы параллельных прямых: Углы, лежащие в области, заключенной между двумя параллельными прямыми, пересекаемыми секущей, также называются внутренними углами.
 На приведенном ниже рисунке (b) \(L_1\) и \(L_2\) параллельны, а L является поперечной. Углы ∠1, ∠2, ∠3 и ∠4 являются внутренними углами.
На приведенном ниже рисунке (b) \(L_1\) и \(L_2\) параллельны, а L является поперечной. Углы ∠1, ∠2, ∠3 и ∠4 являются внутренними углами.
Типы внутренних углов
Существует два типа внутренних углов, образованных при пересечении двух прямых секущей: это параллельные внутренние углы и совмещенные внутренние углы.
- Альтернативные внутренние углы: Эти углы образуются при пересечении двух параллельных прямых секущей. Эта несмежная пара углов образована на противоположных сторонах секущей. На приведенном выше рисунке (b) пары чередующихся внутренних углов равны ∠1 и ∠3, ∠2 и ∠4. Они равны по размеру, если две параллельные прямые пересечены секущей.
- Co-Interior Углы: Эти углы представляют собой пару несмежных внутренних углов на одной стороне поперечной. На приведенном выше рисунке (b) пары внутренних углов равны ∠1 и ∠4, ∠2 и ∠3. Эти углы также называются односторонними внутренними углами или последовательными внутренними углами.
 Сумма двух смежных углов равна 180º, поэтому они также образуют пару дополнительных углов.
Сумма двух смежных углов равна 180º, поэтому они также образуют пару дополнительных углов.
Внутренние углы треугольника
В треугольнике в каждой вершине есть три внутренних угла. Сумма этих внутренних углов всегда равна 180°. Биссектрисы этих углов пересекаются в точке, называемой центром вписанных углов. Поскольку сумма внутренних углов треугольника равна 180 °, в каждом треугольнике может быть только один возможный прямой или тупой угол. Треугольник, у которого все три внутренних угла острые, называется остроугольным, треугольник, у которого один внутренний угол тупой, называется тупоугольным, а треугольник, у которого один внутренний угол является прямым, называется прямоугольным.
Сумма внутренних углов Формула
От простейшего многоугольника, скажем, треугольника, до бесконечно сложного многоугольника с n сторонами, такого как восьмиугольник, все стороны многоугольника образуют вершину, и эта вершина имеет внутренний и внешний углы.
 Согласно теореме о сумме углов, сумма всех трех внутренних углов треугольника равна 180°. Умножение числа сторон на 2, умноженное на 180°, дает нам сумму внутренних углов любого многоугольника.
Согласно теореме о сумме углов, сумма всех трех внутренних углов треугольника равна 180°. Умножение числа сторон на 2, умноженное на 180°, дает нам сумму внутренних углов любого многоугольника.Сумма, S = (n − 2) × 180°
Здесь S = сумма внутренних углов, а n = количество сторон многоугольника.
Применяя эту формулу к треугольнику, получаем:
S = (n − 2) × 180°
S = (3 − 2) × 180°
S = 1 × 180°
S = 180°
Используя ту же формулу, сумма внутренних углов многоугольников рассчитывается следующим образом:
Полигон
Количество сторон, n
Сумма внутренних углов, S
Треугольник 3 180(3-2) = 180° Четырехугольник 4 180(4-2) = 360° Пентагон
5 180(5-2) = 540° Шестигранник
6 180(6-2) = 720° Гептагон
7 180(7-2) = 900° Октагон
8 180(8-2) = 1080° Нонагон 9 180(9-2) = 1260° Декагон 10 180(10-2) = 1440° Нахождение неизвестного внутреннего угла
Мы можем найти неизвестный внутренний угол многоугольника, используя «Формулу суммы внутренних углов».
 Давайте рассмотрим приведенный ниже пример, чтобы найти недостающий угол ∠x в следующем шестиугольнике.
Давайте рассмотрим приведенный ниже пример, чтобы найти недостающий угол ∠x в следующем шестиугольнике.Из приведенных выше внутренних углов многоугольной таблицы сумма внутренних углов шестиугольника составляет 720°. Два внутренних угла шестиугольника выше прямые. Таким образом, мы получаем уравнение:
90 + 90 + 140 + 150 + 130 + x = 720°
Решим это, чтобы найти x.
600 + x = 720
x = 720 — 600 = 120
Таким образом, недостающий внутренний угол x равен 120°.
Внутренние углы многоугольников
Многоугольник можно считать правильным многоугольником, если все его стороны и углы равны. Вот несколько примеров правильных многоугольников:
Мы уже знаем, что формула суммы внутренних углов многоугольника с ‘n’ сторонами равна 180(n-2)°. В правильном многоугольнике с n сторонами/вершинами n углов. Поскольку все внутренние углы правильного многоугольника равны, каждый внутренний угол можно получить, разделив сумму углов на количество сторон.

Каждый внутренний угол = ((180(n-2))/n)°
Применим эту формулу, чтобы найти внутренний угол правильного пятиугольника. Мы знаем, что количество сторон пятиугольника равно 5 (здесь n = 5). Каждый внутренний угол правильного пятиугольника можно найти по формуле:
((180(n-2))/n)° = ((180(5-2))/5)°
= (180 × 3 )/5 = 540/5
= 108°
Таким образом, каждый внутренний угол правильного пятиугольника = 108°.
Используя ту же формулу, внутренние углы многоугольников рассчитываются следующим образом:
Правильный многоугольник
Сумма внутренних углов, S
Измерение каждого внутреннего угла ((180(n-2))/n)°
Треугольник 180(3-2) = 180° 180/3 = 60°, здесь n = 3 Квадрат 180(4-2) = 360° 360/4 = 90°, Здесь n = 4 Пентагон
180(5-2) = 540° 540/5 = 108°, Здесь n = 5 Шестигранник
180(6-2) = 720° 720/6 = 120°, здесь n = 6 Гептагон
180(7-2) = 900° 900/7 = 128,57°, Здесь n = 7· Октагон
180(8-2) = 1080° 1080/8 = 135°, Здесь n = 8 Нонагон 180(9-2) = 1260° 1260/9 = 140°, здесь n = 9 Декагон 180(10-2) = 1440° 1440/10 = 144°, Здесь n = 10 Похожие статьи о внутренних углах
Ознакомьтесь со следующими страницами, посвященными внутренним углам.

- Вертикальные уголки
- Альтернативные углы
- Альтернативные внешние углы
- Внутренние углы с одной стороны
- Калькулятор внутренних углов многоугольника
Важные примечания
Вот несколько моментов, которые следует помнить при изучении внутренних углов:
- Сумма внутренних углов многоугольника с ‘n’ сторонами может быть рассчитана по формуле 180( п-2)°.
- Каждый внутренний угол правильного многоугольника с ‘n’ сторонами можно рассчитать по формуле ((180(n-2))/n)°.
- Согласно теореме о чередующихся внутренних углах, когда секущая пересекает две параллельные прямые, каждая пара чередующихся внутренних углов равна. И наоборот, если секущая пересекает две прямые так, что пара внутренних углов равна, то эти две прямые параллельны.
- Согласно теореме о внутренних углах, если секущая пересекает две параллельные прямые, каждая пара внутренних углов является дополнительной (их сумма равна 180°).
 Наоборот, если секущая пересекает две прямые так, что пара смежных внутренних углов является дополнительной, то эти две прямые параллельны.
Наоборот, если секущая пересекает две прямые так, что пара смежных внутренних углов является дополнительной, то эти две прямые параллельны.
Примеры внутренних углов
Пример 1: Найдите внутренний угол при вершине B на следующем рисунке.
Решение:
Число сторон данного многоугольника равно n = 6, значит, это шестиугольник (у шестиугольника 6 сторон). Таким образом, сумма внутренних углов этого многоугольника равна 180(n-2)º.
= 180(6-2)
= 180 × 4 = 720°
Мы знаем, что сумма всех внутренних углов в этом многоугольнике равна 720°. Сумма всех углов данного многоугольника:
∠A + ∠B + ∠C + ∠D + ∠E + ∠F
= (x — 60) + (x — 20) + 110 + 120 + 130 + (x — 40)
= 3x+ 240
Теперь примем эту сумму равной 720 и решим ее относительно x.
3x+ 240 = 720
3x = 480
x = 480/3 = 160
Теперь найдем ∠B.

∠B = (x — 20)° = (160 — 20)° = 140°
Следовательно, внутренний угол при вершине B равен ∠B = 140°.
Пример 2: На следующем рисунке MN || ОП и ВКЛ || ПК. Если ∠MNO=55°, то найти ∠OPQ.
Решение:
Продлим линии на данном рисунке.
Здесь, МН || OP, а ON — трансверсаль. Таким образом, 55° и x° являются ковнутренними углами и, следовательно, дополнительными (по теореме о ковнутренних углах). т. е.
55° + x° = 180°
x = 180 — 55 = 125°
Снова ВКЛ || PQ и OP — трансверсаль. Таким образом, x° и ∠OPQ являются соответствующими углами и, следовательно, равны. т. е.
∠OPQ = x = 125°
Следовательно, ∠OPQ = 125°
перейти к слайдуперейти к слайду
Разложите сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок
Практические вопросы по внутренним углам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о внутренних углах
Что такое внутренние углы?
Внутренние углы лежат внутри многоугольника. Например, у треугольника 3 внутренних угла. Другой способ определить внутренние углы: «углы, заключенные во внутренней области двух параллельных линий при пересечении их секущей, называются внутренними углами».
Как найти сумму внутренних углов?
Сумма внутренних углов может быть найдена по формуле 180(n-2)°, где n — количество сторон многоугольника. Например, чтобы найти сумму внутренних углов четырехугольника, заменим в формуле n на 4. Получим 180(4-2)°= 360°.
Какова сумма внутренних углов семиугольника?
Семиугольник — это многоугольник с 7 сторонами и 7 углами. Сумма всех внутренних углов семиугольника равна 180(7-2)°, что равно 900°. Следовательно, сумма внутренних углов семиугольника равна 900 градусов.

Чему равна сумма внутренних углов 27-угольника?
Сумма внутренних углов 27-угольника равна 180(27-2)°. Он равен 180 × 25, что составляет 4500°.
Как решить внутренние углы с одной стороны?
Внутренние углы одной стороны являются дополнительными, когда две параллельные прямые пересекаются секущей. Это означает, что их сумма равна 180 градусам. Итак, для решения таких углов воспользуемся этим свойством и найдем недостающее значение.
Чему равна сумма внутренних углов многоугольника?
Сумма внутренних углов многоугольника с n сторонами может быть рассчитана по формуле 180(n-2)°. Это помогает нам найти общую сумму всех углов многоугольника, будь то правильный многоугольник или неправильный многоугольник. Используя эту формулу, мы также можем проверить свойство суммы углов. Сумма всех внутренних углов треугольника равна 180º, сумма внутренних углов четырехугольника равна 360º и так далее.
Какова сумма внутренних углов треугольника?
Рассчитаем сумму внутренних углов треугольника по формуле суммы внутренних углов S = 180(n-2)°, где n — количество сторон многоугольника.
 Здесь n равно 3, так как у треугольника 3 стороны. Следовательно, сумма равна 180(n-2)° = 180(3-2) = 180°. Таким образом, сумма внутренних углов треугольника равна 180°.
Здесь n равно 3, так как у треугольника 3 стороны. Следовательно, сумма равна 180(n-2)° = 180(3-2) = 180°. Таким образом, сумма внутренних углов треугольника равна 180°.Какова сумма внутренних углов шестиугольника?
Рассчитаем сумму внутренних углов шестиугольника, используя формулу суммы внутренних углов S = 180(n-2)°, где n — количество сторон многоугольника. Здесь n равно 6, так как шестиугольник имеет 6 сторон. Следовательно, сумма равна 180(n-2)° = 180(6-2) = 180 × 4 = 720°. Таким образом, сумма внутренних углов шестиугольника равна 720°.
Сколько внутренних углов у восьмиугольника?
Восьмиугольник имеет восемь сторон и, следовательно, восемь внутренних углов. Сумма этих восьми внутренних углов восьмиугольника равна 1080º.
Какова сумма всех внутренних углов пятиугольника?
Рассчитаем сумму внутренних углов пятиугольника, используя формулу суммы внутренних углов S = 180(n-2)°, где n — количество сторон многоугольника. Здесь n равно 5, так как у пятиугольника 5 сторон.
 Следовательно, сумма равна 180(n-2)° = 180(5-2) = 180 × 3 = 540°. Таким образом, сумма внутренних углов пятиугольника равна 540°.
Следовательно, сумма равна 180(n-2)° = 180(5-2) = 180 × 3 = 540°. Таким образом, сумма внутренних углов пятиугольника равна 540°.Скачать БЕСПЛАТНЫЕ учебные материалы
Скачать рабочие листы по геометрии
Рабочие листы по внутренним углам
1.6 ЭТО ВСЁ ЛОЖЬ! (Ну вроде как!)
Вот классическая загадка.
Однажды женщина решает совершить трехмильную прогулку.
Она начинает с того, что направляется прямо на юг и проходит одну милю, бежит счастливой рысью, любуясь солнцем и дикой природой. Затем она поворачивает налево и направляется прямо на восток одну милю, все время наслаждаясь запахом сладкого воздуха и великолепными видами природы вокруг нее. Затем она поворачивает налево еще раз, ровно , и направляется прямо на север еще одну милю. Удивительно, но после этого третьего отрезка в одну милю она возвращается к тому, с чего начала!
Какого цвета был медведь, которого она увидела на прогулке?
Что?! Какой абсурдный вопрос! Во-первых, совершенно невозможно совершить описанное путешествие и вернуться в исходную точку.

И, во-вторых, ни в одной из предоставленных сведений не упоминается медведь и не содержится намека на его окрас. Эта загадка — неразрешимая ерунда!
Или это?
Оказывается, есть одно место на Земле, где можно пройти милю на юг, милю на восток, милю на север и вернуться в исходное положение, и где можно увидеть медведя. Старт на северном полюсе!
(В этом случае любой увиденный медведь должен быть белым медведем и, следовательно, белым.)
Комментарий: На самом деле в южном полушарии тоже есть бесконечно много разных мест, в которых можно совершить описанное путешествие. (Выберите круг, который проходит вокруг южного полюса с периметром в одну милю, или с периметром в полмили, или с периметром в одну треть мили и т. д. Теперь начните свое трехмильное путешествие на одну милю к северу от круга, который вы определили. .) Но так как в Антарктиде нет медведей, то и загадку там загадывать нельзя. Мы должны быть в северном полушарии.
 9{\circ}\) , пол-оборота!
9{\circ}\) , пол-оборота! Представьте, что вы идете по пути этого большого треугольника, начиная с северного полюса и толкая карандаш прямо перед собой по направлению к экватору. Когда вы достигнете экватора, поверните карандаш так, чтобы он указывал на восток. Проведя карандашом прямо вдоль экватора, вы поворачиваете его на север. Затем вы толкаете карандаш прямо на север, пока не вернетесь к северному полюсу, а затем поворачиваете карандаш на этот третий угол. Можете ли вы увидеть мысленным взором, что если вы действительно сможете провести этот эксперимент, карандаш вернется в исходное положение, но будет направлен в противоположном направлении, как если бы он повернулся на 180 градусов?
Что происходит?
Конечно, вы можете возразить, что этот пример неприменим, потому что Земля не плоская и линии, по которым мы водим карандашом, не прямые. Справедливо. Но тогда почему мы готовы верить, что трюк с карандашом работает должным образом для всех (маленьких) треугольников, которые мы рисуем на листах бумаги или на досках? Откуда мы знаем, что бумага плоская? Откуда мы знаем, что плата не слегка деформирована? Трюк с карандашом всегда говорит, что сумма углов в «треугольнике» равна \(180^{\circ}\) ! 9{\circ}\) включить карандаш?
Так что, возможно, карандаш говорит правду только тогда, когда мы уверены, что стороны фигуры, с которой мы работаем, наверняка прямые.
 В конце концов, мы говорили, что скольжение карандаша вдоль стороны фигуры не приводит к ее повороту.
В конце концов, мы говорили, что скольжение карандаша вдоль стороны фигуры не приводит к ее повороту.Но теперь возникает вопрос: как узнать, является ли путь прямым? Если я выйду наружу и пойду прямо на юг, мой путь, я уверен, покажется мне прямым. Кто-нибудь, наблюдающий из космоса, может сказать, что мой путь извилистый, но здесь, на Земле, я не знаю, как бы я это узнал.
Для треугольника, нарисованного на полу в классе, нам может показаться, что его стороны прямые. Для треугольника, нарисованного на футбольном поле, мы можем почувствовать, что его стороны прямые. Если мы нарисуем треугольник размером с штат Айова, будем ли мы чувствовать, что его стороны прямые?
По мере того, как я все больше и больше сомневаюсь в правильности толкания карандаша, на первый план выходит все больше вопросов и беспокойств. Мой мозг начинает болеть!
Так как же нам выбраться из бесконечных философских солений?
Вернемся к тому, во что нам нравится верить.

В теории геометрии мы считаем, что должно быть какое-то понятие о том, что линия является «прямой», и что мы можем создавать фигуры из отрезков этих прямых линий. На листе бумаги или на классной доске, которую мы считаем «плоской», мы проводим эти линии линейкой, которую считаем прямой. На поверхности Земли отрезки линий, которые мы ощущаем прямыми, иные, это участки больших кругов, как разрез экватора. (Эти линии определенно кажутся «прямыми» на поверхности Земли.)
Но эти две геометрии — геометрия на бумаге и геометрия на сфере — будут разными. Мы не думаем о геометрии поверхности Земли как о «плоской».
А какую разницу мы заметили? Это природа углов внутри треугольников.
Итак, давайте превратим все наши спутанные и туманные мысли в определение и утверждение веры.
Определение: Назовем геометрию плоской , если мы можем быть уверены, что три внутренних угла каждого без исключения треугольника в геометрии имеют меры, складывающиеся с \(180^{\circ}\) .

Фундаментальное предположение о геометрии: Мы предпочитаем верить, что геометрия, изучаемая в школе, плоская.
Вот! Философские разногласия разрешились просто благодаря полной открытости и честности и заявлению о том, что мы собираемся сделать фундаментальное предположение о том, как должна работать наша геометрия. Сферическая геометрия не плоская и должна работать иначе, чем геометрия, которую мы изучаем в школе, которую мы предполагаем плоской.
Великий греческий ученый Евклид (ок. 300–260 гг. до н. э.), провозглашенный одним из величайших умов всех времен, почитается за свою серию из 13 томов, Элементы . Здесь Евклид описывает всю теорию геометрии как основанную на небольшом наборе фундаментальных убеждений и их логических следствий. (Евклид начинает с 10 основных верований, но позже ученые поняли, что Евклид неявно делал дополнительные предположения в своей работе. В конце 1800-х годов немецкий математик Давид Гильберт скорректировал список евклидовских верований до 28 аксиом, чтобы получить полный набор исходных верований, необходимых для логически полная теория геометрии.

- (∠2, ∠8) и (∠3, ∠5) — альтернативные внутренние углы.





 Так как по условию задачи сумма внутренних односторонних углов равна 180 градусов, то сторона АС1 ляжет на прямую а, ВС1 — на прямую b. Тогда точка С1 принадлежит двум прямым: а и b. Т.е. две точки С и С1 одновременно принадлежат двум прямым. А это невозможно. Следовательно прямые a и b не пересекаются, они параллельны.
Так как по условию задачи сумма внутренних односторонних углов равна 180 градусов, то сторона АС1 ляжет на прямую а, ВС1 — на прямую b. Тогда точка С1 принадлежит двум прямым: а и b. Т.е. две точки С и С1 одновременно принадлежат двум прямым. А это невозможно. Следовательно прямые a и b не пересекаются, они параллельны.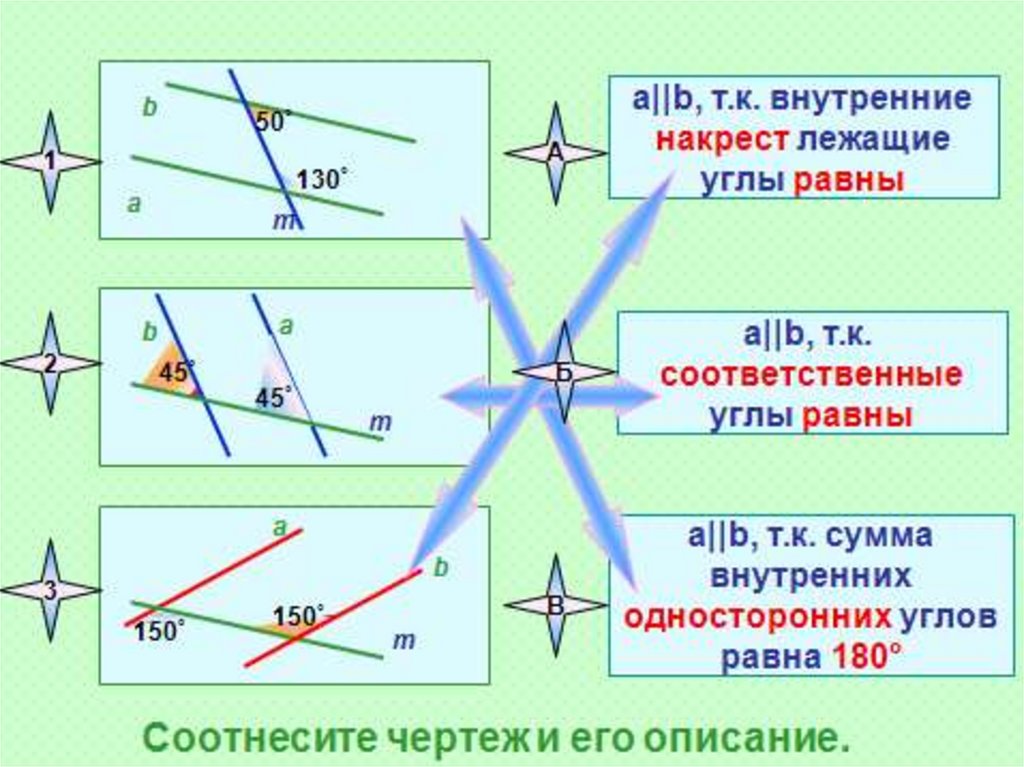
 То в треугольнике АВС образуются два угла 90 градусов, а это невозможно. Следовательно отрезок АВ — это единственный перпендикуляр, проходящий через точку А.
То в треугольнике АВС образуются два угла 90 градусов, а это невозможно. Следовательно отрезок АВ — это единственный перпендикуляр, проходящий через точку А.
 В равнобедренном треугольнике медиана, проведенная из вершины угла к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике медиана, проведенная из вершины угла к основанию, является биссектрисой и высотой. 7 Свойство медианы равнобедренного треугольника.
7 Свойство медианы равнобедренного треугольника.
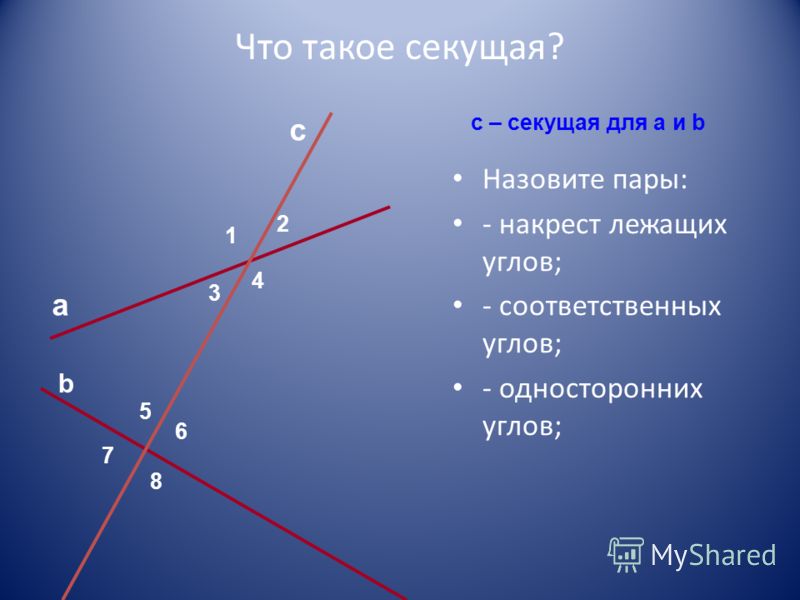 (Рис.8)
(Рис.8) ..
.. Следовательно, биссектрисы d1 и d2 делят углы α и β пополам.
Следовательно, биссектрисы d1 и d2 делят углы α и β пополам.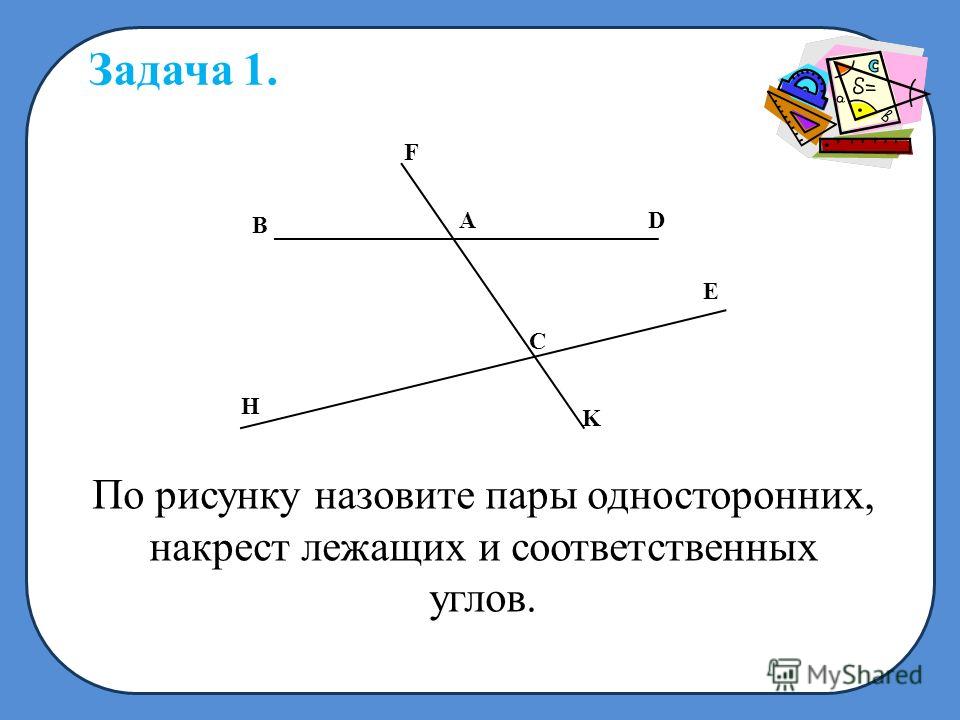 10). Найти остальные углы треугольника.
10). Найти остальные углы треугольника. 11). Найдите угол С треугольника АВС.
11). Найдите угол С треугольника АВС.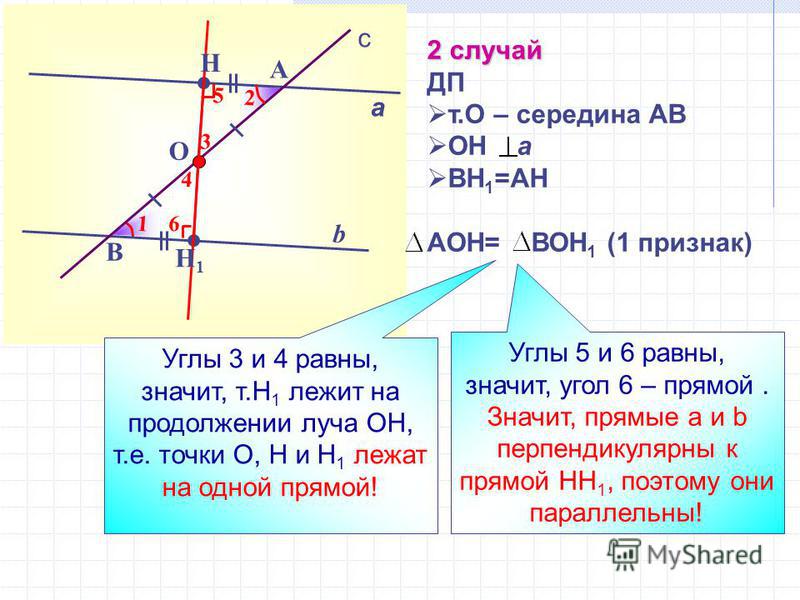 Угол при вершине В составляет 36° (Рис.12). Докажите, что треугольники CDA и ADB равнобедренные.
Угол при вершине В составляет 36° (Рис.12). Докажите, что треугольники CDA и ADB равнобедренные.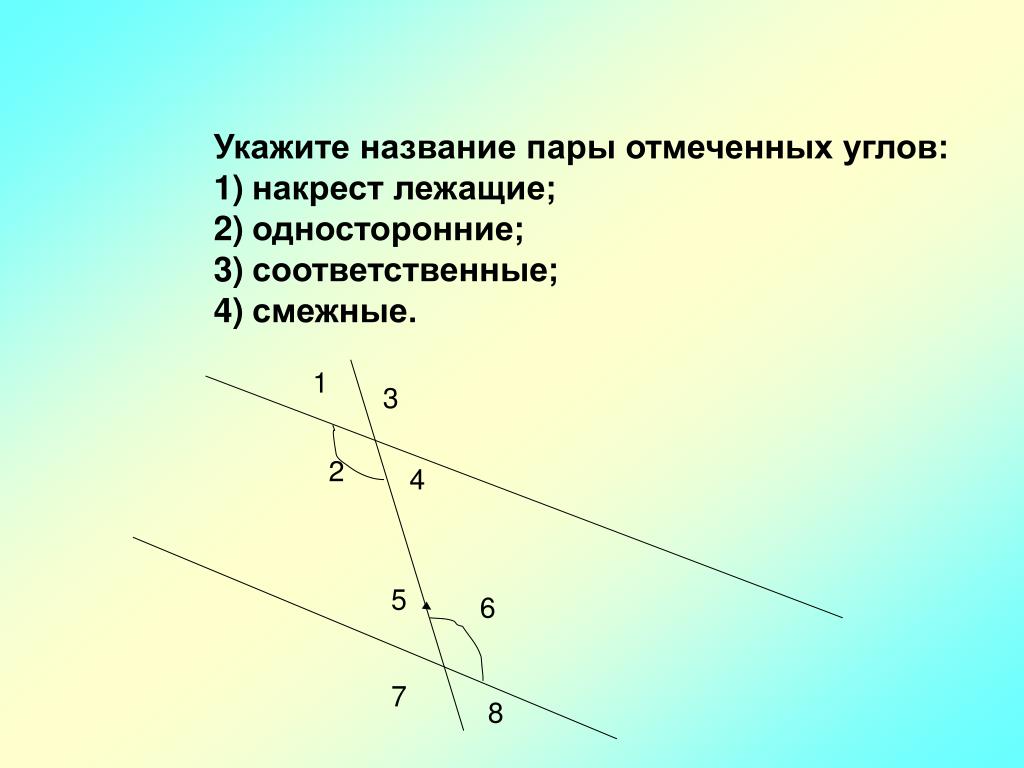 12 Задача. В равнобедренном треугольнике АВС …
12 Задача. В равнобедренном треугольнике АВС …