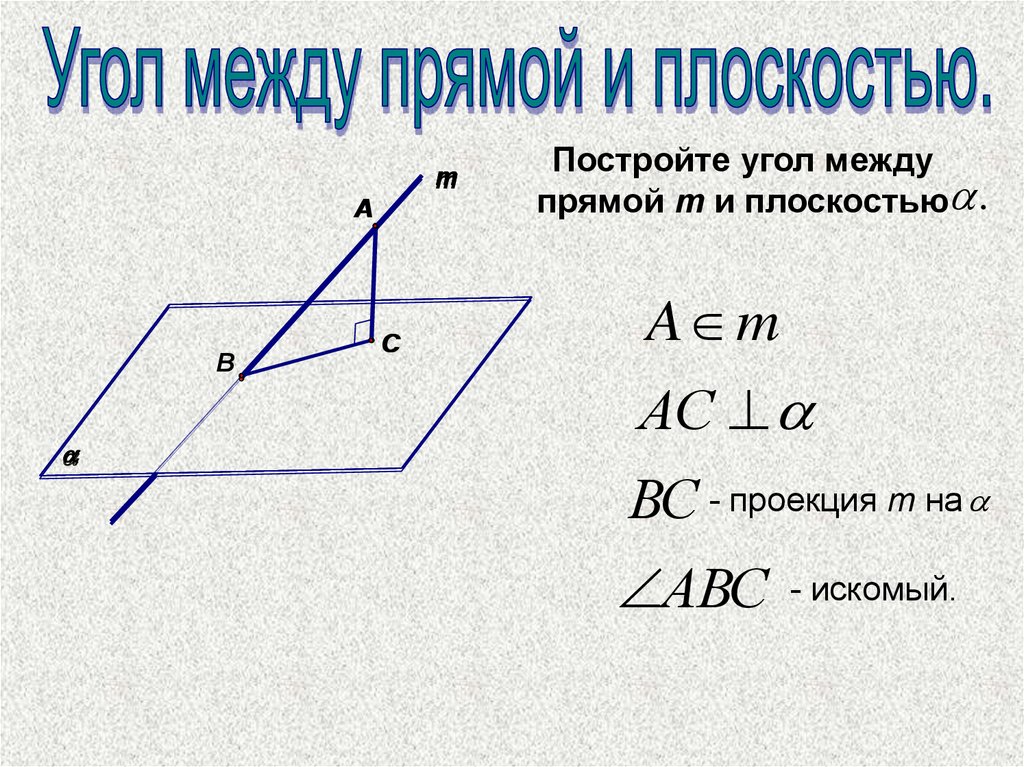
Угол между прямыми онлайн: Онлайн калькулятор. Угол между прямыми

Угол между двумя прямыми на плоскости

• Угол между прямыми, заданными общими уравнениями
• Угол между прямыми, заданными каноническими уравнениями
• Угол между прямыми, заданными уравненями с угловым коэффициентом

Пусть две прямые и заданы общими уравнениями

и .

Так как нормальным вектором прямой является вектор , а нормальным вектором прямой является вектор , то задача об определении угла между прямыми и сводится к определению угла между векторами и .

Из определения скалярного произведения и из выражения в координатах длин векторов и и их скалярного произведения получим

.  (1)

Итак, угол между прямыми, заданными общими уравнениями, определяется с помощью формулы (1).

• Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Пример 1.

Найти угол между прямыми, заданными общими уравнениями и .

Решение. Используя формулу (1), получаем:

Получаем угол .

Пусть две прямые и заданы каноническими уравнениями

и .

Так как направляющими векторами прямых и служат векторы и , то в полной аналогии со случаем, разобранным в предыдущем параграфе, мы получим следующую формулу для определения угла между прямыми:

.   (2)

Итак, угол между прямыми, заданными каноническими уравнениями, определяется с помощью формулы (2).

• Пригодится: тригонометрическая таблица

Пример 2. Найти угол между прямыми, заданными каноническими уравнениями и .

Решение. По формуле (2) находим:

Нет времени вникать в решение? Можно заказать работу!

Пусть две прямые и заданы уравнениями с

угловым коэффициентом

и .

Если и — углы наклона прямых и к оси Ox, то из элементарных соображений следует, что

.

Таким образом,

Получаем следующую формулу для определения угла между прямыми:

.   (3)

Пример 3. Найти угол между прямыми, заданными уравнениями с угловым коэффициентом и .

Решение. По формуле (3) находим:

.

Искомый угол

• Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)

Назад

Листать

Вперёд>>>

Пройти тест по теме Прямая и плоскость

Всё по теме «Прямая на плоскости

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой на плоскости

Уравнение прямой в отрезках

Каноническое уравнение прямой на плоскости

Параметрические уравнения прямой на плоскости

Нормальное уравнение прямой на плоскости, расстояние от точки до прямой

Угол между двумя прямыми | matematicus.

ru

Skip to content

09.04.2019 Artman Аналитическая геометрия на плоскости

Если две не перпендикулярные прямые, обозначенные как L₁, L₂, представляются уравнениями:

y=k₁x+b₁

y=k₂x+b₂

тогда угол между двумя прямыми находится по формуле:

$\tan \theta  = {\text{tan}}\left( {{\alpha _2} — {\alpha _1}} \right) =$

$\frac{{tan{\alpha _2} — tan{\alpha _1}}}{{1 + tan{\alpha _2}tan{\alpha _1}}} = \frac{{{k_2} — {k_1}}}{{1 + {k_1}{k_2}}}$

 таким образом, конечная формула угла между двумя прямыми равна:

Это выражение даёт угол, на который надо повернуть первую прямую L₁, чтобы она стала параллельной второй прямой L₂

---

Примечание 1
Если хотя бы одна из прямых L₁, L₂ параллельна оси OY, то выше написанная формула неприменима.

В этом случае угол θ определяется следующим образом:

1. Если прямая L₂ параллельна оси OY, а прямая L₁ не параллельна, то применяется формула

2. Если прямая L₁

параллельно оси OY, а прямая L₂ не параллельна, то применяется формула

3. Если прямая L₁ и прямая L₂ параллельны оси OY, то они и параллельны друг другом, так что

tgθ = 0

---

Примечание 2
Угол между прямыми, заданными уравнениями

A₁x+B₁y+C1=0 и A₂x+B₂y+C2=0

можно найти по формуле

  
В случае, если A₁A₂+B₁B₂=0, то угол θ=±90 

---

Примечание 3
Если прямые перпендикулярны (θ=±90), то выражение 1+k₁k₂, находящиеся в знаменателе, равно в нулю и тогда θ надо считать равным ±90

---

Пример 1
Найти угол между прямыми

y=3x-2 и y=-2x+3.

Решение
Здесь k₁=3, k₂=-2

 $\tan \theta  = \frac{{{k_2} — {k_1}}}{{1 + {k_1}{k_2}}} =$

$\frac{{ — 2 — 3}}{{1 + 3\cdot\left( { — 2} \right)}} = 1$

Отсюда θ=+45⁰

---

Пример 2
Найти угол между прямыми y=2x−1 и y=−1/2x+5

Решение
Здесь k₁=2, k₂=−1/2   

 $\tan\theta  = \frac{{{k_2} — {k_1}}}{{1 + {k_1}{k_2}}} = $

$\frac{{ — \frac{1}{2} — 2}}{{1 + \left( { — \frac{1}{2}} \right)\cdot2}} = \frac{{ — 2\frac{1}{2}}}{0}$

Отсюда из примечания 3 следует, что θ=±90⁰

---

2???

???y=1???

???(-1,1)???

Нам нужно найти касательные для обеих кривых в каждой из точек пересечения. Помните, что для нахождения касательной мы возьмем производную функции, а затем оценим производную в точке пересечения, чтобы найти там наклон касательной. Затем мы подставим наклон и точку касания в формулу наклона точки, чтобы найти уравнение касательной.

2???: 92-1???:

???y=-4x-3???

???4x+y=-3???

???\langle4,1\rangle???

Подводя итог нашим выводам, мы можем сказать, что нам нужно найти острый угол

между векторами ???a=\langle-2,1\rangle??? и ???b=\langle-4,1\rangle??? в точке ???(1,1)???

между векторами ???c=\langle2,1\rangle??? и ???d=\langle4,1\rangle??? в точке ???(-1,1)???

Прежде чем мы сможем использовать формулу косинуса для нахождения острого угла, нам нужно найти скалярные произведения ???a\cdot b??? и ???c\cdot d??? и величина каждого вектора. 9\циркуляр???

Получить доступ к полному курсу Calculus 3

Угол между двумя линиями — Формула, примеры

Угол между двумя линиями помогает узнать взаимосвязь между двумя линиями. Это мера наклона между двумя линиями. Для двух пересекающихся прямых существует два угла между прямыми: острый угол и тупой угол. Здесь мы рассматриваем острый угол между прямыми, для угла

между двумя прямыми .

Угол между двумя линиями полезен для нахождения меры угла между двумя сторонами замкнутого многоугольника. Проверим формулы и примеры для угла между двумя прямыми в координатной плоскости и трехмерном пространстве..

1.	Как найти угол между двумя линиями?
2.	Формулы для угла между двумя линиями
3.	Угол между двумя линиями в трехмерном пространстве
4.	Примеры угла между двумя линиями
5.	Практические вопросы
6.	Часто задаваемые вопросы об угле между двумя линиями

Как найти угол между двумя линиями?

Угол между двумя линиями можно рассчитать, зная наклон двух линий или зная уравнение двух линий. Угол между двумя линиями обычно дает острый угол между двумя линиями.

Угол между двумя линиями можно вычислить по наклону двух линий и с помощью функции тригонометрического тангенса. Рассмотрим две линии с наклонами \(m_1\) и \(m_2\) соответственно. Острый угол θ между прямыми можно вычислить по формуле функции тангенса. Острый угол между двумя прямыми находится по следующей формуле.

Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\)

Далее, мы можем найти угол между двумя линиями, если даны уравнения двух линий. Пусть уравнения двух линий будут \(l_1 = a_1x + b_1y + c_1 = 0\) и \(l_2 = a_2x + b_2y + c_2 = 0\). Угол между двумя прямыми можно вычислить по тангенсу угла между двумя прямыми.

Tanθ =\(\dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\)

Формулы для угла между двумя линиями

Следующие различные формулы помогают легко найти угол между двумя линиями.

• Угол между двумя линиями, одна из которых представляет собой ax + by + c = 0, а другая линия является осью x, равен θ = Tan ^-1 (-a/b).
• Угол между двумя линиями, одна из которых является линией y = mx + c, а другая линия является осью x, равен θ = Tan 92}{2bc}\)

Угол между двумя линиями в трехмерном пространстве

Угол между двумя линиями в трехмерном пространстве можно вычислить аналогично углу между двумя линиями в координатной плоскости.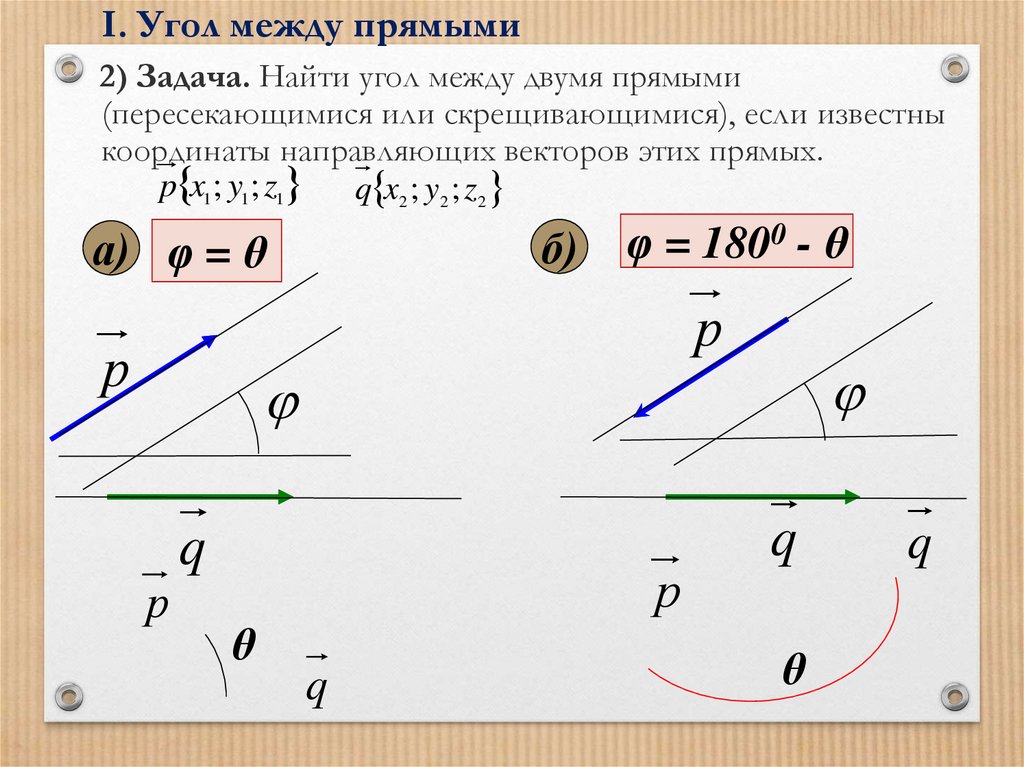 Для двух линий с уравнениями \(r = a_1 + λb_1\) и \(r = a_2 + λb_2\) угол между линиями определяется следующей формулой.

Cosθ = \(\dfrac{b_1.b_2}{|b_1|.|b_2|}\)

Далее для двух линий, имеющих отношение направлений как \((a_1, b_1, c_1)\), и \( (a_2, b_2, c_2)\), угол между линиями можно вычислить по приведенной ниже формуле. 92}}\)

Также для двух прямых, имеющих направляющие косинусы \(l_1, m_1, n_1\) и \(l_2, m_2, n_2\), угол между двумя прямыми можно вычислить по следующей формуле .

Cosθ = \(|l_1.l_2 + m_1.m_2 + n_1.n_2|\)

Связанные темы

Следующие темы помогут лучше понять понятие угла между двумя линиями.

• Координатная геометрия
• Уравнение прямой
• Параллельные линии
• Типы углов

Примеры угла между двумя линиями

1. Пример 1: Найдите угол между двумя линиями, имеющими наклон 1 и 1/2 соответственно.

   Решение:

   Наклоны двух прямых равны \(m_1\) = 1 и \(m_2\) = 1/2.

   Формула для нахождения угла между двумя линиями: Tanθ = \(\frac{m_1 — m_2}{1 + m_1.m_2}\).

   Tanθ = \(\frac{1 — 1/2}{1 + 1/2.1}\) 9{-1} \frac{1}{3}\).

2. Пример 2: Найдите угол между двумя прямыми, используя уравнения 3x + 4y — 10 = 0 и 4x -5y + 2 = 0. + 4y — 10 = 0 и 4x -5y + 2 = 0.

   Здесь мы имеем \(a_1 = 3, b_1 = 4, a_2 = 4, b_2 = -5\)

   Угол между двумя линиями может рассчитать по формуле Tanθ =\(\dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\). 9{-1}-\frac{31}{8}\).

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по углу между двумя линиями

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об угле между двумя линиями

Как найти угол между двумя линиями?

Угол между двумя линиями можно рассчитать по наклону линий или по уравнению двух линий.