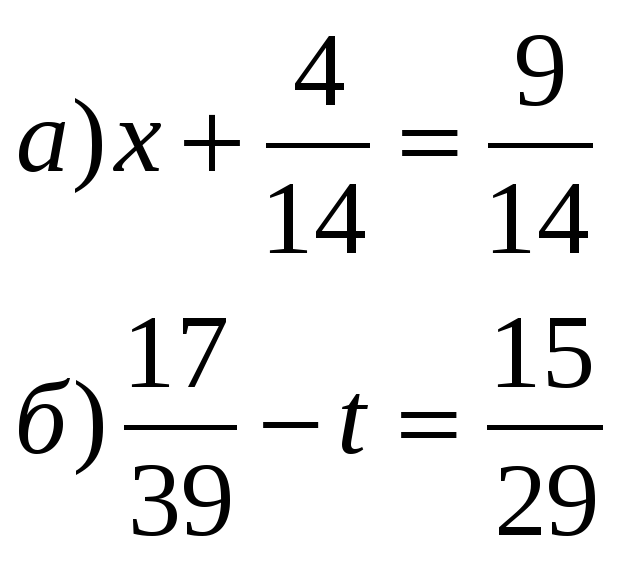Решение уравнений 9 класса по математике
Решение уравнений по математике 9 класс
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Решение уравнений девятого класса подразумевает применение множества разнообразных способов решения: графических, методов алгебраического сложения, введение новых переменных, применение функций и преобразование уравнений из одного вида в более простой и многое другое. Метод решения уравнения выбирается на основании исходных данных, поэтому лучше всего разбирать методы наглядно на примерах.
Допустим, дано уравнение следующего вида:
Чтобы решить данное уравнение поделим левую и правую части на \[x.\]
Далее приведем дробные члены левой части к НОЗ:
Полученные два корня являются решением данного уравнения.
Необходимо найти сумму всех корней данного уравнения. Для этого необходимо выполнить замену:
Для этого необходимо выполнить замену:
Корнями данного уравнения будут 2 числа: -1 и 4. Следовательно:
Сумма всех 3 корней равна 4, что и будет являться ответом в решении данного уравнения.
Где можно решить уравнения онлайн 9 класс?
Решить уравнение вы можете на нашем сайте https://pocketteacher. ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk. com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Корнями данного уравнения будут 2 числа -1 и 4.
Pocketteacher. ru
17.04.2019 19:59:34
2019-04-17 19:59:34
Источники:
Https://pocketteacher. ru/solve-equations-ru
Решение уравнений в рамках подготовки к ОГЭ. 9 класс | План-конспект урока по алгебре (9 класс): | Образовательная социальная сеть » /> » /> .keyword { color: red; }
Решение уравнений по математике 9 класс
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Предварительный просмотр:
Урок в 9А классе на тему «Решение уравнений в рамках подготовки к ОГЭ»
Учебник Алгебра 9: для общеобразовательных учреждений. Макарычев Ю. Н.
Цель урока: отработка предметного навыка решения уравнений в формате ОГЭ.
- Повторить все известные нам виды уравнений; Вспомнить способы решения этих уравнений; Решать уравнения из заданий демонстрационных вариантов ОГЭ 2018-2018 года.
 Способствовать развитию логического мышления. Развивать коммуникативные навыки.
Способствовать развитию логического мышления. Развивать коммуникативные навыки.Оборудование: компьютер, проектор, экран, раздаточный материал, тетради, учебник.
I. Организационный момент (1 мин)
— Здравствуйте! Посмотрите, пожалуйста, друг на друга и от всей души улыбнитесь.
II. Актуализация знаний.
1. Установите соответствие между выражением и значением выражения ( Слайд 3).
Выражения: А) Б) В)
Значения выражений: 1) 6 2) 7,5 3) 1,3 4) 1,75 Ответ: 214
Решить устно: ( Слайд 4)
1) 0x = 5 ; 2) 0,5x = 0; 3) 0x = 0; 4) 2x = 19. 5) ;
III. Основная часть.
Виды уравнений. Алгоритмы решения уравнений.
— Что мы сейчас делали? (решали уравнение)
— А какие виды уравнений и способы мы использовали? (
— Значит, чем мы будем заниматься на уроке? (решать различные уравнения)
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее большинство задач реального мира сводится к решению различных видов уравнений. Начнем наш урок с повторения теоретического материала. Вспомним о видах уравнений (слайды 5-13).
Подавляющее большинство задач реального мира сводится к решению различных видов уравнений. Начнем наш урок с повторения теоретического материала. Вспомним о видах уравнений (слайды 5-13).
Устно Я проговариваю предложения. Если оно справедливо – вы хлопаете, если нет – то топаете. ( Слайд 14)
2. Формирование умений и навыков.
1. По учебнику стр 13 № 29(а), 30 (б, г,е), 31 (а, в).
2. Раздаточный материал. Решить уравнения с сайта «Решу ОГЭ».
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания Ответ: -40
На листочках, по вариантами решить с/р (5 уравнений на «5»)
1 вариант. Решить уравнения
2 вариант. Решить уравнения
(х + 2) 2 = (х – 4) 2 Если корней несколько, запишите их в ответ без пробелов в порядке возрастания 10х + 9 = 7х 3 – х 2 + 8х + 12 = 0 Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
6. * х 4 – 5х 2 – 6 = 0
х 2 + 3х + 2 = 0 Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. 2 – 3(2х + 2) = 5 – 4х Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. х 2 + 3х = 4
6. * х(х 2 + 2х + 1) = 2(х+1)
Ответы: 1 вариант: 1; -3; 6,3; -6-2; -46,5 №6
2 вариант: -2-1; -4,5; -41; -1,25; -20; №6 -2, -, 1
IV. Подведение итогов урока : и так, мы проделали большую работу. Как вы думаете, достигли ли мы цели, которую мы поставили в начале урока? Повторили всю теорию, касающуюся целых рациональных уравнений. Прорешали различные их виды
V. Домашняя работа : 925, 935 (а, в,д)
Резервное задание: по учебнику стр 229 № 935 (г)
По теме: методические разработки, презентации и конспекты
Повторение теории и решение тригонометрических уравнений в рамках подготовки к ЕГЭ
В рамках подгоовки к ЕГЭ: — Повторить и систематизировать раннее изученный материал по решению простейших тригонометрических уравнений. — Решение уравнений, с выбором ответов.- Воспиты.
— Решение уравнений, с выбором ответов.- Воспиты.
Урок по теме «Решение уравнений и систем уравнений в рамках подготовки к ЕГЭ» — Конспект урока
Цели:Систематизировать, расширить и углубить знания по данной темеСпособствовать развитию умения сравнивать, обобщать, классифицировать, анализировать, делать выводыПрививать умение сотрудничать, оказ.
Если оно справедливо вы хлопаете, если нет то топаете.
Nsportal. ru
08.06.2019 22:47:49
2019-06-08 22:47:49
Источники:
Https://nsportal. ru/shkola/algebra/library/2019/03/05/reshenie-uravneniy-v-ramkah-podgotovki-k-oge-9-klass
Конспект урока по алгебре в 9 классе по теме: «Целое уравнение и его корни. Решение упражнений» » /> » /> .keyword { color: red; }
Решение уравнений по математике 9 класс
Методы обучения: словесный, наглядный, практический, проблемный.
Цели: закрепить умения и навыки решения целых уравнений используя методы разложения многочлена на множители и введения новой переменной, использовать полученные знания для решения уравнений высших степеней; формирование умения применять накопленные знания для решения заданий повышенного уровня сложности в ОГЭ.
Планируемые результаты:
Предметные: научить в процессе реальной ситуации использовать определения следующих понятий: «корень уравнения», «степень уравнения», повторить способы решения уравнений первой и второй степени.
Личностные: приобретают навыки сотрудничества со взрослыми и сверстниками; установка на здоровый образ жизни, наличие мотивации к творческому труду, к работе на результат.
Регулятивные: умение обрабатывать информацию и ранжировать ее по указанным основаниям; формировать коммуникативную компетенцию учащихся; выбирать способы решения уравнений; контроль и оценка процесса и результатов деятельности.
Познавательные: овладение логическими действиями сравнения, анализа, синтеза.
Коммуникативные: готовность слушать собеседника и вести диалог; готовность признать возможность существования различных точек зрения и права каждого иметь свою; излагать своё мнение и аргументировать свою точку зрения.
Оборудование: классная доска, учебник, раздаточные материалы, ноутбук.
Организационный момент. Мотивация учебной деятельности.
Приветствие, создание рабочей атмосферы.
Здравствуйте, ребята! Какое у вас сегодня настроение? Улыбнитесь друг другу. Давайте проверим готовность к уроку! Садитесь! Начинаем наш урок! (дети осуществляют самоконтроль готовности к уроку).
Наш урок я хотела бы начать со следующих слов:
Человек родился быть господином, повелителем, царём природы, но мудрость, с которой он должен править, не дана ему от рождения:
Она приобретается учением.
Николай Иванович Лобачевский
Я желаю, чтобы сегодня наш урок был полезен для Вас, и вы приобрели частицу своей мудрости.
У каждого из Вас на столах лежат листы самооценки. Давайте заполним их, отметим настроение, с которым вы пришли на урок.
Актуализация опорных знаний. Определение темы и цели урока.
— Ребята что вы видите на доске? (Уравнения).
— Что такое уравнение? (Равенство, содержащее переменную)
-А что с уравнением обычно делают? (Решают)
— А что значит решить уравнение? (Найти все его корни, или доказать, что
— Что называется корнем уравнения? (Значение переменной, при котором уравнение
Обращается в верное числовое равенство).
А сейчас каждый из Вас решит уравнения, которые вы видите на доске.
Самопроверка.
(В листах самооценки те, кто получил оценку 3 ставят 1 балл; 4 или 5 – 2 балла)
Сообщение темы урока, определение целей урока.
Ребята, как называются уравнения, которые вы только что решали? (учащиеся могут ответить линейные, квадратные – но ы итоге сделают вывод, что это Целые уравнения)
Верно. На прошлом уроке, мы с Вами начали знакомство с целыми уравнениями. Сегодня мы продолжим о них говорить, углубим наши знания и закрепим умение решать эти уравнения.
Итак, запишите тему урока: «Целое уравнение и его корни. Решение упражнений».
Давайте определим цели, которые мы поставим перед собой.
3. Усвоение новых знаний.
Продолжим урок повторением теоретического материала (фронтальный опрос учащихся).
Какое уравнение называется Целым?
Уравнение с одной переменной называют целым уравнением, если обе его части являются целыми выражениями.
Если рациональное выражение не содержит деление на выражение с переменной, то его называют целым, в противном случае дробным.
Что называется Степенью Уравнения?
Всякое целое уравнение с одной переменной можно преобразовать в равносильное ему уравнение вида Р(х)=0, где Р(х)-многочлен стандартного вида.
Наибольший показатель степени, в которой переменная содержится в уравнении Р(х)=0, называется степенью уравнения.
Если уравнение с одной переменной записано в виде Р(х)=0, где Р(х)-многочлен стандартного вида, то степень этого многочлена называют степенью уравнения.
Давайте выполним, следующее задание (устно):
Какова степень уравнения и сколько корней имеет каждое из уравнений:
Ответы: а) 5, б) 6, в) 5, г) 2, д) 1.
Уравнение N-ой степени может иметь не более N Корней.
Мы знаем формулы, по которым решают линейные и квадратные уравнения. Для уравнений 3 и 4 степени также известны формулы корней, но они очень сложны и неудобны для практического применения. Что касается уравнений пятой и более высоких степеней, то общих формул корней не существует.
Для уравнений 3 и 4 степени также известны формулы корней, но они очень сложны и неудобны для практического применения. Что касается уравнений пятой и более высоких степеней, то общих формул корней не существует.
Уравнение вида, где х — переменная, а,B,с – некоторые числа, причём а≠0, называется биквадратным.
Целое уравнение можно решить несколькими способами:
Вам предстоит итоговая аттестация по математике в форме ОГЭ Чтобы успешно сдать ОГЭ, вы должны знать математику не только на базовом уровне, но и применить ваши знания в нестандартных ситуациях. Во II части экзаменационной работы №21 часто встречаются уравнения высших степеней, а впервой части №4 – это уравнения первой и второй степеней.
4. Первичное закрепление.
Теперь давайте решим уравнения используя эти методы.
(Каждый, кто решал уравнение у доски ставит в листах самооценки 1 балл)
А) (Метод разложения на множители)
Б ) (Метод введения новой переменной)
Минутка релаксации.
«Сядьте в удобное положение. Расслабьтесь. Теперь закройте глаза и слушайте меня.
Представьте себе чудесное солнечное утро. Вы находитесь возле тихого озера. Слышны лишь ваше дыхание и плеск воды.
Солнце ярко светит, и это заставляет вас чувствовать себя все лучше и лучше. Вы чувствуете, как солнечные лучи согревают вас. Вы слышите щебет птиц и стрекотанье кузнечика. Вы абсолютно спокойны. Солнце светит, воздух чист и прозрачен. Вы ощущаете всем телом тепло солнца. Вы спокойны и неподвижны, как это тихое утро.
Вы чувствуете себя спокойными и счастливыми, вам лень шевелиться. Каждая клеточка вашего тела наслаждается покоем и солнечным теплом. Вы отдыхаете…
А теперь открываем глаза. Мы снова в школе, мы хорошо отдохнули, у нас бодрое настроение, и приятные ощущения не покинут нас в течение всего дня»
В) (Метод введения новой переменной)
4. Творческое применение знаний.
Самостоятельное решение уравнений:
Х³+2х²−4х−8=0 (Ответ: х= ±2)
Х 4 – 7х 2 + 12 = 0. (Ответ: х= ±2, ± )
(Ответ: х= ±2, ± )
(Каждое верно решенное уравнение оценивается в 1 балл:
2 верно решенных – 2 балла; 1 верно решенное – 1 балл)
5.Подведение итогов урока. Рефлексия
— Какое уравнение с одной переменной называется целым? Приведите пример.
— Как найти степень целого уравнения? Сколько корней имеет уравнение с одной переменной первой, второй степени?
-Дайте определение биквадратного уравнения. Объясните, как решают биквадратные уравнения?
-Уравнения каких степеней мы рассмотрели?
Для курса высшей математики известны формулы для нахождения корней третьей и четвёртой степени, однако они сложны и громоздки и не имеют практического применения. Для уравнений пятой и более высоких степеней формул не существует. Это было доказано в 19 веке Нильсом Абелем и Эваристом Галуа.
х 4 – 7х 2 + 12 = 0. (Ответ: х= ±2, ± )
А сейчас каждый из Вас решит уравнения, которые вы видите на доске.
Ответы а 5, б 6, в 5, г 2, д 1.
Multiurok. ru
19.10.2017 7:39:26
2017-10-19 07:39:26
Источники:
Http://multiurok. ru/files/konspekt-uroka-po-algebre-v-9-klasse-po-teme-tselo. html
10 Методы решения уравнений, содержащих целые или дробные части
К числу нестандартных относятся методы решения уравнений, которые содержат целые и (или) дробные части действительных чисел. В программе школьной математики методы решения таких уравнений не изучаются. В настоящем разделе применение существующих методов и приемов иллюстрируется на примерах решения ряда уравнений.
Целой частью действительного числа (илиАнтье) называется наибольшее целое число, не превосходящее , и это число обозначается. Очевидно, чтоРазностьназывается дробной частью числа(илиМантисса) и обозначается через Из определения следует, чтоКроме того, справедливо равенство
(10.1)
Например, имеет место
Отметим
некоторые свойства введенного выше
понятия целой части действительного
числа.
Для произвольных действительных чисел имеет место неравенство
Кроме того, для любого действительного числа справедливо
. (10.2)
Перейдем теперь к рассмотрению уравнений, содержащих целую и (или) дробную части неизвестной переменной.
Задачи и решений
Пример 10.1. Решить уравнение
(10.3)
Решение. Поскольку являются целым числом, то- тоже целое число. Следовательно, числотакже является целым. В таком случаеи уравнение (10.3) принимает видЦелыми корнями последнего уравнения являются
Ответ:
Пример 10.2. Решить уравнение
(10.4)
Решение. Рассмотрим
последовательно три случая.
Рассмотрим
последовательно три случая.
Если , т.е. решением уравнения (10.4) могут быть только
Пусть тогда из уравнения (10.4) следует, чтоТак как, то получаем систему неравенств
Решением данной системы неравенств являются .
Если Следовательно, уравнение (10.4) не имеет корней среди
Ответ:
Пример 10.3. Решить уравнение
(10.5)
Решение. Используя свойство (10.2), можно записать
Так как то, складывая почленно три приведенные выше неравенства, получим
Отсюда, принимая во внимание уравнение (10.5), следуют неравенства
(10.6)
Поскольку
в этом случае
следует,
что. Так как- целое число, то отсюда получаем, чтоСледовательно, имеем
Так как- целое число, то отсюда получаем, чтоСледовательно, имеем
Из уравнения (10.5) следует, что – целое число. Так както остается лишь проверить целые значенияНетрудно установить, что решениями (10.5) являются
Ответ:
Пример 10.4. Решить уравнение
(10.7)
Решение. Из формулы (10.1) следует, что В этой связи уравнение (10.7) можно переписать, как
Отсюда следует уравнение
(10.8)
Очевидно, что является корнем уравнения (10.8). Положим, чтоТогда разделим обе части уравнения (10.9) наи получим уравнение
(10.9)
Рассмотрим последовательно несколько случаем.
Если В таком случае
Если
Если
Если
Отсюда следует, что уравнение (10. 9) корней
не имеет.
9) корней
не имеет.
Следовательно, уравнение (10.7) имеет единственный корень
Ответ:
Пример 10.5. Решить уравнение
(10.10)
Решение. Решая тригонометрическое уравнение (10.10), получаем
(10.11)
где – целое число. Из уравнения (10.11) получаем совокупность двух уравненийЛевые части обоих уравнений являются целыми числами, в то время как их правые части (за исключением случаяв первом уравнении) принимают иррациональные значения.
Следовательно, равенство в уравнениях совокупности может иметь место только в том случае, когда правые их части являются рациональными (точнее, целыми) числами. А это возможно лишь в первом уравнении при условии, что В этом случае получаем уравнениеоткуда следует
Ответ:
Пример
10.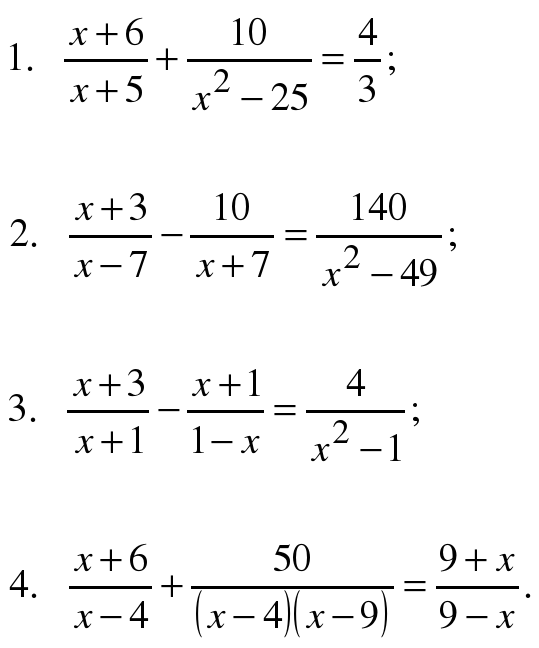 6. Решить
уравнение
6. Решить
уравнение
(10.12)
Решение. Левая часть уравнения (10.12) принимает только целые значения, поэтому число является целым.
Так как то при любом целоммногочленпредставляет собой произведение трех последовательно расположенных на числовой осицелых чисел, среди которых имеется хотя бы одно четное число и число, кратное трем. Следовательно, многочленделится набез остатка, т.е.является целым числом.
В этой связи и уравнение (10.12) принимает видили
(10.13)
Так как то корнями уравнения (10.13) являются
Ответ:
Пример 10.7. Доказать равенство
(10.14)
для произвольного действительного числа
Доказательство. Любое число
можно представить или какгде- целое число и
Любое число
можно представить или какгде- целое число и
Рассмотрим два возможных случая.
Пусть Так как
и
Пусть тогда
и
Таким образом, равенство (10.14) выполняется для каждого из двух рассмотренных выше случаем. Следовательно, равенство (10.14) доказано.
Заключение
В результате работы над дипломным проектом был проведен анализ решения нестандартных типов решения тестовых задач. Все рассмотренные задачи, решаемые нестандартными методами, классифицированы по следующим типам:
метод функциональной подстановки
методы, основанные на применении численных неравенств,
метод тригонометрической подстановки;
методы, основанные на монотонности функций,
методы решения функциональных уравнений,
методы, основанные на применении векторов,
комбинированные методы,
методы, основанные на использовании ограниченности функций,
методы решения симметрических систем уравнений,
методы решения уравнений, содержащих целые или дробные части числа.

В каждом из этих типов рассмотрены конкретные примеры и методы их решения.
Материал, содержащийся в дипломной работе, представляет собой основу методического пособия, которое можно при определенной доработке, внедрять как в школьный процесс, так и при подготовке абитуриентов к поступлению.
Список использованных источников
Азаров, В.И. Функциональные методы решения задач [текст] : учебное пособие / В.И. Азаров, О.П. Тавгень, В.С. Федосенко. – Мн. :БГУ,1994.
Азаров, А.И Экзамен по математике: руководство к решению задач [текст] : справочное пособие / С.В. Пруцко, В.С. Федосенко. – Мн. :ТетраСистем, 2001.
Ивлев, Б.М. Задачи повышенной трудности по алгебре и началам анализа [текст] : учебное пособие / Б.М. Ивлев, А.М.Абрамов, Ю.П. Дудницин, С.И. Шварцбург. -М. :Просвещение, 1990.
Габринович, В.
 А. Решим любую задачу [текст] : учебное
пособие / В.А. Габринович, В.И. Громак. –
Мн. :Асар, 1996.
А. Решим любую задачу [текст] : учебное
пособие / В.А. Габринович, В.И. Громак. –
Мн. :Асар, 1996.Мандрик, П.А. Экзамен по математике на пять [текст] : учебное пособие / П.А. Мандрик, В.И. Репников. – Мн. :тетраСистемс, 1999.
Олехник, С.Н. Нестандартные методы решений уравнений и неравенств [текст] : учебное пособие / С.Н. Олехник, М.К. Потапов, П.И. Пасаиченуо. – М. :МГУ, 1991.
Пруцко, С.В. Экзамен по математике [текст] : руководство к решению задач : учебное пособие / С.В. Пруцко, А.И. Азаров, В.С. Федосенко. – МН. :тетраСистемс, 2001.
Пруцко, С.В. руководство к решению конкурсных задач по математике [текст] : учебное пособие / С.В. Пруцко, А.И. Азаров, В.С. Федосенко. – МН. :тетраСистемс, 1999.
Сборник задач по математике для поступающих во втузы [текст] / под редакцией М.И.Сканави. – Мн. :Высшая школа, 1990.

Супрун, В.П. Избранные задачи повышенной сложности по математике [текст] / В.П. Супрун. Мн. :Полымя, 1998.
Супрун, В.П. Нестандартные методы решения задач по математике [текст] / В.П. Супрун. –Мн. :Полымя, 2000.
Исчисление дробей 分数阶微积分 Дифференциальные уравнения дробных чисел 分数阶微分方程
В математике дифференциальное уравнение в частных производных (УЧП) — это дифференциальное уравнение, содержащее неизвестные функции многих переменных и их частные производные. УЧП используются для формулировки задач, включающих функции нескольких переменных,
и либо решаются компьютерами, либо используются для создания компьютерной модели. Особый случай — обыкновенные дифференциальные уравнения (ОДУ), которые имеют дело с функциями одной переменной и их производными.
УЧП используются для формулировки задач, включающих функции нескольких переменных,
и либо решаются компьютерами, либо используются для создания компьютерной модели. Особый случай — обыкновенные дифференциальные уравнения (ОДУ), которые имеют дело с функциями одной переменной и их производными.
PDE можно использовать для описания широкого спектра явлений, таких как звук, тепло, диффузия, электростатика, электродинамика, гидродинамика, упругость, гравитация и квантовая механика. Эти, казалось бы, разные физические явления можно аналогичным образом формализовать в терминах УЧП. Точно так же, как обыкновенные дифференциальные уравнения часто моделируют одномерные динамические системы, уравнения в частных производных часто моделируют многомерные системы.
Дифференциальные уравнения дробного порядка (ДДУ) могут описывать динамику нескольких сложных и нелокальных систем с памятью. Они возникают во многих областях науки и техники, таких как физика, химия, биология, биофизика, экономика,
теория управления, обработка сигналов и изображений и т. д. В частности, нелинейные системы, описывающие различные явления, можно моделировать с помощью дробных производных. В некоторых фракционных моделях также сообщалось о хаотическом поведении.
Имеются теоретические результаты, касающиеся существования и единственности решений начальных и краевых задач с дробными дифференциальными уравнениями [1-5].
д. В частности, нелинейные системы, описывающие различные явления, можно моделировать с помощью дробных производных. В некоторых фракционных моделях также сообщалось о хаотическом поведении.
Имеются теоретические результаты, касающиеся существования и единственности решений начальных и краевых задач с дробными дифференциальными уравнениями [1-5].
В этой статье показано, что аналитическое решение уравнения дробного деления решается с помощью MathHand.com. MathHand.com — математический онлайн-калькулятор, бывший SymbMath [6-7].
Он рассматривается как Math Handbook Calculator [8].
Примеры включали дробное дифференциальное уравнение, дробное уравнение в частных производных, дробное интегральное уравнение, уравнение смешанного дробного дифференциального и интегрального порядков,
система дифференциального уравнения дробного порядка, дифференциальное уравнение комплексного порядка и дифференциальное уравнение переменного порядка.
По умолчанию определение дробного исчисления Капуто [9] используется здесь.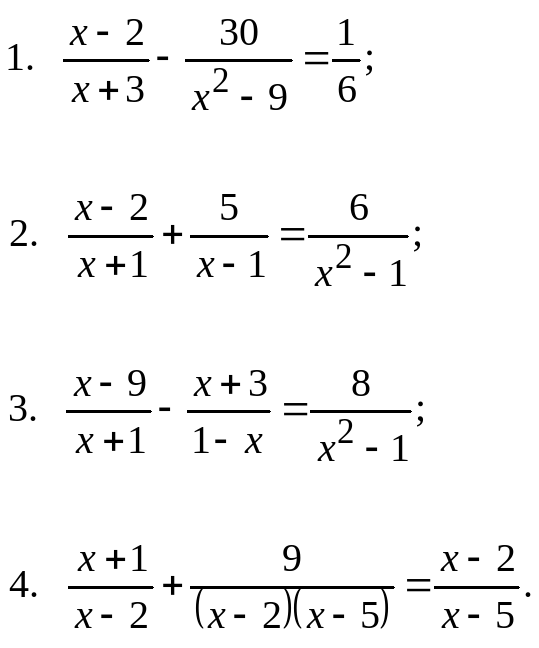
Таблица 1. Сравнение различных заказов
9((1))(х) — 2у = ехр(х)`
Или введите функцию dsolve(), нажмите кнопку « = » для решения, затем нажмите кнопку « test «, чтобы проверить решение.
например
введите dsolve( ds(y) — 2y = exp(x)) для
dsolve `dy/dx — 2y = exp(x)`
Ее решение находится в таблице 2.
Таблица 2. Сравнение дифференциальных уравнений разных порядков
| Заказ | наименование 9cos(x))` | -exp(x) |
|---|
Приведенная выше таблица показывает, что частные решения их дифференциальных уравнений одинаковы независимо от их порядка.
Решить ОДУ графически
Некоторые дифференциальные уравнения не могут быть решены в символьном виде, но могут быть решены численно и графически с помощью функции графика ОДУ odeplot(), например вход sin(x)-cos(y) для y’ = sin(x)-cos(y), затем отметьте y’= или y»= флажок для решения дифференциального уравнения первого или второго порядка. по умолчанию это ODE первого порядка.y»=y’-y для ОДУ второго порядка
Его решение находится в таблице 2. Свойство дифференциального уравнения дробного типа такое же, как и у дифференциального уравнения:
Решение уравнения линейной дроби = общее решение + частное решение = gsolution( ) + psolution( )
Оно похоже на линейное дифференциальное уравнение, поэтому метод решения дробного дифференциального уравнения аналогичен дифференциальному уравнению [3-5].
Уравнение теплопроводности с дробным временным порядком 90,5` — 2у = ехр(х)
Его решение находится в Таблице 2. По умолчанию определение дробного исчисления Капуто используется функцией dsolve() . Если вы хотите использовать определение Римана, используйте решатель преобразования Лапласа lasolve() . Разница между определением Капуто и определением Римана-Лиувилля (RL) заключается в разделе 6 дробного исчисления [8]. например
dsolve(y(-0.5,x)=1) дают ноль.
lasolve(y(-0.5,x)=1) дает ненулевое значение. 9n x` на анимации ниже Рис.1.
Рис. 1. Анимация изменения порядка между 1 и -1.
f:= 2y+1, eq:=y’-f=0, s:=dsolve(eq), test(s, eq)
f:= 2y+1, eq:=ds(y,x,0.5)-f=0, s:=dsolve(eq), test(s, eq)

Мы надеемся, что примеры и идеи, изложенные в этой статье, будут полезны для элементарные и углубленные курсы по дифференциальным уравнениям, а также для решение дифференциальных уравнений, возникающих в исследовательских и конструкторских задачах на практике.
- К.Б. Олдхэм, Дж. Спаниер, Дробное исчисление, Academic Press, Нью-Йорк, Лондон (1974).
- Б.Росс. дробное исчисление и его приложения. Springer, Берлин, Гейдельберг, 1975.
- К.Б. Миллер, Б. Росс, Введение в дробное исчисление и дробные дифференциальные уравнения, Wiley, Нью-Йорк (1993).
- И. Подлубный, Дробные дифференциальные уравнения, Academic Press, Нью-Йорк (1999).

- Ю. Ху, Ю. Луо, З. Лу, Аналитическое решение линейного дробно-дифференциального уравнения методом разложения Адомиана, Том 215, Выпуск 1, 15 мая 2008 г., стр. 220-229.
- В. Хуанг, SymbMath: программа символической математики, Int. Дж. Матем. Эду. науч. Техн., 1992, 23(1), 160-165.
- В. Хуанг, SymbMath Update to Version 2.0, Abs. амер. Мат. Соц., 1992, 13(6), 535.
- Math Handbook Calculator, https://blog.actorsfit.com/a?ID=00550-3e2ed6ca-f8f1-49ba-aafd-2b44cee0ab44, последний доступ 21/07/2021.
- Дробное исчисление, http://drhuang.com/science/mathematics/fractional_calculus/, последний доступ 21/07/2021.
- Примеры системы компьютерной алгебры дробного исчисления, http://drhuang.com/index/example/, последний доступ 21/07/2021.
- Специальное дифференциальное уравнение, https://jingyan.baidu.com/article/19020a0a6bb358529d284293.html, последний доступ 21//07/2021.
- Ошибки Wolfram, http://drhuang.com/index/bugs/, последний доступ 21/07/2021.

Дом | список | вики | о | пожертвовать | показатель | Форум | помощь |中文 | переведено с китайского
Сложные дроби и уравнения с рациональными выражениями
Сложные дроби и уравнения с рациональными выражениями
Сложные дроби
Сначала мы начнем со сложной дроби, которая не содержит переменных.
Пример
1
5
1
5
—
12 —
12
2 6
2
6
знак равно
Умножить
Числитель и
1 2
1
2
Знаменатель на 12
+ 12 +
12
4
3
4 3
6 —
10
4
знак равно
знак равно
—
3 +
8
11
Обратите внимание, что сначала мы умножаем на общий наименьший общий знаменатель, а затем
упрощенный.
Сложные дроби, включающие выражения
Когда у нас есть сложная дробь с рациональными выражениями в качестве числителя и знаменатель, мы делаем аналогичные шаги, за исключением, конечно, разложения на множители ключевую роль.
Шаг 1 Учитывать все.
Шаг 2 Определить общий наименьший общий знаменатель, используя максимальная мощность каждого фактора.
Шаг 3 Умножьте все термины на ЖК-дисплее.
Шаг 4 Объедините похожие термины.
Шаг 5 Умножить и отменить.
Примечание: Обычно вам не нужно выполнять все шаги.
Пример:
7
7
1 –
1(х + 1) —
(x + 1)
x
+ 1
х + 1
знак равно
Умножить
Числитель и
4
4
Знаменатель на (x+1)
+
1
(Икс
+ 1) + 1(х + 1)
х +
1
х +
1
х + 1 —
7
х — 6
знак равно
=
4 +
х + 1
х + 5
Перекрестное умножение
Напомним, что если
а c
=
б г
затем
ad = bc
То же верно для функций:
f g
=
ч к
затем
fg = hk
Пример
Решать.
3x — 1 x + 2
=
5x —
2 3x + 4
Раствор
Скрещиваем множим
(3x — 1)(3x + 4) = (5x — 2)(x + 2)
9x 2 + 12x — 3x — 4 = 5x 2 + 10x — 2x — 4
9x 2 + 9x — 4 = 5x 2 + 8x — 4
4x 2 + х = 0
х (4х + 1) = 0
1
x = 0 или x = —
4
Внимание! Всегда проверяйте работоспособность решения, подключая его к исходному уравнение!
Уравнения с рациональными выражениями
Чтобы решить уравнения, включающие рациональные выражения, мы следуем следующему шаги:
Шаг 1 Умножить, если возможно.

Шаг 2 Умножьте левую и правую части на ЖК-дисплей.
Шаг 3 Объедините похожие термины.
Шаг 4 Перенесите все в левую часть уравнения.
Шаг 5 Решите методом нулевого произведения или элементарной алгеброй.
Шаг 6 Вновь подключитесь к исходному уравнению, чтобы проверить посторонние решения.
Пример
Решить
3 4
48
—
=
Икс —
6 х +
6 x 2 — 36
Решение
Первый фактор.
3
4 48
—
=
Икс —
6 х +
6 (x —
6)(x + 6)
Затем умножьте на LCD (x
— 6)(х+6).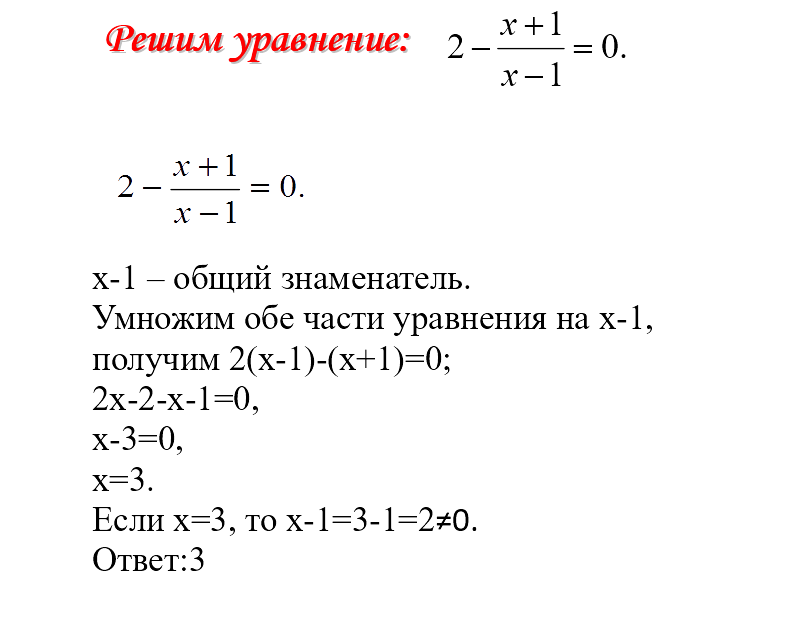


 А. Решим любую задачу [текст] : учебное
пособие / В.А. Габринович, В.И. Громак. –
Мн. :Асар, 1996.
А. Решим любую задачу [текст] : учебное
пособие / В.А. Габринович, В.И. Громак. –
Мн. :Асар, 1996.