Укажите неравенство: 1) x^2+9x-790; 3) x^2+9x+790.

Вариант 11. Часть 1. Задание 8. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Укажите неравенство, решение которого изображено на рисунке

Вариант 11. Часть 1. Задание 8. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Укажите неравенство, решение которого изображено на рисунке – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Укажите неравенство, решение которого изображено на рисунке.

 
1) x²+25<0          2) x²-25<0           3) х²+25>0          4) x²-25>0
 

ответы

2) x²-25<0

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Олимпиады

Экзамены

Оценки

3 класс

похожие вопросы 5

Вариант 1. Часть 2. Задание 26. ОГЭ 36 вариантов ответов по Математике 9 класс Ященко. Помогите найти АН.

На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту АD в точке М, АD (Подробнее…)

ГДЗМатематикаОГЭ9 классЯщенко И.В.

ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№26. Зад.№9.Под руководством Ященко. Помогите установить соответствие.

   Здравствуйте! Помогите установить соответствие между величинами и их возможными значениями: к каждому элементу первого столбца (Подробнее…)

ЕГЭЭкзаменыМатематикаЯщенко И.В.

Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

Всем привет, поделитесь ответом на задание
Прочитайте.
Рассмотрите условные обозначения однородных членов. (Подробнее…)

ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс

А что интересного будет происходить в эти выходные? Куда сходить с учителем?

А что интересного будет происходить в эти выходные? Куда сходить с учителем?

9 класс

4. Теорему синусов можно записать в виде… Ященко И. В. Математика ЕГЭ-2017 ГДЗ. Вариант 23.

(Подробнее. 2-15>0

00:04:22

Валерий Волков 38 05.02.2015

Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями!

Новости образования

ЕГЭ по математике

Профильный уровень

Задание 1     Задание 2

Задание 3     Задание 4

Задание 5     Задание 6

Задание 7     Задание 8

Задание 9     Задание 10

Задание 11     Задание 12

Задание 13     Задание 14

Задание 15     Задание 16

Задание 17     Задание 18

Задание 19     Задание 20

Задание 21

ГИА по математике

Задача 1     Задача 2

Задача 3     Задача 4

Задача 5     Задача 6

Задача 7     Задача 8

Задача 9     Задача 10

Задача 11     Задача 12

Задача 13     Задача 14

Задача 15     Задача 16

Задача 17     Задача 18

Задача 19     Задача 20

Задача 21     Задача 22

Задача 23     Задача 24

Задача 25     Задача 26

Демонстрационные варианты ОГЭ по математике

Математика. 5 класс.

Натуральные числа

Обыкновенные дроби

Десятичные дроби

Проценты

Математика. 6 класс.

Делимость чисел

Сложение и вычитание дробей с разными знаменателями

Умножение и деление обыкновенных дробей

Отношения и пропорции

Положительные и отрицательные числа

Измерение величин

Математика. 7 класс.

Преобразование выражений

Многочлены

Формулы сокращенного умножения

Математика. 8 класс.

Модуль числа. Уравнения и неравенства.

Квадратные уравнения

Квадратные неравенства

Уравнения с параметром

Задачи с параметром

Математика. 9 класс.

Функции и их свойства

Прогрессии

Векторы

Комбинаторика, статистика и теория вероятностей

Математика. 10 — 11 класс.

Числовые функции

Тригонометрические функции

Тригонометрические уравнения

Преобразование тригонометрических выражений

Производная

Степенные функции

Показательная функция

Логарифмические функции

Первообразная и интеграл

Уравнения и неравенства

Комбинаторика

Создаёте видеоуроки?

Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала.

Актуально

---

Физкультминутки для школьников и дошкольников

Подготовка к ЕГЭ Подготовка к ОГЭ

© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.

При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Символы неравенства

Символы неравенства — это символы, которые используются для обозначения отношений неравенства. Вместе с другими математическими символами, такими как знак равенства (=), который указывает на отношение равенства, их иногда называют символами отношения.

Строгие неравенства включают менее () символов, описанных ниже. Хотя знак равенства технически не является символом неравенства, он обсуждается вместе с символами неравенства, поскольку он включен как часть нестрогих неравенств, таких как больше или равно (≥) и меньше или равно (≤) .

Знак равенства: =

Знак равенства, обозначенный символом «=», указывает на равенство. Выражения по обе стороны от знака равенства либо имеют одинаковое значение, либо имеют одинаковое значение для определенных значений. Равенство (как и неравенство) является основой для решения алгебраических уравнений и неравенств.

2 = 2

5 + 3 = 1 + 7

x = x

Все приведенные выше уравнения верны. В случаях, когда значения не равны, мы можем использовать ряд различных символов неравенства, например, знак не равно.

Знак не равно: ≠

Знак не равно, также называемый знаком не равно, представляет собой символ, указывающий на неравенство значений или выражений по обе стороны от символа.

12 ≠ 17

x ² ≠ x ³

x — 7 ≠ x + 7

Хотя приведенное выше использование ≠ верно для всех случаев, за исключением случаев, это мало что нам говорит.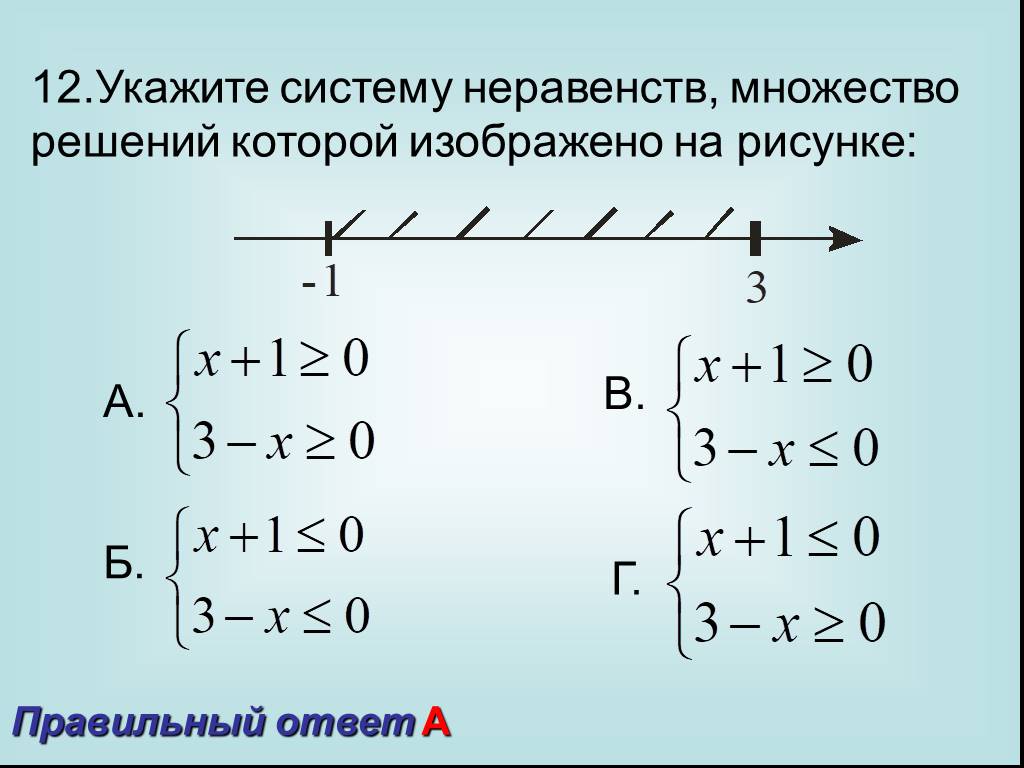 выражения по обе стороны от символа не равны. Существуют и другие, более конкретные отношения неравенства, подобные приведенным ниже.

Знак больше, чем: >

Знак больше, чем — это символ, указывающий на строгое неравенство между двумя значениями; в частности, что значение слева от знака «больше» больше, чем значение справа. Больше — это строгое неравенство, означающее, что значение слева от знака должно быть больше значения справа; они не могут быть равны. Допустимы следующие варианты использования знака «больше»:

5 > 4

x ² > x

x + 12 > x + 7

Как правило, при заданном

a > b

a должно быть больше b. Таким образом, если бы b было равно 4, то а могло бы быть любым значением больше 4, но не 4. В случаях, когда а также может равняться 4, вместо этого мы использовали бы знак больше или равно.

Знак «больше» или «равно»: ≥

Знак больше или равно — это символ, указывающий, что значение в левой части символа больше или равно значению справа. Это также можно прочитать, поскольку значение в левой части как минимум равно значению в правой части. Учитывая

a ≥ b

a может равняться b, в отличие от знака больше. Это связано с тем, что ≥ не означает строгого неравенства. Это единственная разница между «>» и «≥».

Знак меньше:

Знак «меньше» соответствует знаку «больше». Это указывает на строгое неравенство между двумя значениями; в частности, значение слева от знака «меньше» меньше значения справа. Ниже приведены допустимые варианты использования знака «меньше»:

3

х ² 4

х — 12

Как правило, учитывая

а

значение a должно быть меньше значения b. Они не могут быть равны. Если мы хотим обозначить, что a может быть меньше или равно b, мы должны вместо этого использовать знак меньше или равно (≤).

Меньше или равно знаку: ≤

Знак «меньше или равно» — это символ, указывающий, что значение в левой части символа меньше или равно значению справа.

Это также может быть прочитано как означающее, что значение или выражение в левой части символа может быть не более чем равным значению в правой части, но не больше. Как правило, учитывая

а ≤ b

a может быть равно b. В отличие от знака меньше, ≤ не означает строгого неравенства. Это единственная разница между »

Символы и графики неравенства | College Algebra Corequisite

Результаты обучения

• Представление неравенств с помощью символа неравенства
• Представление неравенств на числовой прямой

Неравенство – это математическое утверждение, в котором сравниваются два выражения с использованием такой фразы, как  больше или меньше . В этих операторах используются специальные символы. В алгебре неравенства используются для описания наборов значений, а не отдельных значений переменной. Иногда несколько чисел удовлетворяют неравенству, но в других случаях решение может дать бесконечное множество чисел.

Вместо того, чтобы пытаться перечислить, возможно, бесконечно большой набор чисел, математики разработали несколько эффективных способов описания таких больших списков.

Символы неравенства

Одним из способов представления такого списка чисел, неравенства, является использование символа неравенства:

• [латекс]{х}\lt{9}[/латекс] указывает список чисел, которые меньше [ латекс]9[/латекс]. Поскольку этот список бесконечен, было бы невозможно перечислить все числа меньше [латекс]9[/латекс].
• [латекс]-5\le{t}[/латекс] указывает все числа, которые больше или равны [латекс]-5[/латекс].

Если бы вы прочитали приведенное выше утверждение слева направо, оно бы перешло как [латекс]-5[/латекс] меньше или равно t . Направление символа зависит от заявления, которое вы хотите сделать. Например, следующие операторы эквивалентны. Оба представляют собой список всех чисел меньше 9. Обратите внимание, как открытый конец символа неравенства обращен к большему значению, а меньший заостренный конец указывает на меньшее из значений:

• [латекс]{x}\lt{ 9}[/латекс]
• [латекс]{9}\gt{x}[/латекс]

Вот еще один способ взглянуть на это:

• [латекс]x\lt5[/латекс] означает все действительные числа, которые меньше 5, тогда как;
• [latex]5\lt{x}[/latex] означает, что 5 меньше x, или мы могли бы переписать это с x слева: [latex]x\gt{5}[/latex]. Обратите внимание, что неравенство по-прежнему указывает то же направление относительно x. Это утверждение представляет все действительные числа, которые больше 5, что легче интерпретировать, чем 5 меньше x.

В поле ниже показаны символ, значение и пример для каждого знака неравенства, как они должны быть переведены при чтении слева направо.

Символ	слов	Пример
[латекс]\neq [/латекс]	не равно	[латекс]{2}\neq{8}[/латекс], 2   равно , не равному до 8 .
[латекс]\gt[/латекс]	больше	[латекс]{5}\gt{1}[/латекс], 5   больше, чем   1
[латекс]\lt[/латекс]	меньше	[латекс]{2}\lt{11}[/латекс], 2   меньше, чем   11
[латекс] \geq [/латекс]	больше или равно	[латекс]{4}\geq{ 4}[/латекс], 4   больше или равно   4
[латекс]\leq [/латекс]	меньше или равно	[латекс]{7}\leq{9}[/латекс], 7   меньше или равно   9

Неравенство [латекс]x>y[/латекс] можно также записать как [латекс]{у}<{х}[/латекс]. Стороны любого неравенства можно поменять местами, если символ неравенства между ними также перевернут.

Графическое представление неравенства

Другой способ представить неравенство — изобразить его на числовой прямой:

Ниже приведены три примера неравенств и их графики. Графики часто помогают визуализировать информацию.

[латекс]x\leq -4[/латекс]. Это переводится во все действительные числа на числовой прямой, которые меньше или равны [латекс]4[/латекс].

[латекс]{x}\geq{-3}[/латекс]. Это переводится во все действительные числа на числовой прямой, которые больше или равны -3.

Каждый из этих графиков начинается с круга — открытого или закрытого (заштрихованного) круга. Эту точку часто называют конечной точкой решения. Замкнутый или заштрихованный круг используется для обозначения неравенств больше или равно  [латекс] \displaystyle \left(\geq\right) [/latex] или меньше или равно  [латекс] \displaystyle \left(\leq\right) [/latex].